The Detection and Characterization of Arctic Sea Ice Leads with Satellite Imagers
Abstract
1. Introduction
2. Data and Methods
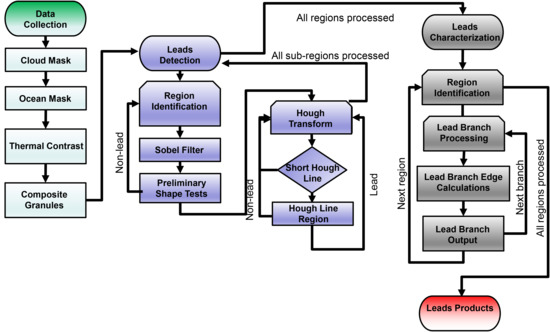
2.1. Algorithm Description
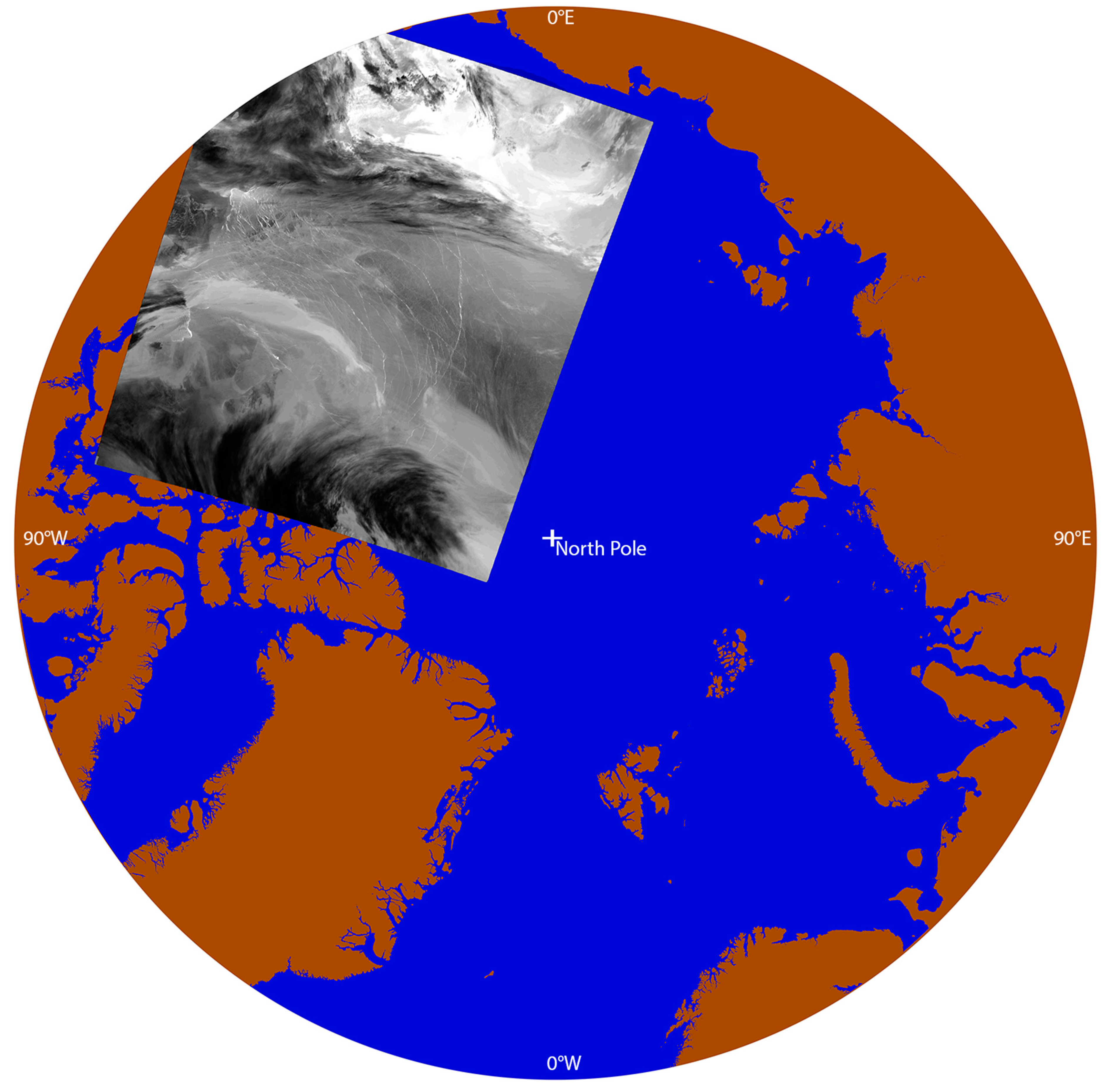
2.1.1. Step 1: Aggregate Imager Data, Identify Potential Leads
2.1.2. Step 2: Bulk Lead Detection
2.1.3. Step 3: Lead Branch Characterization
2.2. Output Format
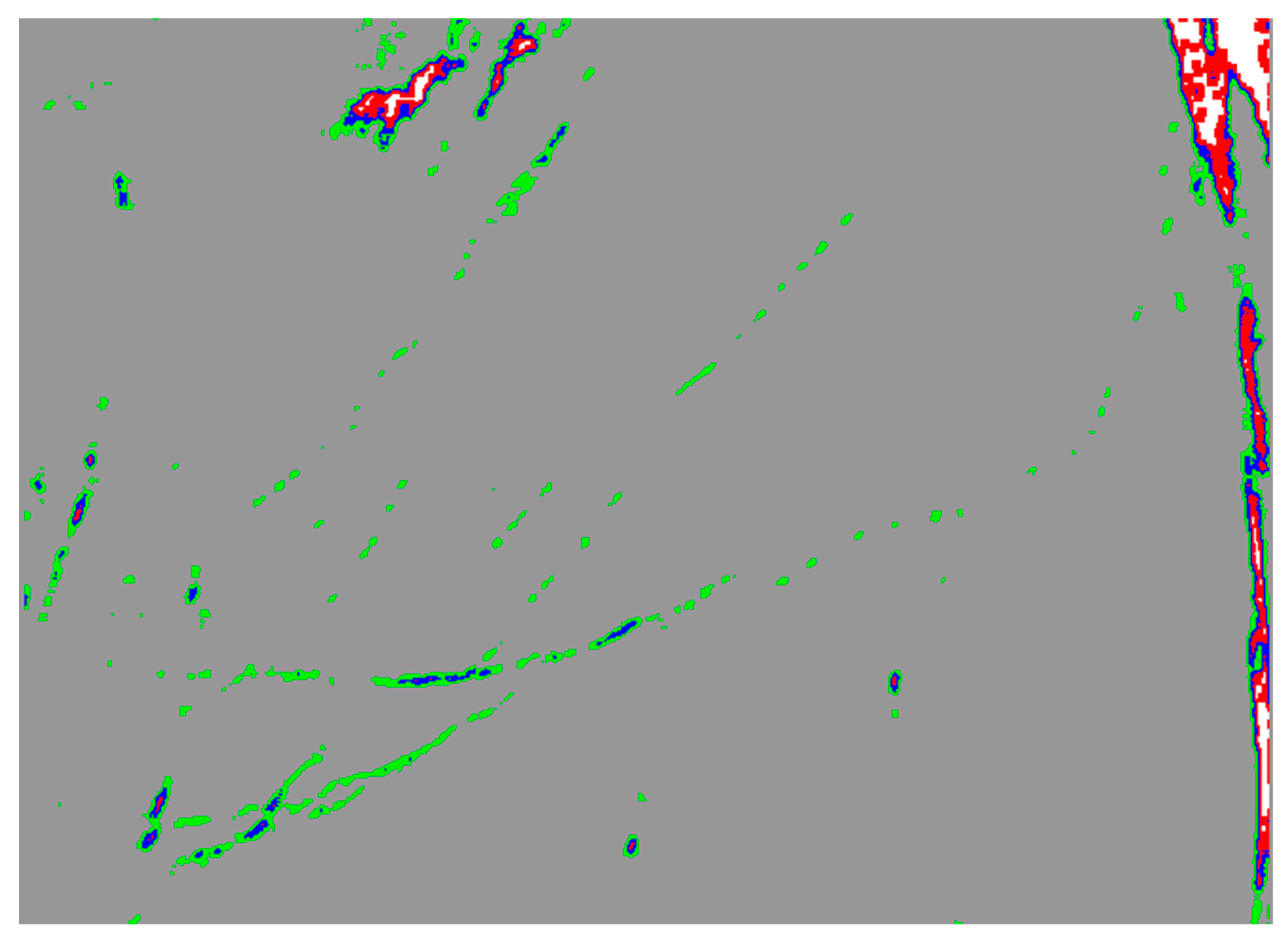
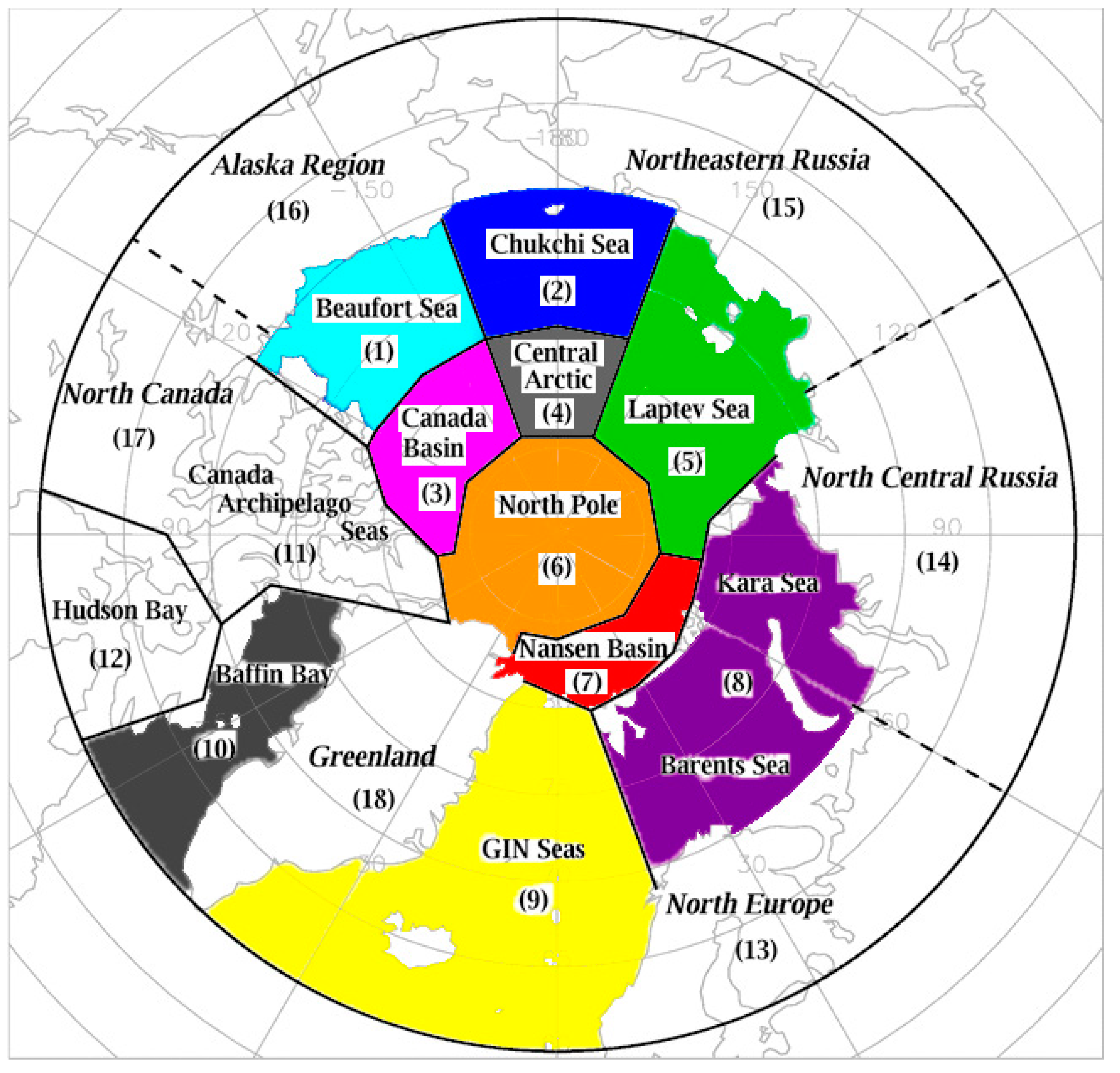
3. Results
3.1. Synthetic Test
3.2. Case Studies
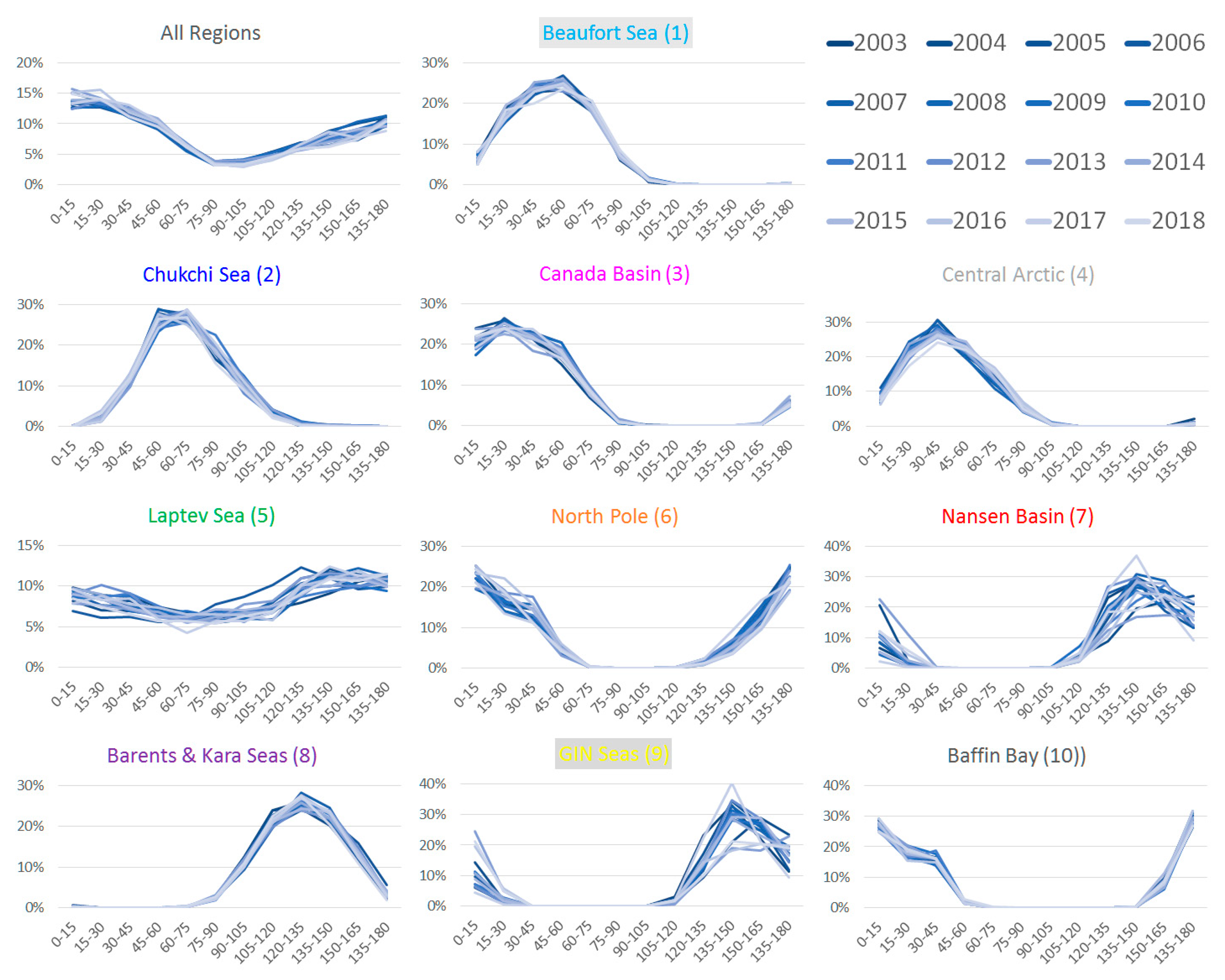
3.3. Lead Timeseries
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smith, S.D.; Muench, R.D.; Pease, C.H. Polynyas and leads: An overview of physical processes and environment. J. Geophys. Res. Oceans 1990, 95, 9461–9479. [Google Scholar] [CrossRef]
- Alam, A.; Curry, J. Lead-induced atmospheric circulations. J. Geophys. Res. Oceans 1995, 100, 4643–4651. [Google Scholar] [CrossRef]
- Maykut, G.A. Energy exchange over young sea ice in the central arctic. J. Geophys. Res. Oceans 1978, 83, 3646–3658. [Google Scholar] [CrossRef]
- Lüpkes, C.; Vihma, T.; Birnbaum, G.; Wacker, U. Influence of leads in sea ice on the temperature of the atmospheric boundary layer during polar night. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Douglas, T.; Sturm, M.; Simpson, W.; Brooks, S.; Lindberg, S.; Perovich, D. Elevated mercury measured in snow and frost flowers near arctic sea ice leads. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Steiner, N.; Lee, W.; Christian, J. Enhanced gas fluxes in small sea ice leads and cracks: Effects on CO2 exchange and ocean acidification. J. Geophys. Res. Oceans 2013, 118, 1195–1205. [Google Scholar] [CrossRef]
- Wadhams, P.; Davis, N.R. Further evidence of ice thinning in the Arctic Ocean. Geophys. Res. Lett. 2000, 27, 3973–3975. [Google Scholar] [CrossRef]
- Vaughan, D.G.; Comiso, J.C.; Allison, I.; Carrasco, J.; Kaser, G.; Kwok, R.; Mote, P.; Murray, T.; Paul, F.; Ren, J. Observations: Cryosphere. Clim. Chang. 2013, 2103, 317–382. [Google Scholar]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C. Cryosat-2 estimates of arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef]
- Rampal, P.; Weiss, J.; Marsan, D. Positive trend in the mean speed and deformation rate of arctic sea ice, 1979–2007. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Key, J.; Stone, R.; Maslanik, J.; Ellefsen, E. The detectability of sea-ice leads in satellite data as a function of atmospheric conditions and measurement scale. Ann. Glaciol. 1993, 17, 227–232. [Google Scholar] [CrossRef]
- Key, J.; Maslanik, J.; Ellefsen, E. The effects of sensor field-of-view on the geometrical characteristics of sea ice leads and implications for large-area heat flux estimates. Remote Sens. Environ. 1994, 48, 347–357. [Google Scholar] [CrossRef]
- Lindsay, R.; Rothrock, D. Arctic sea ice leads from advanced very high resolution radiometer images. J. Geophys. Res. Oceans 1995, 100, 4533–4544. [Google Scholar] [CrossRef]
- Miles, M.W.; Barry, R.G. A 5-year satellite climatology of winter sea ice leads in the western arctic. J. Geophys. Res. Oceans 1998, 103, 21723–21734. [Google Scholar] [CrossRef]
- Drüe, C.; Heinemann, G. High-resolution maps of the sea-ice concentration from MODIS satellite data. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Willmes, S.; Heinemann, G. Pan-arctic lead detection from MODIS thermal infrared imagery. Ann. Glaciol. 2015, 56, 29–37. [Google Scholar] [CrossRef]
- Willmes, S.; Heinemann, G. Sea-ice wintertime lead frequencies and regional characteristics in the arctic, 2003–2015. Remote Sens. 2015, 8, 4. [Google Scholar] [CrossRef]
- Röhrs, J.; Kaleschke, L. An algorithm to detect sea ice leads by using AMSR-E passive microwave imagery. Cryosphere 2012, 6, 343–352. [Google Scholar] [CrossRef]
- Röhrs, J.; Kaleschke, L.; Bröhan, D.; Siligam, P.K. Corrigendum to “An algorithm to detect sea ice leads by using amsr-e passive microwave imagery.”. Cryosphere 2012, 6, 365. [Google Scholar]
- Bröhan, D.; Kaleschke, L. A nine-year climatology of arctic sea ice lead orientation and frequency from AMSR-E. Remote Sens. 2014, 6, 1451–1475. [Google Scholar] [CrossRef]
- Ivanova, N.; Rampal, P.; Bouillon, S. Error assessment of satellite-derived lead fraction in the arctic. Cryosphere 2016, 10, 585–595. [Google Scholar] [CrossRef]
- Murashkin, D.; Spreen, G.; Huntemann, M.; Dierking, W. Method for detection of leads from Sentinel-1 SAR images. Ann. Glaciol. 2018, 59, 124–136. [Google Scholar] [CrossRef]
- Zakharova, E.A.; Fleury, S.; Guerreiro, K.; Willmes, S.; Remy, F.; Kouraev, A.V.; Heinemann, G. Sea ice leads detection using Saral/Altika altimeter. Mar. Geod. 2015, 38, 522–533. [Google Scholar] [CrossRef]
- Wernecke, A.; Kaleschke, L. Lead detection in arctic sea ice from Cryosat-2: Quality assessment, lead area fraction and width distribution. Cryosphere 2015, 9, 1955–1968. [Google Scholar] [CrossRef]
- Frey, R.A.; Ackerman, S.A.; Liu, Y.; Strabala, K.I.; Zhang, H.; Key, J.R.; Wang, X. Cloud detection with MODIS. Part i: Improvements in the MODIS cloud mask for Collection 5. J. Atmos. Ocean. Technol. 2008, 25, 1057–1072. [Google Scholar] [CrossRef]
- Liu, Y.; Key, J.R.; Frey, R.A.; Ackerman, S.A.; Menzel, W.P. Nighttime polar cloud detection with MODIS. Remote Sens. Environ. 2004, 92, 181–194. [Google Scholar] [CrossRef]
- Brodzik, M.J. EASE-Grid: A versatile set of equal-area projections and grids. In Discrete Global Grids; Goodchild, M., Knowles, K.W., Eds.; National Center for Geographic Information & Analysis: Santa Barbara, CA, USA, 2002. [Google Scholar]
- MODIS Science Data Support Team (SDST). Available online: http://dx.doi.org/10.5067/MODIS/MOD021KM.006 (accessed on 29 January 2019).
- MODIS Science Data Support Team (SDST). Available online: http://dx.doi.org/10.5067/MODIS/MYD021KM.006 (accessed on 29 January 2019).
- MODIS Science Data Support Team (SDST). Available online: http://dx.doi.org/10.5067/MODIS/MYD03.006 (accessed on 29 January 2019).
- MODIS Science Data Support Team (SDST). Available online: http://dx.doi.org/10.5067/MODIS/MOD03.006 (accessed on 29 January 2019).
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. Atmos. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Baum, B.A. Modis cloud-top property refinements for collection 6. J. Appl. Meteorol. Climatol. 2012, 51, 1145. [Google Scholar] [CrossRef]
- Fraser, A.D.; Massom, R.A.; Michael, K.J. A method for compositing polar MODIS satellite images to remove cloud cover for landfast sea-ice detection. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3272–3282. [Google Scholar] [CrossRef]
- Sobel, I. Camera Models and Perception. Ph.D. Thesis, California: Artificial Intelligence Lab. Stanford University, Stanford, CA, USA, 1970. [Google Scholar]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Willmes, S.; Heinemann, G. Daily pan-arctic sea-ice lead maps for 2003–2015, with links to maps in netCDF format. In Supplement to: Willmes, S; Heinemann, G (2015): Sea-Ice Wintertime Lead Frequencies and Regional Characteristics in the Arctic, 2003–2015. Remote Sens. 2015, 8, 4. [Google Scholar] [CrossRef]
- Integrated Climate Date Center. AMSR-E Lead Area Fraction for the Arctic, 3 March 2009, Ed; University of Hamburg: Hamburg, Germany.
- Wang, X.; Key, J.R. Arctic surface, cloud, and radiation properties based on the AVHRR Polar Pathfinder dataset. Part I: Spatial and temporal characteristics. J. Clim. 2005, 18, 2558–2574. [Google Scholar] [CrossRef]
- Key, J.R. The area coverage of geophysical fields as a function of sensor field-of-view. Remote Sens. Environ. 1994, 48, 339–346. [Google Scholar] [CrossRef]
- Paul, S.; Willmes, S.; Heinemann, G. Long-term coastal-polynya dynamics in the southern Weddell Sea from MODIS thermal-infrared imagery. Cryosphere 2015, 9, 2027–2041. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; Barton, J.; Casey, K.; Chien, J.; DiGirolamo, N.; Klein, A.; Powell, H.; Tait, A. Algorithm Theoretical Basis Document (ATBD) for the MODIS Snow and Sea Ice-Mapping Algorithms; NASA GSFC: Greenbelt, MD, USA, 2001.
- Riggs, G.A.; Hall, D.K.; Salomonson, V.V. Modis Sea Ice Products User Guide to Collection 5; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2006.
- Riggs, G.A.; Hall, D.K.; Salomonson, V.V. Modis Sea Ice Products User Guide to Collection 6; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2015.
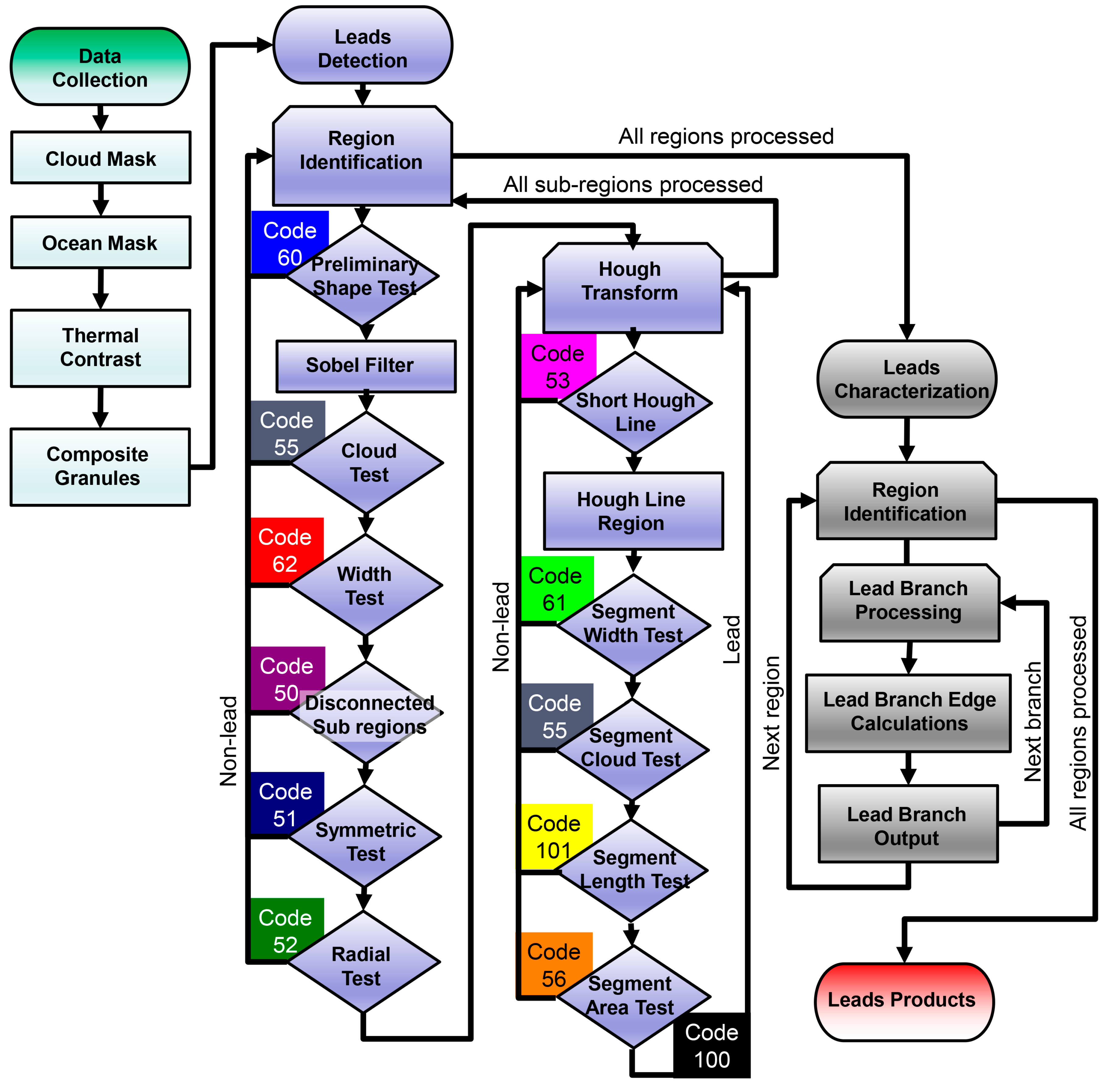

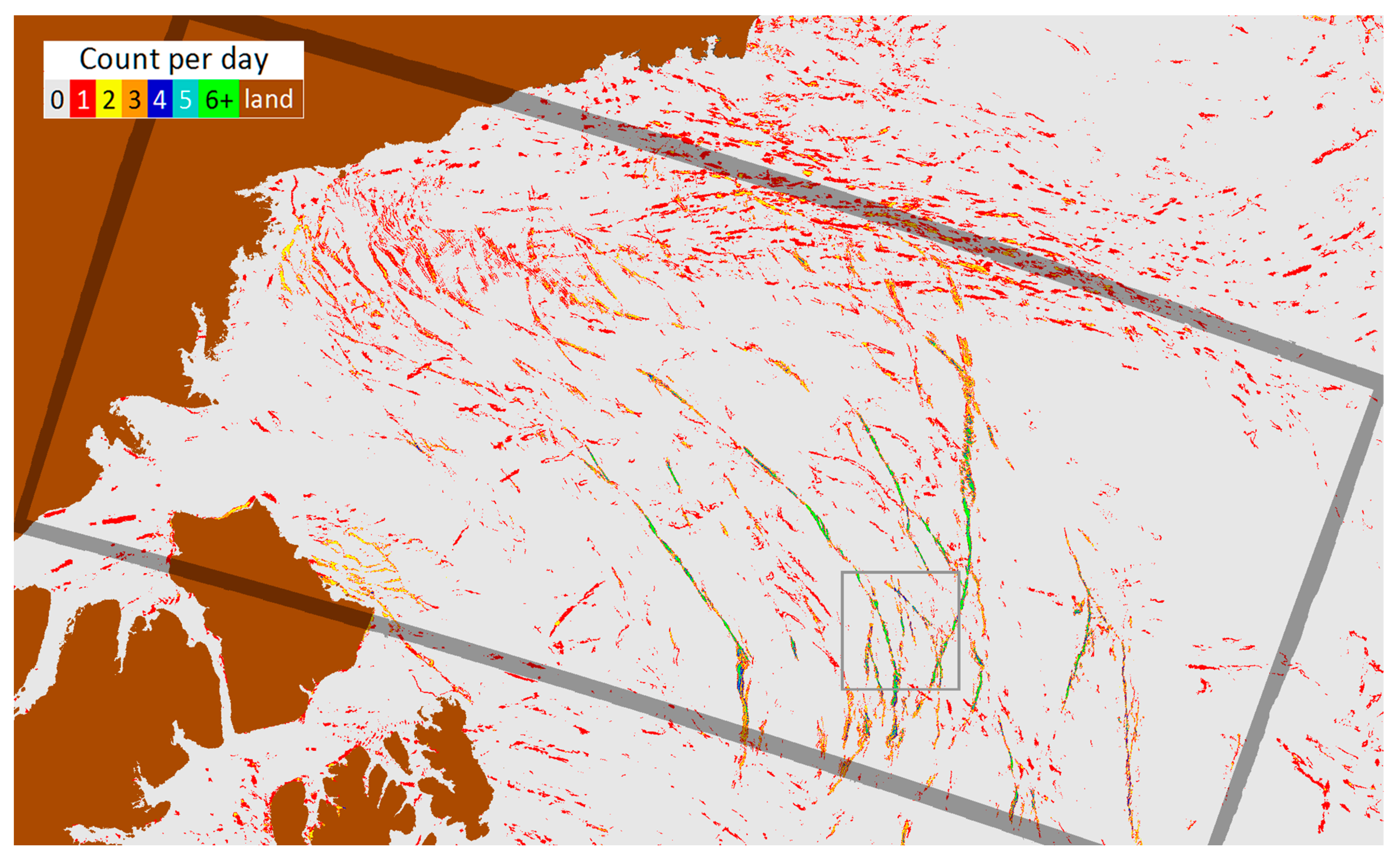
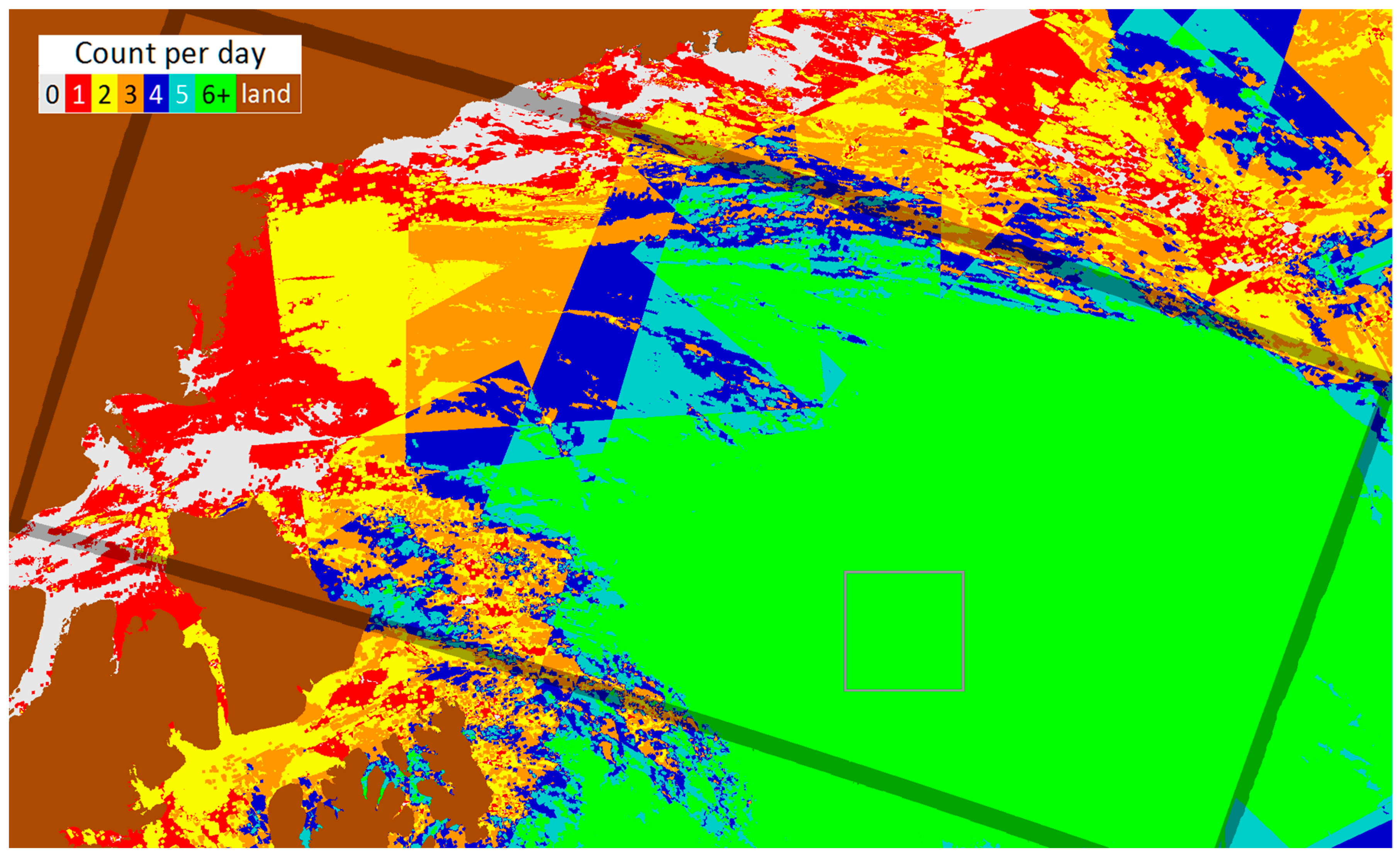



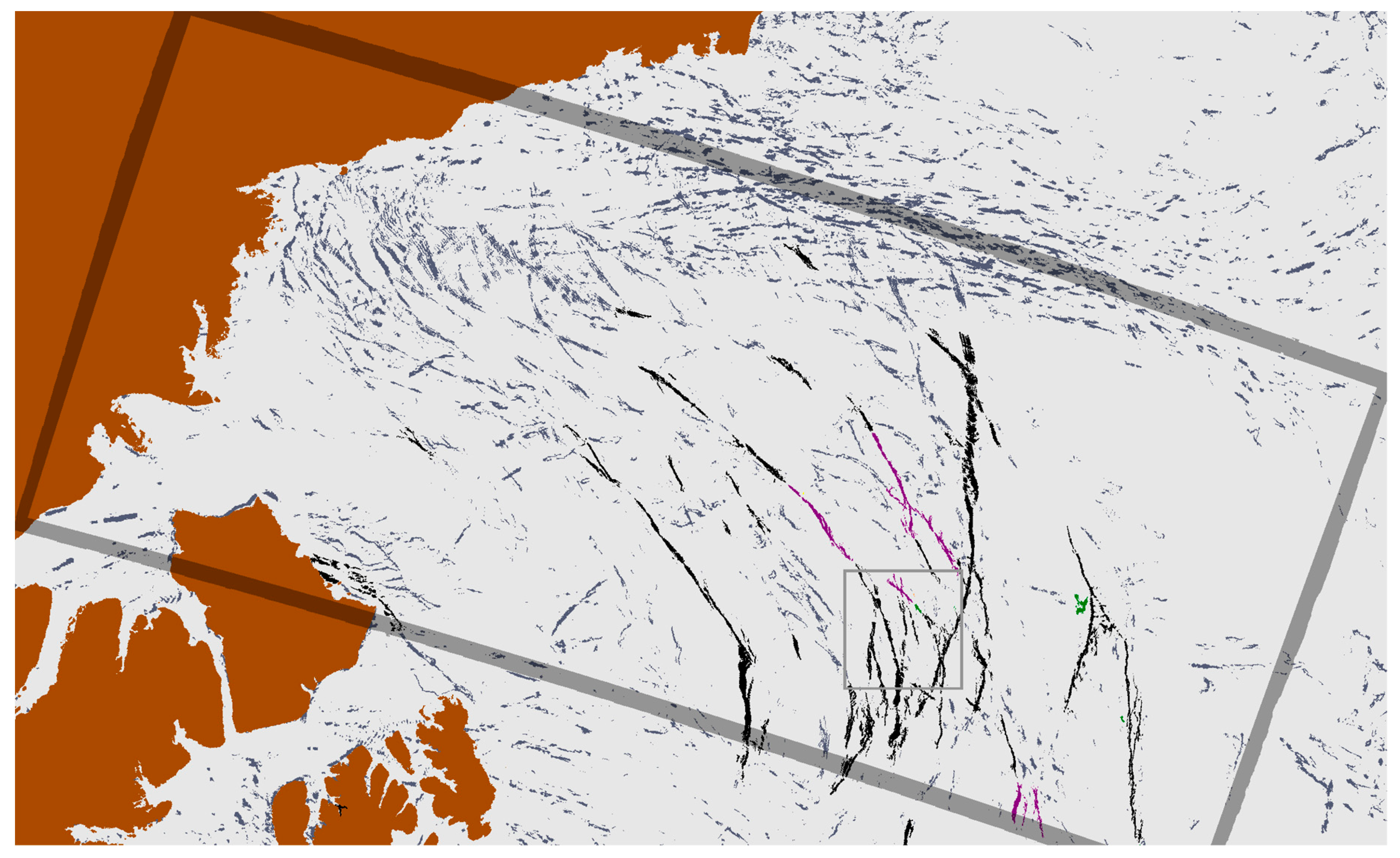




| Color | Name | Code | Description |
|---|---|---|---|
| Water | 10 | Water or ice, fails thermal contrast test; not a lead. | |
| Disconnected Sub Regions | 50 | Less than 1% of potential lead area: A continuous object after Sobel filter is applies contains more than 1 discontinuous region in the unfiltered mask, and more than 50% of the object area comes from sub-regions smaller than 5 km2, and there is between 3–5 sub regions with more 5 km2 or more. | |
| Symmetric | 51 | Less than 1% of potential lead area: A circumscribed rectangle over the object and is divided into 4 equal quadrants. If each quadrant contains +/−5% of 25% of the object area, the object is too symmetric. | |
| Radial | 52 | Approximately 1% of potential lead area: A circle is defined where the radius as half of the average of the span of the object in the x and y direction. If more than half of the object area is within 1.5 km of the edge of the test circle, the object fails to be a lead. | |
| Short Hough Line | 53 | Much less than 1% of potential lead area: Hough line contains 3 points or less. | |
| Cloud | 55 | Approximately 55% of potential lead area: Greater than 90% of object area occurred in 2 overpasses or less. | |
| Segment Area | 56 | Much less than 1% of potential lead area: Object area less than 4 km2. | |
| Large region | 60 | Approximately 8% of potential lead area: Object area divided by diagonal length greater than 60 km. Similar to code 62 test, this test is performed on the object before the image filter is applied. | |
| Segment Width | 61 | Less than 1% of potential lead area: Object area divided by length of the diagonal line greater than 25 and object area divided by circumscribed rectangle over the object greater than 5. | |
| Width | 62 | Approximately 6% of potential lead area: Object area divided by length of the diagonal line greater than 60; same test as code 60, this test is performed on the object after the Sobel filter is applied. | |
| Lead | 100 | Approximately 28% of potential lead area: All tests pass. | |
| Segment Length | 101 | Much less than 1% of potential lead area: Great-circle length of lead squared divided by area less than 2. | |
| Land | 200 | Land, not tested for leads. | |
| No coverage | 201 | Outside of domain, south of 65°N. |
| Year | Leads | Potential Leads | Willmes and Heinemann Leads | Leads with overlapping Willmes and Heinemann coverage | Potential Leads with overlapping Willmes and Heinemann coverage | Willmes and Heinemann with overlapping coverage |
|---|---|---|---|---|---|---|
| 2003 | 3.5% | 11.2% | 8.1% | 3.7% | 11.4% | 8.7% |
| 2004 | 3.2% | 10.2% | 6.6% | 3.4% | 10.1% | 7.1% |
| 2005 | 2.9% | 9.8% | 6.2% | 3.2% | 9.8% | 6.7% |
| 2006 | 2.9% | 10.0% | 7.0% | 3.2% | 10.2% | 7.6% |
| 2007 | 2.9% | 10.0% | 7.8% | 3.3% | 10.6% | 8.4% |
| 2008 | 2.9% | 10.1% | 7.8% | 3.4% | 10.7% | 8.4% |
| 2009 | 2.9% | 10.2% | 7.6% | 3.4% | 10.7% | 8.3% |
| 2010 | 3.0% | 10.2% | 7.9% | 3.5% | 10.8% | 8.5% |
| 2011 | 3.2% | 11.3% | 11.5% | 3.7% | 13.1% | 12.5% |
| 2012 | 2.8% | 10.5% | 12.0% | 3.3% | 12.5% | 12.5% |
| 2013 | 3.3% | 10.9% | 12.3% | 3.7% | 12.3% | 13.3% |
| 2014 | 3.1% | 10.9% | 6.6% | 3.7% | 11.8% | 7.2% |
| 2015 | 3.3% | 10.8% | 6.3% | 3.5% | 10.8% | 6.9% |
| 2016 | 2.9% | 10.2% | Not available | Not available | Not available | Not available |
| 2017 | 3.0% | 10.5% | Not available | Not available | Not available | Not available |
| 2018 | 2.8% | 10.3% | Not available | Not available | Not available | Not available |
| All | 3.0% | 10.2% | 7.7% | 3.4% | 10.7% | 8.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffman, J.P.; Ackerman, S.A.; Liu, Y.; Key, J.R. The Detection and Characterization of Arctic Sea Ice Leads with Satellite Imagers. Remote Sens. 2019, 11, 521. https://doi.org/10.3390/rs11050521
Hoffman JP, Ackerman SA, Liu Y, Key JR. The Detection and Characterization of Arctic Sea Ice Leads with Satellite Imagers. Remote Sensing. 2019; 11(5):521. https://doi.org/10.3390/rs11050521
Chicago/Turabian StyleHoffman, Jay P., Steven A. Ackerman, Yinghui Liu, and Jeffrey R. Key. 2019. "The Detection and Characterization of Arctic Sea Ice Leads with Satellite Imagers" Remote Sensing 11, no. 5: 521. https://doi.org/10.3390/rs11050521
APA StyleHoffman, J. P., Ackerman, S. A., Liu, Y., & Key, J. R. (2019). The Detection and Characterization of Arctic Sea Ice Leads with Satellite Imagers. Remote Sensing, 11(5), 521. https://doi.org/10.3390/rs11050521