1. Introduction
The Meteosat Visible and Infrared Imager (MVIRI) on board the Meteosat First Generation (MFG) of geostationary satellites scanned Earth radiance every 30 min in a 0.4
to 1.1
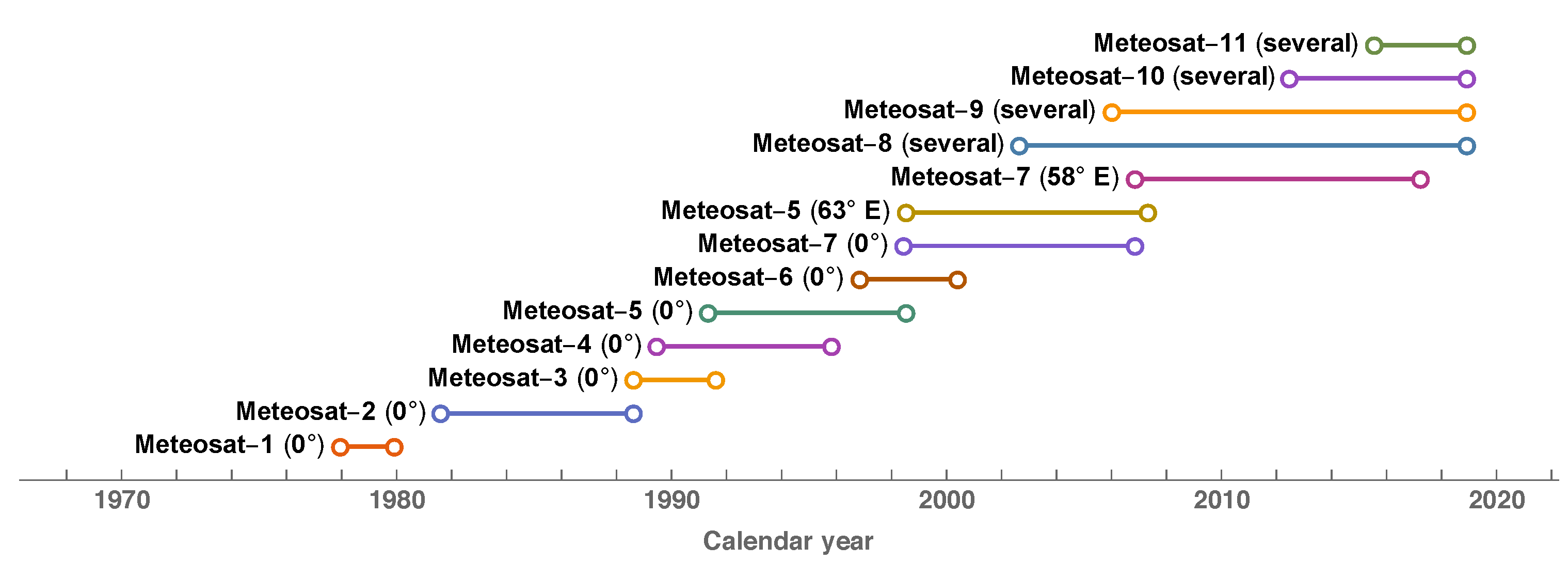
broad band, referred to as the Visible (VIS). Succeeding the Meteosat-1 prototype (1977–1979), the Meteosat 2–7 satellites (1981–2017) acquired full Earth disc images with an on-ground resolution of
km at the sub-satellite point, while operating from geostationary orbits at longitudinal positions of 0
and 58
E to 63
E for the Prime and Indian Ocean Data Coverage (IODC) services, respectively (see
Figure 1).
Originally intended to provide the meteorological community with information on atmospheric circulation and weather, the rapid cycle of Meteosat VIS observations facilitates the respective separation of surface reflectance and atmospheric scattering contributions, making VIS images pre-eminently suited to create a Climate Data Record (CDR) of Surface Albedo and Aerosol Optical Depth [
3,
4,
5]. The prerequisite for any CDR usually is a Fundamental Climate Data Record (FCDR) of Earth radiance (or equivalent) with accurate and traceable quantification of uncertainty per datum [
6]. The missing clue to create such an FCDR from MVIRI images is adequate knowledge of the in-flight VIS spectral response function of each MFG satellite, which is not available because the VIS spectral response functions were characterised inaccurately before launch [
7] and degraded continuously in Space in an unknown manner [
8], a problem that has been investigated [
9,
10,
11] but not been solved.
While the forward problem—of calculating a satellite measurement from a given instrument spectral response function and a given top-of-atmosphere (TOA) spectral radiance—has a unique solution, the inverse problem—of inferring the instrument spectral response function from a given set of satellite measurements and TOA spectral radiance—has multiple solutions (maybe an infinite number). For that reason, any available prior information on forward model parameters needs to be made explicit, and measurement (and modelling) uncertainties need to be represented carefully.
Let
t denote the time passed since launch of a satellite, let
denote the TOA spectral radiance reflected from a target on Earth’s surface, and let
denote the corresponding digital count number taken by the satellite’s radiometer. Ideally, both quantities are related by the measurement model
where
is the instrument digital count number taken from dark Space, and
denotes the absolute in-flight spectral response function of the radiometer. The radiometer measures the average TOA spectral radiance
where the area under the absolute spectral response curve defines the instrument gain factor
Under idealized conditions when the target, its illumination, and the atmosphere above do not change, the measured average TOA spectral radiance
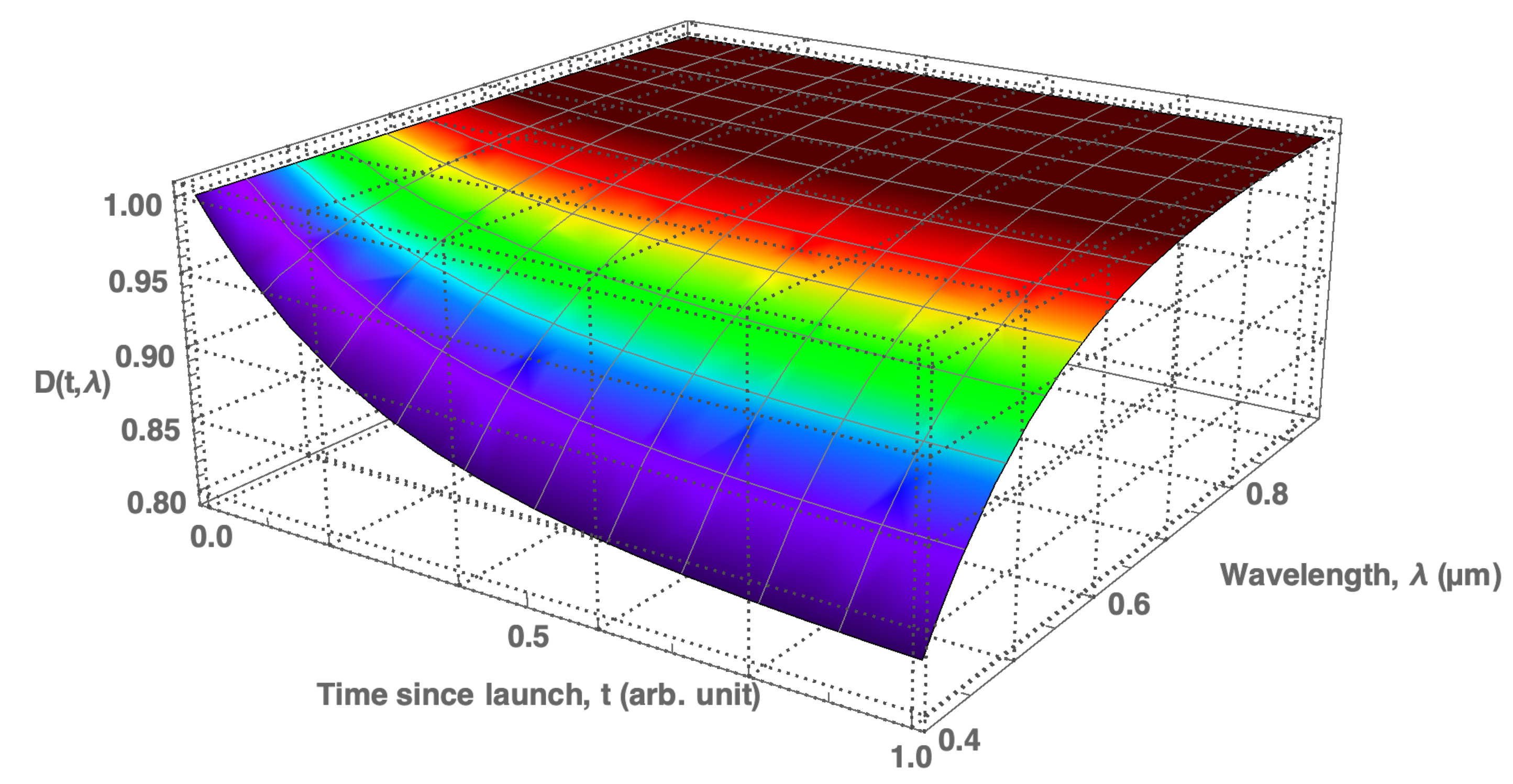
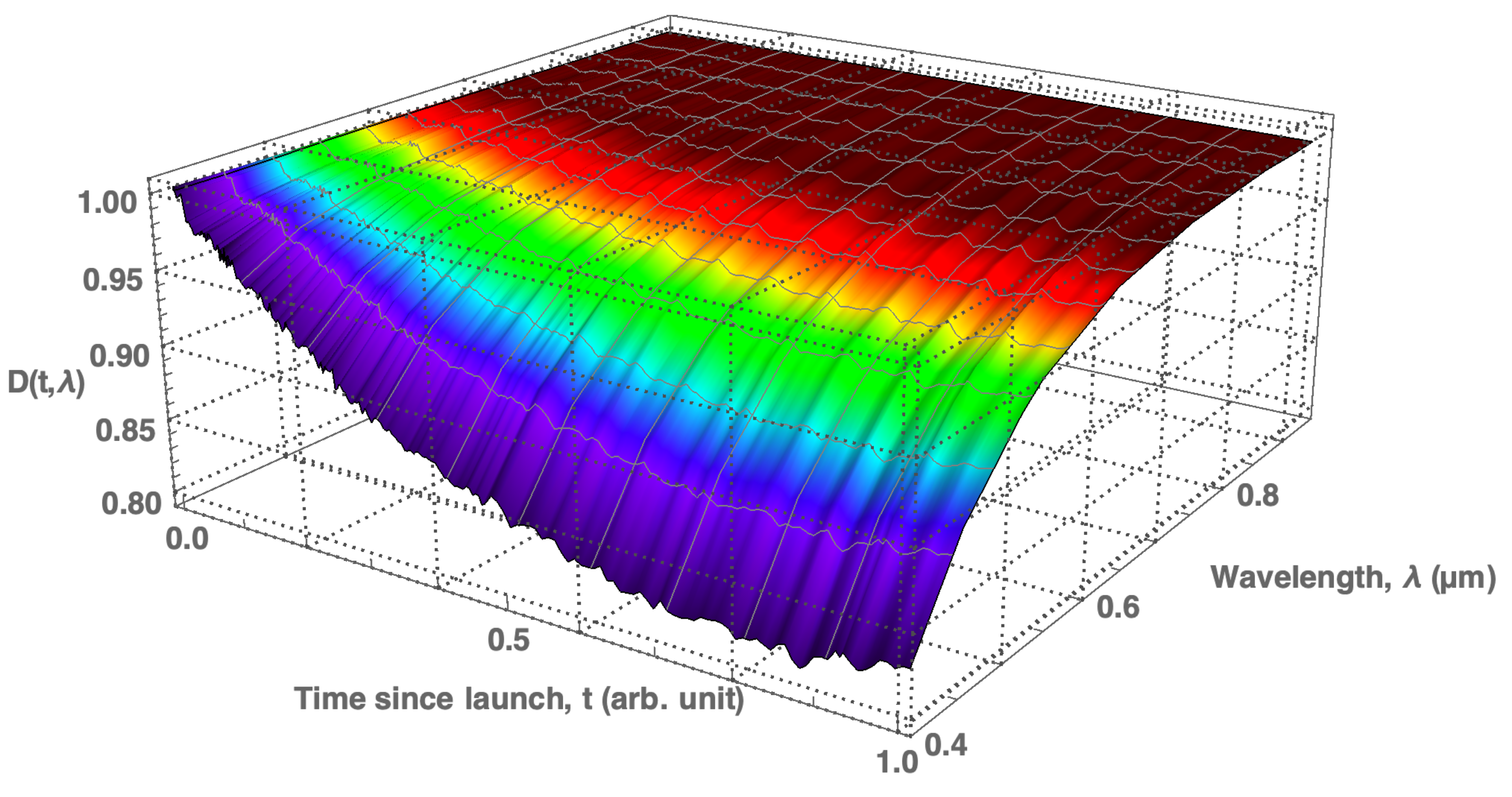
does not change either, even if the in-flight sensitivity of the instrument is not constant over time. If the in-flight spectral response is degrading over time, its generic functional form is
where
such that
is the degradation function and
denotes the absolute spectral response function before launch of the satellite. When the degradation of the instrument is not monitored and the data on its spectral response function is not adjusted to the degrading instrument performance, Equation (
2) will delude the observer into believing that Earth radiance is changing over time in an obscure way, and eventually into believing that trends in Earth’s essential climate variables are weaker or stronger than they actually are.
Instrument degradation that is independent of spectral wavelength is termed grey, whereas the general form expressed in Equation (
4) is termed spectral (or chromatic). While monitoring grey degradation is established practice, monitoring chromatic degradation is more problematic. The difference between grey and chromatic degradation is most clearly noticeable for broad band rather than narrow band optical devices.
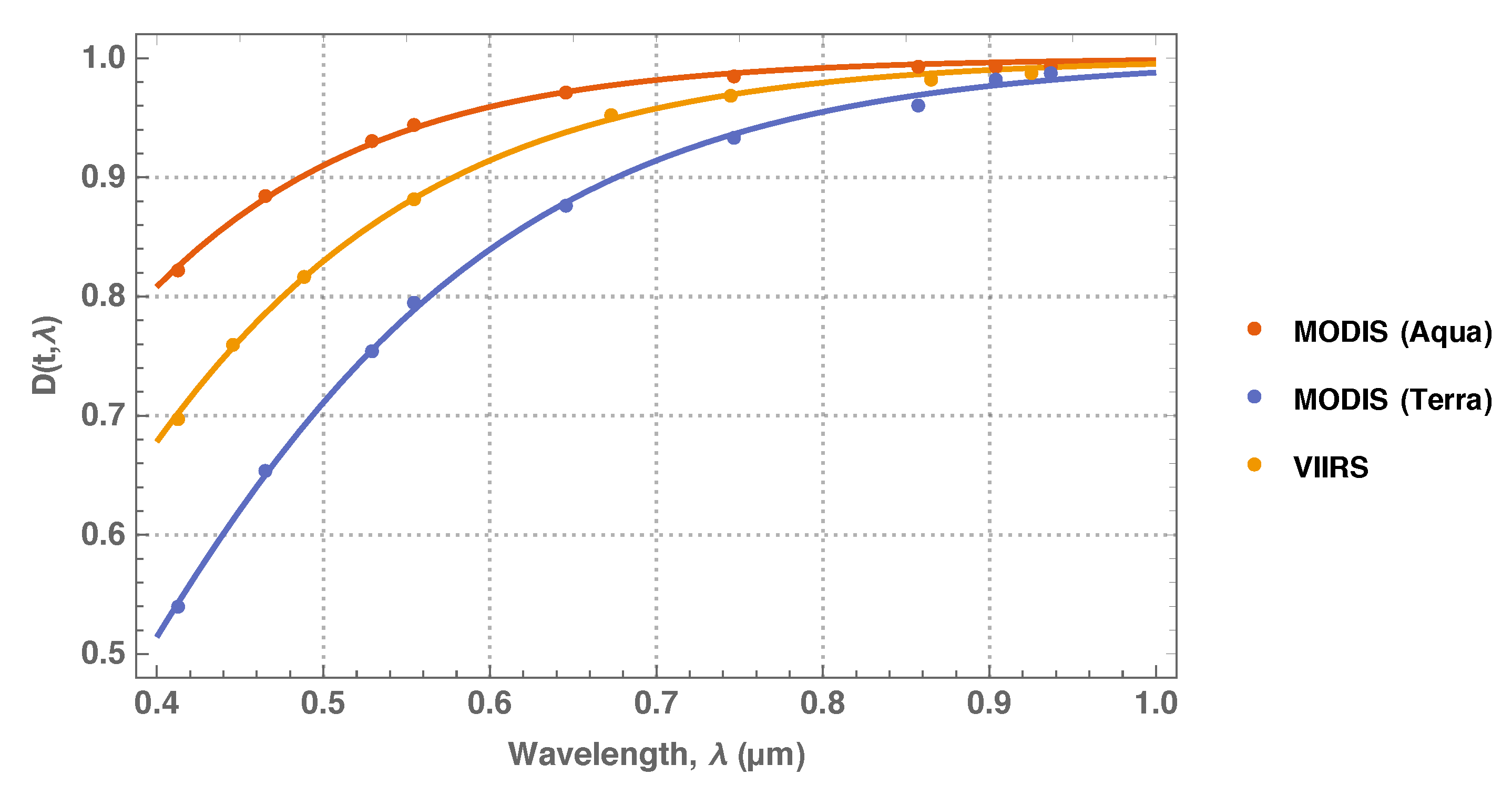
Figure 2 illustrates an example of chromatic degradation picked-up from the monitoring of the MODIS solar diffusers [
12,
13], which are broad band optical devices and though not in the optical path for Earth observations are nevertheless an example of degradation due to contamination of reflective optical elements in Space.
The phenomenon of chromatic degradation has been well known from the monitoring and in-flight calibration of numerous optical Earth Observation instruments (e.g., SeaWiFS [
14], CERES [
15], MERIS [
16], VIIRS [
17,
18,
19]) and space-borne astronomical telescopes. Contaminants evaporated from an instrument’s interior and condensation or UV-stimulated deposition and polymerisation of contaminant films onto the surface of optical elements have been considered as the main reasons for degradation of optical instruments in Space [
20,
21,
22,
23]. For instance, after the first Hubble servicing mission the Wide Field and Planetary Camera (WPFC) was returned to ground and several optical elements were analysed in detail to find the cause and understand the mechanism behind the observed spectral degradation of instrument performance. Laboratory analyses revealed a contaminant film about 45 thick covering the WPFC pickoff mirror [
24]. The contamination contained multiple chemical species, some of which had been polymerised by exposure to Earth-reflected UV. Causes and mechanisms of instrument degradation in Space are manifold in detail and have been elucidated in a few real cases [
18,
23,
24] but not in general. Generic approaches, based on physical models to describe and quantify optical effects like mirror contamination in Space [
25], have been rare.
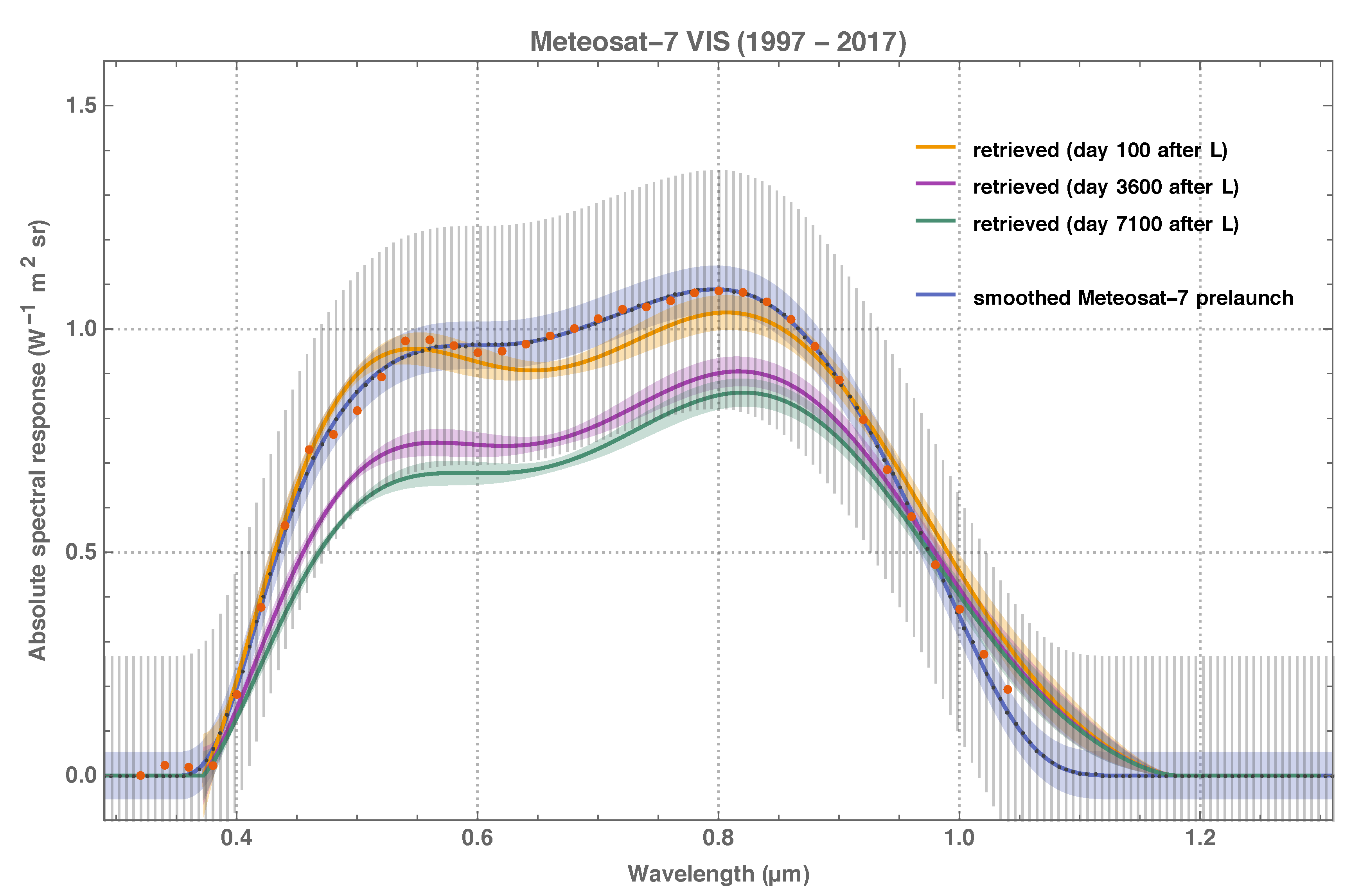
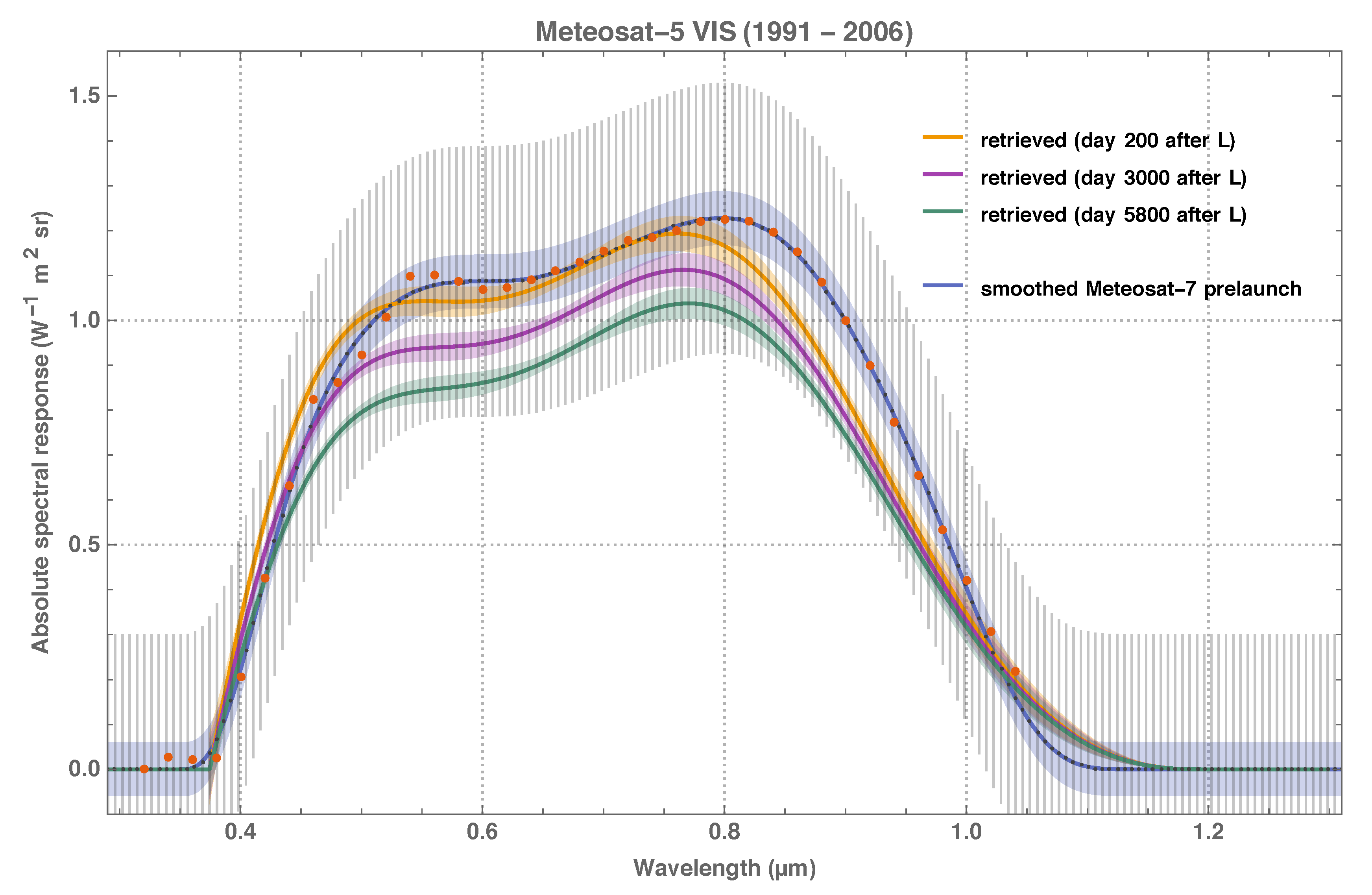
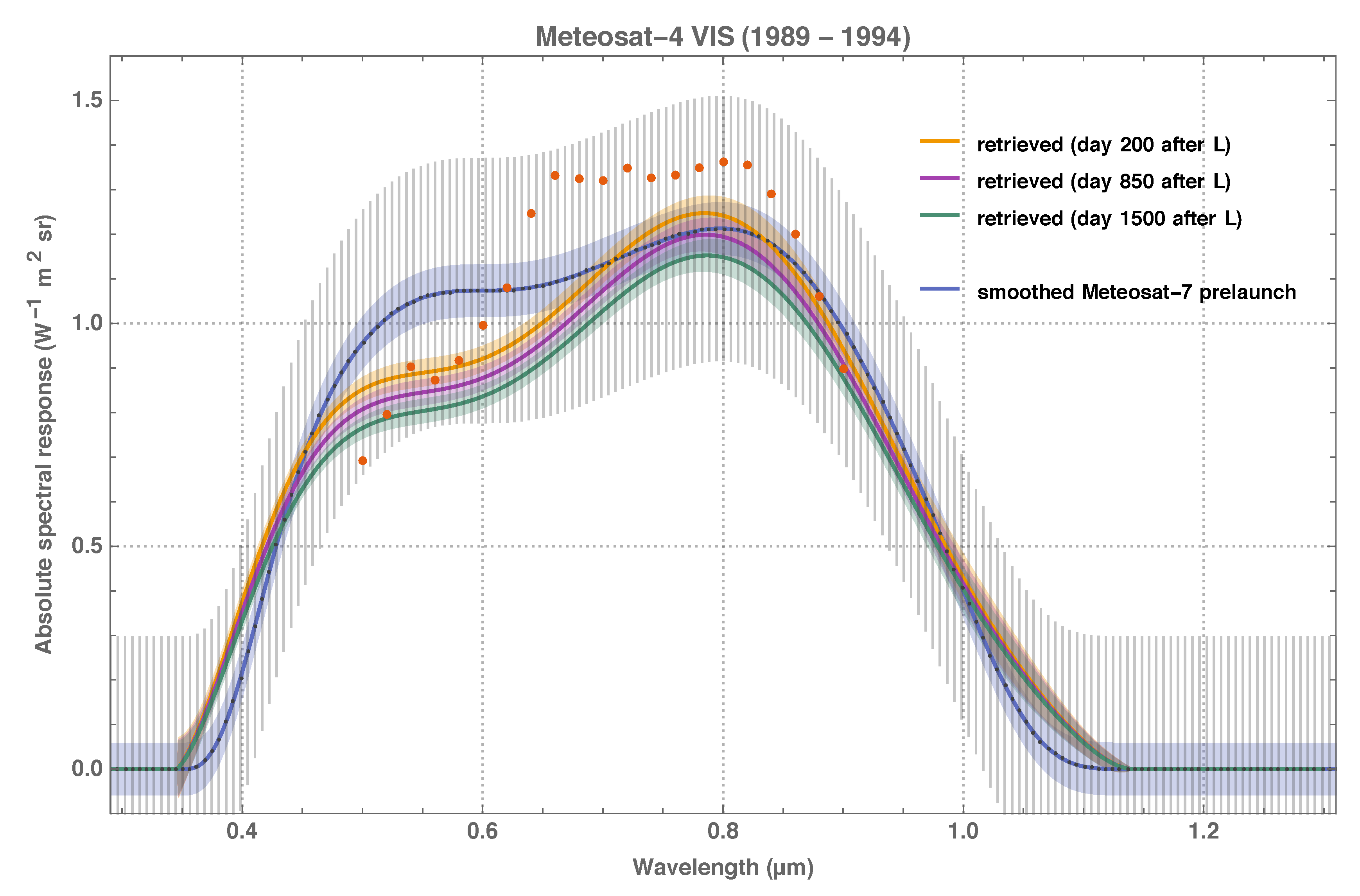
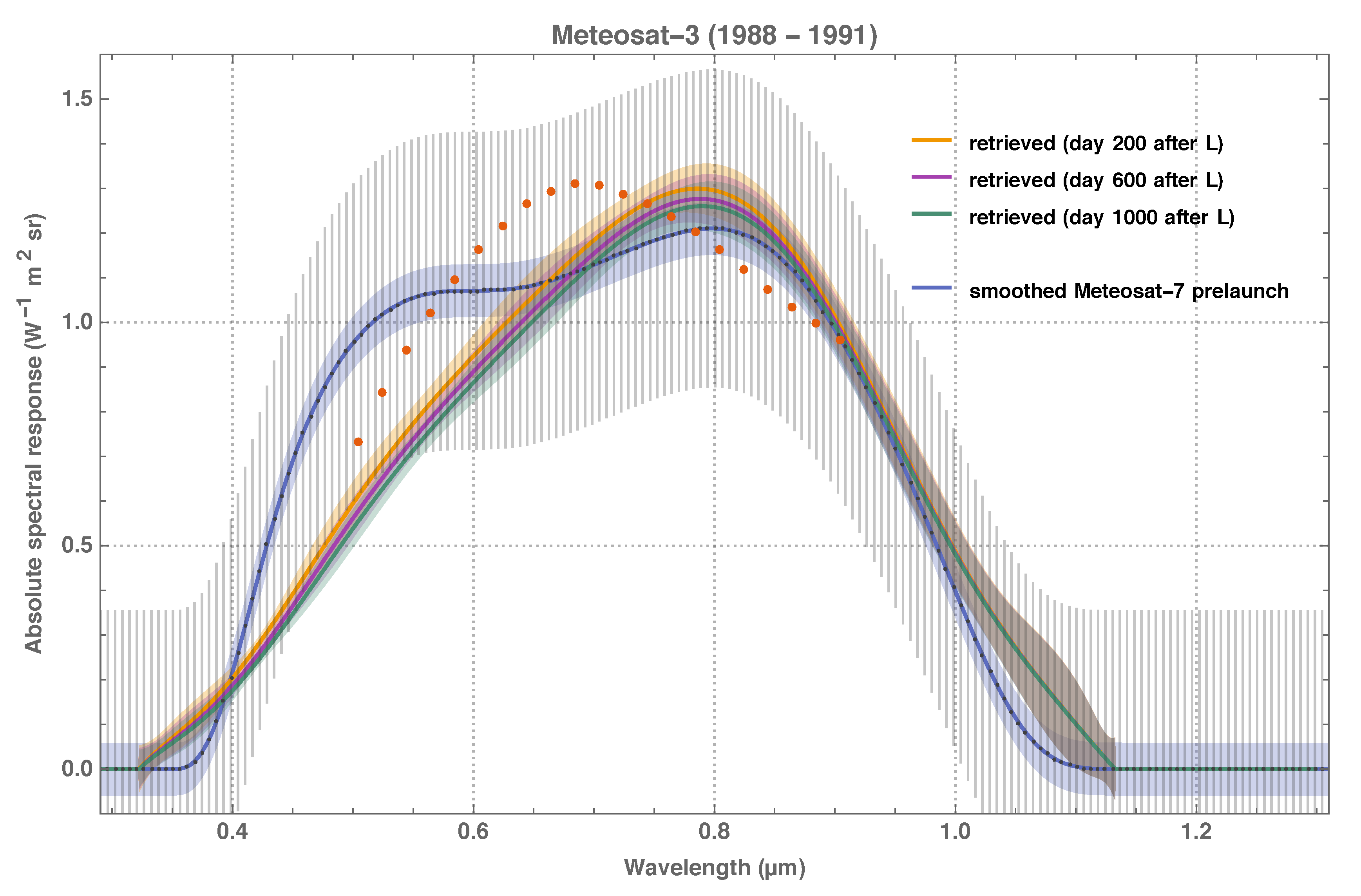
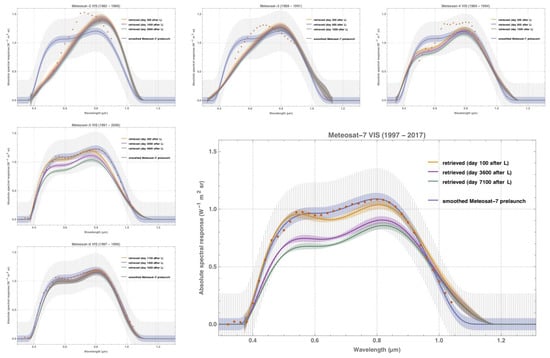
The poorness of the prelaunch characterisation of some Meteosat VIS radiometers has become apparent since 1997–1998, when Meteosat-5, -6 and -7 were located in Prime position and a more consistent vicarious calibration was achieved by calibrating the Meteosat-5 and -6 radiometers with the spectral response of Meteosat-7, which was assessed with improved experimental methods before launch [
7]. Finding evidence for chromatic degradation of Meteosat optics has been facilitated by the SEVIRI Solar Channel Calibration (SSCC) algorithm [
26] to assess the performance of the High-Resolution Visible (HRV) channel of the Meteosat Second Generation (MSG) Spinning Enhanced Visible and Infrared Imager (SEVIRI). SSCC monitors the in-flight performance of MSG HRV radiometers on pseudo-invariant calibration sites (PICS) in bright desert and open ocean target areas in terms of
. Adapting and applying SSCC to MFG satellites [
8] has revealed chromatic degradation of the VIS sensitivity, which was apparently decreasing stronger in the blue (i.e., for open ocean targets) than in the rest of the visible-to-infrared spectrum (i.e., for bright desert sites). Pragmatic efforts to model the chromatic degradation of the VIS radiometers have used an
ad hoc improvised degradation function [
9,
11]. A comparison study of Meteosat-7 VIS and Meteosat-8 HRV observations has concluded that the prelaunch characterisation of the Meteosat-7 VIS spectral response is problematic in the blue, and has suggested the Meteosat-8 HRV spectral response function be used to calibrate the Meteosat-7 VIS radiometer [
10]. All in all, insufficient information and partly inconclusive studies on the Meteosat VIS spectral response make the use of current operationally calibrated VIS images for climate applications doubtful. In consequence, it is not surprising that attempts to create climate data records of Surface Albedo from VIS observations have exhibited temporal inconsistency and instability [
27], indirectly confirming the problematic nature of the VIS spectral response characterisation.
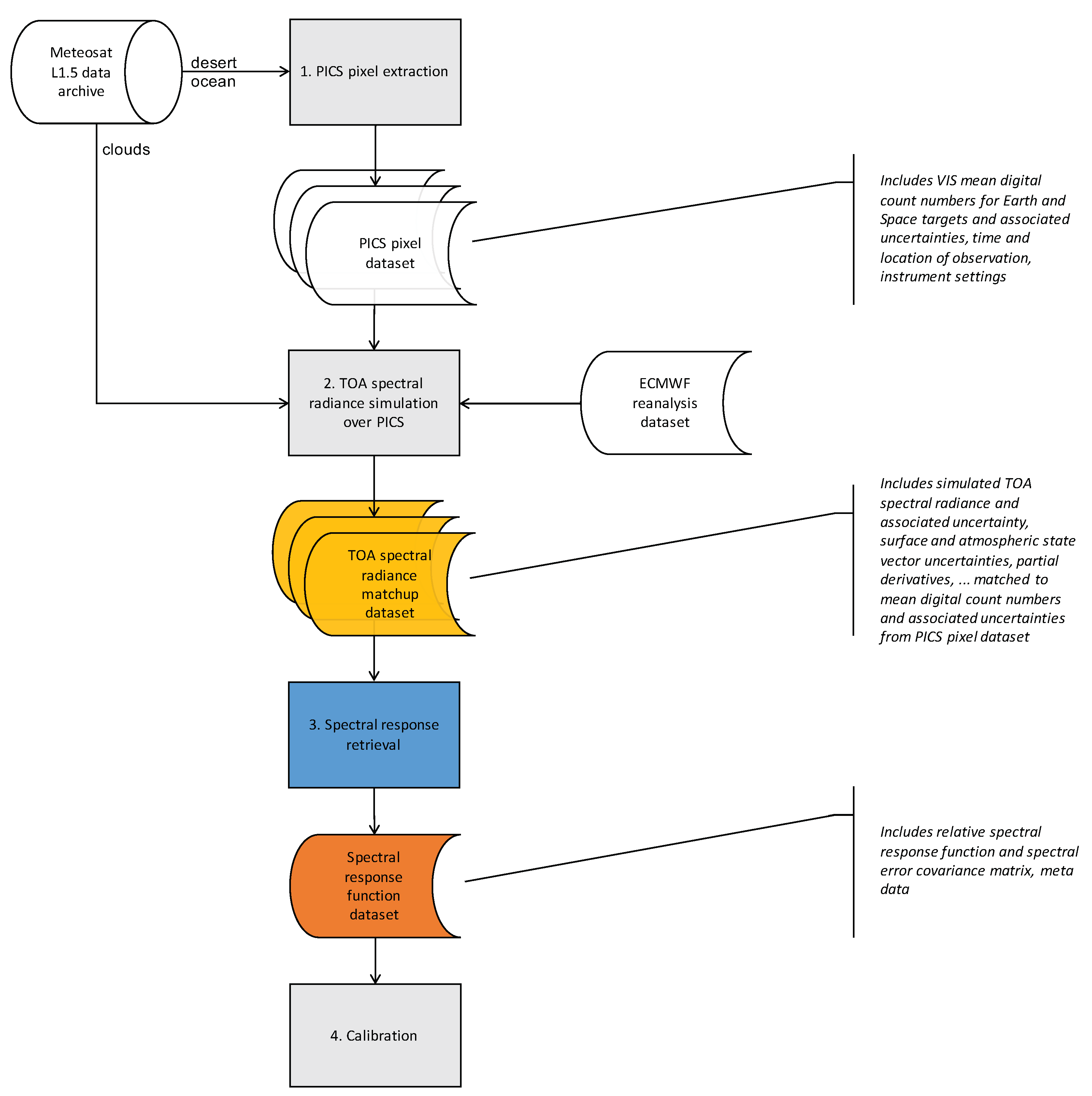
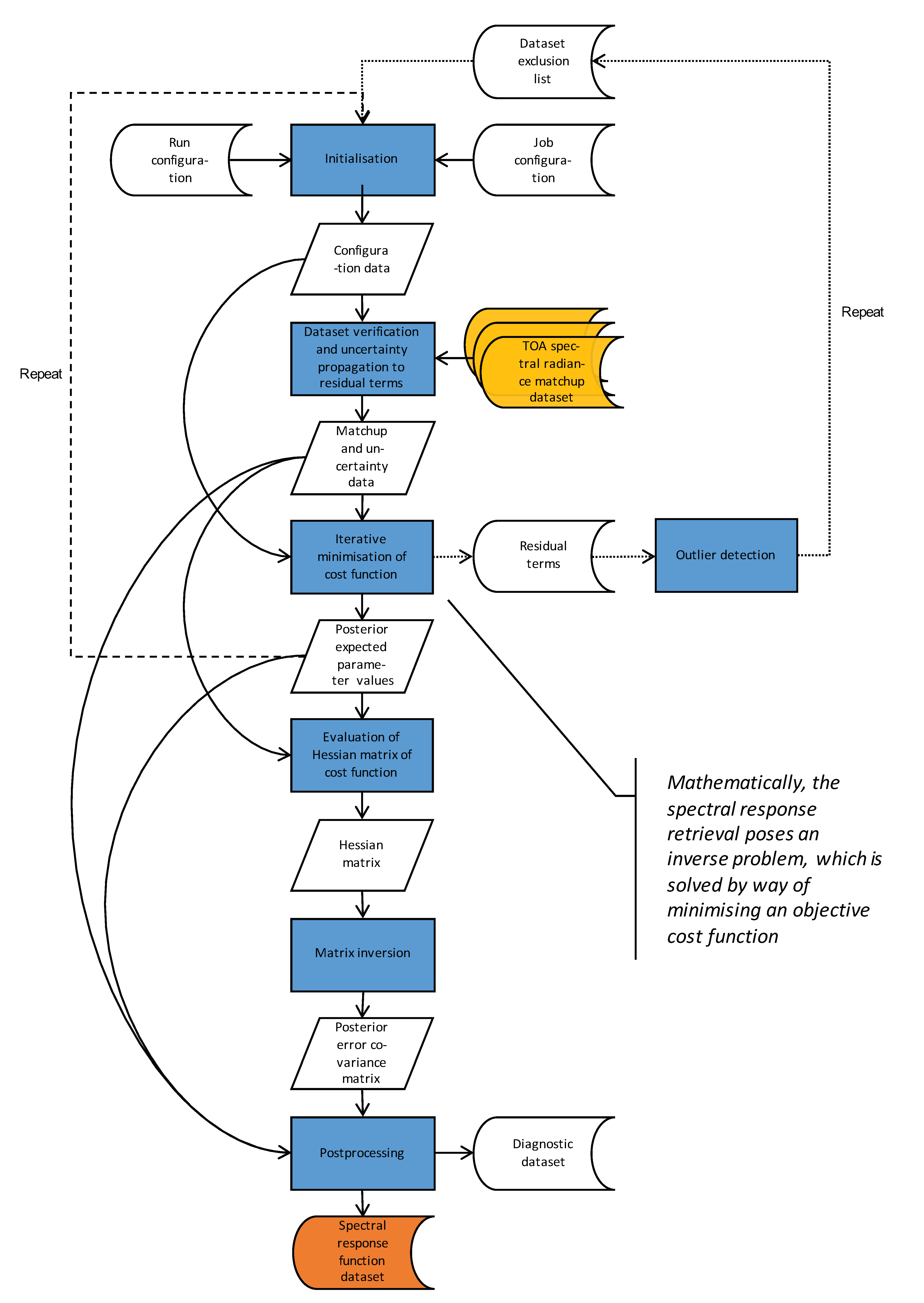
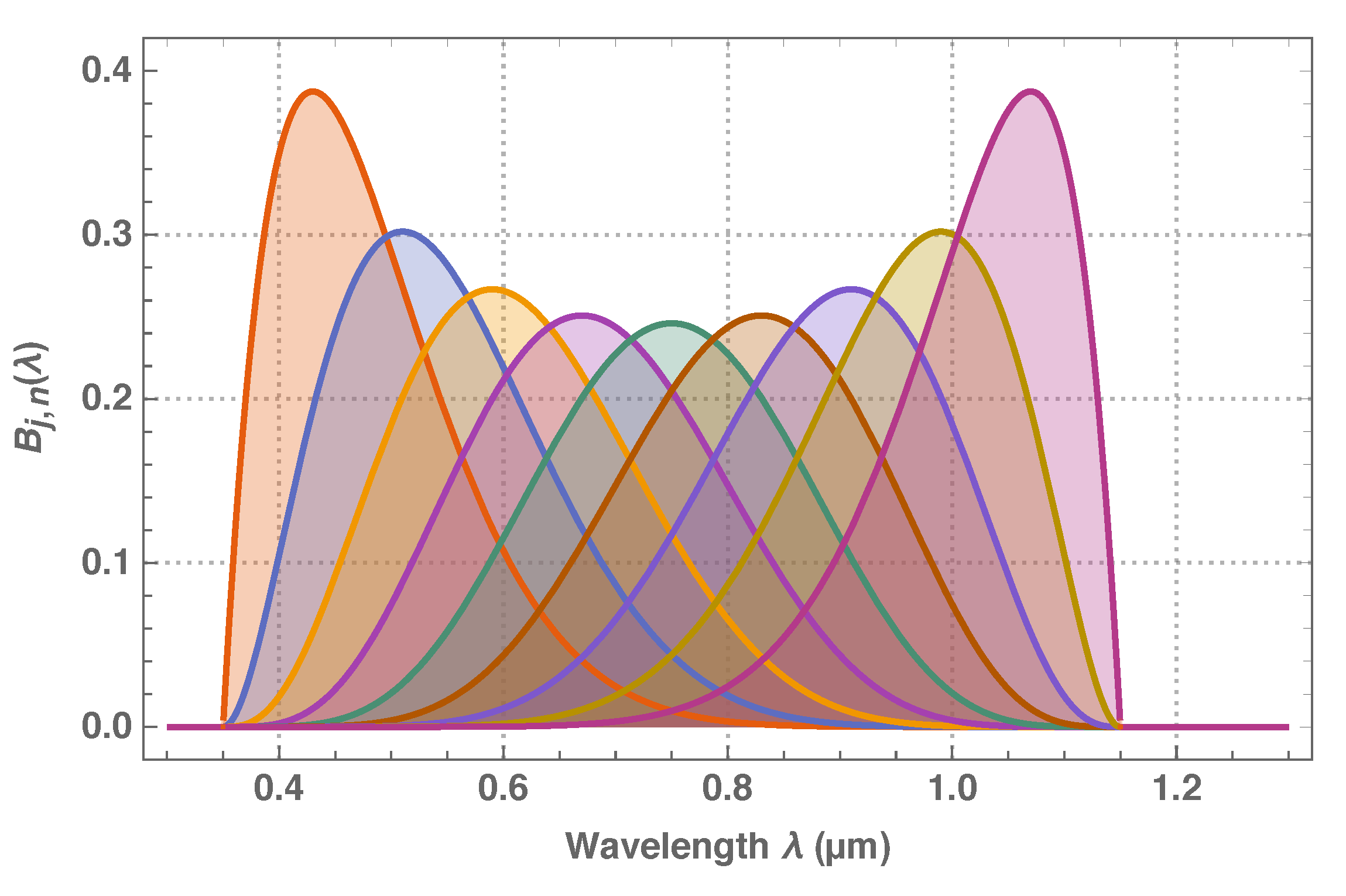
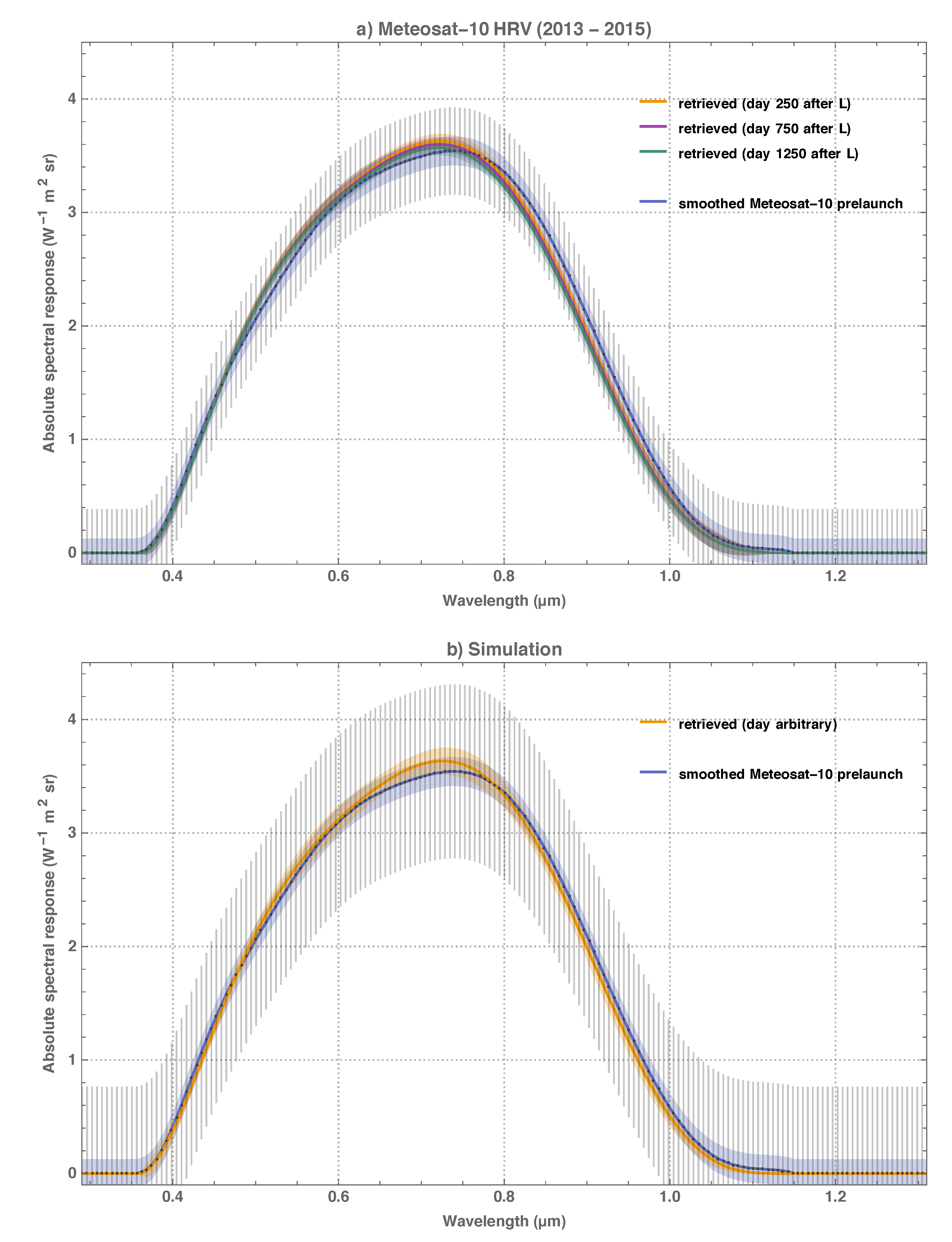
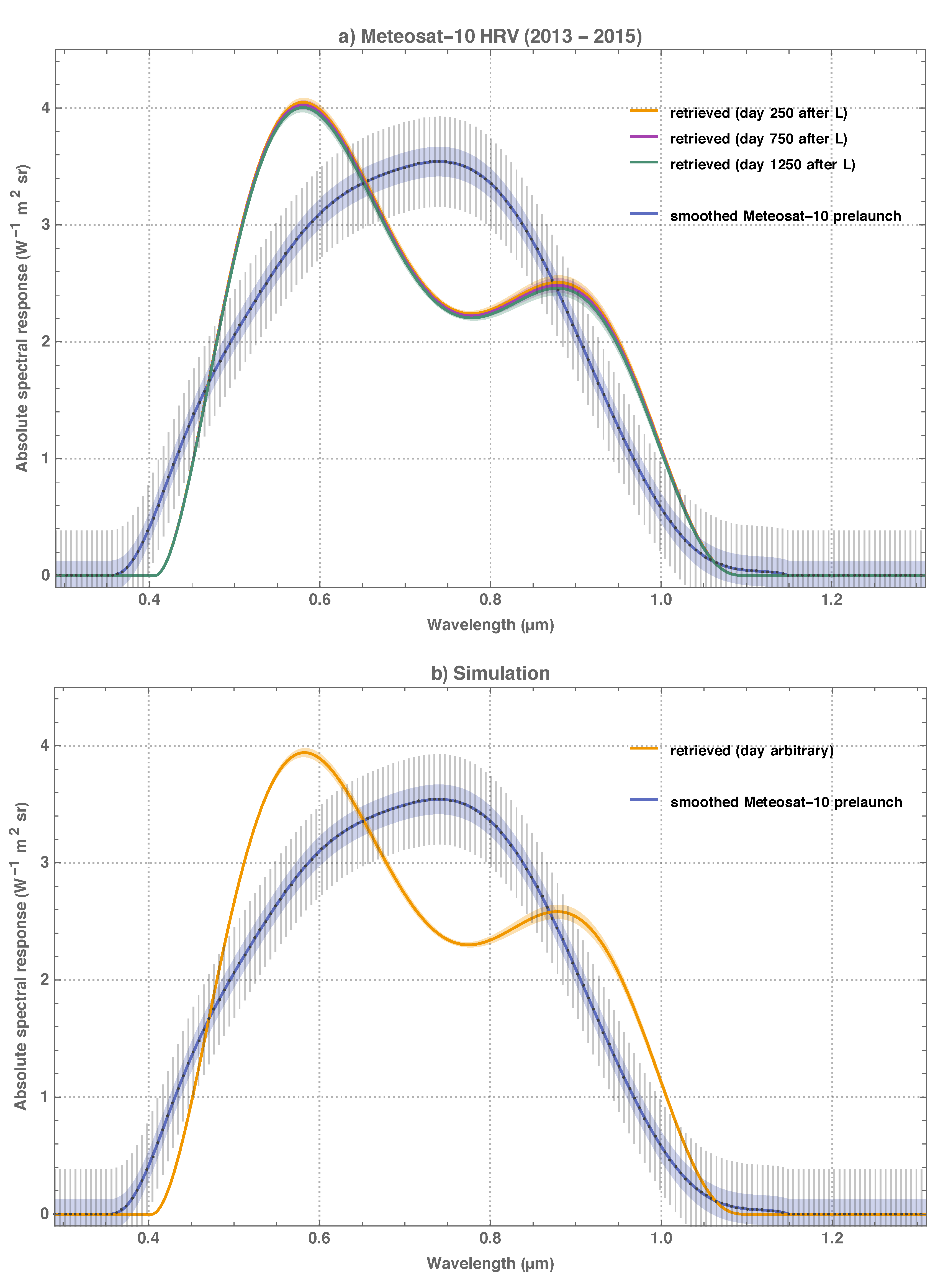
This study describes the retrieval of the in-flight Meteosat VIS spectral response function as a self-standing method and generic application and demonstrates metrologically sound practices to quantify the retrieval uncertainty and spectral error covariance. The absolute instrument spectral response function is decomposed into generalised Bernstein basis [
28,
29] polynomials and a degradation function that is based on plain physical considerations. The method has been validated with well-understood MSG HRV image data and has retrieved meaningful results for all MFG satellites apart from Meteosat-1, which was not available for analysis as it had not been archived at EUMETSAT.
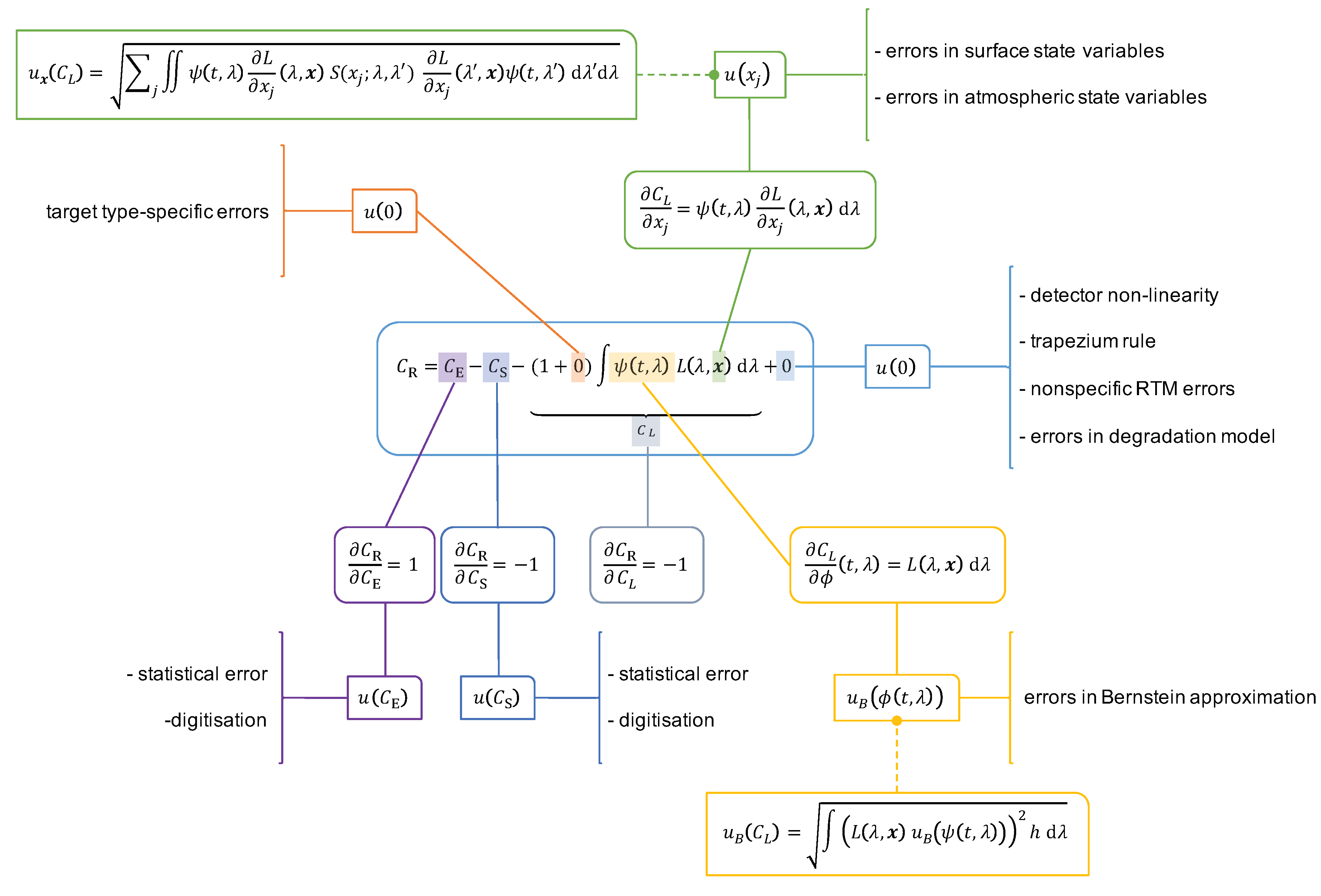
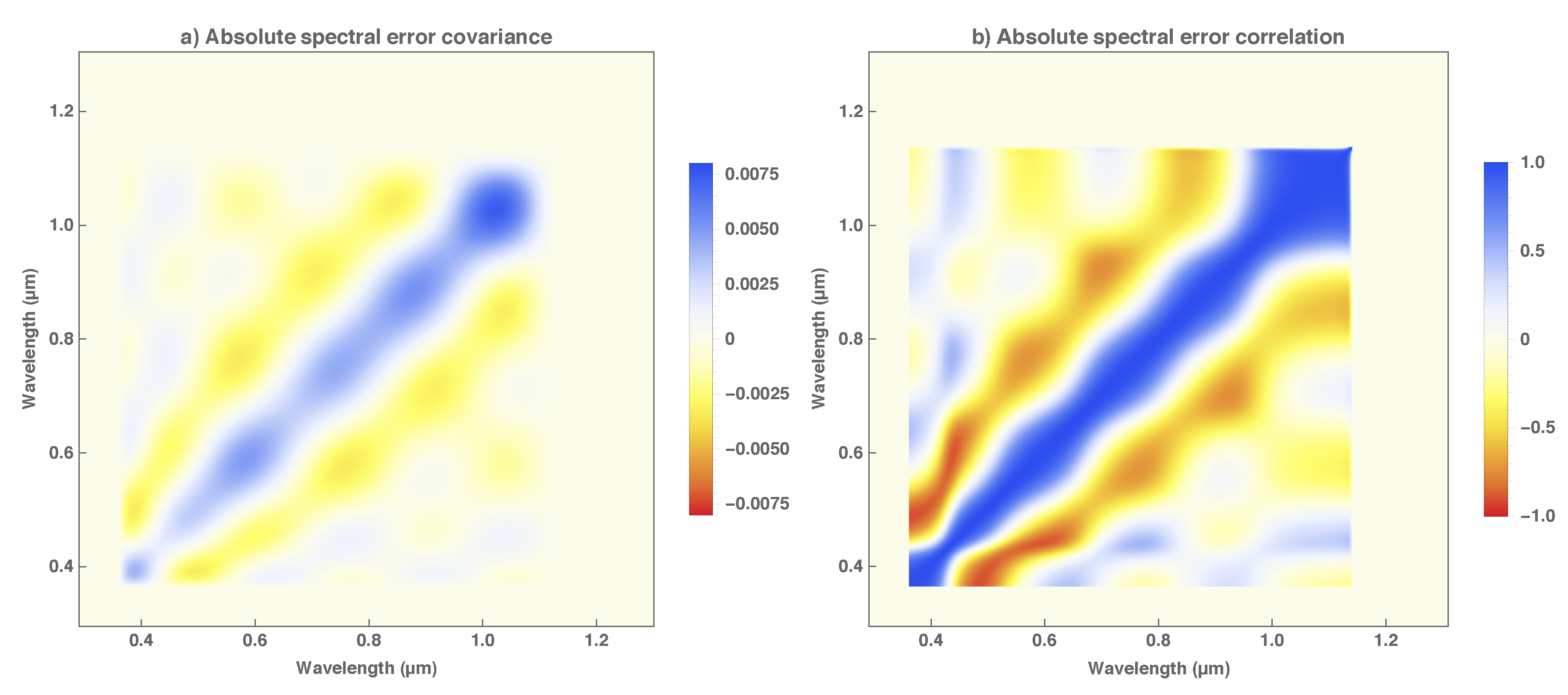
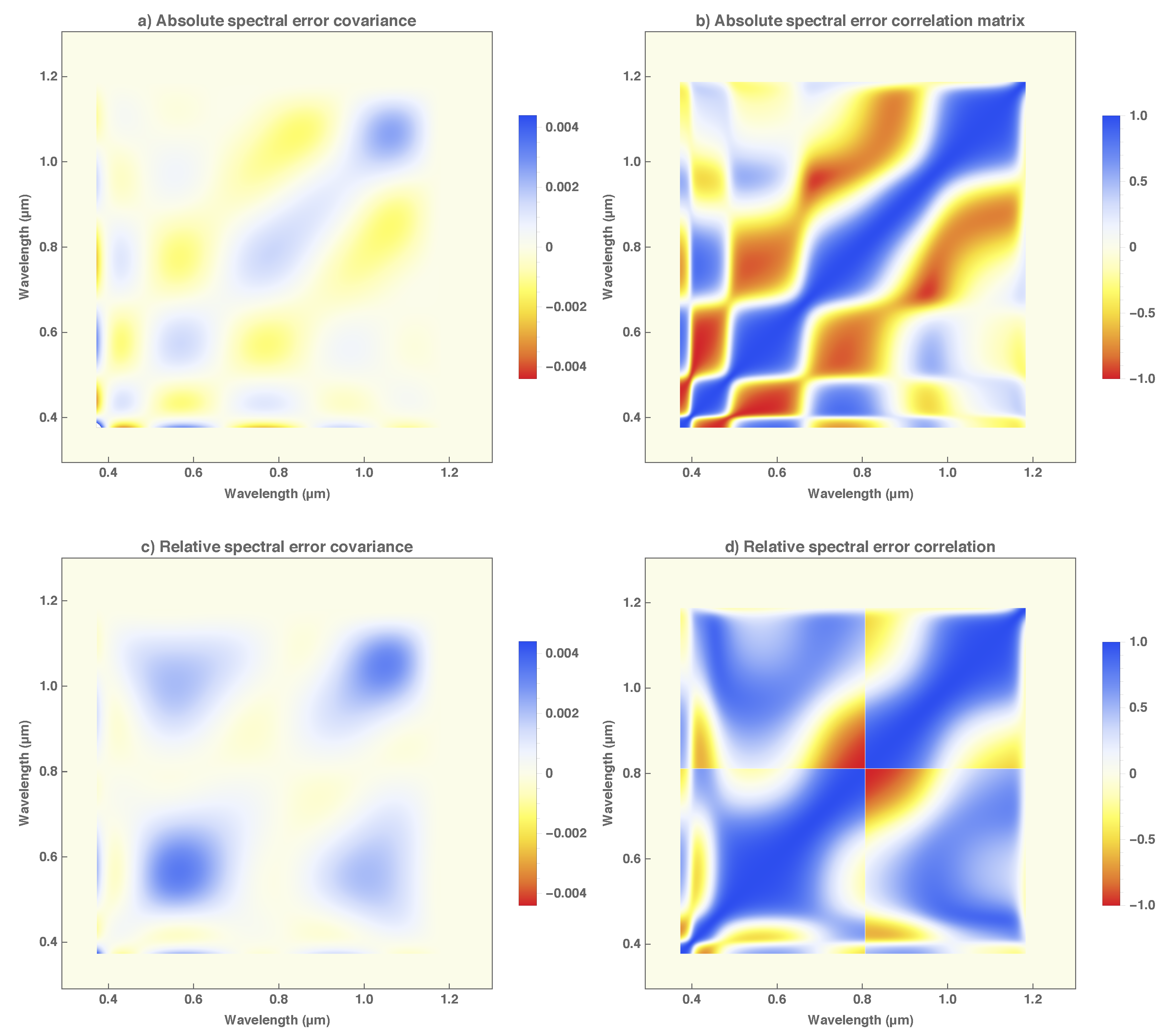
The nomenclature and notation of quantities, such as time, radiance, uncertainty and error covariance, follows the example of Merchant et al. [
6] unless noted otherwise. In a nutshell, the uncertainty of any quantity
q is denoted
. The uncertainty of
q due to the error in any particular variable
x or vector
is denoted
or
. Similarly, the covariance matrix of the errors in the individual components of a vector
is denoted
,
or
. In the same way, the covariance function of the errors in a spectral quantity
q at different spectral wavelengths
and
is denoted
,
or
. The notation analogously applies to spectral quantities
q that depend on time
t. For instance, the covariance function of the errors in a spectral quantity
q at different instants
t and
is denoted
. Materials and methods are presented in
Section 2, results are presented in
Section 3 and discussed in
Section 4.
4. Discussion
Previous studies [
9,
10,
11] that attempted to model the degradation of the MFG VIS spectral response were based on
ad hoc practices to reduce the variance and inconsistency of MFG TOA reflectance time series, but not on metrological sound and traceable methods.
Table 11 presents a conceptual comparison of this and previous studies, the most evident difference of which is the spectral degradation model.
Let
designate the central wavelength of the VIS channel before launch, then the degradation function that has been suggested previously [
9,
10,
11] is
If the chromatic degradation rate
is positive (or negative), the factor
reduces (or enhances) the instrument spectral response for
, but enhances (or reduces) it for
. In other words, chromatic degradation is modelled as a linear function with a tipping point at the central wavelength. Such (unphysical) behaviour does not agree with the (physical) working hypothesis of this paper, which is that the absolute spectral response of the MFG VIS channel degrades over time (in a possibly asymmetric and differential way). Equation (
27) must be interpreted in the context of modelling the change of the relative spectral response over time, which is not a physical approach and not the perspective of this study. A quantitative comparison of results between this and previous studies is therefore not feasible. Qualitatively, all previous studies agree with the result of this study, which is that the spectral degradation of the MFG VIS channels is stronger in the UV and blue than in the red and NIR. From the viewpoint of this study, however, the previous evidence of a prelaunch characterisation problem of the Meteosat-7 VIS spectral response [
10] must be reinterpreted as evidence of an inadequate assessment of spectral degradation by Equation (
27).
Another main conclusion from previous studies is the prognosis that the application of a spectral degradation model will induce a decadal stability of Meteosat-7 time series of Earth-reflected net radiation flux of about
−2 −1 [
9]. Now considering this study, multiplying the residual trend of the Meteosat-7 retrieval (
Table 10) with the Meteosat-7 prelaunch calibration coefficient (
Table 3) induces the tentative conclusion that a stability of
is achievable for a data record of VIS TOA radiant exitance. Repeating this reckoning for the rest of MFG satellites yields tentative stability estimates (listed in
Table 12) which, apart from Meteosat-6, are in tune with the Global Climate Observing System’s requirement on stability of the reflected TOA Earth Radiation Budget product of
−2 −1 [
48].
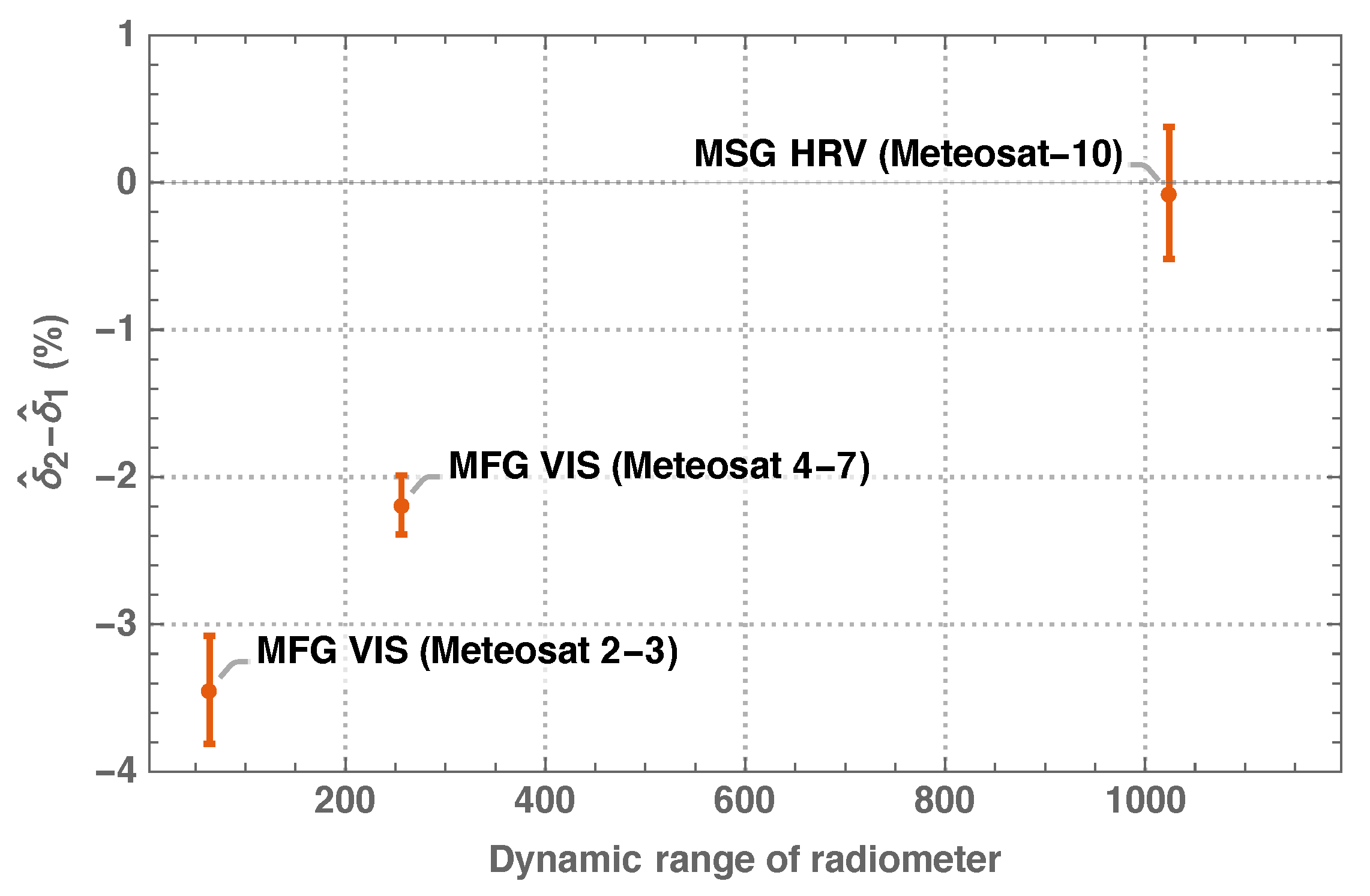
The accuracy of results presented in this paper is in principle limited by two shortcomings. Firstly, the lack of ample prior information on the prelaunch VIS spectral response of all MFG satellites, in particular Meteosat-2 and Meteosat-3 which had been acquiring image data with a binary resolution of 6 only. Secondly, the presence of unknown target type-specific biases due to errors in, e.g., the target pixel selection and the simulation of TOA spectral radiance, which perturb the retrieval. Relative to the retrieved target type-specific bias for desert sites, the retrieved bias for ocean areas is considerably larger for the MFG VIS than for the MSG HRV radiometer. Assuming that the selection of desert and ocean pixels is accurate for MSG HRV scenes, the target type-specific biases retrieved for the MSG validation case (
Table 7, V1.a) yield a mean relative error in the simulation of TOA spectral radiance over ocean targets with respect to desert sites of
percent. Repeating this calculation for the MFG radiometers reveals a statistical correlation of
with the dynamic range of the radiometer: the lower the dynamic range, the more negative is
.
Figure 16 illustrates this correlation. The RTM is the same for MFG and MSG and therefore cannot explain the observed correlation. A possible reason for negative differences
are, e.g., undetected clouds over desert sites, the detection of which is less accurate for low dynamic range. In part, the presence of target type-specific biases may indeed be causally related to the dynamic range of the radiometer. The (number) frequency distribution of (non-digitised) radiance from specific Earth targets may displace when subjected to digitisation. The measure of possible absolute displacement depends on the binary resolution of the digitisation but the possible relative displacement will be largest for dark targets like ocean.
Despite the lack of prior information and the presence of target type-specific biases due to several reasons, the accuracy of the presented method can be improved by refining the identification of ocean and DCC pixels and augmenting the existing MFG matchup datasets with complementary target types, such as green vegetation. Within the composition of target type we have used, ocean targets contribute information in the UV and blue part of the spectrum only, desert targets provide information predominantly in the green to far red part of the spectrum, while DCC targets provide information predominantly in the UV to orange-red and some in the near infrared. This does not mean that DCC targets do not provide information in the red in general, but within the present composition of target types, most information in the red comes from desert targets. Targets with green vegetation, like the Nile delta, may contribute complementary information in the green to near infrared, despite the difficulty that the reflective properties of green vegetation targets are highly controlled by precipitation and will therefore exhibit considerable inter-annual variability. Another considerable improvement were the extraction of PICS data from original Level-0 rather than already processed Level-1.5 data, which would facilitate an individual treatment of the different detectors used in each MFG radiometer.
A companion report on the recalibration and uncertainty tracing of the MFG VIS channel [
31] comes up with definite conclusions on the results and discussion presented in this study.