Modulation of Dual-Polarized X-Band Radar Backscatter Due to Long Wind Waves

Abstract

Investigation of microwave scattering mechanisms is extremely important for developing methods for ocean remote sensing. Recent studies have shown that a common two-scale scattering model accounting for resonance (Bragg) scattering has some drawbacks, in particular it often overestimates the vertical-to-horizontal polarization radar return ratio and underestimates the radar Doppler shifts if the latter are assumed as associated with quasi linear resonance surface waves. It is supposed nowadays that radar backscattering at moderate incidence angles is determined not only by resonance Bragg mechanism but also contains non polarized (non Bragg) component which is associated supposedly with wave breaking but which is still insufficiently studied. Better understanding of the scattering mechanisms can be achieved when studying variations of radar return due to long wind waves. In this paper, results of experiments from an Oceanographic Platform on the Black Sea using dual co-polarized X-band scatterometers working at moderate incidence are presented and variations of Bragg and non-Bragg components (BC and NBC, respectively) and radar Doppler shifts are analysed. It is established that BC and NBC are non-uniformly distributed over profile of dominant (decametre-scale) wind waves (DWW). Variations of BC are characterized by some “background” return weakly modulated with the dominant wind wave periods, while NBC is determined mostly by rare and strong spikes occurred near the crests of the most intense individual waves in groups of DWW. We hypothesize that the spikes are due to intensification of nonlinear structures on the profile of short, decimetre-scale wind waves when the latter are amplified by intense DWW. Bragg scattering in slicks under the experimental conditions was suppressed stronger than NBC and spikes dominated in total radar return. It is obtained that radar Doppler shifts at HH-polarization are larger than at VV-polarization, particularly in slicks, the same relation is for NBC and BC Doppler shifts, thus indicating different scattering mechanisms for these components.

1. Introduction

The problem of scattering of microwaves on the rough surface in application to radar remote sensing of the ocean has been actively discussed in the literature for some decades (see, for example, [1,2,3,4,5,6,7] and references therein). Some recent studies are focused on the role of wind wave breaking in the formation of radar return [8,9,10,11,12,13]. It is supposed nowadays that multipolarization radar observations can improve our understanding of the physical processes responsible for radar backscattering and to extend our capabilities in the characterization of marine currents, internal waves, slicks and so forth (see [14,15,16,17,18] and cited literature). Analysis of radar return at different polarizations, in particular, for dual co-polarized radar signals has revealed that the traditional two-scale Bragg model cannot explain some important characteristics of radar backscatter, in particular, relationship between the radar cross sections at vertical (VV-) and horizontal (HH-) co-polarizations. It was hypothesized in [9] that this inconsistence is a result of the contribution of some additional, non-polarized (or we can call it non Bragg) component in the radar return. The non-Bragg component can be associated with quasi specular reflection of microwaves from tilted facets which can appear due to small-scale features formed on the profile of nonlinear surface wind waves, including wave breaking features [8]. Strictly speaking one can hardly characterize this reflection as quasi specular but as diffraction on the features since the latter are comparable or smaller than the wavelengths of microwave radiation. We suppose that better understanding of the nature of scattering mechanisms can be achieved when studying variability of radar backscattering due to different physical processes. The variability of Bragg and non-Bragg components of radar return due to surfactant films was investigated in [15,16,17,18] and the important role of wave nonlinearity—in particular of wave microbreaking—was emphasized in References [16,18] when trying to describe radar return reduction due to film. It is also well known that radar return is modulated due to decametre-scale dominant wind waves (DWW), whose wavelengths are larger than the antenna footprint. The problem refers to the so-called Modulation Transfer Function (MTF) (see, for example, [19,20,21,22]). It has been shown that the modulation is determined by several physical mechanisms. They are geometric modulation (tilt and range effects) and hydrodynamic modulation due to variations of the spectrum of short wind waves responsible for radar backscattering. The hydrodynamic modulation was traditionally described in a relaxation approximation taking into account modulation of resonance Bragg waves by orbital horizontal velocities of DWW. Modulation effects and MTF were studied also in the presence of films in [23]. The concept of MTF does not take strongly nonlinear effects into account, in particular, the influence of wave breaking on radar backscatter modulation. At present the role of strongly nonlinear effects of wave breaking on radar backscattering is not completely understood and these effects need to be investigated in more detail, particularly in experiment.

This paper presents the results of recent experiments on the modulation of radar return due to wind waves and is focused on the investigation of the variability of Bragg and non-Bragg radar backscattering components and on better understanding of the physical mechanisms of radar backscattering. The results, as shown in the paper, indicate that the distributions of Bragg and non-Bragg components over the DWW profile are different. This conclusion can be very helpful, for example, for the development of an improved combined model of radar backscatter. Namely, since Bragg scattering dominates almost all over the DWW profile, the two-scale scattering model can be approximately applied everywhere except for the regions near the crests of the most intense DWW. In the vicinity of the intense wave crests the radar return can be supposedly described as quasi specular reflection or, more precisely, diffraction of electromagnetic waves. The development of new models of radar backscattering is, however, a subject of future work.

2. Methods and Instruments

2.1. Experiment

The experiments were carried out from an Oceanographic Platform of the Marine Hydrophysical Institute (MHI) in the autumn of 2018. Similar observations were also performed in the spring of 2017 and results of analysis of the archived data are presented here, too. Dual co-polarized (VV/HH polarizations) microwave radar instruments, an X-band Doppler scatterometer and an X-/C-/S-band Doppler radar, were mounted at the Platform at heights of 12 and 13 m, respectively, close to each other and looking nearly in the same directions (Figure 1). The antenna beam width of the X-band scatterometer is about 5.5° and the observations were carried out at an incidence angle of 60°, so that the radar footprint scale was about 1.5 m for the X-band scatterometer, that is, about ten times less than the wavelengths of the dominant wind waves in our experiments. The X-band scatterometer operated in a continuous wave regime with linear frequency modulation. The sampling rate was 2000 Hz and Doppler spectra of radar return were analysed over time intervals of 0.25 s. The radar Doppler shift was determined as a ‘centre of gravity’ of the Doppler spectrum. Since the spatial and temporal resolutions for the scatterometer were essentially smaller than the wave lengths and periods of dominant wind waves, it allowed us to study variations of radar return over the profile of DWW and all the results on the backscatter modulation were obtained with the X-band scatterometer. The three-band Doppler radar with a parabolic 90 cm-diameter antenna operates in a pulse regime and the antenna beam width and the footprint in X-band range are comparable with those for the scatterometer. The radar is capable to form an image of the water surface with a pixel size determined by the time gating (5 ns) and the antenna footprint. In X-band and at incidence angles of about 60° the pixel size was nearly the same as the footprint scale, so the radar was working actually as a scatterometer. For S- and C-bands we chose the pixels corresponding to the centre of the X-band footprint. The sampling rate for the three band radar when operating at three bands and two polarizations is about 1 Hz. Due to the low sampling rate the radar was unable to study modulation of radar return over the period of DWW and was used as an auxiliary instrument to study mean polarization ratio in different radar bands. We believe that this may be useful to extrapolate the results obtained with X-band scatterometer to C- and S-bands. The wind velocity and direction were measured with an acoustic anemometer WindSonic mounted at a height of 16 m. Surface gravity waves were measured with a wire wave gauge mounted at a distance of about 10 m from the radar illuminated areas. Some experiments were carried out to study the influence of films on the radar backscatter modulation. Film slicks were created in the experiments using solutions of oleic acid in ethanol poured out on the water surface. The observations were carried out at wind velocities ranged from about 7 to 10 m/s, mean heights of dominant wind waves were about 0.2 m–0.4 m. This wind velocity range was chosen for our observations because film slicks were quickly disrupted at higher wind velocities, while at lower wind velocities the modulating DWW were too short to be reliably resolved due to the scatterometer footprint limitations.

Figure 1. An Oceanographic Platform (left) and X-/C-/S-band radar and X-band scatterometer mounted at the Platform (right).

2.2. Theoretical Background

We assume that scattering of microwaves is composed of resonance (Bragg) and non-Bragg components. The first component is determined by surface waves whose lengths satisfy to resonance with electromagnetic wavelengths. The second, non-Bragg (or non-polarized) component is associated with scattering from small quasi specular facets on the profile of surface waves longer than Bragg ones, the structures appear due to wave nonlinearity, in particular, due to wave breaking. The total NRCS is supposed to be a sum of the two components (see, for example, [8])

$${\sigma }_{pp}^0={\sigma }_{B\_pp}^0+{\sigma }_{NBC}^0.$$

(1)

Here ${\sigma }_{pp}^0$ is the total NRCS, p denotes vertical (V) or horizontal (H) transmit/receive polarizations, ${\sigma }_{B\_pp}^0$ is Bragg (polarized) component of radar backscatter described by the two-scale Bragg model, ${\sigma }_{NBC}^0$ is non Bragg component. The Bragg component according to the two-scale radar model can be written as (see, for example, [1])

$${\sigma }_{BC\_pp}^0=16\pi k_{em}^4{R}_{pp}(\theta )F(\overrightarrow{k_B}),$$

(2)

where $F(\overrightarrow{k_B})$ is the spectrum of wind waves at the Bragg wave vector ${\overrightarrow{k}}_B=2k_{em}{\overrightarrow{n}}_s$, $k_{em}$ is the wave number of an incident electromagnetic wave, ${\overrightarrow{n}}_s$ is a projection of the unit wave vector of an incident electromagnetic wave on the sea surface, $\left|{\overrightarrow{n}}_s\right|=\sin \theta$, θ is the incidence angle, $R_{pp}(\theta )$ is the reflection coefficient which depends on polarizations of incident/reflected electromagnetic waves.

Assuming that the non-Bragg component is non polarized, being the same for both VV and HH radar return, one can remove NBC from the total radar backscatter (1) when subtracting ${\sigma }_{HH}^0$ from ${\sigma }_{VV}^0$. Under this assumption thus obtained polarization difference (PD) can be described by the two-scale scattering theory, that is,

$$PD={\sigma }_{B\_VV}^0-{\sigma }_{В\_HH}^0=(R_{VV}-R_{HH})F({\overrightarrow{k}}_B),$$

(3)

The non-Bragg component can be found from (1)–(3) as

$${\sigma }_{NBC}^0=\frac{1}{2}[{\sigma }_{VV}^0+{\sigma }_{HH}^0-\frac{R_{VV}+R_{HH}}{R_{VV}-R_{HH}}PD],$$

(4)

A polarization ratio (PR) introduced as

$$PR={\sigma }_{VV}^0/{\sigma }_{HH}^0,$$

(5)

characterizes contribution of NBC to the total radar return when comparing experimental values of PR with two-scale Bragg theory, which predicts $PR=R_{VV}/R_{HH}$.

One should note that all the components of radar return should be considered either as averaged over the periods of DWW or as ‘instantaneous’ time dependent variables, if the latter are analysed on the time scales less than the periods of DWW.

In the latter case

$${\sigma }_{pp}^0(t)=<{\sigma }_{pp}^0>[1+M(t)],$$

(6)

where $<{\sigma }_{pp}^0>$ denotes the mean NRCS and $<{\sigma }_{pp}^0>M(t)=<{\sigma }_{B\_pp}^0>M_{B\_pp}(t)+<{\sigma }_{NBC}^0>M_{NBC}(t)$ its variable part. One should emphasize that the modulation function $M_{B\_pp}(t)$ of the Bragg component describes variations of BC with DWW frequencies Ω in terms of the Modulation Transfer Function $m_{B\_pp}(\mathsf{\Omega })$ as

$$M_{B\_pp}(t)={\displaystyle \int m_{B\_pp}(\mathsf{\Omega })\frac{U(\mathsf{\Omega })}{C(\mathsf{\Omega })}}{e}^{i\mathsf{\Omega }t}d\mathsf{\Omega }.$$

(7)

The MTF in (7) includes geometric (tilt and range) modulation and hydrodynamic modulation.

The geometric modulation is associated mostly with tilting of the surface by DWW leading to variations of the local Bragg wavelength and of the reflection coefficient (“tilt modulation”) and “range modulation” due to different distances from the antenna to crests and troughs of DWW, the “range modulation” is usually negligible. The hydrodynamic modulation is direct modulation due to “straining” of surface waves by non-uniform orbital velocities of DWW.

Modulation of Bragg cm-scale waves due to the mentioned mechanisms results in some weak, “background” backscatter variations, which are of the order of DWW slopes and typically are about 10–20%.

Variations of NBC as it is shown below appear as strong spikes whose periods are larger than the DWW periods and are mostly comparable with the periods of surface wave groups. This strong modulation cannot be described in terms of the traditional MTF and related theory will be developed elsewhere.

The instantaneous radar Doppler shift $F_D$ can be found as a centre of gravity of the radar Doppler spectrum and can be written as (see, for example, [20])

$$F_D=1/2\pi \cdot \overrightarrow{k_B}[\overrightarrow{V_s}+{\overrightarrow{U}}_{orb}(t)].$$

(8)

Here $\overrightarrow{V_s}$ denotes velocity of scattering elements: either Bragg waves or scatterers associated with breaking of short wind waves, the $\overrightarrow{V_s}$-values can also contain the velocity of large-scale and slowly varying surface currents, ${\overrightarrow{U}}_{orb}(t)$ is the orbital velocity of DWW. It follows from (8) that the orbital velocities of DWW are proportional to variations $\delta F_D(t)=F_D(t)-<F_D>$ of the radar Doppler shift and can be easily estimated.

3. Results and Discussion

3.1. Characteristics of Wind Waves

First of all let us characterize wind waves in the experiments from the Oceanographic Platform. It has been mentioned that the observations were carried out at moderate wind velocities ranged from about 7 m/s to 10 m/s. Typical examples of the frequency spectra of wave heights at different wind speeds are shown in Figure 2. The periods T_DWW of DWW were in the range of 2.5 s–3.5 s at wind velocities of 7 m/s–10 m/s, respectively. Mean wave heights varied from about 20 cm to 40 cm. Significant waves heights H_S were estimated as 35 cm at wind velocity of 7 m/s and 60 cm at wind velocity of 10 m/s. One should remind that the experiments were conducted in the coastal zone, therefore the characteristics of DWW differ from those for the open ocean.

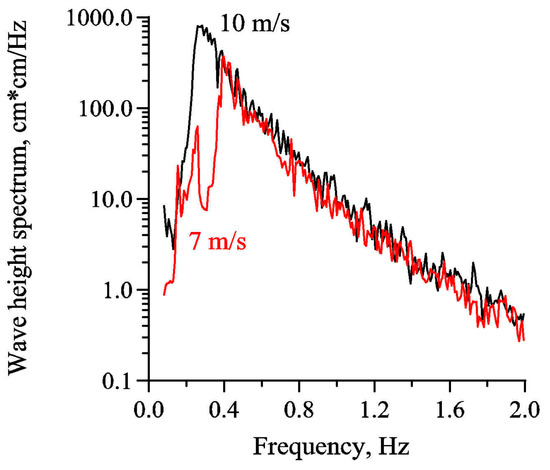
Figure 2. Wave height frequency spectrum at 7 m/s (red) and 10 m/s (black).

3.2. Mean Polarization Ratio

First, we illustrate using three-band radar data that non Bragg scattering significantly contributes to radar return. According to Bragg theory the ratio of mean VV-to-HH radar returns (polarization ratio) $P{R}_{mean}=<{\sigma }_{VV}^0{>}_{lw}/<{\sigma }_{HH}^0>{}_{lw}$ is equal to the ratio of the reflection coefficients at two polarizations, which is about 10 and larger at moderate incidence angles (see, [1]) as shown in Figure 3.

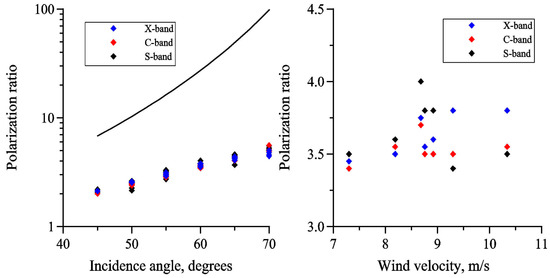
Figure 3. Experimental values of the mean PR vs. radar incidence angle (left) and vs. wind velocity (right) obtained from measurements with the three-band radar for clean water in X-, C- and S-bands (blue, red and black symbols, respectively). The curve is PR calculated according to two-scale Bragg theory [1]. Wind velocities range is 7 m/s to 10 m/s, radar azimuth angles vary from zero to ±30°, that is, close to upwind directions.

The experimentally obtained PR-values are presented in Figure 3, too and appear to be several times smaller than the theoretical values thus demonstrating that non Bragg scattering contributes significantly to radar backscatter. Note, that according to Figure 3 the PR-values in X-, C- and S-bands are very close to each other. Therefore, one can expect that the scattering in these radar bands is determined by similar physical mechanisms.

3.3. Variations of Radar Return at VV and HH-Polarizations

3.3.1. Clean Water Surface

Now we illustrate variability of radar backscattering when analysing the Doppler spectrum of radar return. The Doppler spectrum has a peak in the frequency domain and the peak location characterizes the radar Doppler shift. The spectrum peak intensity and frequency vary due to radar backscatter modulation and due to orbital velocity of DWW, respectively and the spectra are different in different phases of a long wave, as the examples in Figure 4 illustrate.

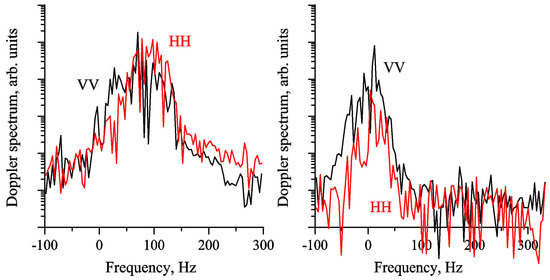
Figure 4. Examples of radar Doppler spectrum near a DWW crest (left) and near a DWW through (right). Black curves–VV-polarization, red curves–HH-polarization. Upwind observations, wind velocity is 10 m/s.

Variations of the radar Doppler spectrum can be seen very clearly in spectrograms (see, Figure 5) illustrating temporal variations of the spectrum. In Figure 5 spectrograms for radar Doppler spectra for VV- and HH-polarized backscatter and for Bragg and non-Bragg components are shown. One can conclude that BC is nearly the same as VV-polarized radar return, at least for the case of a 60° incidence angle and NBC is quite similar to the HH-component. Very short and strong peaks of intensity (spikes) in the instantaneous Doppler spectrum can be recognized in the spectrograms, particularly at HH-polarization. The spikes are very prominent in the spectrum of NBC, too. The intensity of radar backscattering at HH-polarization and of NBC is rather weak everywhere with the exception of the areas of spikes. The appearance of the spikes is not correlated with DWW period. On the contrary, the modulation of VV-polarized radar return and BC with the periods of DWW is well pronounced and the spikes are not much stronger than the long wave modulation.

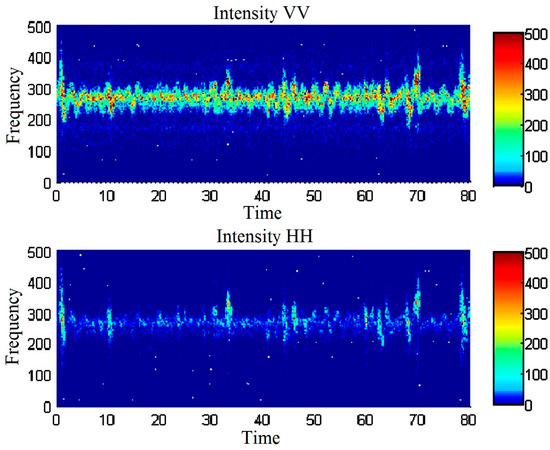
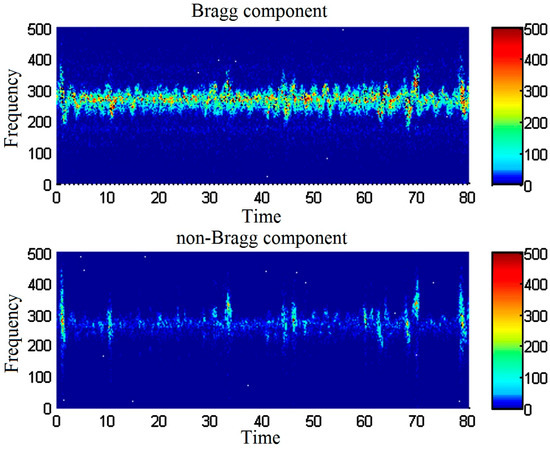
Figure 5. Spectrograms of radar backscatter at VV and HH polarizations (two upper panels) and of Bragg and non-Bragg components of radar return (two bottom panels). Upwind observations, wind velocity of 8 m/s, incidence angle of 60°. The frequency offset 250 Hz corresponds to “zero” Doppler shift, time in seconds. Clean water.

Let us now discuss the radar backscatter variations due to DWW in more detail and consider time series of radar return. Typical time series of X-band radar return at VV and HH-polarizations are shown in Figure 6. It is clearly seen that the backscatter variations at HH-polarization can be characterized by the occurrence of rare but strong peaks (spikes) whose intensities are in general much larger than the adjacent “background” radar return modulated with periods of DWW. Note that at VV-polarization the peaks are not significantly larger than the “background” modulation. Even without special data processing one can conclude that the spikes at VV- and HH-polarizations have practically the same intensities, thus indicating that the radar return in the spikes can be characterized as nearly independent on polarization, that is, as non-polarized backscattering.

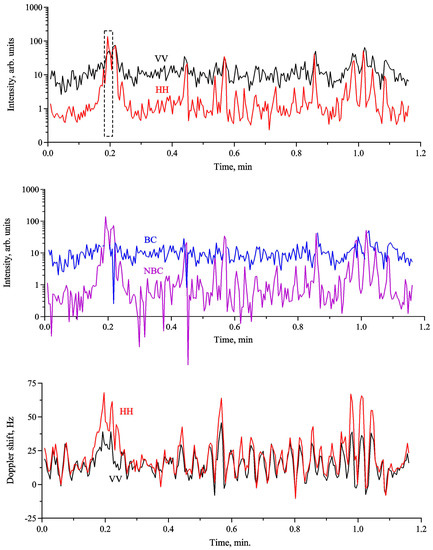
Figure 6. Time series of radar backscatter (upper panel) and radar Doppler shifts (bottom panel) at VV-polarization (black) and at HH-polarization (red). Clean water. Time series for BC (blue) and NBC (violet) are in the middle. The selected fragment (dashed rectangle) in the upper panel denotes a domain where ${\sigma }_{VV}^0<{\sigma }_{HH}^0$, wind velocity is 10 m/s.

The spikes often but not always, occur near the largest maxima of the orbital wave velocity, that is, near the crests of the most intense DWW and only one of about 3 to 10 crests is characterized by the occurrence of spikes (see Figure 5 and Figure 6). The fact that the spikes are mostly pronounced in HH polarization but not in VV polarization, is because Bragg scattering at moderate-to-large incidence angles at VV polarization is much larger according to theory than at HH polarization, since the scattering coefficient $R_{VV}$ is up to some tens of $R_{HH}$ (see Figure 3). BC and NBC in Figure 6 demonstrate some similarity with VV- and HH-polarized radar backscatter, respectively. There are some time intervals, however, like one shown in Figure 6, where VV-polarized backscatter is smaller than HH, that is inconsistent with Bragg theory.

3.3.2. Slick

Variations of backscattering at VV- and HH-polarizations in slicks are in general similar to ones in non-slick areas, namely, moderate radar backscatter variations with periods of DWW alternate with more rare spikes. Figure 7 shows simultaneous time series of radar VV-/HH-backscatter, BC and NBC and radar Doppler shift. The slick is characterized by the following averaged contrasts: K_VV ≈ 8, K_HH ≈ 4, K_BC ≈ 17, K_NBC ≈ 4. The contrasts, although being of the same order of magnitude, nevertheless differ from each other and show that VV-polarised radar backscatter, as well as BC component, is more strongly suppressed in slick than HH- and non-Bragg components. The suppression of BC is associated with enhanced viscous damping of Bragg cm-scale waves due to films, while the suppression of NBC is related to weaker damping of longer dm-scale waves and suppression of related nonlinear structures, presumably responsible for formation of NBC. The relation between different contrasts, however, is not universal (see, for example, [18]) and can vary depending on meteorological conditions, film characteristics, sea state and so forth.

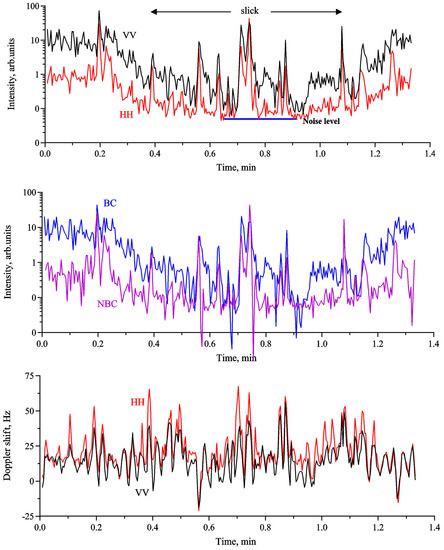
Figure 7. Same as in Figure 6 but for the case of slick, wind velocity is 10 m/s.

Although VV- and HH- intensities in slick can approach values rather close to the noise floor, the backscatter intensity in many spikes remains comparable with those in non-slick areas and the peak of the VV-backscatter becomes similar to the HH-backscatter variations. Similar to the non-slick case, the intensities of VV- and HH-polarized backscatter spikes are nearly equal to each other and the spikes are often located near the crests of the highest DWW. The Doppler shifts in the spikes are normally larger at HH-polarization than at VV-polarization (see below in more detail) and the difference can be even more pronounced than outside slicks. This is partly because the phase velocities of Bragg cm-scale waves, contributing mostly to VV-backscatter, are smaller in slick than in non-slick because of reduction of the surface tension coefficient of the film covered sea surface.

3.4. Relative Energy of Spikes

We have already noticed that spikes in radar return are very intense, short and relatively rare. But we also should emphasize the importance of spikes and give some quantitative estimates of the contribution of spikes to the total radar backscatter. Some conclusions regarding the role of spikes can be made from histograms presented below. In Figure 8 histograms of radar backscatter maxima at HH and VV-polarization are plotted. One can conclude that almost all maxima of radar backscatter at VV-polarization are contained within a narrow range of small intensity values up to 5–10 arb. units in Figure 8. This is because HH-polarized backscatter is characterized by strong and rare spikes and by the low maxima of the “background” modulation with the periods of DWW. For VV-polarization the situation is different because the maxima of “background” modulation are larger than at HH-polarization and are not so small compared to spikes as for the HH-polarization, so the backscatter maxima occupy wider range (up to 20–25 arb. units). The characteristic widths of the histograms for both polarizations, however, are significantly smaller than typical intensities of the spikes. In order to estimate the significance of the spikes in radar backscatter we plotted the summed energy of the maxima which are contained in given intensity interval (see Figure 8, bottom row). Figure 8 shows that the energy of maxima with intensities larger than 10–15 for HH-polarization, which correspond to spikes, is not small compared to low intensity modulation maxima. In fact, the total energy of spikes with intensities over 10 arb. units is about 35% of the total energy of maxima, although the number of the spikes is just about 2% of the total number of maxima.

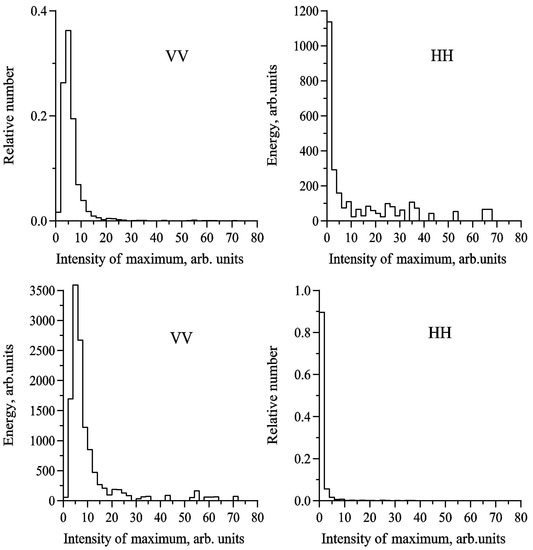
Figure 8. Histograms of local backscatter maxima (top panels) and distributions of total energy of local backscatter maxima within a given intensity interval vs. intensity of local backscatter maximum (bottom panels) at HH-polarization (left column) and VV-polarization (right columns). Wind velocity is 10 m/s, incidence angle 60°.

Similar conclusions can be made from histograms of local intensity maxima and from distribution of energy of the maxima versus their intensity for the case of slick (see, Figure 9). The main difference from the previous case is that the energy contained in spikes is even larger than in the “background” modulation maxima and this effect is stronger for VV-polarization. We can explain this by stronger damping of the Bragg component (contrast about 17, see above) contributing mostly to VV-component in slick compared to NBC which mostly relates to spikes.

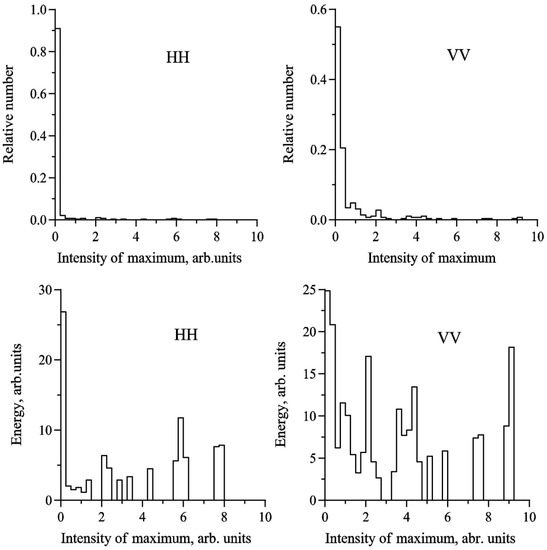
Figure 9. Same as in Figure 8 but for slicks. Wind velocity is 10 m/s, incidence angle of 60°.

3.5. Doppler Shifts of VV and HH-Polarized Backscatter

Let us discuss in more detail radar Doppler shifts and their variations in the presence of long waves. First, we consider histograms of the shifts which are plotted in Figure 10 both for non-slick and slick areas. The width of the shift distributions is determined mostly (but not only, see below) by the orbital velocities of DWW and maxima of the Doppler shift correspond to some mean shift values. It is clearly seen that the mean Doppler shifts at HH-polarization are larger than at VV-polarization both in non-slicks and slicks and the Doppler shift difference in slicks is quite substantial.

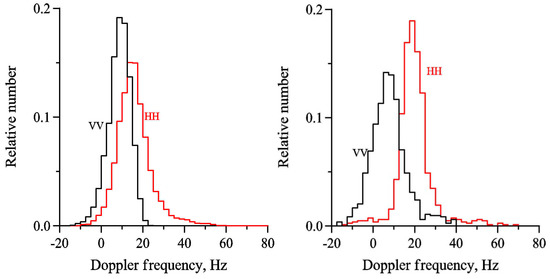
Figure 10. Histograms of radar Doppler shifts in non-slicks (left) and in slicks (right). Wind velocity is 10 m/s.

The difference is negligible in the “background” modulation domain, while the Doppler shifts at HH-polarization in spikes exceed noticeably the shifts at VV-polarization. This result is illustrated by Figure 11, where red symbols denote Doppler shifts in spikes whose intensities are two times larger than the mean backscatter value for HH-polarization. In slicks the Doppler shifts at HH-polarization are systematically larger than at VV-polarization, not only in spikes as for the case of clean water.

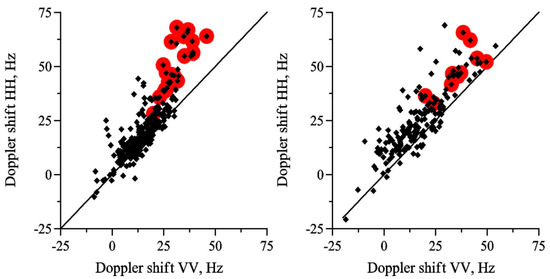
Figure 11. Doppler shifts of HH-polarized backscatter vs. Doppler shifts of VV-polarized radar return for clean water (left) and for slick (right). Red symbols denote Doppler shift in spikes, which intensity is two times greater than the mean HH-backscatter level. Wind velocity is 10 m/s.

From the revealed difference between radar Doppler shifts one can conclude that the scattering mechanisms at VV- and HH-polarizations, and, consequently, formation of NBC and BC are different.

From the revealed distinction between radar Doppler shifts one can conclude that scattering mechanisms at VV- and HH-polarizations, and, consequently, the origin of NBC and BC are different. The arguments supporting a hypothesis of a different nature of BC and NBC can be obtained when estimating the velocities of scatterers responsible for Bragg and non-Bragg scattering. It follows from the data presented above that typical values of radar Doppler shifts F_D in spikes, that is, at the crests of DWW are F_{D_BC} ≈ 35–40 Hz for BC and F_{D_NBC} ≈ 60–65 Hz for NBC. The total velocities ${\overrightarrow{V}}_{\mathsf{\Sigma }}=\overrightarrow{V_s}+{\overrightarrow{U}}_{orb}$ of the scatterers responsible for such Doppler shifts can be retrieved using formula (8) and the BC and NBC velocity values are $V_{\mathsf{\Sigma }\_BC}\approx$ 70–80 cm/s and $V_{\mathsf{\Sigma }\_NBC}\approx$ 120–130 cm/s respectively. Assuming that the Bragg waves propagate according to the dispersion relation of linear gravity-capillary waves and taking into account that the X-band Bragg wavelength at 60° incidence angle is about 2 cm we come to the intrinsic velocity of the Bragg waves $V_{s\_Bragg}=$ 23 cm/s. Then after subtraction of the latter value from the total velocity of BC scatterers the orbital velocity at the crest of DWW can be estimated as ${\overrightarrow{U}}_{orb}\approx$ 47–57 cm/s. The heights $H_{DWW}$ corresponding to such orbital velocities are about $H_{DWW}\approx U_{orb}\cdot T_{DWW}/\pi \approx$ 49–60 cm for DWW of a 3.3 s period. Thus retrieved $H_{DWW}$-values are consistent with those from wave gauge measurements. The intrinsic velocities $V_{s\_NBC}$ of NBC scatterers can be obtained after subtraction the ${\overrightarrow{U}}_{orb}$-values from $V_{\mathsf{\Sigma }}$-values. As a results we come to the values $V_{s\_NBC}\approx$ 63–83 cm/s, so one can conclude that NBC scatterers move with the velocities of gravity waves whose wavelengths are about 25–45 cm.

We believe that the spikes in radar return are associated with strong nonlinearity of short gravity waves of cm-dm-wave lengths. It is known that the profile of short gravity waves is characterized by the presence of some specific nonlinear structures on the wave profile (NSWP)-toe/bulges and parasitic ripples, formed near wave crests [24,25]. Some parts of NSWP can have high slopes and can provide quasi specular scattering of incident microwaves. The slopes /curvature values of NSWP grow very fast with the short gravity wave amplitude/steepness and can be described by a threshold-like dependence. According to [26], NSWP appear when the steepness of short gravity waves is about 0.1–0.12. If the amplitudes of short gravity waves are sufficiently close to the threshold values then the modulation of short gravity waves, for example, due to DWW, even for the case of weak modulation, can result in strong modulation of NSWP. The effect can be characterized as “cascade modulation” which was formerly described in [27] for the case of short wave modulation due to internal waves.

Let us finally discuss polarization ratio modulation over DWW profile which give an additional argument in favour of the hypothesis that non Bragg scattering happens mostly in the areas near the crests of intensive DWW. Instantaneous PR-values in different phases of DWW (different Doppler shifts) are presented in Figure 12. The Polarization Ratio at the smallest Doppler shifts which correspond to DWW troughs tends to large values predicted by Bragg theory, thus demonstrating that in these areas radar backscattering can be described satisfactorily by the Bragg mechanism. At the largest Doppler shifts, that is, at crests of the most intense DWW, where spikes usually exist, the PR-values are close to 1, thus indicating nearly non polarized scattering. The tendency is the same both for the case of clean water and for slicks, as Figure 12 shows. One should note that some PR-values were revealed to be even less than 1, the reason of this is not clear at the moment and the effect needs more detailed investigations.

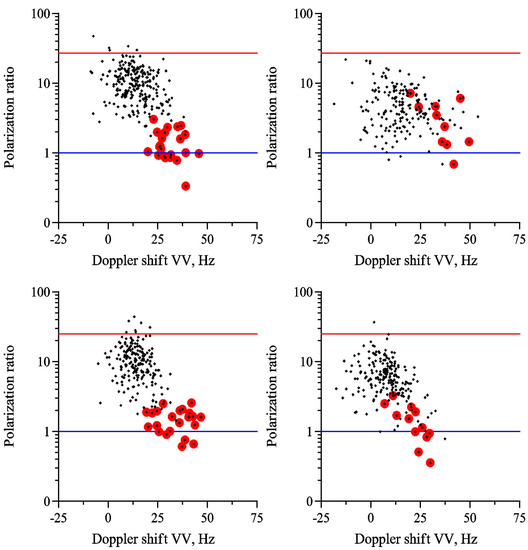
Figure 12. Instantaneous PR-values vs. Doppler shift at VV-polarization for clean water (left) and in slick (right). Red lines are PR-values in Bragg theory, blue line (PR = 1) corresponds to the case of completely non polarized radar return. Incidence angle 60°, wind velocity of 10 m/s (top) and 7 m/s (bottom).

4. Conclusions

Non Bragg scattering of microwaves at moderate incidence angles (of about 60°) and at wind velocities of 7–10 m/s significantly contributes to X-band radar return. The ratio of mean radar returns at VV- and HH-polarizations (PR) varies both for clean water and for slicks in the range from about 20–30 being roughly consistent with Bragg theory, to 1 that corresponds to purely non polarized scattering.

The instantaneous radar backscatter is characterized by the modulation with periods of DWW and by the existence of rare but strong spikes, significantly contributing to the radar backscatter. The spikes at VV- and HH-polarizations have practically the same intensities, thus indicating that radar return in the spikes can be considered as practically nonpolarized. The spikes are mostly pronounced at HH-polarization, while at VV-polarization the spikes are not significantly larger than the “background” modulation with the periods of DWW. The spikes often but not always, occur near the largest maxima of the orbital wave velocity, that is, near the crests of the most intense surface waves. Variations of backscattering in slicks are in general similar to ones in non-slick areas.

Radar Doppler shifts in spikes are normally larger at HH-polarization than at VV-polarization and the difference can be even greater in slicks than outside slicks. From the revealed difference between radar Doppler shifts one can conclude that scattering mechanisms at VV- and HH-polarizations, and, consequently, formation of NBC and BC are different. BC is determined by gravity-capillary Bragg waves (for the considered case of 2-cm wavelength) and its variability can be described in terms of MTF theory. In slick the Bragg waves were damped strongly thus resulting in high contrast values, larger than non-Bragg contrasts. We suppose that spikes in radar return and NBC are in general associated with strong nonlinearity of gravity waves of dm-scale wavelengths, namely with specific nonlinear structures on the wave profile-toe/bulges and parasitic ripples, formed near wave crests. NSWP can have high slopes and can provide quasi specular scattering of incident microwaves. The excitation of NSWP can be described as a threshold-like process. If the amplitudes of short gravity waves are close to the threshold values then even weak modulation of dm-scale gravity waves by DWW can result in strong (“cascade”) modulation of NSWP and appearance of spikes both in HH- and VV-radar backscatter. The spikes remain in slicks if the suppression of dm-scale gravity waves is not sufficient to prevent formation of NSWP. This is a qualitative explanation and the development of a quantitative model of the “cascade” modulation is a subject of future work.

Another unresolved problem left is why VV-polarized radar backscatter in some cases drops below the HH–polarized return, so that PR-values are below unity. This happens mostly for the spikes at DWW crests. At the moment we cannot give any reasonable explanation for this phenomenon, unless we keep up the hypothesis that radar return is a sum of Bragg and non-polarized components. Therefore, further studies are needed to clarify the problem.