Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images
Abstract
1. Introduction
2. Materials
2.1. Study Sites
2.2. Forest Data
2.3. Hemispherical Photographs
2.4. Satellite Image Acquisition and Preprocessing
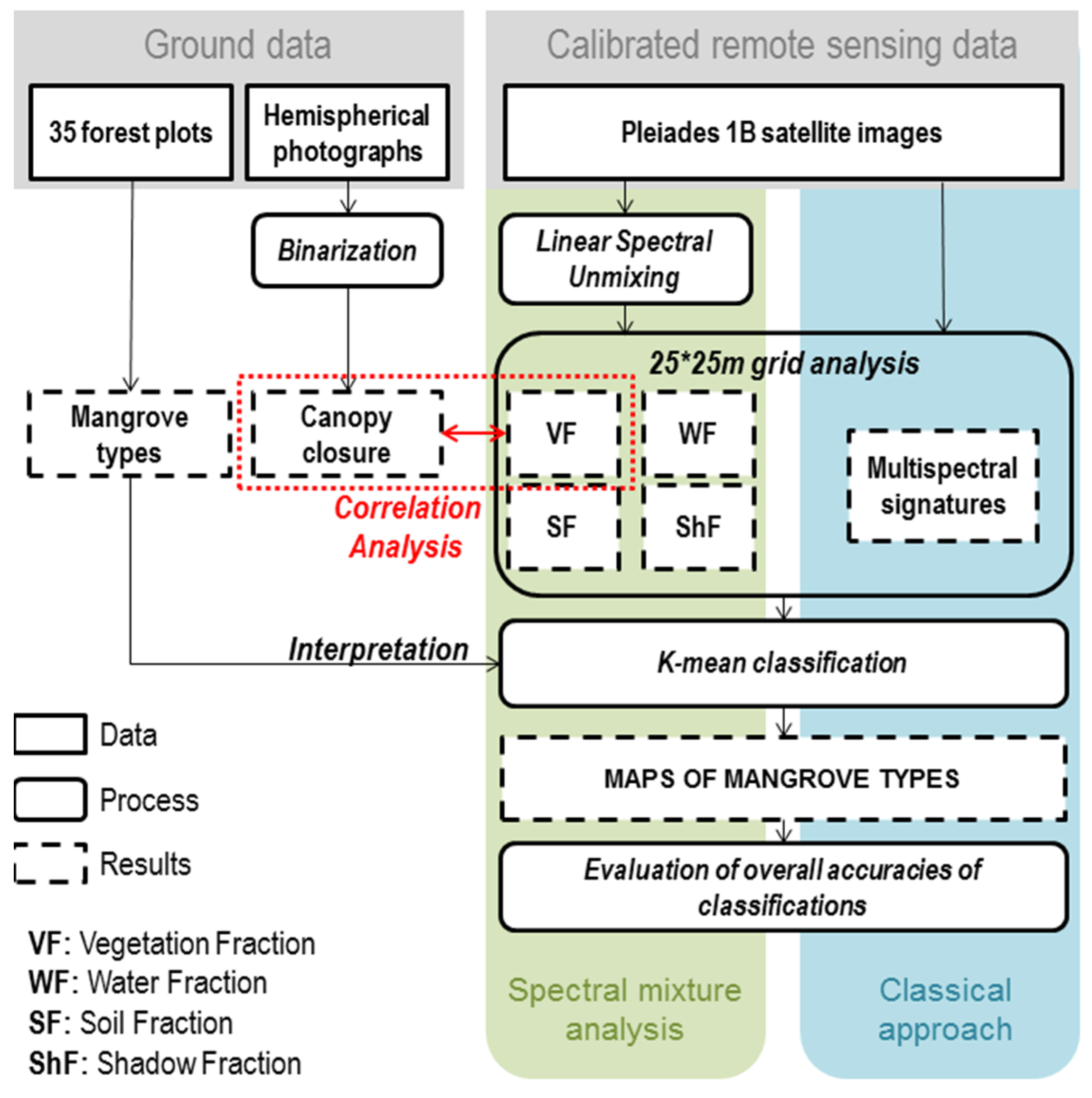
3. Methods
3.1. Fully Constrained Linear Spectral Unmixing (FCLSU)
3.1.1. Endmember Selection
3.1.2. Decomposition of Pixel Spectra according to Endmember Spectral Contributions
3.2. Validation of the FCLSU
3.3. Vegetation Structure Mapping
4. Results
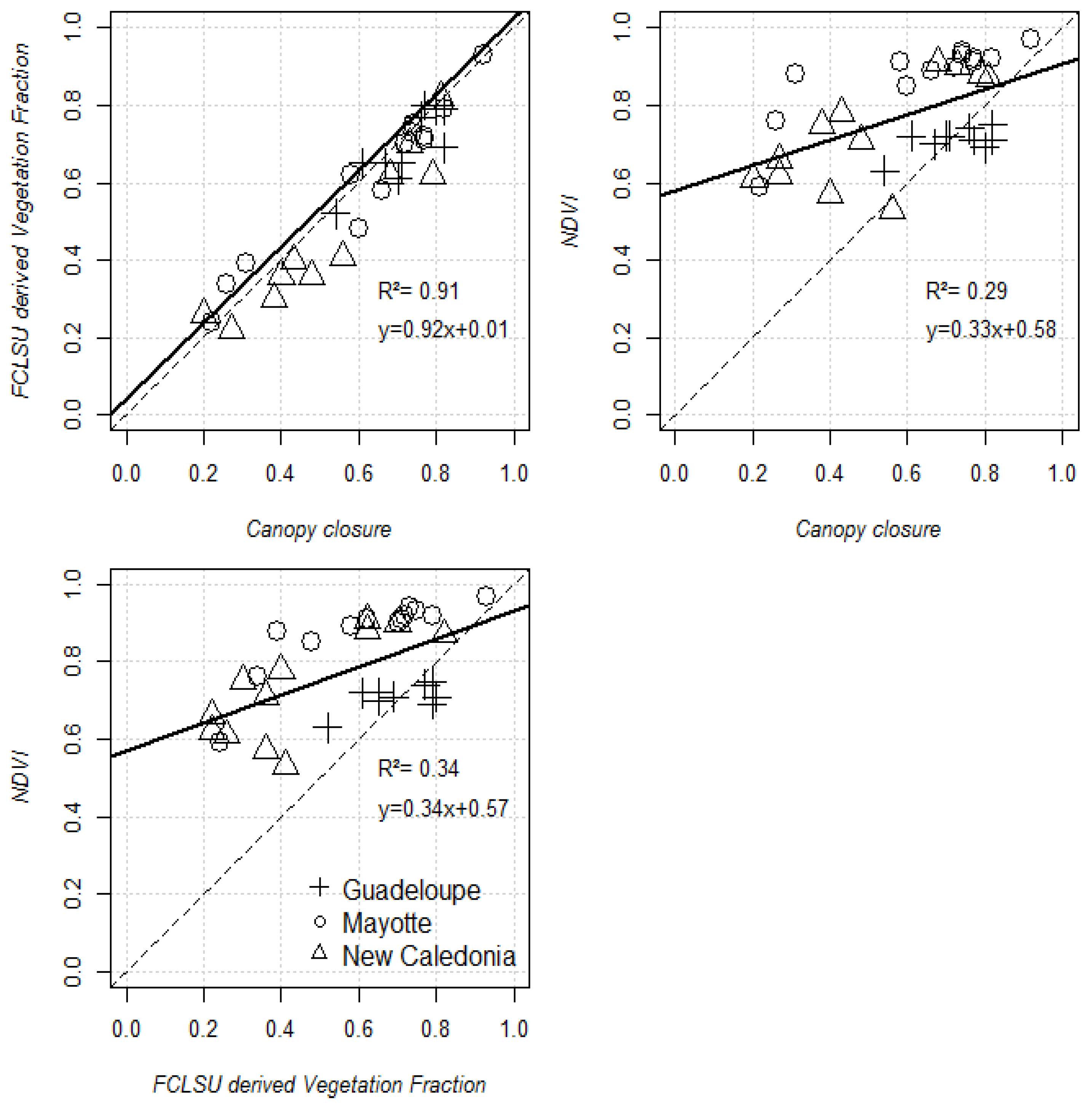
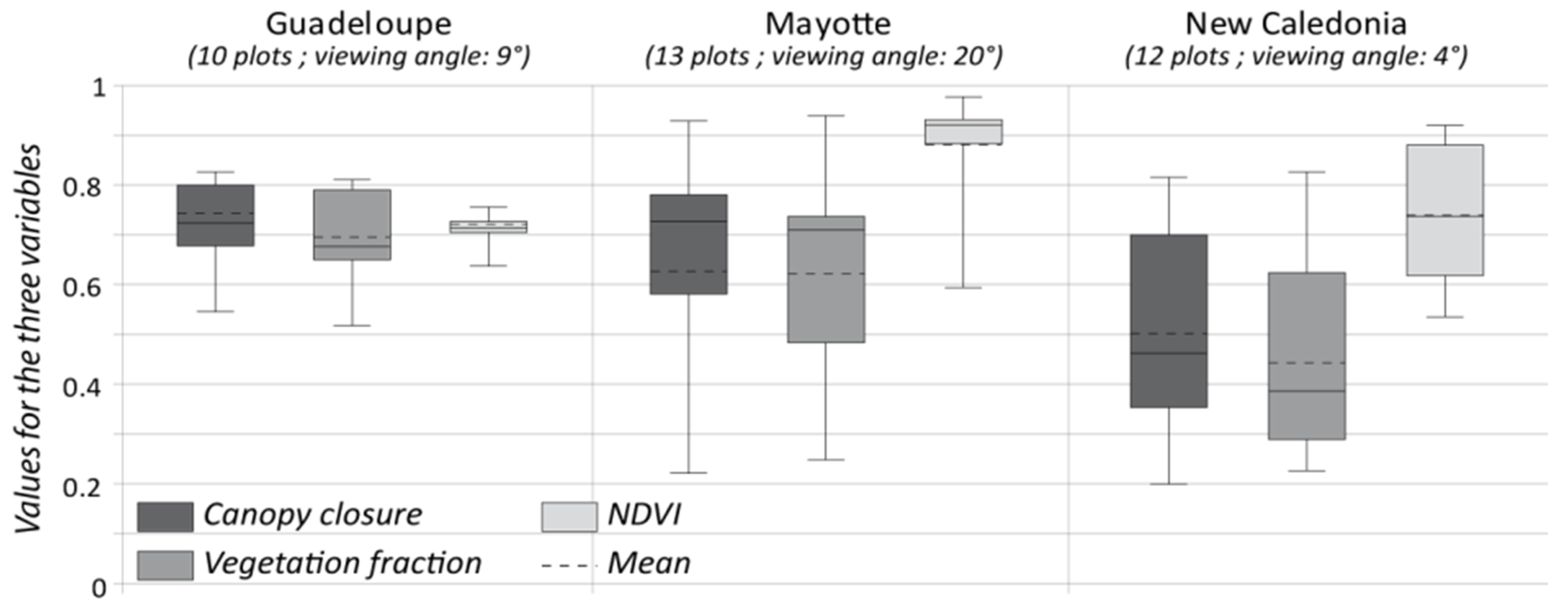
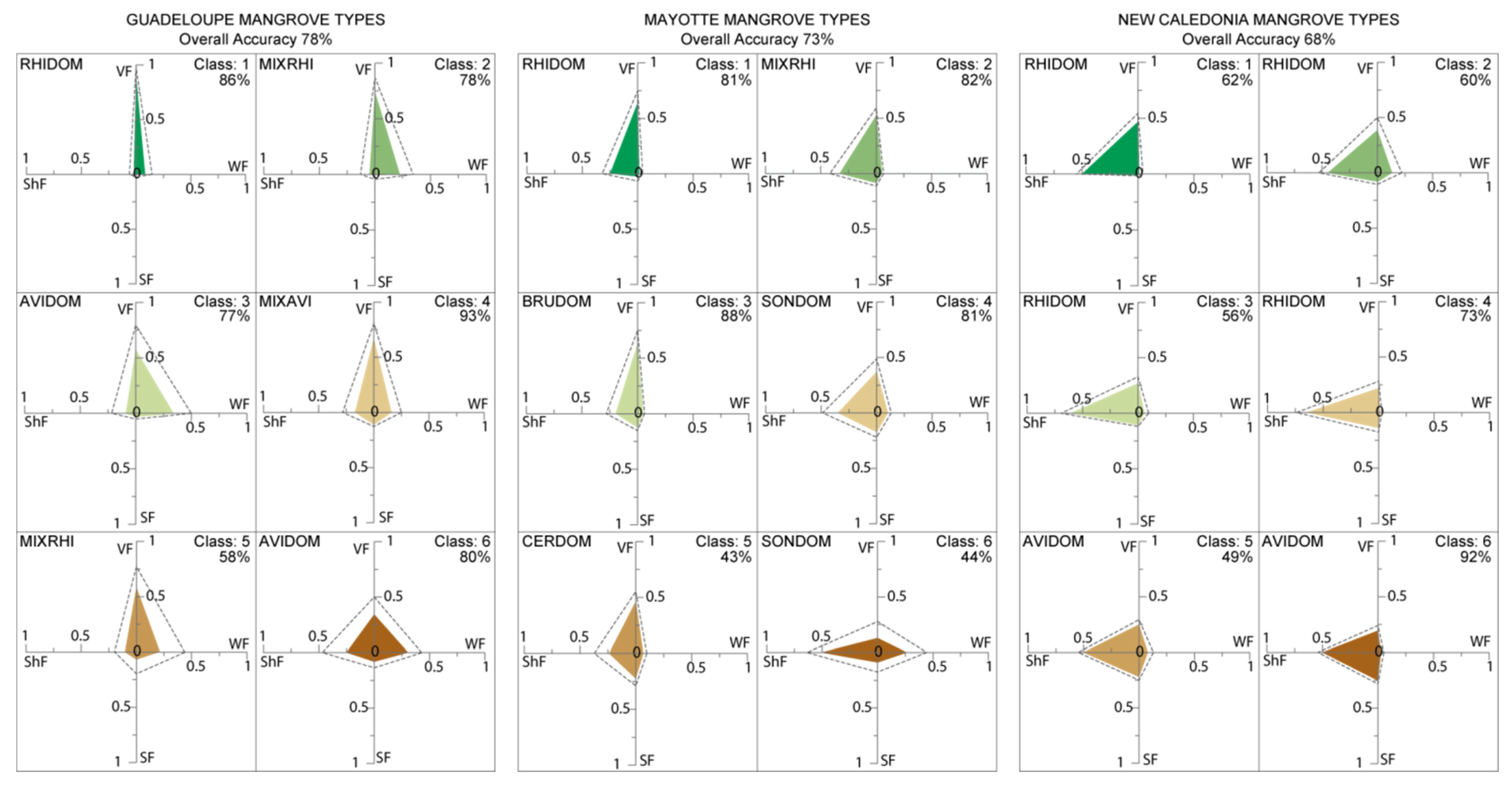
4.1. Performance of the FCLSU Approach for Characterizing Mangrove Forest Structures
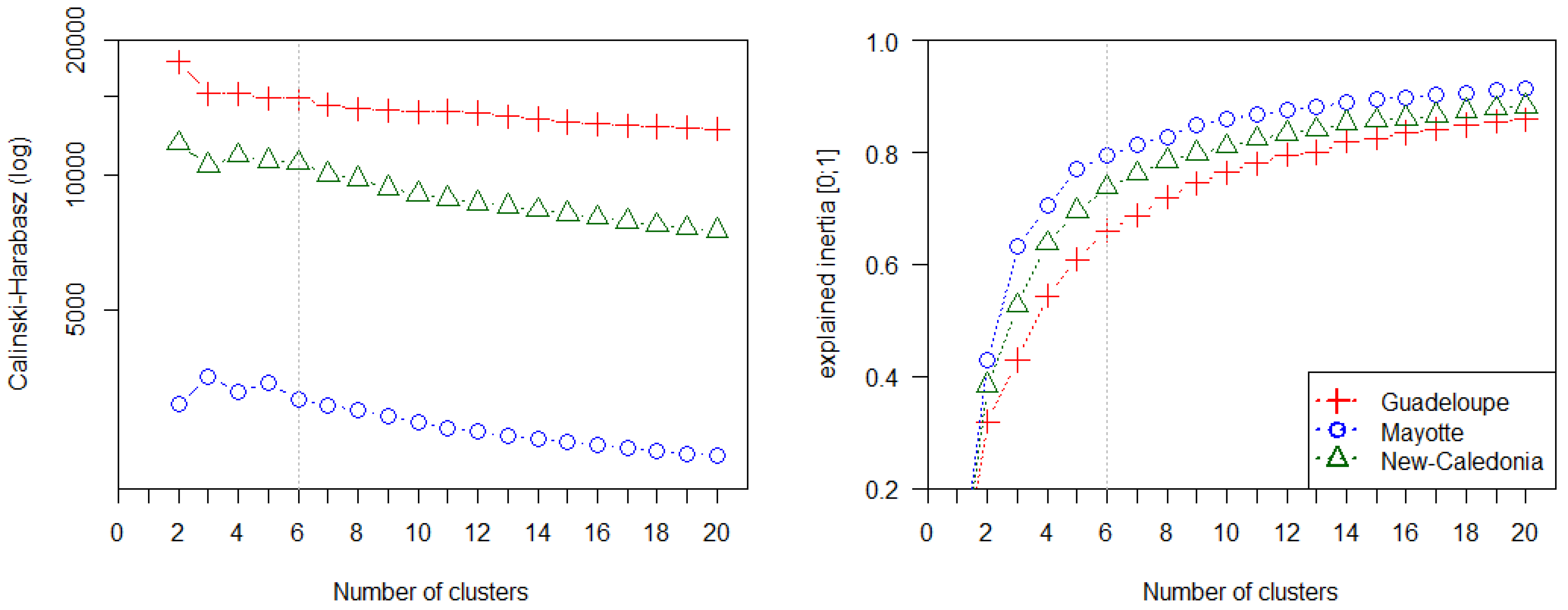
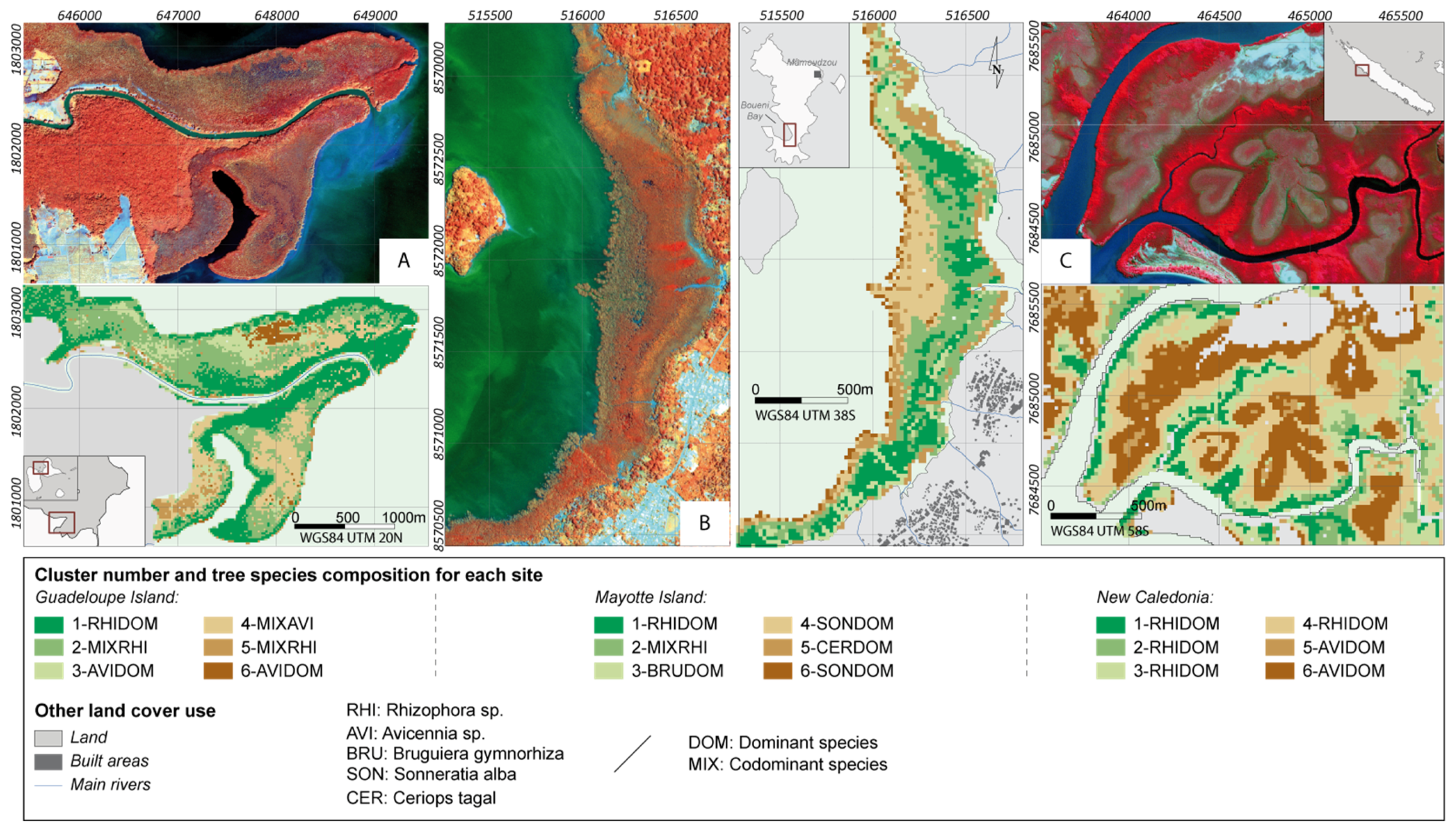
4.2. Potential of Fraction Classification for Mapping Mangrove Forest Structures
4.3. Fraction versus Spectral Classification
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duke, N.C. Mangrove Coast. In Encyclopedia of Marine Geosciences; Harff, J., Meschede, M., Petersen, S., Thiede, J., Eds.; Springer: Berlin, Germany, 2014; pp. 1–17. [Google Scholar]
- Feller, I.C.; Lovelock, C.E.; Berger, U.; McKee, K.L.; Joye, S.B.; Ball, M.C. Biocomplexity in Mangrove Ecosystems. Annu. Rev. Mar. Sci. 2010, 2, 395–417. [Google Scholar] [CrossRef] [PubMed]
- Krauss, K.W.; Lovelock, C.E.; McKee, K.L.; López-Hoffman, L.; Ewe, S.M.; Sousa, W.P. Environmental drivers in mangrove establishment and early development: A review. Aquat. Bot. 2008, 89, 105–127. [Google Scholar] [CrossRef]
- Chapman, V.J. Mangrove Vegetation; Cramer: Vaduz, Liechtenstein, 1976. [Google Scholar]
- Friess, D.A.; Lee, S.Y.; Primavera, J.H. Turning the tide on mangrove loss. Mar. Pollut. Bull. 2016, 109, 673–675. [Google Scholar] [CrossRef] [PubMed]
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Bouillon, S.; Borges, A.V.; Castañeda-Moya, E.; Diele, K.; Dittmar, T.; Duke, N.C.; Kristensen, E.; Lee, S.Y.; Marchand, C.; Rivera-Monroy, V.H.; et al. Mangrove production and carbon sinks: A revision of global budget estimates: Global mangrove carbon budgets. Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Duke, N.C.; Nagelkerken, I.; Agardy, T.; Wells, S.; van Bochove, J.-W. The Importance of Mangroves to People: A Call to Action; United Nations Environment Programme World Conservation Monitoring Centre: Cambridge, UK, 2014. [Google Scholar]
- De Lacerda, L.D. Mangrove Ecosystems: Function and Management; Springer: Berlin, Germany, 2010. [Google Scholar]
- Lee, S.Y.; Primavera, J.H.; Dahdouh-Guebas, F.; McKee, K.; Bosire, J.O.; Cannicci, S.; Diele, K.; Fromard, F.; Koedam, N. Cyril Marchand Ecological role and services of tropical mangrove ecosystems: a reassessment: Reassessment of mangrove ecosystem services. Glob. Ecol. Biogeogr. 2014, 23, 726–743. [Google Scholar] [CrossRef]
- Spalding, M.; Kainuma, M.; Collins, L. World Atlas of Mangroves; Routledge: Abingdon, UK, 2010. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). The World’s Mangroves 1980–2005: A Thematic Study Prepared in the Framework of the Global Forest Resources Assessment 2005; Food and Agriculture Organization of the United Nations: Rome, Italy, 2007. [Google Scholar]
- Ellison, J.C. Vulnerability assessment of mangroves to climate change and sea-level rise impacts. Wetl. Ecol. Manag. 2015, 23, 115–137. [Google Scholar] [CrossRef]
- Ellison, J.; Zouh, I. Vulnerability to Climate Change of Mangroves: Assessment from Cameroon, Central Africa. Biology 2012, 1, 617–638. [Google Scholar] [CrossRef]
- Gilman, E.L.; Ellison, J.; Duke, N.C.; Field, C. Threats to mangroves from climate change and adaptation options: A review. Aquat. Bot. 2008, 89, 237–250. [Google Scholar] [CrossRef]
- Li, S.; Meng, X.; Ge, Z.; Zhang, L. Evaluation of the threat from sea-level rise to the mangrove ecosystems in Tieshangang Bay, Southern China. Ocean Coast. Manag. 2015, 109, 1–8. [Google Scholar] [CrossRef]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Panta, M. Analisys of Forest Canopy Density and Factors Affecting It Using RS and GIS Techniques—A Case Study from Chitwan District of Nepal; International Institue for Geo-Information Science and Earth Observation: Hengelosestraat, The Netherlands, 2003. [Google Scholar]
- Birnbaum, P. Canopy surface topography in a French Guiana forest and the folded forest theory. Plant Ecol. 2001, 153, 293–300. [Google Scholar] [CrossRef]
- Lowman, M.D.; Schowalter, T.; Franklin, J. Methods in Forest Canopy Research; University of California Press: Berkeley, CA, USA, 2012. [Google Scholar]
- Parker, G.G. Structure and microclimate of forest canopies. In Forest Canopies: A Review of Research on a Biological Frontier; Lowman, M., Nadkarni, N., Eds.; Academic Press: San Diego, CA, USA, 1995; pp. 73–106. [Google Scholar]
- Frazer, G.W.; Trofymow, J.A.; Lertzman, K.P. A Method for Estimating Canopy Openness, Effective Leaf Area Index, and Photosynthetically Active Photon Flux Density Using Hemispherical Photography and Computerized Image Analysis Techniques; Canadian Forest Service, Pacific Forestry Centre: Victoria, BC, Canada, 1997. [Google Scholar]
- Smith, M.-L.; Anderson, J.; Fladeland, M. Forest canopy structural properties. In Field Measurements for Forest Carbon Monitoring: A Landscape-Scale Approach; Springer: Berlin, Germany, 2008; pp. 179–196. [Google Scholar]
- Green, E.P.; Clark, C.D.; Mumby, P.J.; Edwards, A.J.; Ellis, A.C. Remote sensing techniques for mangrove mapping. Int. J. Remote Sens. 1998, 19, 935–956. [Google Scholar] [CrossRef]
- Sari, S.P.; Rosalina, D. Mapping and Monitoring of Mangrove Density Changes on tin Mining Area. Procedia Environ. Sci. 2016, 33, 436–442. [Google Scholar] [CrossRef]
- Yuvaraj, E.; Dharanirajan, K.; Saravanan, N.; Karpoorasundarapandian, N. Evaluation of Vegetation Density of the Mangrove Forest in South Andaman Island Using Remote Sensing and GIS Techniques; International Science Congress Association: India, 2014; pp. 19–25. [Google Scholar]
- Garcia-Haro, F.J.; Gilabert, M.A.; Melia, J. Linear spectral mixture modelling to estimate vegetation amount from optical spectral data. Int. J. Remote Sens. 1996, 17, 3373–3400. [Google Scholar] [CrossRef]
- Braun, M.; Martin, H. Mapping imperviousness using NDVI and linear spectral unmixing of ASTER data in the Cologne-Bonn region (Germany). In Proceedings of the SPIE 10th International Symposium on Remote Sensing, Barcelona, Spain, 8–12 September 2003. [Google Scholar]
- Drake, N.A.; Mackin, S.; Settle, J.J. Mapping Vegetation, Soils, and Geology in Semiarid Shrublands Using Spectral Matching and Mixture Modeling of SWIR AVIRIS Imagery. Remote Sens. Environ. 1999, 68, 12–25. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Scarth, P.F.; McVicar, T.R.; Renzullo, L.J.; Malthus, T.J.; Stewart, J.B.; Rickards, J.E.; Trevithick, R. Assessing the effects of site heterogeneity and soil properties when unmixing photosynthetic vegetation, non-photosynthetic vegetation and bare soil fractions from Landsat and MODIS data. Remote Sens. Environ. 2015, 161, 12–26. [Google Scholar] [CrossRef]
- Stagakis, S.; Vanikiotis, T.; Sykioti, O. Estimating forest species abundance through linear unmixing of CHRIS/PROBA imagery. ISPRS J. Photogramm. Remote Sens. 2016, 119, 79–89. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X. Mapping vegetation in an urban area with stratified classification and multiple endmember spectral mixture analysis. Remote Sens. Environ. 2013, 133, 251–264. [Google Scholar] [CrossRef]
- Silvan-Cardenas, J.L.; Wang, L. Fully Constrained Linear Spectral Unmixing: Analytic Solution Using Fuzzy Sets. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3992–4002. [Google Scholar]
- Souza, C. Mapping forest degradation in the Eastern Amazon from SPOT 4 through spectral mixture models. Remote Sens. Environ. 2003, 87, 494–506. [Google Scholar] [CrossRef]
- Ji, M.; Feng, J. Subpixel measurement of mangrove canopy closure via spectral mixture analysis. Front. Earth Sci. 2011, 5, 130–137. [Google Scholar] [CrossRef]
- Tiner, R.W.; Lang, M.W.; Klemas, V.V. Remote Sensing of Wetlands: Applications and Advances; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Haase, D.; Jänicke, C.; Wellmann, T. Front and back yard green analysis with subpixel vegetation fractions from earth observation data in a city. Landsc. Urban Plan. 2019, 182, 44–54. [Google Scholar] [CrossRef]
- Dronova, I. Object-Based Image Analysis in Wetland Research: A Review. Remote Sens. 2015, 7, 6380–6413. [Google Scholar] [CrossRef]
- Fei, S.X.; Shan, C.H.; Hua, G.Z. Remote Sensing of Mangrove Wetlands Identification. Procedia Environ. Sci. 2011, 10, 2287–2293. [Google Scholar] [CrossRef]
- Heumann, B.W. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Proisy, C.; Couteron, P.; Fromard, F. Predicting and mapping mangrove biomass from canopy grain analysis using Fourier-based textural ordination of IKONOS images. Remote Sens. Environ. 2007, 109, 379–392. [Google Scholar] [CrossRef]
- Imbert, D.; Labbé, P.; Rousteau, A. Hurricane damage and forest structure in Guadeloupe, French West Indies. J. Trop. Ecol. 1996, 12, 663–680. [Google Scholar] [CrossRef]
- Herteman, M.; Fromard, F.; Lambs, L. Effects of pretreated domestic wastewater supplies on leaf pigment content, photosynthesis rate and growth of mangrove trees: A field study from Mayotte Island, SW Indian Ocean. Ecol. Eng. 2011, 37, 1283–1291. [Google Scholar] [CrossRef]
- Cremades, C. Cartographie des Habitats Naturels des Mangroves de Mayotte; Direction de l’Agriculture et de la Forêt Service Environnement et Forêt: Mamoudzou, Mayotte, 2010. [Google Scholar]
- Jeanson, M. Morphodynamique du Littoral de Mayotte: des Processus au Réseau de Surveillance; Université du Littoral Côte d’Opale: Dunkerque, France, 2009. [Google Scholar]
- Marchand, C.; Dumas, P. Typologies et Biodiversité des Mangroves de Nouvelle-Calédonie; IRD: Nouméa, Nouvelle-Calédonie, 2007. [Google Scholar]
- Glatthorn, J.; Beckschäfer, P. Standardizing the Protocol for Hemispherical Photographs: Accuracy Assessment of Binarization Algorithms. PLoS ONE 2014, 9, e111924. [Google Scholar] [CrossRef] [PubMed]
- Betbeder, J.; Nabucet, J.; Pottier, E.; Baudry, J.; Corgne, S.; Hubert-Moy, L. Detection and Characterization of Hedgerows Using TerraSAR-X Imagery. Remote Sens. 2014, 6, 3752–3769. [Google Scholar] [CrossRef]
- Betbeder, J.; Hubert-Moy, L.; Burel, F.; Corgne, S.; Baudry, J. Assessing ecological habitat structure from local to landscape scales using synthetic aperture radar. Ecol. Indic. 2015, 52, 545–557. [Google Scholar] [CrossRef]
- Betbeder, J.; Rapinel, S.; Corgne, S.; Pottier, E.; Hubert-Moy, L. TerraSAR-X dual-pol time-series for mapping of wetland vegetation. ISPRS J. Photogramm. Remote Sens. 2015, 107, 90–98. [Google Scholar] [CrossRef]
- Reference Book, eCognition Developer 8.9’; Trimble: Sunnyvale, CA, USA, 2013.
- Lobell, D.B.; Asner, G.P.; Law, B.E.; Treuhaft, R.N. View angle effects on canopy reflectance and spectral mixture analysis of coniferous forests using AVIRIS. Int. J. Remote Sens. 2002, 23, 2247–2262. [Google Scholar] [CrossRef]
- Viennois, G.; Proisy, C.; Feret, J.B.; Prosperi, J.; Sidik, F.; Suhardjono; Rahmania, R.; Longépé, N.; Germain, O.; Gaspar, P. Multitemporal Analysis of High-Spatial-Resolution Optical Satellite Imagery for Mangrove Species Mapping in Bali, Indonesia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3680–3686. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Felde, J.W.; Hoke, M.L.; et al. Atmospheric Correction for Short-wave Spectral Imagery Based on MODTRAN4. Soc. Photo-Opt. Instrum. Eng. 1999, 3753, 61–70. [Google Scholar]
- Adeline, K.R.M.; Chen, M.; Briottet, X.; Pang, S.K.; Paparoditis, N. Shadow detection in very high spatial resolution aerial images: A comparative study. ISPRS J. Photogramm. Remote Sens. 2013, 80, 21–38. [Google Scholar] [CrossRef]
- Heinz, D.C. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Asner, G.P.; Warner, A.S. Canopy shadow in IKONOS satellite observations of tropical forests and savannas. Remote Sens. Environ. 2003, 87, 521–533. [Google Scholar] [CrossRef]
- Dennison, P.E.; Halligan, K.Q.; Roberts, D.A. A comparison of error metrics and constraints for multiple endmember spectral mixture analysis and spectral angle mapper. Remote Sens. Environ. 2004, 93, 359–367. [Google Scholar] [CrossRef]
- Kuusk, A. The Hot Spot Effect in Plant Canopy Reflectance. In Photon-Vegetation Interactions: Applications in Optical Remote Sensing and Plant Ecology; Myneni, R.B., Ross, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 139–159. [Google Scholar]
- Barbier, N.; Proisy, C.; Véga, C.; Sabatier, D.; Couteron, P. Bidirectional texture function of high resolution optical images of tropical forest: An approach using LiDAR hillshade simulations. Remote Sens. Environ. 2011, 115, 167–179. [Google Scholar] [CrossRef]
- Fromard, F.; Vega, C.; Proisy, C. Half a century of dynamic coastal change affecting mangrove shorelines of French Guiana. A case study based on remote sensing data analyses and field surveys. Mar. Geol. 2004, 208, 265–280. [Google Scholar] [CrossRef]
- Ozdemir, I. Linear transformation to minimize the effects of variability in understory to estimate percent tree canopy cover using RapidEye data. GIS Remote Sens. 2014, 51, 288–300. [Google Scholar] [CrossRef]
- Proisy, C.; Féret, J.B.; Lauret, N.; Gastellu-Etchegorry, J.P. Mangrove Forest Dynamics Using Very High Spatial Resolution Optical Remote Sensing A2—Baghdadi, Nicolas. In Land Surface Remote Sensing in Urban and Coastal Areas; Zribi, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 269–295. [Google Scholar]
| Plot ID. | DBH (cm) | Stem Density (Trees.ha−1) | Basal Area (m2.ha−1) | Mean Height (m) | Dominating Species | Canopy Closure (from HP) | Vegetation Fraction | Water Fraction | Soil Fraction | Shadow Fraction | Cluster ID |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G02 | 13 | 1825 | 31 | 4 | A+R | 0.82 | 0.68 | 0.21 | 0.00 | 0.09 | 4 |
| G04 | 7 | 1500 | 9 | 3 | A+R | 0.61 | 0.64 | 0.19 | 0.00 | 0.14 | 2 |
| G05 | 10 | 3900 | 34 | 6 | R | 0.82 | 0.78 | 0.18 | 0.00 | 0.03 | 2 |
| G06 | 7 | 3700 | 19 | 4 | Lr | 0.54 | 0.51 | 0.23 | 0.02 | 0.21 | 4 |
| G09 | 9 | 2100 | 28 | 4 | R | 0.71 | 0.64 | 0.26 | 0.00 | 0.08 | 2 |
| G14 | 5 | 3200 | 13 | 2 | R | 0.8 | 0.78 | 0.12 | 0.09 | 0.00 | 5 |
| G15 | 9 | 3600 | 25 | 7 | R+A | 0.77 | 0.80 | 0.10 | 0.04 | 0.04 | 5 |
| G19 | 6 | 1475 | 7 | 4 | Lr | 0.67 | 0.65 | 0.21 | 0.00 | 0.13 | 2 |
| G20 | 6 | 4125 | 19 | 4 | A+Lr | 0.76 | 0.77 | 0.08 | 0.03 | 0.11 | 1 |
| G21 | 12 | 2400 | 34 | 9 | A+R | 0.7 | 0.60 | 0.16 | 0.00 | 0.22 | 4 |
| M01 | - | 300 | - | 5 | Sa | 0.26 | 0.34 | 0.08 | 0.23 | 0.33 | 5 |
| M02 | 23 | 1400 | 62 | 7 | R | 0.74 | 0.74 | 0.00 | 0.01 | 0.23 | 1 |
| M03 | 21 | 1500 | 90 | 8 | A+R | 0.74 | 0.73 | 0.00 | 0.01 | 0.24 | 1 |
| M06 | 9 | 4300 | 51 | 5 | C+B+R | 0.72 | 0.70 | 0.03 | 0.12 | 0.13 | 3 |
| M07 | 4 | 31,746 | 45 | 3 | C+B+R | 0.77 | 0.70 | 0.02 | 0.06 | 0.19 | 3 |
| M08 | 4 | 46,031 | 57 | 2 | C | 0.6 | 0.48 | 0.05 | 0.18 | 0.27 | 5 |
| M09 | 11 | 1244 | 19 | 4 | R+C | 0.66 | 0.57 | 0.07 | 0.08 | 0.26 | 2 |
| M10 | 11 | 888 | 11 | 7 | R+B+C | 0.58 | 0.62 | 0.0 | 0.03 | 0.29 | 2 |
| M12 | 3 | 3100 | 49 | 5 | R+C+B | 0.92 | 0.93 | 0.00 | 0.00 | 0.06 | 1 |
| M13 | - | 225 | - | 4 | A | 0.22 | 0.24 | 0.06 | 0.50 | 0.18 | 4 |
| M14 | 10 | 2755 | 36 | 4 | C+B+R | 0.82 | 0.79 | 0.02 | 0.06 | 0.12 | 3 |
| M16 | 26 | 1200 | 64 | 10 | R | 0.77 | 0.71 | 0.05 | 0.02 | 0.19 | 1 |
| M17 | - | 250 | - | 4 | A | 0.31 | 0.39 | 0.05 | 0.06 | 0.48 | 5 |
| NC06 | 20 | 1000 | 33 | 5 | R | 0.79 | 0.61 | 0.00 | 0.00 | 0.36 | 1 |
| NC07 | 1 | 18,400 | 2 | 1 | A | 0.27 | 0.22 | 0.01 | 0.18 | 0.57 | 6 |
| NC08 | 2 | 4900 | 2 | 1 | R | 0.38 | 0.29 | 0.04 | 0.14 | 0.51 | 3 |
| NC10 | 4 | 825 | 2 | 2 | R | 0.2 | 0.25 | 0.01 | 0.06 | 0.65 | 4 |
| NC16 | 10 | 2600 | 22 | 3 | R+A | 0.43 | 0.39 | 0.07 | 0.03 | 0.49 | 3 |
| NC17bis | 2 | 24000 | 5 | 1 | A | 0.27 | 0.22 | 0.05 | 0.18 | 0.53 | 6 |
| NC17ter | 6 | 1422 | 4 | 2 | R | 0.48 | 0.35 | 0.00 | 0.04 | 0.59 | 4 |
| NC27 | 18 | 800 | 23 | 6 | B + R | 0.73 | 0.70 | 0.00 | 0.00 | 0.29 | 2 |
| NC28 | 13 | 500 | 7 | 6 | E | 0.68 | 0.62 | 0.03 | 0.01 | 0.32 | 1 |
| NC29 | 7 | 1350 | 16 | 3 | B | 0.56 | 0.40 | 0.02 | 0.10 | 0.46 | 4 |
| NC30 | 6 | 500 | 1 | 3 | Lu | 0.4 | 0.35 | 0.13 | 0.22 | 0.29 | 3 |
| NC31 | 12 | 1400 | 18 | 8 | R | 0.81 | 0.81 | 0.12 | 0.03 | 0.02 | 2 |
| Site | Sensor | Bands Used | Pixel Size | Acquisition Date | High Tide Time | θs (°) | θv (°) | φs-v (°) |
|---|---|---|---|---|---|---|---|---|
| Guadeloupe | 1B | MS | 2 m | 14 December 2013 | 2 h before | 43 | 9 | 25 |
| Mayotte | 1B | MS | 2 m | 18 April 2013 | 2 h after | 33 | 20 | 135 |
| New Caledonia | 1B | MS | 2 m | 27 June 2013 | 1 h before | 51 | 4 | 149 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taureau, F.; Robin, M.; Proisy, C.; Fromard, F.; Imbert, D.; Debaine, F. Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images. Remote Sens. 2019, 11, 367. https://doi.org/10.3390/rs11030367
Taureau F, Robin M, Proisy C, Fromard F, Imbert D, Debaine F. Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images. Remote Sensing. 2019; 11(3):367. https://doi.org/10.3390/rs11030367
Chicago/Turabian StyleTaureau, Florent, Marc Robin, Christophe Proisy, François Fromard, Daniel Imbert, and Françoise Debaine. 2019. "Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images" Remote Sensing 11, no. 3: 367. https://doi.org/10.3390/rs11030367
APA StyleTaureau, F., Robin, M., Proisy, C., Fromard, F., Imbert, D., & Debaine, F. (2019). Mapping the Mangrove Forest Canopy Using Spectral Unmixing of Very High Spatial Resolution Satellite Images. Remote Sensing, 11(3), 367. https://doi.org/10.3390/rs11030367






