Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass
Abstract
:1. Introduction
2. Materials and Methods
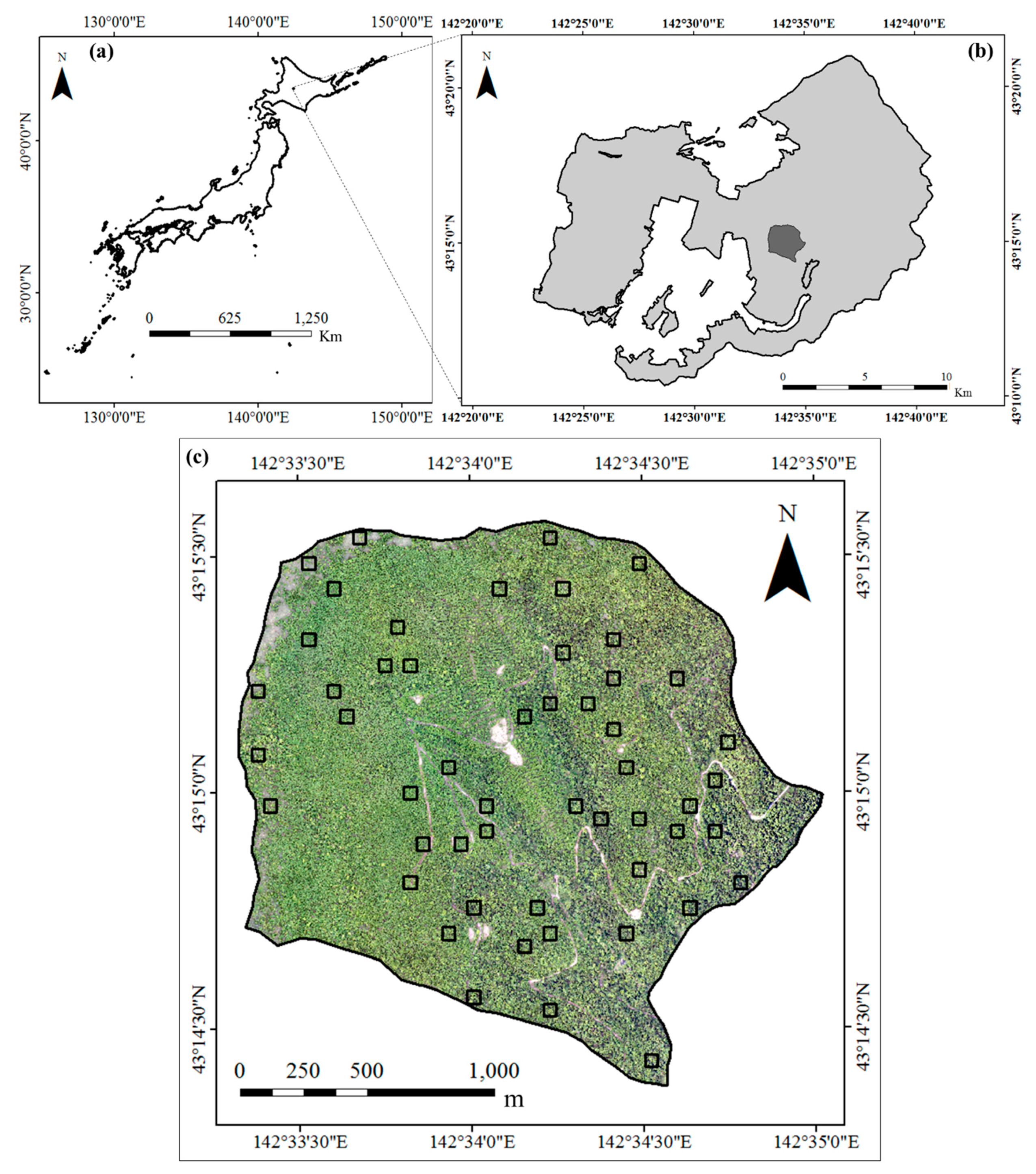
2.1. Study Site
2.2. Data
2.2.1. Field Data
2.2.2. RS Data
2.3. Processing of RS Data
2.3.1. Photogrammetric Processing
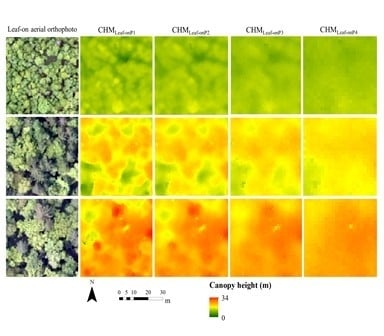
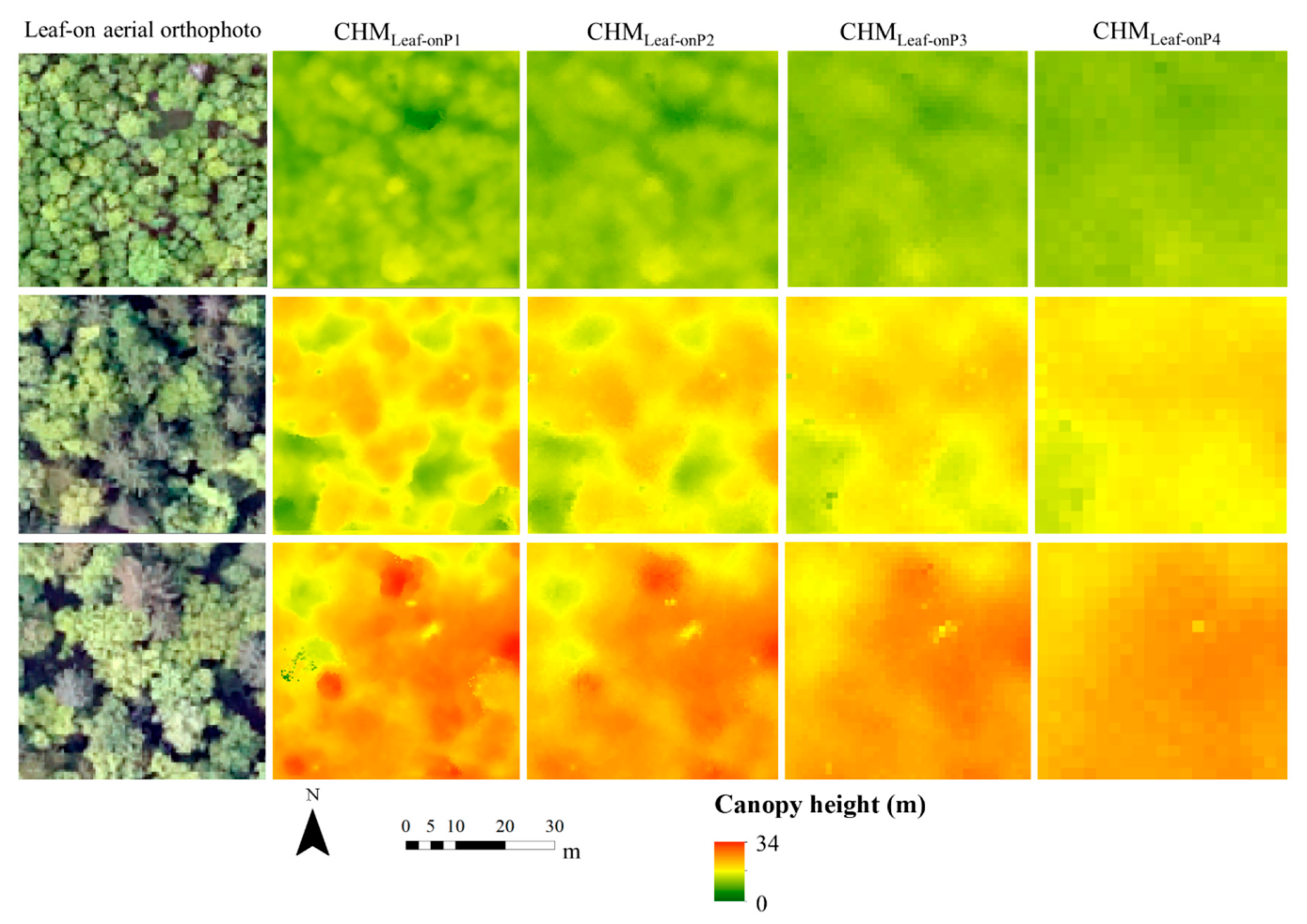
- Leaf-on P1: Built point cloud using downscaled images (original images by a factor of 4);
- Leaf-on P2: Built point cloud using downscaled images (original images by a factor of 16);
- Leaf-on P3: Built point cloud using downscaled images (original images by a factor of 64);
- Leaf-on P4: Built point cloud using downscaled images (original images by a factor of 256).
2.3.2. Development of CHMs and Extraction of Vegetation Metrics from Point Clouds and CHMs
2.4. Estimation of Forest Structural Attributes
2.4.1. Leaf-On Aerial Imagery for Estimation of Forest Structural Attributes in Uneven-Aged Forests
2.4.2. Leaf-Off Aerial Imagery for Forest Attribute Estimation in Uneven-Aged Forests
3. Results
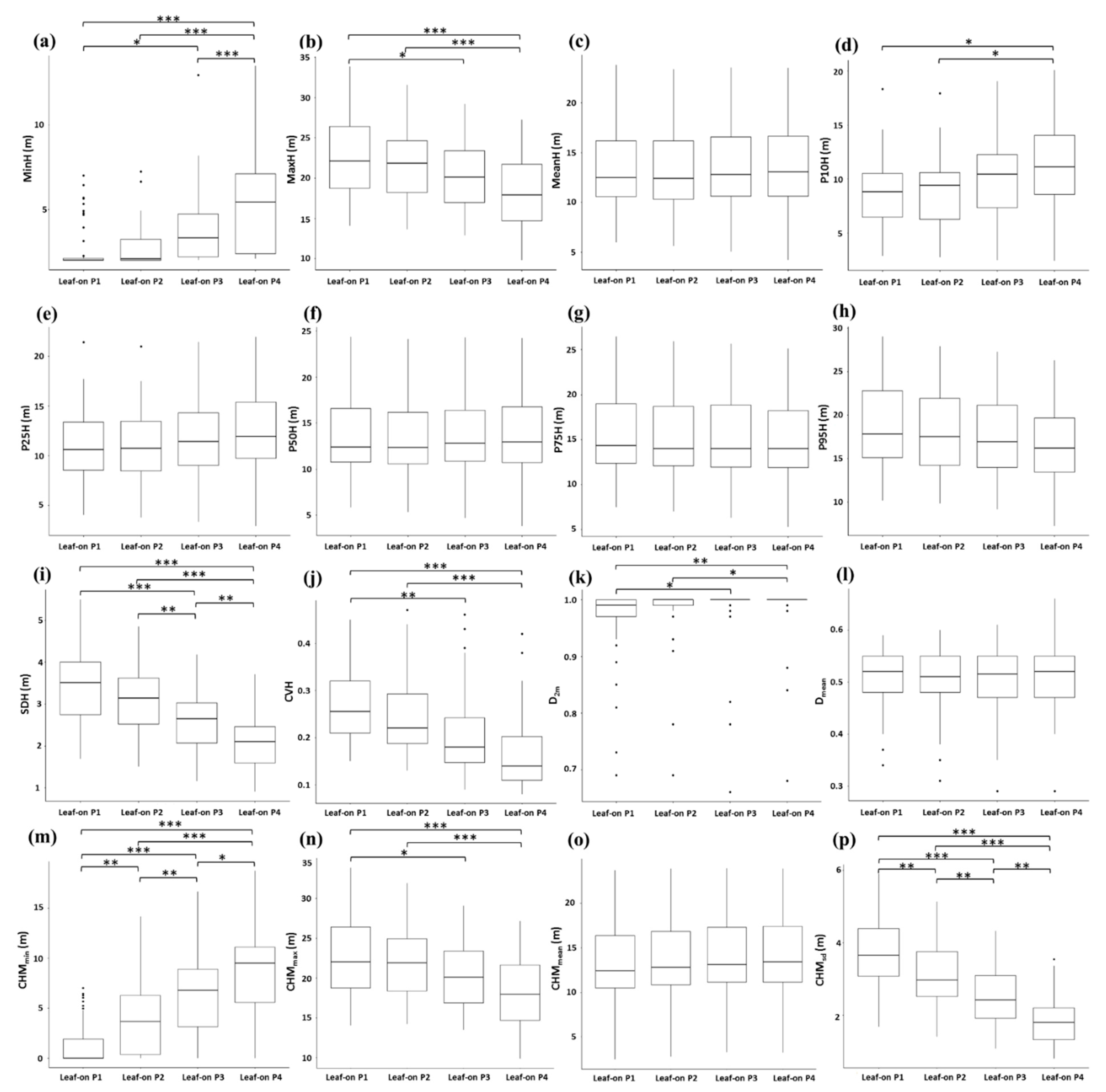
3.1. Reconstruction of Canopy Surface and Derivation of Vegetation Metrics
3.2. Estimation of Plot-Level Forest Structural Attributes
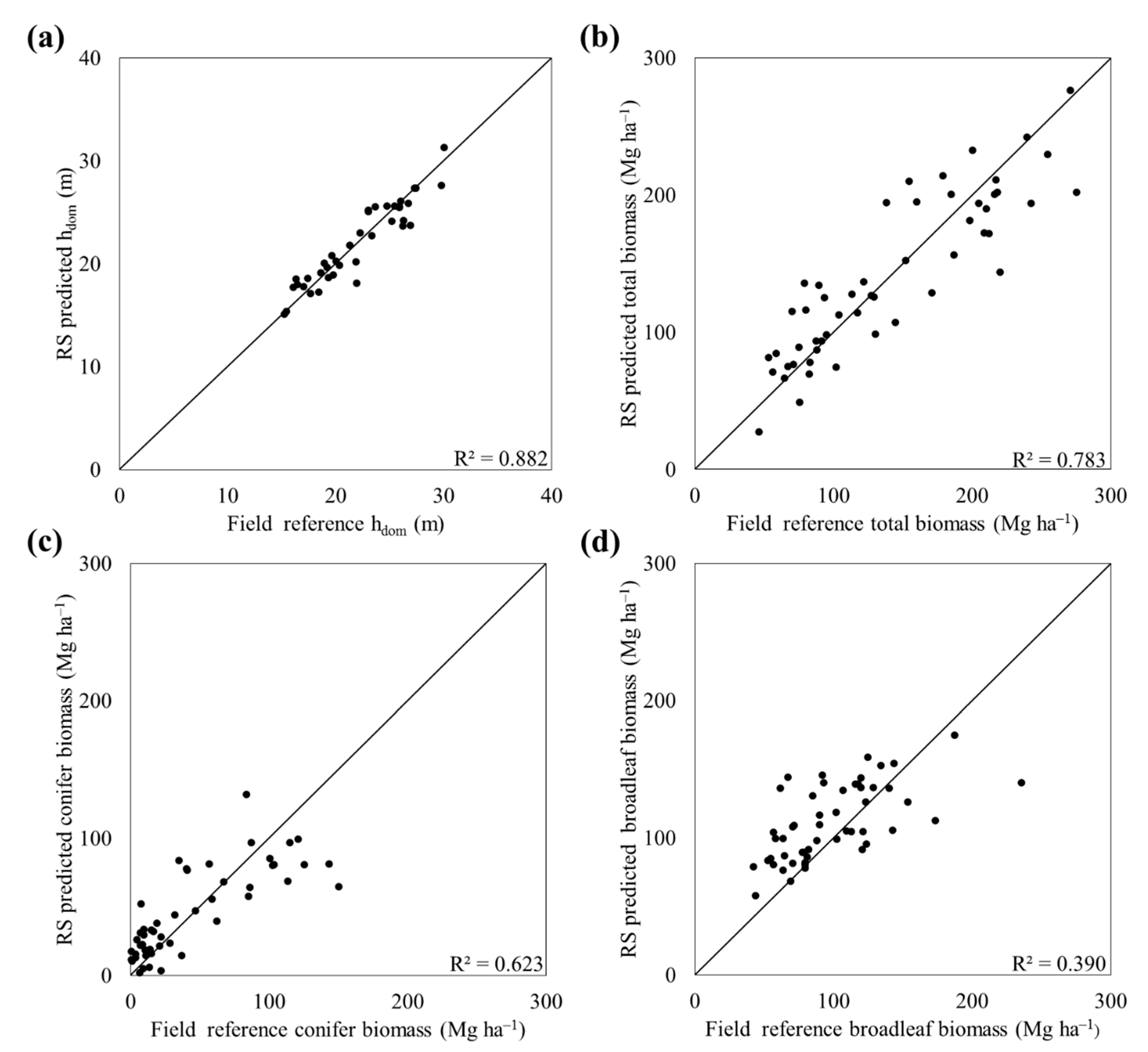
3.2.1. Comparison of the Accuracy of Height and Biomass Estimation Using SLR Modeling for Different Image Downscaling Levels
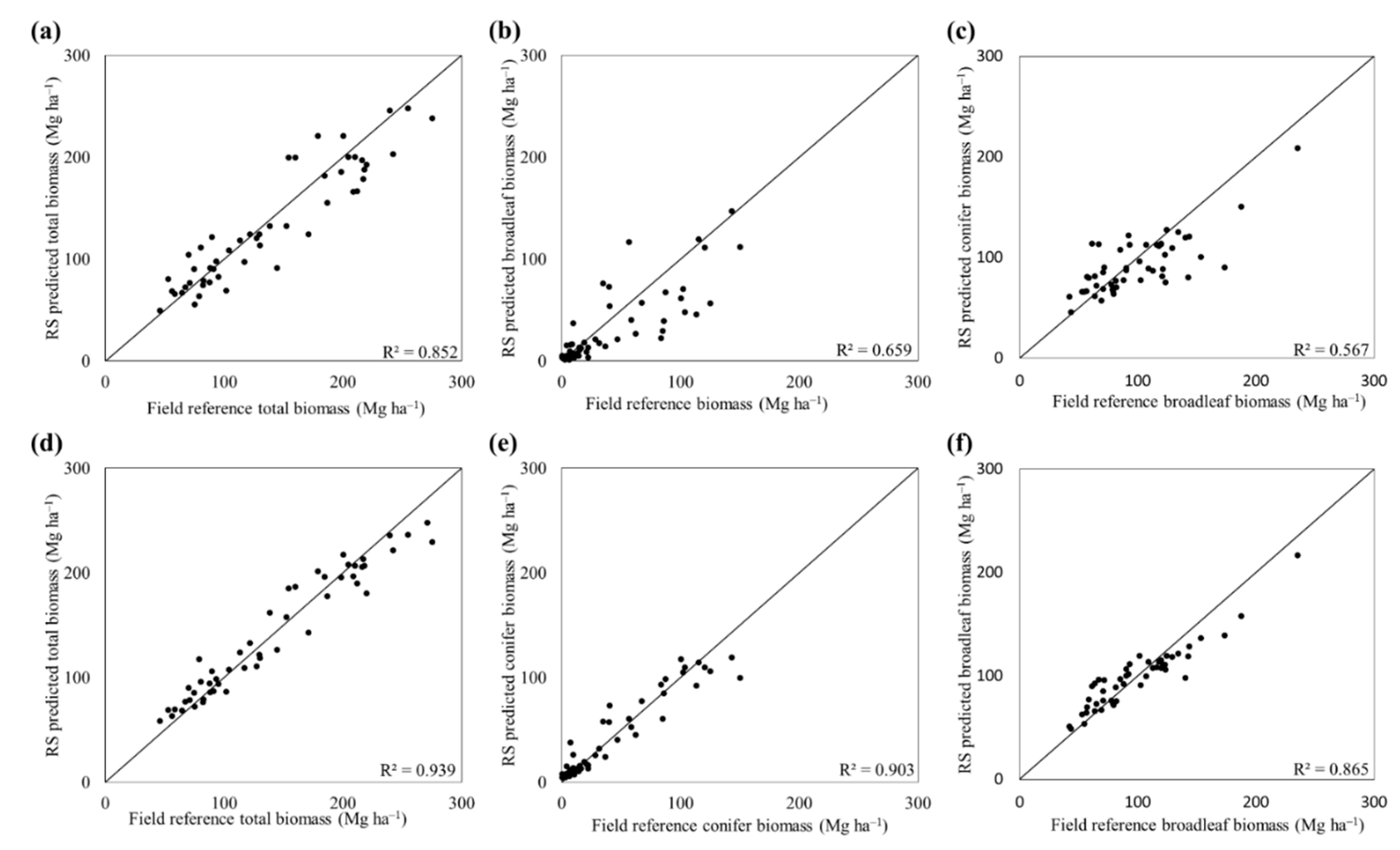
3.2.2. Comparison of the Model Performance in Biomass Estimation
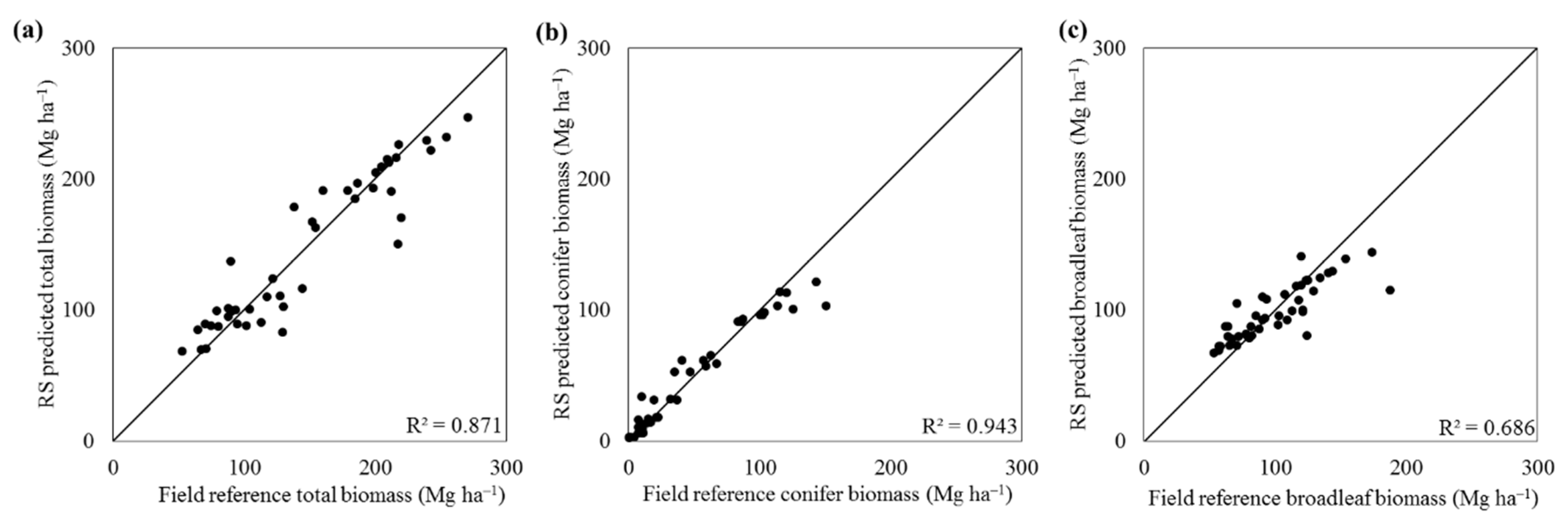
3.2.3. Leaf-Off DAP for Biomass Estimation
4. Discussion
4.1. Reconstruction of 3D Forest Structure Using DAP
4.2. Leaf-On DAP for Biomass Estimation in Uneven-Aged Forests
4.3. Leaf-Off DAP for Biomass Estimation over Uneven-Aged Forests
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erb, K.-H.; Kastner, T.; Plutzar, C.; Bais, A.L.S.; Carvalhais, N.; Fetzel, T.; Gingrich, S.; Haberl, H.; Lauk, C.; Niedertscheider, M.; et al. Unexpectedly large impact of forest management and grazing on global vegetation biomass. Nature 2017, 553, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Millar, C.I.; Stephenson, N.L.; Stephens, S.L. Climate change and forests of the future: Managing in the face of uncertainty. Ecol. Appl. 2007, 17, 2145–2151. [Google Scholar] [CrossRef] [PubMed]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity: Evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- Noss, R.F. Beyond Kyoto: Forest management in a time of rapid climate change. Conserv. Biol. 2001, 15, 578–590. [Google Scholar] [CrossRef]
- Kuuluvainen, T.; Tahvonen, O.; Aakala, T. Even-aged and uneven-aged forest management in boreal fennoscandia: A review. Ambio 2012, 41, 720–737. [Google Scholar] [CrossRef] [PubMed]
- Pukkala, T.; Lähde, E.; Laiho, O.; Salo, K.; Hotanen, J.-P. A multifunctional comparison of even-aged and uneven-aged forest management in a boreal region. Can. J. For. Res. 2011, 41, 851–862. [Google Scholar] [CrossRef]
- Nyland, R. Silviculture: Concepts and Applications; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Hanewinkel, M. Comparative economic investigations of even-aged and uneven-aged silvicultural systems: A critical analysis of different methods. Forestry 2002, 75, 473–481. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: a review. J. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Ma, Z.; Hart, M.M.; Redmond, R.L. Mapping vegetation across large geographic areas: integration of remote sensing and GIS to classify multisource data. Eng. Remote Sens. 2001, 67, 295–307. [Google Scholar]
- Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.A.; Gersonde, R.F.; Franklin, J.F. Examining conifer canopy structural complexity across forest ages and elevations with LiDAR data. Can. J. For. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
- Brosofske, K.D.; Froese, R.E.; Falkowski, M.J.; Banskota, A. A review of methods for mapping and prediction of inventory attributes for operational forest management. For. Sci. 2014, 60, 733–756. [Google Scholar] [CrossRef]
- Wulder, M.A.; Coops, N.C.; Hudak, A.T.; Morsdorf, F.; Nelson, R.F.; Newnham, G.J.; Vastaranta, M. Status and prospects for LiDAR remote sensing of forested ecosystems.pdf. Can. J. Remote Sens. 2013, 39, S1–S5. [Google Scholar] [CrossRef]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manage. 2006, 225, 378–390. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; Alho, P. Advances in forest inventory using airborne laser scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The utility of image-based point clouds for forest inventory: A comparison with airborne laser scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Alonzo, M.; Andersen, H.-E.; Morton, D.; Cook, B. Quantifying boreal forest structure and composition using UAV structure from motion. Forests 2018, 9, 119. [Google Scholar] [CrossRef]
- Puliti, S.; Olerka, H.; Gobakken, T.; Næsset, E. Inventory of small forest areas using an unmanned aerial system. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Järnstedt, J.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Holopainen, M.; Viitala, R. Forest variable estimation using a high-resolution digital surface model. ISPRS J. Photogramm. Remote Sens. 2012, 74, 78–84. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparison of airborne laser scanning and digital stereo imagery for characterizing forest canopy gaps in coastal temperate rainforests. Remote Sens. Environ. 2018, 208, 1–14. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef]
- Aicardi, I.; Garbarino, M.; Lingua, A.; Lingua, E.; Marzano, R.; Piras, M. Monitoring post-fire forest recovery using multi-temporal digital surface models generated from different platforms. EARSeL eProceedings 2016, 15, 1–8. [Google Scholar] [CrossRef]
- Tenenbaum, D.E.; Band, L.E.; Kenworthy, S.T.; Tague, C.L. Analysis of soil moisture patterns in forested and suburban catchments in Baltimore using high-resolution photogrammetric and LiDAR digital elevation datasets. Hydrol. Process. An Int. J. 2006, 240, 219–240. [Google Scholar] [CrossRef]
- Pierzchała, M.; Talbot, B.; Astrup, R. Estimating soil displacement from timber extraction trails in steep terrain: Application of an unmanned aircraft for 3D modelling. Forests 2014, 5, 1212–1223. [Google Scholar] [CrossRef]
- Albertz, J. A Look Back: 140 Years of Photogrammetry. Photogramm. Eng. Remote Sens. 2007, 73, 504–506. [Google Scholar]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Mlambo, R.; Woodhouse, I.H.; Gerard, F.; Anderson, K. Structure from motion (SfM) photogrammetry with drone data: A low cost method for monitoring greenhouse gas emissions from forests in developing countries. Forests 2017, 8, 68. [Google Scholar] [CrossRef]
- Leberl, F.; Irschara, A.; Pock, T.; Meixner, P.; Gruber, M.; Scholz, S.; Wiechert, A. Point Clouds: Lidar versus 3D Vision. Photogramm. Eng. Remote Sens. 2010, 76, 1123–1134. [Google Scholar]
- Wolf, P.R.; Dewitt, B.A. Elements of Photogrammetry: With Applications in Gis, 3rd ed.; McGraw-Hill: New York, NY, USA, 2000; Volume 3, ISBN 0-07-292454-3. [Google Scholar]
- Kasser, M.; Egels, Y. Digital Photogrammetry, 2nd ed.; Taylor & Francis: London, UK, 2002; ISBN 978-3-662-50462-8. [Google Scholar]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Gobakken, T.; Bollandsås, O.M.; Næsset, E. Comparing biophysical forest characteristics estimated from photogrammetric matching of aerial images and airborne laser scanning data. Scand. J. For. Res. 2015, 30, 73–86. [Google Scholar] [CrossRef]
- Bohlin, J. Data Collection for Forest Management Planning Using Stereo Photogrammetry. 2017. Available online: https://pub.epsilon.slu.se/14752/ (accessed on 7 February 2019).
- White, J.; Stepper, C.; Tompalski, P.; Coops, N.; Wulder, M.A. Comparing ALS and image-based point cloud metrics and modelled forest inventory attributes in a complex coastal forest environment. Forests 2015, 6, 3704–3732. [Google Scholar] [CrossRef]
- Kachamba, D.J.; Ørka, H.O.; Gobakken, T.; Eid, T.; Mwase, W. Biomass estimation using 3D data from unmanned aerial vehicle imagery in a tropical woodland. Remote Sens. 2016, 8, 968. [Google Scholar] [CrossRef]
- Cunliffe, A.M.; Brazier, R.E.; Anderson, K. Ultra-fine grain landscape-scale quantification of dryland vegetation structure with drone-acquired structure-from-motion photogrammetry. Remote Sens. Environ. 2016, 183, 129–143. [Google Scholar] [CrossRef]
- Puliti, S.; Ene, L.T.; Gobakken, T.; Næsset, E. Use of partial-coverage UAV data in sampling for large scale forest inventories. Remote Sens. Environ. 2017, 194, 115–126. [Google Scholar] [CrossRef]
- Fryer, J.; Mclntosh, K. Enhancement of Image Resolution rn Digital Photogrammetry. Available online: https://bit.ly/2MVdR8Z (accessed on 10 February 2019).
- Li, A.; Dhakal, S.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Lidar aboveground vegetation biomass estimates in shrublands: Prediction, uncertainties and application to coarser scales. Remote Sens. 2017, 9, 903. [Google Scholar] [CrossRef]
- Bohlin, J.; Bohlin, I.; Jonzén, J.; Nilsson, M. Mapping forest attributes using data from stereophotogrammetry of aerial images and field data from the national forest inventory. Silva Fenn. 2017, 51, 1–18. [Google Scholar] [CrossRef]
- Tatewaki, M. Forest Ecology of the Islands of. J. Fac. Agric. Hokkaido Univ. 1958, 50, 371–486. [Google Scholar]
- The 13th education and research plan of the university of Tokyo Hokkaido forest (2011–2020). Available online: https://repository.dl.itc.u-tokyo.ac.jp/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=26186&item_no=1&page_id=28&block_id=31 (accessed on 8 February 2019).
- Brief on national forest inventory (NFI), Japan; Rome, 2007; MAR-SFM Working Paper 19/2007. Available online: http://www.fao.org/docrep/016/ap187e/ap187e.pdf (accessed on 8 February 2019).
- Commonwealth Forestry Association. The commonwealth forestry review; 57 (3). 1978. Available online: https://www.jstor.org/stable/42607466?seq=1#page_scan_tab_contents (accessed on 8 February 2019).
- Maezawa, K.; Fukushima, Y.; Nakagawa, I.; Kawahara, S. A report on volume table for broad-leaved trees of Tokyo University Forest in Hokkaido. Misc. Inf. Tokyo Univ. For. 1968, 17, 77–100. [Google Scholar]
- Maezawa, K.; Kawahara, S. A preparation of the volume table for Saghalien Fir (Abies sachalinensis) trees of the University Forest in Hokkaido. Bull. Tokyo Univ. For. 1986, 74, 17–37. [Google Scholar]
- National Institute for Environmental Studies. National Greenhouse Gas Inventory Report of Japan 2017. Available online: http://www.cger.nies.go.jp/publications/report/i134/i134.pdf (accessed on 8 February 2019).
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground biomass estimation using structure from motion approach with aerial photographs in a seasonal tropical forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Forest variable estimation using photogrammetric matching of digital aerial images in combination with a high-resolution DEM. Scand. J. For. Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- McGaughey, R. FUSION/LDV: Software for LIDAR Data Analysis and Visualization. Available online: https://bit.ly/2Gl48Zh (accessed on 8 February 2019).
- Jayathunga, S.; Owari, T.; Tsuyuki, S. The use of fixed–wing UAV photogrammetry with LiDAR DTM to estimate merchantable volume and carbon stock in living biomass over a mixed conifer–broadleaf forest. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 767–777. [Google Scholar] [CrossRef]
- Jayathunga, S.; Owari, T.; Tsuyuki, S. Evaluating the Performance of Photogrammetric Products Using Fixed-Wing UAV Imagery over a Mixed Conifer–Broadleaf Forest: Comparison with Airborne Laser Scanning. Remote Sens. 2018, 10, 187. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Probst, A.; Gatziolis, D.; Strigul, N. Intercomparison of photogrammetry software for three-dimensional vegetation modelling. R. Soc. Open Sci. 2018, 5. [Google Scholar] [CrossRef] [PubMed]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Baccini, A.; Friedl, M.A.; Woodcock, C.E.; Warbington, R. Forest biomass estimation over regional scales using multisource data. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Næsset, E.; Økland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Snowdon, P. A ratio estimator for bias correction in logarithmic regression. Can. J. For. Res. 1991, 21, 720–724. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Available online: https://bit.ly/2jNQhzW (accessed on 8 February 2019).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by Random Forest. Available online: https://www.r-project.org/doc/Rnews/Rnews_2002-3.pdf (accessed on 8 February 2019).
- Lisein, J.; Michez, A.; Claessens, H.; Lejeune, P. Discrimination of deciduous tree species from time series of unmanned aerial system imagery. PLoS ONE 2015, 10, 1–20. [Google Scholar] [CrossRef]
- Moudrý, V.; Urban, R.; Štroner, M.; Komárek, J.; Brouček, J.; Prošek, J. Comparison of a commercial and home-assembled fixed-wing UAV for terrain mapping of a post-mining site under leaf-off conditions. Int. J. Remote Sens. 2018, 1–18. [Google Scholar] [CrossRef]
- Carr, J.C.; Slyder, J.B. Individual tree segmentation from a leaf-off photogrammetric point cloud. Int. J. Remote Sens. 2018, 39, 5195–5210. [Google Scholar] [CrossRef]
- Fankhauser, K.E.; Strigul, N.S.; Gatziolis, D. Augmentation of traditional forest inventory and airborne laser scanning with unmanned aerial systems and photogrammetry for forest monitoring. Remote Sens. 2018, 10, 1562. [Google Scholar] [CrossRef]
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal altitude, overlap, and weather conditions for computer vision uav estimates of forest structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef]
- Dandois, J.P.; Baker, M.; Olano, M.; Parker, G.G.; Ellis, E.C. What is the Point? Evaluating the structure, color, and semantic traits of computer vision point clouds of vegetation. Remote Sens. 2017, 9, 355. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. Available online: https://arxiv.org/abs/1511.05741 (accessed on 8 February 2019).
- Kattenborn, T.; Hernández, J.; Lopatin, J.; Kattenborn, G.; Fassnacht, F.E. Pilot study on the retrieval of dbh and diameter distribution of deciduous forest stands using cast shadows in UAV-based orthomosaics. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 93–99. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; de Castro, A.I.; Peña, J.M.; Jiménez-Brenes, F.M.; Arquero, O.; Lovera, M.; López-Granados, F. Mapping the 3D structure of almond trees using UAV acquired photogrammetric point clouds and object-based image analysis. Biosyst. Eng. 2018, 176, 172–184. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Deciduous forest mapping using change detection of multi-temporal canopy height models from aerial images acquired at leaf-on and leaf-off conditions. Scand. J. For. Res. 2016, 31, 517–525. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
| Field Attributes | Unit | Mean (SD) | Range |
|---|---|---|---|
| Dominant height (hdom) | M | 22.0 (4.2) | 15.2–30.0 |
| Mean DBH (D) | Cm | 13.3 (3.9) | 6.5–20.9 |
| Basal area (BA) | m2 ha−1 | 23.1 (8.6) | 7.1–39.7 |
| Living tree biomass (total biomass) | Mg ha−1 | 140 (65.5) | 45.8–275.1 |
| Living biomass of conifer trees (conifer biomass) | Mg ha−1 | 42.1 (43.3) | 0.13–150.1 |
| Living biomass of broadleaf trees (broadleaf biomass) | Mg ha−1 | 98.3 (38.5) | 41.78–235.2 |
| Stem density (N) | ha−1 | 1276 (796) | 228–4636 |
| Data Source | Abbreviation | Description |
|---|---|---|
| Point cloud-derived metrics | MinH | The minimum height of all points within each plot |
| MaxH | The maximum height of all points within each plot | |
| MeanH | The mean height of all points within each plot | |
| P10H, P25H, P50H, P75H, and P95H | 10th, 25th, 50th, 75th, and 95th percentile heights of all points within each plot | |
| SDH | Standard deviation of point height within each plot | |
| CVH | Coefficient of variation of point height within each plot | |
| D2m | Proportion of points with >2-m height relative to the total number of points | |
| Dmean | Proportion of points with >mean height relative to the total number of points | |
| CHM-derived metrics | CHMmin | The minimum value of all pixels within each plot |
| CHMmax | The maximum value of all pixels within each plot | |
| CHMmean | The mean value of all pixels within each plot | |
| CHMsd | The standard deviation of all pixels within each plot |
| Leaf-On P1 | Leaf-On P2 | Leaf-On P3 | Leaf-On P4 | |
|---|---|---|---|---|
| Average point spacing (m) | 0.18 | 0.41 | 0.96 | 2.10 |
| Maximum point spacing (m) | 0.29 | 0.59 | 1.18 | 2.35 |
| Average point density (m−2) | 11.5 | 3.1 | 0.72 | 0.18 |
| Time taken for building point cloud (hours) | ~28 | ~15 | ~4 | ~2 |
| DSM/CHM resolution (m) | 0.30 | 0.60 | 1.2 | 2.4 |
| Forest Structural Attribute | Explanatory Variable | Leaf-On P1 | Leaf-On P2 | Leaf-On P3 | Leaf-On P4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | ||
| hdom | P75 | 0.88 | 6.4 | 0.88 | 6.6 | 0.87 | 6.9 | 0.86 | 7.0 |
| Total biomass | P95 | 0.78 | 21.1 | 0.77 | 21.7 | 0.76 | 22.3 | 0.74 | 23.4 |
| Conifer biomass | P75 | 0.62 | 63.8 | 0.60 | 64.8 | 0.57 | 67.0 | 0.53 | 69.7 |
| Broadleaf biomass | P95 | 0.39 | 33.2 | 0.42 | 29.7 | 0.43 | 31.1 | 0.43 | 29.2 |
| Forest Structural Attribute | Explanatory Variable | Leaf-On P1 | Leaf-On P2 | Leaf-On P3 | Leaf-On P4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | ||
| hdom | CHMmax | 0.83 | 7.7 | 0.80 | 8.3 | 0.78 | 8.7 | 0.75 | 9.3 |
| Total biomass | CHMmax | 0.76 | 22.8 | 0.74 | 23.6 | 0.71 | 24.8 | 0.71 | 24.9 |
| Conifer biomass | CHMmean | 0.54 | 68.9 | 0.54 | 68.9 | 0.53 | 69.8 | 0.52 | 70.4 |
| Broadleaf biomass | CHMmean | 0.35 | 31.4 | 0.35 | 31.2 | 0.36 | 31.1 | 0.37 | 30.8 |
| Forest Structural Attribute | SLR | MLR | RF | |||
|---|---|---|---|---|---|---|
| R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | |
| Total biomass | 0.78 | 21.1 | 0.85 | 18.1 | 0.94 | 12.0 |
| Conifer biomass | 0.62 | 63.8 | 0.66 | 60.5 | 0.90 | 32.1 |
| Broadleaf biomass | 0.39 | 33.2 | 0.57 | 26.3 | 0.87 | 22.7 |
| Forest Structural Attribute | SLR | MLR | RF | |||
|---|---|---|---|---|---|---|
| R2 | %RMSE | R2 | %RMSE | R2 | %RMSE | |
| Total biomass | 0.70 | 23.1 | 0.72 | 22.2 | 0.87 | 15.0 |
| Conifer biomass | 0.64 | 56.3 | 0.71 | 53.2 | 0.94 | 23.8 |
| Broadleaf biomass | 0.28 | 56.7 | 0.30 | 48.3 | 0.69 | 35.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayathunga, S.; Owari, T.; Tsuyuki, S. Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sens. 2019, 11, 338. https://doi.org/10.3390/rs11030338
Jayathunga S, Owari T, Tsuyuki S. Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sensing. 2019; 11(3):338. https://doi.org/10.3390/rs11030338
Chicago/Turabian StyleJayathunga, Sadeepa, Toshiaki Owari, and Satoshi Tsuyuki. 2019. "Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass" Remote Sensing 11, no. 3: 338. https://doi.org/10.3390/rs11030338
APA StyleJayathunga, S., Owari, T., & Tsuyuki, S. (2019). Digital Aerial Photogrammetry for Uneven-Aged Forest Management: Assessing the Potential to Reconstruct Canopy Structure and Estimate Living Biomass. Remote Sensing, 11(3), 338. https://doi.org/10.3390/rs11030338