Calibration of a Ground-Based Array Radar for Tomographic Imaging of Natural Media
Abstract
1. Introduction
- Mutual coupling between antenna elements in the array may produce side-lobes that interfere with the scene reflectivity.
- Magnitude and phase imbalances between antenna elements are usually large enough to completely defocus a rendered scene’s reflectivity.
- The impulse response function of the rendered reflectivity image is space-variant, distorting the scene reflectivity represented by the pixel intensities.
2. Instrument Description
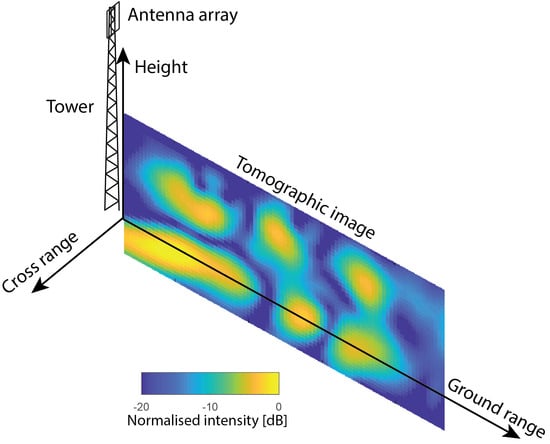
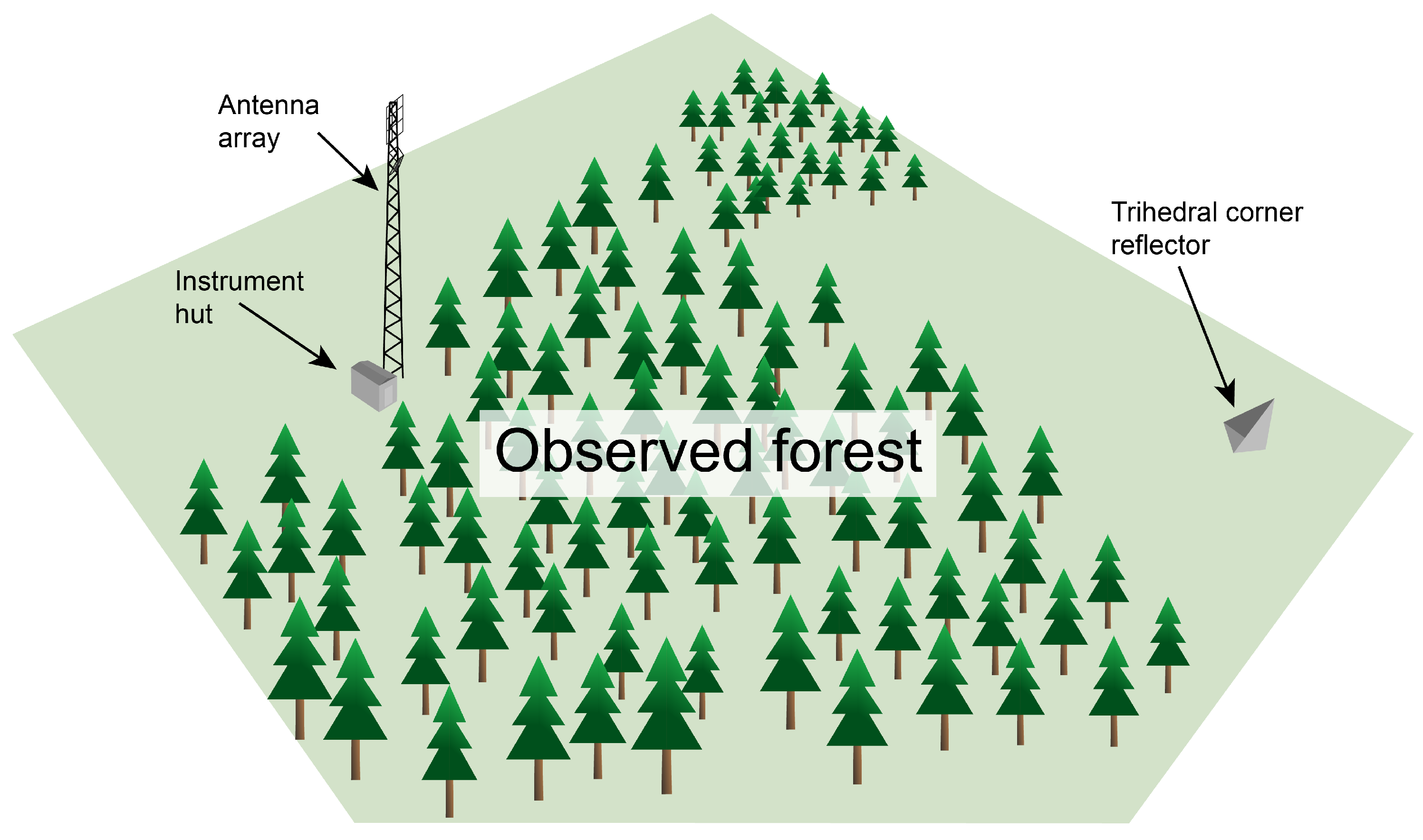
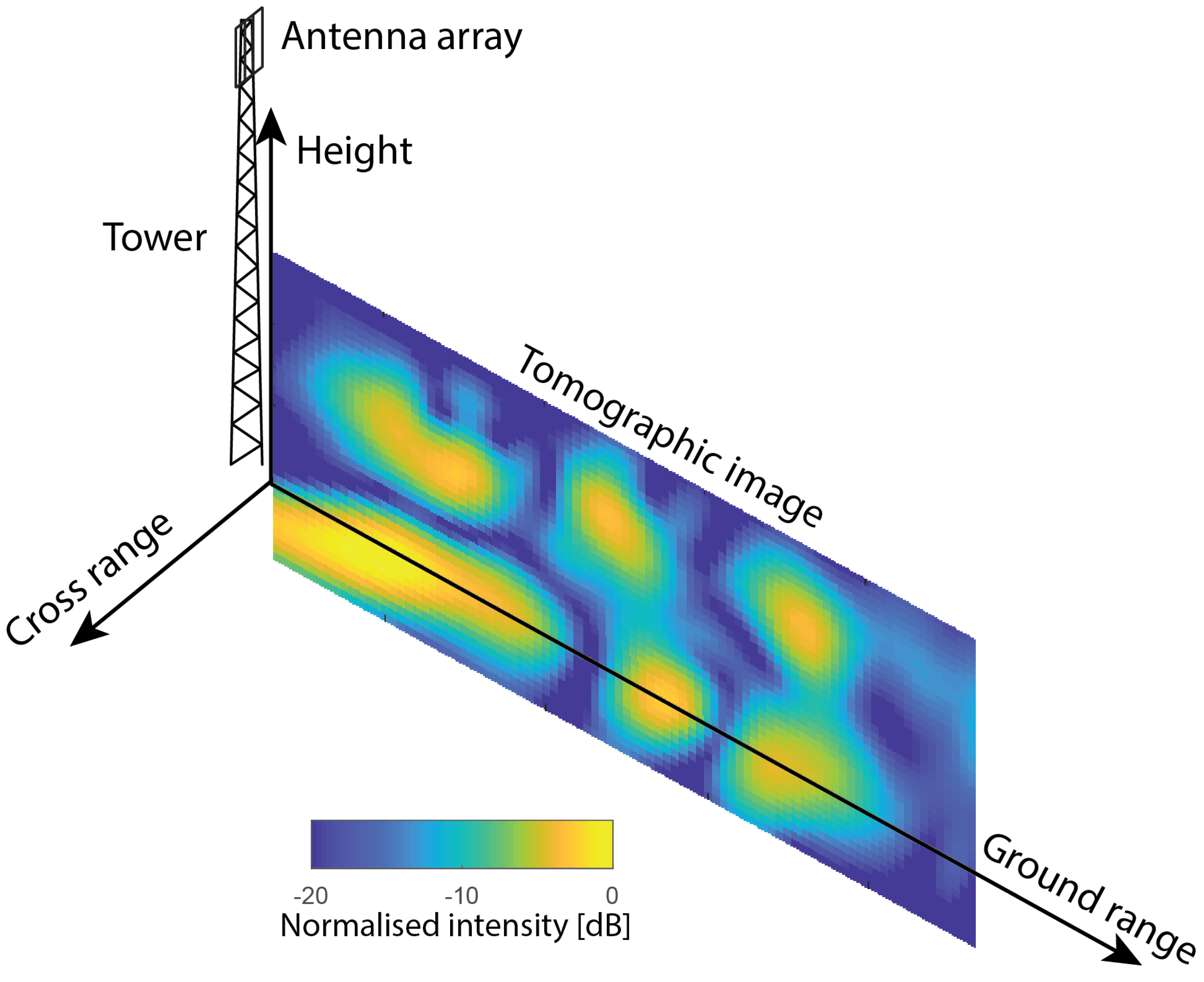
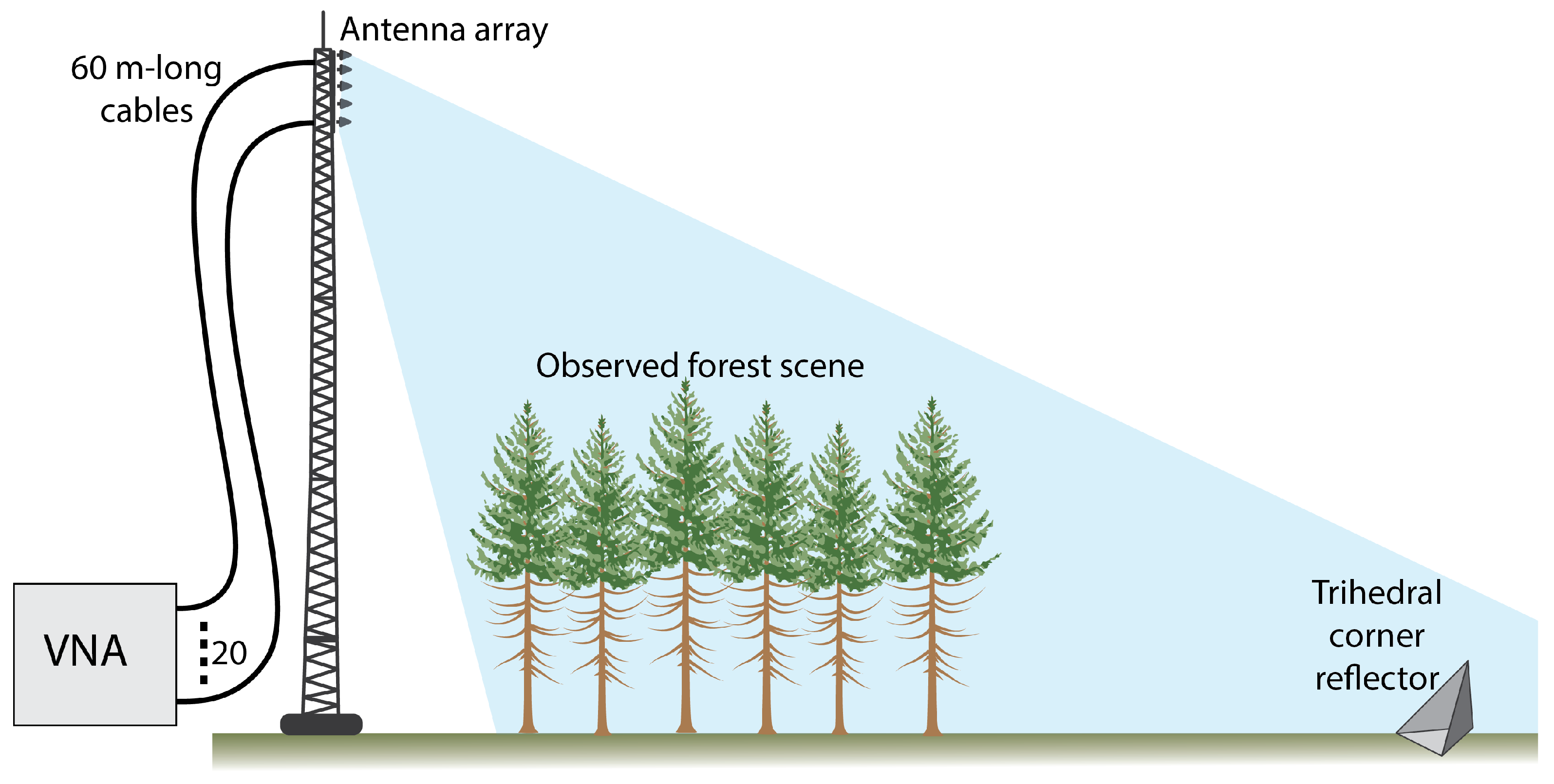
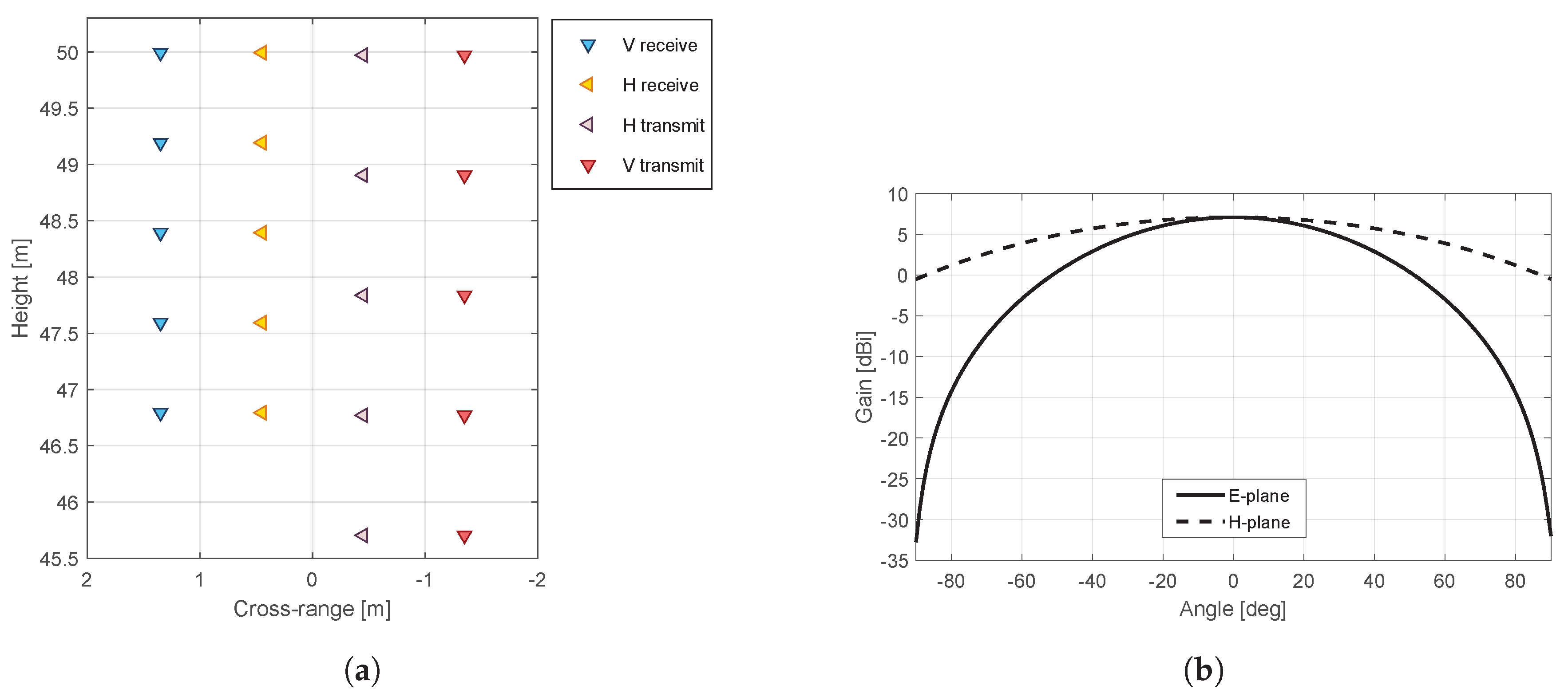
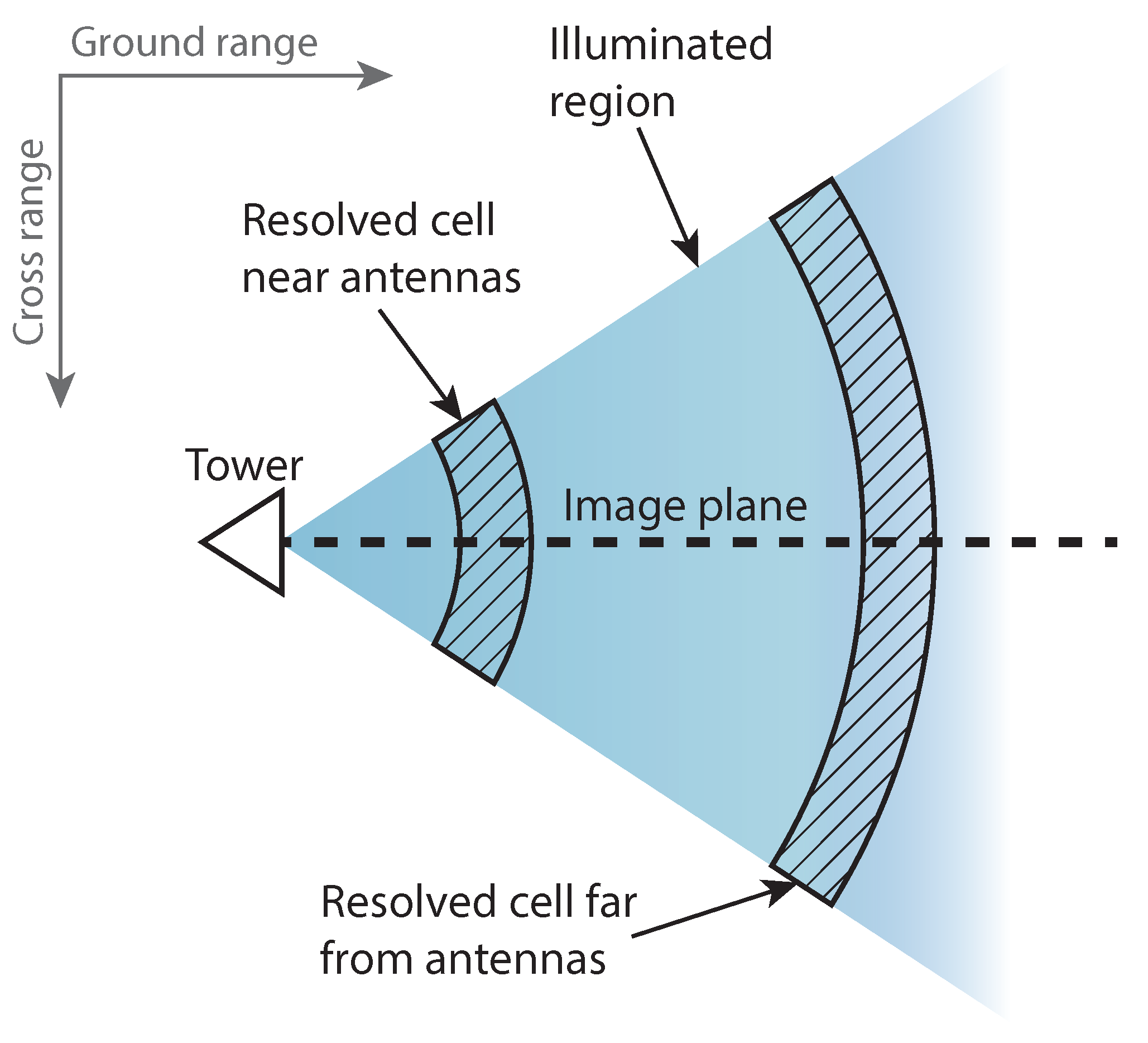
2.1. Observation Geometry
2.2. Radar Instrument
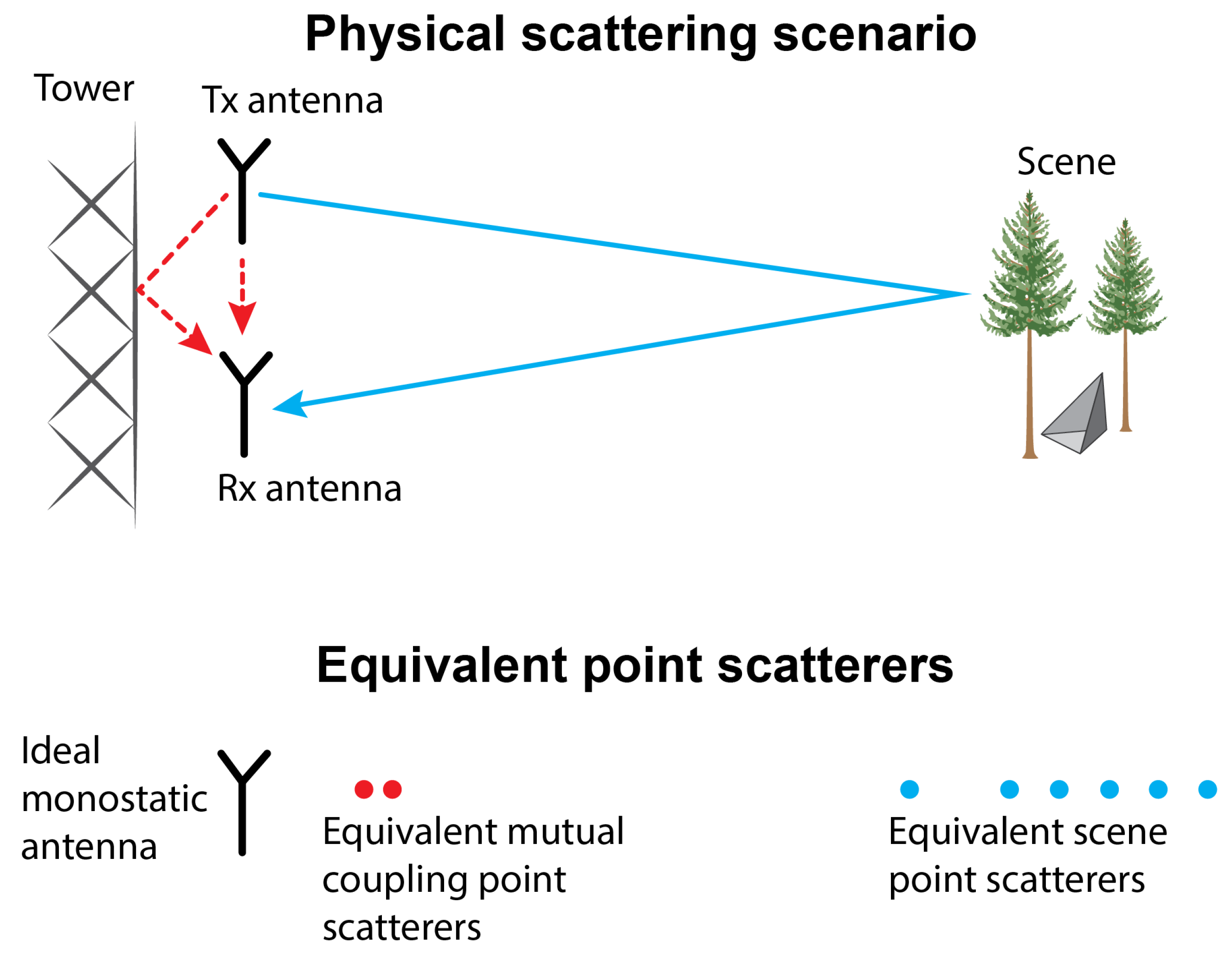
3. Mutual Coupling Suppression
3.1. Signal Model for a Single Channel
3.2. When Mutual Coupling Is a Problem
- The mutual coupling amplitude. A large relative to the scene reflectivity amplitude causes strong interference by mutual coupling. This is the case for BorealScat’s P to L-band observations.
- Signal bandwidth. If B is small, high side-lobes of spread out in range, increasing the interference by mutual coupling. This is the case for BorealScat’s P-band observations.
- Antenna-scene separation. The side-lobe amplitude of decreases with increasing R. A small antenna-scene separation, which is true for most ground-based experiments, increases the interference by mutual coupling.
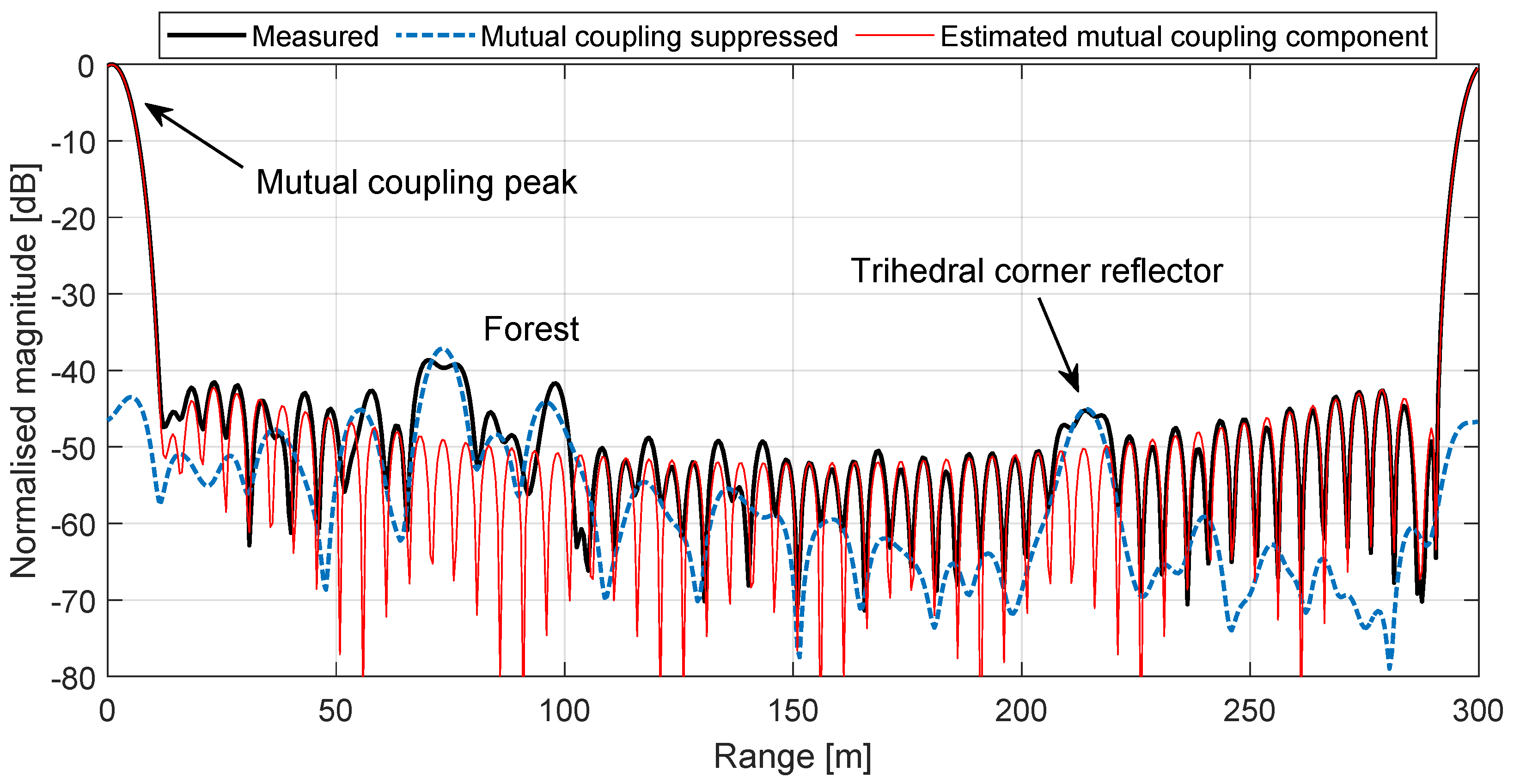
- Unambiguous range. Due to the circular convolution in (4), the mutual coupling peak is repeated at . The side-lobes from this peak may interfere with scatterers near , such as BorealScat’s trihedral corner reflector.
3.3. Mutual Coupling Side-Lobe Suppression
3.4. Range Profiles
4. Magnitude and Phase Error Calibration
4.1. Properties of the Magnitude and Phase Errors
4.2. Calibration between Polarisation Channels Using a Trihedral Corner Reflector
4.3. Model for Single-Channel Observations of a Reference Target
4.4. Model for Multi-Channel Observations of a Reference Target
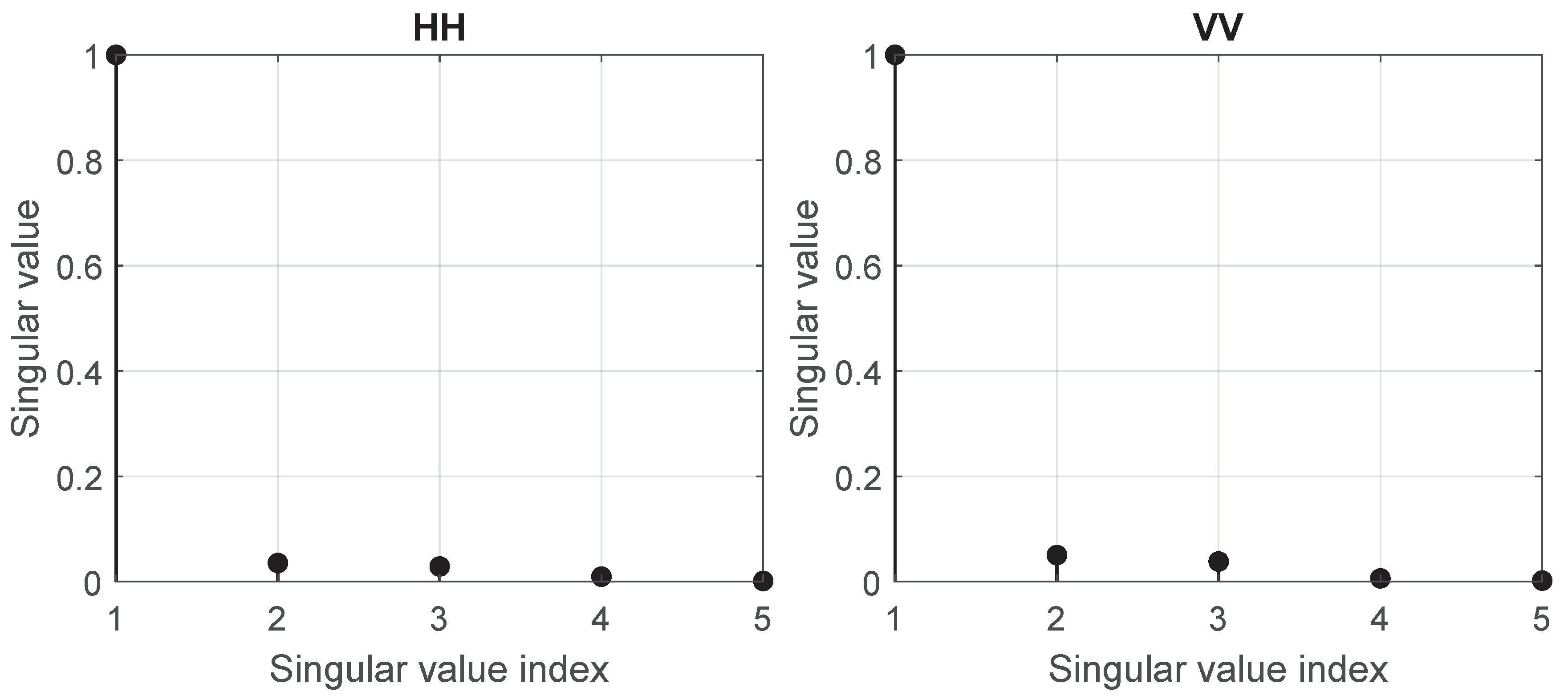
4.5. Decomposition of Co-Polarised Channel Errors
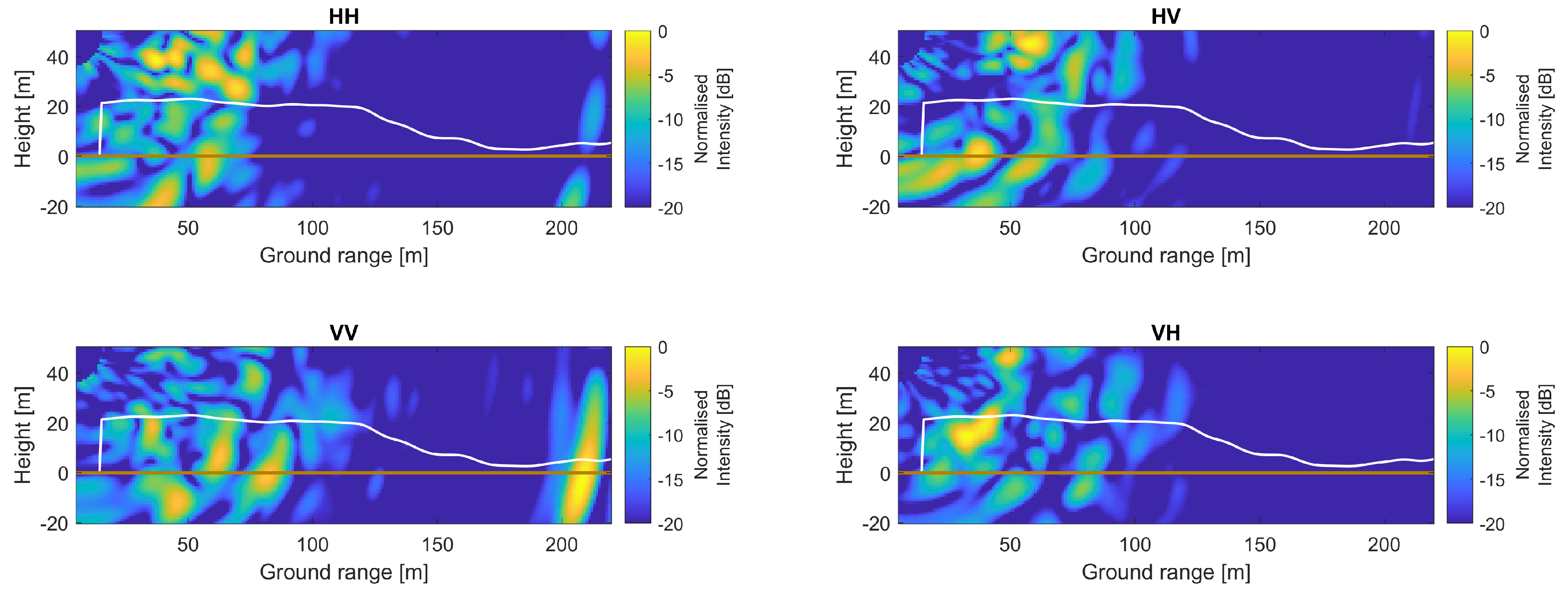
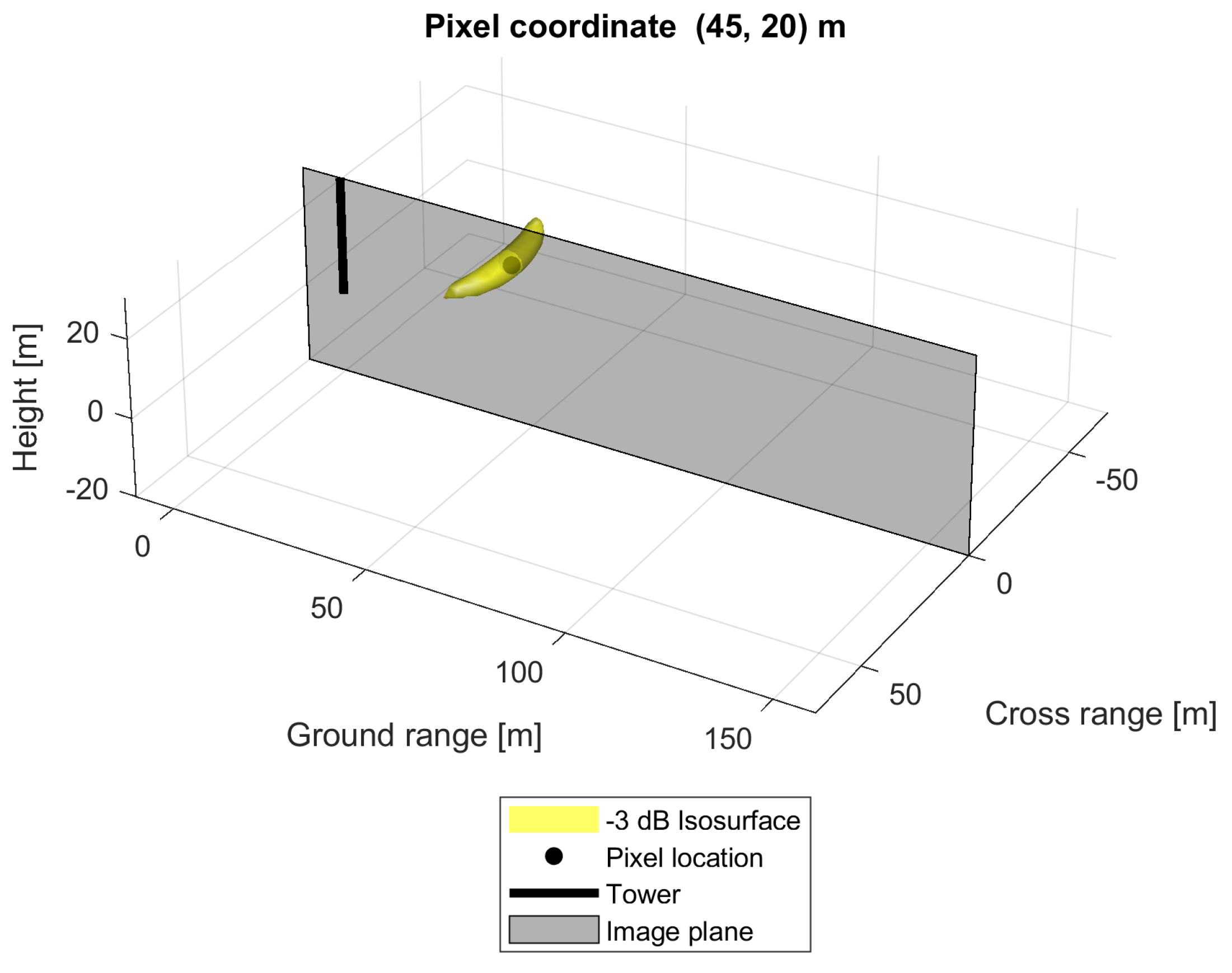
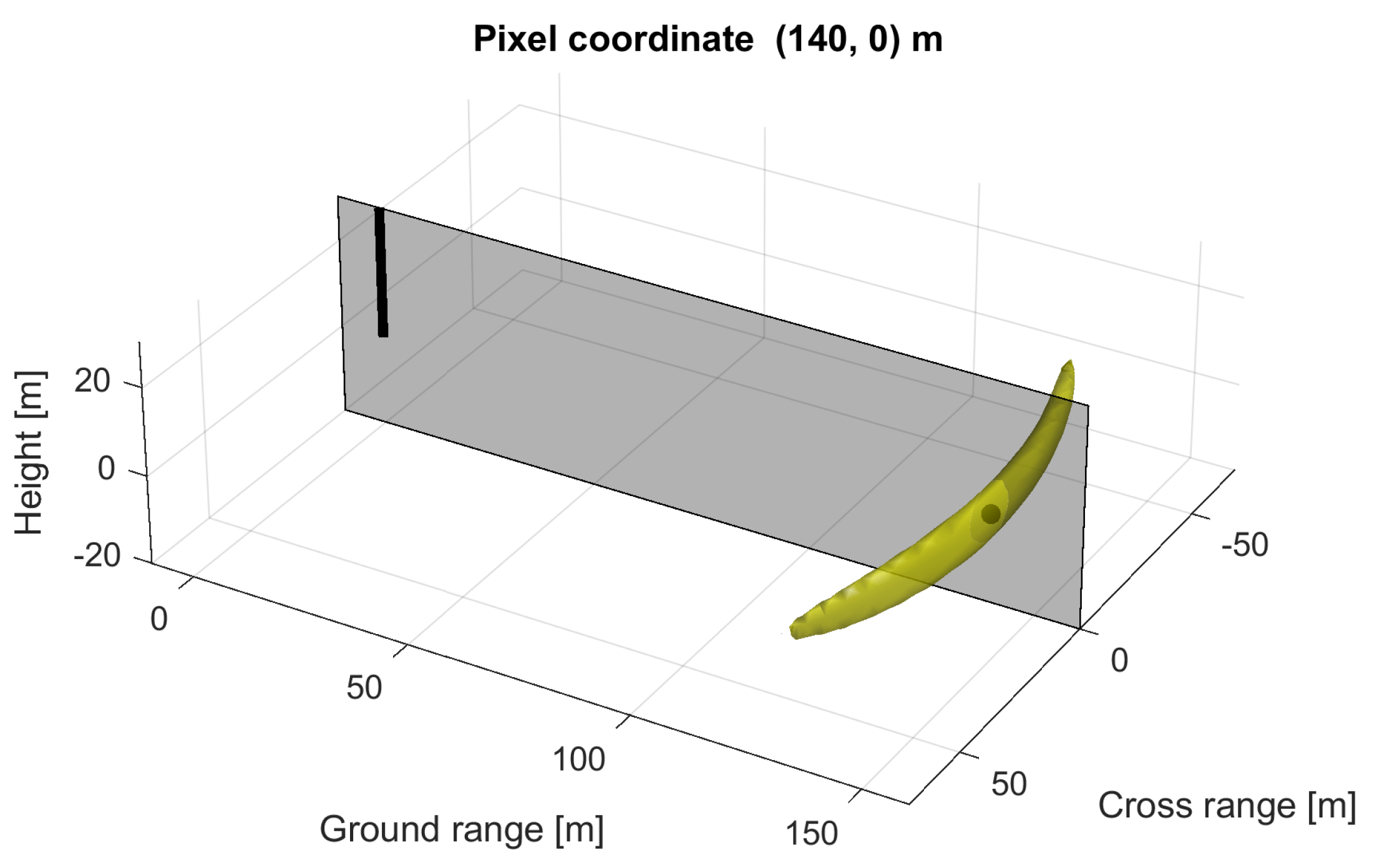
4.6. Tomographic Image Formation Validation
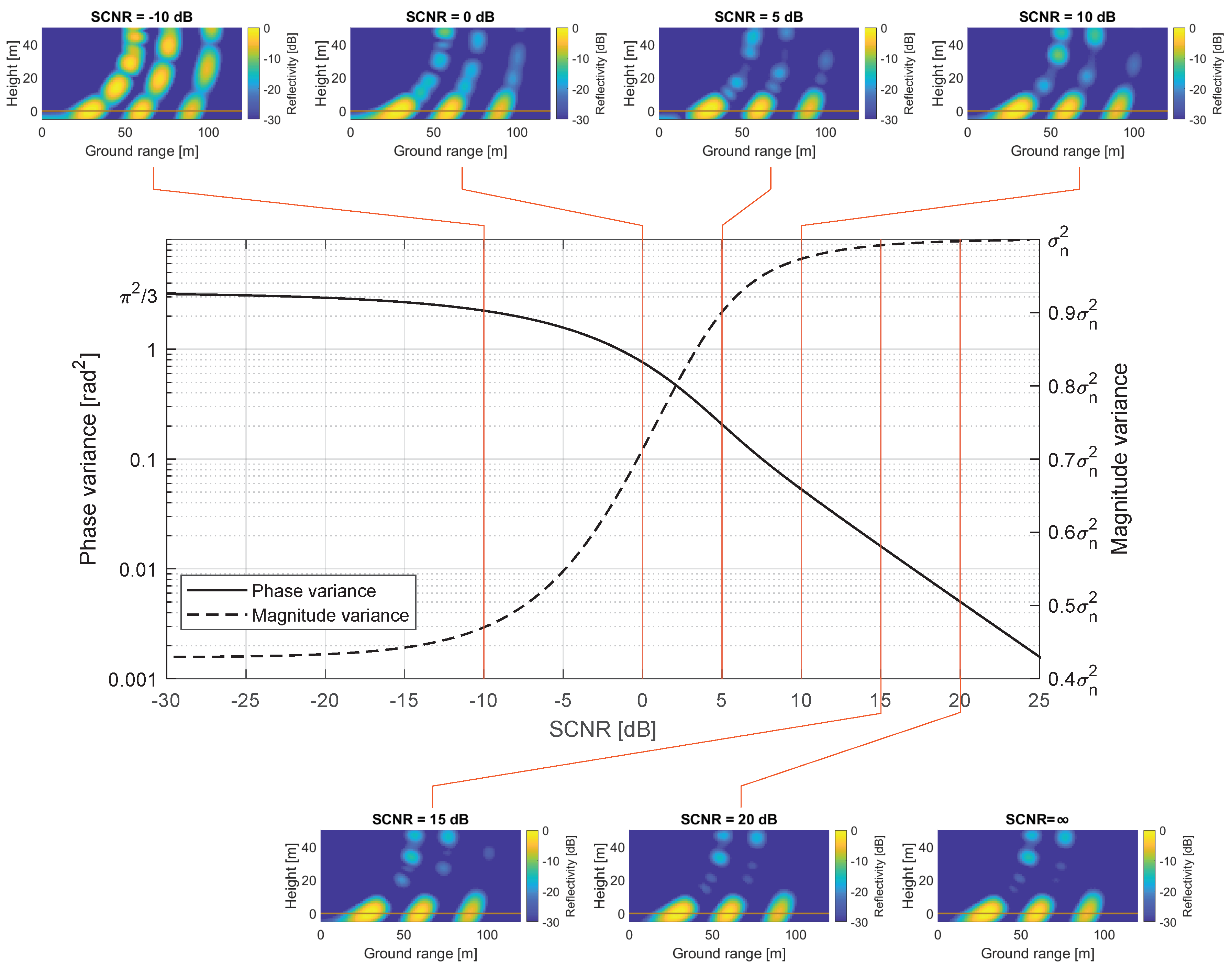
4.7. Signal to Clutter and Noise Ratio Requirement
5. Impulse Response Compensation
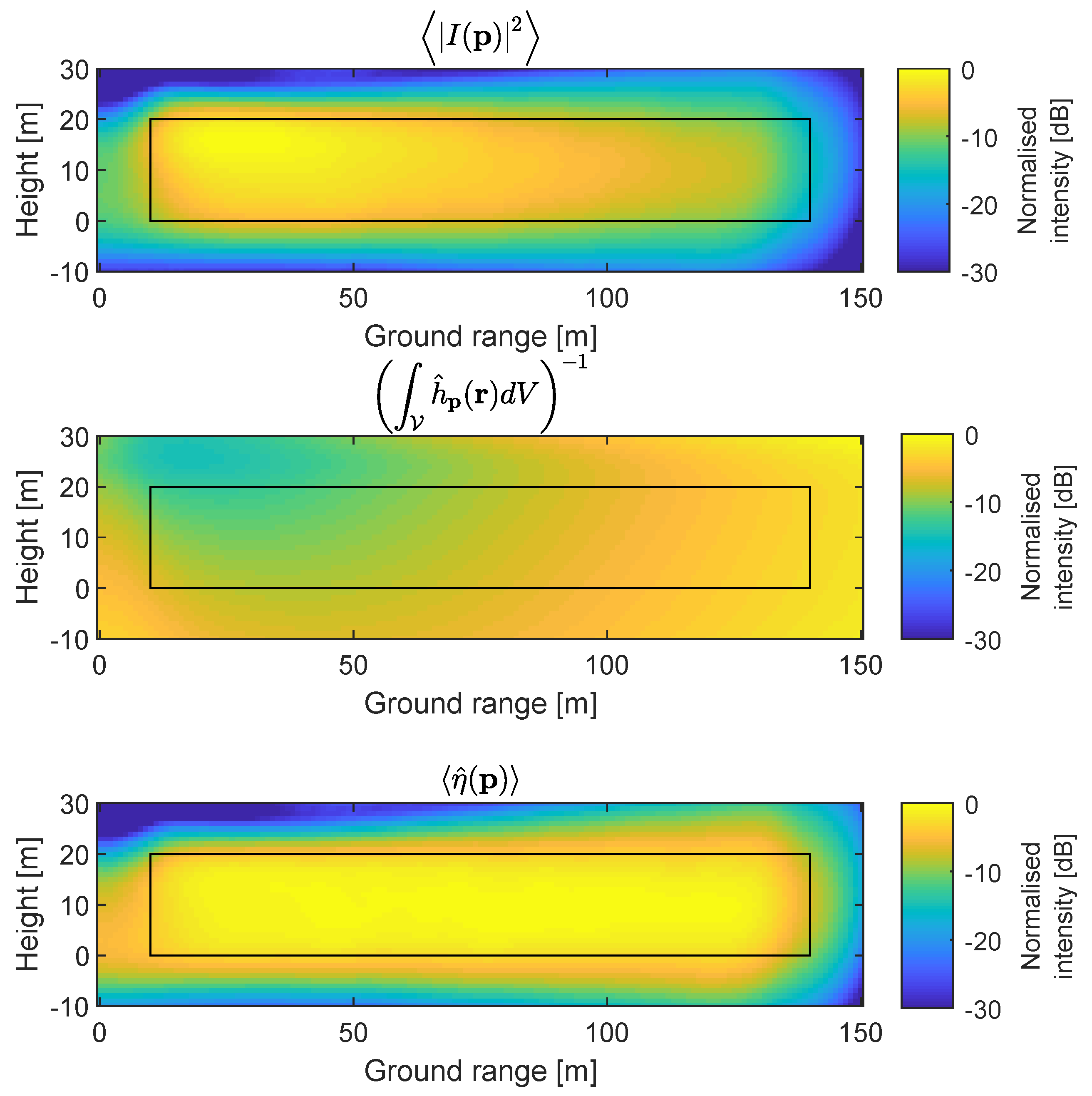
5.1. Systematic Pixel Gain
5.2. Image Intensity Model
5.3. Impulse Response Estimation
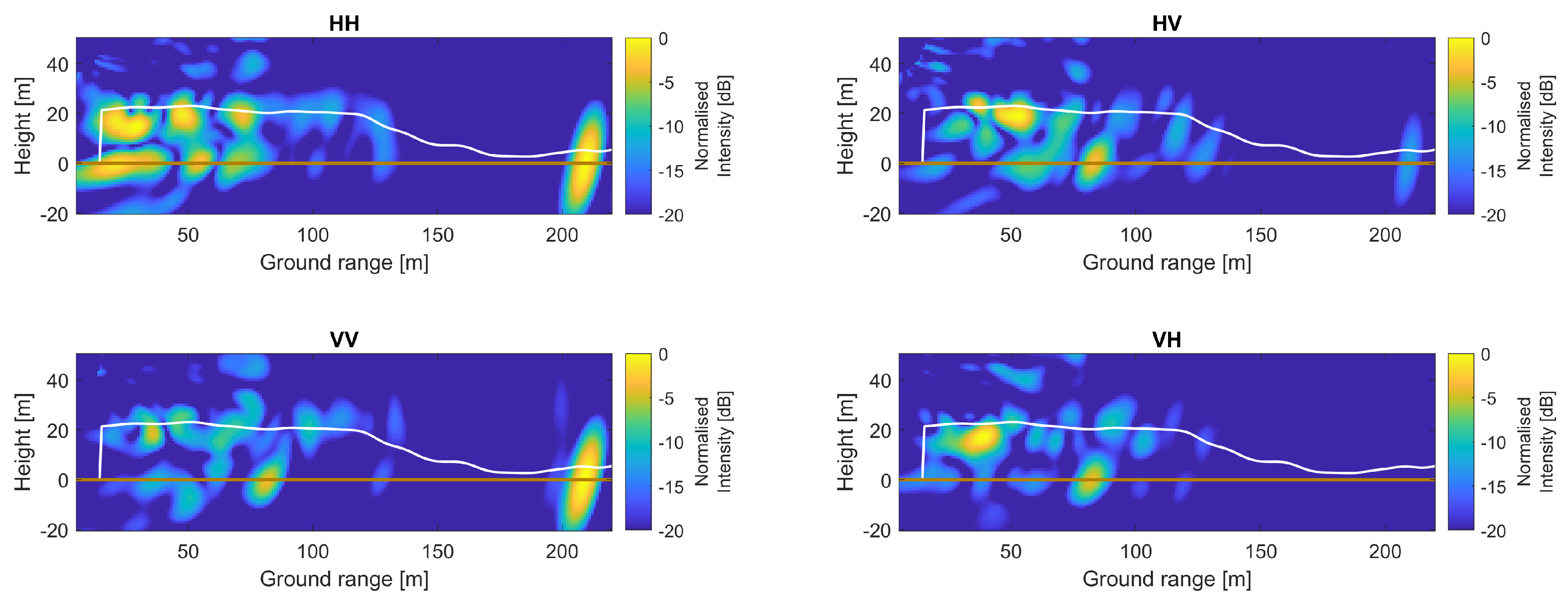
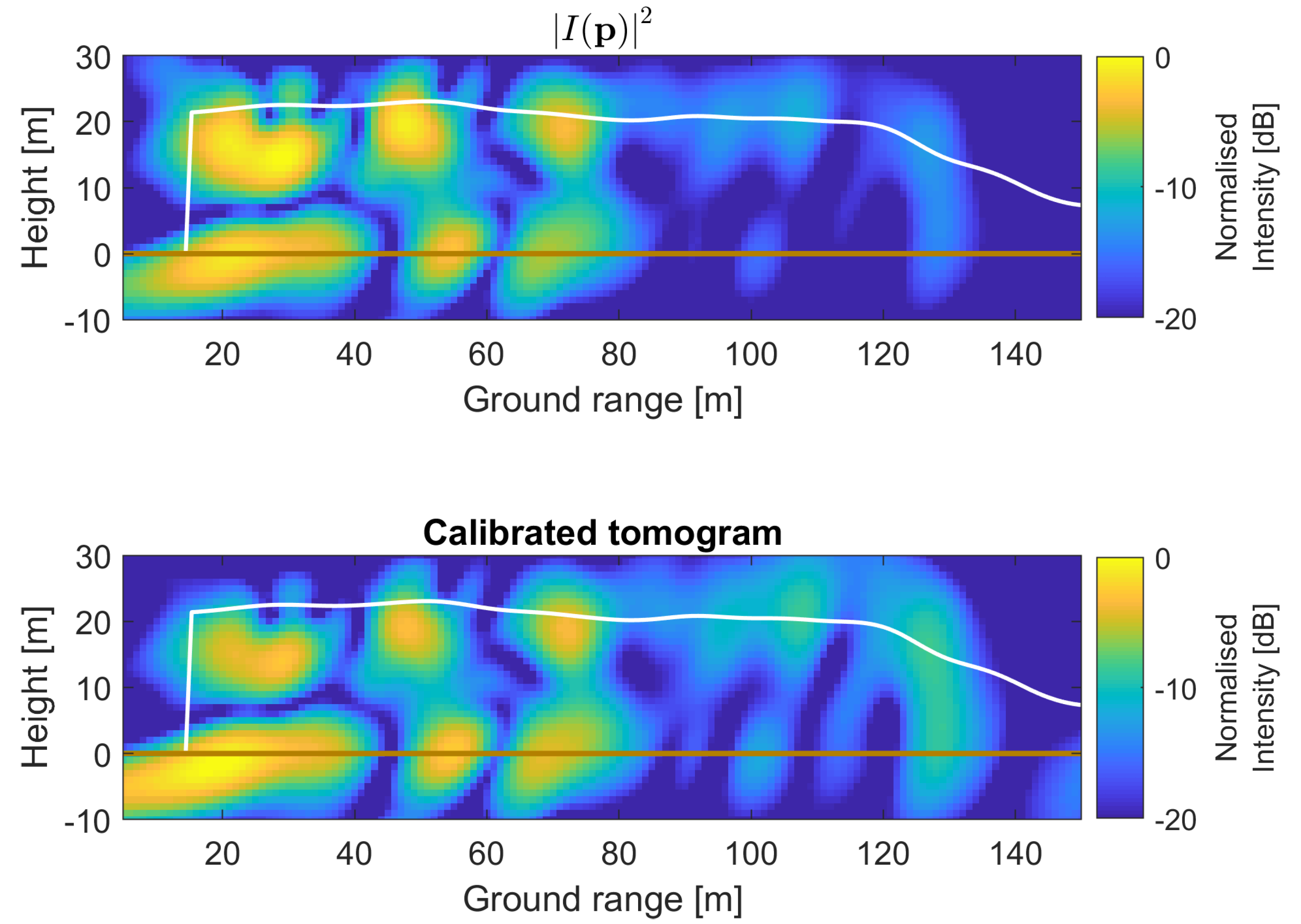
5.4. Impulse Response Compensation
5.5. Validation of Impulse Response Compensation
6. Summary of Calibration Procedure
7. Limitations of the Proposed Calibration
- There exists an unknown magnitude and phase offset between tomographic images of different polarisations. Care should, therefore, be taken when interpreting polarimetric combinations of images such as HH/VV, HH/HV and VV/HV.
- The images are not calibrated in an absolute sense. This means that the intensity and phase distributions in the images are correct, but have an unknown constant offset from the true geophysical value.
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, X.; Bamler, R. Very high resolution spaceborne SAR tomography in urban environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef]
- Tebaldini, S.; Nagler, T.; Rott, H.; Heilig, A. Imaging the internal structure of an Alpine glacier via L-band airborne SAR tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7197–7209. [Google Scholar] [CrossRef]
- Morrison, K. Mapping Subsurface Archaeology with SAR. Archaeol. Prospect. 2013, 20, 149–160. [Google Scholar] [CrossRef]
- Hanafy, S.; al Hagrey, S. Ground-penetrating radar tomography for soil-moisture heterogeneity. Geophysics 2006, 71, K9–K18. [Google Scholar] [CrossRef]
- Tebaldini, S.; Ho Tong Minh, D.; Mariotti d’Alessandro, M.; Villard, L.; Le Toan, T.; Chave, J. The status of technologies to measure forest biomass and structural properties: State of the art in SAR tomography of tropical forests. Surv. Geophys. 2019, 40, 779–801. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Le Toan, T.; Rocca, F.; Tebaldini, S.; D’Alessandro, M.; Villard, L. Relating P-band synthetic aperture radar tomography to tropical forest biomass. IEEE Trans. Geosci. Remote Sens. 2014, 52, 967–979. [Google Scholar] [CrossRef]
- Blomberg, E.; Ferro-Famil, L.; Soja, M.J.; Ulander, L.M.H.; Tebaldini, S. Forest biomass retrieval from L-Band SAR using tomographic ground backscatter removal. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1030–1034. [Google Scholar] [CrossRef]
- Hallberg, B.; Smith-Jonforsen, G.; Ulander, L.M.H.; Sandberg, G. A physical-optics model for double-bounce scattering from tree stems standing on an undulating ground surface. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2607–2621. [Google Scholar] [CrossRef]
- Soja, M.J.; Sandberg, G.; Ulander, L.M.H. Regression-based retrieval of boreal forest biomass in sloping terrain using P-band SAR backscatter intensity data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2646–2665. [Google Scholar] [CrossRef]
- Frey, O.; Werner, C.; Wiesmann, A. Tomographic profiling of the structure of a snow pack at X-/Ku-Band using SnowScat in SAR mode. In Proceedings of the 2015 European Radar Conference (EuRAD 2015), Paris, France, 9–11 September 2015; pp. 21–24. [Google Scholar]
- Albinet, C.; Borderies, P.; Koleck, T.; Rocca, F.; Tebaldini, S.; Villard, L.; Le Toan, T.; Hamadi, A.; Ho Tong Minh, D. TropiSCAT: A ground based polarimetric scatterometer experiment in tropical forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1060–1066. [Google Scholar] [CrossRef]
- Ulander, L.M.H.; Monteith, A.R.; Soja, M.J.; Eriksson, L.E.B. Multiport vector network analyzer radar for tomographic forest scattering measurements. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1897–1901. [Google Scholar] [CrossRef]
- Dinh, H.; Tebaldini, S.; Rocca, F.; Koleck, T.; Borderies, P.; Albinet, C.; Villard, L.; Hamadi, A.; Le Toan, T. Ground-based array for tomographic imaging of the tropical forest in P-band. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4460–4472. [Google Scholar] [CrossRef]
- Albinet, C.; Koleck, T.; Le Toan, T.; Borderies, P.; Villard, L.; Hamadi, A.; Laurin, G.; Nicolini, G.; Valentini, R. First results of AfriScat, a tower-based radar experiment in African forest. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5356–5358. [Google Scholar]
- Monteith, A.R.; Ulander, L.M.H. Long-term P-band tomosar observations from the BorealScat tower experiment. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 8594–8597. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2013. [Google Scholar]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation: Theory and Application; Prentice Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Barabell, A. Improving the resolution performance of eigenstructure-based direction-finding algorithms. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Boston, MA, USA, 14–16 April 1983; pp. 336–339. [Google Scholar]
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: London, UK, 1995. [Google Scholar]
- Rice, S.O. Mathematical Analysis of Random Noise. Bell Syst. Tech. J. 1945, 24, 46–156. [Google Scholar] [CrossRef]
- Vinokur, M. Optimisation dans la Recherche d’une Sinusoïde de Période Connue en Présence de Bruit. Ann. d’Astrophys. 1965, 28, 412–445. [Google Scholar]
- Ulaby, F.; Elachi, C. Radar Polarimetry for Geoscience Applications; Artech House: Norwood, MA, USA, 1990. [Google Scholar]
- Ulander, L.M.H. Accuracy of using point targets for SAR calibration. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 139–148. [Google Scholar] [CrossRef]
- Carlström, A.; Ulander, L.M.H. C-Band backscatter signatures of old sea ice in the central Arctic during freeze-Up. IEEE Trans. Geosci. Remote Sens. 1993, 31, 819–829. [Google Scholar] [CrossRef]


| HH | VV | HV | VH | |||||
|---|---|---|---|---|---|---|---|---|
| Orig. | Cal. | Orig. | Cal. | Orig. | Cal. | Orig. | Cal. | |
| Standard deviation [dB] | 3.42 | 1.64 | 4.57 | 1.52 | 3.22 | 1.52 | 3.24 | 1.52 |
| Median absolute deviation [dB] | 2.24 | 0.77 | 2.14 | 0.69 | 1.91 | 0.67 | 1.96 | 0.73 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteith, A.R.; Ulander, L.M.H.; Tebaldini, S. Calibration of a Ground-Based Array Radar for Tomographic Imaging of Natural Media. Remote Sens. 2019, 11, 2924. https://doi.org/10.3390/rs11242924
Monteith AR, Ulander LMH, Tebaldini S. Calibration of a Ground-Based Array Radar for Tomographic Imaging of Natural Media. Remote Sensing. 2019; 11(24):2924. https://doi.org/10.3390/rs11242924
Chicago/Turabian StyleMonteith, Albert R., Lars M. H. Ulander, and Stefano Tebaldini. 2019. "Calibration of a Ground-Based Array Radar for Tomographic Imaging of Natural Media" Remote Sensing 11, no. 24: 2924. https://doi.org/10.3390/rs11242924
APA StyleMonteith, A. R., Ulander, L. M. H., & Tebaldini, S. (2019). Calibration of a Ground-Based Array Radar for Tomographic Imaging of Natural Media. Remote Sensing, 11(24), 2924. https://doi.org/10.3390/rs11242924