Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA
Abstract
:1. Introduction
2. Methodology
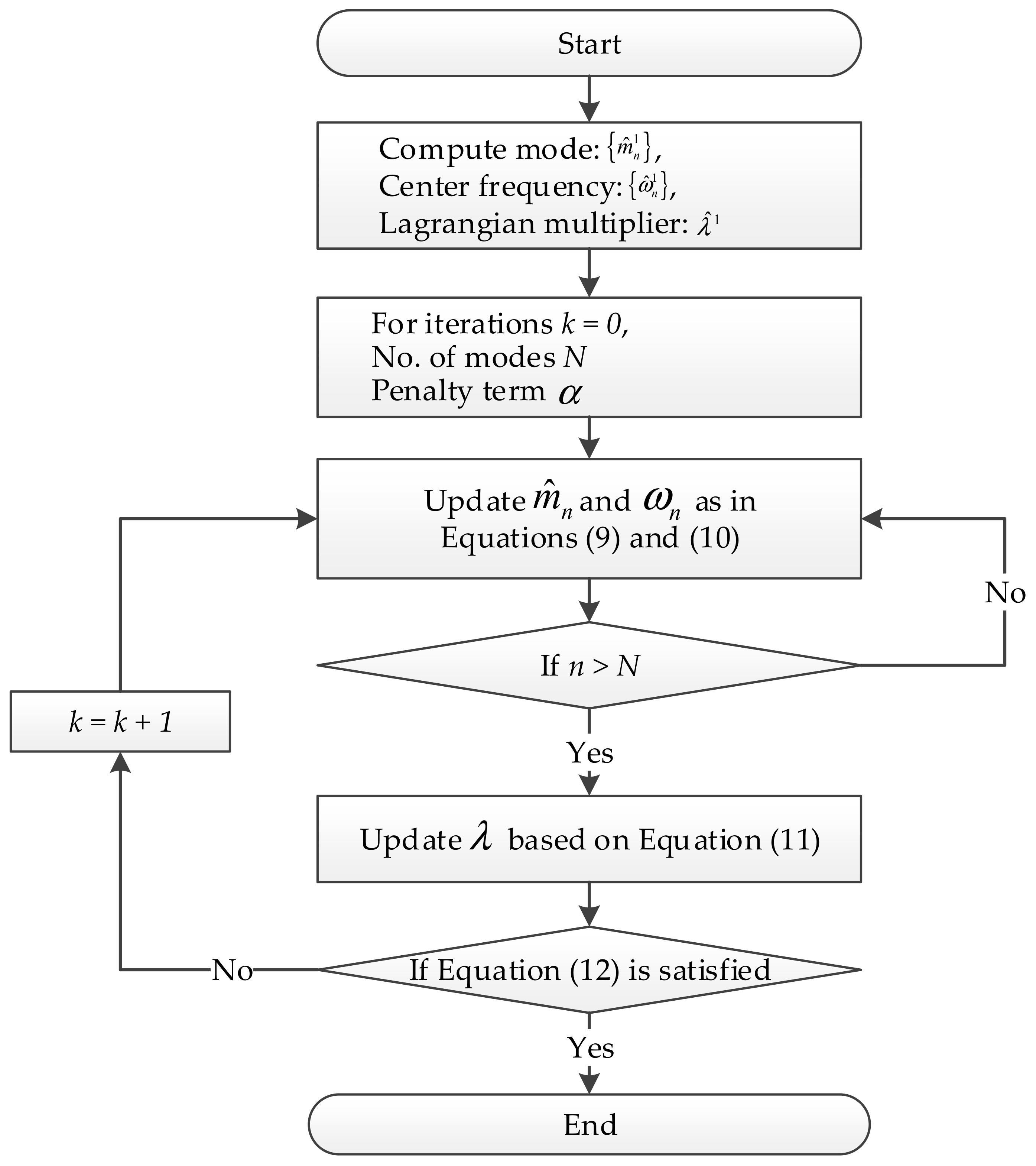
2.1. Variational Mode Decomposition (VMD)
2.2. Multifractal Detrended Fluctuation Analysis
2.3. GNSS Signal Decomposition with VMD
3. Merits and Features of VMD
3.1. VMD Reconfiguration of Signal
3.2. Signal Smoothing Filtering
3.3. VMD Adaptivity
3.4. Orthogonality of IMFs
4. Experimental Results
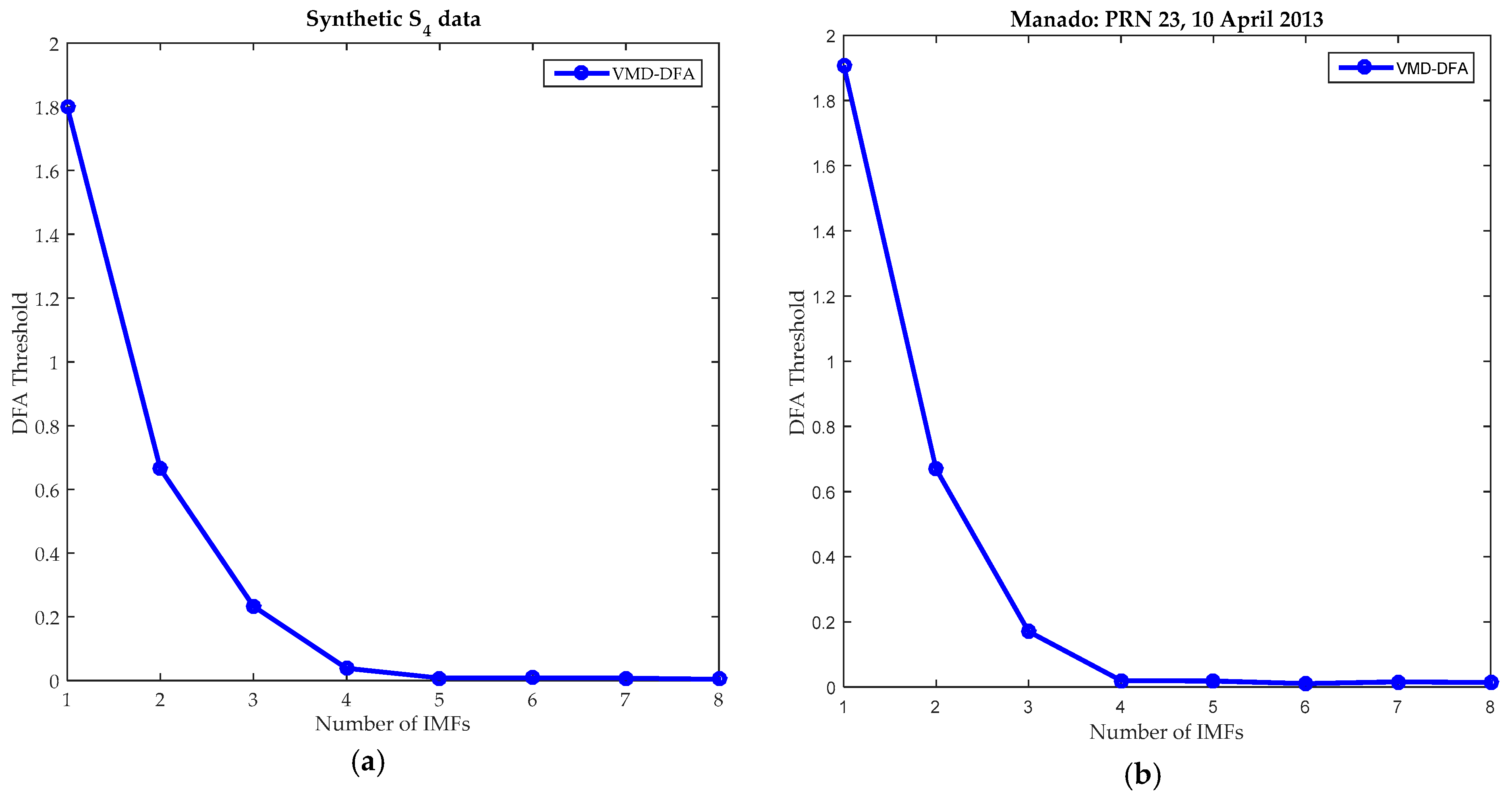
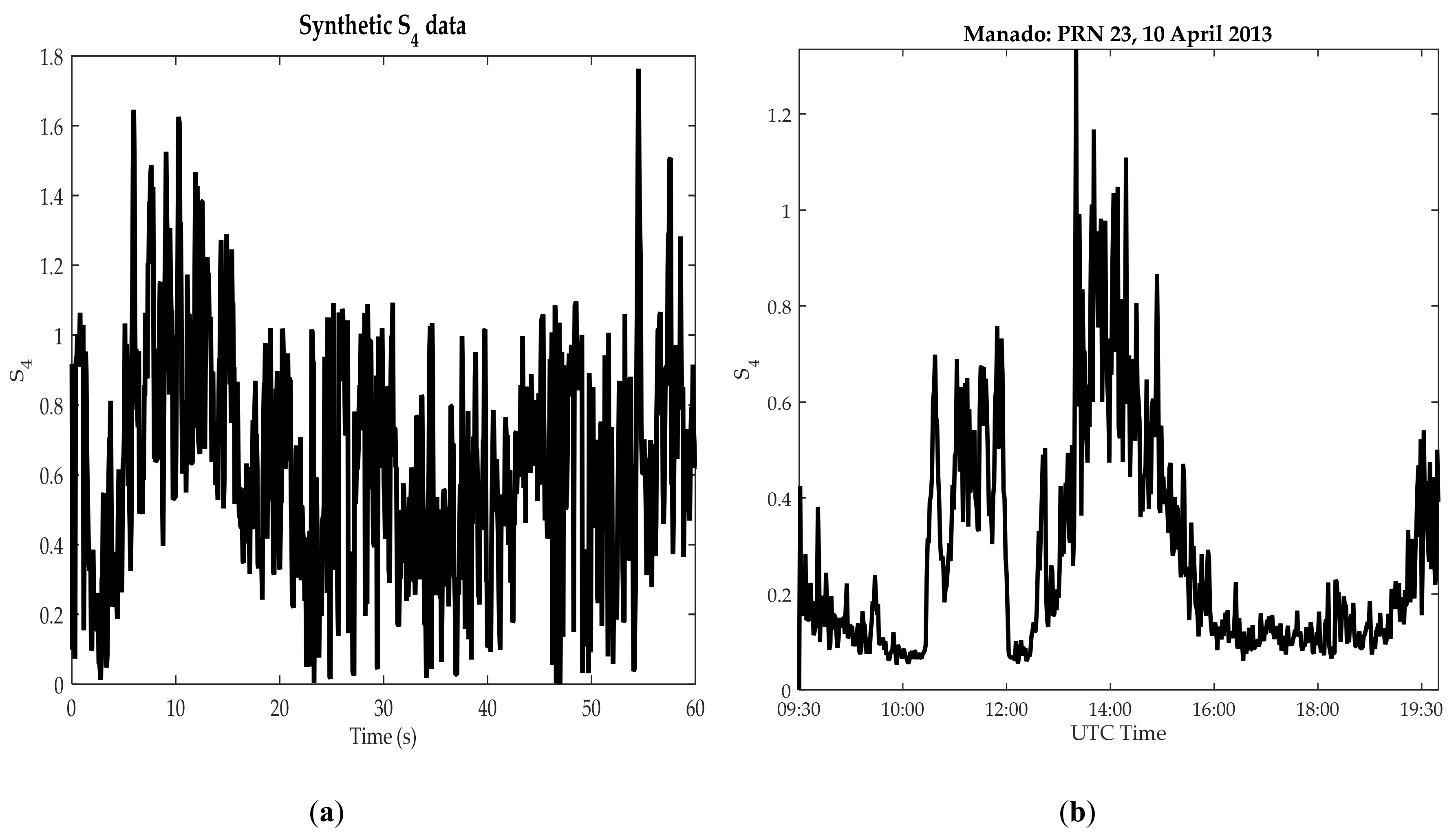
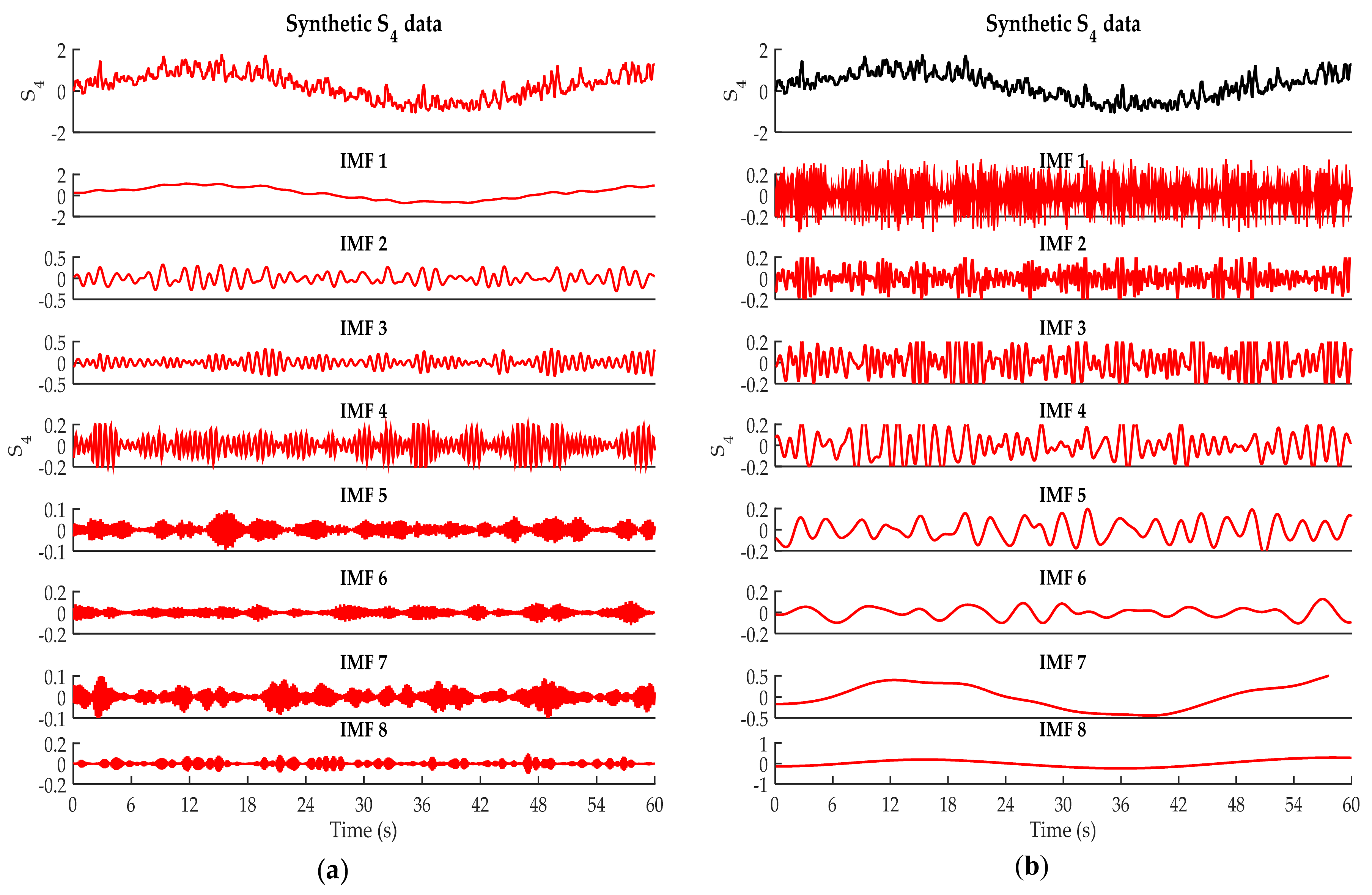
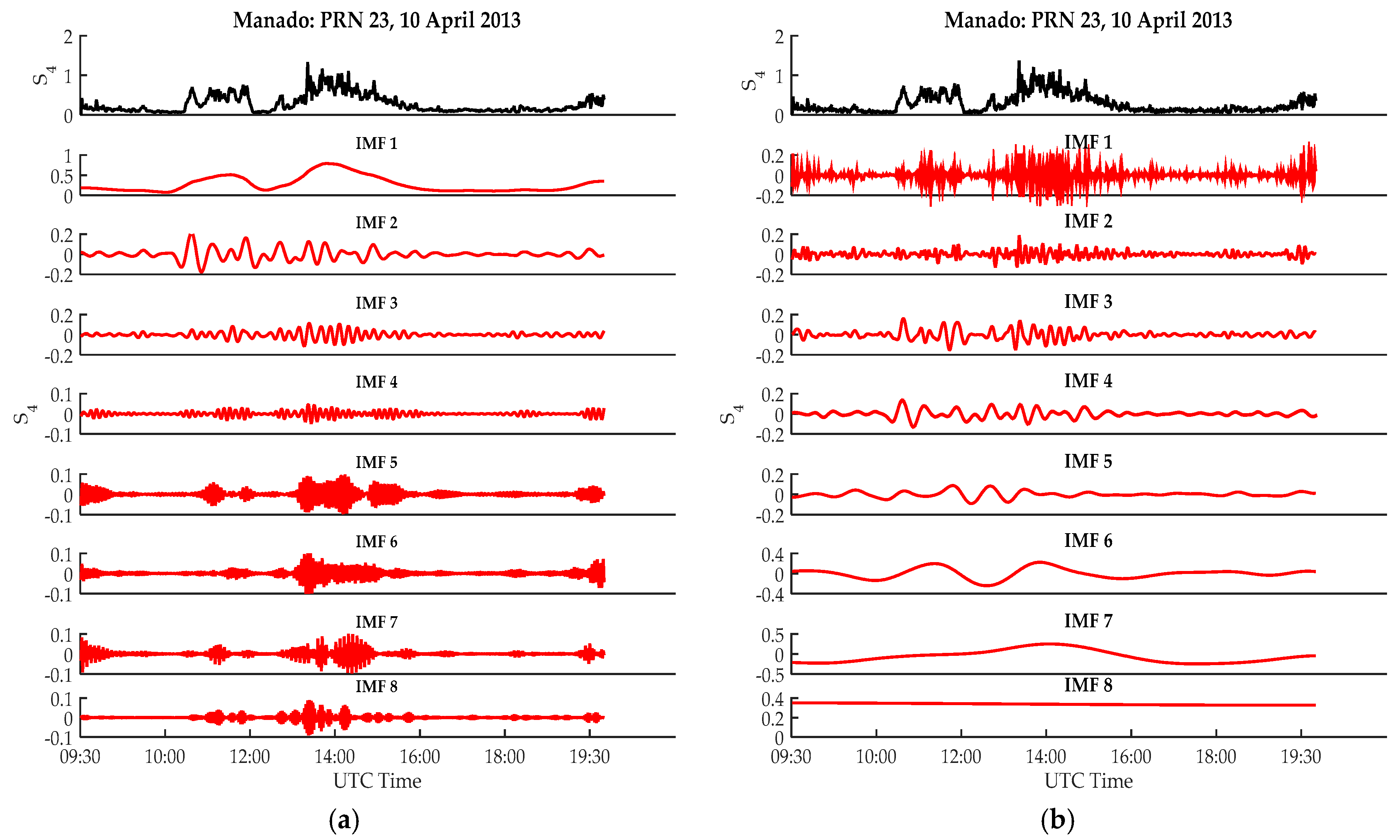
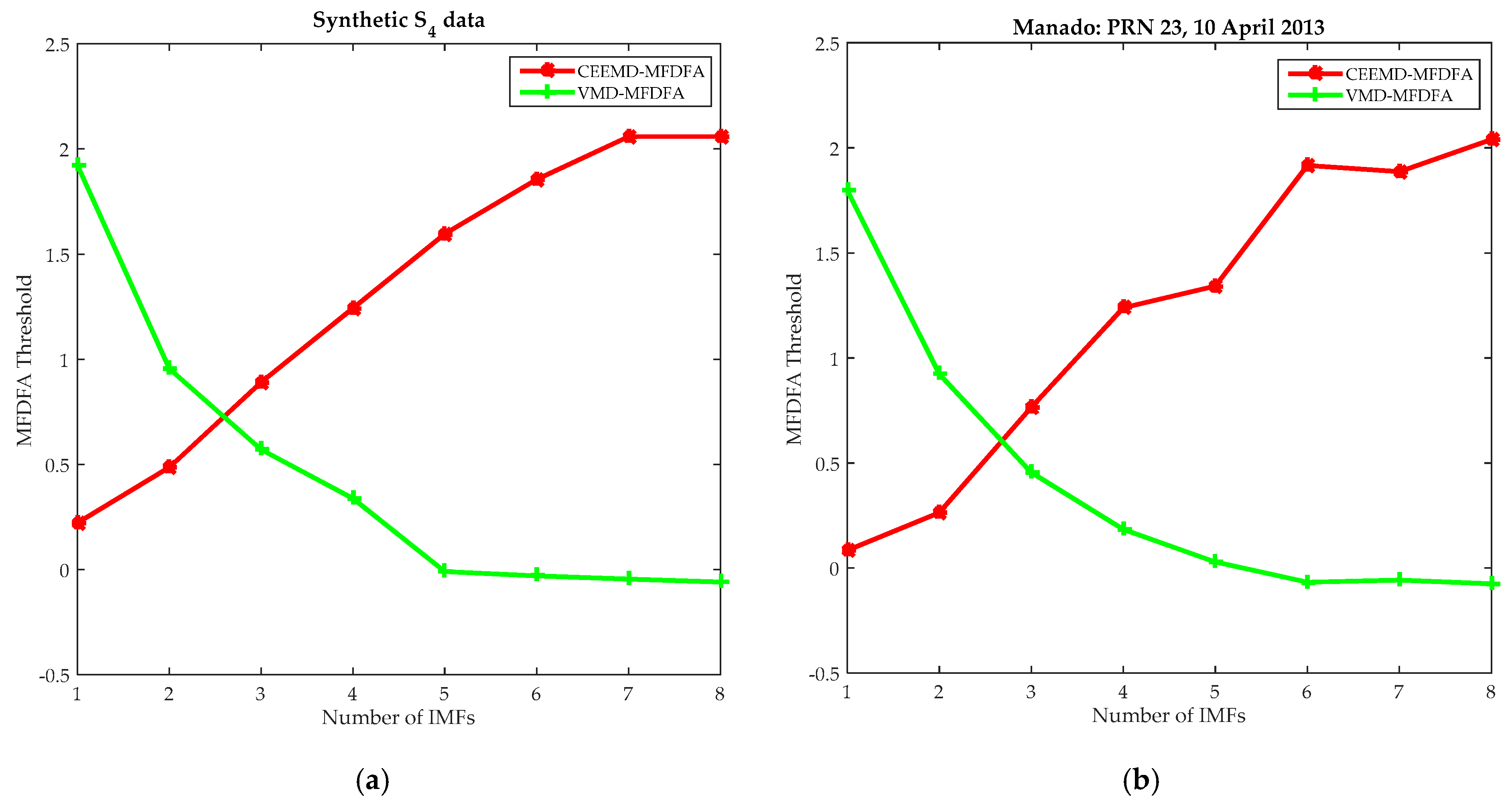
4.1. Signal Decomposition Analysis
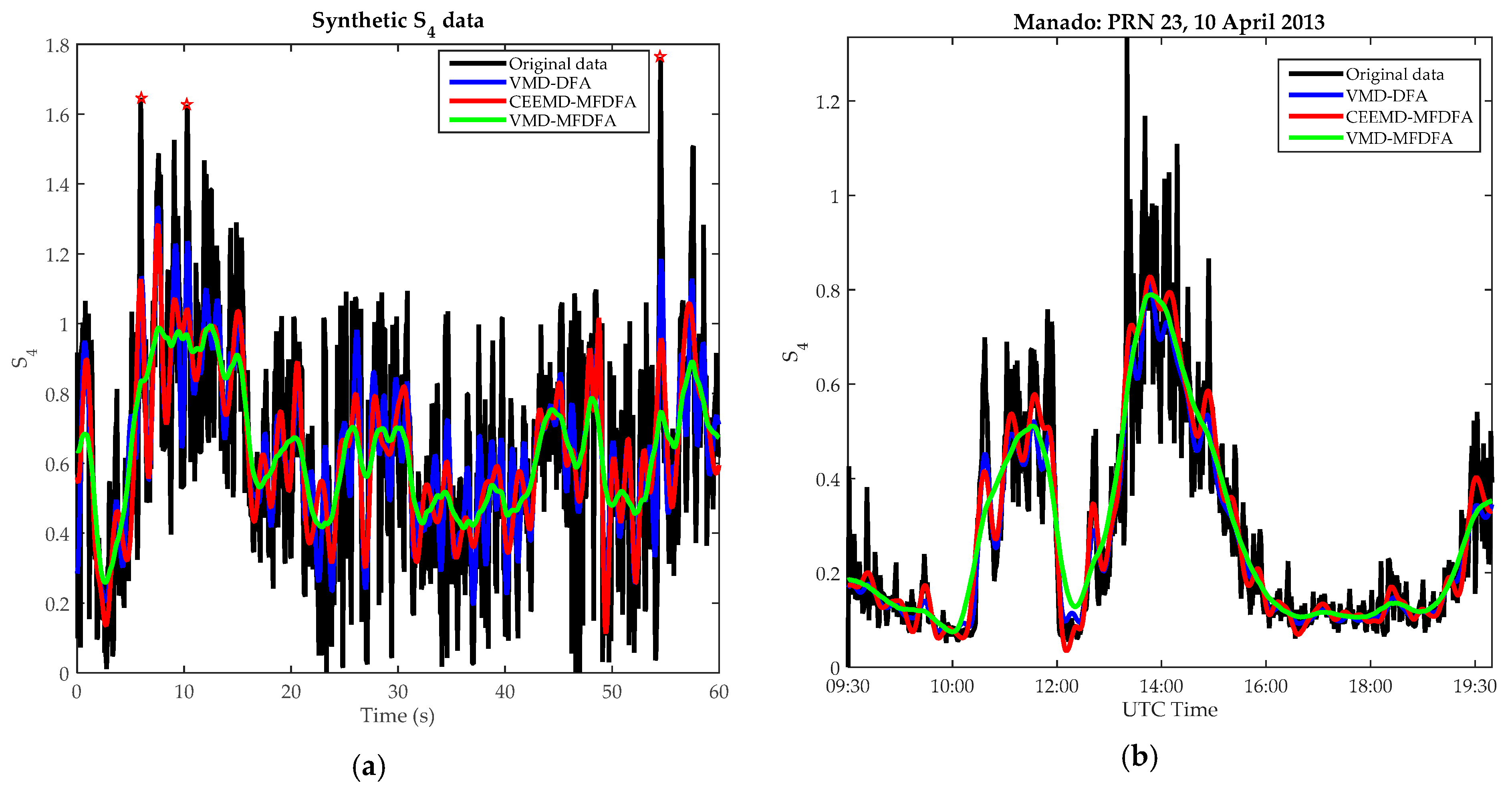
4.2. Signal Reconfiguration Analysis
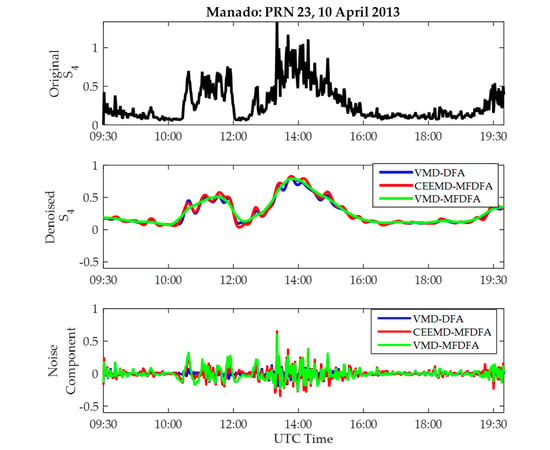
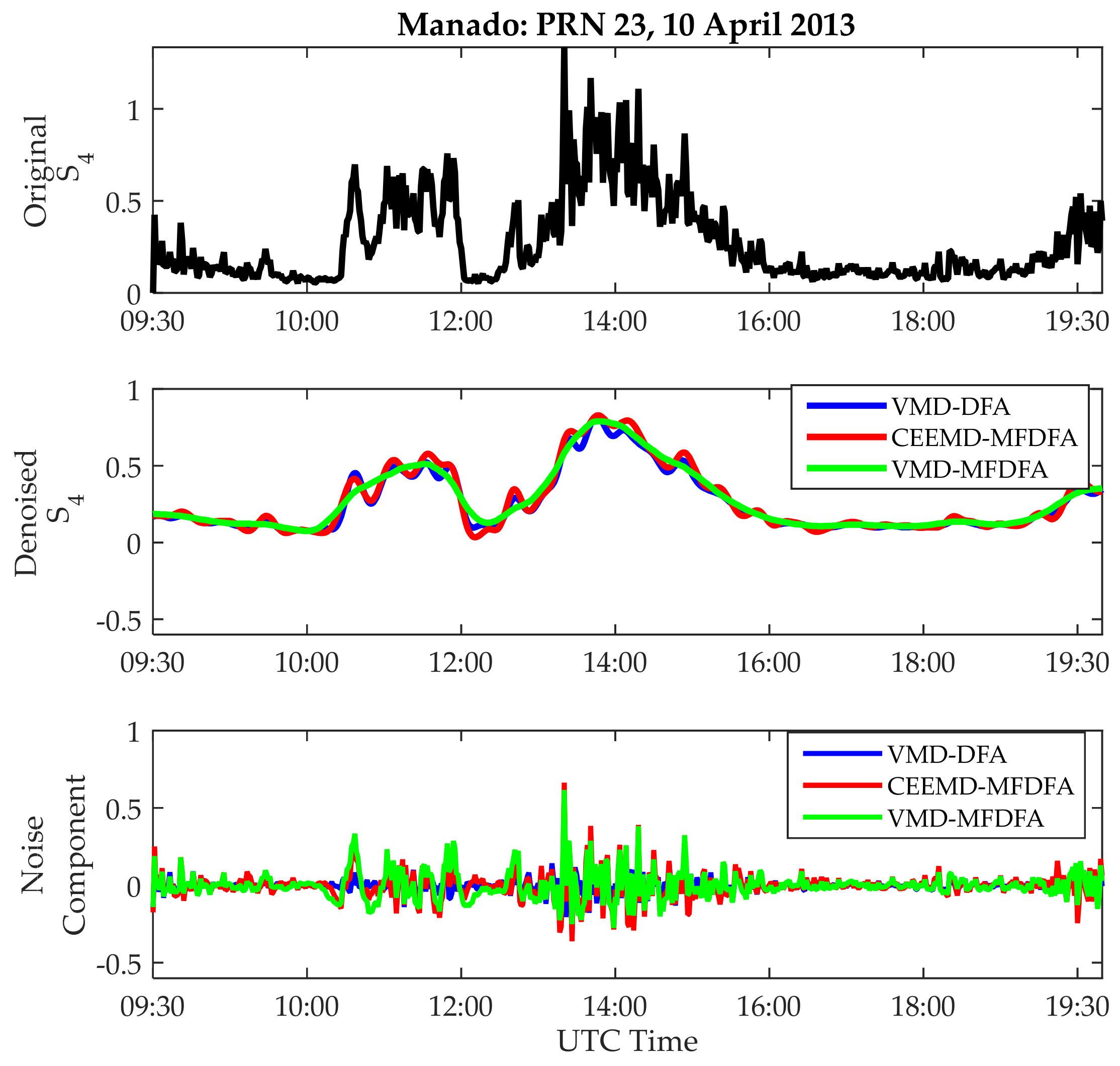
4.3. Signal Denoising
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sivavaraprasad, G.; Sree, R.P.; Venkata, D.R. Mitigation of Ionospheric Scintillation Effects on GNSS Signals Using Variational Mode Decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 389–893. [Google Scholar] [CrossRef]
- De Paula, E.; Rodrigues, F.S.; Iyer, K.N.; Kantor, I.J.; Abdu, M.A.; Kintner, P.M.; Kil, H. Equatorial anomaly effects on GPS scintillations in Brazil. Adv. Space Res. 2003, 31, 749–754. [Google Scholar] [CrossRef]
- Ahmed, W.A.; Wu, F.; Agbaje, G.I.; Ednofri, E.; Marlia, D.; Zhao, Y. Seasonal Ionospheric Scintillation Analysis during Increasing Solar Activity at Mid-Latitude. In Optics in Atmospheric Propagation and Adaptive Systems; SPIE Remote Sensing: Warsaw, Poland, 2017; Volume 10425, pp. 1–14. [Google Scholar]
- Aquino, M.; Sreeja, V. Correlation of scintillation occurrence with interplanetary magnetic field reversals and impact on Global Navigation Satellite System receiver tracking performance. Space Weather 2013, 11, 219–224. [Google Scholar] [CrossRef]
- Kintner, P.M.; Ledvina, B.M.; De Paula, E.R. GPS and ionospheric scintillations. Space Weather 2007, 5, 1–23. [Google Scholar] [CrossRef]
- Pongracic, B.; Wu, F.; Fathollahi, L.; Brčić, D. Midlatitude Klobuchar correction model based on the k—means clustering of ionospheric daily variations. GPS Solut. 2019, 23, 1–13. [Google Scholar] [CrossRef]
- Wernik, A.W.; Alfonsi, L.; Materassi, M. Ionospheric irregularities, scintillation and its effect on systems. Acta Geophys. Pol. 2004, 52, 237–249. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Liu, H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ahmed, W.A.; Wu, F.; Agbaje, G.I. Analysis of GPS ionospheric scintillation during solar maximum at mid-latitude. In International Geoscience and Remote Sensing Symposium; IGARSS: Beijing, China, 2016; pp. 4151–4154. [Google Scholar]
- Sridhar, M.; Ratnam, D.V.; Sirisha, B.; Sasanka, C.R.; Kumar, B.S.; Ajay, C.; Rao, C.S. Characterization of Low Latitude Ionospheric Scintillations using EEMD-DFA Method. In Proceedings of the Sponsored 2nd International Conference on Innovations in Information Embedded and Communication Systems, Tamil Nadu, India, 19–20 March 2015; pp. 1–6. [Google Scholar]
- Xia, J.; Yue, F.; Wang, P.; Wang, S. Robust GNSS Signal Tracking Algorithm Based on Vector Tracking Loop Under Ionospheric Scintillation Conditions. In Proceedings of the 12th International Conference on Signal Processing, Hangzhou, China, 17–19 December 2014; pp. 2385–2389. [Google Scholar]
- Ahmed, A.; Tiwari, R.; Strangeways, H.J.; Rutter, N.; Boussakta, S. GPS tracking loop performance using wavelet denoising. In Proceedings of the 7th ESA workshop on Satellite Navigation Technologies (NAVITEC 2014), Space Research and Technology Centre, European Space Agency, Noordwijk, The Netherlands, 5–7 December 2014. [Google Scholar]
- Lyer, K.; Souza, J.; Pathan, B.; Abdu, M.; Jivani, M.N.; Joshi, H.P. A model of equatorial and low latitude VHF scintillation in India. Indian J. Radio Space Phys. 2006, 34, 98. [Google Scholar]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 23, 87–114. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A New View of Non-linear Water Waves: The Hilbert Spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2008, 1, 1–41. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Miriyala, S.; Koppireddi, P.R.; Chanamallu, S.R. Robust detection of ionospheric scintillations using MF-DFA technique. Earth Planets Space 2015, 67, 1–5. [Google Scholar] [CrossRef]
- Chen, Q.; Cai, W. Algorithm of VMD for the detection of APF harmonics. In Proceedings of the 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 1260–1263. [Google Scholar]
- Kun, Y.; Yu, M.; Yueyu, L.Z.; Xiangjun, Z.; Liwei, X. VMD-S Traveling Wave Signal Extraction Method Under Strong Noise. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 1739–1743. [Google Scholar]
- Jiao, S.; Shi, W.; Yang, Y. Denoising of UHF Partial Discharge Signals by Using VMD Based on Shannon Entropy and Kurtosis- Approximation Entropy. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1742–1747. [Google Scholar]
- Lahmiri, S.; Boukadoum, M. Biomedical Image Denoising Using Variational Mode Decomposition. In Proceedings of the 2014 IEEE Biomedical Circuits and Systems Conference (BioCAS), Lausanne, Switzerland, 22–24 October 2014; pp. 340–343. [Google Scholar]
- Liu, W.; Cao, S.Y.; He, Y. Ground Roll Attenuation Using Variational Mode Decomposition. In Proceedings of the 77th EAGE Conference & Exhibition, Madrid, Spain, 1–5 June 2015; pp. 63–68. [Google Scholar]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos An Interdiscip. J. Nonlinear Sci. 1995, 5, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Mert, A.; Akan, A. Detrended fluctuation thresholding for empirical mode decomposition based denoising. Digit. Signal Process. 2014, 32, 48–56. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Nonstationary Data Analysis. In Random Data (Analysis and Measurement Procedures), 2nd ed.; John Wiley & Sons: New York, NY, USA, 2010; pp. 417–472. [Google Scholar]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rego, H.H.A.; Havlin, S. Detecting long-range correlations in fire sequences with Detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2001, 295, 441–454. [Google Scholar] [CrossRef]
- Liao, Y.; He, C. Denoising of Magnetocardiography Based on Improved Variational Mode Decomposition and Interval Thresholding Method. J. MDPI Remote Sens. 2018, 10, 269. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 3, 1–18. [Google Scholar] [CrossRef]
- Fosso, O.B.; Molinas, M. EMD Mode Mixing Separation of Signals with Close Spectral Proximity in Smart Grids. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia, 21–25 October 2018; pp. 1–6. [Google Scholar]
- Mushini, S.C.; Jayachandran, P.T.; Langley, R.B.; Macdougall, J.W.; Pokhotelov, D. Improved amplitude- and phase-scintillation indices derived from wavelet detrended high-latitude GPS data. GPS Solut. 2012, 16, 363–373. [Google Scholar] [CrossRef]
| Time (s) | Before Denoising | After Denoising | ||
|---|---|---|---|---|
| S4 | CEEMD-MFDFA | VMD-DFA | VMD-MFDFA | |
| 6 | 1.64 | 1.12 | 1.01 | 0.65 |
| 11 | 1.62 | 1.04 | 0.80 | 0.56 |
| 54 | 1.76 | 0.95 | 0.82 | 0.74 |
| UTC Time (hh:mm) | Before Denoising (S4) | After Denoising | ||
|---|---|---|---|---|
| CEEMD-MFDFA | VMD-DFA | VMD-MFDFA | ||
| 13:47 | 1.3 | 0.67 | 0.62 | 0.58 |
| 14:04 | 1.2 | 0.80 | 0.78 | 0.75 |
| 14:35 | 1.1 | 0.71 | 0.66 | 0.62 |
| Before Denoising | After Denoising | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CEEMD-MFDFA | VMD-DFA | VMD-MFDFA | |||||||
| Data | PRN | STD | RMSE | STD | RMSE | STD | RMSE | STD | RMSE |
| Syn. data | 0.23 | 0.48 | 0.21 | 0.46 | 0.20 | 0.45 | 0.17 | 0.43 | |
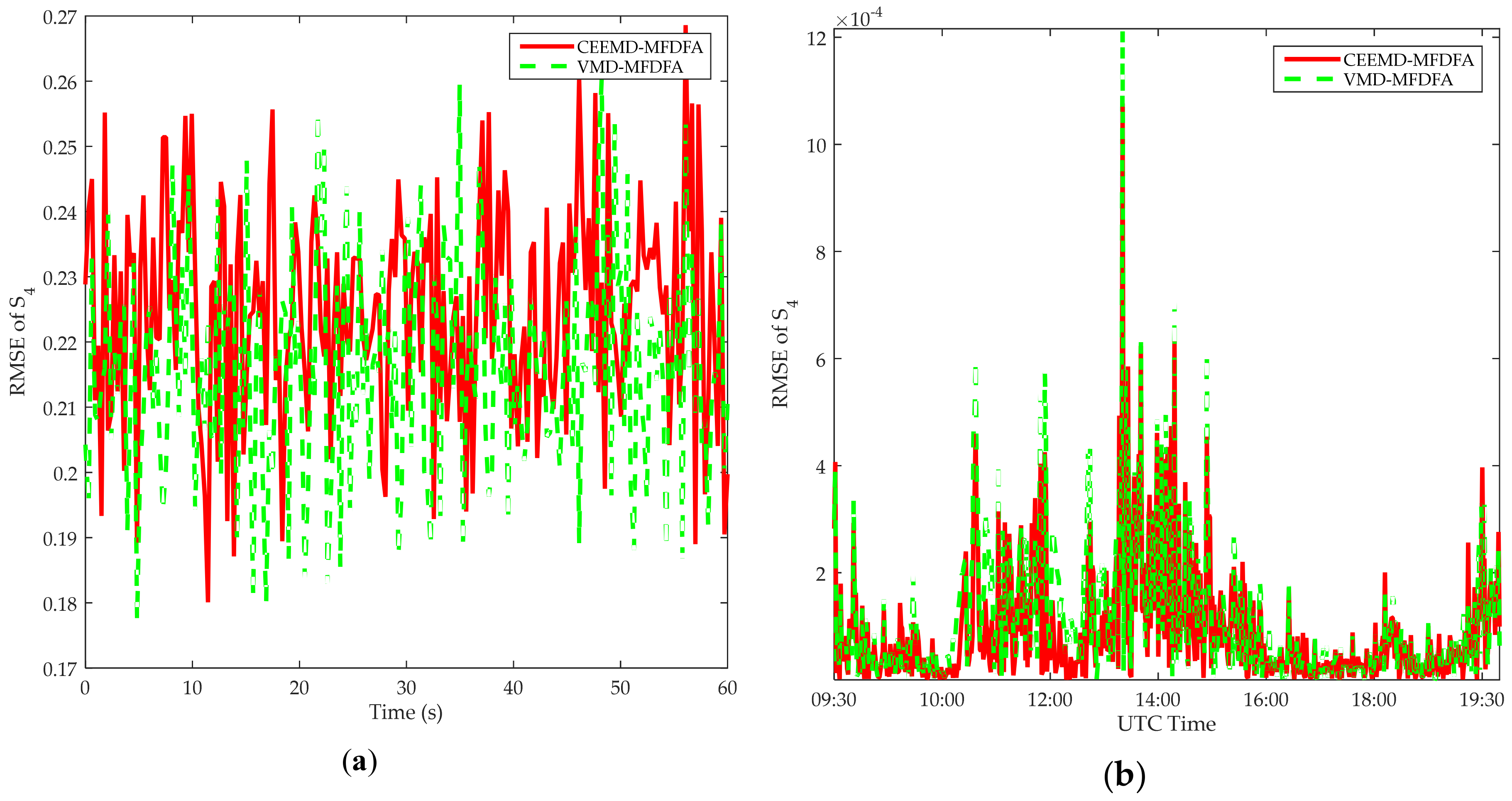
| 10 April 2013 | 23 | 0.23 | 0.13 | 0.21 | 0.11 | 0.19 | 0.10 | 0.17 | 0.09 |
| 26 September 2013 | 12 | 0.24 | 0.10 | 0.22 | 0.08 | 0.20 | 0.07 | 0.10 | 0.05 |
| 12 October 2013 | 29 | 0.13 | 0.05 | 0.11 | 0.03 | 0.10 | 0.02 | 0.09 | 0.01 |
| Method | 50 MC Runs | 100 MC Runs | 150 MC Runs | 200 MC Runs | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| CEEMD-MFDFA | 0.20 | 0.28 | 0.25 | 0.20 | 0.31 | 0.25 | 0.19 | 0.32 | 0.24 | 0.21 | 0.33 | 0.33 |
| VMD-DFA | 0.19 | 0.27 | 0.24 | 0.17 | 0.27 | 0.23 | 0.16 | 0.26 | 0.22 | 0.16 | 0.25 | 0.21 |
| VMD-MFDFA | 0.16 | 0.24 | 0.22 | 0.14 | 0.23 | 0.21 | 0.14 | 0.22 | 0.21 | 0.12 | 0.21 | 0.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, W.A.; Wu, F.; Marlia, D.; Ednofri; Zhao, Y. Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA. Remote Sens. 2019, 11, 2867. https://doi.org/10.3390/rs11232867
Ahmed WA, Wu F, Marlia D, Ednofri, Zhao Y. Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA. Remote Sensing. 2019; 11(23):2867. https://doi.org/10.3390/rs11232867
Chicago/Turabian StyleAhmed, Wasiu Akande, Falin Wu, Dessi Marlia, Ednofri, and Yan Zhao. 2019. "Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA" Remote Sensing 11, no. 23: 2867. https://doi.org/10.3390/rs11232867
APA StyleAhmed, W. A., Wu, F., Marlia, D., Ednofri, & Zhao, Y. (2019). Mitigation of Ionospheric Scintillation Effects on GNSS Signals with VMD-MFDFA. Remote Sensing, 11(23), 2867. https://doi.org/10.3390/rs11232867