Retrieval of Snow Depth over Arctic Sea Ice Using a Deep Neural Network
Abstract
1. Introduction
2. Data and Methods
2.1. Satellite Data
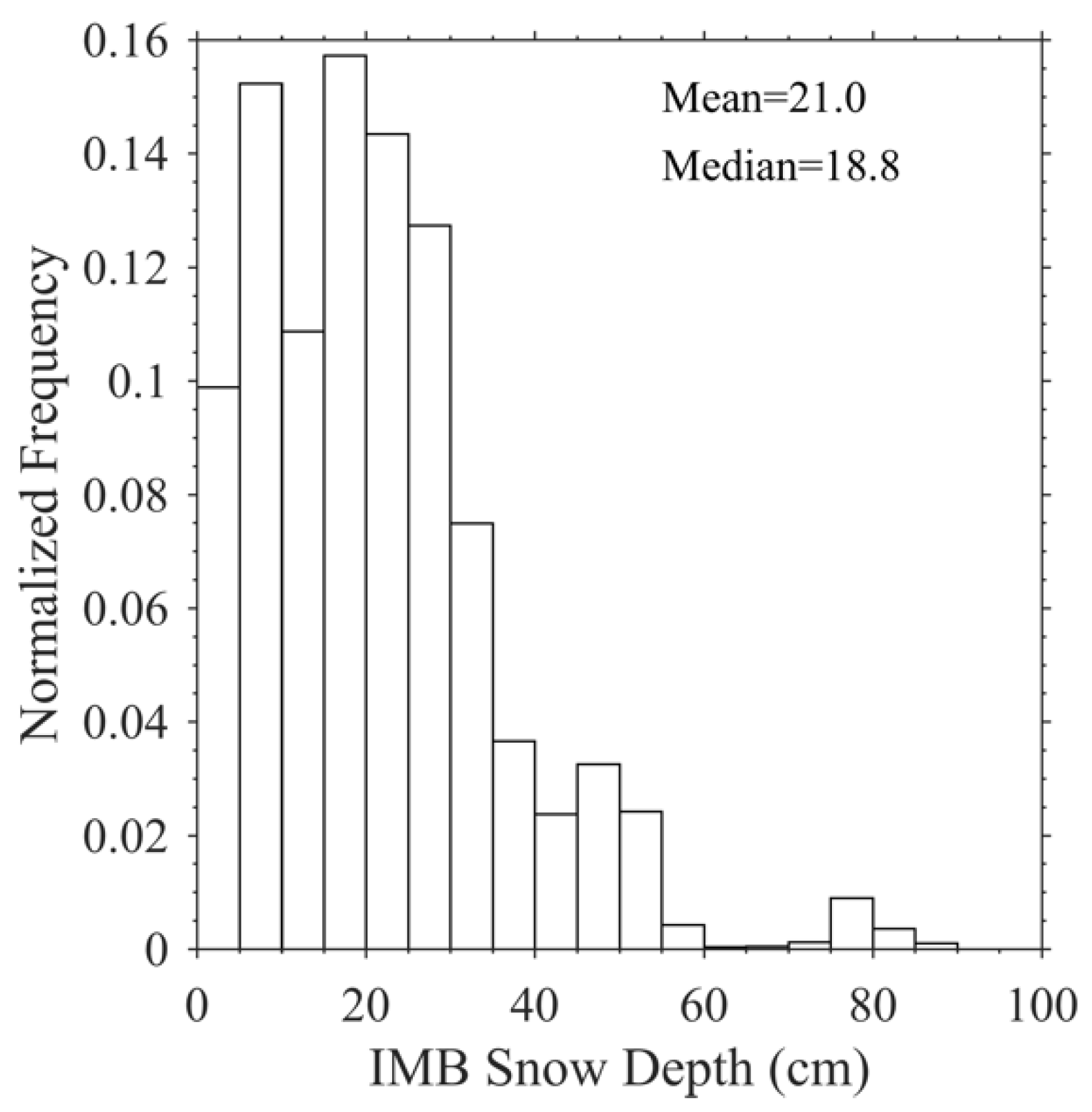
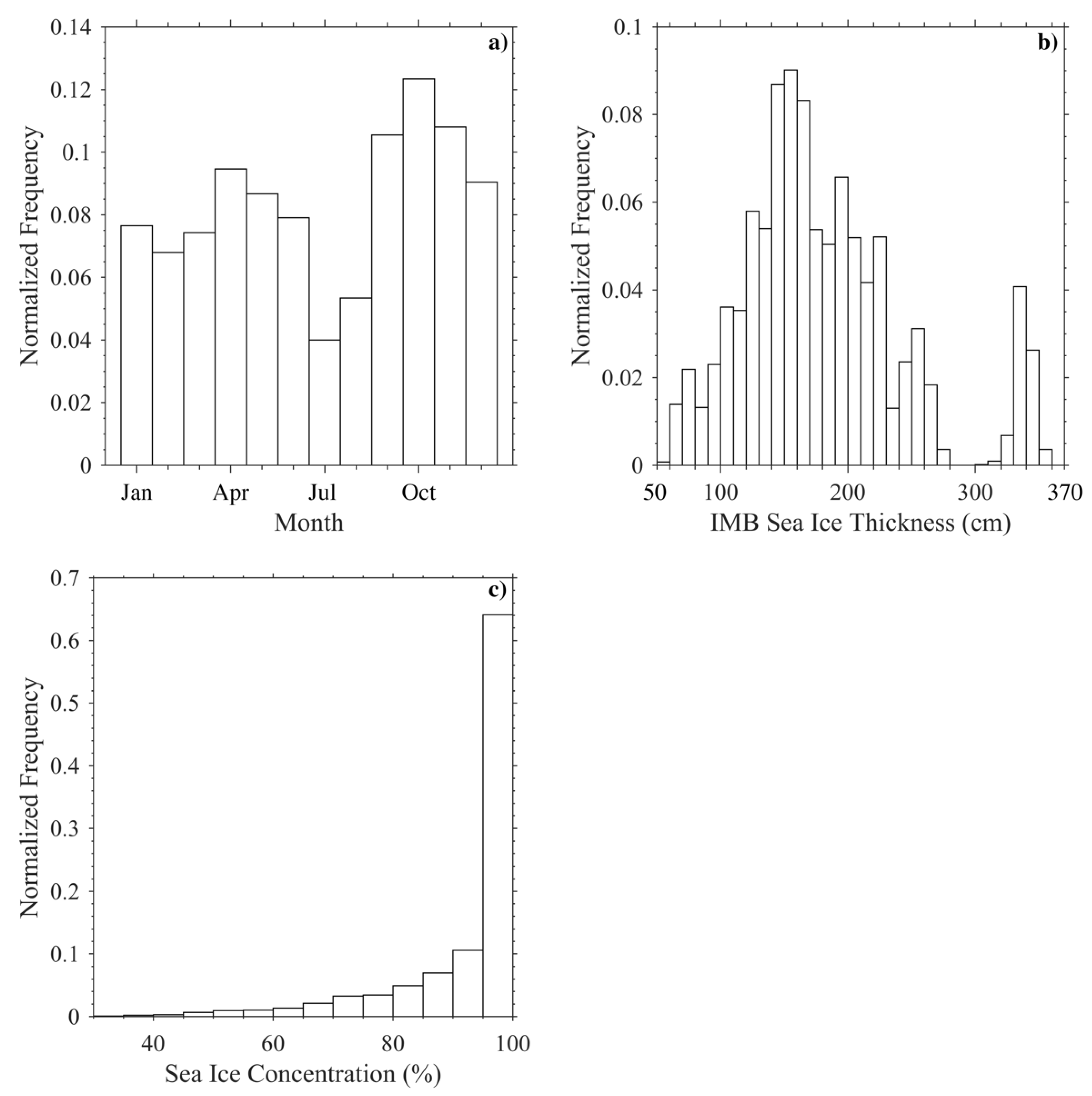
2.2. Sea Ice Mass Balance Buoy Data
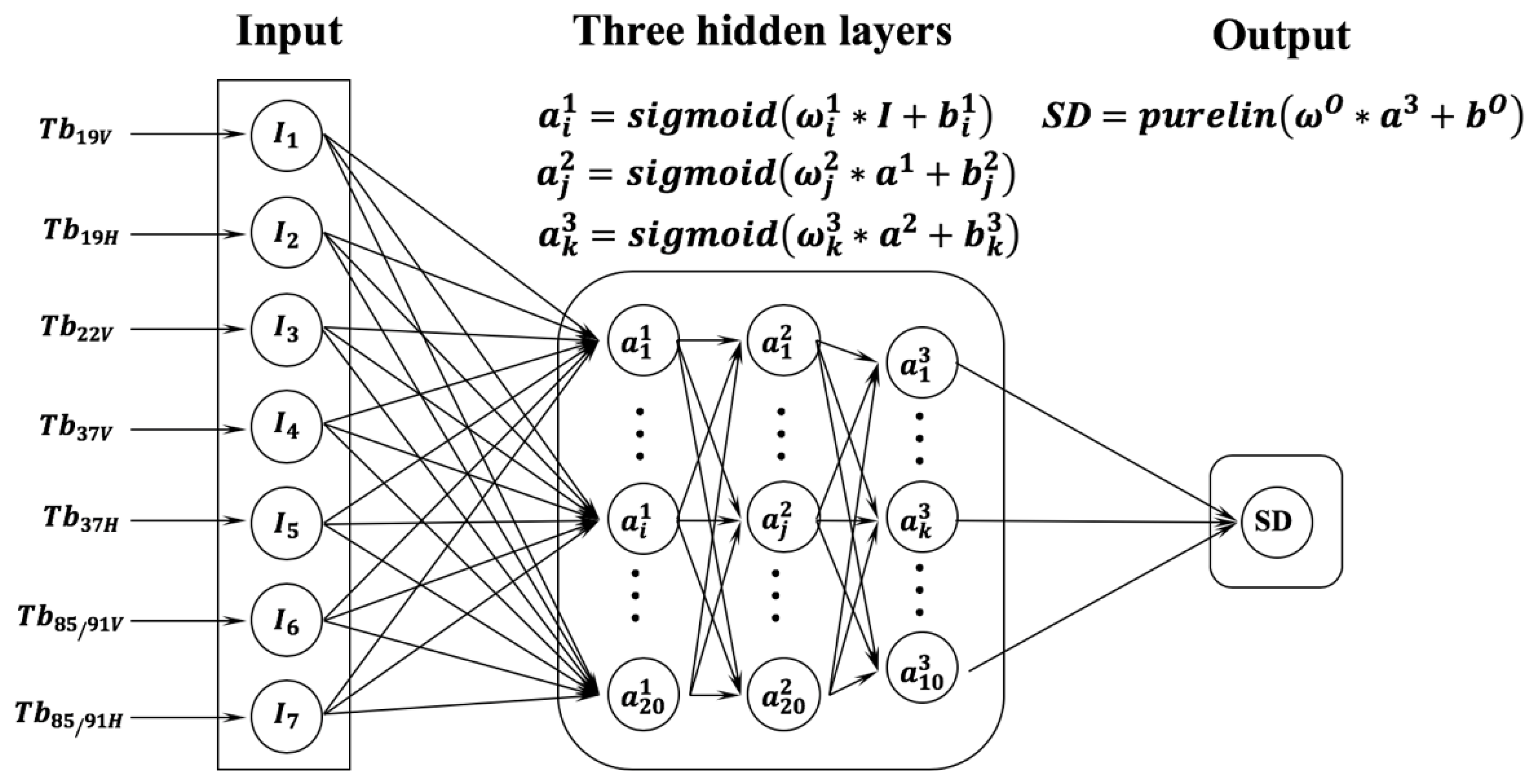
2.3. Deep Neural Network
2.4. Two Available Long-Term Basin-Scale Snow Depth Retrievals for Intercomparison
3. Results
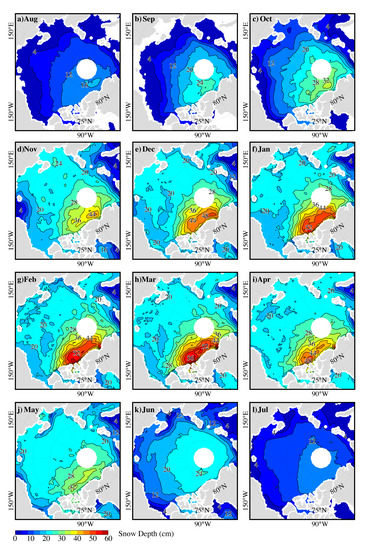
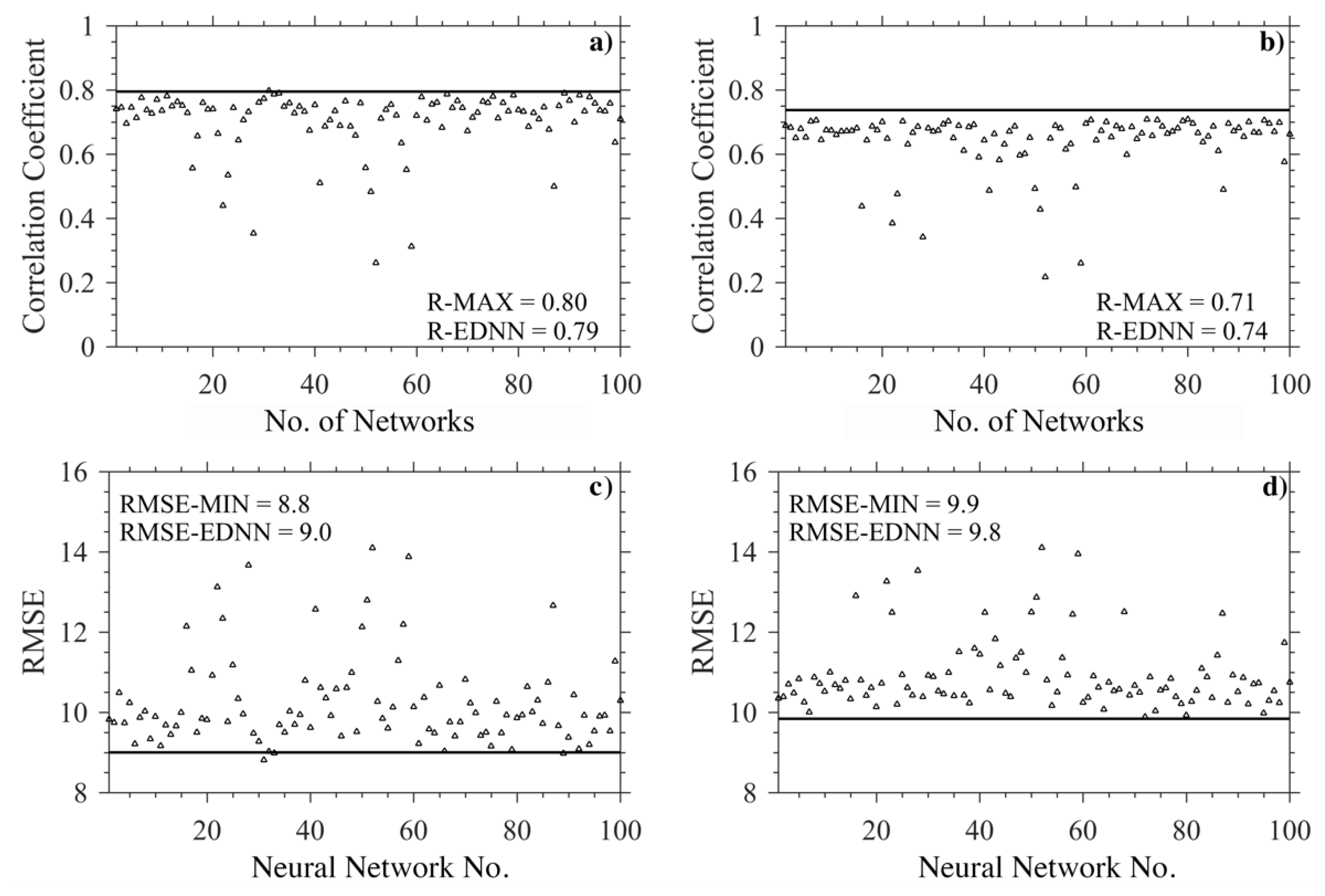
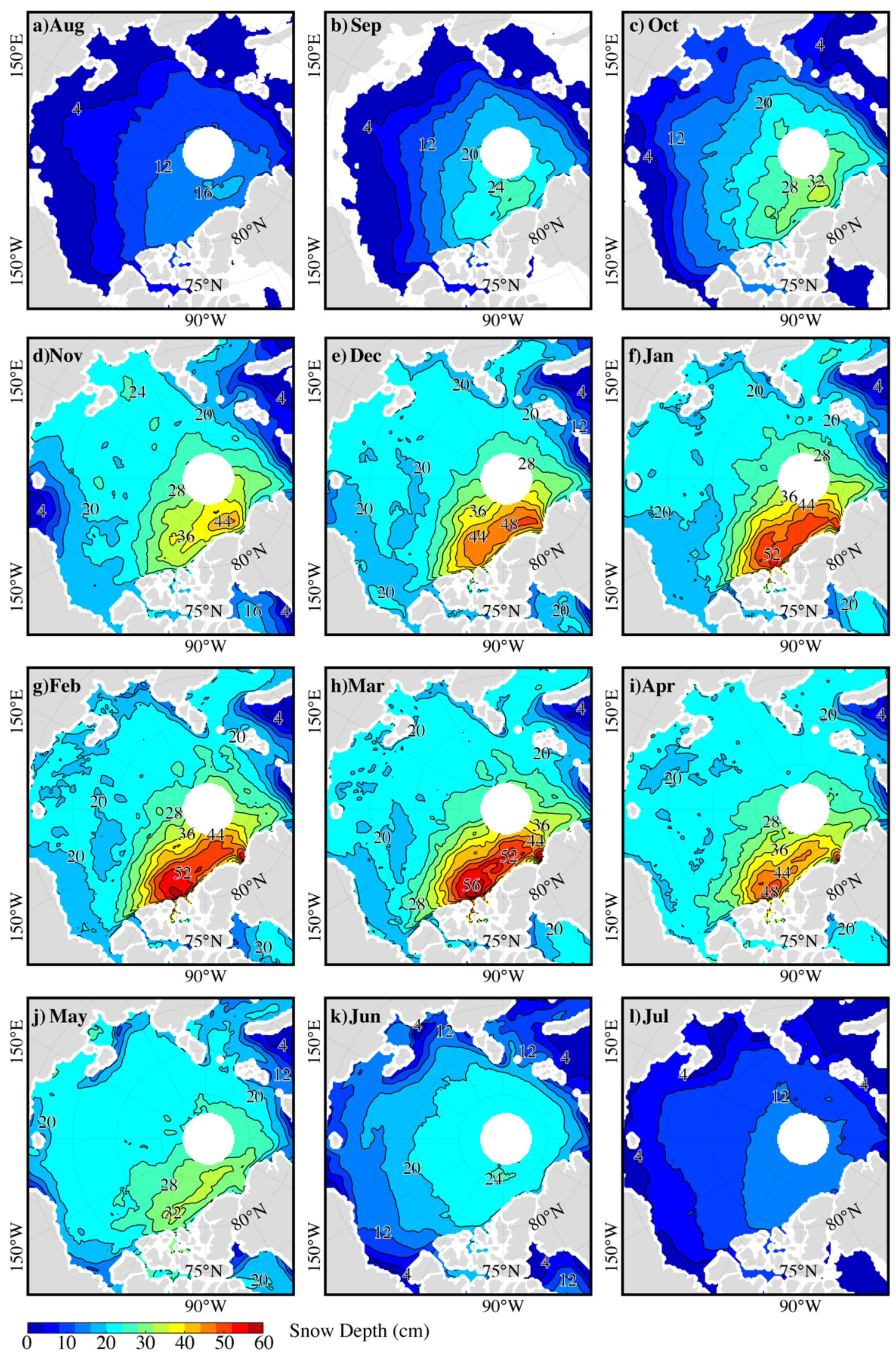
3.1. Ensemble-Based Deep Neural Network
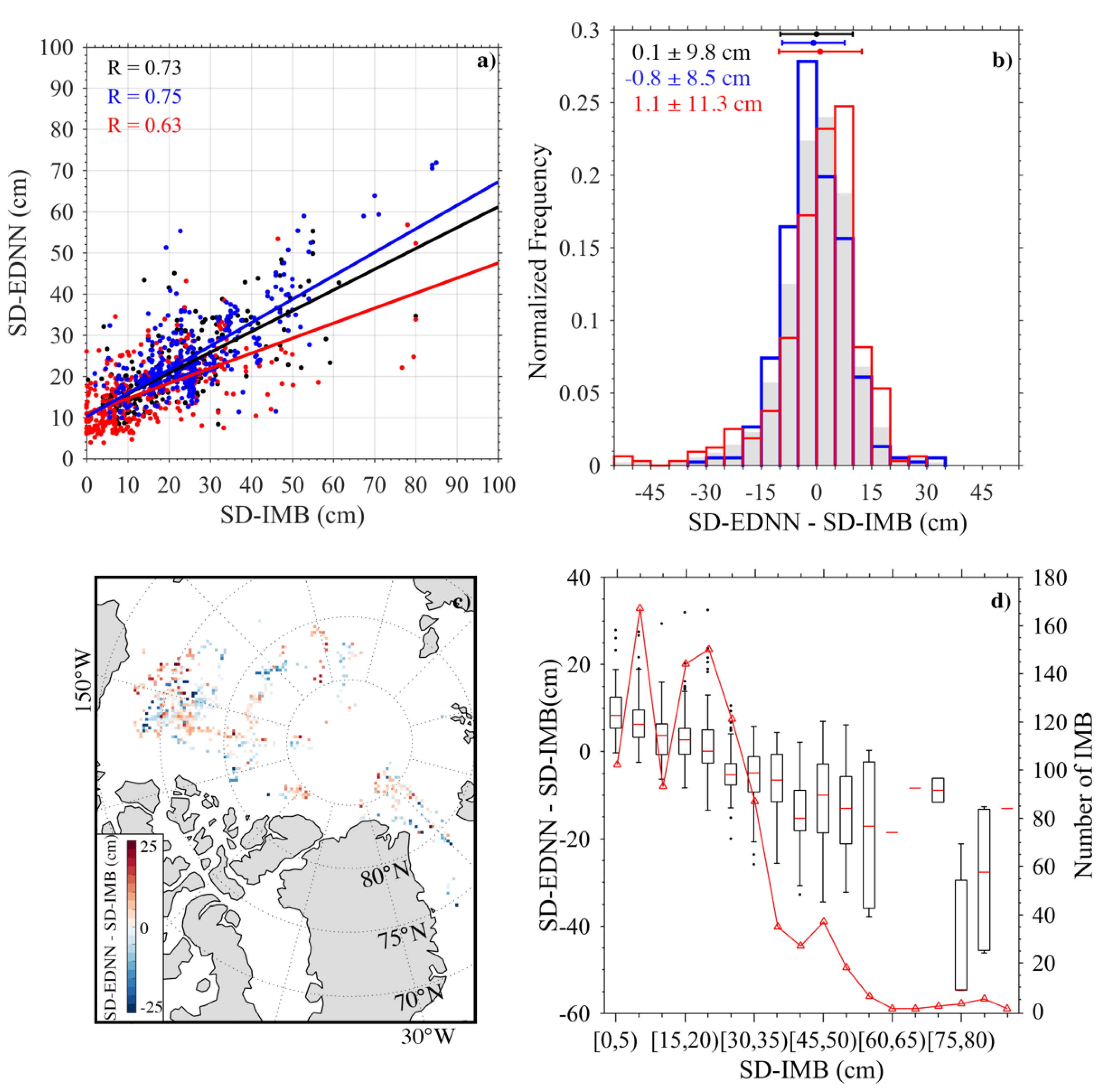
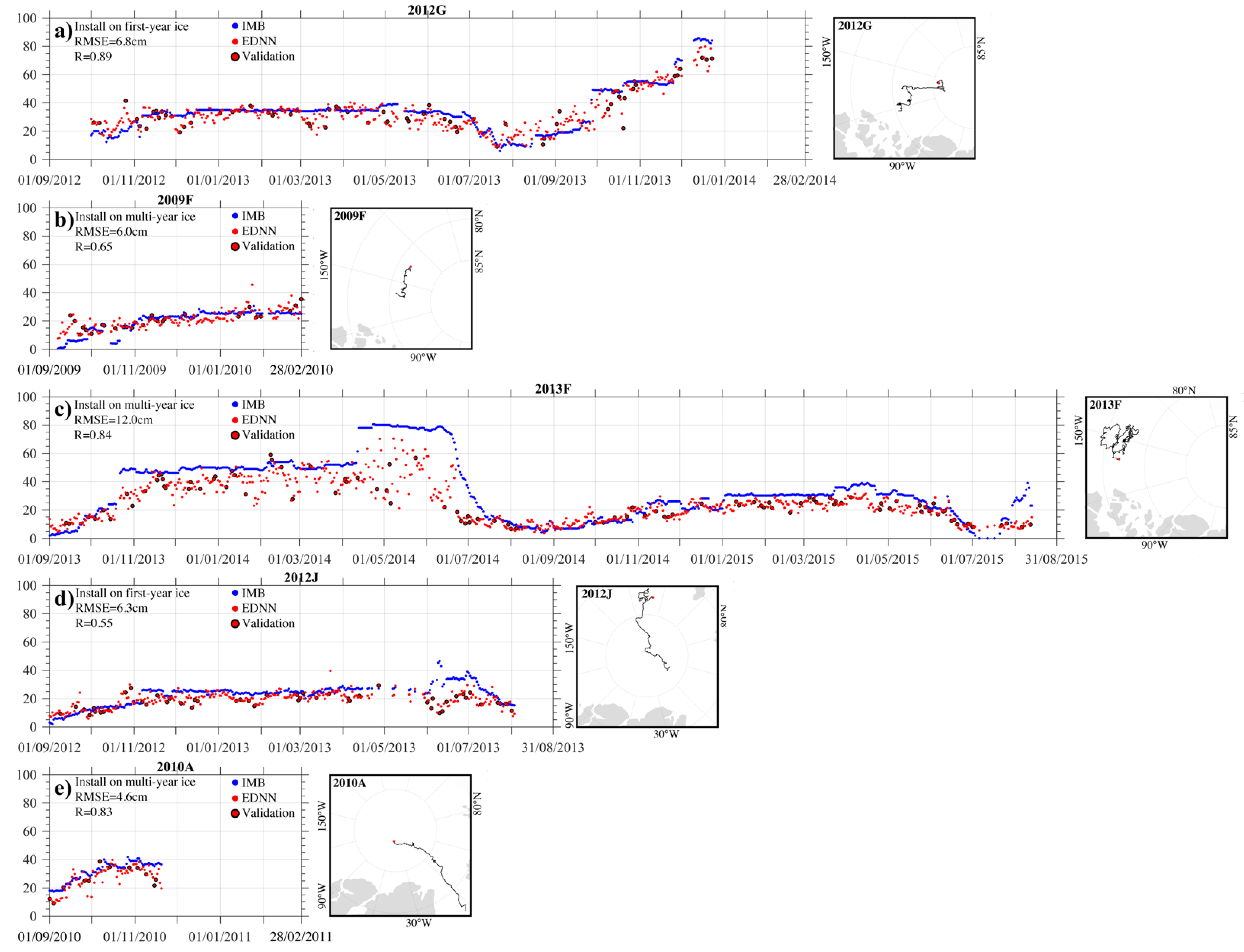
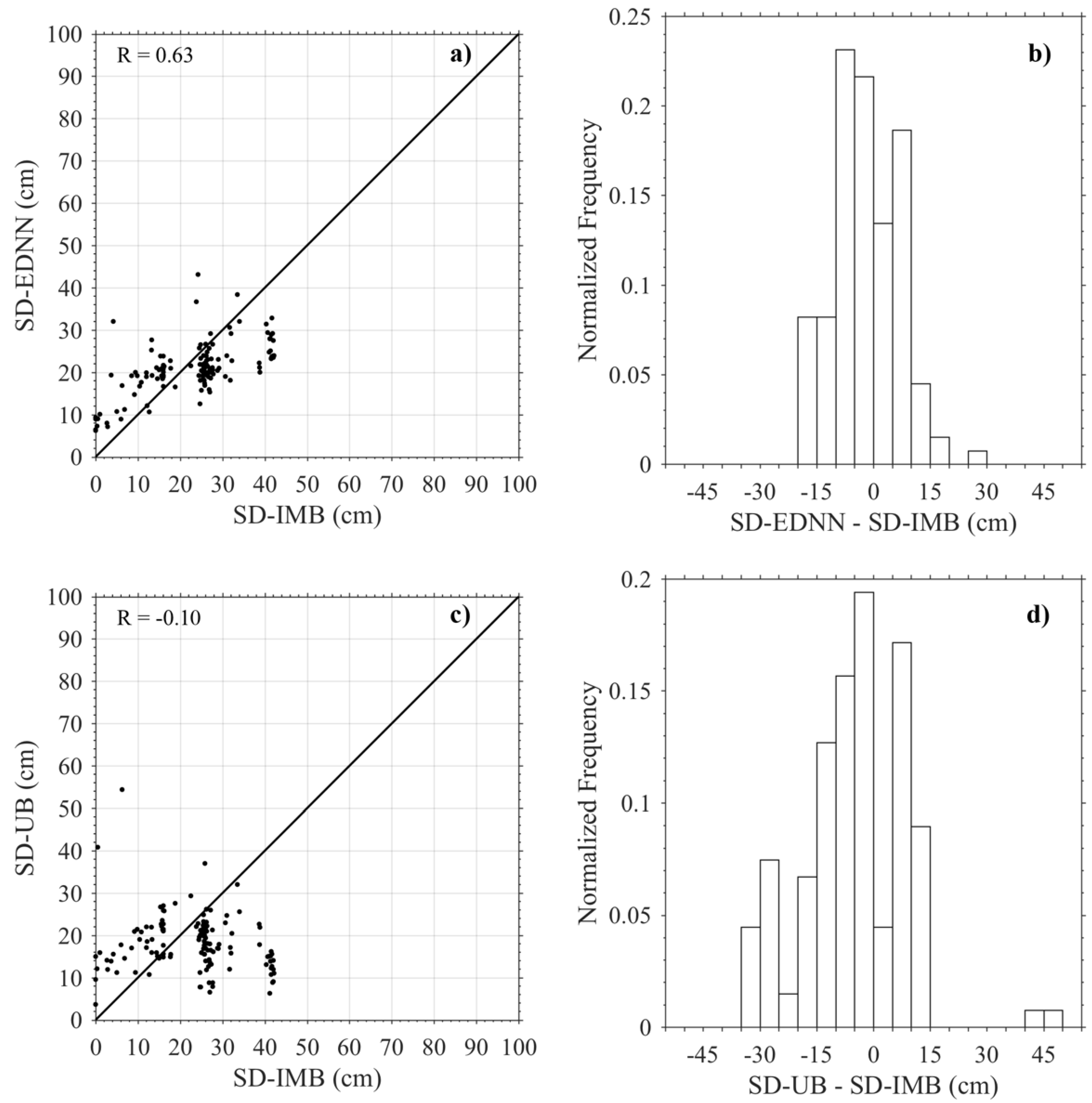
3.2. Comparison with the Validation Data
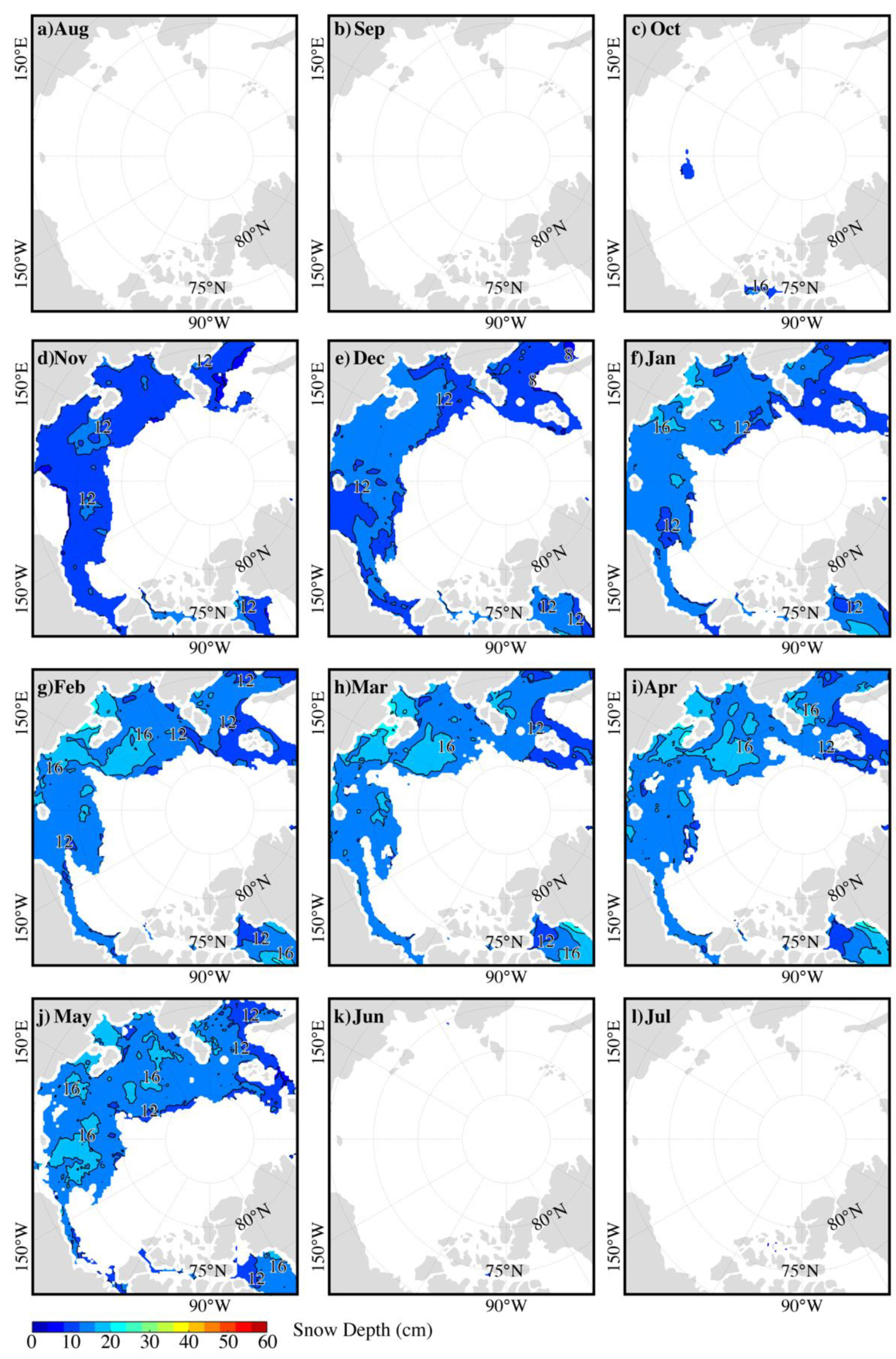
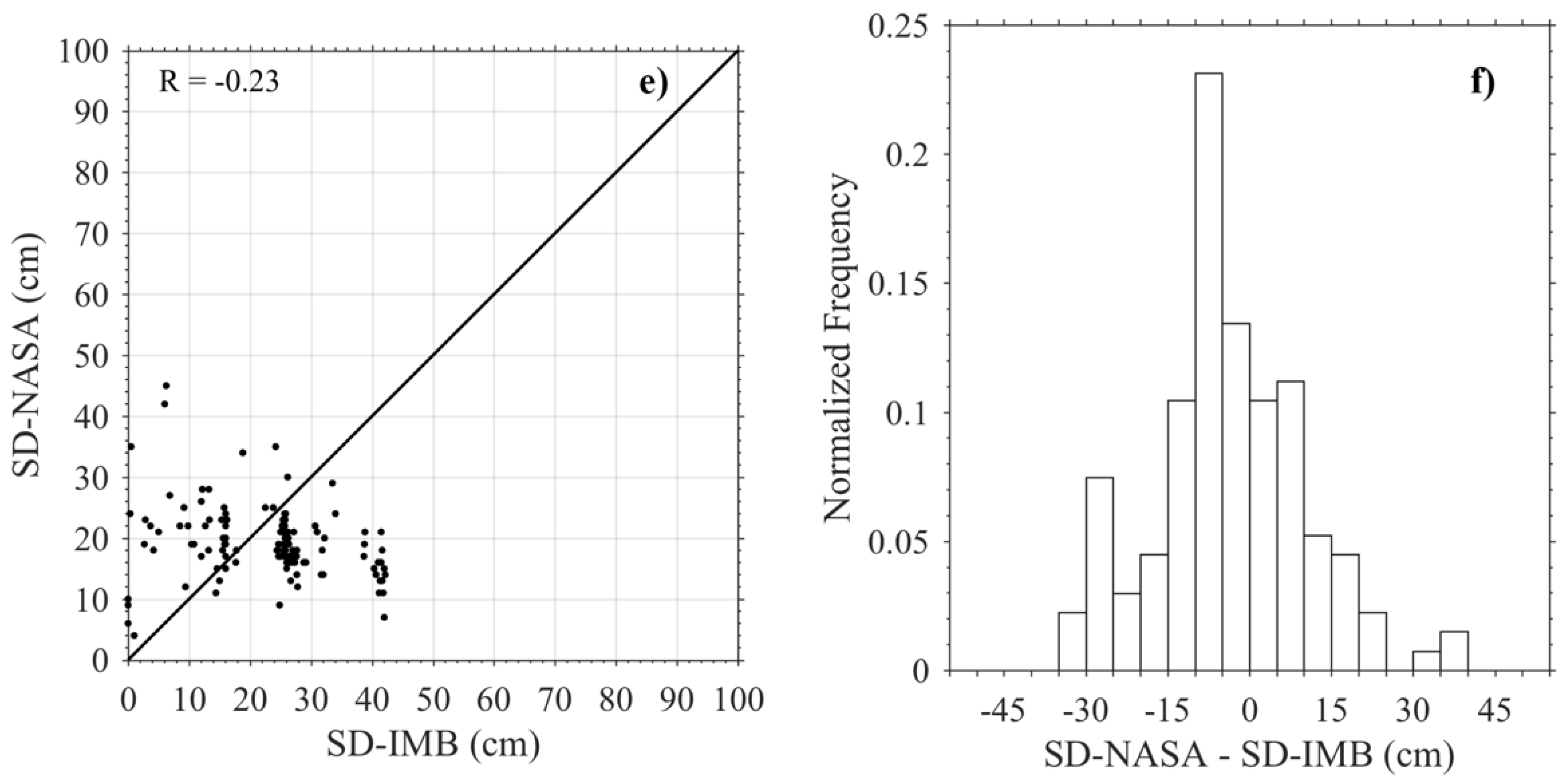
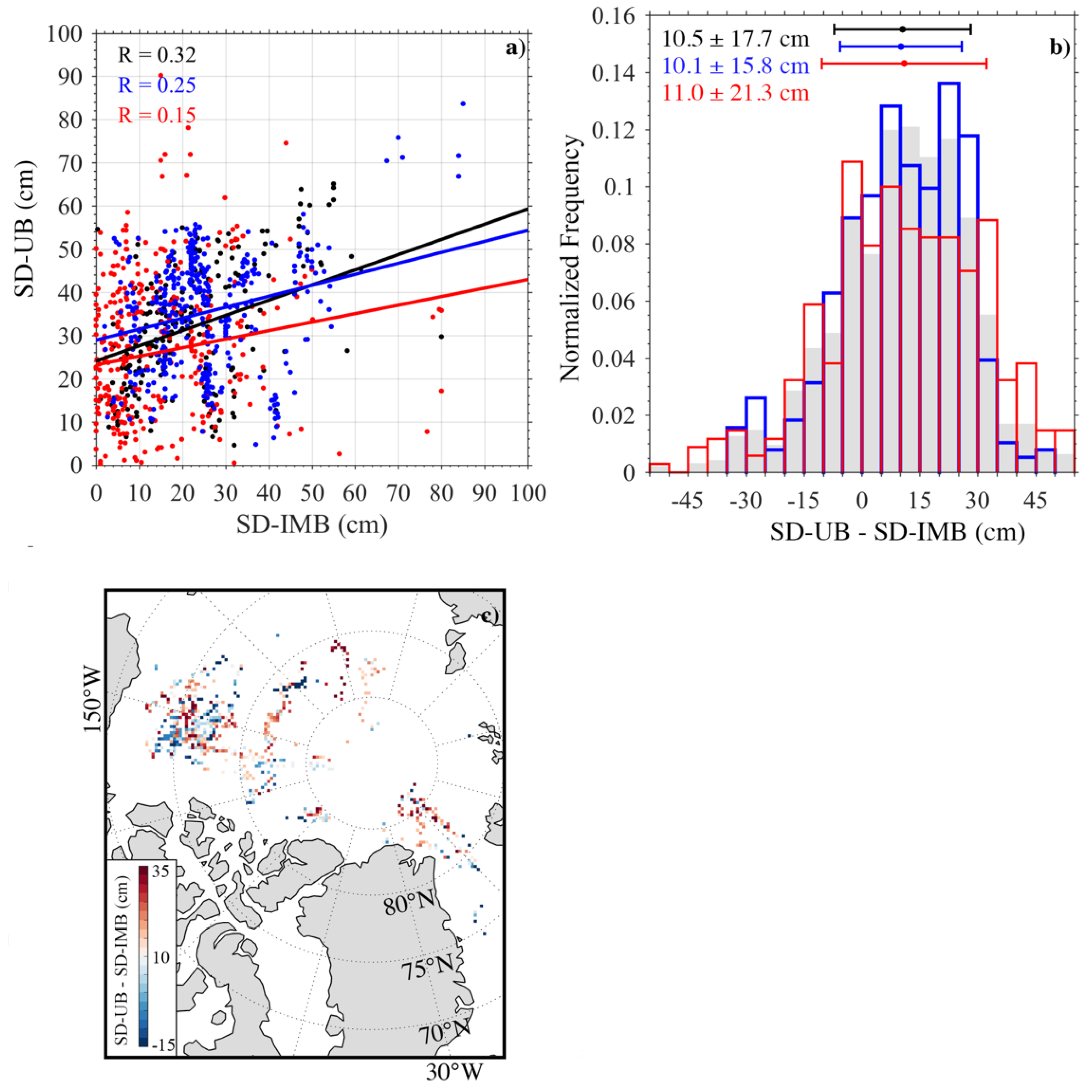
3.3. Comparison with Other Retrieved Snow Depth Data
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Perovich, D.; Grenfell, T.; Light, B.; Hobbs, P. Seasonal evolution of the albedo of multiyear Arctic sea ice. J. Geophys. Res. Ocean. 2002, 107, SHE 20-1–SHE 20-13. [Google Scholar] [CrossRef]
- Sturm, M.; Perovich, D.K.; Holmgren, J. Thermal conductivity and heat transfer through the snow on the ice of the Beaufort Sea. J. Geophys. Res. Ocean. 2002, 107, SHE 19-1–SHE 19-17. [Google Scholar] [CrossRef]
- Maykut, G.A.; Untersteiner, N. Some results from a time-dependent thermodynamic model of sea ice. J. Geophys. Res. 1971, 76, 1550–1575. [Google Scholar] [CrossRef]
- Perovich, D.; Polashenski, C.; Arntsen, A.; Stwertka, C. Anatomy of a late spring snowfall on sea ice. Geophys. Res. Lett. 2017, 44, 2802–2809. [Google Scholar] [CrossRef]
- Untersteiner, N.; Badgley, F. The roughness parameters of sea ice. J. Geophys. Res. 1965, 70, 4573–4577. [Google Scholar] [CrossRef]
- Fichefet, T.; Maqueda, M.M. Modelling the influence of snow accumulation and snow-ice formation on the seasonal cycle of the Antarctic sea-ice cover. Clim. Dyn. 1999, 15, 251–268. [Google Scholar] [CrossRef]
- Schröder, D.; Feltham, D.L.; Flocco, D.; Tsamados, M. September Arctic sea-ice minimum predicted by spring melt-pond fraction. Nat. Clim. Chang. 2014, 4, 353. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Horton, R.M.; Hu, Y. Revisiting the potential of melt pond fraction as a predictor for the seasonal Arctic sea ice extent minimum. Environ. Res. Lett. 2015, 10, 054017. [Google Scholar] [CrossRef]
- Alou-Font, E.; Mundy, C.-J.; Roy, S.; Gosselin, M.; Agustí, S. Snow cover affects ice algal pigment composition in the coastal Arctic Ocean during spring. Mar. Ecol. Prog. Ser. 2013, 474, 89–104. [Google Scholar] [CrossRef]
- Lund-Hansen, L.C.; Hawes, I.; Holtegaard Nielsen, M.; Dahllöf, I.; Sorrell, B.K. Summer meltwater and spring sea ice primary production, light climate and nutrients in an Arctic estuary, Kangerlussuaq, west Greenland. Arct. Antarct. Alp. Res. 2018, 50, S100025. [Google Scholar] [CrossRef]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef]
- Kern, S.; Ozsoy-Çiçek, B. Satellite remote sensing of snow depth on Antarctic sea ice: An inter-comparison of two empirical approaches. Remote Sens. 2016, 8, 450. [Google Scholar] [CrossRef]
- Webster, M.; Gerland, S.; Holland, M.; Hunke, E.; Kwok, R.; Lecomte, O.; Massom, R.; Perovich, D.; Sturm, M. Snow in the changing sea-ice systems. Nat. Clim. Chang. 2018, 8, 946–953. [Google Scholar] [CrossRef]
- Warren, S.G.; Rigor, I.G.; Untersteiner, N.; Radionov, V.F.; Bryazgin, N.N.; Aleksandrov, Y.I.; Colony, R. Snow depth on Arctic sea ice. J. Clim. 1999, 12, 1814–1829. [Google Scholar] [CrossRef]
- Bunzel, F.; Notz, D.; Pedersen, L.T. Retrievals of Arctic sea-ice volume and its trend significantly affected by interannual snow variability. Geophys. Res. Lett. 2018, 45, 11751–11759. [Google Scholar] [CrossRef]
- Gerland, S.; Barber, D.; Meier, W.; Mundy, C.J.; Holland, M.; Kern, S.; Li, Z.; Michel, C.; Perovich, D.K.; Tamura, T. Essential gaps and uncertainties in the understanding of the roles and functions of Arctic sea ice. Environ. Res. Lett. 2019, 14, 043002. [Google Scholar] [CrossRef]
- Shalina, E.V.; Sandven, S. Snow depth on Arctic sea ice from historical in situ data. Cryosphere 2018, 12, 1867–1886. [Google Scholar] [CrossRef]
- Dai, A.; Luo, D.; Song, M.; Liu, J. Arctic amplification is caused by sea-ice loss under increasing CO2. Nat. Commun. 2019, 10, 121. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic sea ice cover. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Kwok, R. Arctic sea ice thickness, volume, and multiyear ice coverage: Losses and coupled variability (1958–2018). Environ. Res. Lett. 2018, 13, 105005. [Google Scholar] [CrossRef]
- Webster, M.A.; Rigor, I.G.; Nghiem, S.V.; Kurtz, N.T.; Farrell, S.L.; Perovich, D.K.; Sturm, M. Interdecadal changes in snow depth on Arctic sea ice. J. Geophys. Res. Ocean. 2014, 119, 5395–5406. [Google Scholar] [CrossRef]
- Kurtz, N.T.; Farrell, S.L. Large-scale surveys of snow depth on Arctic sea ice from Operation IceBridge. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Giles, K.; Laxon, S.; Wingham, D.; Wallis, D.; Krabill, W.; Leuschen, C.; McAdoo, D.; Manizade, S.; Raney, R. Combined airborne laser and radar altimeter measurements over the Fram Strait in May 2002. Remote Sens. Environ. 2007, 111, 182–194. [Google Scholar] [CrossRef]
- Uttal, T.; Curry, J.A.; McPhee, M.G.; Perovich, D.K.; Moritz, R.E.; Maslanik, J.A.; Guest, P.S.; Stern, H.L.; Moore, J.A.; Turenne, R. Surface heat budget of the Arctic Ocean. Bull. Am. Meteorol. Soc. 2002, 83, 255–276. [Google Scholar] [CrossRef]
- Sturm, M.; Holmgren, J.; Perovich, D.K. Winter snow cover on the sea ice of the Arctic Ocean at the Surface Heat Budget of the Arctic Ocean (SHEBA): Temporal evolution and spatial variability. J. Geophys. Res. Ocean. 2002, 107, SHE 23-1–SHE 23-17. [Google Scholar] [CrossRef]
- Richter-Menge, J.A.; Perovich, D.K.; Elder, B.C.; Claffey, K.; Rigor, I.; Ortmeyer, M. Ice mass-balance buoys: A tool for measuring and attributing changes in the thickness of the Arctic sea-ice cover. Ann. Glaciol. 2006, 44, 205–210. [Google Scholar] [CrossRef]
- Brucker, L.; Markus, T. Arctic-scale assessment of satellite passive microwave-derived snow depth on sea ice using Operation IceBridge airborne data. J. Geophys. Res. Ocean. 2013, 118, 2892–2905. [Google Scholar] [CrossRef]
- Rösel, A.; Itkin, P.; King, J.; Divine, D.; Wang, C.; Granskog, M.A.; Krumpen, T.; Gerland, S. Thin sea ice, thick snow, and widespread negative freeboard observed during N-ICE2015 north of Svalbard. J. Geophys. Res. Ocean. 2018, 123, 1156–1176. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, C.T.; Chang, A.T.; Guo, J.; Ding, K.H. Dense media radiative transfer theory based on quasicrystalline approximation with applications to passive microwave remote sensing of snow. Radio Sci. 2000, 35, 731–749. [Google Scholar] [CrossRef]
- Langlois, A.; Barber, D.G. Passive microwave remote sensing of seasonal snow-covered sea ice. Prog. Phys. Geogr. 2007, 31, 539–573. [Google Scholar] [CrossRef]
- Markus, T.; Powell, D.C.; Wang, J.R. Sensitivity of passive microwave snow depth retrievals to weather effects and snow evolution. IEEE Trans. Geosci. Remote Sens. 2006, 44, 68–77. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J.; Gasiewski, A.J.; Klein, M.; Maslanik, J.A.; Powell, D.C.; Stankov, B.B.; Stroeve, J.C.; Sturm, M. Microwave signatures of snow on sea ice: Observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3081–3090. [Google Scholar] [CrossRef]
- Drobot, S.D.; Barber, D.G. Towards development of a snow water equivalence (SWE) algorithm using microwave radiometry over snow covered first-year sea ice. Photogramm. Eng. Remote Sens. 1998, 64, 415–423. [Google Scholar]
- Rostosky, P.; Spreen, G.; Farrell, S.L.; Frost, T.; Heygster, G.; Melsheimer, C. Snow depth retrieval on Arctic sea ice from passive microwave radiometers—Improvements and extensions to multiyear ice using lower frequencies. J. Geophys. Res. Ocean. 2018, 123, 7120–7138. [Google Scholar] [CrossRef]
- Chang, A.; Foster, J.; Hall, D.K. Nimbus-7 SMMR derived global snow cover parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef]
- Kaleschke, L.; Maaß, N.; Haas, C.; Hendricks, S.; Heygster, G.; Tonboe, R. A sea-ice thickness retrieval model for 1.4 GHz radiometry and application to airborne measurements over low salinity sea-ice. Cryosphere 2010, 4, 583–592. [Google Scholar] [CrossRef]
- Maaß, N.; Kaleschke, L.; Tian-Kunze, X.; Drusch, M. Snow thickness retrieval over thick Arctic sea ice using SMOS satellite data. Cryosphere 2013, 7, 1971–1989. [Google Scholar] [CrossRef]
- Zhou, L.; Xu, S.; Liu, J.; Wang, B. On the retrieval of sea ice thickness and snow depth using concurrent laser altimetry and L-band remote sensing data. Cryosphere 2018, 12, 993–1012. [Google Scholar] [CrossRef]
- Lawrence, I.R.; Tsamados, M.C.; Stroeve, J.C.; Armitage, T.W.; Ridout, A.L. Estimating snow depth over Arctic sea ice from calibrated dual-frequency radar freeboards. Cryosphere 2018, 12, 3551–3564. [Google Scholar] [CrossRef]
- Zwally, H.J.; Yi, D.; Kwok, R.; Zhao, Y. ICESat measurements of sea ice freeboard and estimates of sea ice thickness in the Weddell Sea. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Nandan, V.; Geldsetzer, T.; Yackel, J.; Mahmud, M.; Scharien, R.; Howell, S.; King, J.; Ricker, R.; Else, B. Effect of snow salinity on CryoSat-2 Arctic first-year sea ice freeboard measurements. Geophys. Res. Lett. 2017, 44, 10419–10426. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J. Snow depth distribution over sea ice in the Southern Ocean from satellite passive microwave data. Antarct. Sea Ice Phys. Process. Interact. Var. 1998, 74, 19–39. [Google Scholar]
- Kelly, R.E.; Chang, A.T.; Tsang, L.; Foster, J.L. A prototype AMSR-E global snow area and snow depth algorithm. IEEE Trans. Geosci. Remote Sens. 2003, 41, 230–242. [Google Scholar] [CrossRef]
- Comiso, J.C.; Cavalieri, D.J.; Markus, T. Sea ice concentration, ice temperature, and snow depth using AMSR-E data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 243–252. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Markus, T.; Ivanoff, A.; Miller, J.A.; Brucker, L.; Sturm, M.; Maslanik, J.A.; Heinrichs, J.F.; Gasiewski, A.J.; Leuschen, C. A comparison of snow depth on sea ice retrievals using airborne altimeters and an AMSR-E simulator. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3027–3040. [Google Scholar] [CrossRef]
- Kilic, L.; Tonboe, R.T.; Prigent, C.; Heygster, G. Estimating the snow depth, the snow–ice interface temperature, and the effective temperature of Arctic sea ice using Advanced Microwave Scanning Radiometer 2 and ice mass balance buoy data. Cryosphere 2019, 13, 1283–1296. [Google Scholar] [CrossRef]
- Guerreiro, K.; Fleury, S.; Zakharova, E.; Rémy, F.; Kouraev, A. Potential for estimation of snow depth on Arctic sea ice from CryoSat-2 and SARAL/AltiKa missions. Remote Sens. Environ. 2016, 186, 339–349. [Google Scholar] [CrossRef]
- Tsang, L.; Chen, Z.; Oh, S.; Marks, R.J.; Chang, A.T. Inversion of snow parameters from passive microwave remote sensing measurements by a neural network trained with a multiple scattering model. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1015–1024. [Google Scholar] [CrossRef]
- Davis, D.T.; Chen, Z.; Tsang, L.; Hwang, J.-N.; Chang, A.T. Retrieval of snow parameters by iterative inversion of a neural network. IEEE Trans. Geosci. Remote Sens. 1993, 31, 842–852. [Google Scholar] [CrossRef]
- Tedesco, M.; Pulliainen, J.; Takala, M.; Hallikainen, M.; Pampaloni, P. Artificial neural network-based techniques for the retrieval of SWE and snow depth from SSM/I data. Remote Sens. Environ. 2004, 90, 76–85. [Google Scholar] [CrossRef]
- Tedesco, M.; Jeyaratnam, J. A new operational snow retrieval algorithm applied to historical AMSR-E brightness temperatures. Remote Sens. 2016, 8, 1037. [Google Scholar] [CrossRef]
- Braakmann-Folgmann, A.; Donlon, C. Estimating snow depth on Arctic sea ice using satellite microwave radiometry and a neural network. Cryosphere 2019, 13, 2421–2438. [Google Scholar] [CrossRef]
- Maslanik, J.A.; Stroeve, J.C. DMSP SSM/I-SSMIS Daily Polar Gridded Brightness Temperatures, Version 4. Available online: https://nsidc.org/data/nsidc-0001 (accessed on 1 April 2019).
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1. Available online: https://nsidc.org/data/nsidc-0051 (accessed on 1 April 2019).
- Perovich, D.; Richter-Menge, J.; Polashenski, C. Observing and Understanding Climate Change: Monitoring the Mass Balance, Motion, and Thickness of Arctic Sea Ice. Available online: http://imb-crrel-dartmouth.org (accessed on 1 April 2019).
- Blanchard-Wrigglesworth, E.; Webster, M.; Farrell, S.; Bitz, C. Reconstruction of snow on Arctic sea ice. J. Geophys. Res. Ocean. 2018, 123, 3588–3602. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C. Lessons in Neural Network Training: Overfitting May be Harder than Expected. In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Innovative Applications of Artificial Intelligence Conference; AAAI Press: Menlo Park, CA, USA, 1997; pp. 540–545. [Google Scholar]
- Snow Depth Product Archived at the NASA Cryosphere Science Research Portal. Available online: https://neptune.gsfc.nasa.gov/csb/index.php?section=53 (accessed on 1 April 2019).
- Snow Depth Product Archived at the Sea Ice Remote Sensing Group of the University of Bremen. Available online: https://seaice.uni-bremen.de/data/amsre/snow_daygrid (accessed on 1 April 2019).
- Snow Depth Product Archived at the Sea Ice Remote Sensing Group of the University of Bremen. Available online: https://seaice.uni-bremen.de/data/amsr2/snow_daygrid (accessed on 1 April 2019).
- Lee, A.; Geem, Z.; Suh, K.-D. Determination of optimal initial weights of an artificial neural network by using the harmony search algorithm: Application to breakwater armor stones. Appl. Sci. 2016, 6, 164. [Google Scholar] [CrossRef]
- Maslanik, J.; Stroeve, J.; Fowler, C.; Emery, W. Distribution and trends in Arctic sea ice age through spring 2011. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Peng, G.; Steele, M.; Bliss, A.; Meier, W.; Dickinson, S. Temporal means and variability of Arctic sea ice melt and freeze season climate indicators using a satellite climate data record. Remote Sens. 2018, 10, 1328. [Google Scholar] [CrossRef]
- Petty, A.A.; Webster, M.; Boisvert, L.; Markus, T. The NASA Eulerian Snow on Sea Ice Model (NESOSIM) v1. 0: Initial model development and analysis. Geosci. Model Dev. 2018, 11, 4577–4602. [Google Scholar] [CrossRef]

| Data Set | Spatial Resolution | Temporal Resolution |
|---|---|---|
| SD-NASA | 25 km | 1978.11–2018.06 |
| SD-UB | 6.25 km | 2002.06–2011.09; 2012.07–2018.12 |
| SD-EDNN (cm) | SD-UB (cm) | |||
|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | |
| All | 0.1 | 9.8 | 10.5 | 17.7 |
| Freeze-up | −0.8 | 8.5 | 10.1 | 15.8 |
| Melting | 1.1 | 11.3 | 11.0 | 21.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Y.; Cheng, X.; Hu, Y. Retrieval of Snow Depth over Arctic Sea Ice Using a Deep Neural Network. Remote Sens. 2019, 11, 2864. https://doi.org/10.3390/rs11232864
Liu J, Zhang Y, Cheng X, Hu Y. Retrieval of Snow Depth over Arctic Sea Ice Using a Deep Neural Network. Remote Sensing. 2019; 11(23):2864. https://doi.org/10.3390/rs11232864
Chicago/Turabian StyleLiu, Jiping, Yuanyuan Zhang, Xiao Cheng, and Yongyun Hu. 2019. "Retrieval of Snow Depth over Arctic Sea Ice Using a Deep Neural Network" Remote Sensing 11, no. 23: 2864. https://doi.org/10.3390/rs11232864
APA StyleLiu, J., Zhang, Y., Cheng, X., & Hu, Y. (2019). Retrieval of Snow Depth over Arctic Sea Ice Using a Deep Neural Network. Remote Sensing, 11(23), 2864. https://doi.org/10.3390/rs11232864