Effects of Distinguishing Vegetation Types on the Estimates of Remotely Sensed Evapotranspiration in Arid Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Models and Estimating Process
2.2. Site Description and Measurements
2.3. Data and Processing
2.3.1. Daily ET and ET0 Data
2.3.2. Landsat OLI Imagery and Processing
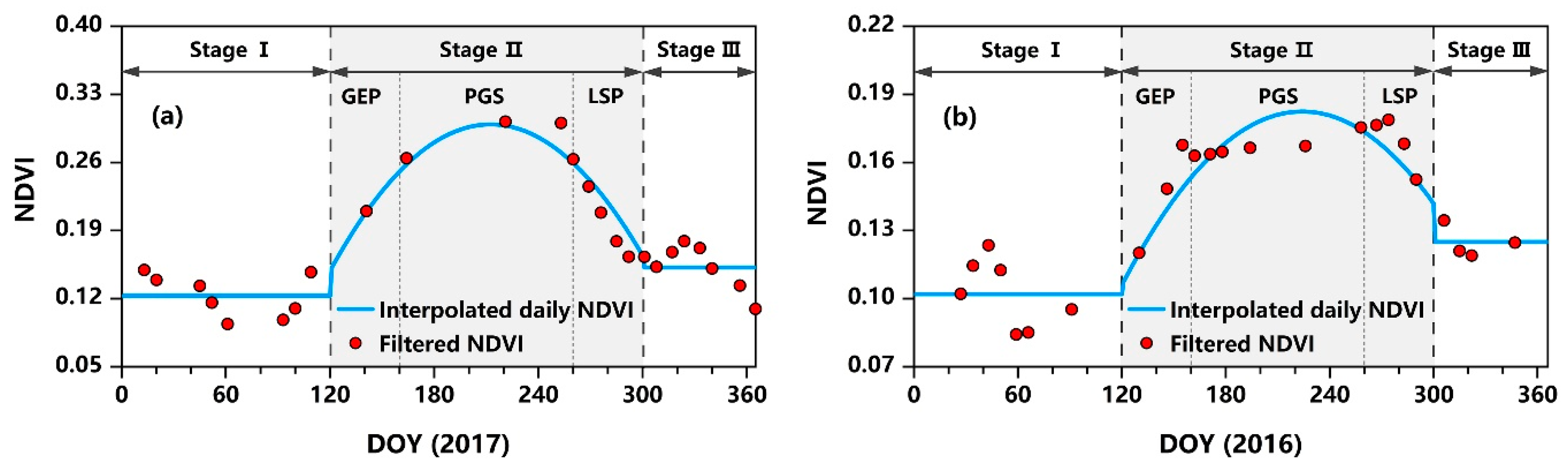
2.3.3. Derivation of NDVI
2.3.4. Statistical Analyses
2.4. Evaluation of Model Performance
3. Results
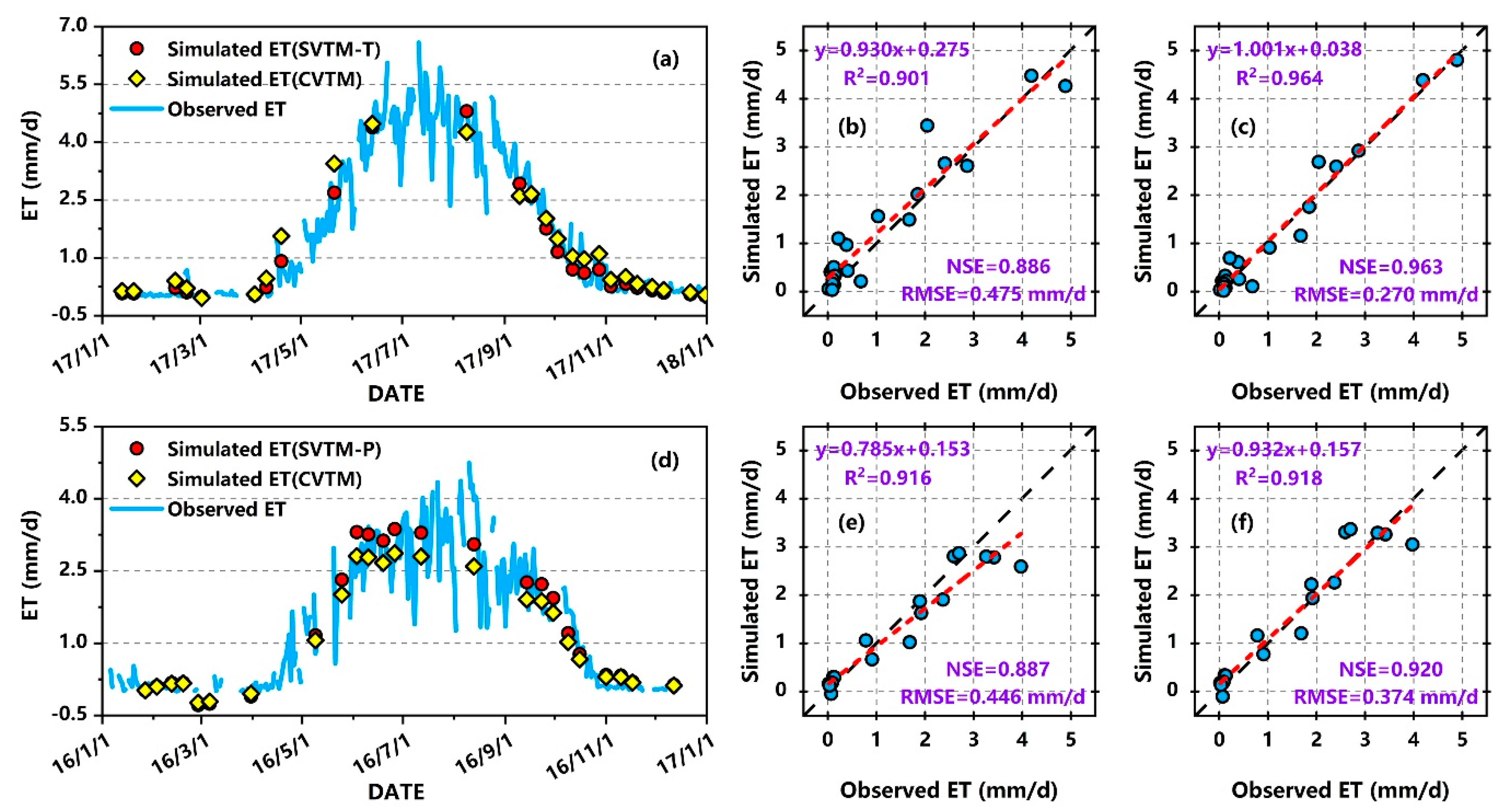
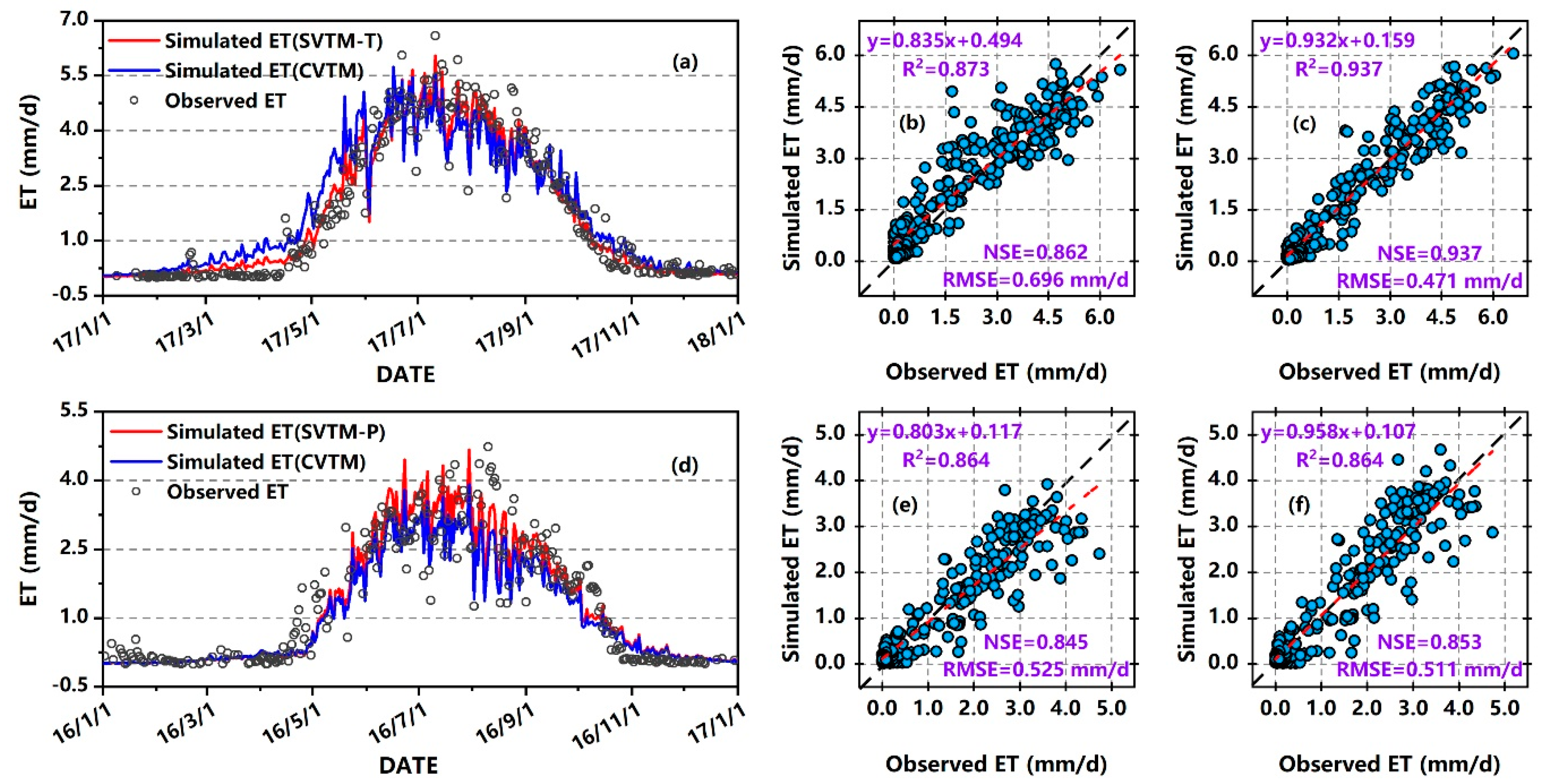
3.1. Calibration and Validation of CVTM and SVTM
3.2. Comparison of Estimates from CVTM and SVTM
3.2.1. Estimation Accuracy at Site Scale
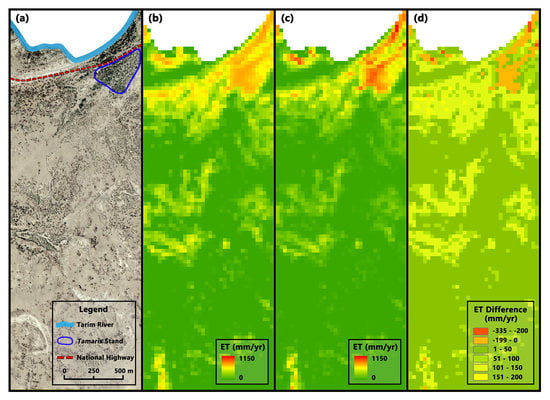
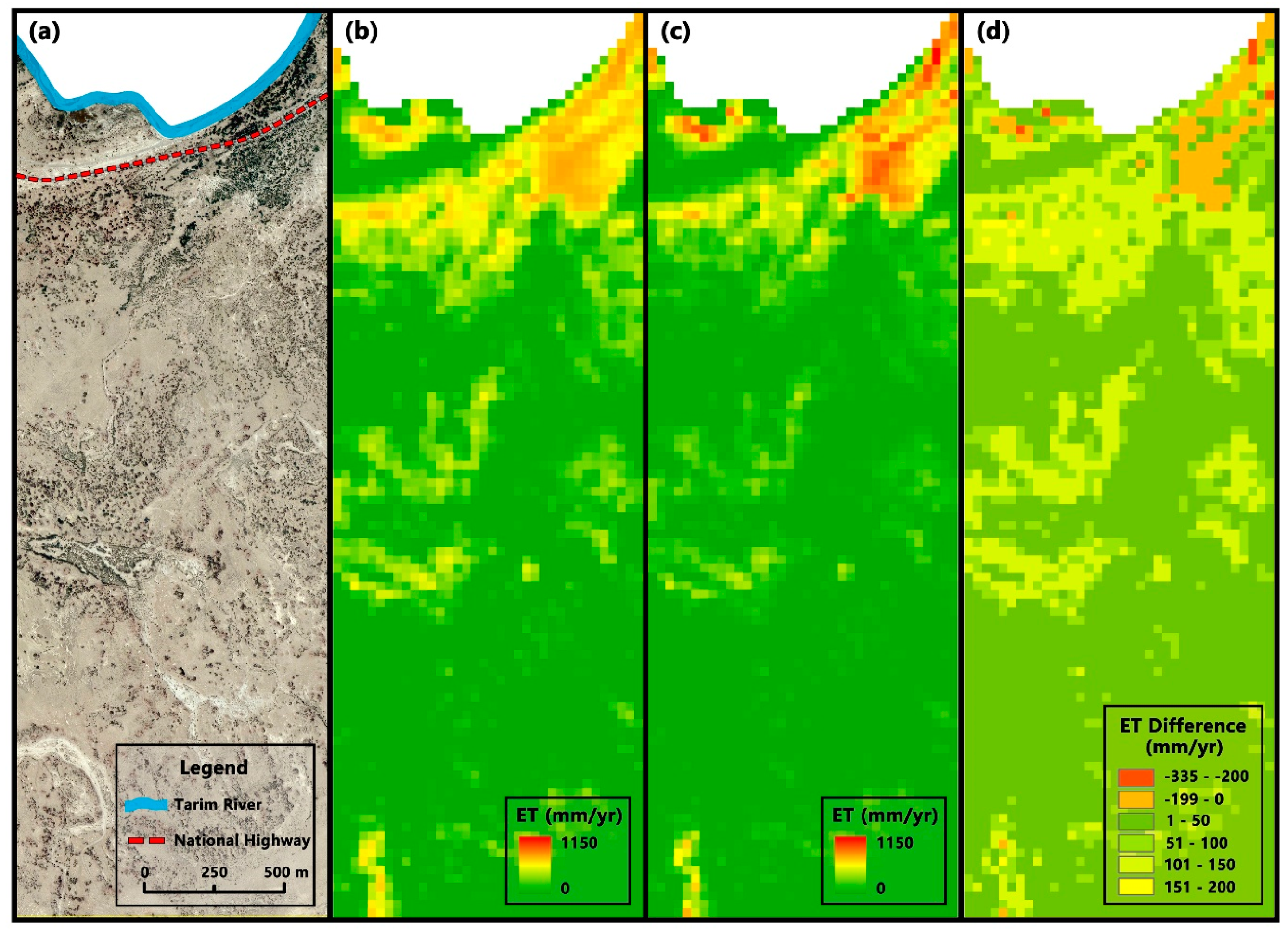
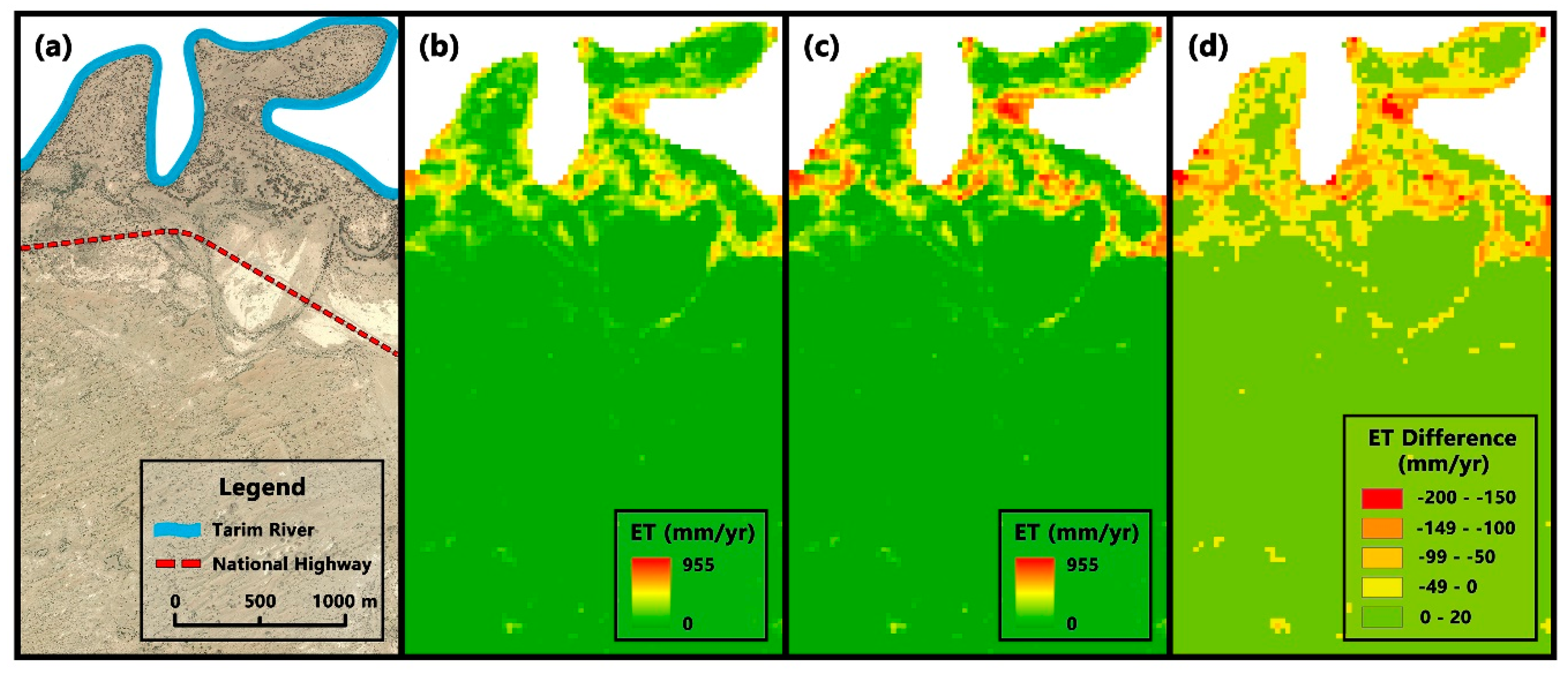
3.2.2. Differences in Regional Scale
4. Discussion
4.1. Effects of Distinguishing Vegetation Types
4.2. Feasibility of the Application of SVTM
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Wang, S.; Pan, M.; Mu, Q.; Shi, X.; Mao, J.; Brümmer, C.; Jassal, R.S.; Krishnan, P.; Li, J.; Black, T.A. Comparing Evapotranspiration from Eddy Covariance Measurements, Water Budgets, Remote Sensing, and Land Surface Models over Canada. J. Hydrometeorol. 2015, 16, 1540–1560. [Google Scholar] [CrossRef]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ. 2006, 105, 271–285. [Google Scholar] [CrossRef]
- Cleverly, J.R.; Dahm, C.N.; Thibault, J.R.; Mcdonnell, D.E.; Coonrod, J.E.A. Riparian ecohydrology: Regulation of water flux from the ground to the atmosphere in the Middle Rio Grande, New Mexico. Hydrol. Process. 2006, 20, 3207–3225. [Google Scholar] [CrossRef]
- Falkenmark, M.; Rockström, J. Balancing Water for Humans and Nature: The New Approach in Ecohydrology; Earthscan: London, UK, 2004. [Google Scholar]
- Nagler, P.L.; Cleverly, J.; Glenn, E.; Lampkin, D.; Huete, A.; Wan, Z. Predicting riparian evapotranspiration from MODIS vegetation indices and meteorological data. Remote Sens. Environ. 2005, 94, 17–30. [Google Scholar] [CrossRef]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western US rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ. 2005, 97, 337–351. [Google Scholar] [CrossRef]
- Groeneveld, D.P.; Baugh, W.M.; Sanderson, J.S.; Cooper, D.J. Annual groundwater evapotranspiration mapped from single satellite scenes. J. Hydrol. 2007, 344, 146–156. [Google Scholar] [CrossRef]
- Scott, R.L.; Cable, W.L.; Huxman, T.E.; Nagler, P.L.; Hernandez, M.; Goodrich, D.C. Multiyear riparian evapotranspiration and groundwater use for a semiarid watershed. J. Arid Environ. 2008, 72, 1232–1246. [Google Scholar] [CrossRef]
- Nagler, P.L.; Morino, K.; Murray, R.S.; Osterberg, J.; Glenn, E.P. An Empirical Algorithm for Estimating Agricultural and Riparian Evapotranspiration Using MODIS Enhanced Vegetation Index and Ground Measurements of ET. I. Description of Method. Remote Sens. 2009, 1, 1273–1297. [Google Scholar] [CrossRef]
- Nagler, P.L.; Glenn, E.P.; Nguyen, U.; Scott, R.L.; Doody, T. Estimating riparian and agricultural actual evapotranspiration by reference evapotranspiration and MODIS enhanced vegetation index. Remote Sens. 2013, 5, 3849–3871. [Google Scholar] [CrossRef]
- Bunting, D.P.; Kurc, S.A.; Glenn, E.P.; Nagler, P.L.; Scott, R.L. Insights for empirically modeling evapotranspiration influenced by riparian and upland vegetation in semiarid regions. J. Arid Environ. 2014, 111, 42–52. [Google Scholar] [CrossRef]
- Glenn, E.P.; Scott, R.L.; Nguyen, U.; Nagler, P.L. Wide-area ratios of evapotranspiration to precipitation in monsoon-dependent semiarid vegetation communities. J. Arid Environ. 2015, 117, 84–95. [Google Scholar] [CrossRef]
- Yuan, G.; Zhu, X.; Tang, X.; Du, T.; Yi, X. A Species-Specific and spatially-Explicit Model for Estimating Vegetation Water Requirements in Desert Riparian Forest Zones. Water Resour. Manag. 2016, 30, 1–19. [Google Scholar] [CrossRef]
- Groeneveld, D.P. Remotely-sensed groundwater evapotranspiration from alkali scrub affected by declining water table. J. Hydrol. 2008, 358, 294–303. [Google Scholar] [CrossRef]
- Murray, R.S.; Nagler, P.L.; Morino, K.; Glenn, E.P. An Empirical Algorithm for Estimating Agricultural and Riparian Evapotranspiration Using MODIS Enhanced Vegetation Index and Ground Measurements of ET. II. Application to the Lower Colorado River, U.S. Remote Sens. 2009, 1, 1125–1138. [Google Scholar] [CrossRef]
- Nagler, P.L.; Pearlstein, S.; Glenn, E.P.; Brown, T.B.; Bateman, H.L.; Bean, D.W.; Hultine, K.R. Rapid dispersal of saltcedar (Tamarix spp.) biocontrol beetles (Diorhabda carinulata) on a desert river detected by phenocams, MODIS imagery and ground observations. Remote Sens. Environ. 2014, 140, 206–219. [Google Scholar] [CrossRef]
- Nagler, P.L.; Doody, T.M.; Glenn, E.P.; Jarchow, C.J.; Barreto-Muñoz, A.; Didan, K. Wide-area estimates of evapotranspiration by red gum (Eucalyptus camaldulensis) and associated vegetation in the Murray–Darling River Basin, Australia. Hydrol. Process. 2016, 30, 1376–1387. [Google Scholar] [CrossRef]
- Tillman, F.D.; Wiele, S.M.; Pool, D.R. A comparison of estimates of basin-scale soil-moisture evapotranspiration and estimates of riparian groundwater evapotranspiration with implications for water budgets in the Verde Valley, Central Arizona, USA. J. Arid Environ. 2016, 124, 278–291. [Google Scholar] [CrossRef]
- Jarchow, C.J.; Nagler, P.L.; Glenn, E.P.; Ramírez-Hernández, J.; Rodríguez-Burgueño, J.E. Evapotranspiration by remote sensing: An analysis of the Colorado River Delta before and after the Minute 319 pulse flow to Mexico. Ecol. Eng. 2017, 106, 725–732. [Google Scholar] [CrossRef]
- Khand, K.; Taghvaeian, S.; Hassan-Esfahani, L. Mapping Annual Riparian Water Use Based on the Single-Satellite-Scene Approach. Remote Sens. 2017, 9, 832. [Google Scholar] [CrossRef]
- Knipper, K.; Hogue, T.; Scott, R.; Franz, K. Evapotranspiration Estimates Derived Using Multi-Platform Remote Sensing in a Semiarid Region. Remote Sens. 2017, 9, 184. [Google Scholar] [CrossRef]
- Shanafield, M.; Gutiérrez-Jurado, H.; Rodríguez-Burgueño, J.E.; Ramírez-Hernández, J.; Jarchow, C.J.; Nagler, P.L. Short- and long-term evapotranspiration rates at ecological restoration sites along a large river receiving rare flow events. Hydrol. Process. 2017, 31, 4328–4337. [Google Scholar] [CrossRef]
- Nagler, P.L.; Morino, K.; Didan, K.; Erker, J.; Osterberg, J.; Hultine, K.R.; Glenn, E.P. Wide-area estimates of saltcedar (Tamarix spp.) evapotranspiration on the lower Colorado River measured by heat balance and remote sensing methods. Ecohydrology 2009, 2, 18–33. [Google Scholar] [CrossRef]
- Nagler, P.L.; Nguyen, U.; Bateman, H.L.; Jarchow, C.J.; Glenn, E.P.; Waugh, W.J.; van Riper, C., III. Northern tamarisk beetle (Diorhabda carinulata) and tamarisk (Tamarix spp.) interactions in the Colorado River basin. Restor. Ecol. 2018, 26, 348–359. [Google Scholar] [CrossRef]
- Bresloff, C.J.; Nguyen, U.; Glenn, E.P.; Waugh, J.; Nagler, P.L. Effects of grazing on leaf area index, fractional cover and evapotranspiration by a desert phreatophyte community at a former uranium mill site on the Colorado Plateau. J. Environ. Manag. 2013, 114, 92–104. [Google Scholar] [CrossRef] [PubMed]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating Remote Sensing and Ground Methods to Estimate Evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Eamus, D.; Zolfaghar, S.; Villalobos-Vega, R.; Cleverly, J.; Huete, A. Groundwater-dependent ecosystems: Recent insights from satellite and field-based studies. Hydrol. Earth Syst. Sci. 2015, 19, 4229–4256. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation index methods for estimating evapotranspiration by remote sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Yuan, G.; Luo, Y.; Shao, M.; Zhang, P.; Zhu, X. Evapotranspiration and its main controlling mechanism over the desert riparian forests in the lower Tarim River Basin. Sci. China Earth Sci. 2015, 58, 1–11. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Zhou, H.; Chen, Y.; Hao, X.; Fu, A.; Ma, J. Experimental study on water transport observations of desert riparian forests in the lower reaches of the Tarim River in China. Int. J. Biometeorol. 2017, 61, 1055–1062. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.L.; James Shuttleworth, W.; Goodrich, D.C.; Maddock, T., III. The water use of two dominant vegetation communities in a semiarid riparian ecosystem. Agric. For. Meteorol. 2000, 105, 241–256. [Google Scholar] [CrossRef]
- Satchithanantham, S.; Wilson, H.F.; Glenn, A.J. Contrasting patterns of groundwater evapotranspiration in grass and tree dominated riparian zones of a temperate agricultural catchment. J. Hydrol. 2017, 549, 654–666. [Google Scholar] [CrossRef]
- Fu, A.; Chen, Y.; Li, W. Water use strategies of the desert riparian forest plant community in the lower reaches of Heihe River Basin, China. Sci. China Earth Sci. 2014, 57, 1293–1305. [Google Scholar] [CrossRef]
- Li, J.; Yu, B.; Zhao, C.; Nowak, R.S.; Zhao, Z.; Sheng, Y.; Li, J. Physiological and morphological responses of Tamarix ramosissima and Populus euphratica to altered groundwater availability. Tree Physiol. 2013, 33, 57–68. [Google Scholar] [CrossRef]
- Merritt, D.M.; Poff, N.L. Shifting dominance of riparian Populus and Tamarix along gradients of flow alteration in western North American rivers. Ecol. Appl. 2010, 20, 135–152. [Google Scholar] [CrossRef]
- Nippert, J.B.; Butler, J.J.; Kluitenberg, G.J.; Whittemore, D.O.; Arnold, D.; Spal, S.E.; Ward, J.K. Patterns of Tamarix water use during a record drought. Oecologia 2010, 162, 283–292. [Google Scholar] [CrossRef]
- Wang, D.D.; Yu, Z.T.; Peng, G.; Zhao, C.Y.; Ding, J.L.; Zhang, X.L. Water use strategies of Populus euphratica seedlings under groundwater fluctuation in the Tarim River Basin of Central Asia. Catena 2018, 166, 89–97. [Google Scholar] [CrossRef]
- Gries, D.; Zeng, F.; Foetzki, A.; Arndt, S.K.; Bruelheide, H.; Thomas, F.M.; Zhang, X.; Runge, M. Growth and water relations of Tamarix ramosissima and Populus euphratica on Taklamakan desert dunes in relation to depth to a permanent water table. Plant Cell Environ. 2003, 26, 725–736. [Google Scholar] [CrossRef]
- Zhu, X.; Yuan, G.; Yi, X.; Du, T. Quantifying the impacts of river hydrology on riparian vegetation spatial structure: Case study in the lower basin of the Tarim River, China. Ecohydrology 2017, 10, e1887. [Google Scholar] [CrossRef]
- Thevs, N.; Zerbe, S.; Peper, J.; Succow, M. Vegetation and vegetation dynamics in the Tarim River floodplain of continental-arid Xinjiang, NW China. Phytocoenologia 2008, 38, 65–84. [Google Scholar] [CrossRef]
- Nouri, H.; Glenn, E.P.; Beecham, S.; Boroujeni, S.C.; Sutton, P.; Alaghmand, S.; Noori, B.; Nagler, P. Comparing Three Approaches of Evapotranspiration Estimation in Mixed Urban Vegetation: Field-Based, Remote Sensing-Based and Observational-Based Methods. Remote Sens. 2016, 8, 492. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Wendland, E.; Nearing, M.A.; Scott, R.L.; Rosolem, R.; Da Rocha, H.R. The water balance components of undisturbed tropical woodlands in the Brazilian cerrado. Hydrol. Earth Syst. Sci. 2015, 19, 2899–2910. [Google Scholar] [CrossRef]
- Chen, Y.J.; Li, W.H.; Liu, J.Z.; Yang, Y.H. Effects of water conveyance embankments on riparian forest communities at the middle reaches of the Tarim River, Northwest China. Ecohydrology 2013, 6, 937–948. [Google Scholar] [CrossRef]
- Huang, T.M.; Pang, Z.H. Changes in groundwater induced by water diversion in the Lower Tarim River, Xinjiang Uygur, NW China: Evidence from environmental isotopes and water chemistry. J. Hydrol. 2010, 387, 188–201. [Google Scholar] [CrossRef]
- Tao, H.; Gemmer, M.; Bai, Y.; Su, B.; Mao, W. Trends of streamflow in the Tarim River Basin during the past 50 years: Human impact or climate change? J. Hydrol. 2011, 400, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Xu, C.; Ye, Z.; Li, Z.; Zhu, C.; Ma, X. Effects of ecological water conveyance on groundwater dynamics and riparian vegetation in the lower reaches of Tarim River, China. Hydrol. Process. 2009, 24, 170–177. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, P.; Shao, M.; Luo, Y.; Zhu, X. Energy and water exchanges over a riparian Tamarix spp. stand in the lower Tarim River basin under a hyper-arid climate. Agric. For. Meteorol. 2014, 194, 144–154. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Loheide, S.P.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Wang, P.; Niu, G.-Y.; Fang, Y.H.; Wu, R.J.; Yu, J.J.; Yuan, G.F.; Pozdniakov, S.P.; Scott, R.L. Implementing Dynamic Root Optimization in Noah-MP for Simulating Phreatophytic Root Water Uptake. Water Resour. Res. 2018, 54, 1560–1575. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Foken, T. The Energy Balance Closure Problem: An Overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef] [PubMed]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- USGS Global Visualization Viewer (GloVis). Available online: https://glovis.usgs.gov/ (accessed on 26 November 2019).
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; NASA Special Publication: Washington, DC, USA, 1974; pp. 309–317. [Google Scholar]
- Hird, J.N.; McDermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- Kobayashi, H.; Dye, D.G. Atmospheric conditions for monitoring the long-term vegetation dynamics in the Amazon using normalized difference vegetation index. Remote Sens. Environ. 2005, 97, 519–525. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. J. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Geng, L.; Ma, M.; Wang, X.; Yu, W.; Jia, S.; Wang, H. Comparison of eight techniques for reconstructing multi-satellite sensor time-series NDVI data sets in the Heihe river basin, China. Remote Sens. 2014, 6, 2024–2049. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, X.; Ye, M.; Yue, N.; Kan, F. Bayesian performance evaluation of evapotranspiration models based on eddy covariance systems in an arid region. Hydrol. Earth Syst. Sci. 2019, 23, 2877–2895. [Google Scholar] [CrossRef]
- Lian, J.; Huang, M. Comparison of three remote sensing based models to estimate evapotranspiration in an oasis-desert region. Agric. Water Manag. 2016, 165, 153–162. [Google Scholar] [CrossRef]
- Hao, X.M.; Li, W.H.; Huang, X.; Zhu, C.G.; Ma, J.X. Assessment of the groundwater threshold of desert riparian forest vegetation along the middle and lower reaches of the Tarim River, China. Hydrol. Process. 2010, 24, 178–186. [Google Scholar] [CrossRef]
- Nagler, P.; Glenn, E.P.; Hursh, K.; Curtis, C.; Huete, A. Vegetation Mapping for Change Detection on an Arid-Zone River. Environ. Monit. Assess. 2005, 109, 255–274. [Google Scholar] [CrossRef] [PubMed]
- Alrababah, M.A.; Alhamad, M.N. Land use/cover classification of arid and semi-arid Mediterranean landscapes using Landsat ETM. Int. J. Remote Sens. 2006, 27, 2703–2718. [Google Scholar] [CrossRef]
- Thakkar, A.K.; Desai, V.R.; Patel, A.; Potdar, M.B. An effective hybrid classification approach using tasseled cap transformation (TCT) for improving classification of land use/land cover (LU/LC) in semi-arid region: A case study of Morva-Hadaf watershed, Gujarat, India. Arab. J. Geosci. 2016, 9, 180. [Google Scholar] [CrossRef]
- Langley, S.K.; Cheshire, H.M.; Humes, K.S. A comparison of single date and multitemporal satellite image classifications in a semi-arid grassland. J. Arid Environ. 2001, 49, 401–411. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Paz, A.R.; Collischonn, W.; Aragao, L.; Rocha, H.R.; Malhi, Y.S. A MODIS-Based Energy Balance to Estimate Evapotranspiration for Clear-Sky Days in Brazilian Tropical Savannas. Remote Sens. 2012, 4, 703–725. [Google Scholar] [CrossRef]
- Rao, Y.H.; Zhu, X.L.; Chen, J.; Wang, J.M. An Improved Method for Producing High Spatial-Resolution NDVI Time Series Datasets with Multi-Temporal MODIS NDVI Data and Landsat TM/ETM plus Images. Remote Sens. 2015, 7, 7865–7891. [Google Scholar] [CrossRef]
- Carroll, R.W.; Pohll, G.M.; Morton, C.G.; Huntington, J.L. Calibrating a Basin-Scale Groundwater Model to Remotely Sensed Estimates of Groundwater Evapotranspiration. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1114–1127. [Google Scholar] [CrossRef]
- Schilling, O.; Doherty, J.; Kinzelbach, W.; Wang, H.; Yang, P.; Brunner, P. Using tree ring data as a proxy for transpiration to reduce predictive uncertainty of a model simulating groundwater–surface water–vegetation interactions. J. Hydrol. 2014, 519, 2258–2271. [Google Scholar] [CrossRef]
| Empirical Remotely Sensed ET Models | Vegetation Types | References |
|---|---|---|
| Saltcedar (flooded and unflooded); Cottonwood (flooded and unflooded). | [6] | |
| Saltcedar (flooded and unflooded); Cottonwood (flooded and unflooded); Mesquite woodland; Mesquite shrubland; Giant Sacaton grassland; Dense saltcedar; Arrowweed. | [7] | |
| Mesquite woodland; Sacaton grassland; Mixed mesquite/sacaton shrubland. | [9] | |
| Saltcedar; Cottonwood; Arrowweed; Quailbush shrubs; Screwbean Mesquite; Alfalfa. | [10] | |
| Mesquite woodland; Mesquite shrubland; Sacaton grass; Aafalf; Cotton; Saltcedar; Reed; Crops. | [11] | |
| Mesquite woodland; Mesquite shrubland; Sacaton grassland; Brunchgrass; Mesquite savannah. | [12] | |
| Mesquite savanna; Grass; Forbs; Larrea tridentata, Parthenium incanum; Acacia constricta; E. lehmanniana; Prosopis velutina. | [13] |
| Models | a | b | c | R2 | Reduced chi-sqr |
|---|---|---|---|---|---|
| CVTM | 2.364 | 11.681 | 1.597 | 0.809 | 0.492 |
| SVTM-T | 17.993 | 0.221 | 0.374 | 0.862 | 0.433 |
| SVTM-P | 2.652 | 9.598 | 1.611 | 0.845 | 0.312 |
| Sites | Dataset | N | ME (mm/d) | MaxError (mm/d) | ||||
|---|---|---|---|---|---|---|---|---|
| CVTM | SVTM-T | SVTM-P | CVTM | SVTM-T | SVTM-P | |||
| Tamarix site | Validation Data | 21 | 0.197 | 0.040 | 1.399 | 0.646 | ||
| Throughout 2017 | 294 | 0.177 | 0.029 | 3.235 | 2.103 | |||
| Populus site | Validation Data | 18 | −0.158 | 0.059 | 1.380 | 0.922 | ||
| Throughout 2016 | 264 | −0.163 | 0.047 | 2.336 | 1.870 | |||
| Month | ET for Tamarix Site | ET for Populus Site | ||||||
|---|---|---|---|---|---|---|---|---|
| N | Observed (mm) | CVTM (mm) | SVTM-T (mm) | N | Observed (mm) | CVTM (mm) | SVTM-P (mm) | |
| January | 11 | 0.51 | 1.56 | 0.82 | 20 | 3.48 | 0.54 | 0.49 |
| February | 23 | 2.43 | 6.03 | 3.16 | 14 | 0.64 | 0.80 | 0.73 |
| March | 19 | 1.16 | 11.63 | 6.10 | 13 | 1.51 | 2.08 | 1.90 |
| April | 24 | 11.71 | 27.66 | 15.01 | 28 | 9.79 | 7.11 | 6.59 |
| May | 30 | 64.07 | 98.12 | 74.14 | 14 | 23.06 | 16.03 | 17.83 |
| June | 27 | 113.23 | 118.79 | 115.66 | 29 | 82.28 | 79.87 | 93.26 |
| July | 29 | 138.30 | 122.31 | 133.59 | 27 | 84.13 | 80.39 | 95.47 |
| August | 28 | 117.74 | 103.23 | 112.94 | 26 | 77.09 | 60.80 | 72.52 |
| September | 30 | 83.38 | 82.53 | 80.20 | 30 | 64.08 | 55.15 | 65.31 |
| October | 28 | 24.19 | 32.63 | 24.68 | 26 | 25.38 | 20.64 | 23.91 |
| November | 22 | 5.67 | 8.50 | 5.08 | 24 | 2.06 | 6.24 | 6.96 |
| December | 23 | 3.39 | 4.82 | 2.88 | 13 | 0.73 | 1.54 | 1.71 |
| Average | 25 | 47.15 | 51.48 | 47.85 | 22 | 31.18 | 27.60 | 32.22 |
| Total | 294 | 565.78 | 617.80 | 574.25 | 264 | 374.22 | 331.17 | 386.68 |
| Residual Error | 52.02 (9.19%) | 8.47 (1.50%) | −43.04 (−11.50%) | 12.47 (3.33%) | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, T.; Wang, L.; Yuan, G.; Sun, X.; Wang, S. Effects of Distinguishing Vegetation Types on the Estimates of Remotely Sensed Evapotranspiration in Arid Regions. Remote Sens. 2019, 11, 2856. https://doi.org/10.3390/rs11232856
Du T, Wang L, Yuan G, Sun X, Wang S. Effects of Distinguishing Vegetation Types on the Estimates of Remotely Sensed Evapotranspiration in Arid Regions. Remote Sensing. 2019; 11(23):2856. https://doi.org/10.3390/rs11232856
Chicago/Turabian StyleDu, Tao, Li Wang, Guofu Yuan, Xiaomin Sun, and Shusen Wang. 2019. "Effects of Distinguishing Vegetation Types on the Estimates of Remotely Sensed Evapotranspiration in Arid Regions" Remote Sensing 11, no. 23: 2856. https://doi.org/10.3390/rs11232856
APA StyleDu, T., Wang, L., Yuan, G., Sun, X., & Wang, S. (2019). Effects of Distinguishing Vegetation Types on the Estimates of Remotely Sensed Evapotranspiration in Arid Regions. Remote Sensing, 11(23), 2856. https://doi.org/10.3390/rs11232856