On the Adequacy of Representing Water Reflectance by Semi-Analytical Models in Ocean Color Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
2.1. Reflectance Models
2.2. Inversion Scheme
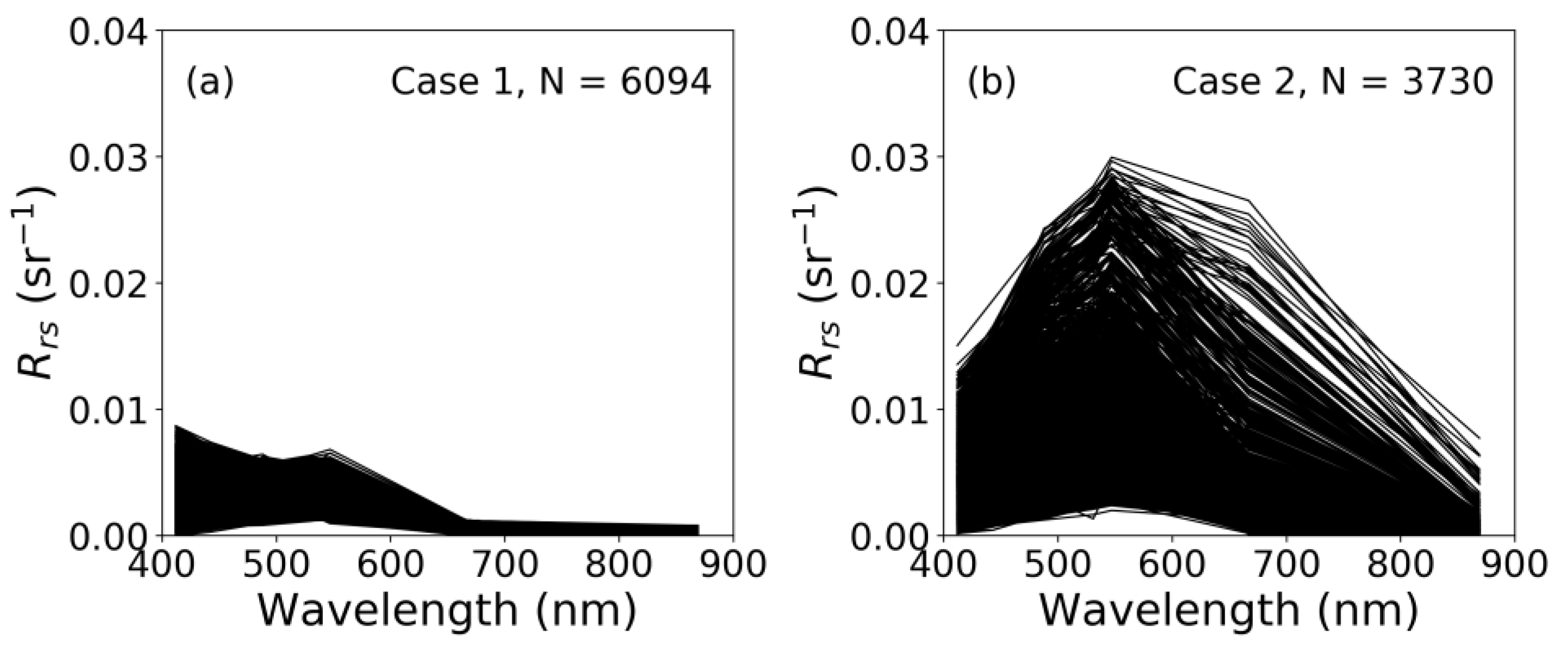
2.3. Data Source
- Phytoplankton absorption. The phytoplankton absorption, aph, is expressed as aph = [Chla] a*ph, where a*ph is the chlorophyll-specific absorption coefficient, both provided in the IOCCG dataset. The values of a*ph at 350–400 nm were adopted from Morel [25] and extrapolated to 300 nm, which was then normalized to the IOCCG a*ph value at 400 nm to ensure continuity. The a*ph values in the 800-900 nm range were assumed constant and fixed at the value at 800 nm.
- CDOM absorption. The CDOM absorption, ag, was modeled as ag(λ) = ag(440) exp(−Sg(λ − 440)), with Sg and ag(440) provided by IOCCG [18].
- Detritus/mineral absorption. The absorption of detritus/mineral, adm, was modeled as adm(λ) = adm(440) exp(−Sdm(λ − 440)), with Sdm and adm(440) provided by IOCCG [18].
- Backscattering of phytoplankton. The attenuation of phytoplankton, cph, was modeled as cph = cph(550) (550/λ)n1 in the IOCCG dataset. The value of n1 was determined using cph at 400–800 nm, which was then used to extend cph to 300-1000 nm. The backscattering of phytoplankton, bbph, was thus obtained using bbph = ph(cph − aph) with ph equal to 0.01.
- Backscattering of detritus, mineral, and other particles. The backscattering of detritus, mineral, and others, bbdm, was modeled as bbdm = bbdm(550) (550/ λ)n2. The value of n2 was determined using bbdm at 400–800 nm, which was then used to extend bbdm to 300–900 nm.
3. Results and Discussion
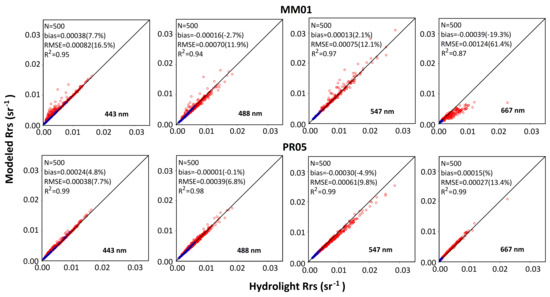
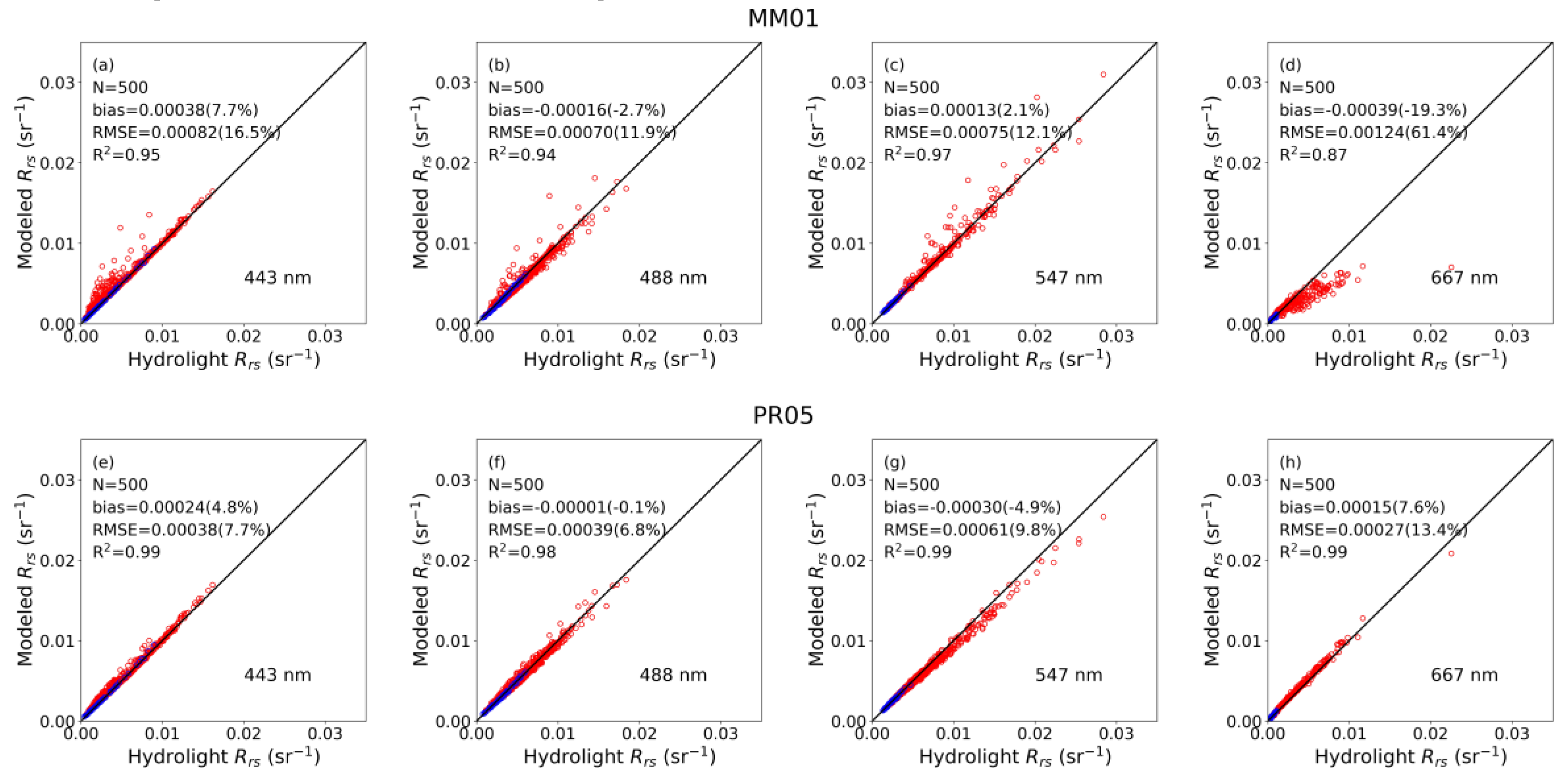
3.1. Model Performance with Hydrolight Simulations
3.2. Sensivity of Rrs Reconstruction to Atmospheric Transmittance
3.3. Model Performance Using AERONET-OC Dataset
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frouin, R.J.; Franz, B.A.; Ibrahim, A.; Knobelspiesse, K.; Ahmad, Z.; Cairns, B.; Chowdhary, J.; Dierssen, H.M.; Tan, J.; Dubovik, O.; et al. Atmospheric Correction of Satellite Ocean-Color Imagery During the PACE Era. Front. Earth Sci. 2019, 7, 145. [Google Scholar] [CrossRef]
- Chomko, R.M.; Gordon, H.R. Atmospheric correction of ocean color imagery: use of the Junge power-law aerosol size distribution with variable refractive index to handle aerosol absorption. Appl. Opt. 1998, 37, 5560. [Google Scholar] [CrossRef] [PubMed]
- Land, P.E.; Haigh, J.D. Atmospheric correction over case 2 waters with an iterative fitting algorithm: relative humidity effects. Appl. Opt. 1997, 36, 9448. [Google Scholar] [CrossRef] [PubMed]
- Stamnes, K.; Li, W.; Yan, B.; Eide, H.; Barnard, A.; Pegau, W.S.; Stamnes, J.J. Accurate and self-consistent ocean color algorithm: simultaneous retrieval of aerosol optical properties and chlorophyll concentrations. Appl. Opt. 2003, 42, 939. [Google Scholar] [CrossRef] [PubMed]
- Kuchinke, C.P.; Gordon, H.R.; Franz, B.A. Spectral optimization for constituent retrieval in Case 2 waters I: Implementation and performance. Remote Sens. Environ. 2009, 113, 571–587. [Google Scholar] [CrossRef]
- Shi, C.; Nakajima, T.; Hashimoto, M. Simultaneous retrieval of aerosol optical thickness and chlorophyll concentration from multiwavelength measurement over East China Sea. J. Geophys. Res.: Atmos. 2016, 121, 14084–14101. [Google Scholar] [CrossRef]
- Gordon, H.R. Removal of atmospheric effects from satellite imagery of the oceans. Appl. Opt. 1978, 17, 1631. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Prieur, L.; Morel, A. A three-component model of ocean colour and its application to remote sensing of phytoplankton pigments in coastal waters. Int. J. Remote Sens. 1989, 10, 1373–1394. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L.; Del Castillo, C. Bio-optical properties and ocean color algorithms for coastal waters influenced by the Mississippi River during a cold front. Appl. Opt. 2006, 45, 7410. [Google Scholar] [CrossRef]
- D’Sa, E.J.; DiMarco, S.F. Seasonal variability and controls on chromophoric dissolved organic matter in a large river-dominated coastal margin. Limnol. Oceanogr. 2009, 54, 2233–2242. [Google Scholar] [CrossRef]
- Komick, N.M.; Costa, M.P.F.; Gower, J. Bio-optical algorithm evaluation for MODIS for western Canada coastal waters: An exploratory approach using in situ reflectance. Remote Sens. Environ. 2009, 113, 794–804. [Google Scholar] [CrossRef]
- O’Donnell, D.M.; Effler, S.W.; Strait, C.M.; Leshkevich, G.A. Optical characterizations and pursuit of optical closure for the western basin of Lake Erie through in situ measurements. J. Great Lakes Res. 2010, 36, 736–746. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.-Y.; Ramon, D. Atmospheric correction in presence of sun glint: application to MERIS. Opt. Express 2011, 19, 9783. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.; Krasemann, H.; Brewin, R.J.W.; Brockmann, C.; Deschamps, P.-Y.; Doerffer, R.; Fomferra, N.; Franz, B.A.; Grant, M.G.; Groom, S.B.; et al. The Ocean Colour Climate Change Initiative: I. A methodology for assessing atmospheric correction processors based on in-situ measurements. Remote Sens. Environ. 2015, 162, 242–256. [Google Scholar]
- Müller, D.; Krasemann, H.; Brewin, R.J.W.; Brockmann, C.; Deschamps, P.-Y.; Doerffer, R.; Fomferra, N.; Franz, B.A.; Grant, M.G.; Groom, S.B.; et al. The Ocean Colour Climate Change Initiative: II. Spatial and temporal homogeneity of satellite data retrieval due to systematic effects in atmospheric correction processors. Remote Sens. Environ. 2015, 162, 257–270. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res.: Ocean. 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- Park, Y.-J.; Ruddick, K. Model of remote-sensing reflectance including bidirectional effects for case 1 and case 2 waters. Appl. Opt. 2005, 44, 1236. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications; Reports of the International Ocean-Colour Coordinating Group, No. 5; Lee, Z.-P., Ed.; IOCCG: Dartmouth, NS, Canada, 2006. [Google Scholar]
- Zibordi, G.; Mélin, F.; Berthon, J.-F.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A network for the validation of ocean color primary products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters III Implication of bidirectionality for the remote-sensing problem. Appl. Opt. 1996, 35, 4850. [Google Scholar] [CrossRef]
- Ruddick, K.G.; De Cauwer, V.; Park, Y.-J.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Westberry, T.K.; Boss, E.; Lee, Z. Influence of Raman scattering on ocean color inversion models. Appl. Opt. 2013, 52, 5552. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). J. Geophys. Res. 1988, 93, 10749. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water II Integrating cavity measurements. Appl. Opt. 1997, 36, 8710. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177. [Google Scholar] [CrossRef]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. 1995, 100, 13321. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res.: Ocean. 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Roesler, C.S.; Perry, M.J.; Carder, K.L. Modeling in situ phytoplankton absorption from total absorption spectra in productive inland marine waters. Limnol. Oceanogr. 1989, 34, 1510–1523. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Cambridge University Press: Cambridge, UK, 1994; ISBN 0521459664. [Google Scholar]
- Voss, K.J. A spectral model of the beam attenuation coefficient in the ocean and coastal areas. Limnol. Oceanogr. 1992, 37, 501–509. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Lecture Notes on Coastal and Estuarine Studies; American Geophysical Union: Washington, DC, USA, 1983; Volume 4, ISBN 0-387-90923-0. [Google Scholar]
- Loisel, H.; Morel, A. Light scattering and chlorophyll concentration in case 1 waters: A reexamination. Limnol. Oceanogr. 1998, 43, 847–858. [Google Scholar] [CrossRef]
- Morel, A.; Bélanger, S. Improved detection of turbid waters from ocean color sensors information. Remote Sens. Environ. 2006, 102, 237–249. [Google Scholar] [CrossRef]
- Robinson, W.D.; Franz, B.A.; Patt, F.S.; Bailey, S.W.; Werdell, P.J. Masks and flags updates. In SeaWiFS Postlauch Technical Report Series; NASA/TM-2003-206892; Hook, S.B., Firestone, E.R., Eds.; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 2003; Volume 22, pp. 34–40. [Google Scholar]
- Krasemann, H.; Müller, D. Ocean Colour Climate Change Initiative (OC-CCI)—Phase Two: Product Validation and Algorithm Selection Report, Part 1—Atmospheric Correction; Technical Report AO-1/6207/09/I-LG, D2.5, 4.0.3; ESRIN, European Space Agency: Frascati, Italy, 2017; p. 26. [Google Scholar]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res.: Ocean. 1998, 103, 24937–24953. [Google Scholar]
- Werdell, P.J.; Bailey, S.W. An improved in-situ bio-optical data set for ocean color algorithm development and satellite data product validation. Remote Sens. Environ. 2005, 98, 122–140. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res.: Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: an ocean color case study. Opt. Express 2018, 26, 7404. [Google Scholar] [CrossRef]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019. [Google Scholar] [CrossRef]
- Lenoble, J.; Herman, M.; Deuzé, J.L.; Lafrance, B.; Santer, R.; Tanré, D. A successive order of scattering code for solving the vector equation of transfer in the earth’s atmosphere with aerosols. J. Quant. Spectrosc. Radiat. Transf. 2007, 107, 479–507. [Google Scholar] [CrossRef]
- Tanre, D.; Herman, M.; Deschamps, P.Y.; de Leffe, A. Atmospheric modeling for space measurements of ground reflectances, including bidirectional properties. Appl. Opt. 1979, 18, 3587. [Google Scholar] [CrossRef] [PubMed]
- Fitzpatrick, M.F.; Brandt, R.E.; Warren, S.G.; Fitzpatrick, M.F.; Brandt, R.E.; Warren, S.G. Transmission of solar radiation by clouds over snow and ice Surfaces: A parameterization in terms of optical depth, solar zenith angle, and surface albedo. J. Clim. 2004, 17, 266–275. [Google Scholar] [CrossRef]
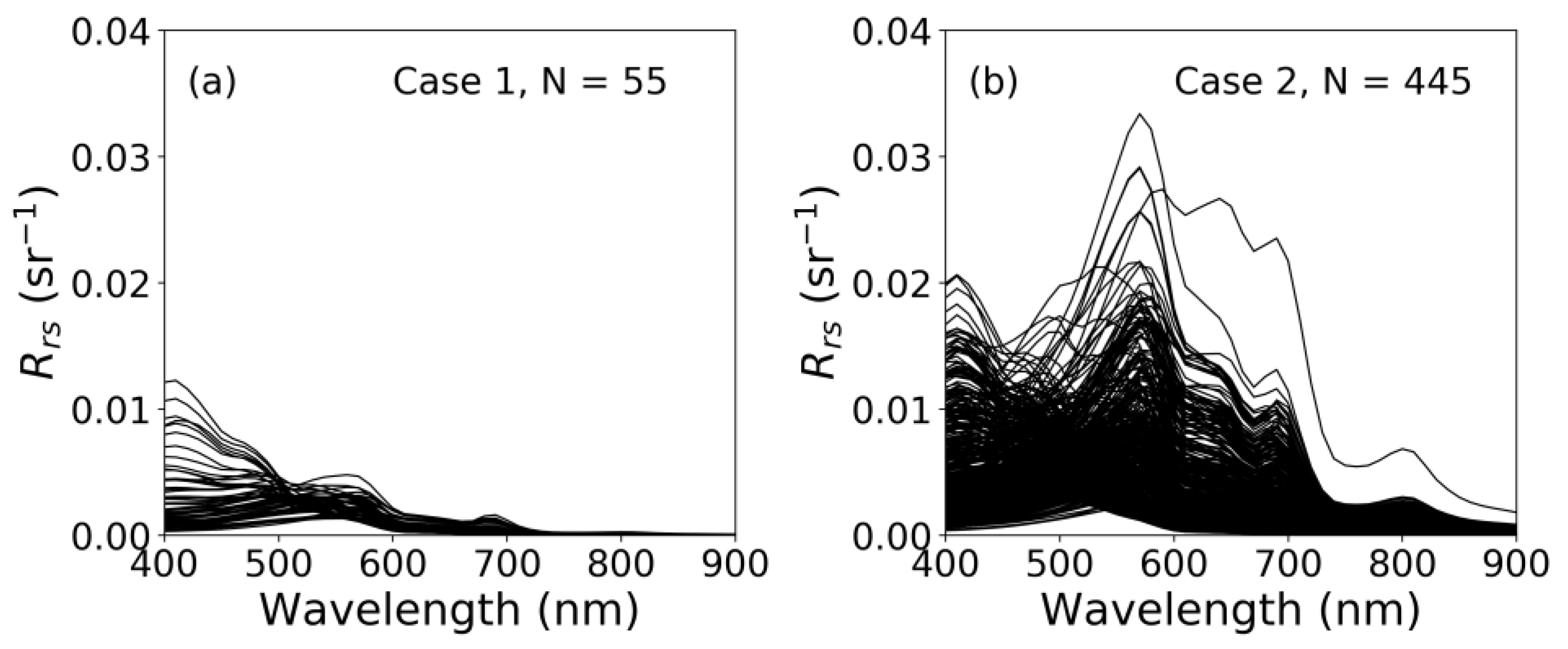

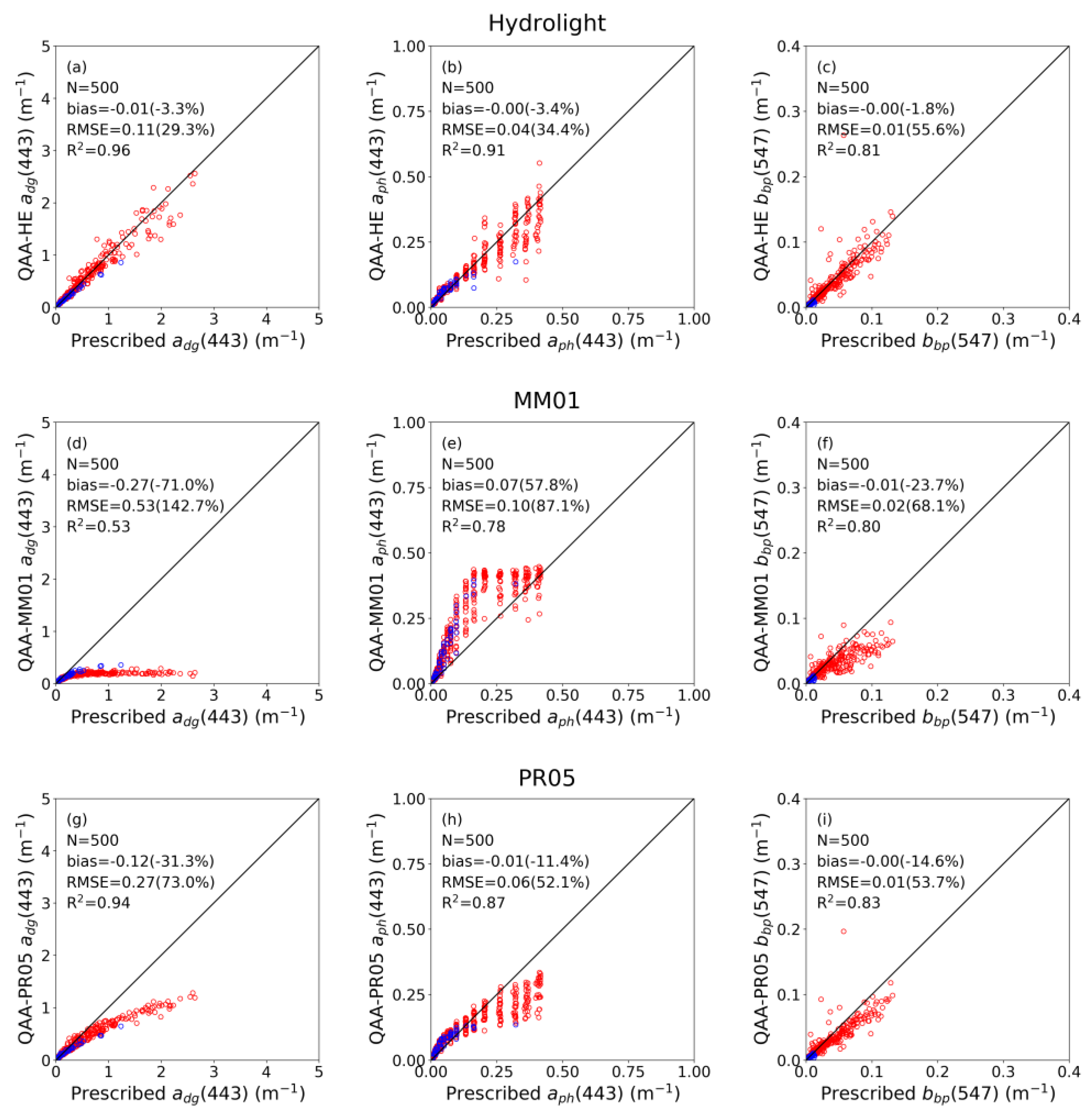
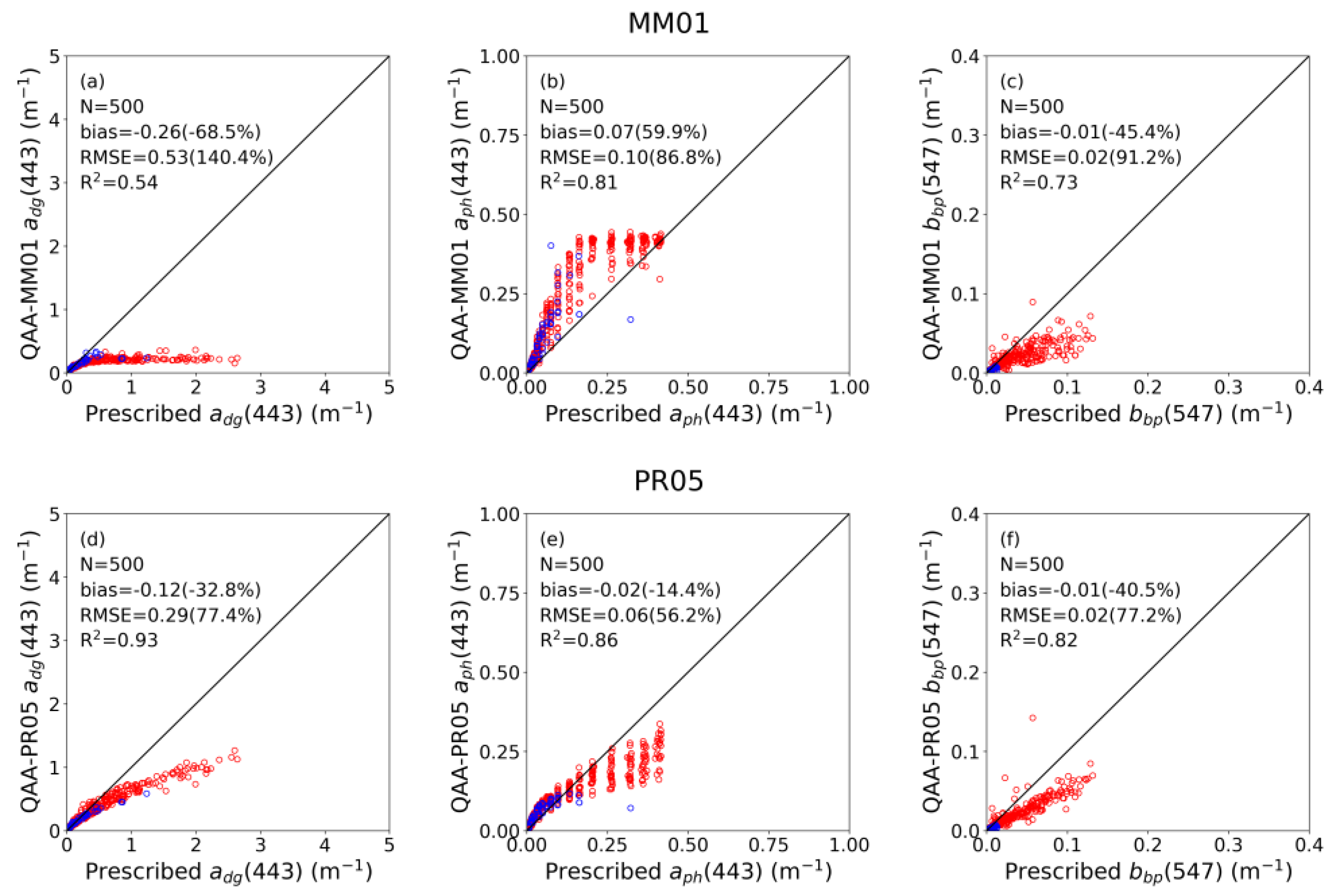
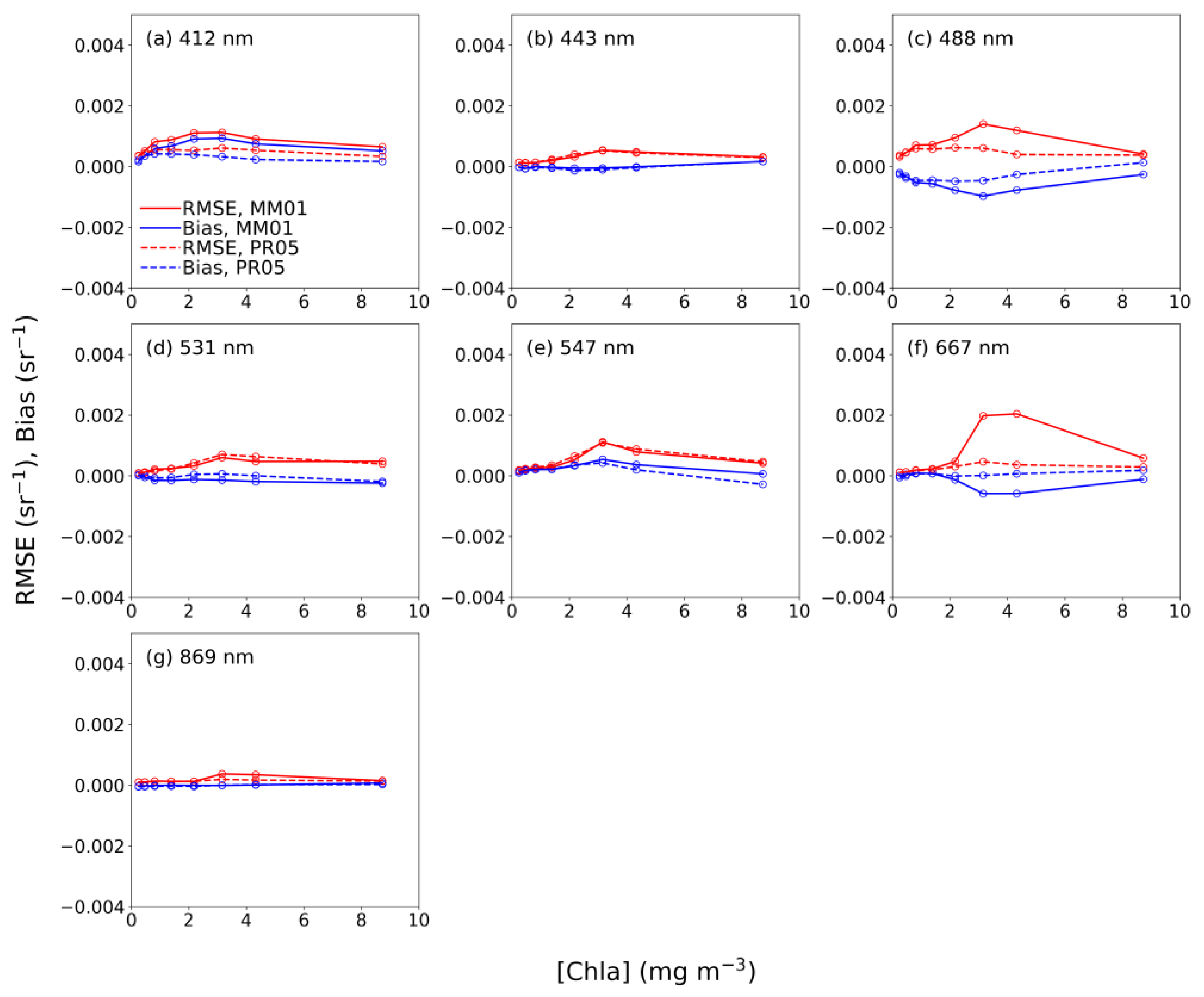
| Parameter | Case 1, N = 55 | Case 2, N = 445 | All Cases, N = 500 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | ||
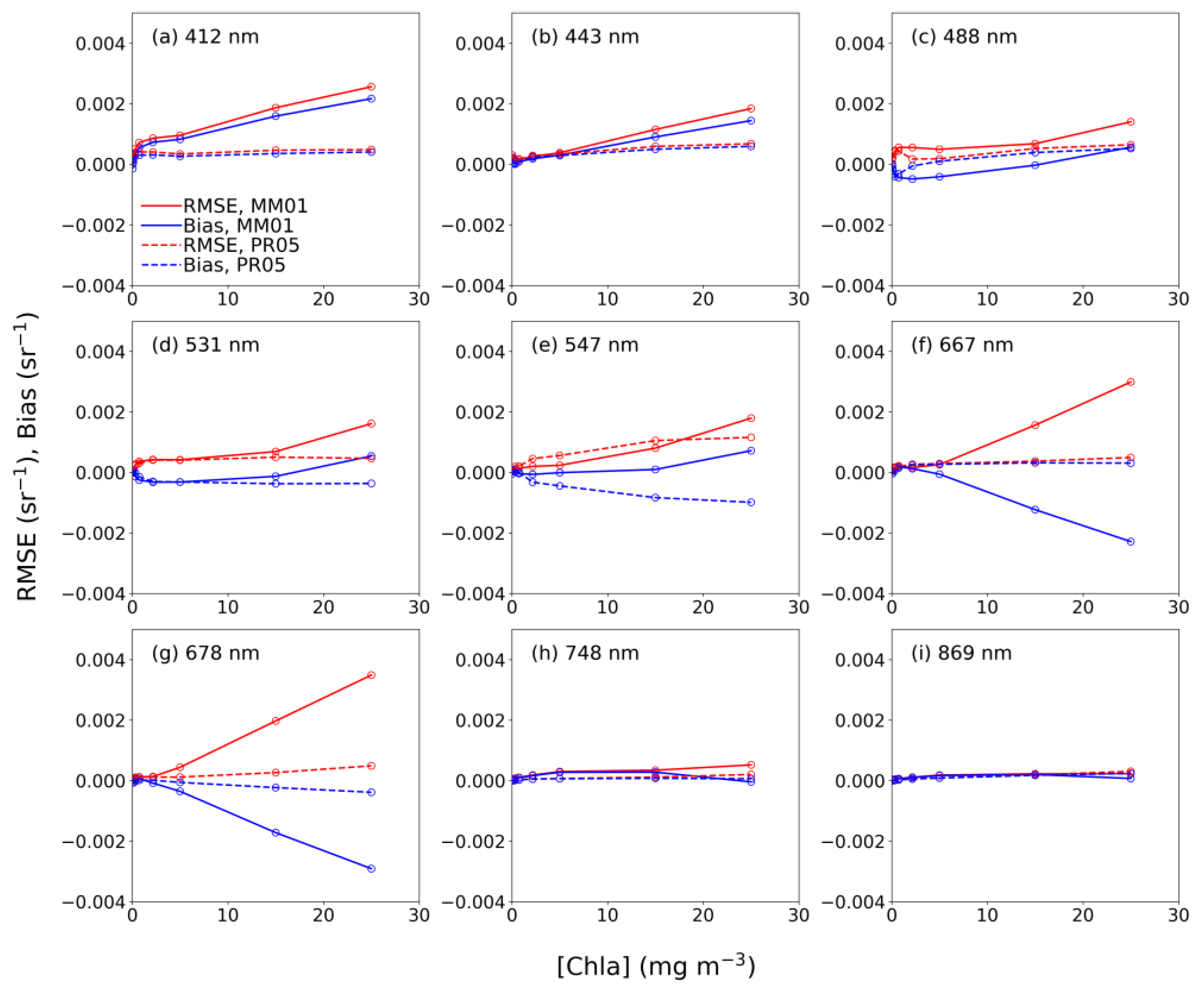
| MM01 | Rrs(412) | 1.00 | 0.11 (3.7) | 0.18 (5.9) | 0.95 | 0.88 (17.0) | 1.35 (26.1) | 0.94 | 0.79 (16.0) | 1.27 (25.8) |
| Rrs(443) | 1.00 | 0.01 (0.4) | 0.08 (2.6) | 0.95 | 0. 43 (8.2) | 0.87 (16.6) | 0.95 | 0.38 (7.7) | 0.82 (16.5) | |
| Rrs(488) | 1.00 | −0.11 (−3.8) | 0.16 (5.4) | 0.93 | −0.16 (−2.6) | 0.74 (11.9) | 0.94 | −0.16 (−2.7) | 0.70 (11.9) | |
| Rrs(531) | 1.00 | −0.04 (−1.5) | 0.06 (2.4) | 0.96 | −0.06 (−0.9) | 0.75 (11.8) | 0.96 | −0.06 (−1.0) | 0.70 (12.0) | |
| Rrs(547) | 1.00 | 0.06 (2.5) | 0.08 (3.4) | 0.97 | 0.14 (2.1) | 0.79 (11.9) | 0.97 | 0.13 (2.1) | 0.75 (12.1) | |
| Rrs(667) | 0.95 | 0.04 (8.1) | 0.07 (15.5) | 0.86 | −0.44 (−20.0) | 1.32 (59.5) | 0.87 | −0.39 (19.3) | 1.24 (61.4) | |
| Rrs(678) | 0.92 | −0.09 (−15.4) | 0.45 (27.3) | 0.87 | −0.69 (−29.3) | 1.55 (65.8) | 0.88 | −0.62 (−28.9) | 1.46 (67.8) | |
| Rrs(748) | 0.97 | 0.06 (80.2) | 0.07 (100.2) | 0.81 | 0.11 (25.1) | 0.28 (63.0) | 0.82 | 0.11 (26.1) | 0.27 (65.7) | |
| Rrs(869) | 0.96 | 0.03 (119.3) | 0.04 (145.7) | 0.82 | 0.09 (44.2) | 0.15 (74.9) | 0.83 | 0.08 (45.6) | 0.14 (78.3) | |
| PR05 | Rrs(412) | 1.00 | 0.05 (1.5) | 0.15 (4.8) | 1.00 | 0.27 (5.2) | 0.42 (8.1) | 1.00 | 0.25 (5.0) | 0.40 (8.0) |
| Rrs(443) | 1.00 | 0.06 (2.1) | 0.12 (4.1) | 0.99 | 0.26 (4.9) | 0.40 (7.7) | 0.99 | 0.24 (4.8) | 0.38 (7.7) | |
| Rrs(488) | 0.99 | −0.05 (−1.7) | 0.12 (4.0) | 0.98 | −0.00 (−0.0) | 0.42 (6.7) | 0.98 | −0.01 (−0.1) | 0.39 (6.8) | |
| Rrs(531) | 0.99 | −0.03 (−1.3) | 0.07 (2.9) | 1.00 | −0.19 (−3.0) | 0.36 (5.6) | 1.00 | −0.17 (−2.9) | 0.34 (5.7) | |
| Rrs(547) | 0.99 | −0.00 (−0.2) | 0.08 (3.3) | 0.99 | −0.34 (−5.1) | 0.64 (9.7) | 0.99 | −0.30 (−4.9) | 0.61 (9.8) | |
| Rrs(667) | 0.99 | 0.06 (13.7) | 0.10 (22.2) | 0.99 | 0.17 (7.5) | 0.28 (12.8) | 0.99 | 0.15 (7.6) | 0.27 (13.4) | |
| Rrs(678) | 0.97 | −0.07 (−12.5) | 0.09 (16.3) | 1.00 | −0.11 (−4.6) | 0.23 (9.8) | 1.00 | −0.10 (−4.8) | 0.22 (10.2) | |
| Rrs(748) | 0.97 | 0.02 (30.7) | 0.03 (47.3) | 0.98 | 0.03 (7.6) | 0.10 (21.7) | 0.98 | 0.03 (8.0) | 0.09 (22.7) | |
| Rrs(869) | 0.97 | 0.02 (67.8) | 0.03 (102.0) | 0.98 | 0.08 (39.6) | 0.14 (72.6) | 0.98 | 0.07 (40.1) | 0.14 (75.8) | |
| Parameter | Case 1, N =55 | Case 2, N = 445 | |||||
|---|---|---|---|---|---|---|---|
| R2 | Bias (bias%) | RMSE (RMSE%) | R2 | Bias (bias%) | RMSE (RMSE%) | ||
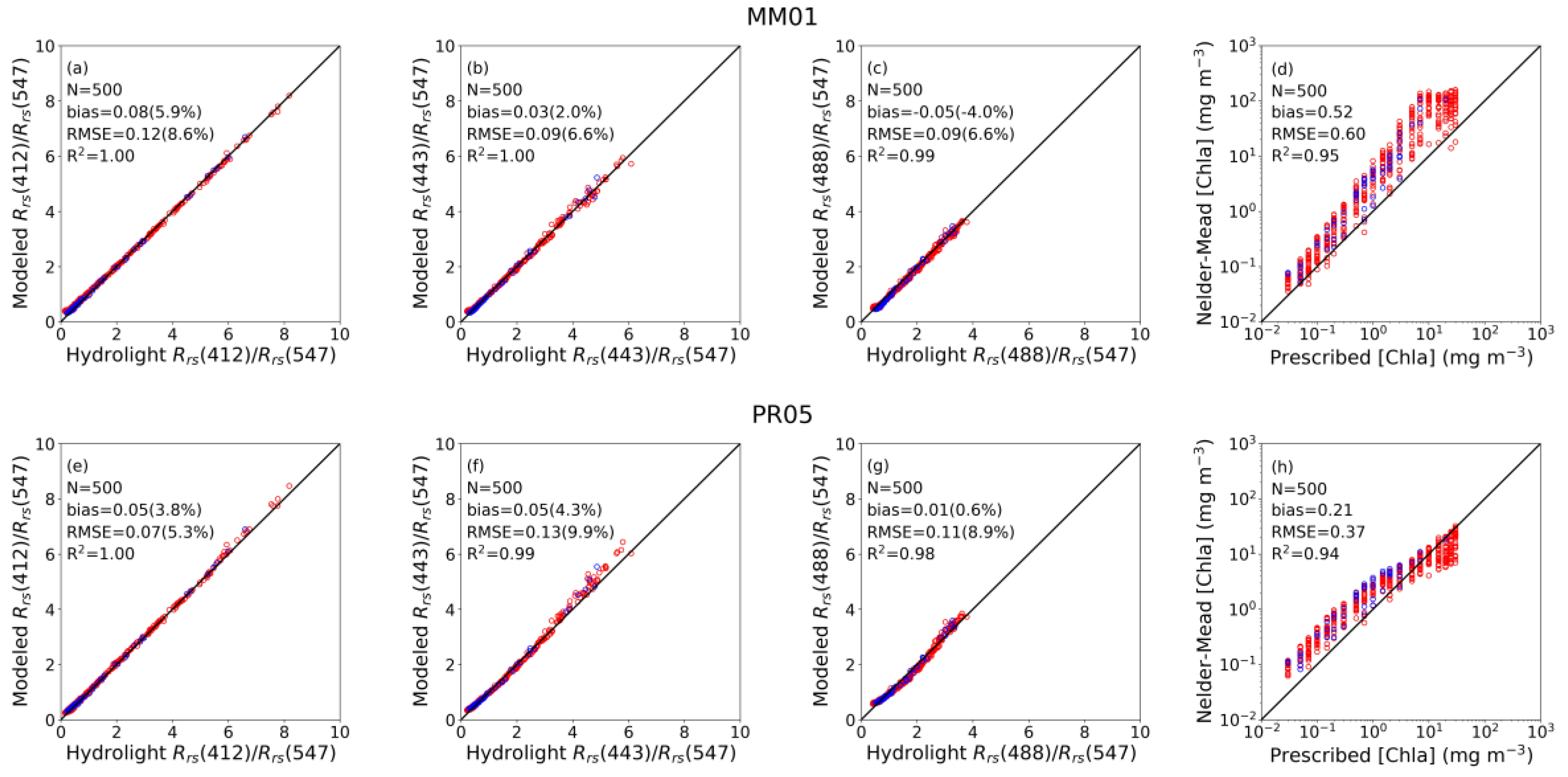
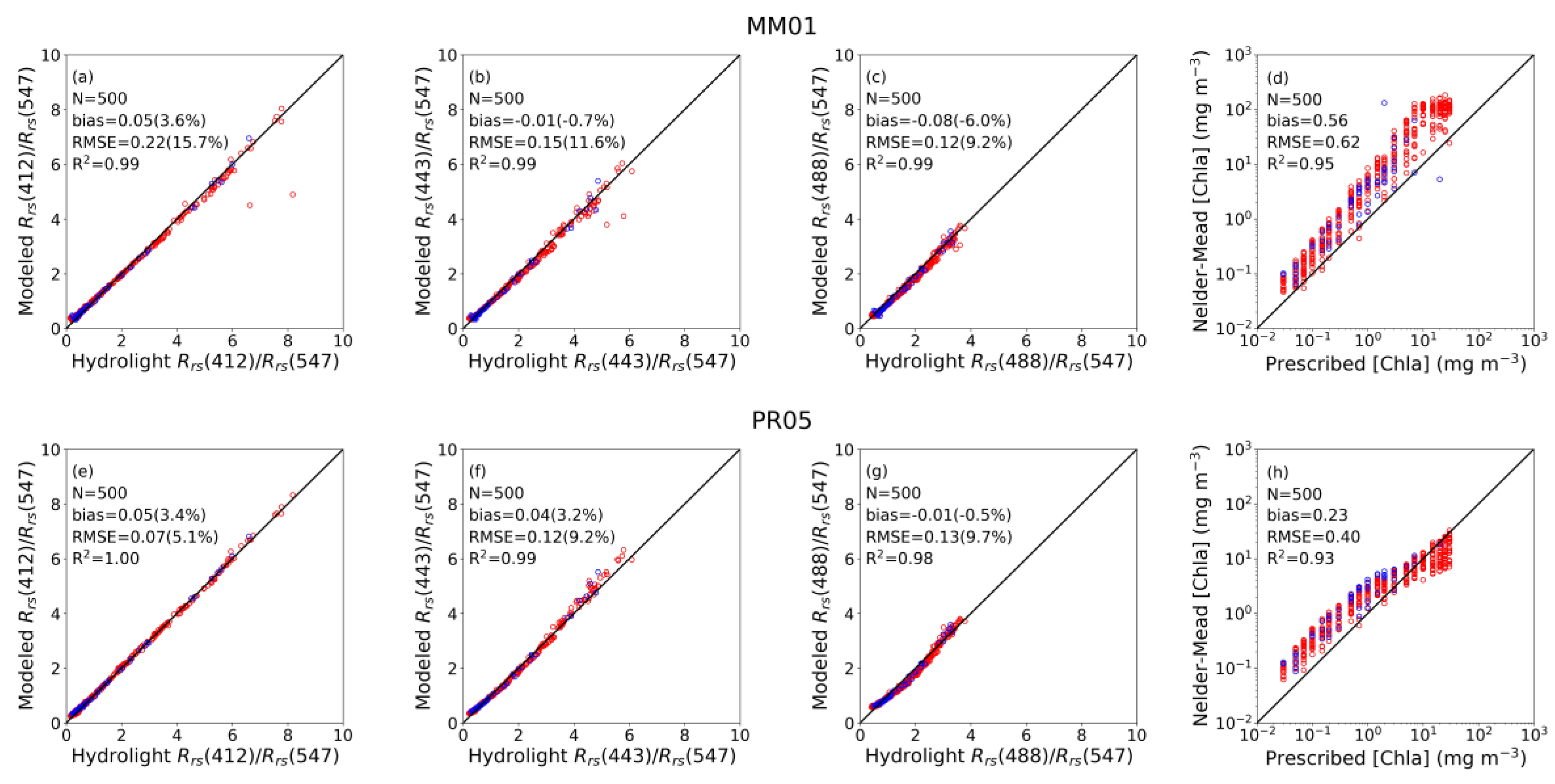
| MM01 | Rrs(412)/Rrs(547) | 1.00 | 0.03 (2.1) | 0.05 (3.6) | 1.00 | 0.09 (6.5) | 0.13 (9.2) |
| Rrs(443)/Rrs(547) | 1.00 | −0.04 (−0.6) | 0.08 (5.7) | 1.00 | 0.03 (2.4) | 0.09 (6.8) | |
| Rrs(488)/Rrs(547) | 1.00 | −0.06 (−4.6) | 0.09 (6.9) | 1.00 | −0.05 (−3.9) | 0.08 (6.6) | |
| log10([Chla]) | 0.94 | 0.49 | 0.56 | 0.95 | 0.52 | 0.61 | |
| PR05 | Rrs(412)/Rrs(547) | 1.00 | 0.03 (2.3) | 0.06 (4.1) | 1.00 | 0.06 (4.0) | 0.07 (5.4) |
| Rrs(443)/Rrs(547) | 1.00 | 0.04 (3.1) | 0.14 (9.9) | 0.99 | 0.06 (4.4) | 0.13 (9.8) | |
| Rrs(488)/Rrs(547) | 0.99 | −0.01 (−0.8) | 0.10 (7.5) | 0.99 | 0.01 (0.8) | 0.12 (9.1) | |
| log10([Chla]) | 0.93 | 0.37 | 0.41 | 0.95 | 0.19 | 0.37 | |
| Parameter | Case 1, N = 55 | Case 2, N = 445 | All Cases, N = 500 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | |
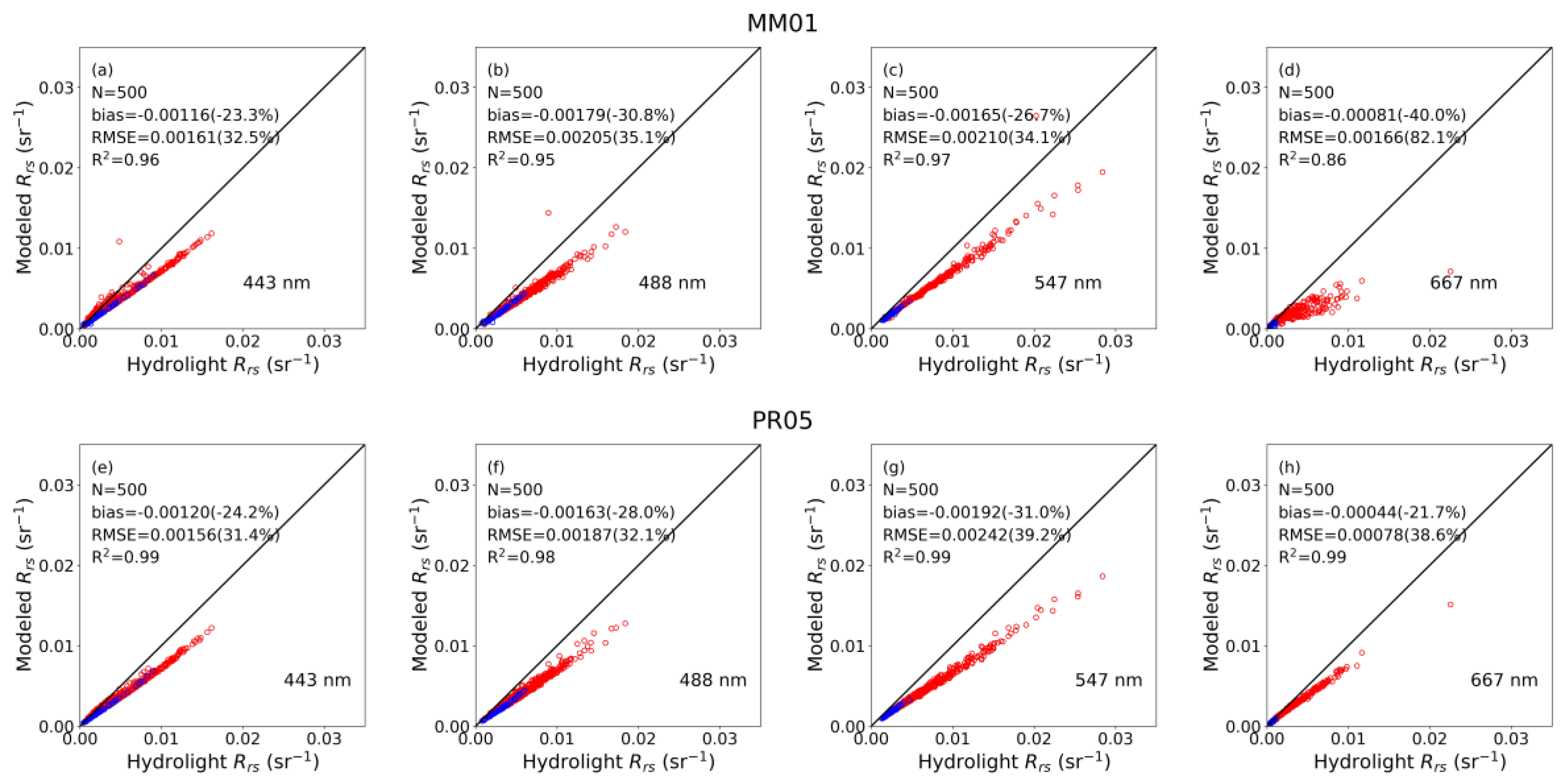
| Rrs(412) | 1.00 | 0.05 (1.7) | 0.07 (2.4) | 1.00 | 0.25 (4.9) | 0.36 (6.9) | 1.00 | 0.23 (4.7) | 0.34 (6.8) |
| Rrs(443) | 1.00 | 0.05 (1.8) | 0.07 (2.3) | 1.00 | 0.24 (4.6) | 0.35 (6.8) | 1.00 | 0.22 (4.5) | 0.33 (6.7) |
| Rrs(488) | 1.00 | −0.05 (−1.7) | 0.08 (2.8) | 0.98 | −0.02 (−0.3) | 0.36 (5.8) | 0.99 | −0.02 (−0.3) | 0.34 (5.8) |
| Rrs(531) | 0.99 | −0.03 (−1.2) | 0.07 (2.7) | 1.00 | −0.20 (−3.1) | 0.36 (5.7) | 1.00 | −0.18 (−3.1) | 0.34 (5.8) |
| Rrs(547) | 0.99 | −0.01 (−0.3) | 0.07 (2.8) | 0.99 | −0.34 (−5.2) | 0.63 (9.5) | 0.99 | −0.31 (−4.9) | 0.59 (9.6) |
| Rrs(667) | 0.99 | 0.07 (14.2) | 0.11 (22.9) | 1.00 | 0.20 (8.8) | 0.29 (13.2) | 1.00 | 0.18 (9.0) | 0.28 (13.7) |
| Rrs(678) | 0.98 | −0.07 (−12.3) | 0.09 (15.4) | 1.00 | −0.08 (−3.2) | 0.14 (5.9) | 1.00 | −0.08 (−3.5) | 0.13 (6.3) |
| Rrs(748) | 0.98 | 0.02 (25.9) | 0.03 (41.4) | 0.99 | 0.01 (2.2) | 0.07 (16.1) | 0.99 | 0.01 (2.6) | 0.07 (17.0) |
| Rrs(869) | 0.96 | 0.02 (57.9) | 0.03 (92.0) | 0.99 | 0.07 (32.7) | 0.11 (53.6) | 0.99 | 0.06 (33.1) | 0.10 (56.1) |
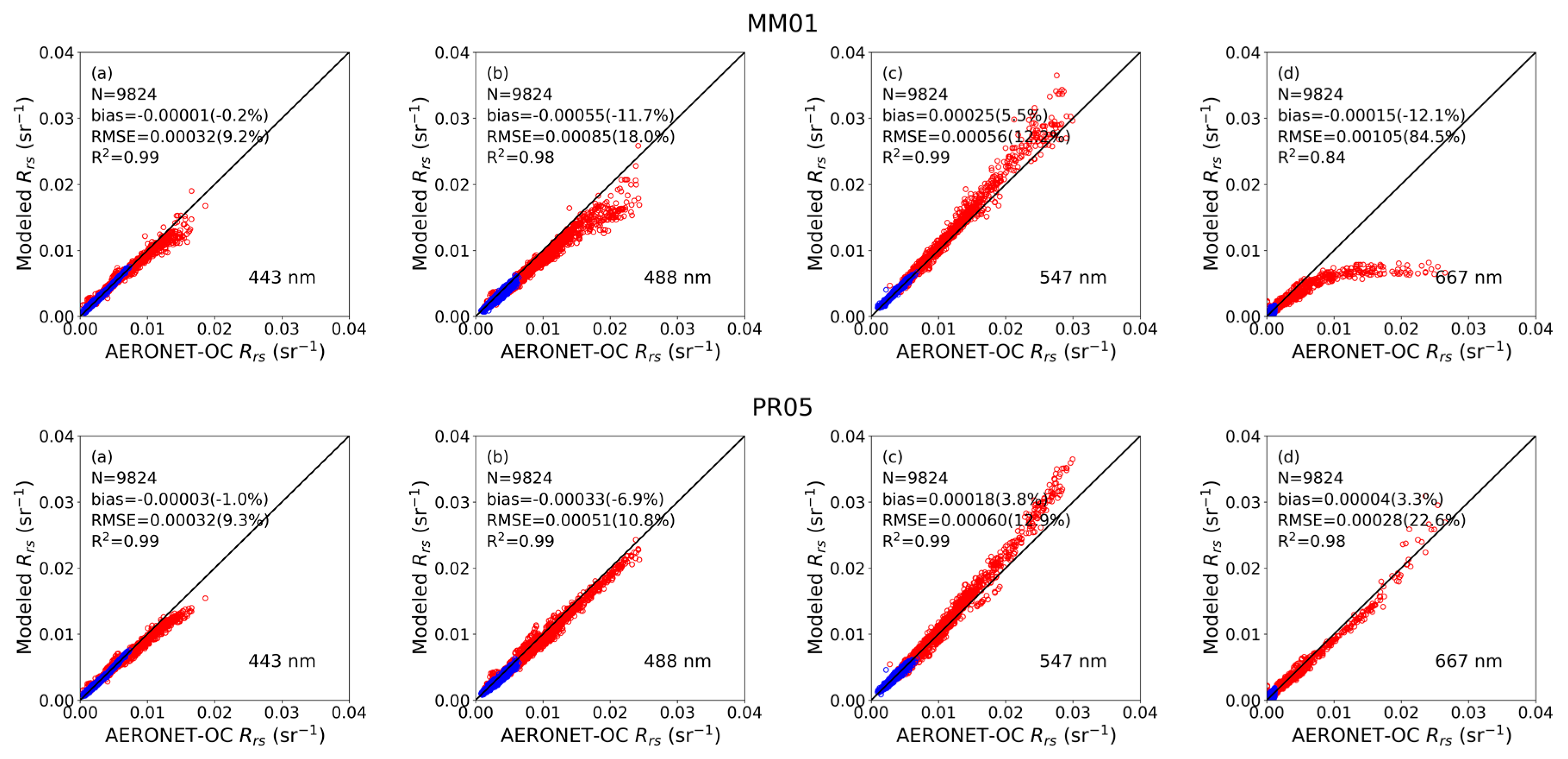
| Parameter | Case 1, N = 6094 | Case 2, N = 3730 | All Cases, N = 9824 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | R2 | Bias, 10−3 sr−1 (bias%) | RMSE, 10−3 sr−1 (RMSE%) | ||
| MM01 | Rrs(412) | 0.97 | 0.32 (12.2) | 0.43 (16.5) | 0.96 | 1.08 (30.8) | 1.23 (35.1) | 0.94 | 0.61 (20.7) | 0.83 (28.2) |
| Rrs(443) | 0.99 | 0.01 (−0.2) | 0.11 (4.1) | 0.99 | −0.03 (−0.8) | 0.50 (10.7) | 0.99 | −0.01 (−0.2) | 0.32 (9.2) | |
| Rrs(488) | 0.94 | −0.29 (−8.7) | 0.38 (11.5) | 0.98 | −0.97 (−13.9) | 1.28 (18.4) | 0.98 | −0.55 (−11.7) | 0.85 (18.0) | |
| Rrs(531) | 0.98 | −0.08 (−2.7) | 0.15 (5.4) | 0.99 | −0.21 (−2.7) | 0.55 (7.1) | 0.99 | −0.13 (−2.7) | 0.36 (7.6) | |
| Rrs(547) | 0.99 | 0.13 (5.0) | 0.16 (6.4) | 0.99 | 0.46 (5.8) | 0.89 (11.1) | 0.99 | 0.25 (5.5) | 0.56 (12.2) | |
| Rrs(667) | 0.82 | 0.03 (6.9) | 0.13 (27.1) | 0.84 | −0.45 (−18.4) | 1.68 (69.1) | 0.84 | −0.15 (−12.1) | 1.05 (84.5) | |
| Rrs(869) | 0.01 | −0.02 (−22.3) | 0.10 (28.1) | 0.44 | 0.01 (5.1) | 0.31 (124.4) | 0.42 | −0.01 (−4.2) | 0.21 (143.8) | |
| PR05 | Rrs(412) | 0.98 | 0.25 (9.4) | 0.33 (12.8) | 0.95 | 0.42 (12.1) | 0.69 (19.6) | 0.96 | 0.31 (10.6) | 0.50 (16.9) |
| Rrs(443) | 0.99 | 0.01 (0.5) | 0.12 (4.2) | 0.99 | −0.11 (−2.4) | 0.50 (10.9) | 0.99 | −0.03 (−1.0) | 0.32 (9.3) | |
| Rrs(488) | 0.95 | −0.25 (−7.4) | 0.33 (10.1) | 0.99 | −0.46 (−6.6) | 0.71 (10.2) | 0.99 | −0.33 (−6.9) | 0.51 (10.8) | |
| Rrs(531) | 0.98 | −0.05 (−1.6) | 0.14 (4.9) | 0.99 | 0.02 (0.2) | 0.63 (8.1) | 0.99 | −0.02 (−0.5) | 0.41 (8.5) | |
| Rrs(547) | 0.97 | 0.08 (3.1) | 0.18 (7.2) | 0.99 | 0.33 (4.2) | 0.94 (11.8) | 0.99 | 0.18 (3.8) | 0.60 (12.9) | |
| Rrs(667) | 0.85 | 0.04 (9.1) | 0.16 (32.3) | 0.98 | 0.03 (1.4) | 0.40 (16.6) | 0.98 | 0.04 (3.3) | 0.28 (22.6) | |
| Rrs(869) | 0.01 | −0.03 (−42.7) | 0.10 (132.3) | 0.82 | −0.01 (−4.0) | 0.18 (71.1) | 0.76 | −0.02 (−17.1) | 0.14 (94.9) | |
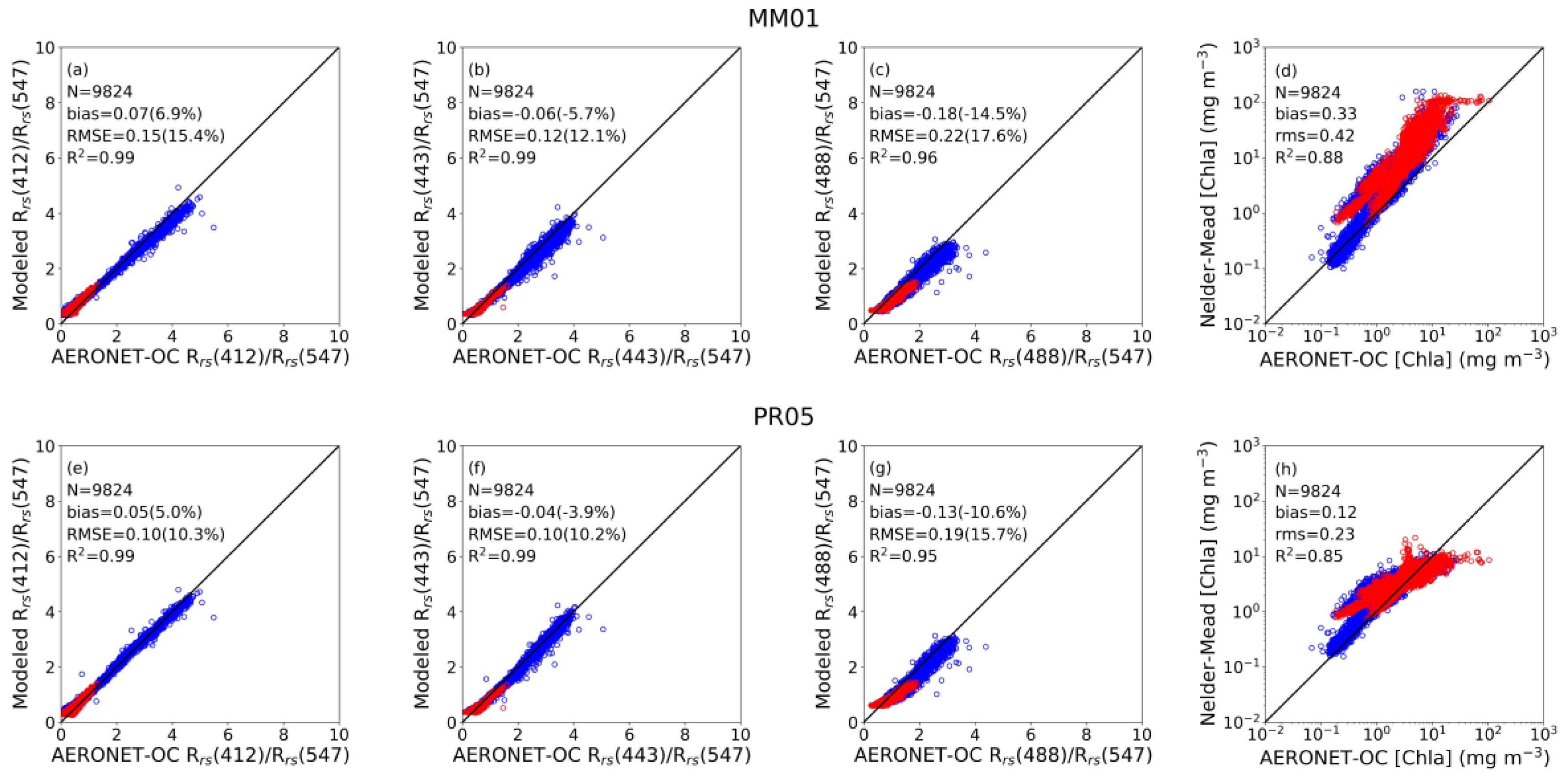
| Parameter | Case 1, N = 6094 | Case 2, N = 3730 | |||||
|---|---|---|---|---|---|---|---|
| R2 | Bias (bias%) | RMSE (RMSE%) | R2 | Bias (bias%) | RMSE (RMSE%) | ||
| MM01 | Rrs(412)/Rrs(547) | 0.99 | 0.03 (2.4) | 0.15 (11.8) | 0.87 | 0.12 (28.7) | 0.14 (32.6) |
| Rrs(443)/Rrs(547) | 0.99 | −0.08 (−6.0) | 0.15 (11.4) | 0.94 | −0.02 (−3.5) | 0.06 (11.0) | |
| Rrs(488)/Rrs(547) | 0.96 | −0.19 (−13.1) | 0.24 (16.4) | 0.89 | −0.16 (−18.2) | 0.18 (20.4) | |
| log10([Chla]) | 0.88 | 0.22 | 0.33 | 0.80 | 0.50 | 0.54 | |
| PR05 | Rrs(412)/Rrs(547) | 0.99 | 0.04 (3.3) | 0.10 (8.0) | 0.85 | 0.06 (13.1) | 0.09 (21.1) |
| Rrs(443)/Rrs(547) | 0.99 | −0.05 (−4.1) | 0.12 (9.1) | 0.91 | −0.02 (−3.1) | 0.08 (13.5) | |
| Rrs(488)/Rrs(547) | 0.95 | −0.16 (−10.9) | 0.22 (15.2) | 0.84 | −0.08 (−9.8) | 0.14 (15.9) | |
| log10([Chla]) | 0.85 | 0.14 | 0.23 | 0.73 | 0.09 | 0.22 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Frouin, R.; Ramon, D.; Steinmetz, F. On the Adequacy of Representing Water Reflectance by Semi-Analytical Models in Ocean Color Remote Sensing. Remote Sens. 2019, 11, 2820. https://doi.org/10.3390/rs11232820
Tan J, Frouin R, Ramon D, Steinmetz F. On the Adequacy of Representing Water Reflectance by Semi-Analytical Models in Ocean Color Remote Sensing. Remote Sensing. 2019; 11(23):2820. https://doi.org/10.3390/rs11232820
Chicago/Turabian StyleTan, Jing, Robert Frouin, Didier Ramon, and François Steinmetz. 2019. "On the Adequacy of Representing Water Reflectance by Semi-Analytical Models in Ocean Color Remote Sensing" Remote Sensing 11, no. 23: 2820. https://doi.org/10.3390/rs11232820
APA StyleTan, J., Frouin, R., Ramon, D., & Steinmetz, F. (2019). On the Adequacy of Representing Water Reflectance by Semi-Analytical Models in Ocean Color Remote Sensing. Remote Sensing, 11(23), 2820. https://doi.org/10.3390/rs11232820