An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment
Abstract
1. Introduction
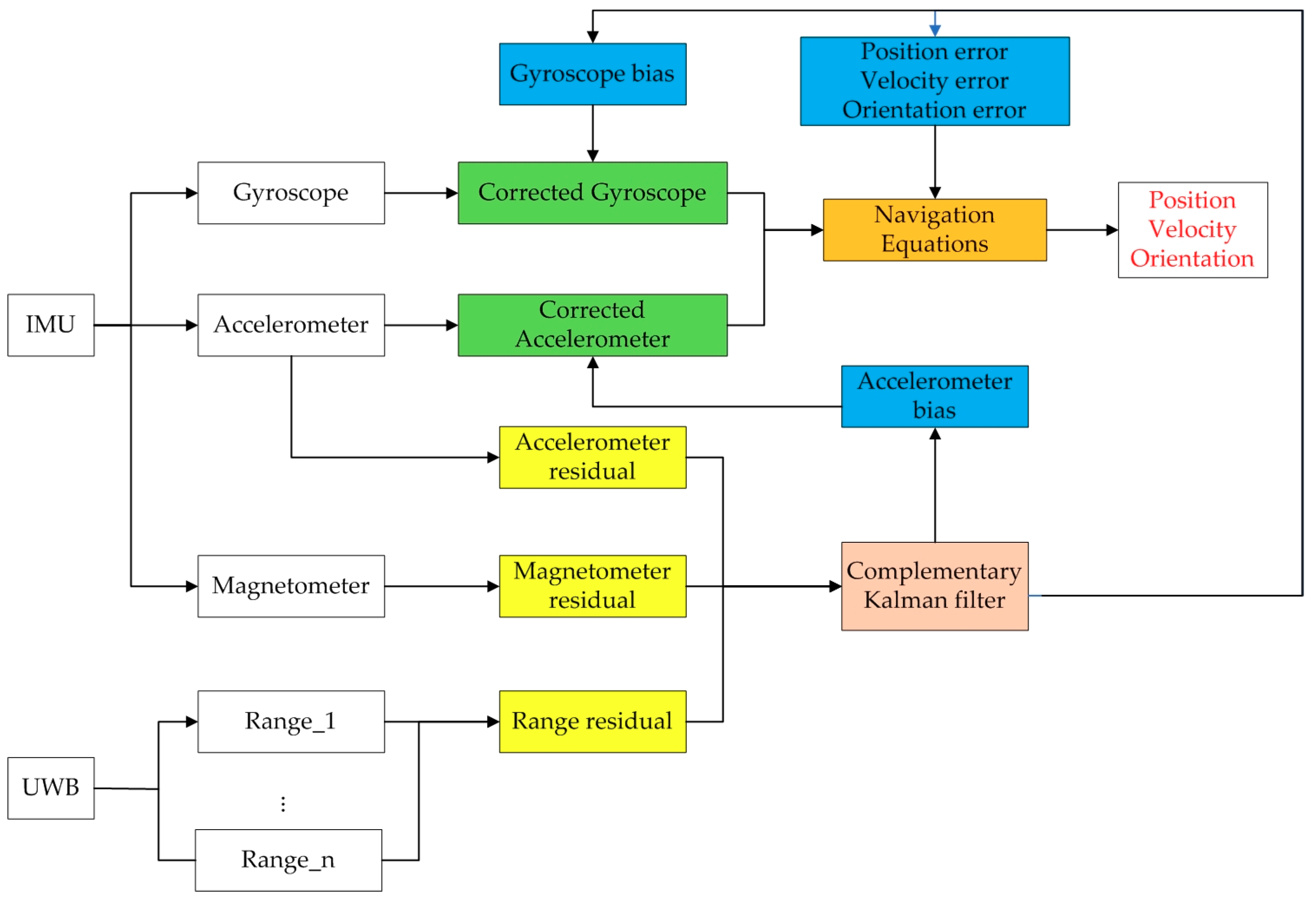
2. Fusion Location Algorithm of IMU/UWB
2.1. State Model
2.1.1. The Equation of Acceleration and Gyroscope Bias
2.1.2. The Directional Error Equation
2.1.3. The Error Equation of Velocity and Position
2.2. The Observation Model
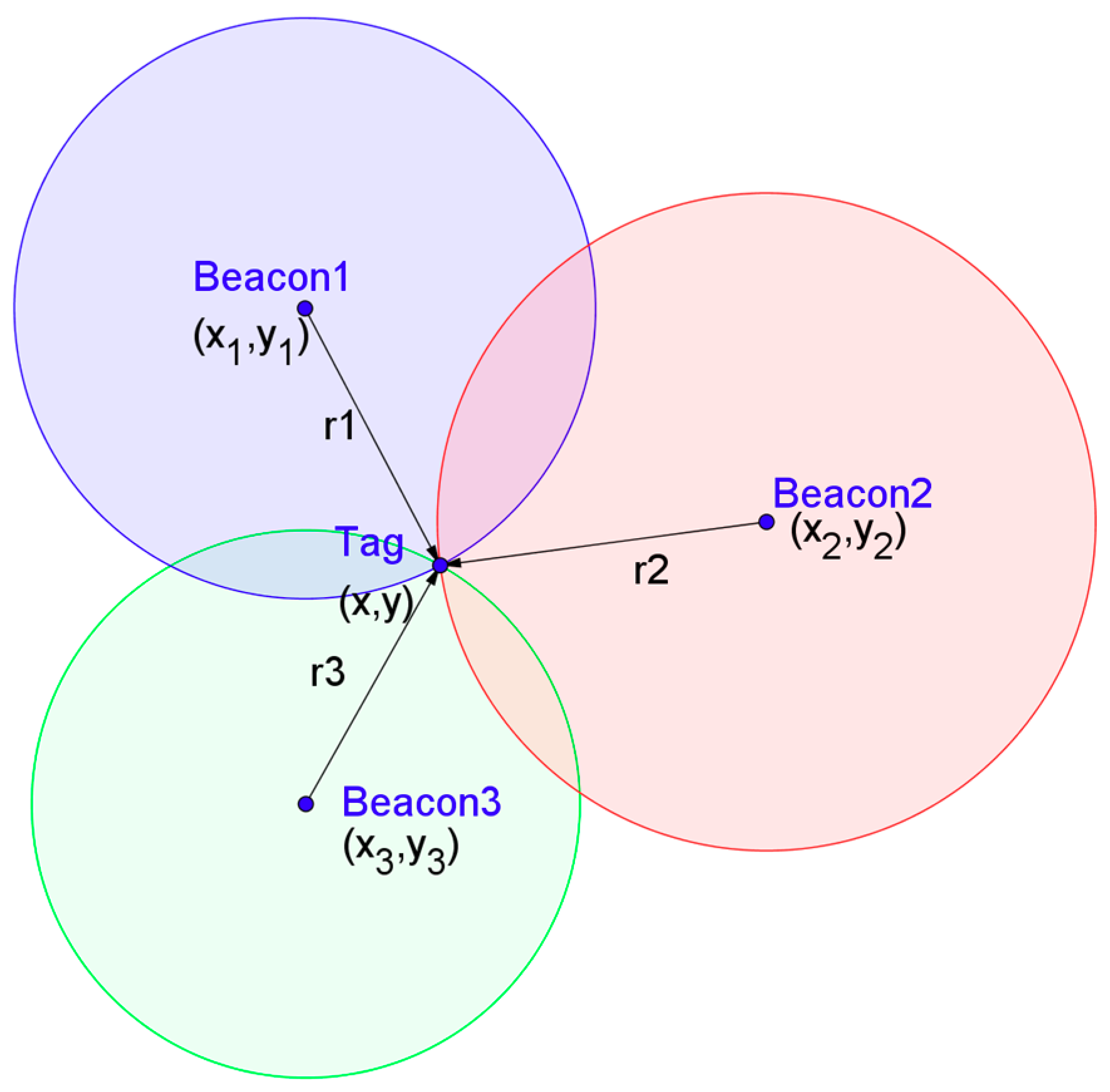
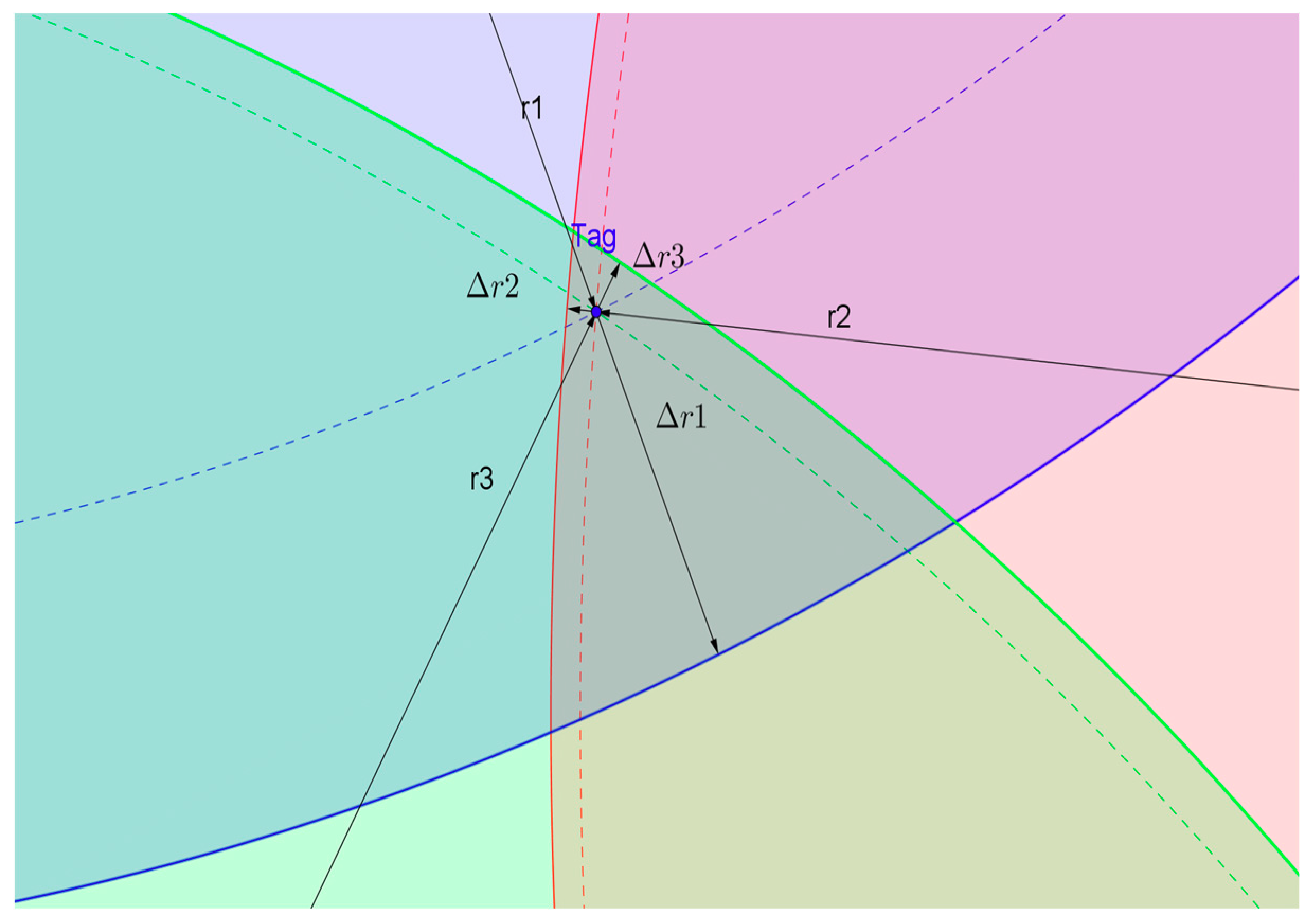
2.2.1. UWB Observations
2.2.2. Observations of Accelerometers and Magnetometers
2.3. INS Navigation Equation
3. Experiment
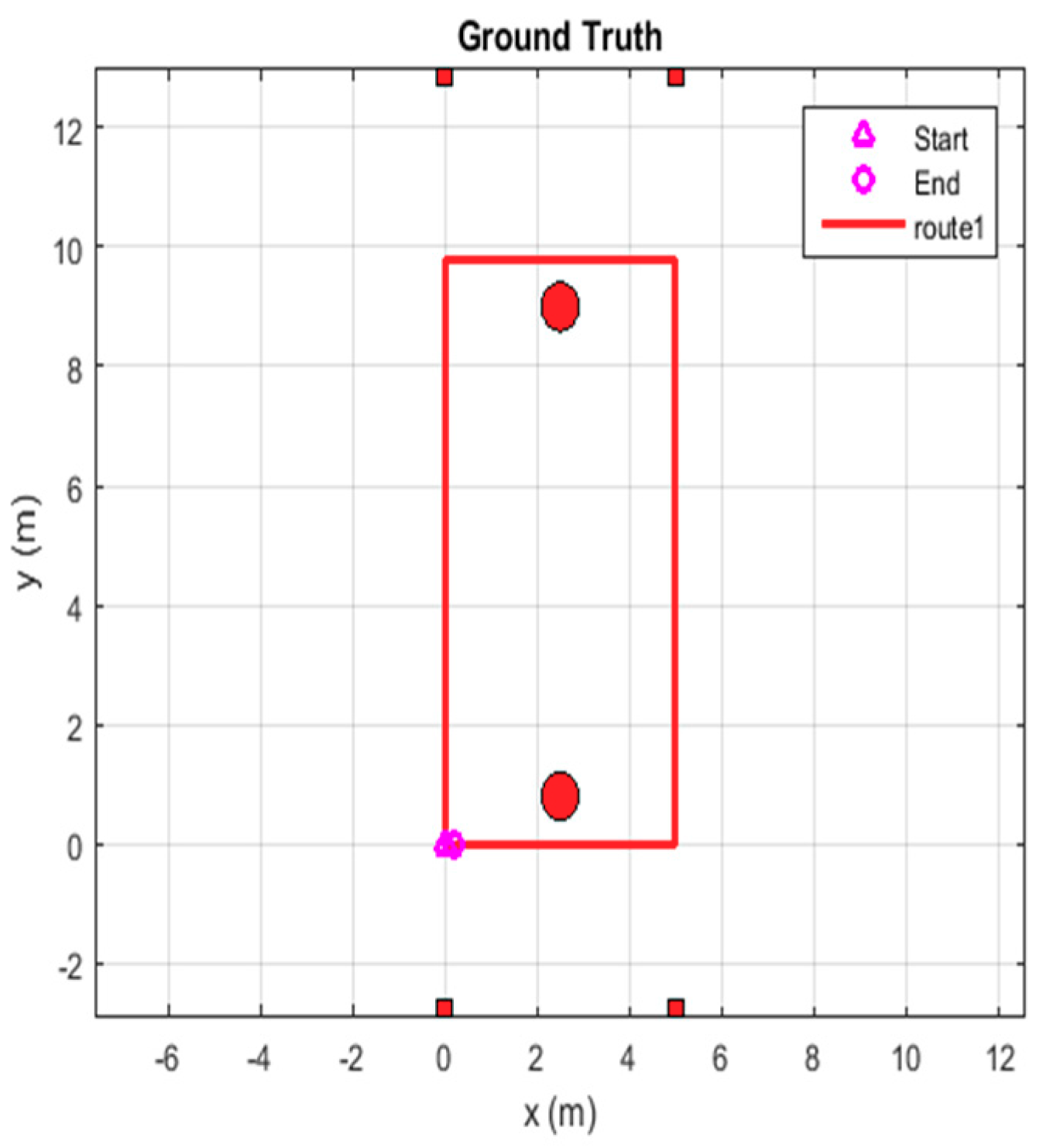
3.1. Analysis of Location Results of Route 1
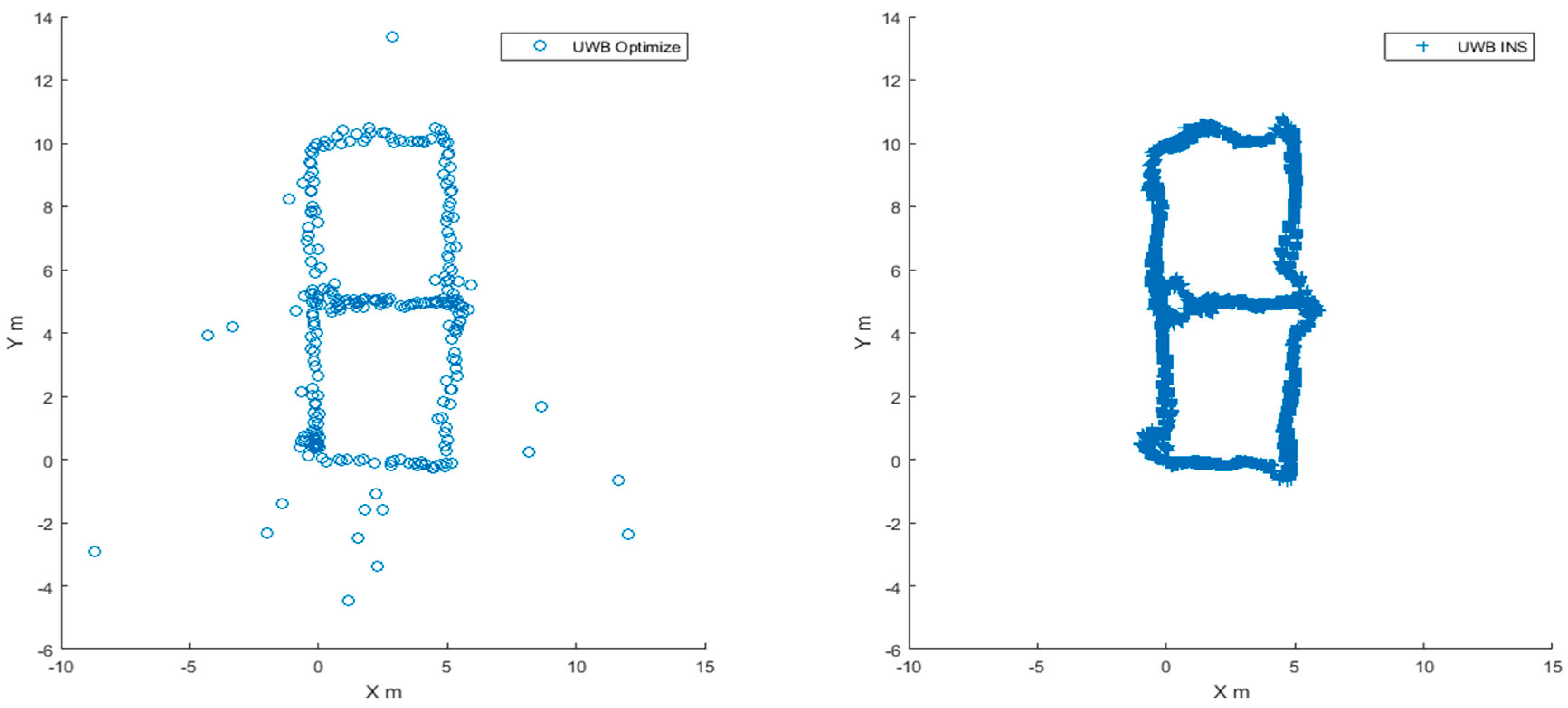
3.1.1. Positioning Trajectory Analysis
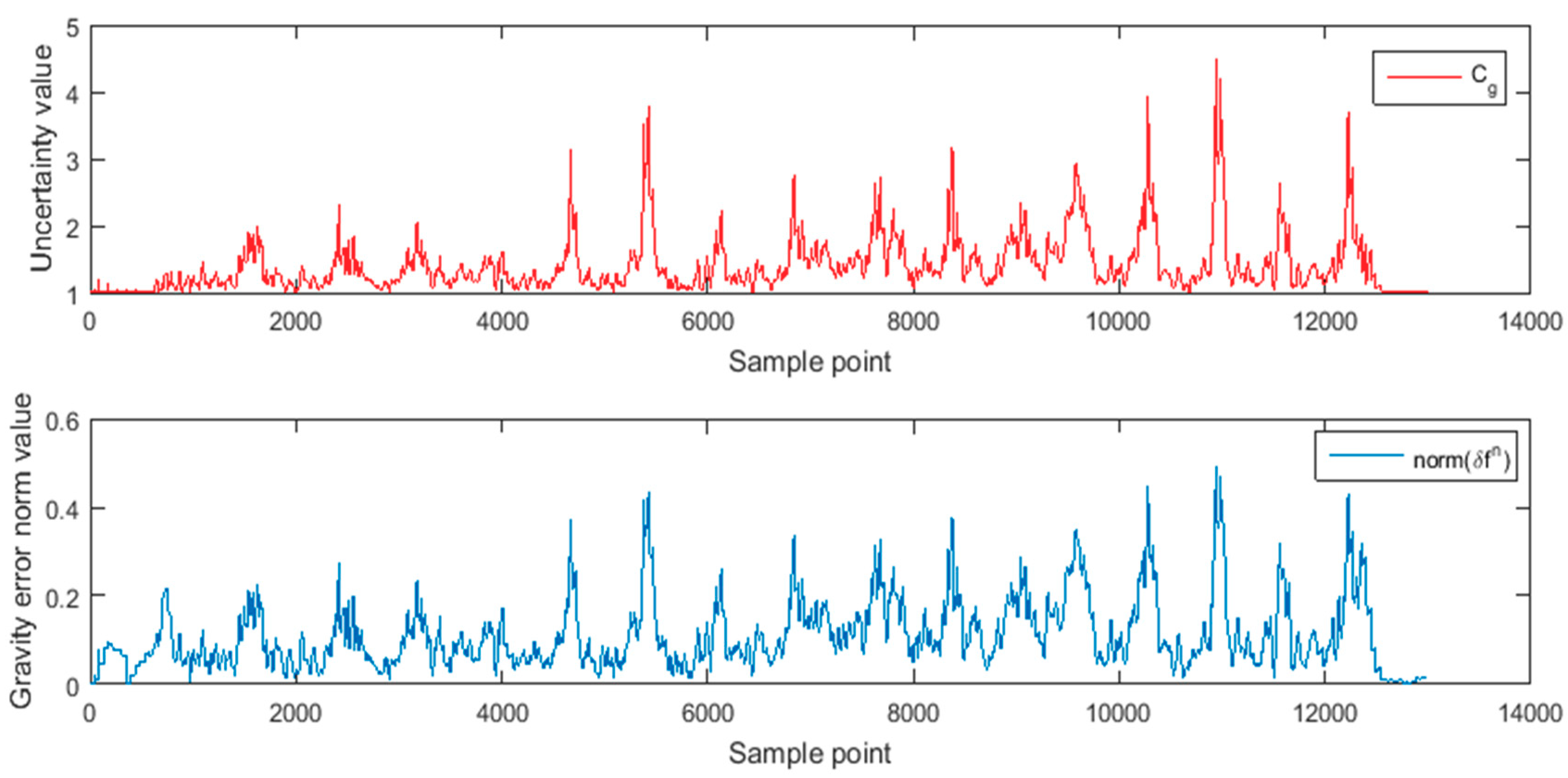
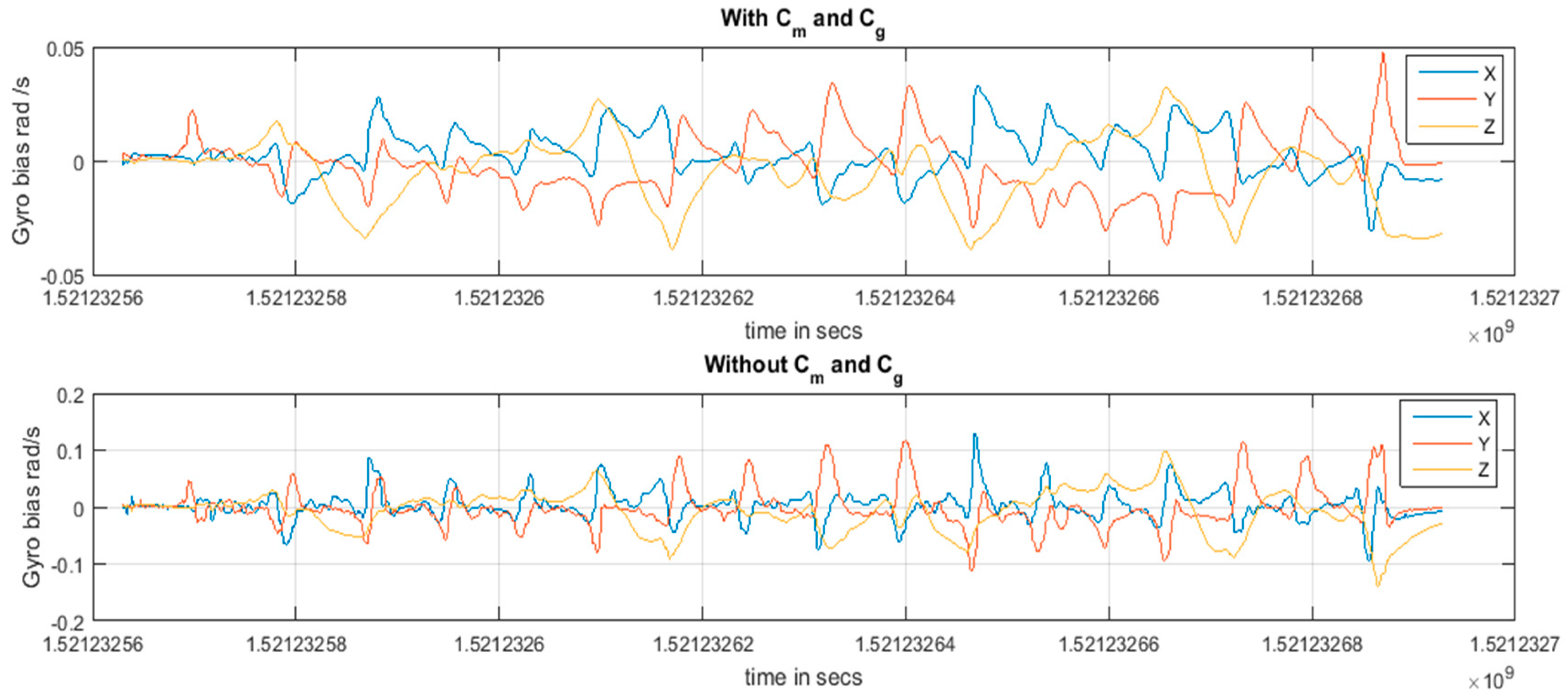
3.1.2. Analysis of Geomagnetism and Gravity Residual
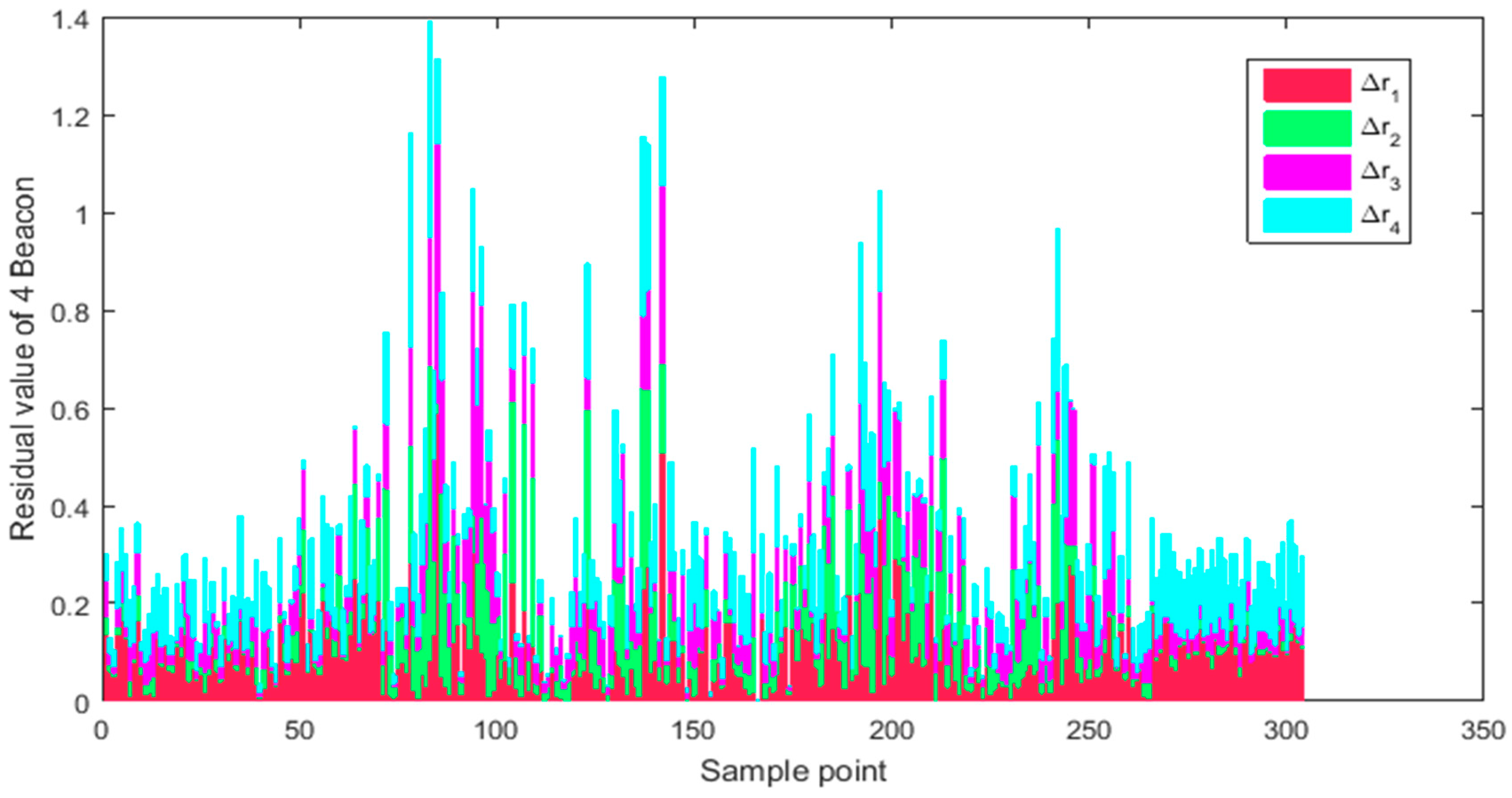
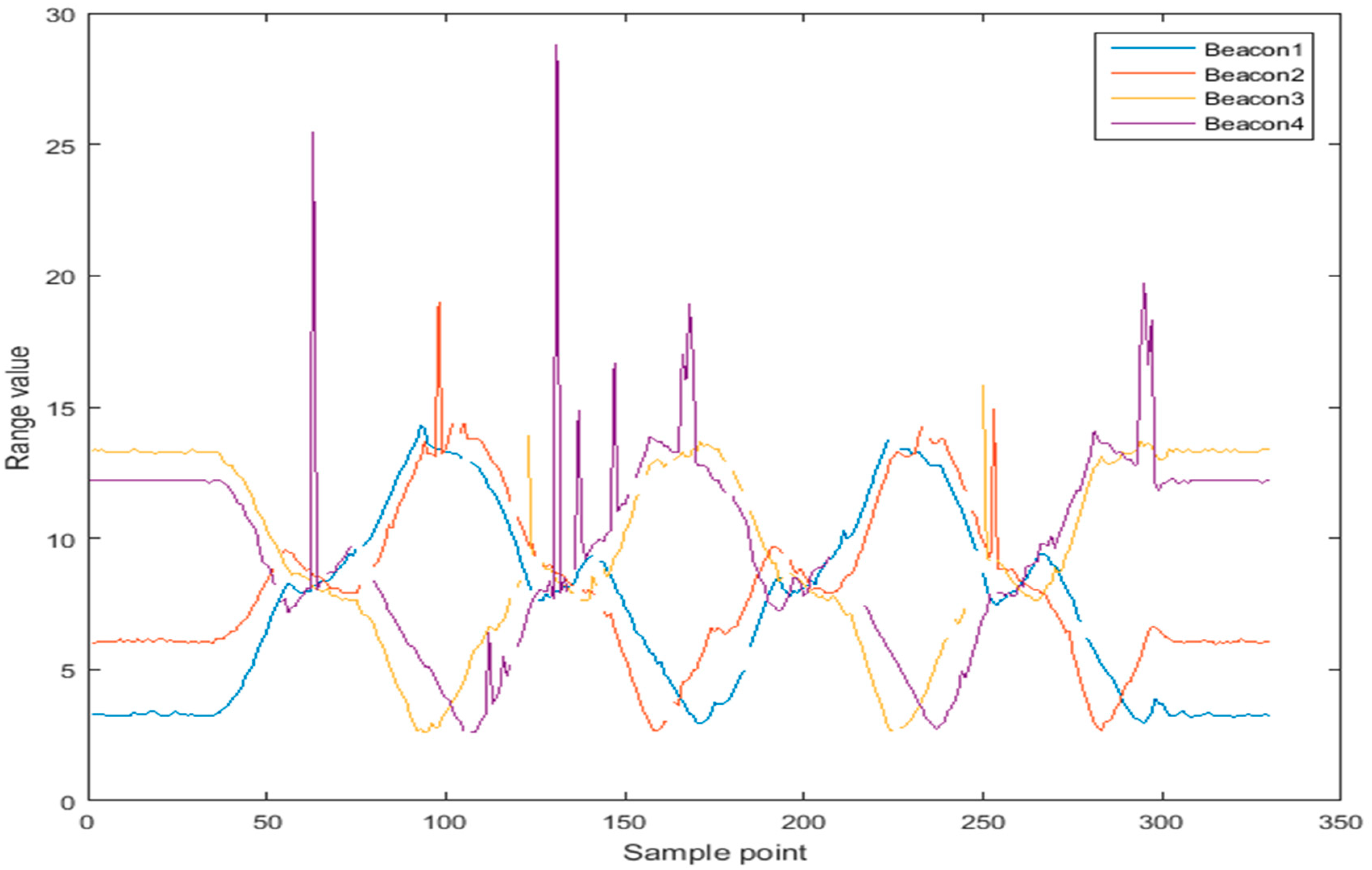
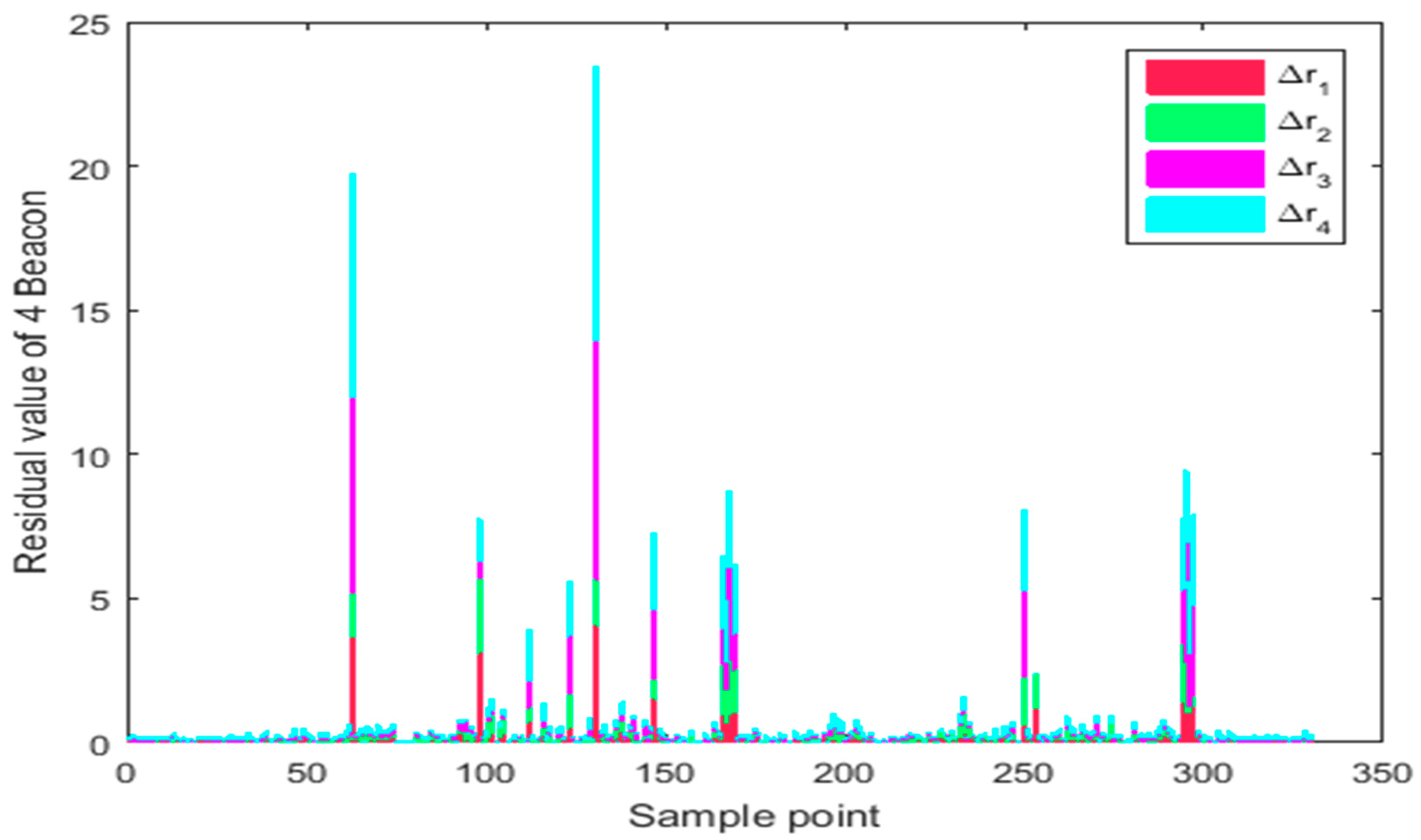
3.1.3. Residual Analysis of UWB Data
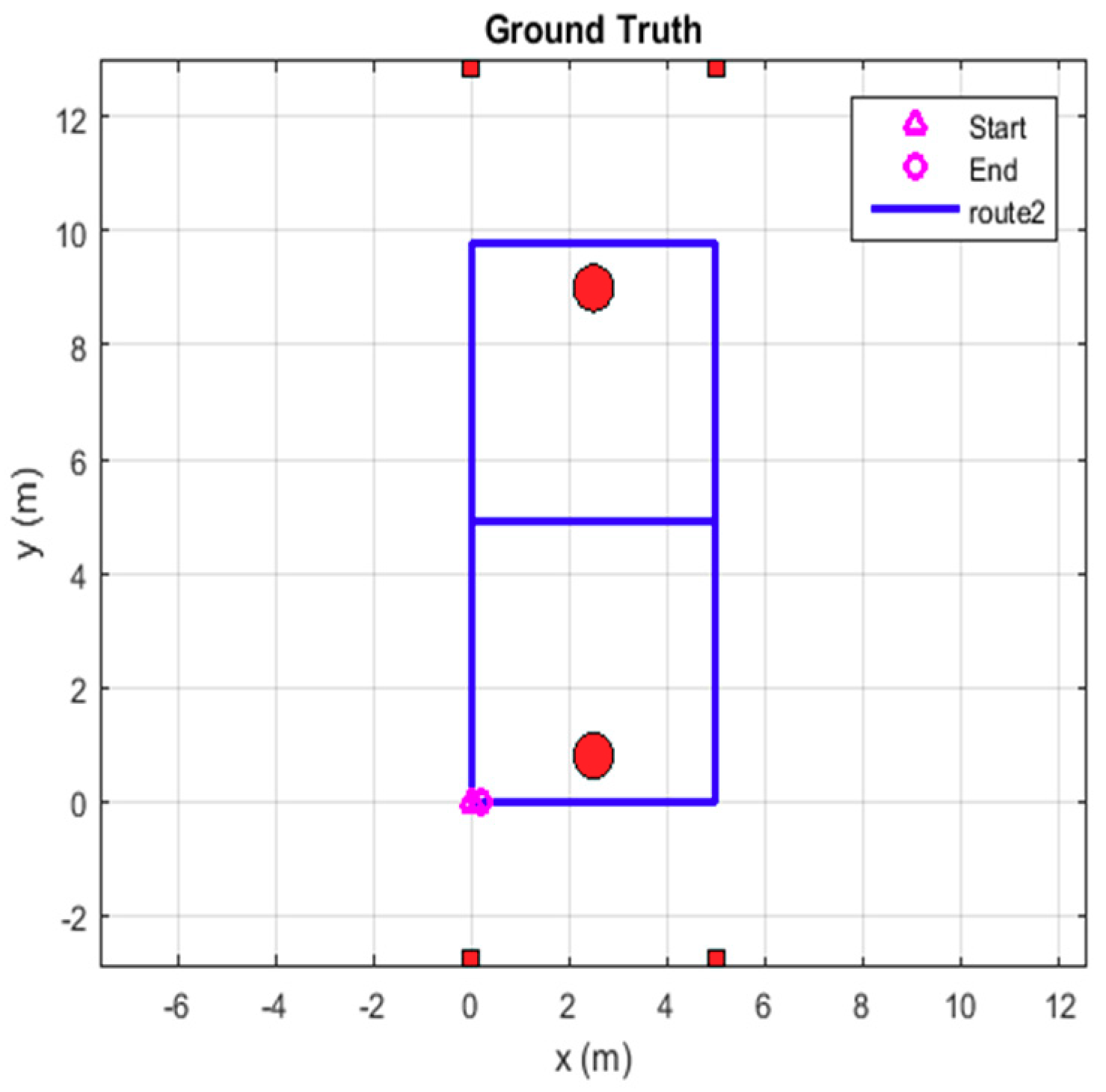
3.2. Analysis of Location Trajectory of Route 2
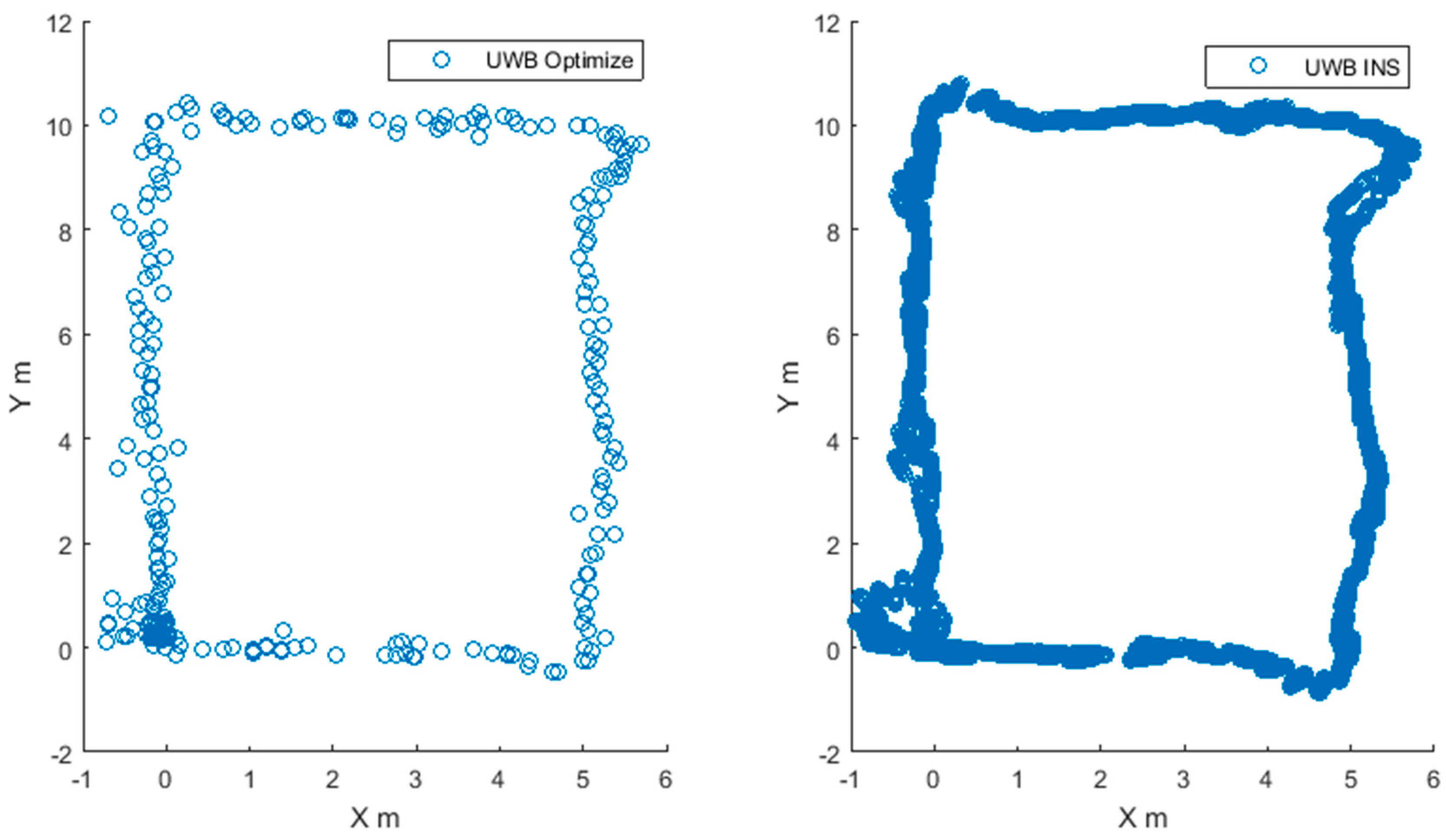
3.2.1. Location Trajectory Analysis
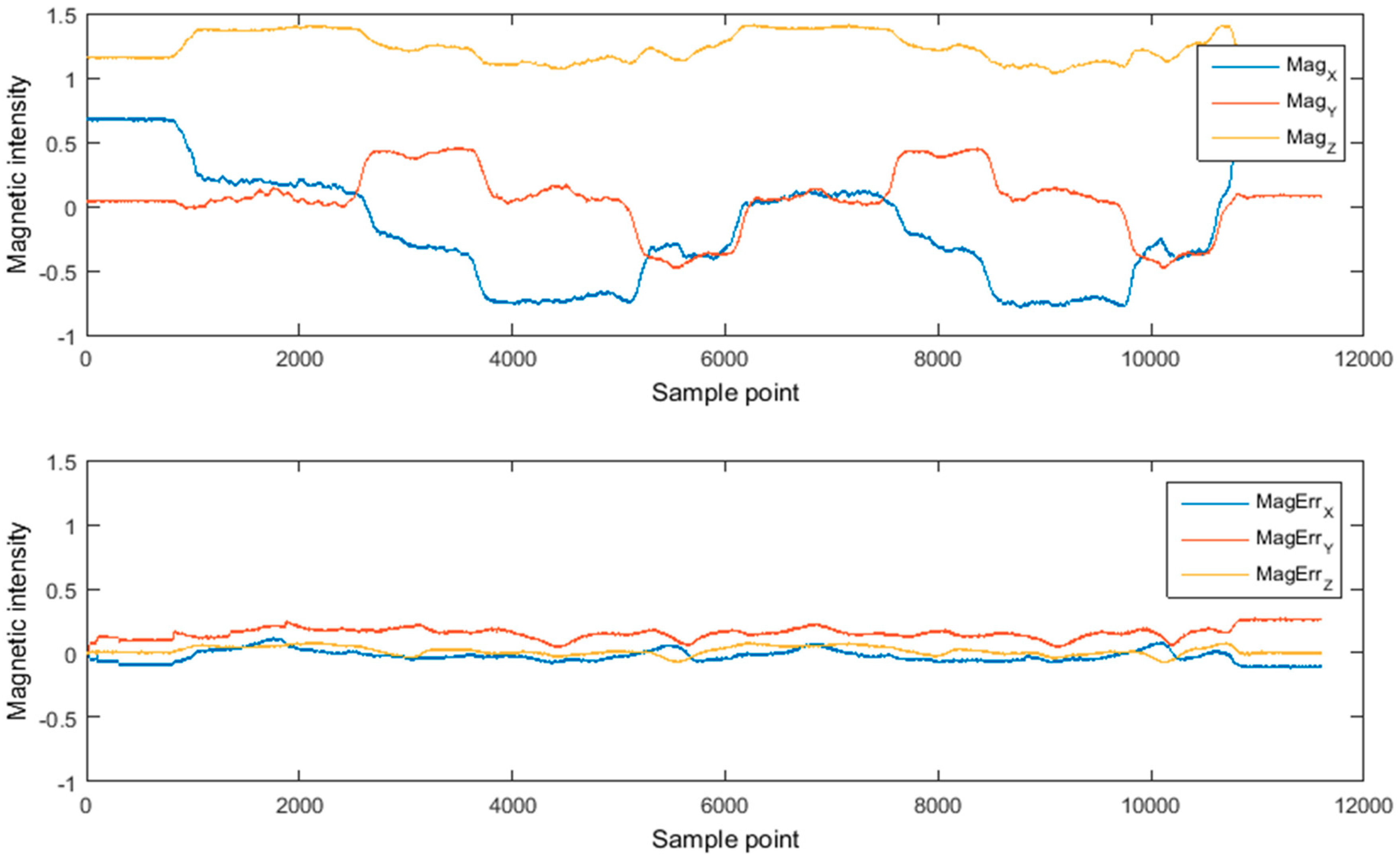
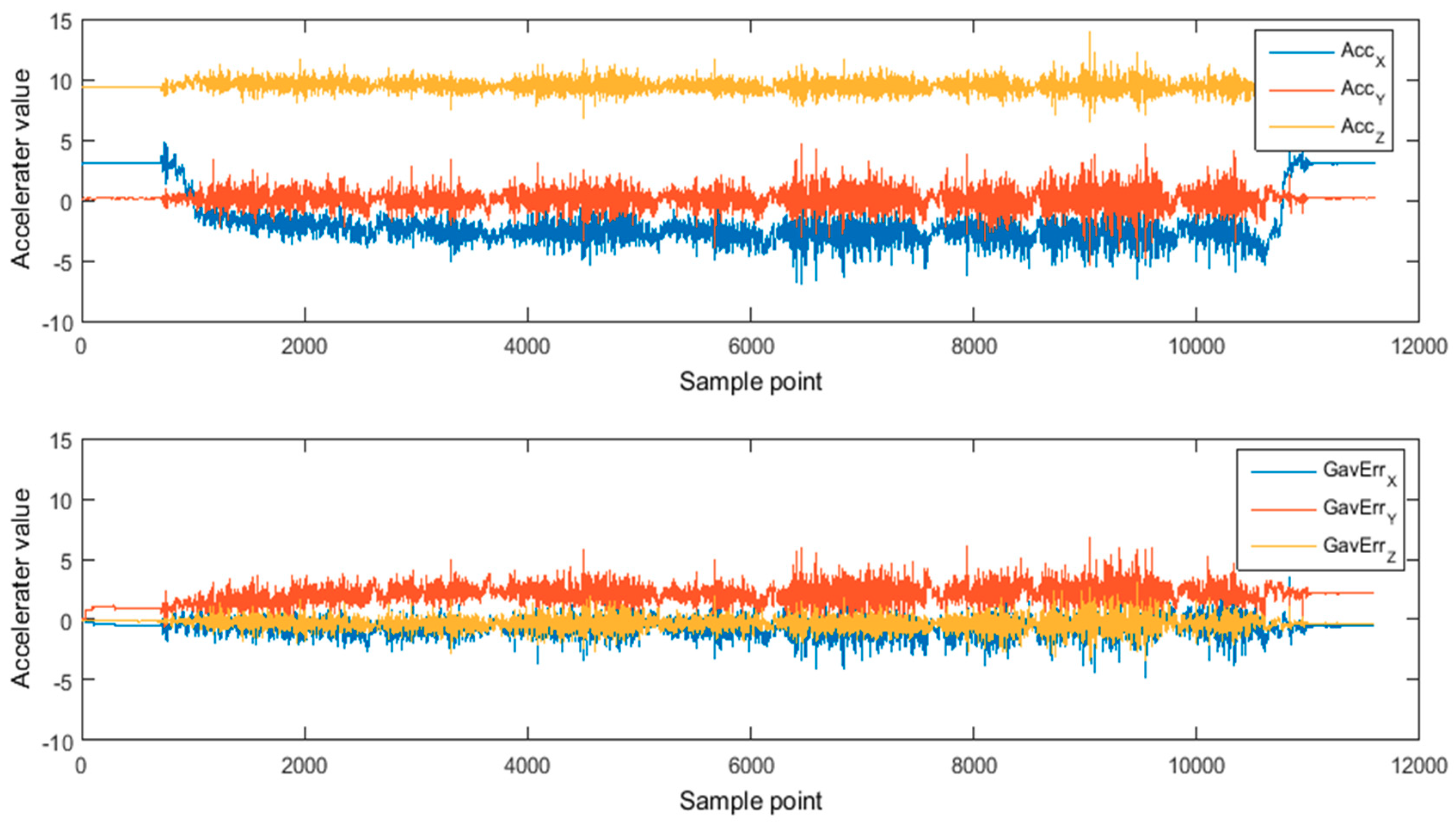
3.2.2. Analysis of Geomagnetism and Gravity Residual
3.2.3. Residual Analysis of UWB Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xin, L.; Jian, W.; Liu, C.; Zhang, L.; Li, Z. Integrated WiFi/PDR/Smartphone Using an Adaptive System Noise Extended Kalman Filter Algorithm for Indoor Localization. Int. J. Geo-Inf. 2016, 5, 8. [Google Scholar]
- Santoso, F.; Redmond, S.J. Indoor location-aware medical systems for smart homecare and telehealth monitoring: State-of-the-art. Physiol. Meas. 2015, 36, R53–R87. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Wang, J.; Zhang, J.; Han, H. An Indoor Localization Method for Pedestrians Base on Combined UWB/PDR/Floor Map. Sensors 2019, 19, 2578. [Google Scholar] [CrossRef] [PubMed]
- Dabove, P.; Di Pietra, V.; Piras, M.; Jabbar, A.A.; Kazim, S.A. Indoor positioning using Ultra-wide band (UWB) technologies: Positioning accuracies and sensors’ performances. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 175–184. [Google Scholar]
- García, E.; Poudereux, P.; Hernández, Á.; Ureña, J.; Gualda, D. A robust UWB indoor positioning system for highly complex environments. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 3386–3391. [Google Scholar]
- Zhang, J.; Shen, C. Research on UWB indoor positioning in combination with TDOA improved algorithm and Kalman filtering. Mod. Electron. Tech. 2016, 39, 1–5. [Google Scholar]
- Fan, Q.; Sun, B.; Yan, S.; Zhuang, X.J.I.S.J. Performance Enhancement of MEMS-Based INS/UWB Integration for Indoor Navigation Applications. IEEE Sens. J. 2017, 17, 3116–3130. [Google Scholar] [CrossRef]
- Denis, B.; Keignart, J.; Daniele, N. Impact of NLOS propagation upon ranging precision in UWB systems. In Proceedings of the IEEE Conference on Ultra Wideband Systems and Technologies, Reston, VA, USA, 16–19 November 2003; pp. 379–383. [Google Scholar]
- Wang, X.; Wang, Z.; O’Dea, B. A TOA-based location algorithm reducing the errors due to non-line-of-sight (NLOS) propagation. IEEE Trans. Veh. Technol. 2003, 52, 112–116. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Mäkelä, M.; Kirkko-Jaakkola, M.; Rantanen, J.; Ruotsalainen, L. Proof of Concept Tests on Cooperative Tactical Pedestrian Indoor Navigation. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1369–1376. [Google Scholar]
- Sczyslo, S.; Schroeder, J.; Galler, S.; Kaiser, T. Hybrid localization using UWB and inertial sensors. In Proceedings of the IEEE International Conference on Ultra-Wideband, Hannover, Germany, 10–12 September 2008. [Google Scholar]
- Yuan, X.; Chen, X.; Jin, C.; Zhao, Q.; Wang, Y. Improving tightly-coupled model for indoor pedestrian navigation using foot-mounted IMU and UWB measurements. In Proceedings of the Instrumentation & Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016. [Google Scholar]
- Fan, Q.; Sun, B.; Yan, S.; Wu, Y.; Zhuang, X. Data Fusion for Indoor Mobile Robot Positioning Based on Tightly Coupled INS/UWB. J. Navig. 2017, 70, 1079–1097. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X. Range-only uwb/ins tightly integrated navigation method for indoor pedestrian. Chin. J. Sci. Instrum. 2016, 37, 142–148. [Google Scholar]
- Wang, J.; Yang, G.; Li, Z.; Meng, X.; Hancock, C.M. A Tightly-Coupled GPS/INS/UWB Cooperative Positioning Sensors System Supported by V2I Communication. Sensors 2016, 16, 944. [Google Scholar] [CrossRef] [PubMed]
- Benini, A.; Mancini, A.; Longhi, S. An IMU/UWB/Vision-based Extended Kalman Filter for Mini-UAV Localization in Indoor Environment using 802.15.4a Wireless Sensor Network. J. Intell. Robot. Syst. 2013, 70, 461–476. [Google Scholar] [CrossRef]
- Li, K.; Wang, C.; Huang, S.; Liang, G.; Wu, X.; Liao, Y. Self-positioning for UAV indoor navigation based on 3D laser scanner, UWB and INS. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 498–503. [Google Scholar]
- González, J.; Blanco, J.L. Mobile robot localization based on Ultra-Wide-Band ranging: A particle filter approach. Robot. Auton. Syst. 2009, 57, 496–507. [Google Scholar] [CrossRef]
- Zwirello, L.; Ascher, C.; Trommer, G.F.; Zwick, T. Study on UWB/INS integration techniques. In Proceedings of the Positioning Navigation & Communication, Dresden, Germany, 7–8 April 2011. [Google Scholar]
- Chen, P.; Kuang, Y.; Chen, X. A UWB/Improved PDR Integration Algorithm Applied to Dynamic Indoor Positioning for Pedestrians. Sensors 2017, 17, 2065. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ahn, C.K.; Shmaliy, Y.S.; Chen, X.; Li, Y. Adaptive robust INS/UWB-integrated human tracking using UFIR filter bank. Measurement 2018, 123, 1–7. [Google Scholar] [CrossRef]
- Hartmann, F.; Rifat, D.; Stork, W. Hybrid indoor pedestrian navigation combining an INS and a spatial non-uniform UWB-network. In Proceedings of the 2016 19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016; pp. 549–556. [Google Scholar]
- Hol, J.D.; Dijkstra, F.; Luinge, H.; Schon, T.B. Tightly coupled UWB/IMU pose estimation. In Proceedings of the IEEE International Conference on Ultra-Wideband, Vancouver, BC, Canada, 9–11 September 2009. [Google Scholar]
- Savioli, A.; Goldoni, E.; Savazzi, P.; Gamba, P. Low Complexity Indoor Localization in Wireless Sensor Networks by UWB and Inertial Data Fusion. Comput. Sci. 2013, 52, 723–732. [Google Scholar]
- Ascher, C.; Zwirello, L.; Zwick, T.; Trommer, G. Integrity monitoring for UWB/INS tightly coupled pedestrian indoor scenarios. In Proceedings of the International Conference on Indoor Positioning & Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011. [Google Scholar]
- Fan, Q.; Wu, Y.; Hui, J.; Wu, L.; Yu, Z.; Zhou, L. Integrated navigation fusion strategy of INS/UWB for indoor carrier attitude angle and position synchronous tracking. Sci. World J. 2014, 2014, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.E.; Sathyan, T. Improved orientation estimation in complex environments using low-cost inertial sensors. In Proceedings of the International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011. [Google Scholar]
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology. Aerosp. Electron. Syst. Mag. IEEE 2004, 20, 33–34. [Google Scholar] [CrossRef]
- Nyqvist, H.E.; Skoglund, M.A.; Hendeby, G.; Gustafsson, F. Pose estimation using monocular vision and inertial sensors aided with ultra wide band. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–10. [Google Scholar]
- Fischer, C.; Sukumar, P.T.; Hazas, M. Tutorial: Implementing a Pedestrian Tracker Using Inertial Sensors. IEEE Pervasive Comput. 2013, 12, 17–27. [Google Scholar] [CrossRef]
- Nilsson, J.O. Navigation System for a Micro-UAV. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2008. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering: With MATLAB Exercises and Solutions, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]




| Coordinate Axis | Average of Absolute Value | Max | Min |
|---|---|---|---|
| X | 0.0449 | 0.1188 | −0.1180 |
| Y | 0.1564 | 0.2720 | −0.0125 |
| Z | 0.0287 | 0.0839 | −0.0783 |
| Axial Direction | Average of Absolute Value | Max | Min |
|---|---|---|---|
| X | 0.7248 | 4.8814 | −3.7402 |
| Y | 2.0226 | 6.0312 | −1.5509 |
| Z | 0.6095 | 3.4986 | −3.4159 |
| Base Station | Average of Absolute Value | Max | Min |
|---|---|---|---|
| Beacon1 | 0.0910 | 0.5882 | 0 |
| Beacon2 | 0.0733 | 0.6012 | 0 |
| Beacon3 | 0.0688 | 0.5283 | 0 |
| Beacon4 | 0.0919 | 0.4413 | 0 |
| Base Station | Average of Absolute Value | Max | Min |
|---|---|---|---|
| Beacon1 | 0.1362 | 4.0561 | 0 |
| Beacon2 | 0.1400 | 2.5900 | 0 |
| Beacon3 | 0.1781 | 8.2678 | 0 |
| Beacon4 | 0.2304 | 9.5135 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Li, X.; Wang, J.; Zhang, J. An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment. Remote Sens. 2019, 11, 2628. https://doi.org/10.3390/rs11222628
Liu F, Li X, Wang J, Zhang J. An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment. Remote Sensing. 2019; 11(22):2628. https://doi.org/10.3390/rs11222628
Chicago/Turabian StyleLiu, Fei, Xin Li, Jian Wang, and Jixian Zhang. 2019. "An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment" Remote Sensing 11, no. 22: 2628. https://doi.org/10.3390/rs11222628
APA StyleLiu, F., Li, X., Wang, J., & Zhang, J. (2019). An Adaptive UWB/MEMS-IMU Complementary Kalman Filter for Indoor Location in NLOS Environment. Remote Sensing, 11(22), 2628. https://doi.org/10.3390/rs11222628






