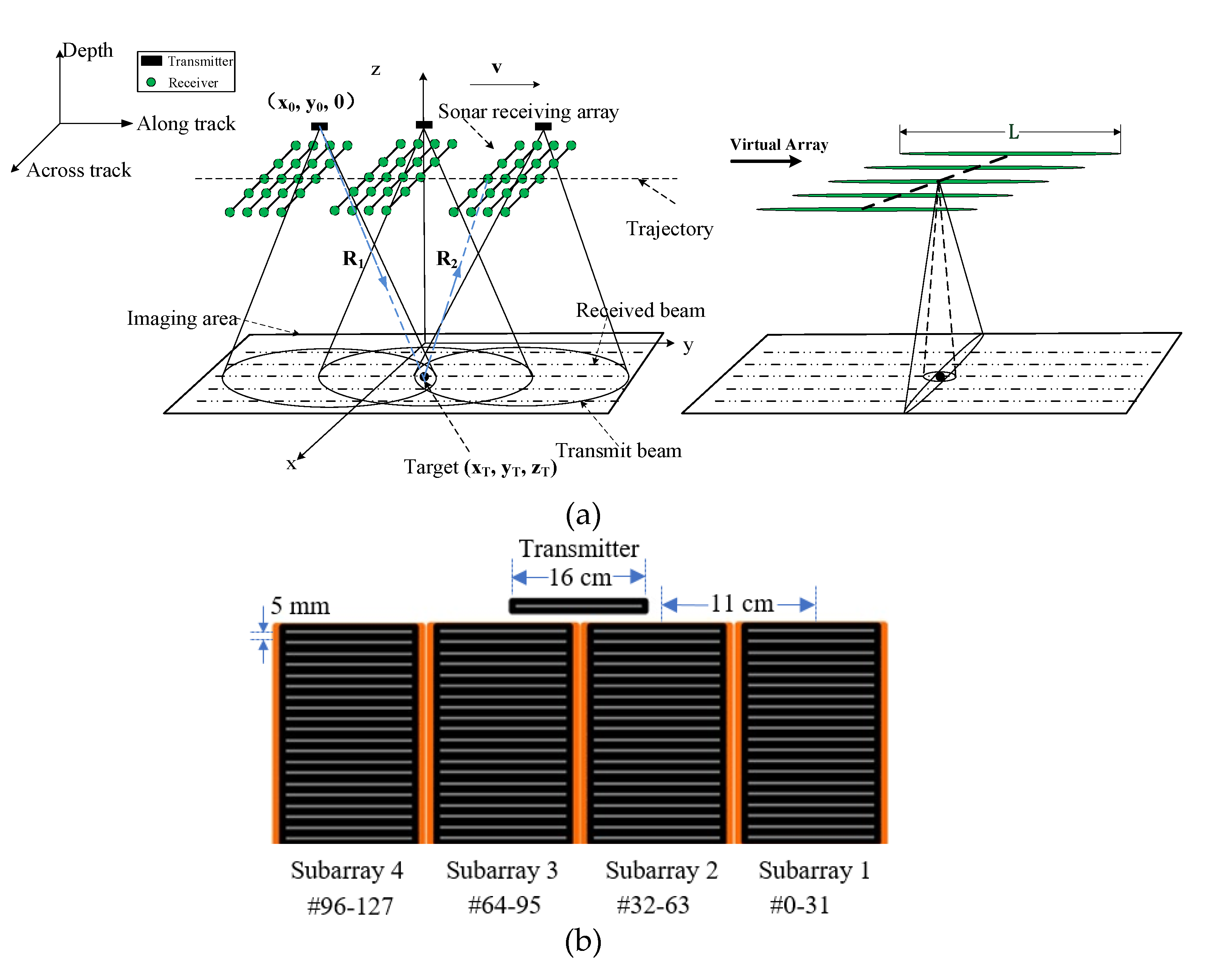
Target simulation is the basic and necessary work of MBSAS modeling. To provide a detailed echo signal to the imaging algorithm, not only the target main body but also the shadows at different synthetic positions should be simulated in detail. An acoustic highlights model is employed to carry the complex target echo simulation. Furthermore, an imaging algorithm is proposed to demonstrate the feasibility of the 2D MBSAS model.
3.1. Target with Shadow Simulation Approach
The basic unit of target simulation is the single highlight, which is widely employed to evaluate the performance of a detection algorithm, such as received beam angle width and sidelobe level [
19]. Thus, the solid target is divided into dozens of highlights through the tangents, as shown in
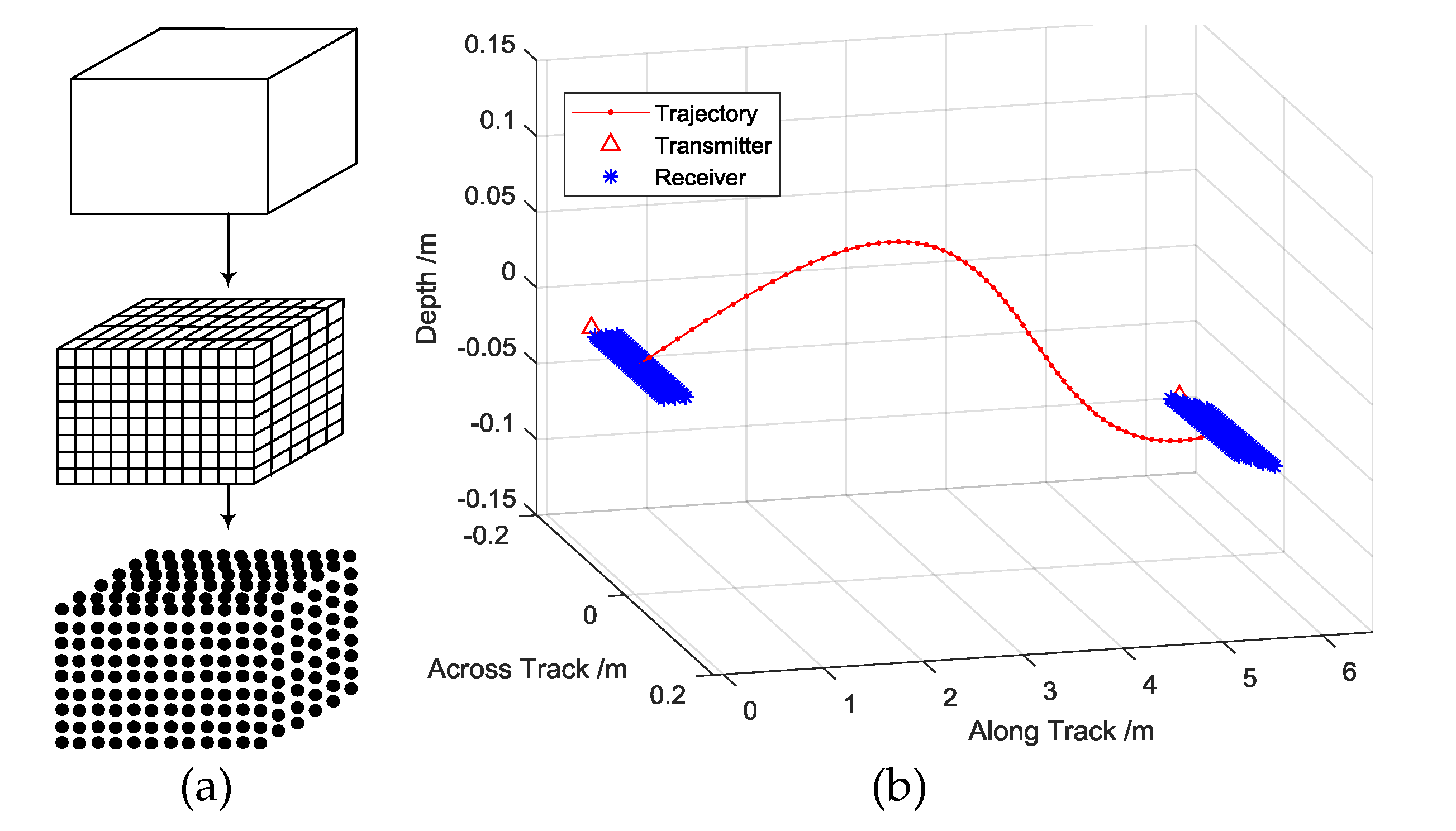
Figure 6a. Highlights on the surface contribute to the echo accumulated on the elements, ignoring the penetration of the echo. Movement of the 2D transducer array is more complex than the SAS which has single-element or multiple receivers on the along-track. The carrier should move as a uniform rectilinear motion in theory, but an ideal trajectory cannot always be maintained that the motion error must be estimated and compensated. The MBSAS can be equipped by surface vessel or AUV that the high accuracy motion sensors (USBL, DVL, and compass) or motion estimation algorithms based on the echo (DPC and PGA) are employed to calculate the position of each element, considering different application scenarios [
20].
The carrier has six dimensional motion parameters, which can be separated by position (sway, surge, and heave) and motion (yaw, roll, and pitch), as shown in
Figure 6b. Assuming that the 2D array has M ULAs on the along-track and each ULA has N elements on the across-track, the array we designed has a
manifold.
The coordinates of each element should be calculated accurately according to position and motion parameters to guarantee the validity of the imaging algorithm. We define the rotation angle along the x-axis, y-axis, and z-axis as
, respectively, then the rotation matrix
,
,
can be expressed as Equation (7)
Assuming the carrier’s translation along the x-axis, y-axis, and z-axis is
,
,
, respectively, the translation matrix can be defined as
, where
is the spanned
vector. The positions of the receiving elements
can be calculated through the rotation matrix and translation matrix from the initial position
as Equation (8)
Similarly, the transmitter’s position can be calculated through Equation (9).
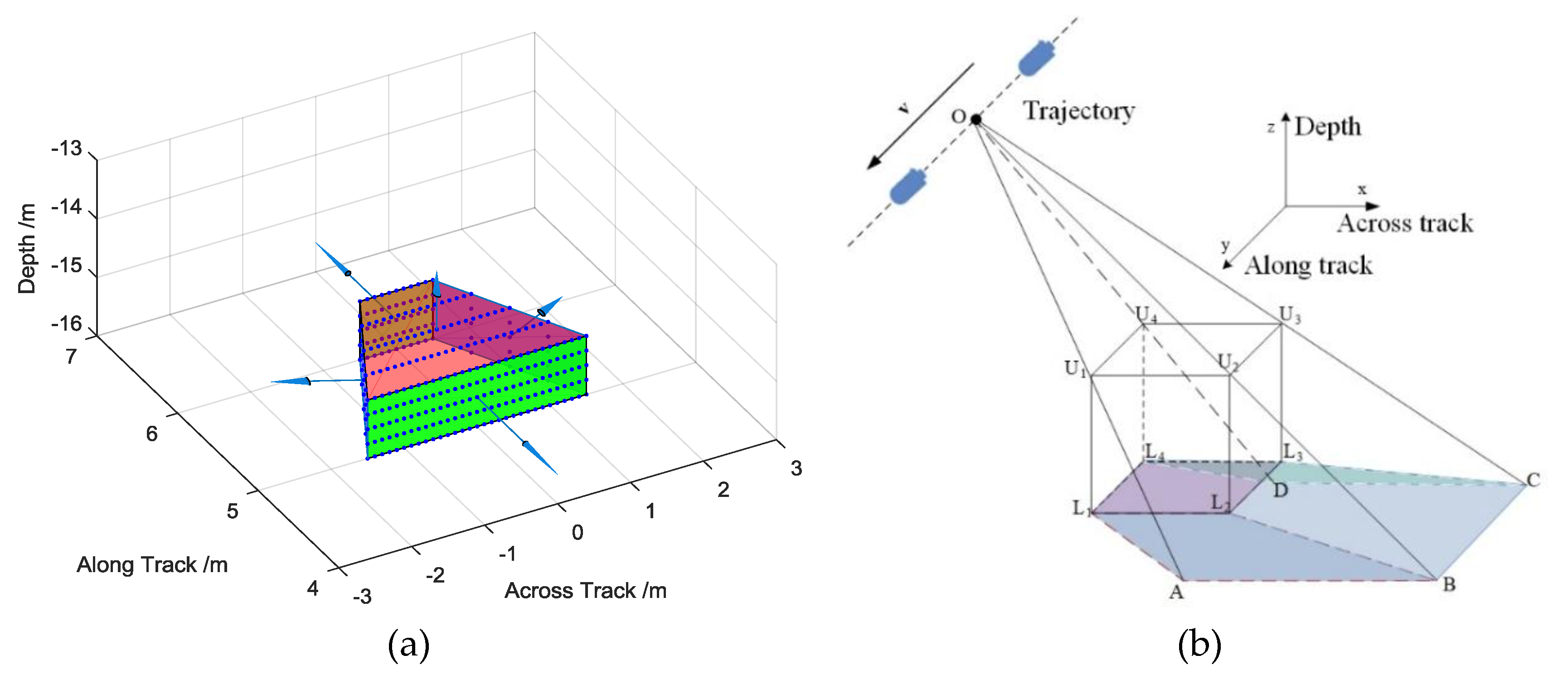
In the simulation of the target, the shadows area is an important factor that also indicates the characteristics of the target. We employ the normal vector of the surface to calculate the shadow area of the target. Any plane in the 3D space can be described by the point normal equation. The surface of the target contributes to the signal when it is illuminated by the transmitted echo. When the included angle between the normal vector and the connection from the transmitter to the surface is an obtuse angle, this surface contributes to the received signal. The normal vector
Figure 7a shows that each surface has its own normal vector and the bottom is never illuminated. The normal vector of the surface can be expressed as
, which is vertical to the plane. Given a certain point
on the surface, any point on the surface
has the limit as
, which is also calculated as Equation (10).
The included angle between the target surface and the coordinate system plane can be expressed as Equation (11)
where
is the normal vector of each coordinate plane, such as
,
,
.
The target echo shadow area is delineated through the line connecting the transmit position
and the seabed as shown in
Figure 7b. The points U
1–U
4 are the top vertices of the target and points L
1–L
4 are the bottom vertices. Points A–D are subpoints of
that connect the top vertices and seabed. The shadow area is defined by the linear function
, which connects the transmit position
and the vertices, together with the seabed. Furthermore, when the target is located on the seabed, the bottom side also cannot contribute to the returned echo. The shadow area can be analytically described according to the connection between the sampling position and the vertices of the target. We define the plane equation of side U
4L
4L
3U
3 as
and that of side U
1L
1L
2U
2 as
, where
and
are constant to indicate the location of the target. The connection between the vertices and the origin varies with different synthetic positions and forms different shadow areas, described by Equation (12). The synthetic shadow area after imaging is the intersection of the shadow areas formed at each sampling position, which is smaller than a single-position shadow
3.2. Imaging Algorithm for 2D MBSAS
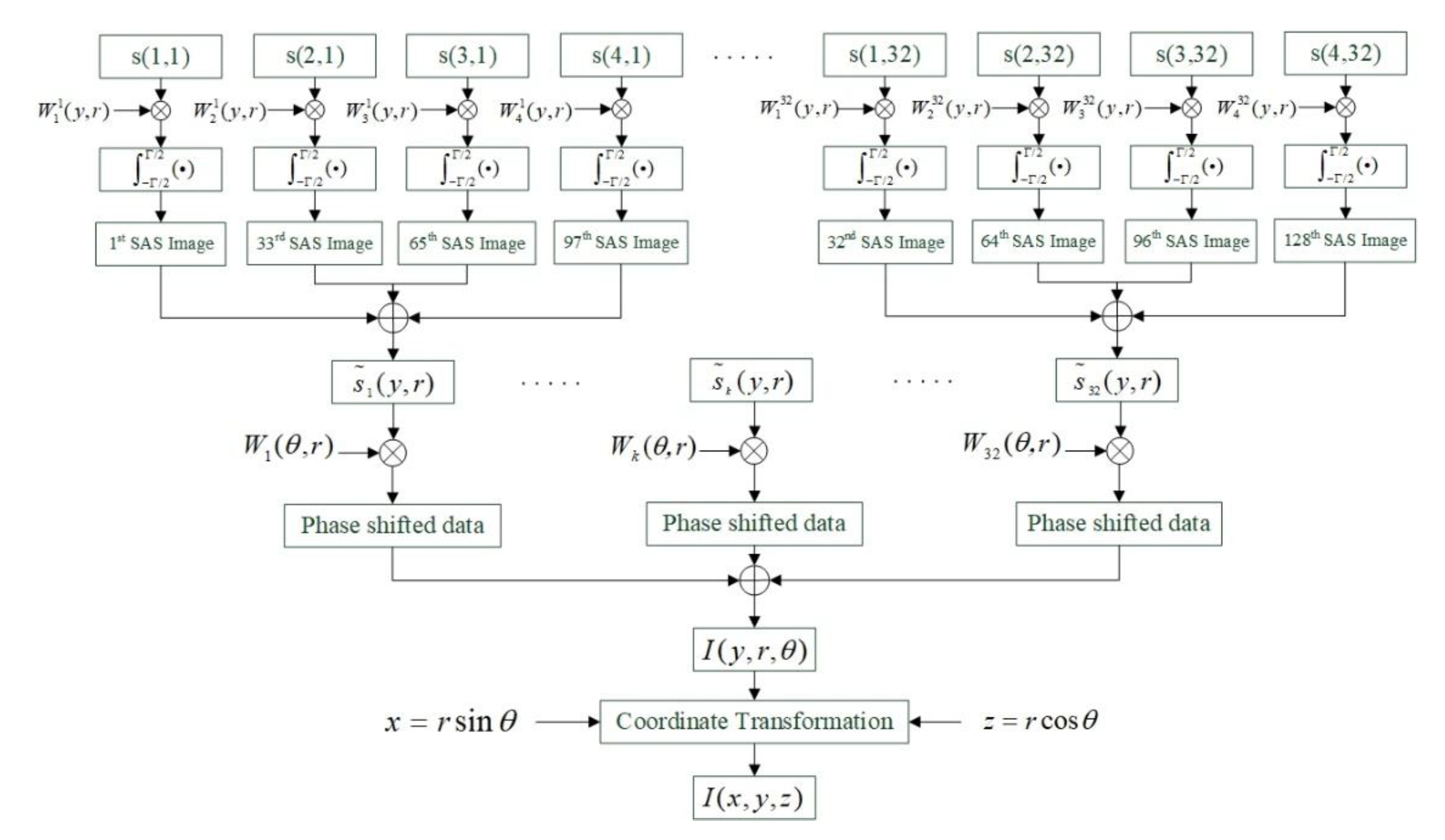
SAS imaging theory separates the detection area into different pixel points. The time delay between the pixel points and the elements is compensated and the echoes accumulate coherently according to the array manifold. The 2D SAS image of the detection area, which only indicates the azimuth and range direction, can be obtained intuitively [
21]. Single-element SAS processing is first performed on the along-track. After that, the multi-element SAS signals are coherently accumulated to convert the multiple elements to a virtual single element. SAS processing of the received echo in the element space is undertaken to obtain the 2D SAS image according to Equation (13), where the center of the virtual array is the origin coordinates
where
is the time-delay of the SAS echo, which is the vector expression of
; and
is the vector of the carrier and
is the vector of the target, which is processed in the synthetic aperture period
.
is the analytic vector in the 3D space and performs scalar in the range and time delay as
. The center frequency of the echo is expressed as
, and
is the bandwidth of the LFM echo. The single-element imaging output of SAS processing is shown in Equation (14), which has been solved analytically [
22]
After traversing all the elements, the 2D transducer array is converted to a virtual ULA on the across-track, which is similar to a conventional MBES system. On the across-track, beamforming is conducted to estimate the echo direction of arrival (DOA). The full-scan 3D imaging result is achieved as Equation (15), and the Taylor expansion is employed to simplify the formula
where
is the
time delay of the element. The average element spacing
and the number of elements
indicates the manifold of the designed transducer array;
is the wavelength of the echo, and
as designed; and
is the preset beam angle and
is the beam angle of the target. In the theory of sonar imaging, when the scanned point matches the target position, the echoes superpose most effectively. It is also shown in Equation (15) that the imaging output
is maximum when
. The output is the 3D image under the coordinates of
, which is not obvious for detection. The image should be transmitted to the coordinates of
to produce the echo image on the across-track and along-track, and the depth direction. The image points are transmitted uniformly according to
.
MBSAS images show the energy output in 3D space, while in actual situations, we pay more attention to detecting of the time of arrival (TOA) of the preformed angles. Accurate TOA estimated from noised echoes is also the thinning of the detailed sonar image. Target detection plays a more important role in the field of engineering [
23]. The output of MBSAS beamforming contains phase information that could be employed for TOA estimation. General energy-based detection methods such as weighted mean time (WMT) and phase difference methods such as the split beam and multi-subarray (MSA) algorithms can also be introduced in MBSAS detection theory, which is similar to the MBES detection system [
24,
25].
3.3. Simulation
To evaluate the performance of the MBSAS modeling and the imaging algorithm, simulations are undertaken according to the echo model we designed in
Figure 1. First, plane targets are simulated. We locate dozens of independent highlights on the same depth plane, which can more directly indicate the performance of the MBSAS imaging algorithm, especially on the along-track. The main parameters are shown in
Table 1. A virtual receiving array with an aperture of 4 m is generated through the processing. The across-track is defined as the direction of x and the along-track as y.
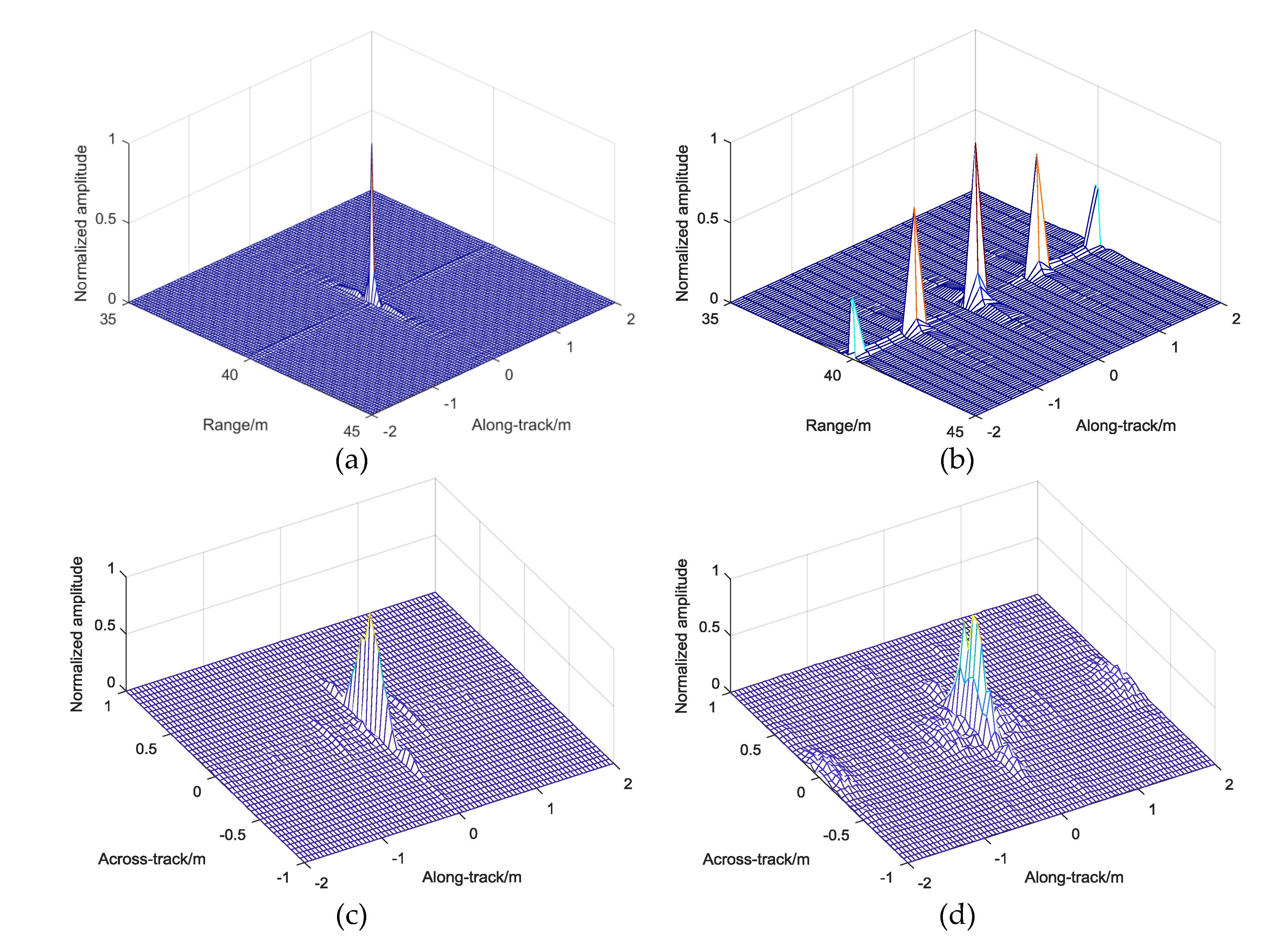
Figure 8 compares different imaging results. The trajectory and position of the element are shown in
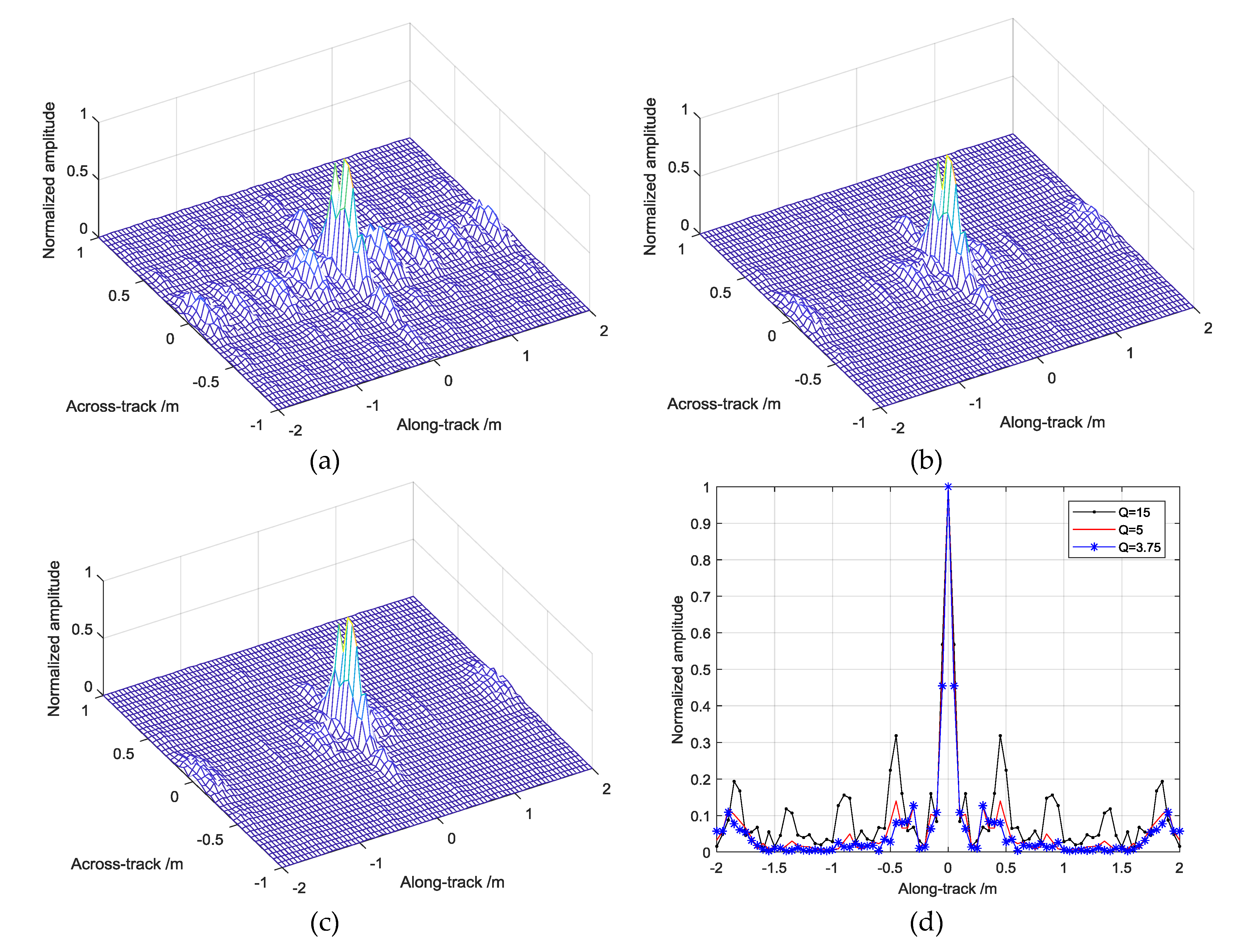
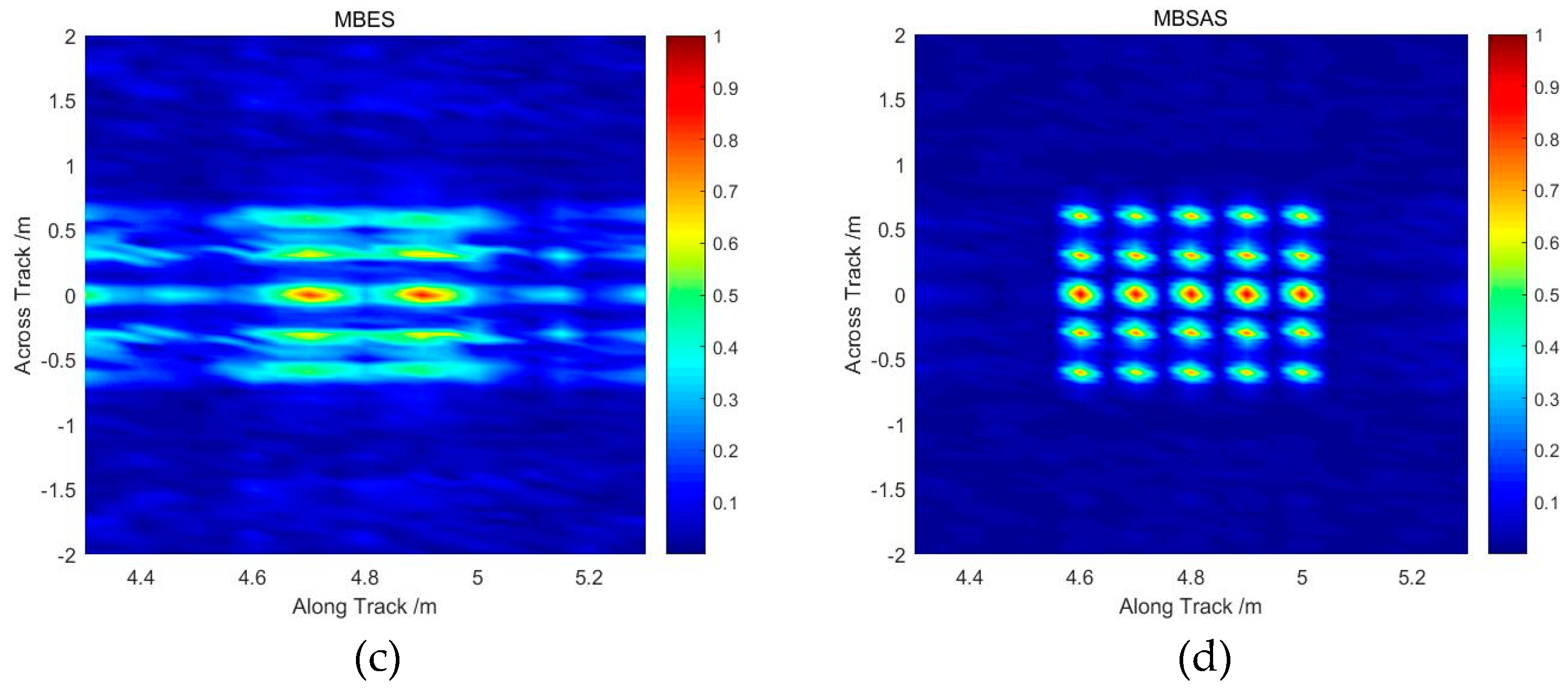
Figure 8a, showing that we locate 25 highlights on the same depth plane with 15 cm spacing. Different imaging algorithms are used to compare the results.
Figure 8b shows the SAS imaging result, with the same number of elements, which can separate the target location on the along-track. However, the SAS theory can only obtain the 2D image, so that the actual location on the across-track is replaced with range. Moreover, the size of the target on the along-track is seriously distorted with a reduced energy focusing ability.
Figure 8c indicates that the aliasing problem damaged the validity of the imaging result obtained via MBES, which was defocused seriously on the along-track. Moreover, the energy leaking to the side lobe also affected the beamforming processing on the across-track. Although the targets can be separated, false peaks appear and the energy focusing ability decreases seriously. The number of targets and locations of highlights are mixed. For comparison, the imaging result obtained via MBSAS is shown in
Figure 8d. The targets can be separated on the along-track with constant resolution. Beamforming on the across-track achieves the same resolution as MBES, which also recognizes the targets. MBSAS also achieves higher energy focusing ability, owing to more echo superposition.
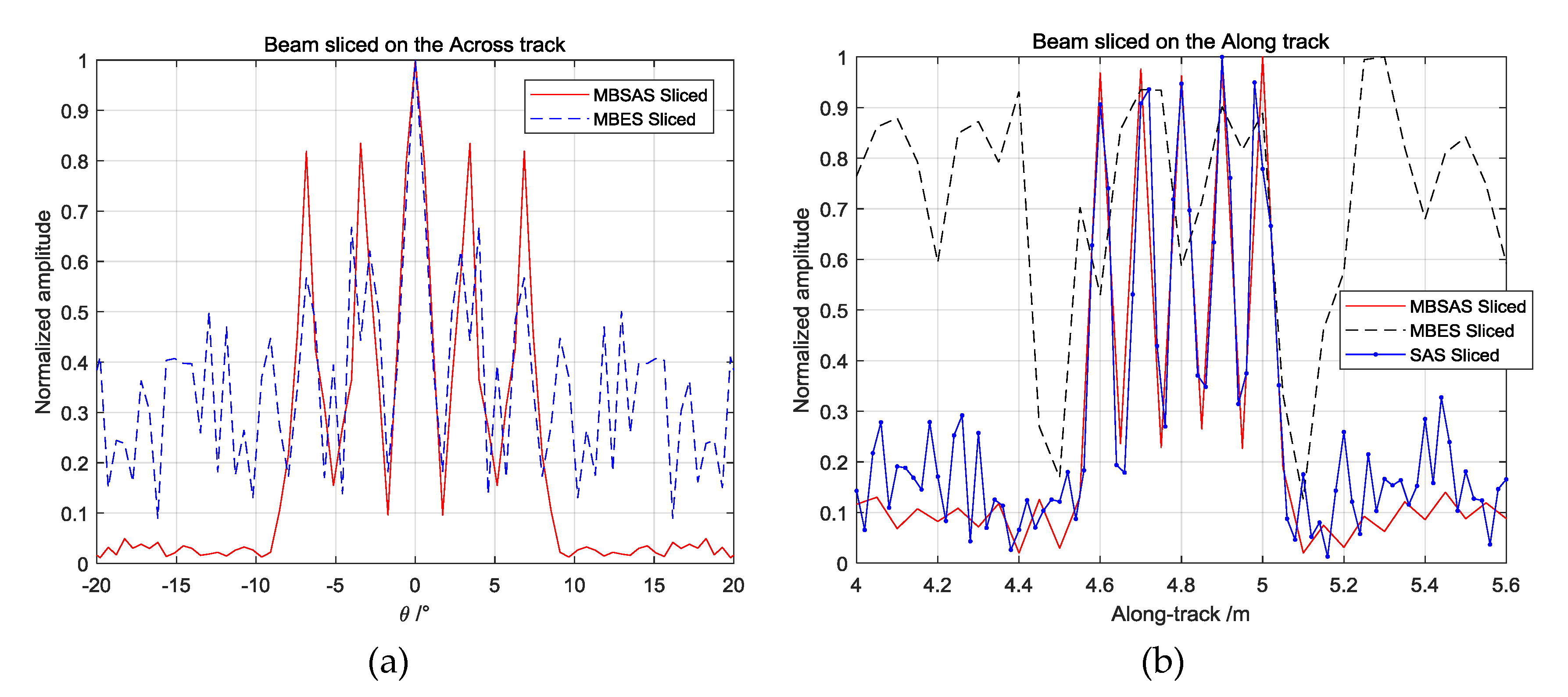
The image above is also sliced and shown on the across-track and along-track to observe the resolution. The beamforming on the along-track of MBSAS is similar to that of MBES, so we can evaluate the results under one angle coordinate. The SAS image is under the coordinates of
, which cannot be compared with the MBES and MBSAS system on the across-track.
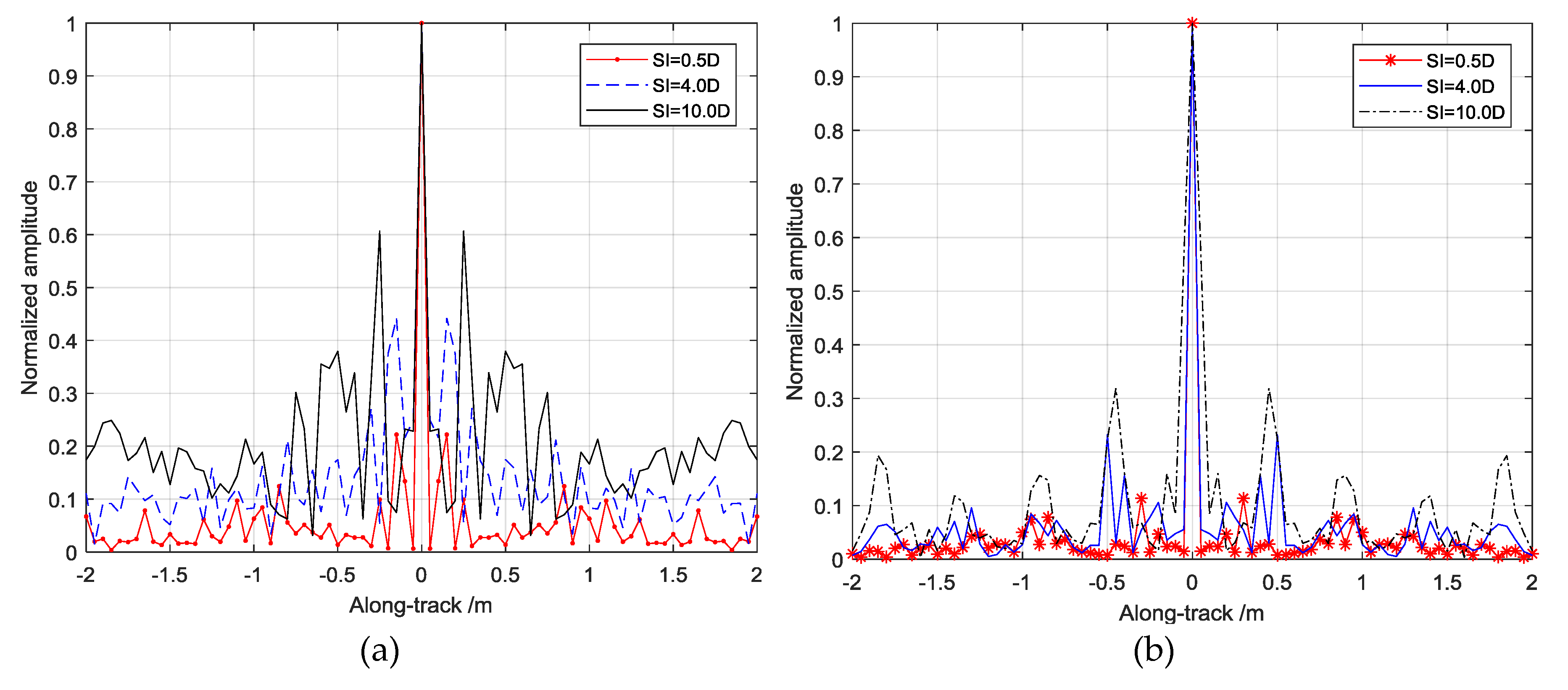
Figure 9a indicates that even if the targets can be separated by MBES on the across-track, some false peaks appear. The sidelobe levels were damaged by the mixed echo from the along-track. MBSAS imaging reveals the beam width of the array and separates the multiple targets by
, which has the same target resolution on the across-track as conventional MBES. The resolution on the along-track of MBSAS does not vary with the beam angle, and we focus more on the constant resolution in engineering situations. Therefore, the imaging resolution on the along-track is sliced under Cartesian coordinates. It is shown in
Figure 9b that the resolution of MBES decreases substantially with increasing beam angle and cannot easily separate the multiple targets. SAS imaging has constant resolution on the along-track that can separate the targets. However, the SAS has a low ability to estimate the DOA on the across-track, so that the mixed echo reduces the sidelobe level of the image. The MBSAS imaging is slice performed with constant high resolution, which has the same ability as SAS. The multiple targets can be separated clearly with high energy focusing ability, given the narrow main lobe width and low sidelobe level.
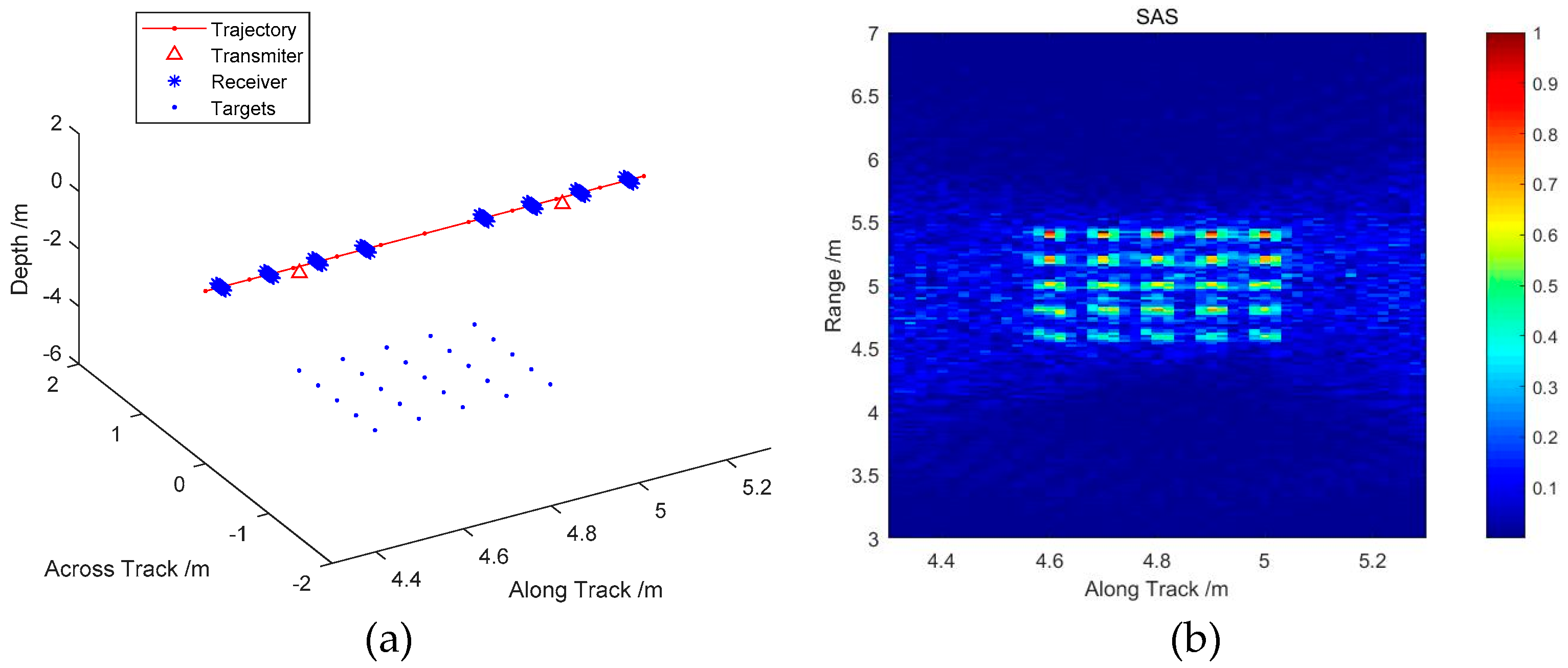
After that, a solid target is simulated to evaluate the performance of different imaging algorithms in the 3D space. Assuming that there is a solid target located in a detection area divided into hundreds of highlights, and the distance between the highlights is 0.3 m on the across-track, 0.1 m on the along-track, and 0.2 m in the depth direction, there are 125 echo highlights located in the detection area. To evaluate the validity of the model, the target is first briefly simulated while ignoring the shadows and seabed, according to the designed 2D MBSAS model and the referred imaging theory. The imaging result is the full 3D detection of the scanned area. Therefore, the sonar image is prospectively sliced to evaluate the performance of the MBSAS imaging algorithm. The simulation parameters are listed in
Table 2.
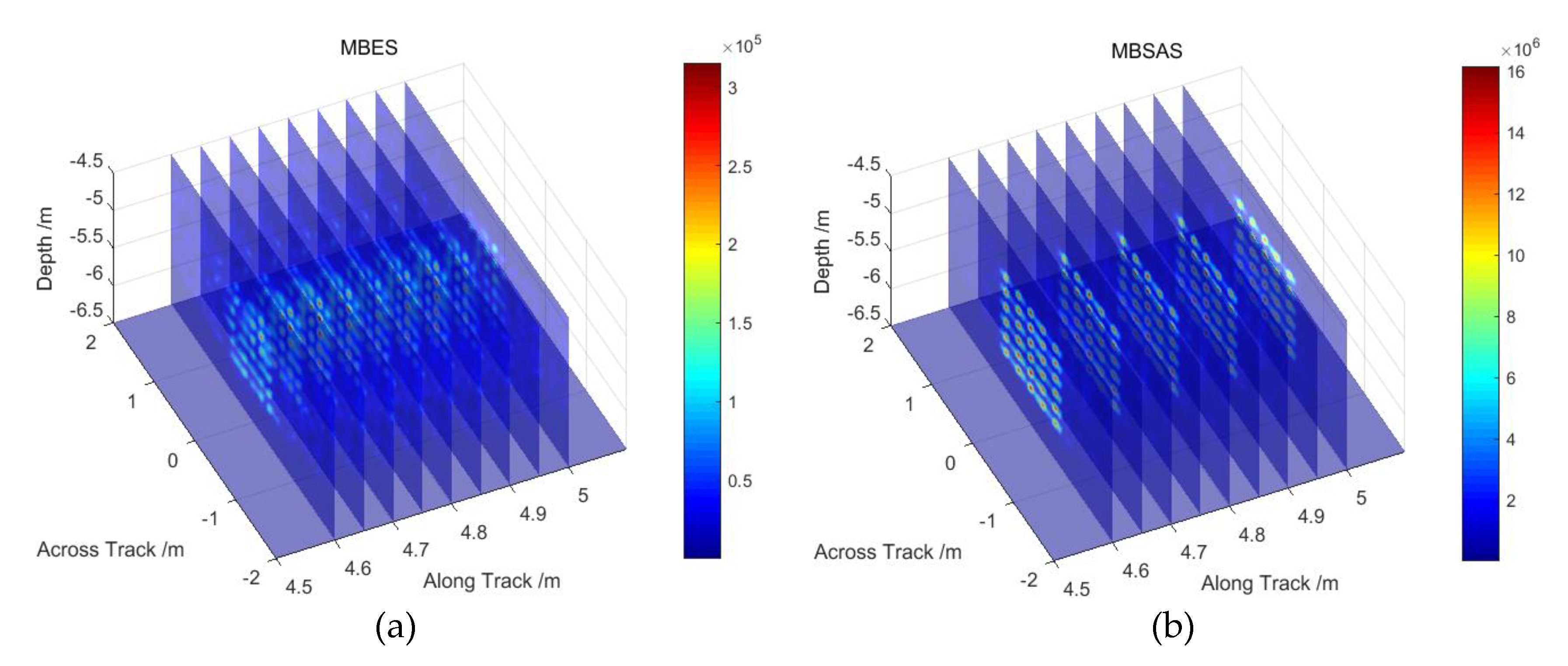
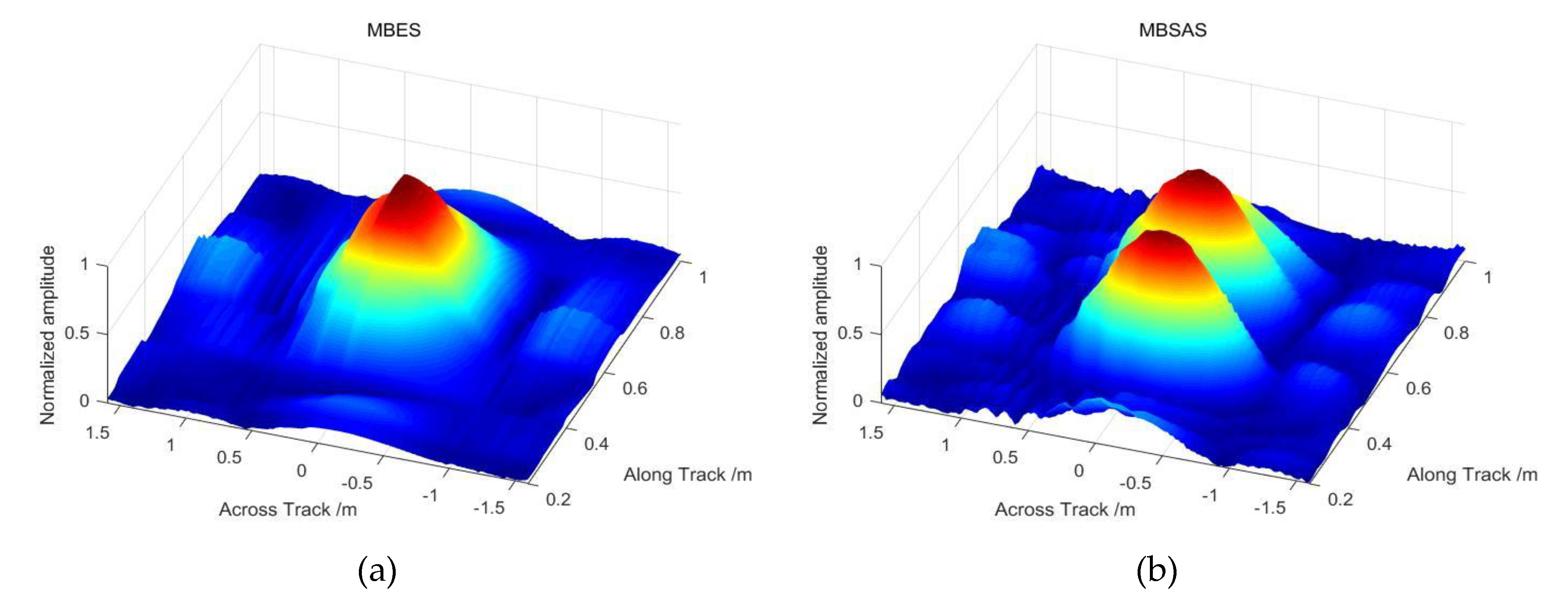
Figure 10a shows the image achieved by the MBES imaging algorithm. The positions and number of targets on the along-track cannot be identified, as such detection is limited by the beam footprint. Moreover, due to echo aliasing throughout the whole space, the sliced perspective image is severely defocused, which introduces false targets.
Figure 10b indicates the image achieved by the MBSAS imaging algorithm. The targets can be effectively recognized with high contrast. The image slices show that the targets can also be identified in detail in 3D space, as shown. Targets located at the vertical bottom area can still be detected, rather than detecting gaps as in the SAS image. Moreover, the MBSAS image has a better echo energy focusing ability than MBES, owing to the array gain of the 2D planar transducer array. The simulation results indicate that the model and the imaging algorithm of MBSAS can effectively improve the resolution of MBES without gaps.
To evaluate the performance of the modeling of targets with shadows, a detailed simulation is conducted under the parameters shown in
Table 3. A cube target is located on the seabed with a shadow area. The echo signal is accumulated in the 2D transducer array according to the designed array manifold and the synthetic position. MBSAS imaging and target detection based on the phase difference method are undertaken.
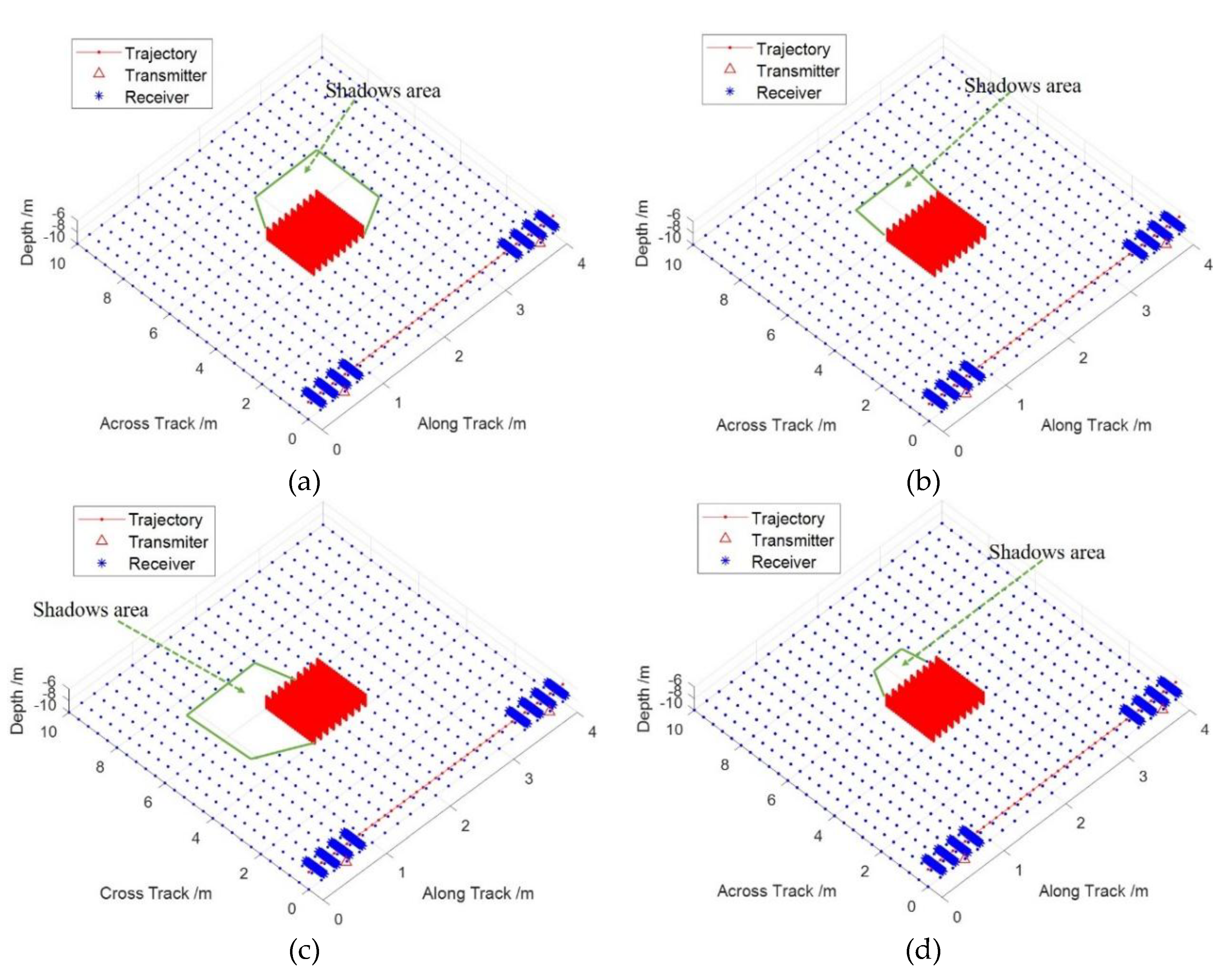
The target highlights and shadow area are simulated, where the shadows vary as the transducer array sails along the trajectory. The target obstructs the echo and forms the shadows area on the designed seabed. The shadow area forms according to the line connecting the transmit position and the seabed at different view positions, as shown in
Figure 11a–c. The shadow area has center symmetry on the whole moving trajectory. The synthetic shadows area is the intersection of the shadows formed at each sampling position and is smaller than a single-position shadow. The synthetic shadow area is constant and does not change with the sampling position, which can effectively demonstrate the location of the target. The synthetic shadow shown in
Figure 11d is smaller than a single-position shadow area. The carrier moving trajectory and the location of the receiving elements at different sampling moments are also shown in the figure. The center of the array is regarded as the origin, which limits the line connecting the transducer array and the seabed.
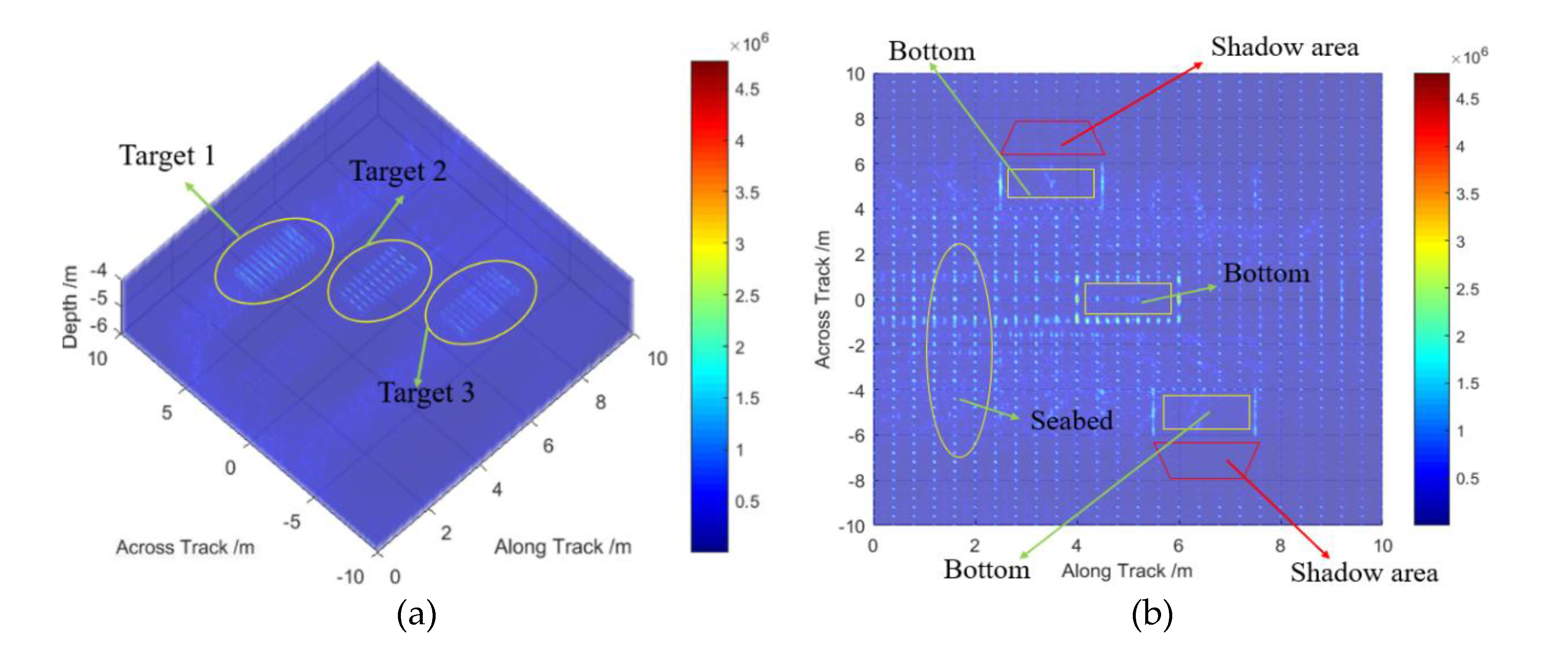
Three cube targets are also simulated to evaluate the performance of distinguishing adjusted targets. We locate the cube targets on both sides and the right bottom of the trajectory. The targets and the shadow area are considered in the model to reveal their mutual influences. The targets are independent of each other, and their positions are parallel and progressive. The image is sliced as shown in
Figure 12, where the targets and the shadows are marked.
The sliced image is shown in
Figure 12a. The adjusted targets can be separated after MBSAS image processing as marked. Then, the 3D image is sliced in the bottom view, which can indicate the shadows and the seabed in more detail. The targets in
Figure 12b match the MBSAS imaging result. The seabed and shadows are the same as calculated in Equation (12). The cube bottom on the seabed is not highlighted because the bottom is not illuminated by echoes. Furthermore, the targets directly below the trajectory do not generate shadows, as they are vertically irradiated. The adjusted targets can be recognized effectively with high resolution according to MBSAS theory. It is important to note that, limited by the beam width, the imaging resolution on the across-track inevitably decreases with increasing distance. Therefore, some high-resolution beamforming algorithms used on the across-track, such as minimum variance distortionless response (MVDR) and deconvolved beamforming, should be researched further but are not the focus of this paper [
26,
27].