Semi-Coupled Convolutional Sparse Learning for Image Super-Resolution
Abstract
1. Introduction
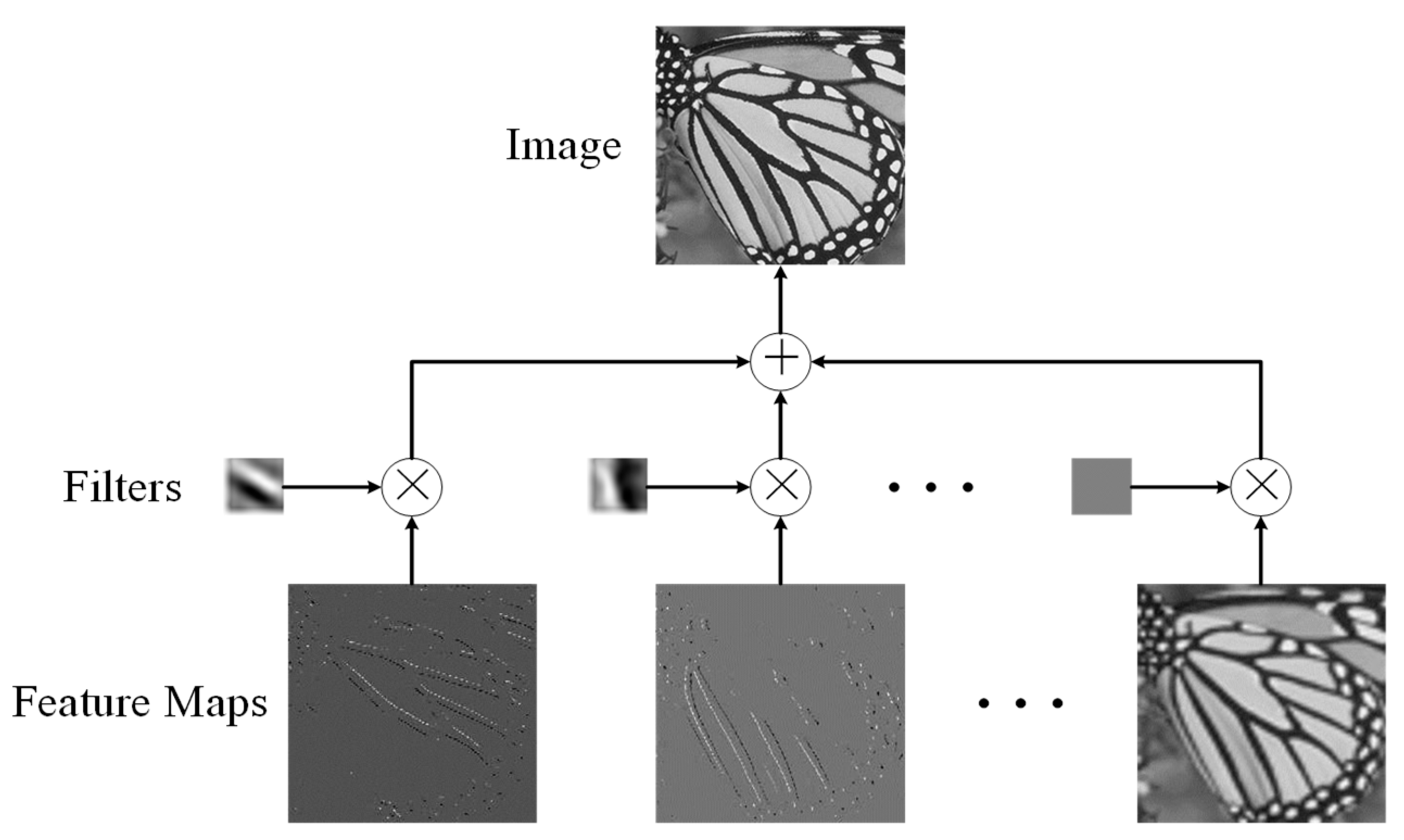
2. Convolutional Sparse Coding
3. Semi-Coupled Convolutional Sparse Learning for Super Resolution
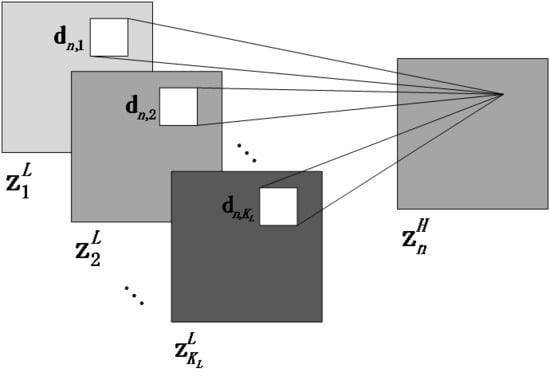
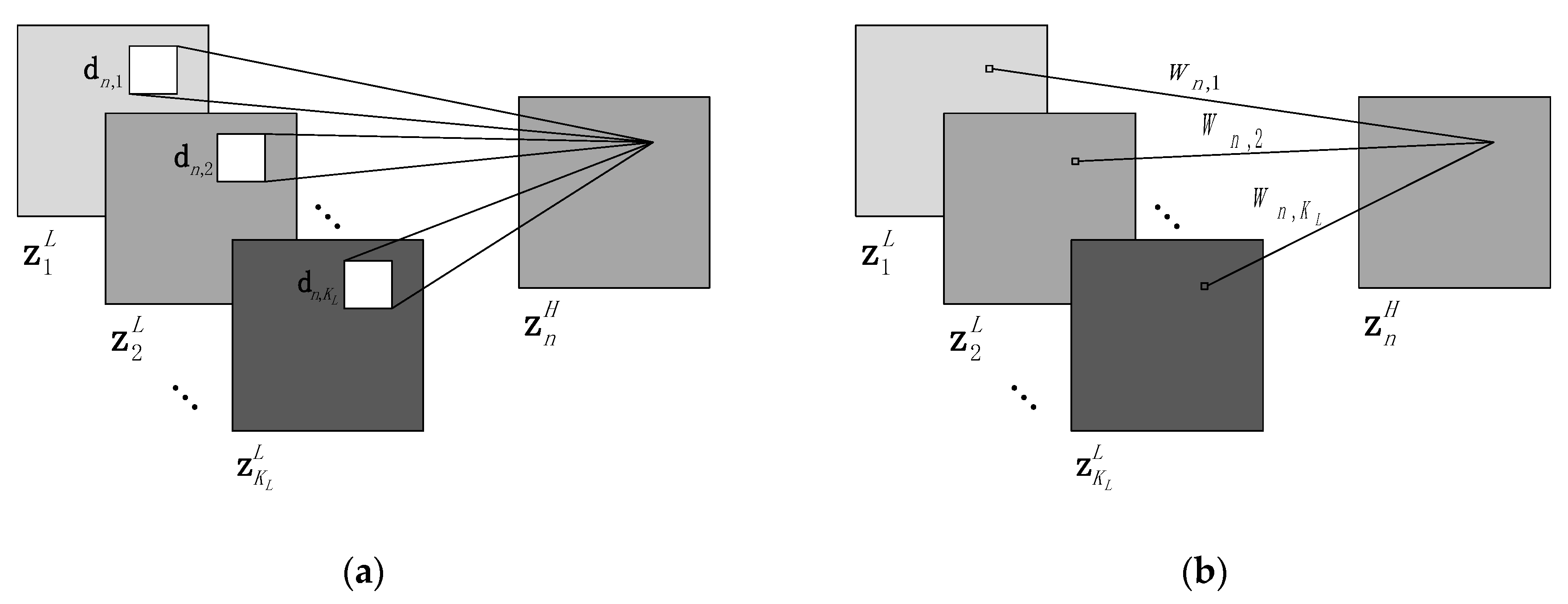
3.1. Formulation
3.2. The Training Phase
3.2.1. LR Filters Learning
3.2.2. Mapping and HR Filters Learning
3.2.3. Algorithm Summary
| Algorithm 1 Semi-Coupled Convolutional Sparse Learning |
| Require: |
| Training image pairs ; |
| Initial LR filters ; |
| Initial HR filters ; |
| Initial mapping filters ; |
| Ensure: |
| Training results of , and ; |
| 1: LR filters learning |
| 2: While stopping criteria not met do |
| 3: Calculate by solving Equation (8); |
| 4: Update via Equation (18); |
| 5: end while |
| 6: Mapping and HR filters learning |
| 7: While stopping criteria not met do |
| 8: Calculate by solving Equation (23); |
| 9: Update via Equation (25); |
| 10: Update via Equation (26); |
| 11: end while |
| 12: return , and |
3.3. The Testing Phase
3.4. Relationship to Linear Mapping Based Model
4. Experiments
4.1. Implementation
4.2. Parameter Analysis
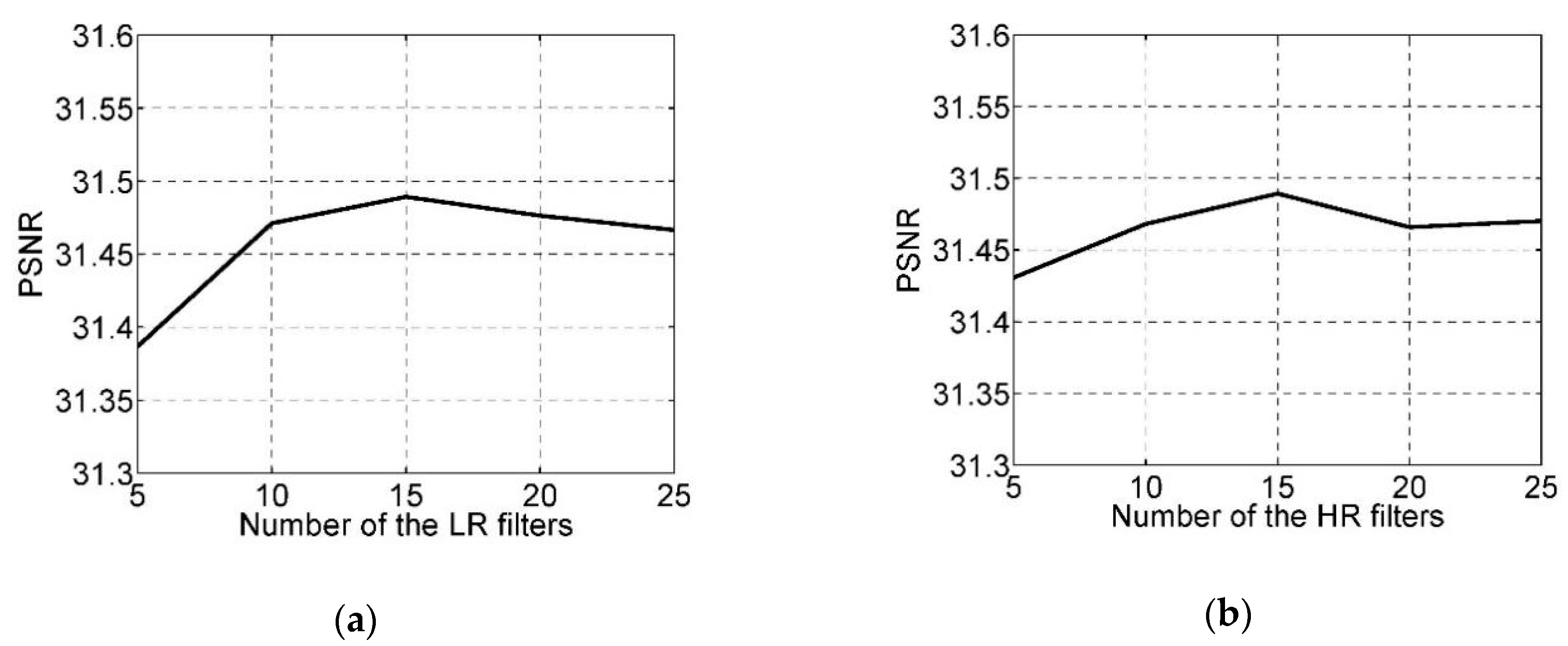
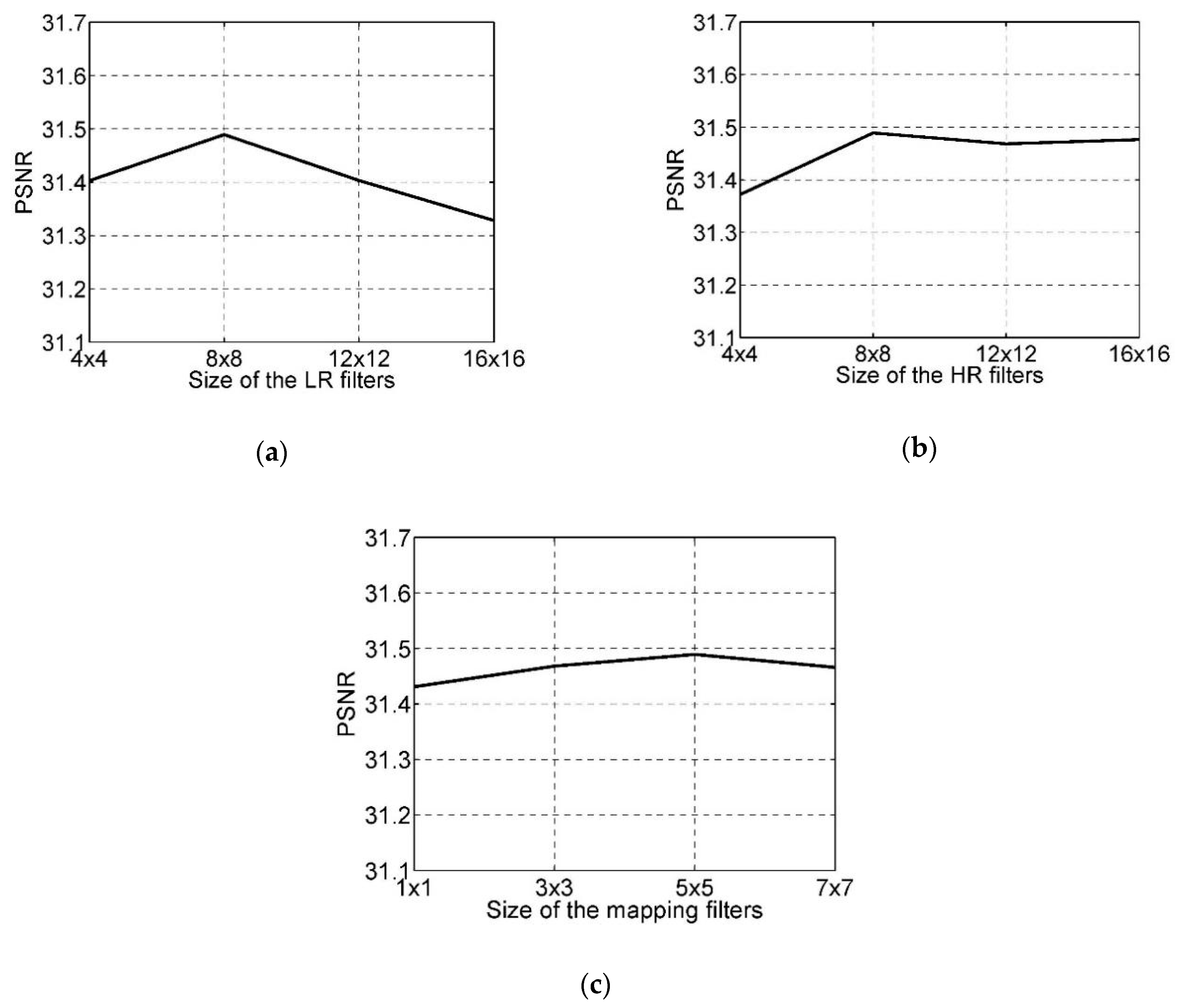
4.2.1. Number of Filters
4.2.2. Size of Filters
4.3. Super-Resolution Experiments
5. Discussions
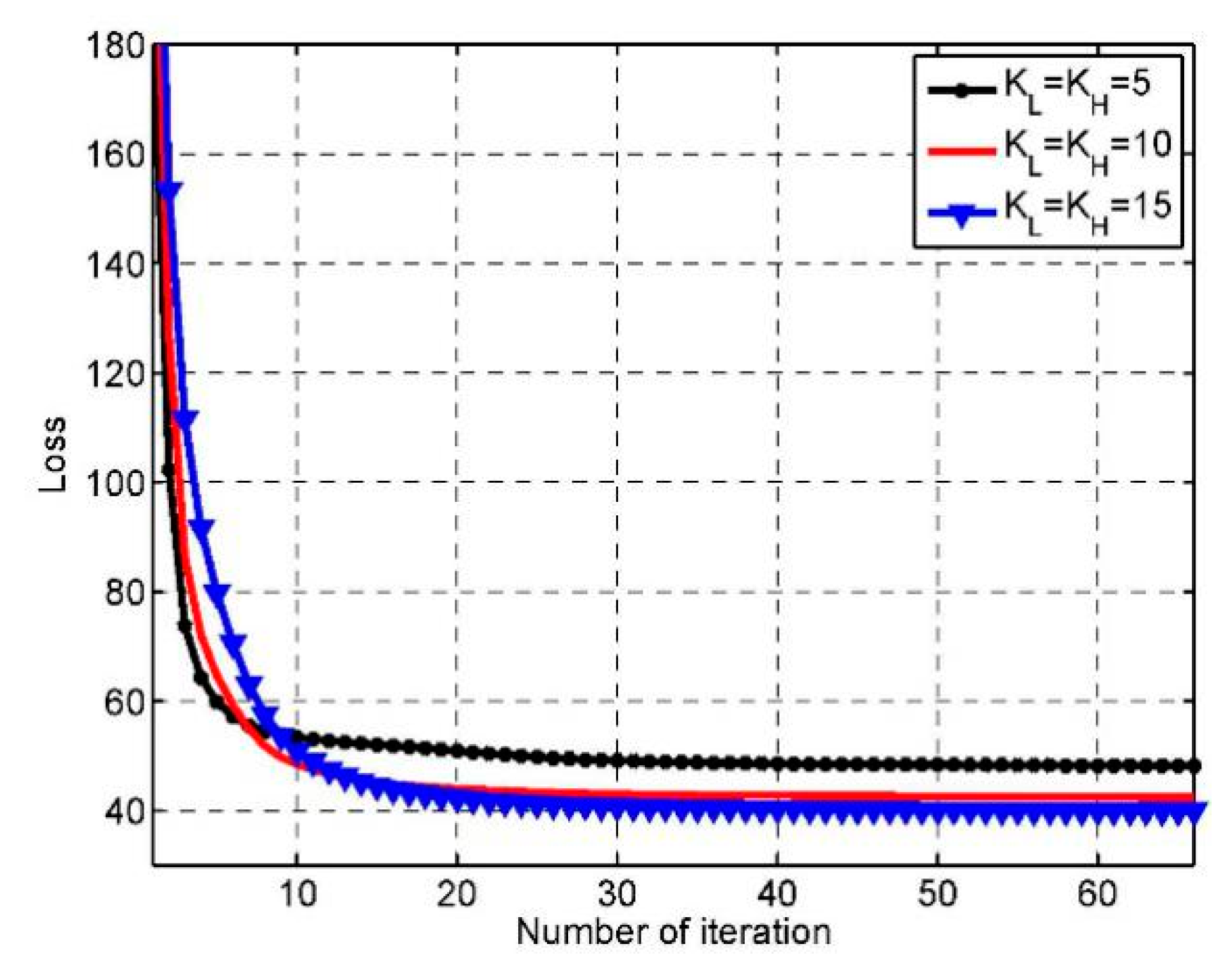
5.1. Convergence
5.2. Time Complexity
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.S.; Yan, S. Sparse Representation for Computer Vision and Pattern Recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inform. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Gan, L. Block Compressed Sensing of Natural Images. In Proceedings of the 2007 IEEE 15th International Conference on Digital Signal Processing, Assam, India, 18–21 December 2007; pp. 403–406. [Google Scholar]
- Fu, Y.; Gao, J.; Tien, D.; Lin, Z.; Hong, X. Tensor LRR and Sparse Coding-Based Subspace Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2017, 27, 2120–2133. [Google Scholar] [CrossRef] [PubMed]
- Zeiler, M.D.; Krishnan, D.; Taylor, G.W.; Fergus, R. Deconvolutional networks. In Proceedings of the Twenty-Third IEEE Conference Computer Vision Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2528–2535. [Google Scholar]
- Papyan, V.; Sulam, J.; Elad, M. Working Locally Thinking Globally: Theoretical Guarantees for Convolutional Sparse Coding. IEEE Trans. Signal Process. 2017, 65, 5687–5701. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Tao, D.; See, S.; Wang, G. Learning Common and Specific Features for RGB-D Semantic Segmentation with Deconvolutional Networks. In Proceedings of the European Conference on Computer Vision ECCV, Amsterdam, The Netherlands, 8–16 October 2016; pp. 664–679. [Google Scholar]
- Dandois, J.P. Remote Sensing of Vegetation Structure Using Computer Vision. Remote Sens. 2010, 2, 1157–1176. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Taylor, G.W.; Fergus, R. Adaptive deconvolutional networks for mid and high level feature learning. In Proceedings of the IEEE International Conference Computer Vision ICCV, Barcelona, Spain, 6–13 November 2011; pp. 2018–2025. [Google Scholar]
- Nekrasov, V.; Ju, J.; Choi, J.; Nekrasov, V.; Ju, J.; Choi, J.; Nekrasov, V.; Ju, J.; Choi, J. Global Deconvolutional Networks for Semantic Segmentation. arXiv 2016, arXiv:1602.03930. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-Image Super-Resolution Using Sparse Regression and Natural Image Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Wang, S.; Yue, B.; Liang, X.; Jiao, L. How Does the Low-Rank Matrix Decomposition Help Internal and External Learnings for Super-Resolution. IEEE Trans. Image Process. 2017, 27, 1086–1099. [Google Scholar] [CrossRef]
- Mei, S.; Xin, Y.; Ji, J.; Zhang, Y.; Shuai, W.; Qian, D. Hyperspectral Image Spatial Super-Resolution via 3D Full Convolutional Neural Network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Dong, W.; Fu, F.; Shi, G.; Cao, X.; Wu, J.; Li, G.; Li, G. Hyperspectral Image Super-Resolution via Non-Negative Structured Sparse Representation. IEEE Trans. Image Process. 2016, 25, 2337–2352. [Google Scholar] [CrossRef] [PubMed]
- Yue, B.; Wang, S.; Liang, X.; Jiao, L. Robust Noisy Image Super-Resolution Using l1-norm Regularization and Non-local Constraint. In Proceedings of the 13th Asian Conference on Computer Vision ACCV, Taipei, Taiwan, 20–24 November 2016; pp. 34–49. [Google Scholar]
- Hou, B.; Zhou, K.; Jiao, L. Adaptive Super-Resolution for Remote Sensing Images Based on Sparse Representation with Global Joint Dictionary Model. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2312–2327. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 545–559. [Google Scholar] [CrossRef]
- Wei, J.; Wang, L.; Liu, P.; Song, W. Spatiotemporal Fusion of Remote Sensing Images with Structural Sparsity and Semi-Coupled Dictionary Learning. Remote Sens. 2016, 9, 21. [Google Scholar] [CrossRef]
- Osendorfer, C.; Soyer, H.; Smagt, P.V.D. Image Super-Resolution with Fast Approximate Convolutional Sparse Coding. In Proceedings of the International Conference on Neural Information Processing ICONIP, Kuching, Malaysia, 3–6 November 2014; Springer: Cham, Switzerland, 2014; pp. 250–257. [Google Scholar]
- Gu, S.; Zuo, W.; Xie, Q.; Meng, D.; Feng, X.; Zhang, L. Convolutional Sparse Coding for Image Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1823–1831. [Google Scholar]
- Wang, S.; Zhang, L.; Liang, Y.; Pan, Q. Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis. In Proceedings of the IEEE Conference Computer Vision Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2216–2223. [Google Scholar]
- Bristow, H.; Eriksson, A.; Lucey, S. Fast Convolutional Sparse Coding. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 391–398. [Google Scholar]
- Heide, F.; Heidrich, W.; Wetzstein, G. Fast and flexible convolutional sparse coding. In Proceedings of the IEEE Conference Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5135–5143. [Google Scholar]
- Wohlberg, B. Efficient Algorithms for Convolutional Sparse Representations. IEEE Trans. Image Process. 2016, 25, 301–315. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Yan, S.; Lin, Z. A Unified Alternating Direction Method of Multipliers by Majorization Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 527–541. [Google Scholar] [CrossRef]
- Mairal, J.; Elad, M.; Sapiro, G. Sparse Representation for Color Image Restoration. IEEE Trans. Image Process. 2008, 17, 53–69. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust Face Recognition via Sparse Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef]
- Wang, J.; Lu, C.; Wang, M.; Li, P.; Yan, S.; Hu, X. Robust face recognition via adaptive sparse representation. IEEE Trans. Cybern 2014, 44, 2368–2378. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, S.; Roth, D. Learning a Sparse Representation for Object Detection. In Proceedings of the European Conference Computer Vision ECCV, Copenhagen, Denmark, 28–31 May 2002; pp. 113–130. [Google Scholar]
- Ren, X.; Ramanan, D. Histograms of Sparse Codes for Object Detection. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition CVPR, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Gu, J.; Jiao, L.; Yang, S.; Liu, F. Fuzzy Double C-Means Clustering Based on Sparse Self-Representation. IEEE Trans. Fuzzy Syst. 2017, 26, 612–626. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, Z.; Feng, H.; Ma, Y. Sparse coding-based topic model for remote sensing image segmentation. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Xue, Z.; Du, P.; Su, H.; Zhou, S. Discriminative Sparse Representation for Hyperspectral Image Classification: A Semi-Supervised Perspective. Remote Sens. 2017, 9, 386. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Wei, Z.; Liang, X.; Le, S. Spatial-Spectral Kernel Sparse Representation for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2462–2471. [Google Scholar] [CrossRef]
- Rida, I.; Al-Maadeed, N.; Al-Maadeed, S.; Bakshi, S. A comprehensive overview of feature representation for biometric recognition. Multimed. Tools Appl. 2018, 1–24. [Google Scholar] [CrossRef]
- Congzhong, W.U.; Changsheng, H.U.; Zhang, M.; Xie, Z.; Zhan, S. Single Image Super-resolution Reconstruction via Supervised Multi-dictionary Learning. Opto Electron. Eng. 2016, 43, 69–75. [Google Scholar]
- Rida, I.; Herault, R.; Gasso, G. An efficient supervised dictionary learning method for audio signal recognition. arXiv 2018, arXiv:1812.04748. [Google Scholar]
- Singhal, V.; Majumdar, A. Supervised Deep Dictionary Learning for Single Label and Multi-Label Classification. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 2161–4407. [Google Scholar]
- Huang, Y.; Liu, X.; Xiang, T.; Fan, Z.; Chen, Y.; Jiang, R. Deep supervised dictionary learning for no-reference image quality assessment. J. Electron. Imaging 2018, 27, 1. [Google Scholar] [CrossRef]
- Jiao, L.; Zhang, S.; Li, L.; Yang, S.; Liu, F.; Hao, H.; Dong, H. A Novel Image Representation Framework Based on Gaussian Model and Evolutionary Optimization. IEEE Trans. Evol. Comput. 2017, 21, 265–280. [Google Scholar] [CrossRef]
- Jiao, L.; Liang, M.; Chen, H.; Yang, S.; Liu, H.; Cao, X. Deep Fully Convolutional Network-Based Spatial Distribution Prediction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5585–5599. [Google Scholar] [CrossRef]
- Lecun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 2014, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the International Conference on Neural Information Processing Systems, NIPS, Lake Tahoe, CA, USA, 3–6 December 2012; pp. 1106–1114. [Google Scholar]
- Jiao, L.; Zhang, S.; Li, L.; Liu, F.; Ma, W. A modified convolutional neural network for face sketch synthesis. Pattern Recognit. 2017, 76, 125–136. [Google Scholar] [CrossRef]
- Feng, J.; Wang, L.; Yu, H.; Jiao, L.; Zhang, X. Divide-and-Conquer Dual-Architecture Convolutional Neural Network for Classification of Hyperspectral Images. Remote Sens. 2019, 11, 484. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, Y.; Jiao, L.; Zhang, X.; Stolkin, R. Single image super-resolution reconstruction based on genetic algorithm and regularization prior model. Inf. Sci. Int. J. 2016, 372, 196–207. [Google Scholar] [CrossRef]
- Yang, S.; Liu, Z.; Wang, M.; Sun, F.; Jiao, L. Multitask dictionary learning and sparse representation based single-image super-resolution reconstruction. Neurocomputing 2011, 74, 3193–3203. [Google Scholar] [CrossRef]
- Bianco, S.; Cusano, C.; Schettini, R. Single and Multiple Illuminant Estimation Using Convolutional Neural Networks. IEEE Trans. Image Process. 2017, 26, 4347–4362. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.; Kwok, J.T. Fast Stochastic Alternating Direction Method of Multipliers. In Proceedings of the International Conference on Machine Learning ICML, Beijing, China, 21–26 June 2014; pp. 46–54. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the European Conference Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Yoon, Y.; Jeon, H.; Yoo, D.; Lee, J.; Kweon, I.S. Learning a Deep Convolutional Network for Light-Field Image Super-Resolution. In Proceedings of the IEEE International Conference Computer Vision Workshops, Santiago, Chile, 7–13 December 2015; pp. 57–65. [Google Scholar]
- Yu, G.; Sapiro, G.; Mallat, S. Solving Inverse Problems with Piecewise Linear Estimators: From Gaussian Mixture Models to Structured Sparsity. IEEE Trans. Image Process. 2012, 21, 2481–2499. [Google Scholar]
- Bo, L.; Rui, Y.; Jiang, H. Remote-Sensing Image Compression Using Two-Dimensional Oriented Wavelet Transform. IEEE Trans. Geosci. Remote Sens. 2010, 49, 236–250. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X. Image Interpolation by Adaptive 2-D Autoregressive Modeling and Soft-Decision Estimation. IEEE Trans. Image Process. 2008, 17, 887–896. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Jing, Y.; Huang, H.; Hu, S.; Sun, W. Super-Resolution Based on Compressive Sensing and Structural Self-Similarity for Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4864–4876. [Google Scholar] [CrossRef]




| Methods | Images | |||||||
|---|---|---|---|---|---|---|---|---|
| Butterfly | Face | Bird | Comic | Woman | Foreman | Coast. | Flowers | |
| BI | 26.87 | 34.14 | 36.29 | 24.52 | 31.60 | 32.08 | 28.59 | 29.81 |
| SAI | 25.18 | 33.02 | 32.24 | 24.14 | 28.66 | 30.36 | 27.46 | 28.05 |
| SCS | 29.93 | 34.83 | 38.19 | 25.20 | 33.52 | 33.40 | 29.72 | 31.64 |
| LMSCS | 30.12 | 35.67 | 39.36 | 25.29 | 34.13 | 34.18 | 30.30 | 32.23 |
| SCCSL | 30.47 | 35.69 | 39.67 | 25.32 | 34.24 | 34.14 | 30.41 | 32.30 |
| Zebra | Lena | Bridge | Baby | Peppers | Man | Barbara | Avg. val. | |
| BI | 28.39 | 34.08 | 27.11 | 36.51 | 32.47 | 28.55 | 27.21 | 30.55 |
| SAI | 26.73 | 31.59 | 24.88 | 33.63 | 31.20 | 27.50 | 26.37 | 28.73 |
| SCS | 28.53 | 35.33 | 26.97 | 37.19 | 33.20 | 29.96 | 28.08 | 31.71 |
| LMSCS | 28.56 | 36.20 | 27.44 | 38.51 | 33.50 | 30.35 | 28.42 | 32.28 |
| SCCSL | 28.64 | 36.28 | 27.42 | 38.52 | 33.78 | 30.42 | 28.45 | 32.38 |
| Methods | Images | |||||||
|---|---|---|---|---|---|---|---|---|
| Butterfly | Face | Bird | Comic | Woman | Foreman | Coast. | Flowers | |
| BI | 0.86 | 0.81 | 0.95 | 0.69 | 0.91 | 0.91 | 0.73 | 0.85 |
| SAI | 0.89 | 0.83 | 0.94 | 0.80 | 0.92 | 0.92 | 0.73 | 0.86 |
| SCS | 0.94 | 0.85 | 0.97 | 0.84 | 0.95 | 0.95 | 0.80 | 0.91 |
| LMSCS | 0.94 | 0.89 | 0.98 | 0.85 | 0.96 | 0.96 | 0.85 | 0.93 |
| SCCSL | 0.95 | 0.89 | 0.98 | 0.86 | 0.96 | 0.96 | 0.85 | 0.93 |
| Zebra | Lena | Bridge | Baby | Peppers | Man | Barbara | Avg. val. | |
| BI | 0.75 | 0.87 | 0.72 | 0.93 | 0.85 | 0.78 | 0.80 | 0.83 |
| SAI | 0.85 | 0.88 | 0.72 | 0.93 | 0.88 | 0.80 | 0.80 | 0.85 |
| SCS | 0.86 | 0.91 | 0.81 | 0.95 | 0.89 | 0.85 | 0.85 | 0.89 |
| LMSCS | 0.88 | 0.93 | 0.84 | 0.97 | 0.91 | 0.88 | 0.87 | 0.91 |
| SCCSL | 0.88 | 0.93 | 0.84 | 0.97 | 0.91 | 0.88 | 0.87 | 0.91 |
| Methods | BI | SAI | CSC | LMCSC | SCCSL |
|---|---|---|---|---|---|
| Time (sec) | 0.01 | 0.07 | 4.14 | 4.23 | 4.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhang, S.; Jiao, L.; Liu, F.; Yang, S.; Tang, X. Semi-Coupled Convolutional Sparse Learning for Image Super-Resolution. Remote Sens. 2019, 11, 2593. https://doi.org/10.3390/rs11212593
Li L, Zhang S, Jiao L, Liu F, Yang S, Tang X. Semi-Coupled Convolutional Sparse Learning for Image Super-Resolution. Remote Sensing. 2019; 11(21):2593. https://doi.org/10.3390/rs11212593
Chicago/Turabian StyleLi, Lingling, Sibo Zhang, Licheng Jiao, Fang Liu, Shuyuan Yang, and Xu Tang. 2019. "Semi-Coupled Convolutional Sparse Learning for Image Super-Resolution" Remote Sensing 11, no. 21: 2593. https://doi.org/10.3390/rs11212593
APA StyleLi, L., Zhang, S., Jiao, L., Liu, F., Yang, S., & Tang, X. (2019). Semi-Coupled Convolutional Sparse Learning for Image Super-Resolution. Remote Sensing, 11(21), 2593. https://doi.org/10.3390/rs11212593