1. Introduction
The constellations of BeiDou-2 and BeiDou-3 are designed to contain geostationary earth orbit (GEO), inclined geosynchronous orbit (IGSO), and medium earth orbit (MEO). In the positioning, navigation, and timing (PNT) service of the BeiDou satellite system (BDS) for the Asia-Pacific region, GEO and IGSO satellites play an important role [
1,
2,
3,
4,
5,
6]. According to the three-step strategy, when BeiDou-3 was under construction, it was planned to complete the constellation consisting of 35 satellites and to provide global service for users around the world [
7,
8,
9]. The main goals of Global Navigation Satellite System (GNSS) in engineering sciences are to describe the Earth’s shape and to determine coordinates, and precise orbit and clock offset products play an important role [
10]. However, the multi-orbit configuration brings great challenges in determining precise orbits, especially the demands of geostationary orbit. As satellites are affected by the Earth’s nonspherical gravity and other perceptual factors, the positions of satellites tend to gradually deviate from the designed orbits. Thus, orbital maneuvering is necessary to optimize the space location of satellites from time to time. The orbits of satellites must be adjusted to the designed position by using a propulsion device. GEO and IGSO satellites are maneuvered more frequently than MEO satellites because they are geosynchronous. The changes of the gravity field coefficients or temporal variations of those coefficients can substantially change the estimated orbits because the coefficients cause secular drifts of Keplerian elements [
11]. We cannot obtain the information of thrust force models and the periods of orbit maneuvering because of secrecy, and the initial orbits of maneuvering satellites cannot be calculated by invalid orbital elements from broadcast ephemeris for about 7 hours after maneuvering, which impedes precise orbit determination. In 2016, the status of the Multi-GNSS Experiment (MGEX) within the International GNSS Service (IGS) was changed to a pilot project in recognition of the high level of maturity already achieved by the multi-GNSS network, data collection, and product generation [
12]. Orbit maneuvers break the integrality and continuity of the precise products from the IGS and International GNSS Monitoring and Assessment System (iGMAS) analysis centers. Thus, it is necessary to study orbit determination for maneuvered satellites to improve the service performance of the precise products for users.
In recent years, there has been some research about orbit maneuver detection and orbit determination for maneuvered GEO satellites. Huang and Cao et al. determined the orbit for GEO by the pseudo-distance between satellites and ground stations monitored by the Chinese Area Positioning System (CAPS) [
13,
14], but common users cannot obtain the CAPS data. Xu et al. proposed two methods of orbit determination for maneuvered GEO satellites. The first method used a Kalman filter with dynamic model compensation to determine the maneuvered satellites, and it performed well when used for orbit determination of GEO satellites. However, the premise is that the dynamic models must be known very well, which is impossible for BDS because its maneuver information is secret. The second method was to build a thrust force model for simulated maneuvering of a GEO satellite using two-way adaptive Kalman filtering, but the real maneuver type might be different from the simulated maneuver type [
15,
16]. A new dynamic orbit determination method for GEO satellites after orbit maneuvering, proposed by Li et al. could not ensure the continuity of orbit before and after maneuvers [
17]. Kelecy and Jah determined the low earth orbit (LEO) satellite orbit for low thrust maneuvers, but post-maneuver data are required for maneuver reconstruction and the method is not suitable for GEO/IGSO [
18]. Li et al. used two-way satellite–station observations to determine GEO satellite orbits by adding empiric force and maneuver force modeling, which needed the information of maneuver thrust. Also, if there was not the proper amount of empiric force, the morbid normal equation would be induced [
19]. Beutler and Jäggi et al. analyzed the effectiveness of GPS and LEO satellite orbit modelling using pseudo-stochastic parameters [
20,
21]. Sośnica et al. studied different orbit parameterizations, particularly different arc lengths and the impact of pseudo-stochastic pulses and dynamical orbit parameters on the quality of solutions for LEO satellites [
22]. Now, pseudo-stochastic pulses are typically used by the Center for Orbit Determination in Europe (CODE) for precise GNSS orbit determination for unmaneuvered satellites [
23,
24,
25].
In summary, the problem of orbit determination for BeiDou satellites could not be solved for various reasons, mainly the lack of secret maneuver information or some valuable observational data for common users. Therefore, it is necessary to study orbit determination for maneuvered satellites using public data, which does not need to rely too much on thrust information about orbit maneuvers. This paper presents a method to determine orbits for maneuvered BDS satellites by adding pseudo-stochastic pulses.
2. Theory of Orbit Determination for Maneuvered Satellites
There are three problems in precise orbit determination for maneuvered satellites.
First, the time information of orbit maneuvers is unknown for common users because of the secrecy. When orbit maneuvers occur, maneuvered satellites are marked as unhealthy for several hours (about 6–8 hours) in broadcast ephemeris, but the real time period is only about half an hour, which means that precise orbits are missing during the unmaneuvered period. Therefore, the time information of orbit maneuvering needs to be detected in order to change the strategy of precise orbit determination.
Second, the initial orbit and clock offset must be the priority because of nonlinear estimates for orbit determination, and observation data with invalid initial orbits will be removed as gross errors. The satellite clock parameters are valid in broadcast ephemeris, which cannot be affected by orbit maneuvers, so the initial clock offsets could be calculated by the parameters in broadcast ephemeris. However, the orbital elements of satellites in broadcast ephemeris cannot be updated for several hours after maneuvering, so the orbital elements are unavailable, which makes the initial orbit calculation for maneuvered satellites difficult. Therefore, the second problem that needs to be solved is valid initial orbit calculation for maneuvered satellites.
Third, when orbit maneuvers occur, there are different orbital elements before, during, and after the maneuvering period, and the information about maneuver thrust is unknown because of secrecy. In addition, the position of a maneuvered satellite cannot be calculated by seam orbit elements and the strategy of precise orbit determination must be changed to estimate different status variables of maneuvered satellites. In order to determine the precise orbits of maneuvered satellites, the above problems need to be solved.
2.1. Metheds of Detecting Orbit Maneuver Periods
Time detection for orbit maneuvers has already been discussed in our previous publications [
26,
27,
28]. The maneuver period can be detected by the pseudo-range residual:
where
are the spatial coordinates of station
;
are spatial coordinates of satellite
before orbit maneuvering;
is the distance calculated by the station and the satellite’s position;
are the spatial coordinates of satellite
after orbit maneuvering; and
is the distance calculated by the position of the station and the satellite. Furthermore,
where
is the value of pseudo-range observation;
is the empirical threshold of pseudo-range residual; and
and
are the start-time and end-time discrimination factors of the satellite orbital maneuver, respectively.
The start time and end time are determined by the start-time and end-time discrimination factors. The start time is the time of the last epoch when
is bigger than zero, and the end time is the time of the first epoch when
is bigger than zero. The details of the method for detecting the orbit maneuvering period are discussed in Reference [
28].
2.2. Methods for Calculating Initial Orbit and Clock Offset of Maneuvered Satellites
The satellite clock cannot be affected by orbit maneuvers, and the initial clock offset can be calculated by the parameters from broadcast ephemeris [
29,
30]:
where
is the satellite clock offset;
is the clock offset of initial epoch
;
is the velocity of the clock at initial epoch
; and
is the time of the initial epoch [
31].
The initial orbit of a satellite before orbit maneuvers can be calculated by the method in Reference [
32] using the orbit elements in broadcast ephemeris. However, the satellite status is changed by the orbit maneuver and the orbit elements in broadcast ephemeris cannot be updated for several hours, which makes it difficult to calculate the initial orbit of the satellite after the maneuvering. In this study, the initial orbit of a maneuvered satellite after maneuvering refers to the method in Reference [
28]. Considering that the orbit elements after a maneuver are consistent with the day after maneuvering, the initial orbit of a satellite after orbit maneuvering can be calculated by backward orbit prediction according to the precise orbit products, with the following formula:
where
is the initial position vector;
is the initial velocity vector;
is the status vector of the perturbation parameter for the satellite; and
is the time vector. The perturbation parameters of the satellite are calculated by orbit fitting by the measured orbit. The orbit is predicted by orbit integrations with parameters, including
,
, and the perturbation parameters. Specific mathematical models of orbit fitting and integration can be found in Reference [
33].
2.3. Precise Orbit Determination for Maneuvered Satellite with Pseudo-Stochastic Pulses
There are problems when determining the orbit of a maneuvered satellite, in that the forces acting on the satellite are unknown and the orbit elements of the satellite are different before and after the maneuver, which means the orbit cannot be integrated by the same status vector and estimated perturbation parameter. In addition, the effective observation data of the maneuvered satellite would be removed as gross errors in the iterative adjustment because of the inaccurate orbit. In order to solve this problem, determining the orbits of maneuvered satellites with pseudo-stochastic pulses is discussed in this study. Measurement noise and system noise have to be considered in data processing. This type of general approach is beyond the scope of our orbit determination process. We will refer to the method of allowing stochastic changes in the orbit, which can be established by the conventional least-squares method [
11]. The method of pseudo-stochastic pulses allows instantaneous velocity change
in predefined directions at predefined epoch
. An instantaneous velocity change
at epoch
in a predetermined direction
is called a pseudo-stochastic pulse. Depending on the application, many such pulses can be set up, up to three pulses in different directions, which can also be set up at different epochs. Pseudo-stochastic pulses are set up in the radial, along-track, and across-track directions (ACR) at the epoch before orbit maneuvering, during the maneuvering period, and after the orbit maneuver is finished in this study. The method of pseudo-stochastic pulses was introduced in References [
11,
29].
At predetermined epoch
(before orbit maneuver, during maneuvering period, and after orbit maneuver), the maneuvered satellite is allowed to change its velocity instantaneously in predetermined directions. The sizes of the velocity changes are controlled by artificial observation equations, and the prescribed weights are shown as follows:
The scalar velocity change is thus constrained as a random variable with the expected value of zero and variance . is the mean error of unit weight of the adjustment.
The associated changes in the initial conditions of a maneuvered satellite at time
may thus be written as follows:
where
is the orbit vector and
is the partial derivative of orbit
. Due to this pulse, the orbit will be modified for times
according to the following:
where
is the unit vector.
Pseudo-stochastic pulses
are in every respect “normal” parameters of a classical least-squares adjustment process. The sizes of the velocity changes are controlled by artificial observation equations, and the strategies for precise orbit determination in this study are described in
Table 1.
The observation data in this study were selected from the Multi-GNSS Experiment (MGEX) [
25], and the distribution of the stations is shown in
Figure 1.
3. Validations
In order to validate the reliability of the method for determining the precise orbit, the clock offset of the maneuvered satellite, and the service performance of the estimated precise orbit, considering that precise orbit products of maneuvered BeiDou satellites are missing from the analysis centers of IGS and iGMAS, we analyze the phase and pseudo-range observation residuals of maneuvered satellites (GEO/IGSO) in the first adjustment for data processing, in the removal ratio of observations, and in the bias of station coordinates calculated by precise point positioning (PPP) using the estimated orbit including the maneuvered satellite. In order to validate the applicability of the method for MEO satellites, considering CODE estimates the maneuvered orbit for GPS, which can be used for reference orbit to validate the correctness of estimated maneuvered orbits, we analyze the phase and pseudo-range observation residuals of maneuvered GPS satellites in the first adjustment for data processing and in the removal ratio of observations. In addition, we use the precise orbit products published by IGS analysis centers (CODE; Natural Resources Canada (EMR); European Space Agency (ESA), GeoForschungsZentrum (GFZ), National Centre for Space Studies (CNES) space geodesy team (GRG), Massachusetts Institute of Technology (MIT), National Oceanic and Atmospheric Administration (NOAA)/National Geodetic Survey (NGS), Scripps Institution of Oceanography (SIO), and Jet Propulsion Laboratory (JPL)). The precise orbits of maneuvered satellite G11 are only included in the products of CODE [
39]. Therefore, the differences of estimated G11 orbits between schemes 1 and 2 and CODE are analyzed.
Positioning and Navigation Data Analyst (PANDA) software is used in this study. For GEO and IGSO satellites, the selection criterion for analysis is stations that can monitor satellites during the maneuvering period. The stations are selected randomly for MEO satellites. Two schemes are set for comparison.
Scheme 1: The initial orbit is calculated by the orbital elements from the broadcast ephemeris, and precise orbit determination is done without pseudo-stochastic pulses.
Scheme 2: The initial orbit of maneuvered satellites after orbit maneuvering is backward predicted according to the precise orbit products from the BeiDou Analysis and Service Center of Chang’an University (CHD), and precise orbit determination is done with pseudo-stochastic pulses in the radial, along-track, and across-track directions at the time of epoch before orbit maneuvering, during the maneuvering period, and after orbit maneuvering is finished.
For GEO satellites, the results of BeiDou C01 are analyzed in this study. The results from 22 MGEX stations (AUCK, CAS1, CHTI, CKIS, COCO, DARW, DUND, FTNA, JFNG, KARR, KIRI, LAUT, LHAZ, MOBS, NAUR, NIUM, PERT, PNGM, SAMO, SOLO, SYDN, and XMIS) were selected on 9 January 2017. These stations can monitor the C01 satellite during the maneuvering period. For IGSO satellites, the results of BeiDou C07 are analyzed in this study. The results from 16 MGEX stations (COCO, DJIG, DYNG, FTNA, HARB, KIRI, KOKV, KZN2, LAUT, MAL2, MAYG, NIUM, SAMO, SEYG, UCAL, and YEL2) were selected on 16 October 2017. The stations can monitor the C07 satellite during the maneuvering period. For MEO satellites, the results of GPS G11 are analyzed in this study. The results from 20 MGEX stations (ASCG, AUCK, CEDU, CHPG, FLIN, HKSL, IQAL, KIRU, KOUR, KUUJ, LAUT, MAL2, MAYG, MGUE, NICO, PADO, SCH2, STFU, THTG, and UCAL) were selected on 1 March 2018. The precise orbit determination was done according to schemes 1 and 2, and the coordinates of the stations are from the IGS Solution Independent Exchange (SINEX) daily product.
3.1. Residuals of Phase and Pseudo-Range
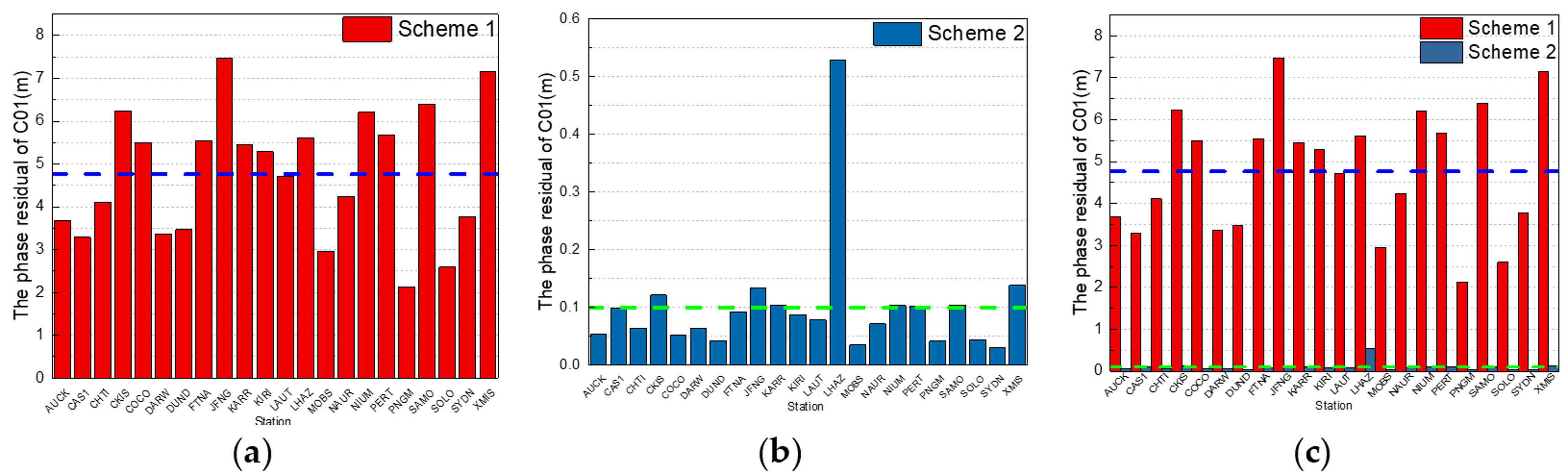
For GEO satellites, the phase observation residuals of C01 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 2.
In
Figure 2, the red columns are the residuals according to scheme 1; the maximum is 7.5 m from JNFG station, the minimum is 2.1 m from PNGM station, and the average value from the 22 stations is 4.8 m, which is denoted by the dotted blue lines in
Figure 2a,c. The dark blue columns are the residuals according to scheme 2; the maximum is 0.5 m from LHAZ station, the minimum is 0.03 m from SYDN station, and the average value from 22 stations is 0.1 m, which is denoted by the dotted green lines in
Figure 2b,c. It is obvious that the phase residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
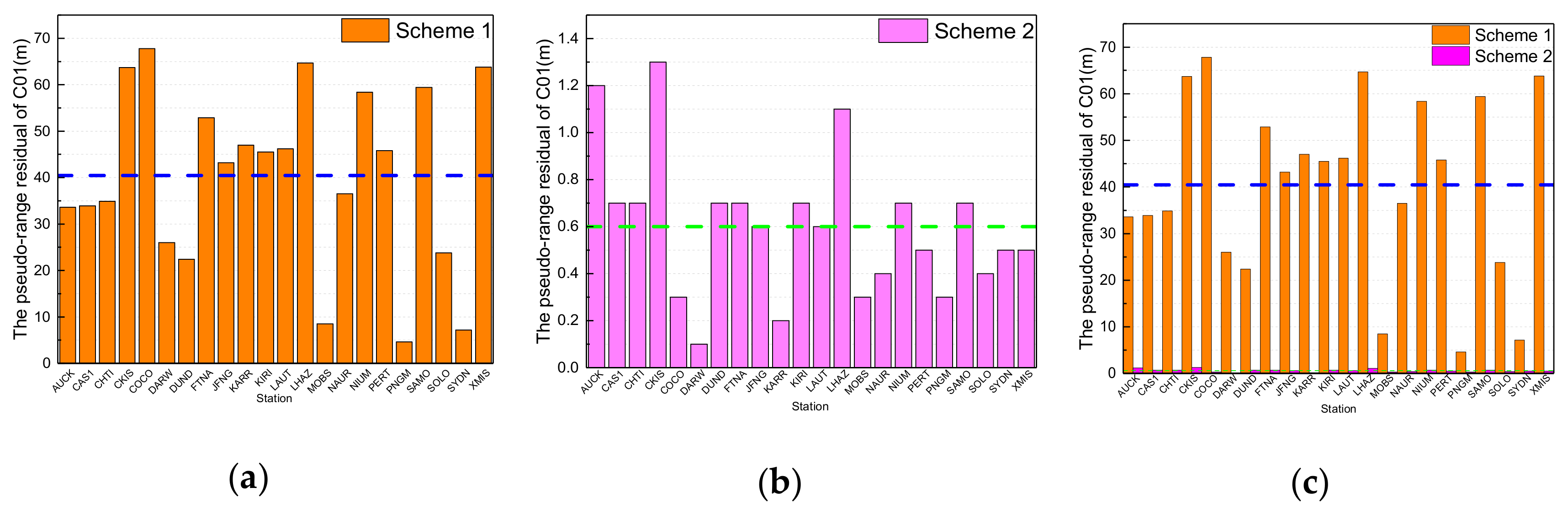
The pseudo-range observation residuals of C01 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 3.
In
Figure 3, the orange columns are the residuals according to scheme 1; the maximum is 67.8 m from COCO station, the minimum is 4.6 m from PNGM station, and the average value from the 22 stations is 40.4 m, which is denoted by the dotted blue lines in
Figure 3a,c. The pink columns are the residuals according to scheme 2; the maximum is 1.3 m from CKIS station, the minimum is 0.1 m from KARW station, and the average value from 22 stations is 0.6 m, which is denoted by the dotted green lines in
Figure 3b,c. It is obvious that the pseudo-range residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, phase and pseudo-range residuals of scheme 2 are much less than those of scheme 1 because of the valid initial orbit and the estimated pseudo-stochastic pulses of maneuvered satellites, which proves the validity of the method for calculating the initial position of maneuvered GEO satellites.
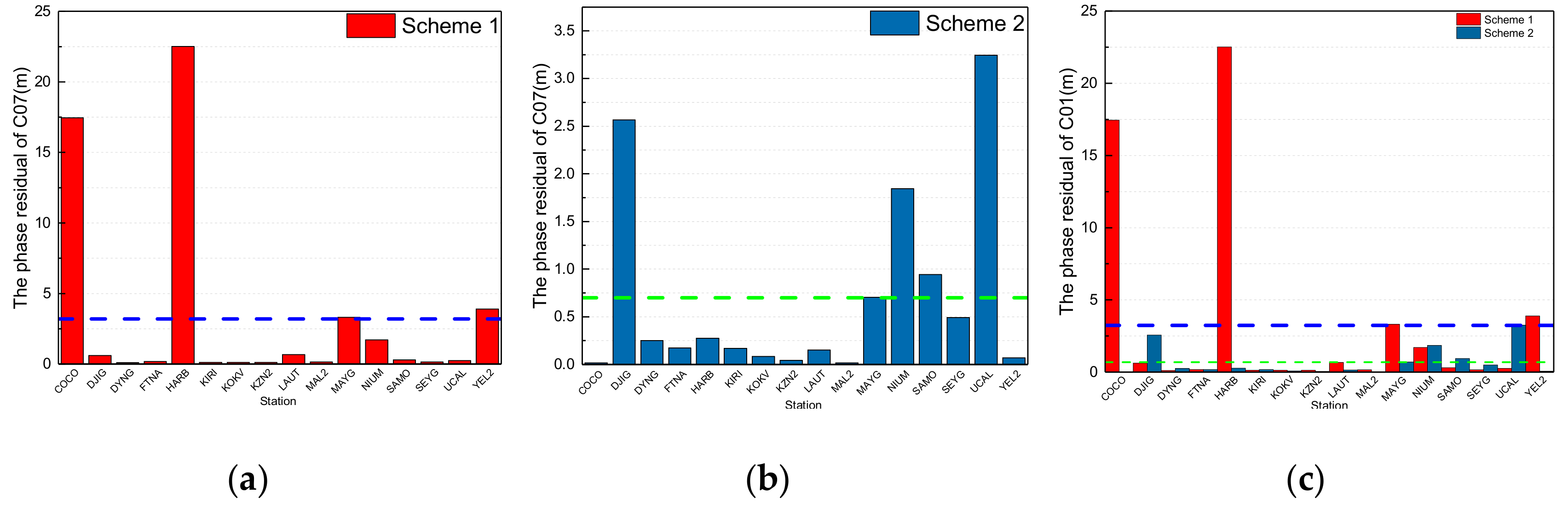
For IGSO satellites, the phase observation residuals of C07 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 4.
In
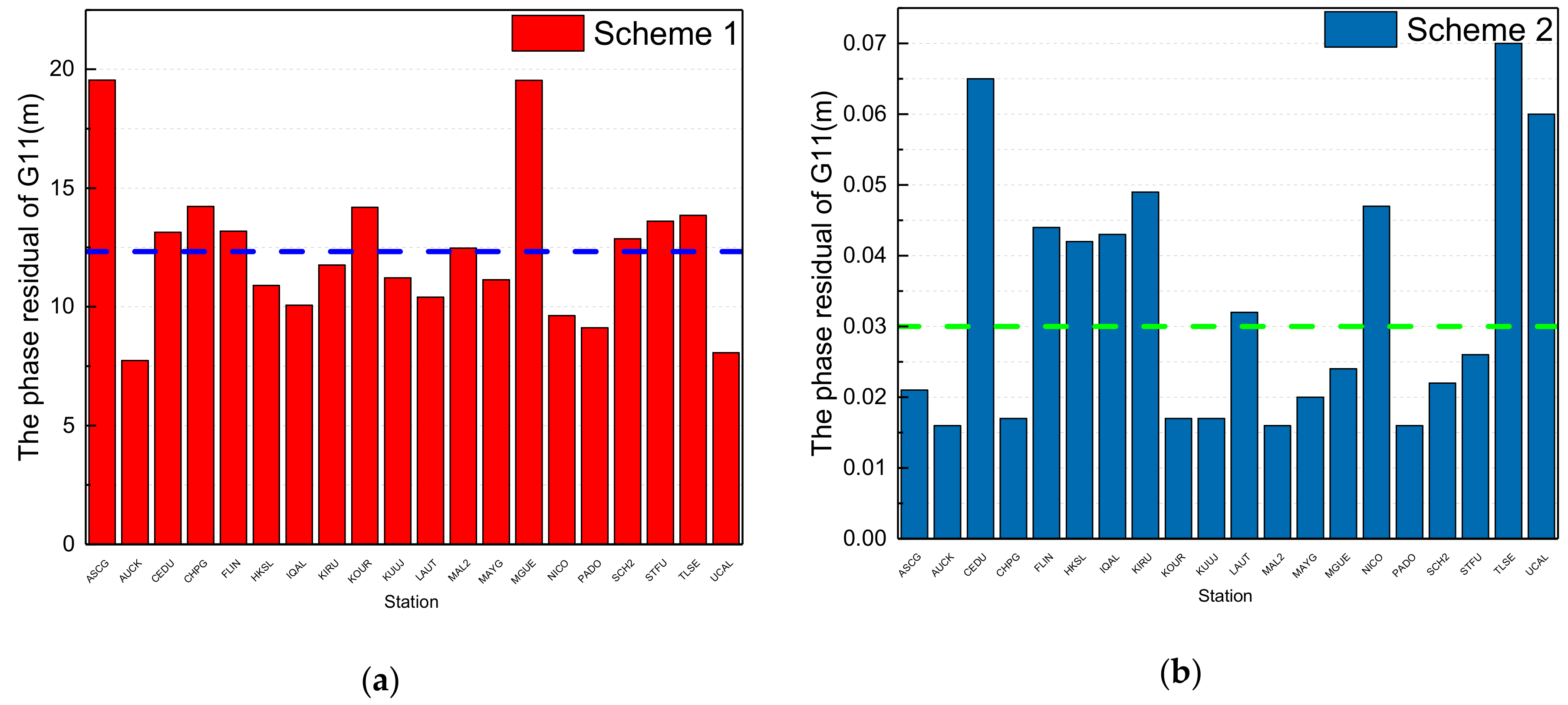
Figure 4, the red columns are the phase residuals according to scheme 1; the maximum is 22.5 m from HARB station, the minimum is 0.12 m from KIRI station, and the average value from the 16 stations is 3.2 m, which is denoted by the dotted blue lines in
Figure 4a,c. The dark blue columns are the phase residuals according to scheme 2; the maximum is 3.2 m from UCAL station, the minimum is 0.02 m from MAL2 station, and the average value from the 16 stations is 0.7 m, which is denoted by the dotted green lines in
Figure 4b,c. It is obvious that the phase residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses. In addition, the phase residuals of some stations from scheme 1 are less than those of scheme 2 because most phase observations were removed due to the invalid initial orbit calculated by using broadcast ephemeris in the data preparation. From the results, the phase residuals of stations for maneuvering IGSO satellites are greater than those of GEO satellites, and the cause needs to be analyzed in further research.
The pseudo-range observation residuals of C07 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 5.
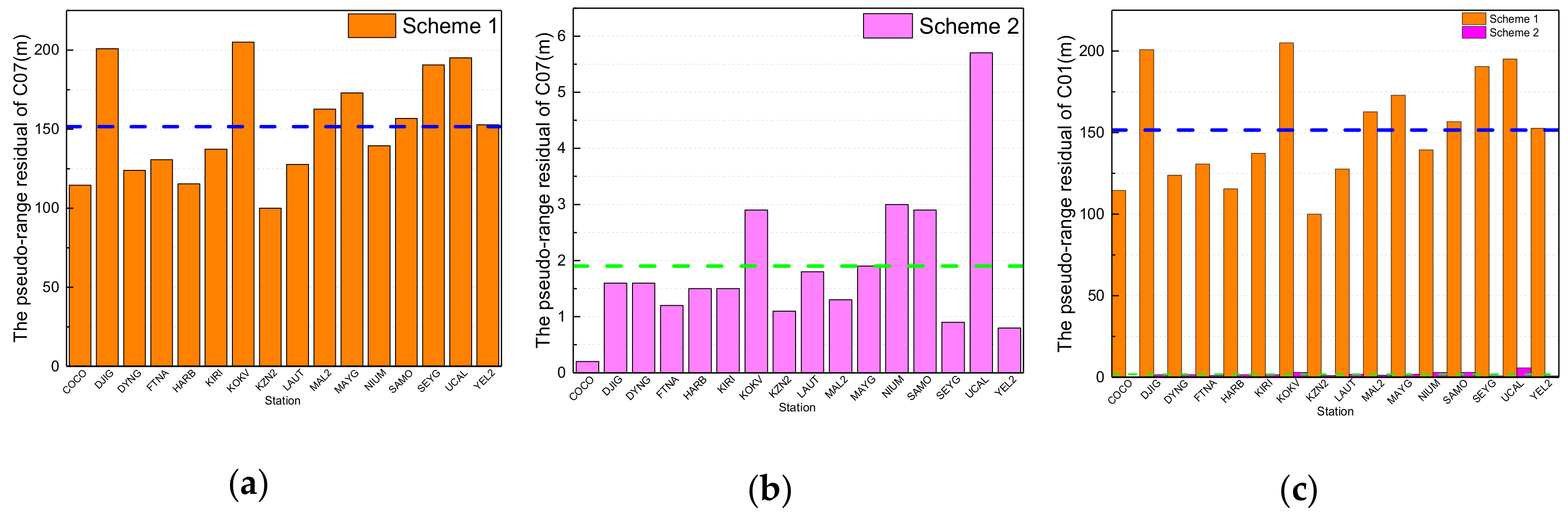
In
Figure 5, the orange columns are the pseudo-range residuals according to scheme 1; the maximum is 205 m from KOKV station, the minimum is 114.6 m from COCO station, and the average value from the 16 stations is 151.6 m, which is denoted by the dotted blue lines in
Figure 5a,c. The pink columns are the pseudo-range residuals according to scheme 2; the maximum is 5.9 m from UCAL station, the minimum is 0.2 m from COCO station, and the average value from the 16 stations is 1.9 m, which is denoted by the dotted green lines in
Figure 5b,c. It is obvious that the pseudo-range residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, phase and pseudo-range residuals of scheme 2 are much less than those of scheme 1 because of the valid initial orbit and estimated pseudo-stochastic pulses of maneuvered satellites, which proves the validity of the method for calculating the initial position of maneuvered satellites. However, the phase residuals of some stations from scheme 1 are less than those of scheme 2 because most of the phase observations were removed due to the invalid initial orbit calculated by using broadcast ephemeris in the data preparation. The phase residuals of stations for maneuvering IGSO satellites are greater than those of GEO satellites, and the influence of orbital maneuvering on the carrier phase observations of GEO and IGSO satellites is different, which needs to be analyzed in further research. For MEO satellites, the phase observation residuals of G11 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 6.
In
Figure 6, the red columns are the phase residuals according to scheme 1; the maximum is 19.5 m from ASCG station, the minimum is 7.7 m from AUCK station, and the average value from the 20 stations is 12.3 m, which is denoted by the dotted blue line in
Figure 6a. The dark blue columns are the phase residuals according to scheme 2; the maximum is 0.065 m from CEDU station, the minimum is 0.016 m from AUCK station, and the average value from the 20 stations is 0.033 m, which is denoted by the dotted green line in
Figure 6b. It is obvious that the phase residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
The pseudo-range observation residuals of G11 in the first adjustment for data processing from schemes 1 and 2 are shown in
Figure 7.
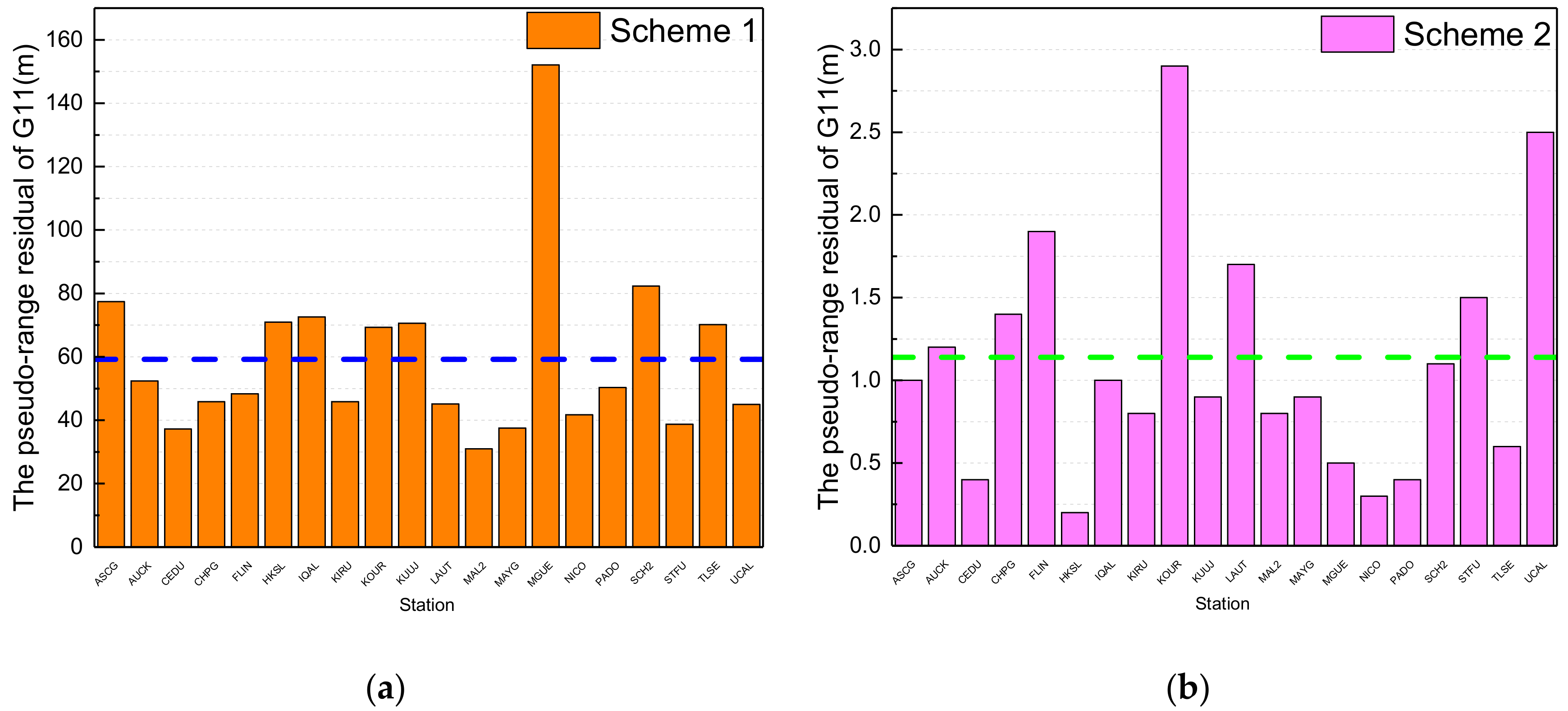
In
Figure 7, the orange columns are the pseudo-range residuals according to scheme 1; the maximum is 152.1 m from MGUE station, the minimum is 31 m from MAL2 station, and the average value from the 20 stations is 59.2 m, which is denoted by the dotted blue line in
Figure 7a. The pink columns are the pseudo-range residuals according to scheme 2; the maximum is 2.9 m from KOUR station, the minimum is 0.2 m from HKSL station, and the average value from the 20 stations is 1.1 m, which is denoted by the dotted green line in
Figure 7b. It is obvious that the pseudo-range residuals from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses are much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, phase and pseudo-range residuals of scheme 2 are much less than those of scheme 1 because of the valid initial orbit and the estimated pseudo-stochastic pulses of maneuvered satellites, which proves the validity of the method for calculating the initial position of a maneuvered MEO satellite.
3.2. Removal Ratio of Observations
In order to further prove the effectiveness of determining orbits with pseudo-stochastic pulses in predetermined directions and epochs, the removal ratio of observations for maneuvered satellites is analyzed.
For GEO satellites, the removal ratio of observations from the 22 MGEX stations for C01 according to schemes 1 and 2 is shown in
Figure 8.
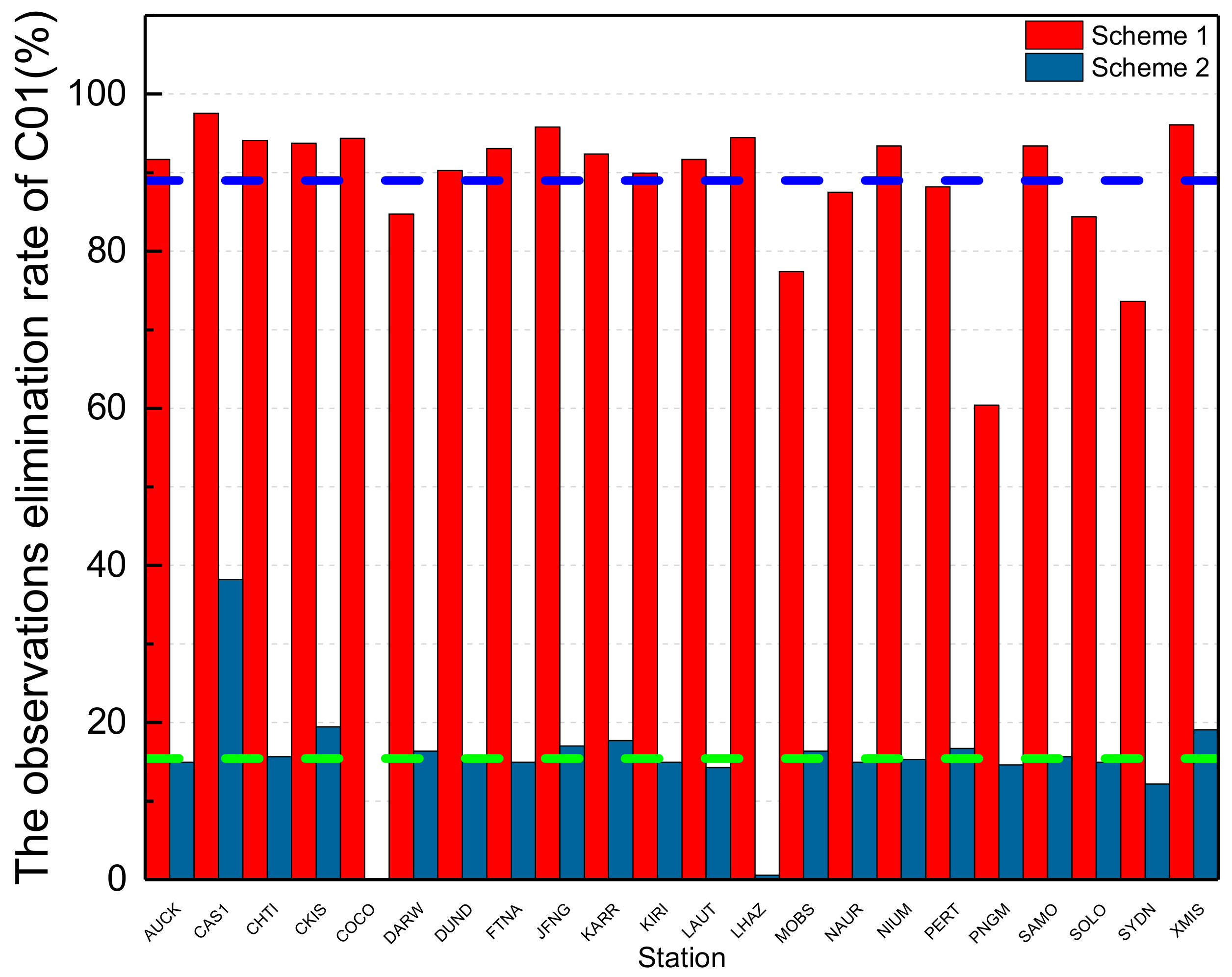
In
Figure 8, the red columns are the removal ratio of observations according to scheme 1; the maximum is 97.57% from CAS1 station, the minimum is 73.61% from SYDN station, and the average value from the 22 stations is 89.01%, which is denoted by the dotted blue line. The dark blue columns are the removal ratio of observations according to scheme 2; the maximum is 38% from CAS1 station, the minimum is 0 from COCO station, and the average value from 22 stations is 15.41%, which is denoted by the dotted green line. It is obvious that the removal rate of observations from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses is much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, the removal rate of observations of scheme 2 is much less than that of scheme 1 because of the valid initial orbit and pseudo-stochastic pulses, which proves that the orbit of a maneuvered satellite cannot be integrated by the same status vector and estimated perturbation parameters, and the effective observation data of maneuvered satellites would be removed as gross errors in the iterative adjustment because of inaccurate estimated parameters. In addition, it verifies the effectiveness of precise orbit determination with pseudo-stochastic pulses for maneuvered satellites.
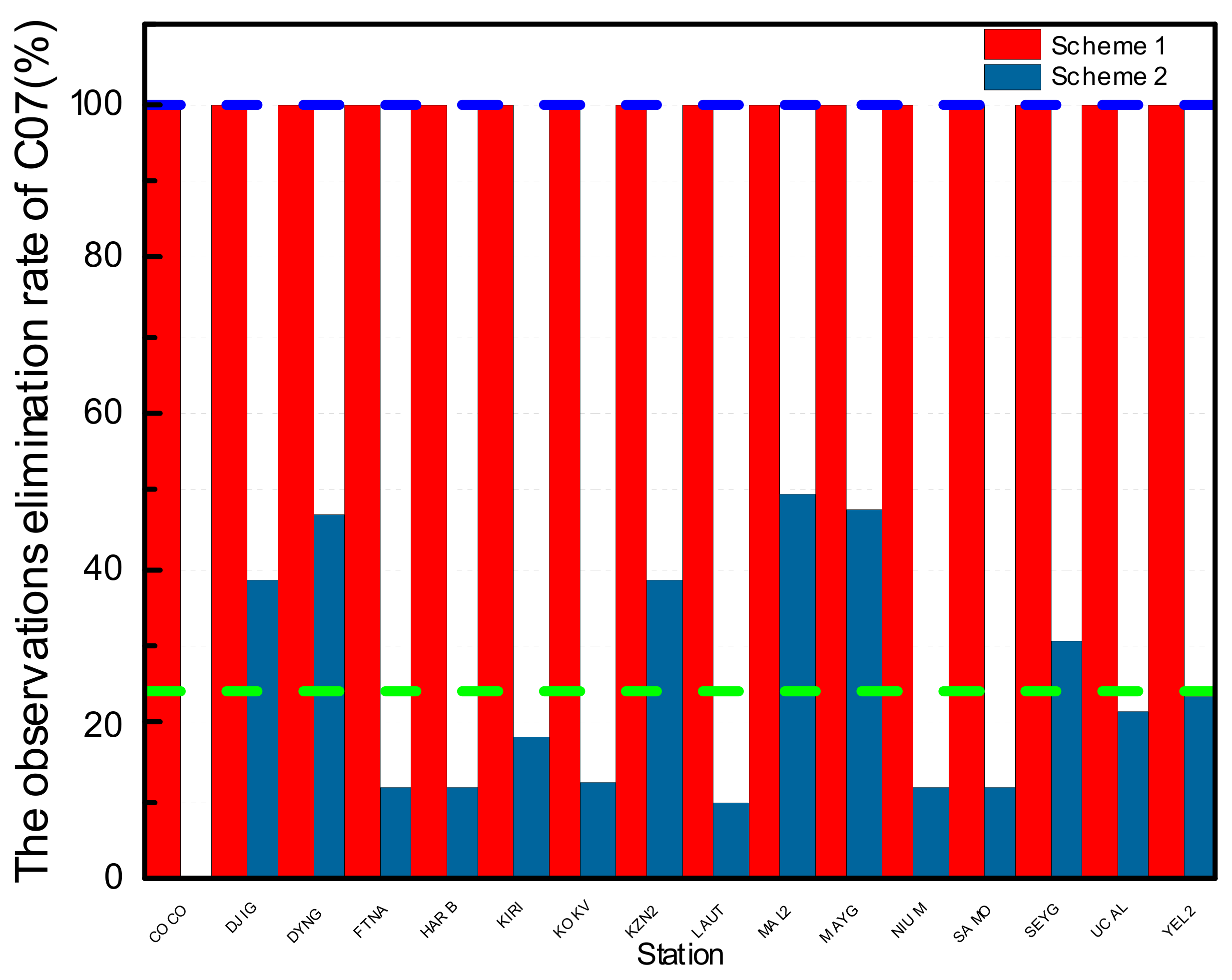
For IGSO satellites, the removal ratio of observations of the 16 MGEX stations for C07 according to schemes 1 and 2 is shown in
Figure 9.
In
Figure 9, the red columns are the ratio of observations removed according to scheme 1; all observation data of 15 stations for C07 have been removed from precise orbit determination, and the removal ratio of the other station is 96.53%. The dark blue columns are the ratios of observations removed according to scheme 2; the maximum is 49.48% from MAL2 station, the minimum is 0 from COCO station, and the average value from 16 stations is 24.08%, which is denoted by the dotted green line. It is obvious that the removal rate of observations from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses is much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, the removal rate of observations of scheme 2 is much less than that of scheme 1 because of the valid initial orbit and pseudo-stochastic pulses, which proves that the orbit of a maneuvered IGSO satellite cannot be integrated by the same status vector and estimated perturbation parameters, and the effective observation data of the maneuvered satellite would be removed as gross errors in the iterative adjustment because of the inaccurate estimated parameters. In addition, it verifies the effectiveness of precise orbit determination with pseudo-stochastic pulses for maneuvered IGSO satellites.
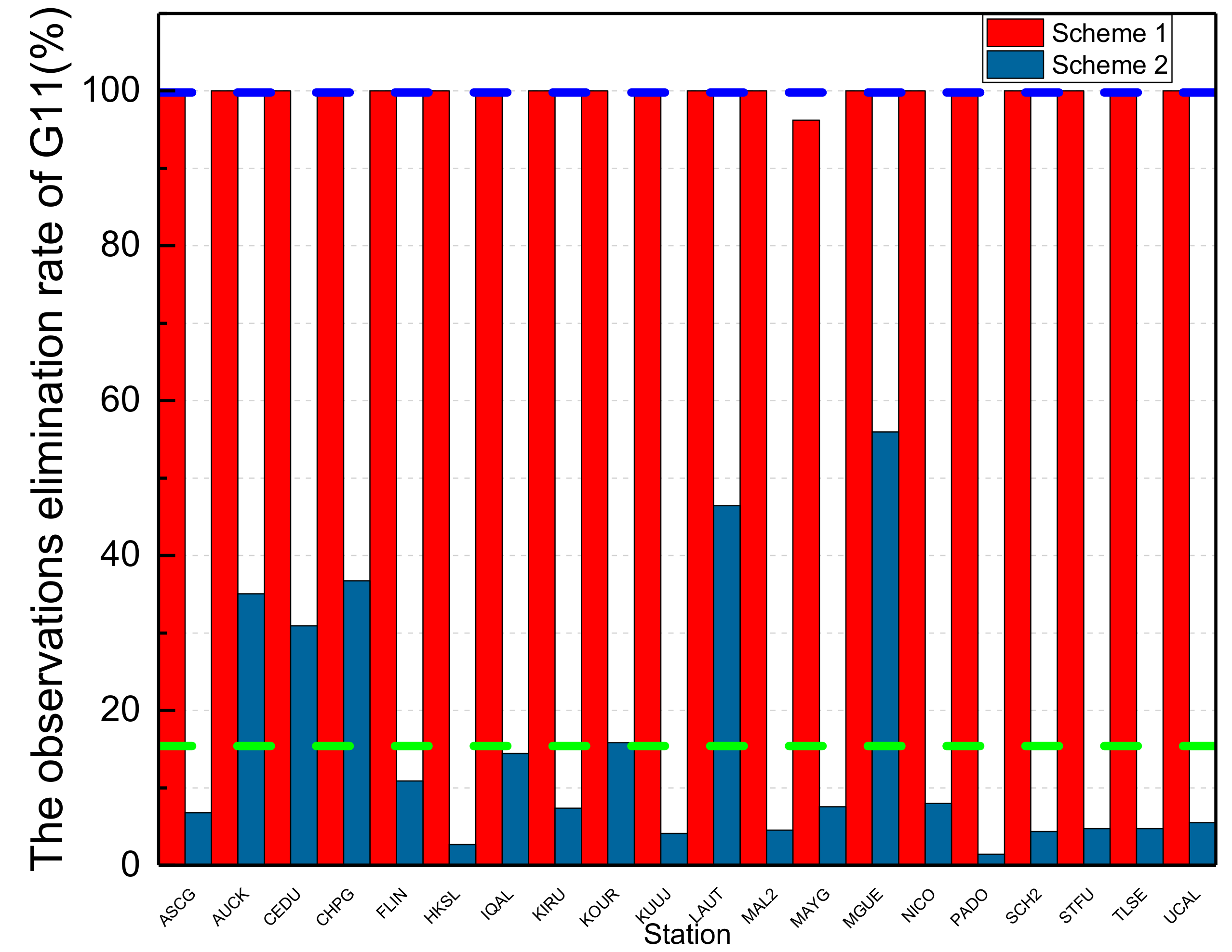
For MEO satellites, the removal ratio of observations of the 20 MGEX stations for G11 according to schemes 1 and 2 is shown in
Figure 10.
In
Figure 10, the red columns are the ratios of observations removed according to scheme 1; all observation data of 19 stations for G11 have been removed from precise orbit determination, and the removal ratio of the other station, MAYG, is 96.23%. The dark blue columns show the ratio of observations removed according to scheme 2; the maximum is 55.95% from MGUE station, the minimum is 1.43% from PADO station, and the average value from 20 stations is 19.40%, which is denoted by the dotted green line. It is obvious that the removal rate of observations from data processing by using the initial orbit calculated by backward predicted orbit and by adding the pseudo-stochastic pulses is much less than by using the initial orbit calculated by orbit elements from broadcast ephemeris and without pseudo-stochastic pulses.
From the above results, the removal rate of observations of scheme 2 is much less than that of scheme 1 because of the valid initial orbit and pseudo-stochastic pulses, which proves that the orbit of a maneuvered MEO satellite cannot be integrated by the same status vector and estimated perturbation parameters, and the effective observation data of the maneuvered satellite would be removed as gross errors in the iterative adjustment because of the inaccurate estimated parameters. In addition, it verifies the effectiveness of precise orbit determination with pseudo-stochastic pulses for maneuvered MEO satellites.
3.3. Bias of PPP by Using the Estimated Orbit
In order to verify the correctness and service performance of the estimated precise orbits of BeiDou satellites and considering that the precise orbit products of maneuvered satellites are missing from the analysis centers of IGS and iGMAS, the coordinate biases of tracking stations calculated through PPP technology using the orbit and clock offset estimated by the method proposed in this study are analyzed, and reference coordinates were acquired from the IGS Solution Independent Exchange product.
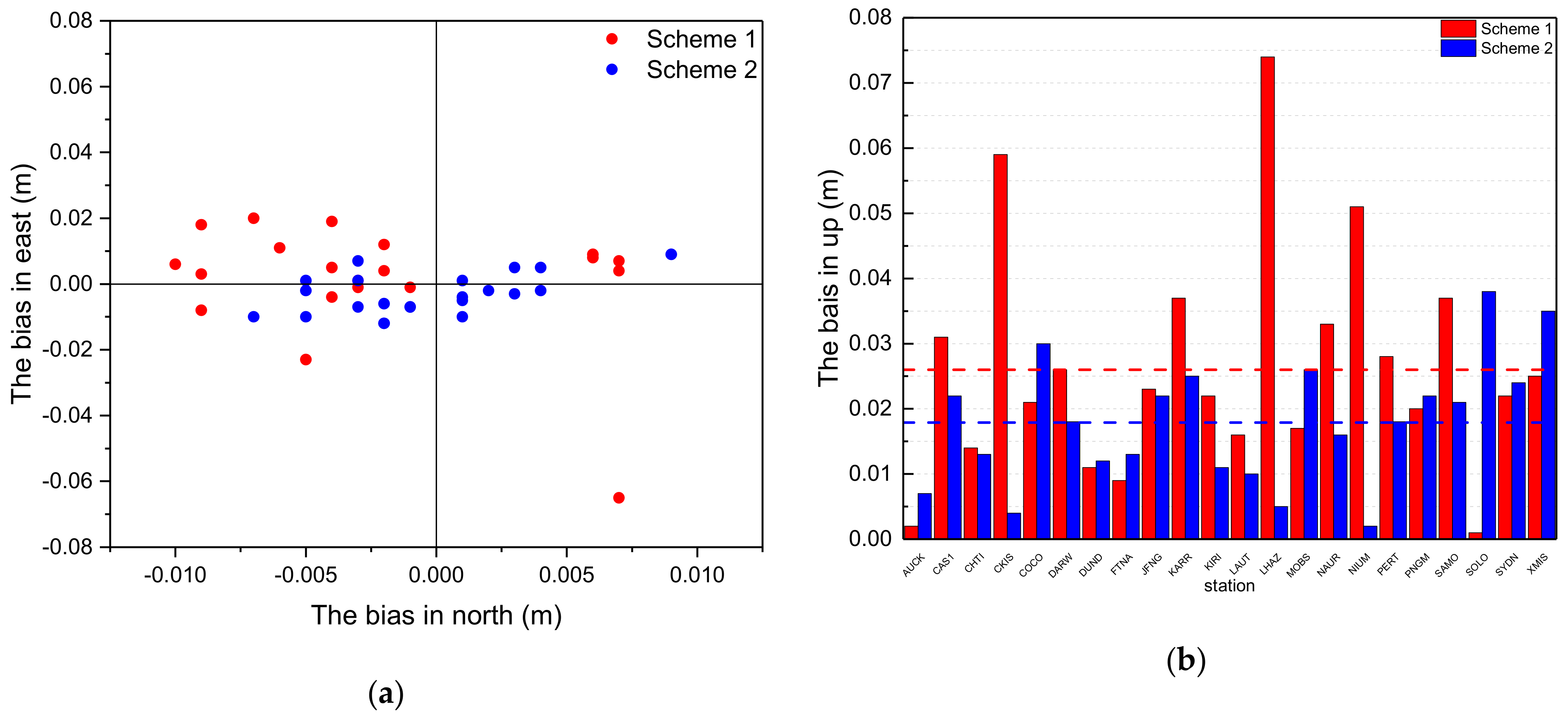
The results of GEO satellites are shown in
Figure 11.
In
Figure 11a, the red points indicate the bias distribution in the north and east (NE) directions of PPP using the estimated orbits of scheme 1 and the blue points indicate the bias distribution in the NE directions using the estimated orbits of scheme 2. From the results in
Figure 11a, the blue points are more concentrated than the red points, which means that the positioning accuracy using the estimated orbits is higher according to scheme 2 than scheme 1. From the results in
Figure 11b, the red columns represent bias in the up (U) direction according to scheme 1 and the average value is denoted by the dotted red line. The blue columns are bias in the up direction according to scheme 2, and the average value is denoted by the dotted blue line. The biases of coordinates calculated by PPP for each station are shown in
Table 2.
It can be seen from
Table 1 that scheme 2 results in a better average bias of NEU directions than scheme 1. Bias in the N direction is 7 mm according to scheme 1 and 3 mm according to scheme 2. Bias in the E direction is 11 mm according to scheme 1 and 6 mm according to scheme 2. Bias in the U direction is 26 mm according to scheme 1 and 18 mm according to scheme 2. When compared with that of scheme 1, bias of the N direction for most stations under scheme 2 is significantly improved, with an average of 4 mm (57%). For the E-component results, the improvement is 5 mm (45%). For the U-component results, the improvement is 8 mm (31%). Therefore, it could improve the accuracy of the coordinate solution for PPP effectively by using estimated orbits with pseudo-stochastic pulses, which verifies the validity of the proposed precise orbit determination method for maneuvered GEO satellites, thereby improving the service performance of precise products for users.
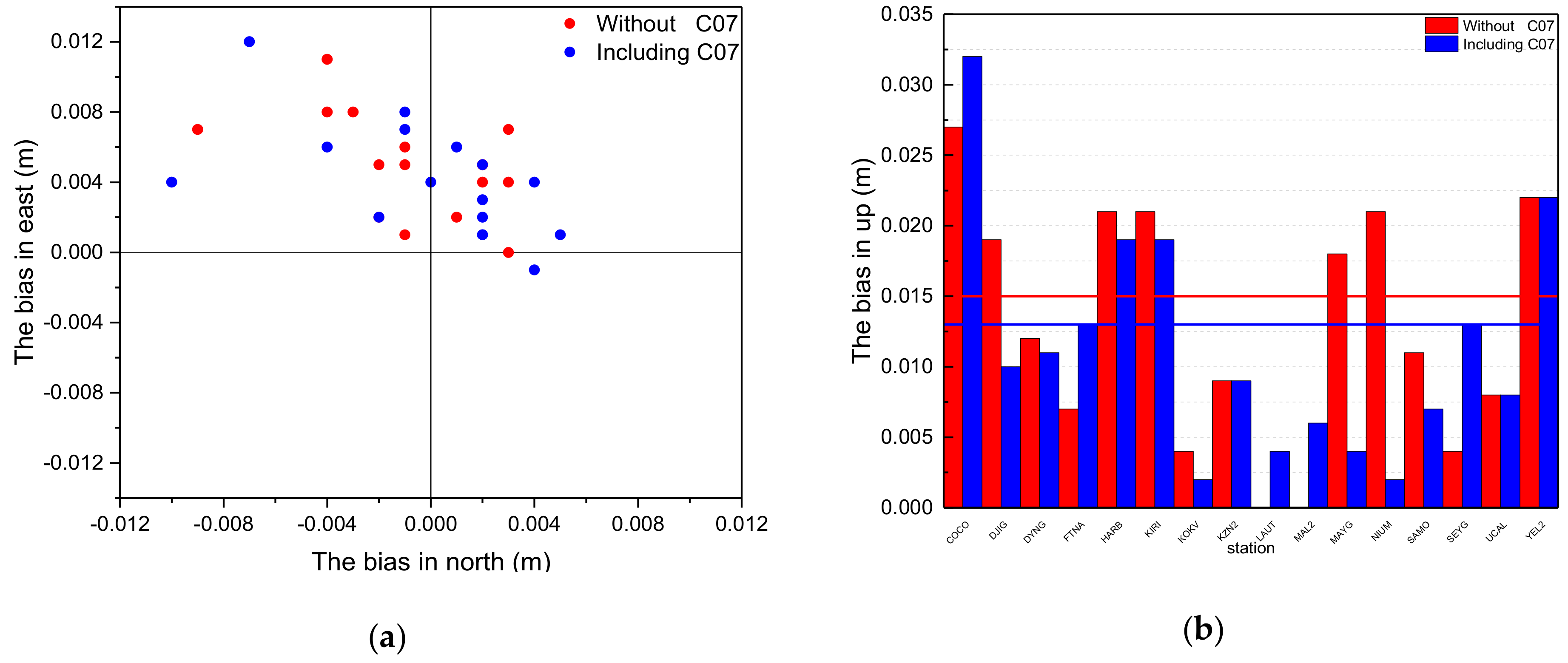
For IGSO satellites, considering that all observations of C07 are removed because of the invalid initial orbit calculated by broadcast ephemeris, the orbit and clock offset of C07 cannot be estimated according to scheme 1. Therefore, the results of PPP using the orbit and clock offset estimated according to scheme 2 is analyzed. In order to verify the validity of orbit estimates for C07, two schemes for PPP are set for comparison. The first PPP scheme uses the precise orbit and clock offset of GPS and BeiDou without the maneuvered satellite C07 to calculate the precise coordinates of 16 selected tracking stations. In the second PPP scheme, the precise orbit and clock offset of GPS and BeiDou, including the maneuvered satellite C07, are used to calculate the precise coordinates of the 16 stations. The biases of coordinates calculated by PPP are shown in
Figure 12.
In
Figure 12a, the red points indicate the bias distribution in the NE directions of PPP using estimated orbits without maneuvered satellite C07 and the blue points represent the bias distribution including C07. From the results of
Figure 12a, the dispersion degree of red and blue is relatively consistent, which means the positioning accuracy in the NE directions is not influenced by maneuvered satellite C07. From the results in
Figure 12b, the red columns are bias in the up direction by PPP using the orbit without C07 and the average value is 13 mm, which is denoted by the dotted red line. The blue columns are bias in the up direction by PPP for stations using the orbit including C07, and the average value is 11 mm, which is denoted by the dotted blue line. The biases of PPP for each station are shown in
Table 3.
It can be seen from
Table 3 that the PPP average bias without C07 in the NEU directions including CO7 was compared. Biases in the N direction are 3 mm and 4 mm, respectively; biases in the E direction are 5 mm and 4 mm, respectively; and biases in the U direction are 13 mm and 11 mm, respectively. For the N-component result, it shares the same deviation degree. For the E-component result, the improvement is 1 mm (20%). For the U-component result, the improvement is 2 mm (18%). Therefore, the positional accuracy of solution for PPP could be effectively improved by using the precise orbit estimated with the maneuvered satellite; it plays an important role in positioning in a complex environment without excess observations. It verifies the validity of the proposed precise orbit determination method for maneuvered IGSO satellites, which can improve the service performance of the precise products for users.
3.4. Difference between Estimated Orbits and CODE for GPS
The precise orbit products are published by IGS Analysis Centers (CODE: EMR, ESA, GFZ, GRG, MIT, NGS, SIO, and JPL), and the precise orbit and clock of maneuvered satellite G11 are only included in the products of CODE [
39]. Therefore, the differences of estimated orbits for G11 between scheme 1 and 2 and CODE are analyzed.
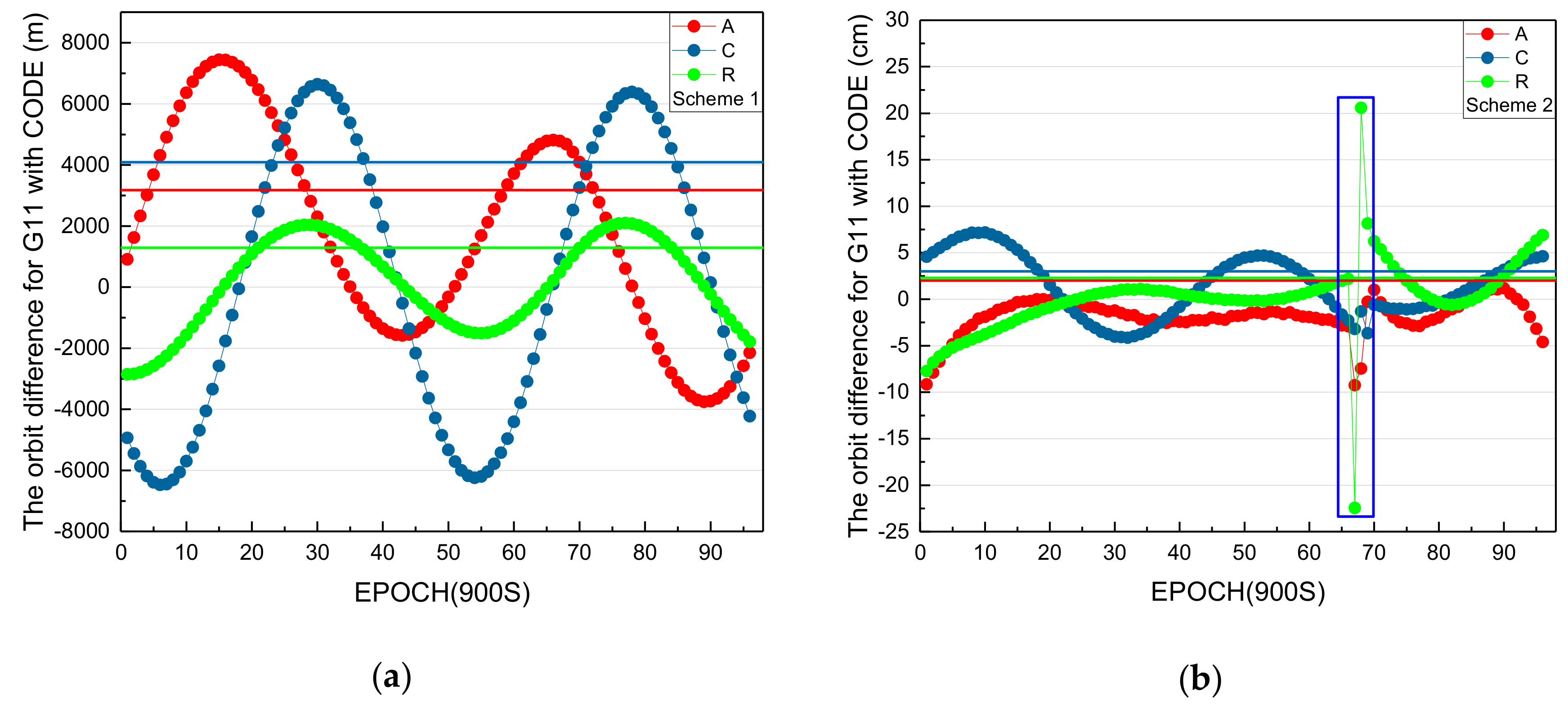
In
Figure 13, the red, dark blue, and green lines denote the average absolute values of orbit differences in the along-track, across-track, and radial directions, respectively. The blue rectangle in
Figure 13b marks the orbit differences during the maneuvering period. From
Figure 13a, the average absolute values of orbit differences in the along-track, across-track, and radial directions are 3179.2 m, 4087.7 m, and 1293.3 m, respectively. From
Figure 13b, the average absolute values of orbit differences in the along-track, across-track, and radial directions are 2.0 cm, 3.0 cm, and 2.3 cm, respectively. It is obvious that the normal orbit determination method according to scheme 1 is unusable for determining maneuvered satellites, and orbits can be estimated correctly by the proposed method in this paper. However, the orbit difference in the radial direction is more than 20 cm and, in the along-track direction, is more than 5 cm during the orbit maneuvering period because of the systematic error of unmodeled maneuvered force, which cannot be absorbed absolutely by the estimated pseudo-stochastic pulses. There are also some questions to be studied to improve the orbit determination accuracy of maneuvered satellites in the future.
3.5. Discussion of Interval and Constraints for Estimating Pseudo-Stochastic Pulses
The intervals and constraints of estimating pseudo-stochastic pulses to determine maneuvered orbits are important. Pseudo-stochastic pulses are estimated by CODE for precise GNSS orbit determination for unmaneuvered satellites. For unmaneuvered satellites, pseudo-stochastic pulses are estimated every 12 hours in the along-track, cross-track, and radial directions. The mean errors of unit weight (sigmas) are 10
– 5 (along-track), 10
–8 (cross-track), and 10
–6 (radial) [
23], but they cannot be used for maneuvered satellites. The variation of velocity in the along-track, cross-track, and radial directions caused by maneuvers are unknown in advance, so the intervals and constraint differences for estimating pseudo-stochastic pulses are not discussed in this paper. For maneuvered satellites, GPS orbits are only estimated by CODE, and the precise orbit products of BDS are missing from all IGS and iGMAS analysis centers. For IGSO satellites, CODE only estimates orbits before orbit maneuvering. Therefore, the intervals and constraints of estimating pseudo-stochastic pulses are analyzed for G11 on 1 March 2018. The period (16:00:00–18:00:00) includes the maneuvering period of G11 [
28].
First, the intervals of estimating pseudo-stochastic pulses to determine maneuvered orbits are analyzed. The constraints (3 × 10–1 m/s) are selected.
From
Table 4, looking at the intervals from 300 to 900 seconds, it is obvious that the orbit differences increase gradually. This verifies that pseudo-stochastic pulses estimated more frequently during the maneuvering period are beneficial for precise orbit determination for maneuvered satellites. In addition, when the interval is set as 12 hours, the orbit differences are more than 5 meters in the along-track and radial directions. Because the variation of velocity in cross-track is small, the orbit difference is 13 cm. The pseudo-stochastic pulses estimated every 12 hours cannot be used for maneuvered satellites. In summary, pseudo-stochastic pulses estimated more frequently during the maneuvering period are beneficial for precise orbit determination for maneuvered satellites.
Second, the constraints of estimating pseudo-stochastic pulses for determining maneuvered orbits are analyzed. The interval 300 seconds is selected.
From
Table 5, for constraints from 3 × 10
–0 to 3 × 10
–4 m/s, the orbit differences are the same. This shows that the variation range of velocity in the along-track, cross-track, and radial directions caused by maneuvers is less than 3 × 10
–4 m/s. When the constraint is set as 3 × 10
–5 m/s, the orbit differences are smaller in the along-track, cross-track, and radial directions, which shows that the selected constraint is proper to estimate pseudo-stochastic pulses for G11 on 1 March 2018. In addition, when the selected constraints are from 3 × 10
–6 m/s to 3 × 10
–8 m/s, the orbit differences of 1D increase to about 5 meters. This verifies that the variation range of velocity in the along-track, cross-track, and radial directions caused by maneuvers is larger than 3 × 10
–6 m/s. The variation of velocity caused by maneuvers is unknown in advance. We suggest that the constraints of estimating pseudo-stochastic pulses be set as more than 10
–5 m/s for maneuvered MEO satellites. The constraints of estimating pseudo-stochastic pulses for GEO/IGSO and MEO satellites are different because of the different maneuvering models. We suggest that the constraints of maneuvered IGSO and GEO satellites be set larger than 10
–4 m/s and 10
–7 m/s, respectively. In future research, in order to improve the accuracy of the precise orbits of maneuvered satellites, the long periodic orbit estimated by this method could be used to analyze the constraints of estimating pseudo-stochastic pulses in the along-track, cross-track, and radial directions.