Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction
Abstract
1. Introduction
- To the best of our knowledge, we are the first to exploit GCS and NSS to construct the nonlocal structure sparsity of HSI that is a faithfully structured sparsity representation form for HSI-CSR task.
- For each cube that is formed by grouping nonlocal similar cubes, the tensor representation based on tensor sparse and low-rank approximation is introduced to encode the intrinsic spatial-spectral correlation.
- The HSI-CSR task is treated as an optimization problem; we resort to alternative direction multiplier method (ADMM) [44] to solve it.
2. Notations and Background of HSI-CS
2.1. Notations
2.2. Background of HSI-CS
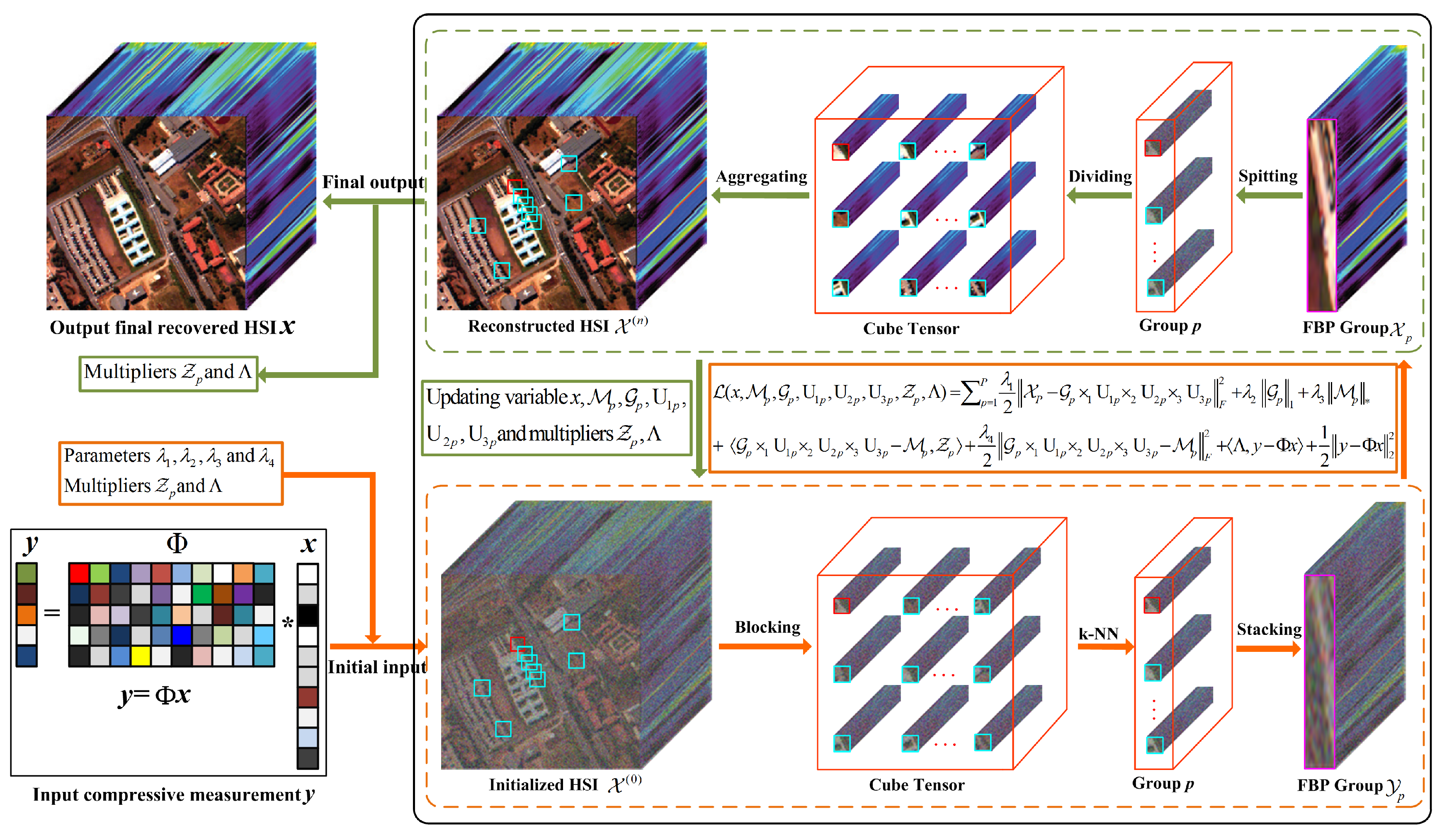
3. The Proposed HSI-CSR via NTSRLR
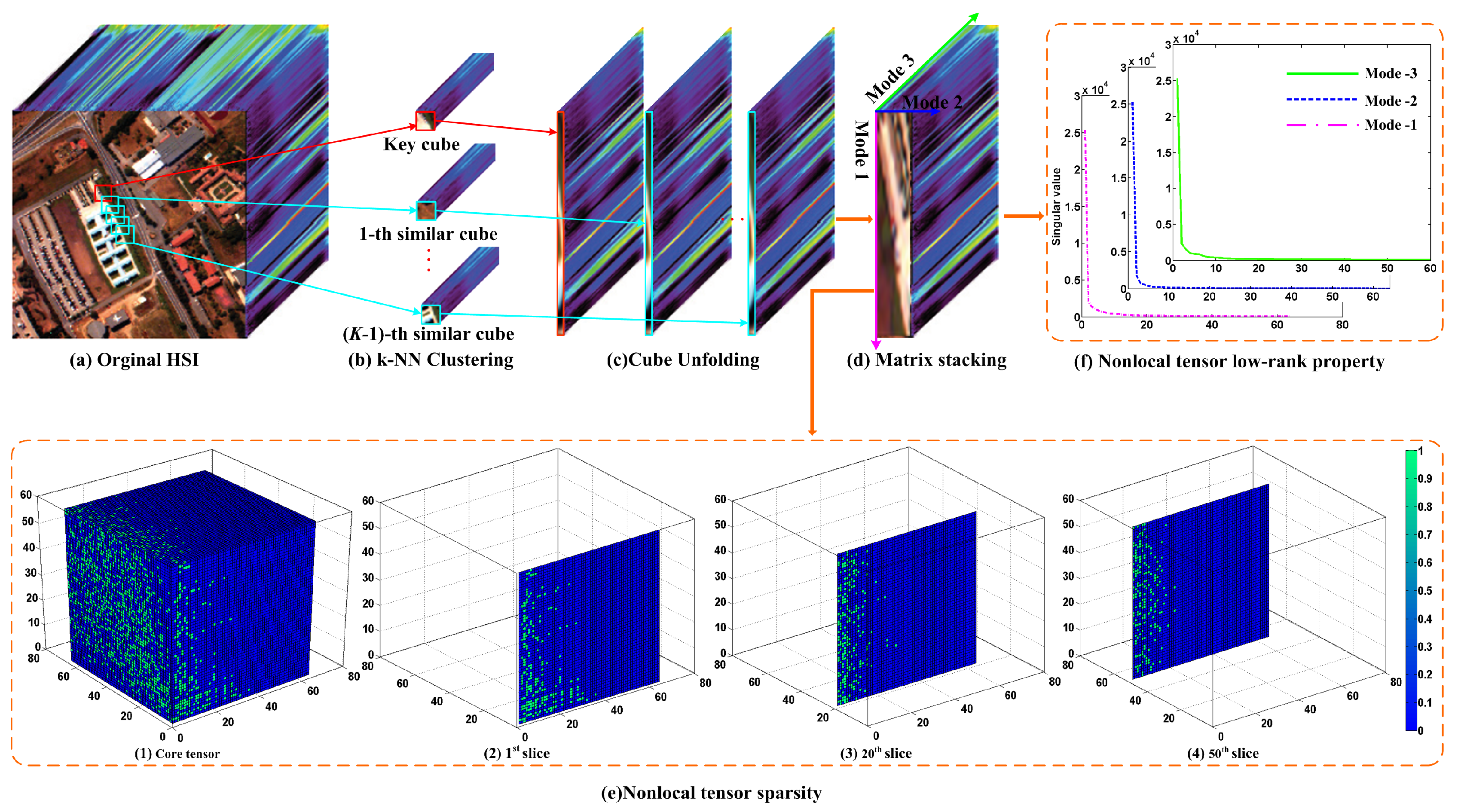
3.1. Non-Local Tensor Formula for Structure Sparsity
3.1.1. Non-Local Structure Sparsity Analysis
3.1.2. Non-Local Structure Sparsity Modeling
3.2. Proposed Model
3.3. Optimization Algorithm
- (a)
- (b)
- sub-problem:It can be rewritten as
- (c)
- sub-problem:It can be briefly reformulated as:where , its equivalent form isAs suggested in [51], its close-form solution is expressed as:For a given matrix X, the singular value shrinkage operator is defined as , and where is the SVD of X and .
- (d)
- x sub-problem:It is easy to observe that optimizing L with respect to x can be treated as solving the following linear system:where , denotes the vectorization operator for a matrix or tensor, and indicates the adjoint of . Obviously, this linear system can be solved by well-known preconditioned conjugate gradient technique.
- (e)
- Update the multiplierswhere is a parameter associated with the convergence rate at values of, e.g., [1.05–1.1]. The whole optimization procedure for the proposed HSI-CSR model can be summarized as Algorithm 1, and we abbreviate the proposed method as NTSRLR.
| Algorithm 1. HSI-CSR based NTSRLR. |
| Input: The compressive measurements y, measurement operator , and the parameters of the algorithm. |
| 1: Initialization: Initializing an HSI via a standard CSR method (e.g., DCT based CSR). |
| 2: Fordo |
| 3: Extract the set of tensor from via k-NN search the each exemplar cube; |
| 4: For do |
| 5: Solve the problem (12) by ADMM; |
| 6: Updating by via Equation (14); |
| 7: Updating via Equation (16); |
| 8: Updating via Equation (20); |
| 9: Updating the multipliers via Equation (23); |
| 10: End for |
| 11: Updating via Equation (22); |
| 12: Updating the multiplier via Equation (23); |
| 13: End for |
| Output: CS Reconstructed HSI . |
4. Experimential Results and Analysis
4.1. Quantitative Metrics
4.2. Experiments on Noiseless HSI Datasets
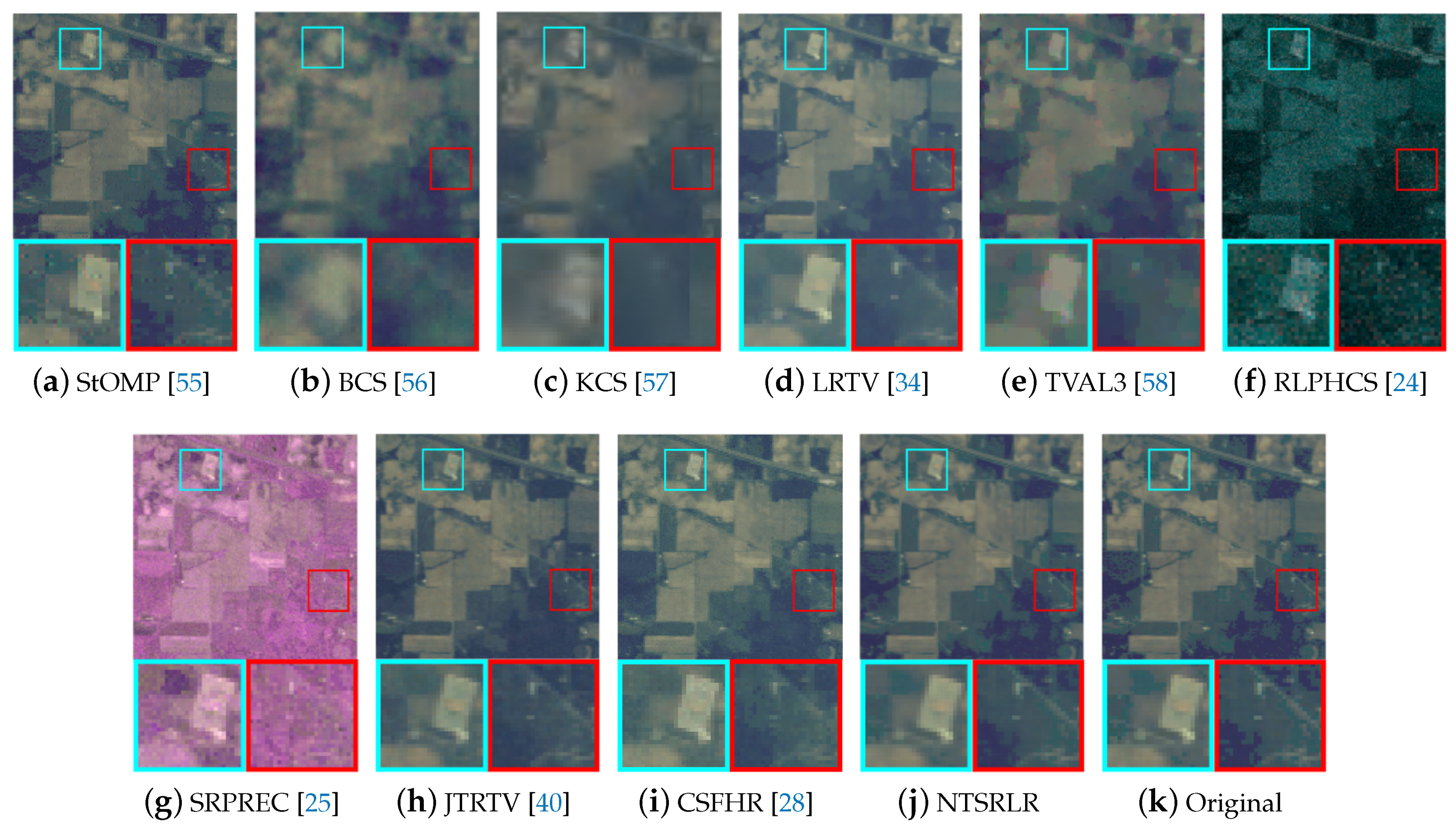
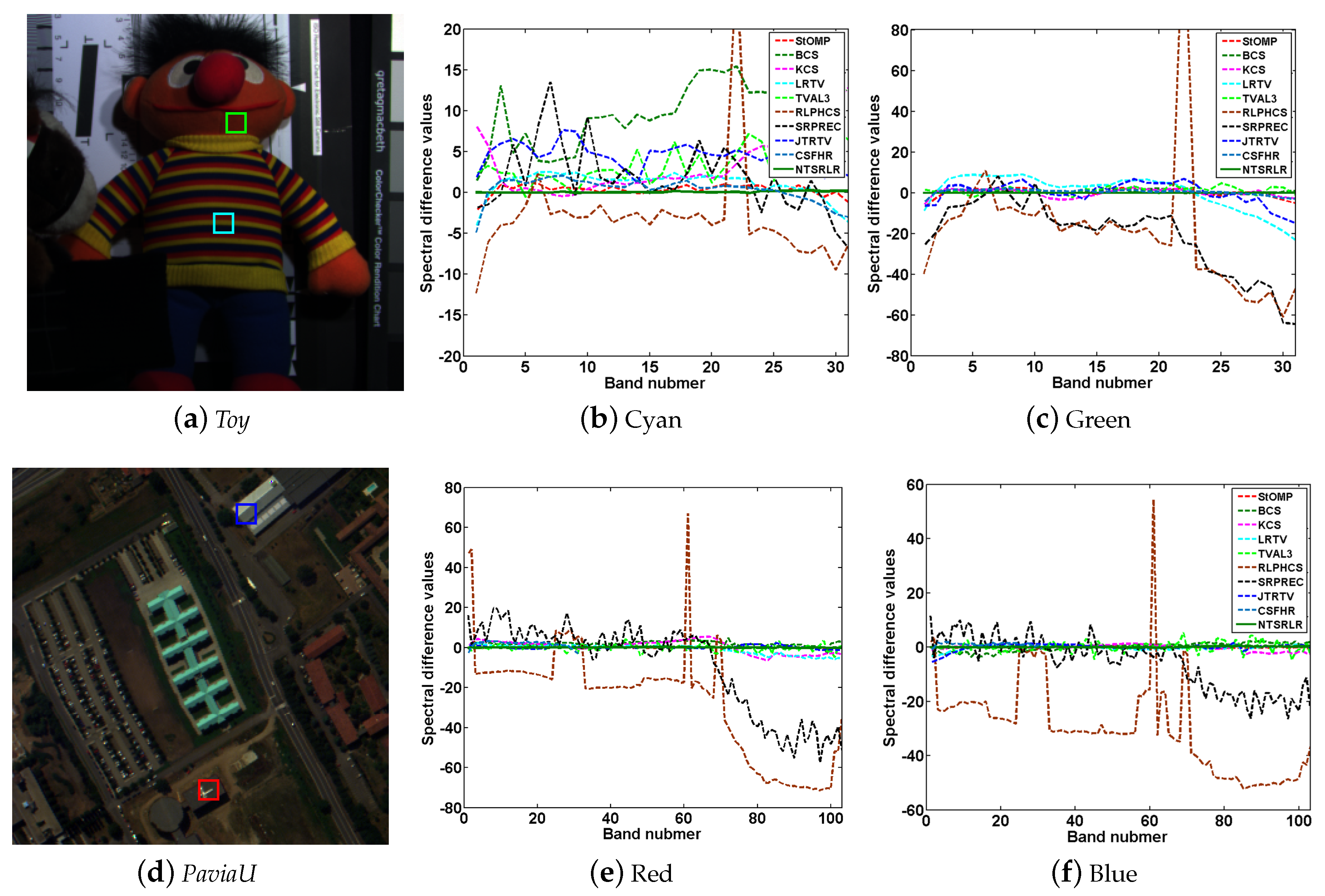
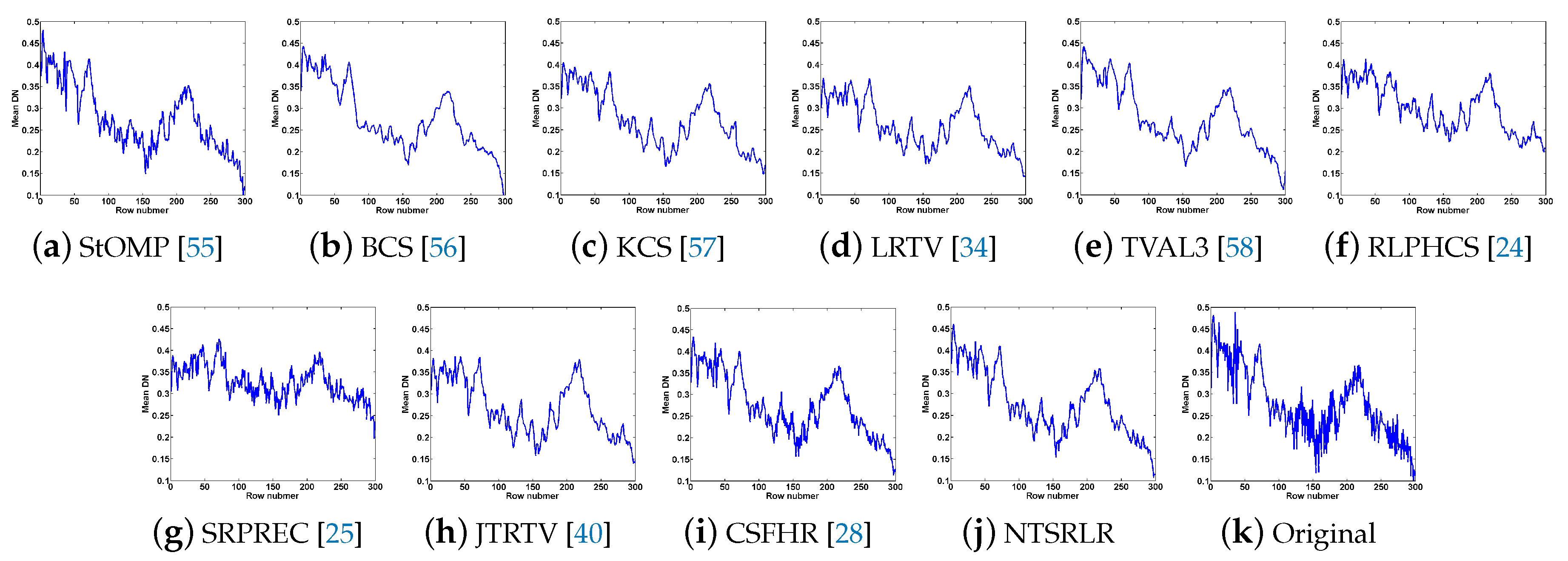
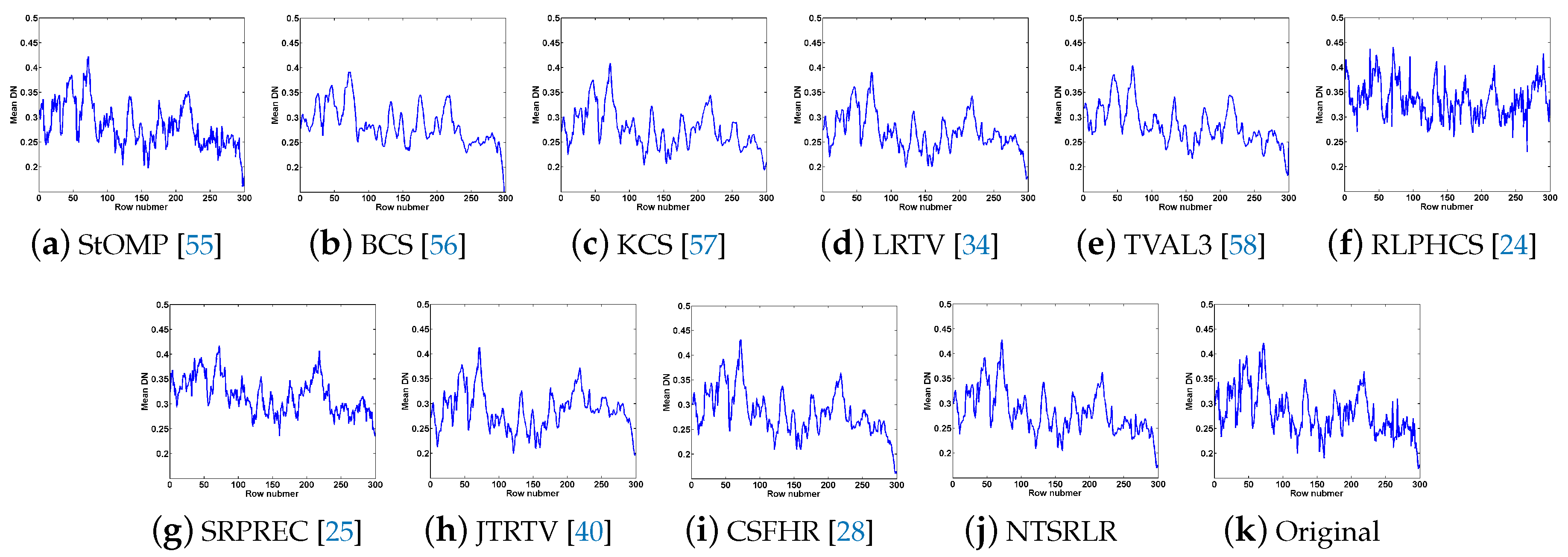
4.2.1. Visual Quality Evaluation
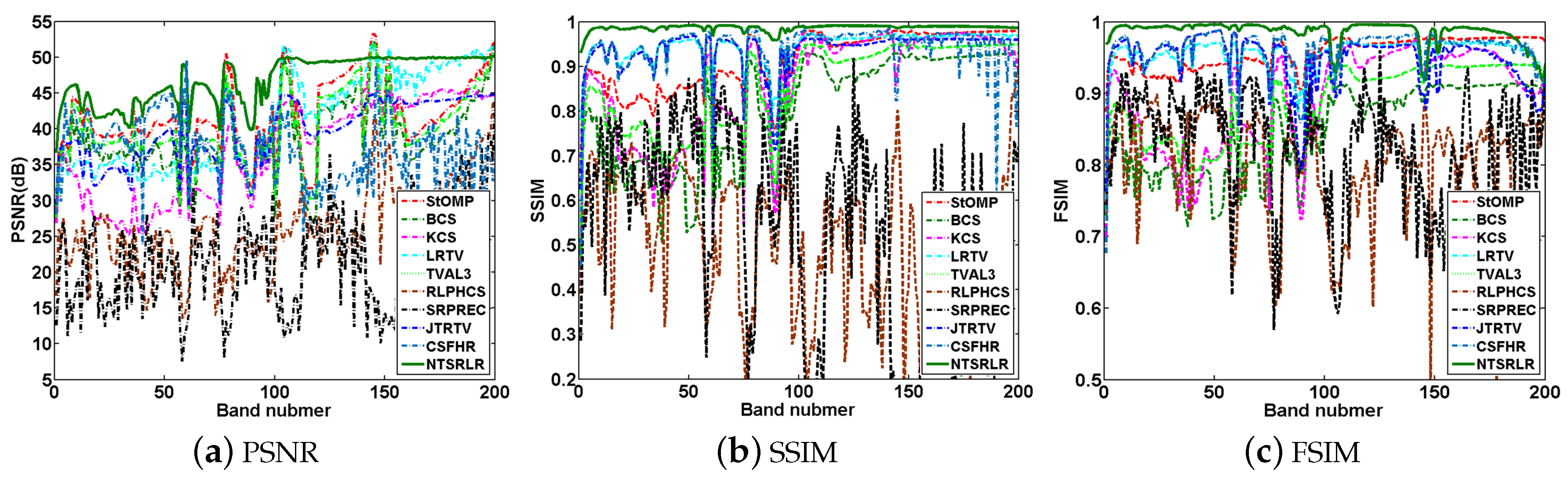
4.2.2. Quantitative Evaluation
4.2.3. Classification Performance on Indian Pines Dataset
4.3. Robustness for Noise Suppression during HSI-CSR
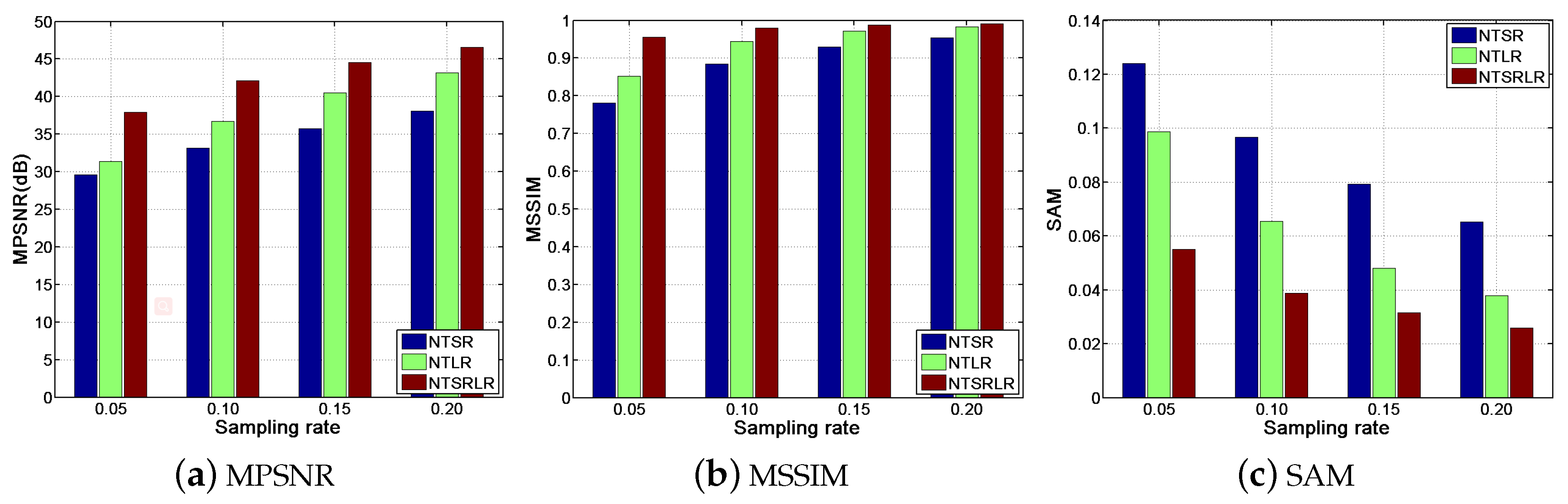
4.4. Effectiveness Analysis of Single NTSR or NTLR Constraint
4.5. Computational Complexity Analysis
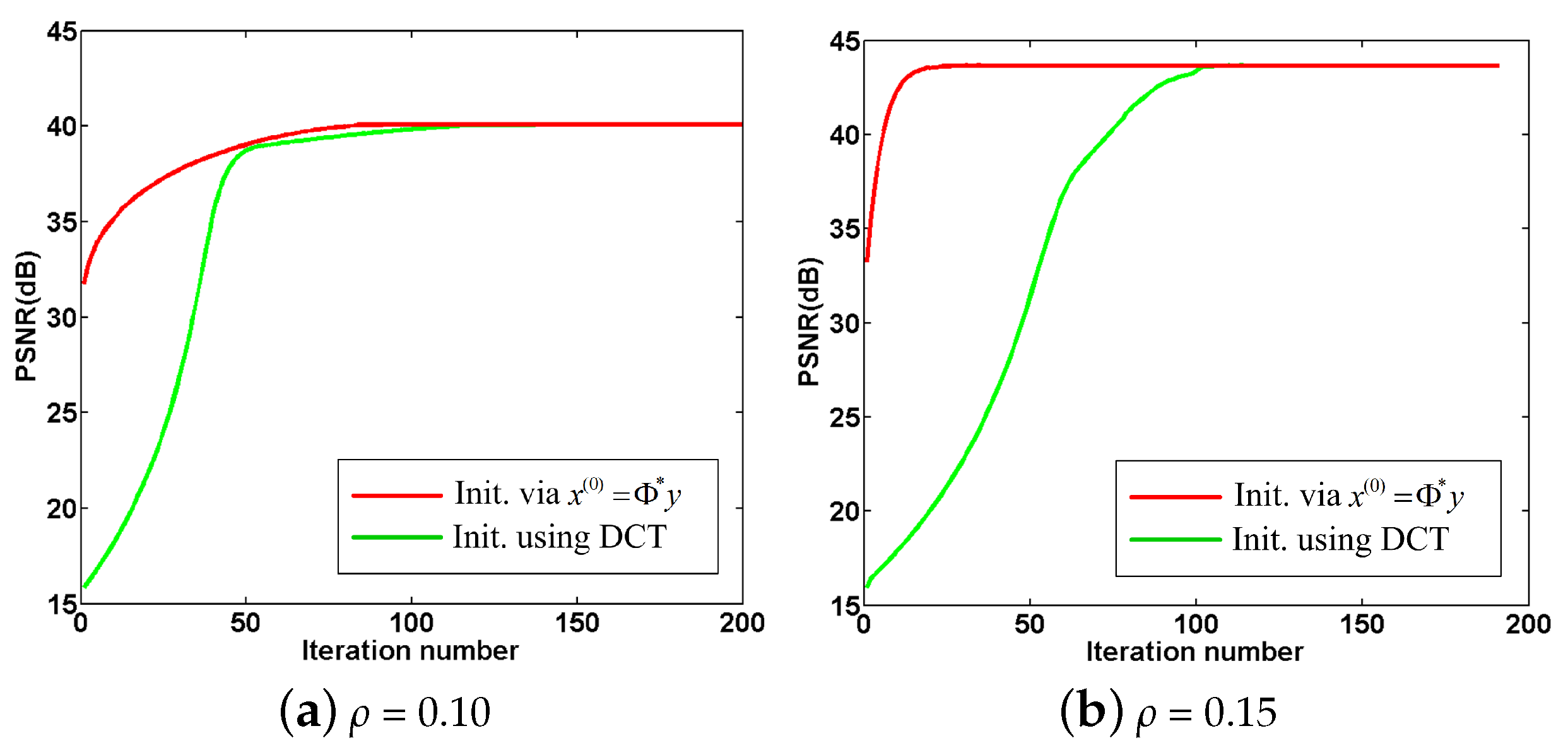
4.6. Convergence Analysis
4.7. Parameters Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, J.; Zhao, Y.; Chan, J.C.-W. Learning and transferring deep joint spectral—Spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral image classification via multitask joint sparse representation and stepwise MRF optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, Z.; Zhang, G.; Chen, Y.; Li, S.; Hong, Y.; Shi, T.; Wang, J.; Liu, Y. Application of Spectrally Derived Soil Type as Ancillary Data to Improve the Estimation of Soil Organic Carbon by Using the Chinese Soil Vis-NIR Spectral Library. Remote Sens. 2018, 10, 1747. [Google Scholar] [CrossRef]
- Khelifi, F.; Bouridane, A.; Kurugollu, F. Joined spectral trees for scalable spiht-based multispectral image compression. IEEE Trans. Multimed. 2008, 10, 316–329. [Google Scholar] [CrossRef]
- Christophe, E.; Mailhes, C.; Duhamel, P. Hyperspectral image compression: Adapting spiht and ezw to anisotropic 3-d wavelet coding. IEEE Trans. Image Process. 2008, 17, 2334–2346. [Google Scholar] [CrossRef] [PubMed]
- Töreyın, B.U.; Yilmaz, O.; Mert, Y.M.; Türk, F. Lossless hyperspectral image compression using wavelet transform based spectral decorrelation. In Proceedings of the IEEE 7th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 16–19 June 2015; pp. 251–254. [Google Scholar]
- Wang, L.; Wu, J.; Jiao, L.; Shi, G. Lossy-to-lossless hyperspectral image compression based on multiplierless reversible integer TDLT/KLT. IEEE Geosci. Remote Sens. Lett. 2009, 6, 587–591. [Google Scholar] [CrossRef]
- Mielikainen, J.; Toivanen, P. Clustered DPCM for the lossless compression of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2943–2946. [Google Scholar] [CrossRef]
- Du, Q.; Fowler, J.E. Hyperspectral image compression using JPEG2000 and principal component analysis. IEEE Geosci. Remote Sens. Lett. 2007, 4, 201–205. [Google Scholar] [CrossRef]
- Du, Q.; Ly, N.; Fowler, J.E. An operational approach to PCA+JPEG2000 compression of hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2237–2245. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Boufounos, D.; Liu, D.; Boufounos, P.T. A lecture on compressive sensing. IEEE Signal Process. Mag. 2007, 24, 1–9. [Google Scholar]
- Huang, J.; Zhang, T.; Metaxas, D. Learning with structured sparsity. J. Mach. Learn. Res. 2011, 12, 3371–3412. [Google Scholar]
- Tan, M.; Tsang, I.W.; Wang, L. Matching pursuit LASSO part I: Sparse recovery over big dictionary. IEEE Trans. Signal Process. 2015, 63, 727–741. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iterative Reweighted Algorithms for Compressive Sensing. In Proceedings of the IEEE International Conference on Acoust. Speech Signal Process, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3869–3872. [Google Scholar]
- Dong, W.; Wu, X.; Shi, G. Sparsity fine tuning in wavelet domain with application to compressive image reconstruction. IEEE Trans. Image Process. 2014, 23, 5249–5262. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X.; Ma, Y.; Huang, F. Compressive sensing via nonlocal low-rank regularization. IEEE Trans. Image Process. 2014, 23, 3618–3632. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Li, X.; Zhang, L.; Shi, G. Sparsity-based image denoising via dictionary learning and structural clustering. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 457–464. [Google Scholar]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar]
- Zhang, L.; Wei, W.; Zhang, Y.; Yan, H.; Li, F.; Tian, C. Locally similar sparsity-based hyperspectral compressive sensing using unmixing. IEEE Trans. Comput. Imaging 2016, 2, 86–100. [Google Scholar] [CrossRef]
- Wang, L.; Feng, Y.; Gao, Y.; Wang, Z.; He, M. Compressed sensing reconstruction of hyperspectral images based on spectral unmixing. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2018, 11, 1266–1284. [Google Scholar] [CrossRef]
- Li, C.; Sun, T.; Kelly, K.F.; Zhang, Y. A compressive sensing and unmixing scheme for hyperspectral data processing. IEEE Trans. Image Process. 2012, 21, 1200–1210. [Google Scholar]
- Zhang, L.; Wei, W.; Tian, C.; Li, F.; Zhang, Y. Exploring structured sparsity by a reweighted laplace prior for hyperspectral compressive sensing. IEEE Trans. Image Process. 2016, 25, 4974–4988. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Zhang, Y.; Shen, C.; Hengel, A.V.D.; Shi, Q. Dictionary learning for promoting structured sparsity in hyperspectral compressive sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7223–7235. [Google Scholar] [CrossRef]
- Fu, W.; Li, S.; Fang, L.; Benediktsson, J.A. Adaptive spectral—Spatial compression of hyperspectral image with sparse representation. IEEE Trans. Geosc. Remote Sens. 2017, 55, 671–682. [Google Scholar] [CrossRef]
- Lin, X.; Liu, Y.; Wu, J.; Dai, Q. Spatial-spectral encoded compressive hyperspectral imaging. ACM Trans. Graphics (TOG) 2014, 33, 233. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, W.; Zhang, Y.; Shen, C.; Hengel, A.V.D.; Shi, Q. Cluster sparsity field: An internal hyperspectral imagery prior for reconstruction. Int. J. Comput. Vis. 2015, 11, 1–25. [Google Scholar] [CrossRef]
- Meza, P.; Ortiz, I.; Vera, E.; Martinez, J. Compressive hyperspectral imaging recovery by spatial-spectral non-local means regularization. Opt. Express 2018, 26, 7043–7055. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Huang, Y.; Lu, K.; Wang, L. Nonlocal low-rank-based compressed sensing for remote sensing image reconstruction. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1557–1561. [Google Scholar] [CrossRef]
- Khan, Z.; Shafait, F.; Mian, A. Joint group sparse pca for compressed hyperspectral imaging. IEEE Trans. Image Process. 2015, 24, 4934–4942. [Google Scholar] [CrossRef] [PubMed]
- Eason, D.T.; Andrews, M. Total variation regularization via continuation to recover compressed hyperspectral images. IEEE Trans. Image Process. 2015, 24, 284–293. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Luo, Z. Weighted total variation iterative reconstruction for hyperspectral pushbroom compressive imaging. J. Image Process. Theory Appl. 2016, 1, 6–10. [Google Scholar]
- Golbabaee, M.; Vandergheynst, P. Joint trace/TV norm minimization: A new efficient approach for spectral compressive imaging. In Proceedings of the 19th IEEE International Conference on Image Processing (ICIP), Orlando, FL, USA, 30 September–3 October 2012; pp. 933–936. [Google Scholar]
- Karami, A.; Yazdi, M.; Mercier, G. Compression of hyperspectral images using discerete wavelet transform and Tucker decomposition. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 444–450. [Google Scholar] [CrossRef]
- Wang, L.; Bai, J.; Wu, J.; Jeon, G. Hyperspectral image compression based on lapped transform and Tucker decomposition. Signal Process. Image Commun. 2015, 36, 63–69. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Compression of hyperspectral remote sensing images by tensor approach. Neurocomputing 2015, 147, 358–363. [Google Scholar] [CrossRef]
- Fang, L.; He, N.; Lin, H. CP tensor-based compression of hyperspectral images. J. Opt. Image Sci. Vis. 2017, 34, 252. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Wang, M.; Li, P.; Jin, L.; Wu, B.; Jiao, L. Compressive hyperspectral imaging via sparse tensor and nonlinear compressed sensing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5943–5957. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, L.; Zhao, Q.; Yue, T.; Meng, D.; Leung, Y. Compressive sensing of hyperspectral images via joint tensor tucker decomposition and weighted total variation regularization. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2457–2461. [Google Scholar] [CrossRef]
- Du, B.; Zhang, M.; Zhang, L.; Hu, R.; Tao, D. PLTD: Patch-based low-rank tensor decomposition for hyperspectral images. IEEE Trans. Multimed. 2016, 19, 67–79. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, Q.; Meng, D.; Xu, Z.; Gu, S.; Zuo, W.; Zhang, L. Multispectral images denoising by intrinsic tensor sparsity regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1692–1700. [Google Scholar]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Hao, J. Tensor non-local low-rank regularization for recovering compressed hyperspectral images. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3046–3050. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Schwab, H. For most large underdetermined systems of linear equations the minimal l1 solution is also the sparsest solution. Commun. Pur Appl. Math. 2006, 59, 797–829. [Google Scholar]
- Daubechies, I.; Defrise, M.; Mol, C.D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Zhang, X.; Burger, M.; Bresson, X.; Osher, S. Bregmanized nonlocal regularization for deconvolution and sparse reconstruction. SIAM J. Imag. Sci. 2010, 3, 253–276. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Kong, S.G. Joint spatial and spectral low-rank regularization for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1940–1958. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Quan, Y.; Huang, Y.; Ji, H. Dynamic texture recognition via orthogonal tensor dictionary learning. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 73–81. [Google Scholar]
- Qi, N.; Shi, Y.; Sun, X.; Yin, B. Tensor: Multi-dimensional tensor sparse representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5916–5925. [Google Scholar]
- Qi, N.; Shi, Y.; Sun, X.; Wang, J.; Yin, B.; Gao, J. Multi-dimensional sparse models. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 163–178. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y.; Drori, I.; Starck, J.L. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit. IEEE Trans. Inf. Theory 2012, 58, 1094–1121. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Duarte, M.F.; Baraniuk, R.G. Kronecker compressive sensing. IEEE Trans. Image Process. 2012, 21, 494–504. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Jiang, H.; Zhang, Y. An efficient augmented lagrangian method with applications to total variation minimization. Comput. Optim. Appl. 2013, 56, 507–530. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. Fsim: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef]
- Wald, L. Data Fusion: Definitions and Architectures: Fusion of Images of Different Spatial Resolutions; Presses des MINES: Paris, France, 2002. [Google Scholar]
- Yuhas, R.H.; Boardman, J.W.; Goetz, A.F. Determination of semi-arid landscape endmembers and seasonal trends using convex geometry spectral unmixing techniques. In Summaries of the 4th Annual JPL Airborne Geoscience Workshop; NASA: Washington, DC, USA, 1993; Volume 4, pp. 205–208. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]





| SRs | PQIs | Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| StOMP | BCS | KCS | LRTV | TVAL3 | RLPHCS | SRPREC | JTRTV | CSFHR | NTSRLR | ||
| [55] | [56] | [57] | [34] | [58] | [24] | [25] | [40] | [28] | |||
| Results on Toy | |||||||||||
| 0.02 | MPSNR | 25.27 | 18.45 | 23.39 | 22.08 | 22.91 | 13.19 | 14.40 | 17.19 | 25.87 | 27.81 |
| MSSIM | 0.7040 | 0.3499 | 0.6565 | 0.6651 | 0.6364 | 0.2089 | 0.2786 | 0.1601 | 0.6639 | 0.7322 | |
| MFSIM | 0.8044 | 0.6937 | 0.7820 | 0.8061 | 0.7397 | 0.6651 | 0.6272 | 0.5033 | 0.8389 | 0.8484 | |
| 0.05 | MPSNR | 29.35 | 24.63 | 26.93 | 26.51 | 27.63 | 13.22 | 13.89 | 22.65 | 29.96 | 34.22 |
| MSSIM | 0.8256 | 0.6672 | 0.7811 | 0.7873 | 0.7817 | 0.2372 | 0.1929 | 0.3374 | 0.7462 | 0.8930 | |
| MFSIM | 0.9189 | 0.7837 | 0.8523 | 0.8783 | 0.8273 | 0.6493 | 0.5480 | 0.6233 | 0.8845 | 0.9423 | |
| 0.10 | MPSNR | 29.71 | 28.24 | 29.94 | 32.06 | 31.81 | 13.06 | 15.92 | 29.93 | 32.35 | 40.12 |
| MSSIM | 0.8416 | 0.8072 | 0.8641 | 0.9233 | 0.8871 | 0.2034 | 0.1267 | 0.6860 | 0.8418 | 0.9640 | |
| MFSIM | 0.9261 | 0.8563 | 0.8987 | 0.9517 | 0.9052 | 0.6163 | 0.4505 | 0.8466 | 0.9255 | 0.9814 | |
| 0.15 | MPSNR | 30.90 | 29.40 | 31.88 | 34.99 | 33.46 | 13.69 | 27.79 | 31.47 | 34.99 | 44.52 |
| MSSIM | 0.8982 | 0.8429 | 0.9025 | 0.9427 | 0.9141 | 0.1993 | 0.7492 | 0.7673 | 0.8985 | 0.9848 | |
| MFSIM | 0.9485 | 0.8777 | 0.9232 | 0.9669 | 0.9282 | 0.5642 | 0.9082 | 0.8894 | 0.9527 | 0.9928 | |
| 0.20 | MPSNR | 31.75 | 31.63 | 33.26 | 40.54 | 37.65 | 13.71 | 25.74 | 33.39 | 38.53 | 47.86 |
| MSSIM | 0.9345 | 0.8845 | 0.9236 | 0.9808 | 0.9593 | 0.2495 | 0.7384 | 0.8504 | 0.9541 | 0.9925 | |
| MFSIM | 0.9617 | 0.9094 | 0.9375 | 0.9876 | 0.9664 | 0.6182 | 0.8942 | 0.9307 | 0.9785 | 0.9965 | |
| Results on PaviaU | |||||||||||
| 0.02 | MPSNR | 28.11 | 21.74 | 23.79 | 23.08 | 22.99 | 15.18 | 14.84 | 28.04 | 25.11 | 29.83 |
| MSSIM | 0.7603 | 0.4767 | 0.5486 | 0.6500 | 0.5014 | 0.1562 | 0.0990 | 0.6708 | 0.6923 | 0.8000 | |
| MFSIM | 0.8246 | 0.6825 | 0.6743 | 0.7974 | 0.6429 | 0.6808 | 0.5758 | 0.8593 | 0.8095 | 0.8884 | |
| 0.05 | MPSNR | 30.06 | 24.26 | 26.59 | 27.49 | 25.29 | 14.38 | 15.46 | 35.73 | 32.74 | 37.96 |
| MSSIM | 0.8571 | 0.5572 | 0.6783 | 0.8099 | 0.5914 | 0.1698 | 0.1266 | 0.9235 | 0.8756 | 0.9551 | |
| MFSIM | 0.9371 | 0.7379 | 0.7854 | 0.8863 | 0.7132 | 0.7123 | 0.6379 | 0.9666 | 0.9442 | 0.9774 | |
| 0.10 | MPSNR | 30.40 | 26.36 | 29.14 | 32.99 | 27.48 | 15.73 | 16.00 | 37.10 | 34.36 | 42.15 |
| MSSIM | 0.8223 | 0.6479 | 0.7871 | 0.9158 | 0.6907 | 0.1225 | 0.1157 | 0.9452 | 0.9062 | 0.9794 | |
| MFSIM | 0.9409 | 0.7963 | 0.8606 | 0.9479 | 0.7894 | 0.5930 | 0.5461 | 0.9761 | 0.9583 | 0.9905 | |
| 0.15 | MPSNR | 31.59 | 27.08 | 30.85 | 33.81 | 28.33 | 26.46 | 28.29 | 37.39 | 36.77 | 44.55 |
| MSSIM | 0.8707 | 0.6812 | 0.8422 | 0.9417 | 0.7268 | 0.6771 | 0.8567 | 0.9487 | 0.9417 | 0.9872 | |
| MFSIM | 0.9523 | 0.8137 | 0.8981 | 0.9683 | 0.8165 | 0.8738 | 0.9255 | 0.9778 | 0.9741 | 0.9944 | |
| 0.20 | MPSNR | 32.49 | 28.54 | 32.13 | 40.56 | 30.46 | 28.14 | 35.38 | 38.03 | 40.56 | 46.55 |
| MSSIM | 0.9020 | 0.7445 | 0.8745 | 0.9740 | 0.8057 | 0.7328 | 0.9547 | 0.9548 | 0.9705 | 0.9917 | |
| MFSIM | 0.9594 | 0.8518 | 0.9198 | 0.9862 | 0.8745 | 0.8964 | 0.9800 | 0.9807 | 0.9871 | 0.9965 | |
| Results on Indian Pines | |||||||||||
| 0.02 | MPSNR | 30.45 | 33.03 | 31.46 | 22.81 | 30.12 | 19.51 | 23.58 | 30.87 | 30.85 | 33.54 |
| MSSIM | 0.7487 | 0.7692 | 0.7385 | 0.4916 | 0.7839 | 0.2234 | 0.4025 | 0.8010 | 0.8089 | 0.8202 | |
| MFSIM | 0.8299 | 0.8128 | 0.7337 | 0.8421 | 0.8026 | 0.7149 | 0.8327 | 0.8102 | 0.8500 | 0.8775 | |
| 0.05 | MPSNR | 35.70 | 37.23 | 33.71 | 26.77 | 37.28 | 16.44 | 21.01 | 37.07 | 36.86 | 41.15 |
| MSSIM | 0.8693 | 0.8153 | 0.7763 | 0.8057 | 0.8221 | 0.0920 | 0.2944 | 0.9240 | 0.8671 | 0.9470 | |
| MFSIM | 0.8639 | 0.8554 | 0.7983 | 0.8936 | 0.8517 | 0.4714 | 0.8125 | 0.9475 | 0.9210 | 0.9553 | |
| 0.10 | MPSNR | 40.77 | 38.97 | 35.38 | 34.10 | 39.66 | 16.06 | 25.10 | 39.29 | 37.38 | 44.12 |
| MSSIM | 0.9395 | 0.8427 | 0.8165 | 0.9153 | 0.8606 | 0.0614 | 0.5336 | 0.9338 | 0.8798 | 0.9719 | |
| MFSIM | 0.9420 | 0.8867 | 0.8491 | 0.9440 | 0.8919 | 0.3846 | 0.8317 | 0.9472 | 0.9439 | 0.9750 | |
| 0.15 | MPSNR | 43.71 | 39.42 | 36.39 | 34.65 | 40.47 | 19.62 | 24.05 | 39.85 | 39.27 | 45.65 |
| MSSIM | 0.9465 | 0.8478 | 0.8417 | 0.9248 | 0.8743 | 0.4756 | 0.4416 | 0.9354 | 0.9197 | 0.9810 | |
| MFSIM | 0.9794 | 0.8942 | 0.8743 | 0.9496 | 0.9056 | 0.7956 | 0.7804 | 0.9476 | 0.9569 | 0.9818 | |
| 0.20 | MPSNR | 44.92 | 40.72 | 37.12 | 41.66 | 42.36 | 20.95 | 26.07 | 39.67 | 41.81 | 46.96 |
| MSSIM | 0.9350 | 0.8740 | 0.8601 | 0.9670 | 0.9052 | 0.5259 | 0.4957 | 0.9367 | 0.9475 | 0.9863 | |
| MFSIM | 0.9772 | 0.9179 | 0.8907 | 0.9748 | 0.9349 | 0.8216 | 0.7966 | 0.9465 | 0.9706 | 0.9858 | |
| SRs | PQIs | Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| StOMP | BCS | KCS | LRTV | TVAL3 | RLPHCS | SRPREC | JTRTV | CSFHR | NTSRLR | ||
| [55] | [56] | [57] | [34] | [58] | [24] | [25] | [40] | [28] | |||
| Results on Toy | |||||||||||
| 0.02 | SAM | 0.3040 | 0.6548 | 0.3062 | 0.5096 | 0.3888 | 0.9853 | 0.9707 | 0.6599 | 0.4014 | 0.2810 |
| ERGAS | 165.5 | 864.5 | 294.7 | 362.5 | 309.7 | 2411 | 2740 | 582.3 | 178.9 | 154.8 | |
| 0.05 | SAM | 0.2500 | 0.2781 | 0.2351 | 0.3967 | 0.2886 | 0.9633 | 0.9210 | 0.6532 | 0.3401 | 0.2029 |
| ERGAS | 147.8 | 257.3 | 193.9 | 204.3 | 181.9 | 2064 | 2536 | 321.4 | 141.5 | 84.65 | |
| 0.10 | SAM | 0.2318 | 0.1968 | 0.1894 | 0.2162 | 0.2080 | 0.6234 | 0.8382 | 0.4129 | 0.2750 | 0.1031 |
| ERGAS | 141.94 | 170.4 | 136.9 | 107.0 | 113.1 | 1273 | 1853 | 140.3 | 108.1 | 35.92 | |
| 0.15 | SAM | 0.2629 | 0.1654 | 0.1635 | 0.1940 | 0.1828 | 0.4228 | 0.4562 | 0.3582 | 0.2151 | 0.0998 |
| ERGAS | 123.9 | 148.6 | 109.9 | 78.40 | 93.82 | 1262 | 1620 | 118.5 | 79.23 | 28.08 | |
| 0.20 | SAM | 0.1123 | 0.1471 | 0.1478 | 0.1112 | 0.1294 | 0.3866 | 0.4250 | 0.2964 | 0.1599 | 0.0733 |
| ERGAS | 112.5 | 116.1 | 94.29 | 41.20 | 58.60 | 978 | 1305 | 95.77 | 53.85 | 20.86 | |
| Results on PaviaU | |||||||||||
| 0.02 | SAM | 0.1819 | 0.2223 | 0.1931 | 0.1576 | 0.2460 | 0.9542 | 0.9950 | 0.1722 | 0.1248 | 0.1128 |
| ERGAS | 137.8 | 345.6 | 264.4 | 329.0 | 284.3 | 2537 | 3585 | 156.7 | 153.8 | 125.8 | |
| 0.05 | SAM | 0.1542 | 0.1749 | 0.1512 | 0.1347 | 0.2021 | 0.8849 | 0.9646 | 0.0817 | 0.1019 | 0.0550 |
| ERGAS | 123.4 | 245.2 | 187.6 | 153.2 | 213.4 | 2079 | 2997 | 67.56 | 96.19 | 50.98 | |
| 0.10 | SAM | 0.1447 | 0.1417 | 0.121 | 0.0862 | 0.1701 | 0.7069 | 0.8168 | 0.0725 | 0.0905 | 0.0389 |
| ERGAS | 118.7 | 188.0 | 138.7 | 90.35 | 165.2 | 1858 | 2425 | 58.58 | 80.19 | 32.53 | |
| 0.15 | SAM | 0.1116 | 0.1326 | 0.1059 | 0.0708 | 0.1596 | 0.2914 | 0.2368 | 0.0708 | 0.0728 | 0.0315 |
| ERGAS | 103.6 | 173.3 | 113.96 | 77.17 | 149.8 | 1247 | 1921 | 56.68 | 61.15 | 24.90 | |
| 0.20 | SAM | 0.0858 | 0.1178 | 0.0957 | 0.0462 | 0.1359 | 0.2407 | 0.0836 | 0.0674 | 0.0521 | 0.0260 |
| ERGAS | 93.40 | 146.2 | 98.66 | 38.73 | 117.7 | 1231 | 1427 | 52.63 | 41.26 | 19.74 | |
| Results on Indian Pines | |||||||||||
| 0.02 | SAM | 0.1511 | 0.1622 | 0.1383 | 0.2774 | 0.1246 | 0.9166 | 0.9476 | 0.1075 | 0.1087 | 0.0821 |
| ERGAS | 143.2 | 161.8 | 138.6 | 759.7 | 126.5 | 1723 | 2297 | 129.7 | 198.7 | 116.0 | |
| 0.05 | SAM | 0.1447 | 0.0830 | 0.1063 | 0.0832 | 0.0911 | 0.5668 | 0.8286 | 0.0553 | 0.0723 | 0.0382 |
| ERGAS | 89.48 | 88.69 | 119.2 | 233.2 | 87.85 | 1558 | 1988 | 64.84 | 152.6 | 49.62 | |
| 0.10 | SAM | 0.0434 | 0.0728 | 0.0888 | 0.0587 | 0.0743 | 0.4821 | 0.6523 | 0.0515 | 0.0659 | 0.0282 |
| ERGAS | 38.77 | 74.77 | 96.91 | 43.08 | 68.53 | 1078 | 1323 | 58.37 | 127.4 | 35.96 | |
| 0.15 | SAM | 0.0365 | 0.0714 | 0.0799 | 0.0498 | 0.0693 | 0.3914 | 0.4663 | 0.0505 | 0.0549 | 0.0229 |
| ERGAS | 34.98 | 72.32 | 86.24 | 37.45 | 62.99 | 917 | 1258 | 56.15 | 78.07 | 30.81 | |
| 0.20 | SAM | 0.0295 | 0.0622 | 0.0741 | 0.0344 | 0.0586 | 0.2749 | 0.4590 | 0.0481 | 0.0553 | 0.0190 |
| ERGAS | 31.39 | 61.87 | 79.43 | 33.59 | 51.61 | 366 | 982 | 50.78 | 59.69 | 27.19 | |
| SRs | StOMP | BCS | KCS | LRTV | TVAL3 | RLPHCS | SRPREC | JTRTV | CSFHR | NTSRLR | Original |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [55] | [56] | [57] | [34] | [58] | [24] | [25] | [40] | [28] | |||
| 0.02 | 71.19% | 50.64% | 52.37% | 60.96% | 51.85% | 29.61% | 10.51% | 20.03% | 53.21% | 73.69% | 86.37% |
| 0.05 | 75.70% | 57.83% | 56.18% | 69.64% | 57.83% | 36.66% | 13.32% | 54.47% | 59.17% | 77.32% | |
| 0.10 | 76.32% | 59.01% | 62.01% | 71.24% | 60.92% | 41.82% | 14.62% | 55.66% | 62.98% | 79.31% | |
| 0.15 | 78.41% | 63.80% | 65.80% | 77.03% | 62.70% | 45.53% | 45.53% | 56.84% | 65.24% | 80.26% | |
| 0.20 | 80.28% | 68.73% | 70.73% | 79.19% | 65.73% | 46.57% | 57.83% | 58.13% | 67.70% | 81.79% |
| SRs | PQIs | Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| StOMP | BCS | KCS | LRTV | TVAL3 | RLPHCS | SRPREC | JTRTV | CSFHR | NTSRLR | ||
| [55] | [56] | [57] | [34] | [58] | [24] | [25] | [40] | [28] | |||
| 0.10 | MPSNR | 19.63 | 16.95 | 23.63 | 24.76 | 17.79 | 22.04 | 15.13 | 27.74 | 26.76 | 30.88 |
| MSSIM | 0.6523 | 0.4147 | 0.8152 | 0.8705 | 0.4423 | 0.8155 | 0.4245 | 0.8959 | 0.8933 | 0.9471 | |
| MFSIM | 0.8841 | 0.6918 | 0.8916 | 0.9277 | 0.6562 | 0.9088 | 0.7711 | 0.9561 | 0.9279 | 0.9746 | |
| ERGAS | 280.2 | 380.4 | 184.2 | 159.6 | 346.3 | 261.6 | 480.9 | 111.5 | 109.8 | 76.89 | |
| SAM | 0.2884 | 0.2157 | 0.1551 | 0.1197 | 0.2644 | 0.2737 | 0.4775 | 0.1196 | 0.1252 | 0.0682 | |
| 0.15 | MPSNR | 20.61 | 17.45 | 25.78 | 26.40 | 18.48 | 24.16 | 20.94 | 27.94 | 28.27 | 33.51 |
| MSSIM | 0.7088 | 0.4546 | 0.8740 | 0.9134 | 0.4924 | 0.8442 | 0.8306 | 0.8992 | 0.9064 | 0.9662 | |
| MFSIM | 0.8972 | 0.7138 | 0.9242 | 0.9575 | 0.6946 | 0.9284 | 0.9016 | 0.9580 | 0.9582 | 0.9845 | |
| ERGAS | 250.4 | 359.7 | 145.4 | 122.9 | 320.0 | 202.4 | 296.3 | 108.9 | 91.23 | 56.89 | |
| SAM | 0.2461 | 0.2076 | 0.1310 | 0.1024 | 0.2518 | 0.2202 | 0.2885 | 0.1180 | 0.1075 | 0.0564 | |
| 0.20 | MPSNR | 20.93 | 18.72 | 27.37 | 33.26 | 20.35 | 25.99 | 25.24 | 28.40 | 30.11 | 35.62 |
| MSSIM | 0.7274 | 0.5509 | 0.9051 | 0.9664 | 0.6133 | 0.8583 | 0.9034 | 0.9040 | 0.9275 | 0.9762 | |
| MFSIM | 0.9011 | 0.7645 | 0.9418 | 0.9840 | 0.7810 | 0.9459 | 0.9445 | 0.9608 | 0.9705 | 0.9896 | |
| ERGAS | 241.4 | 310.8 | 122.3 | 59.45 | 259.0 | 165.8 | 183.7 | 103.1 | 67.60 | 44.66 | |
| SAM | 0.2323 | 0.1879 | 0.1156 | 0.0592 | 0.2207 | 0.1831 | 0.1859 | 0.1149 | 0.0828 | 0.0481 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.-W. Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sens. 2019, 11, 193. https://doi.org/10.3390/rs11020193
Xue J, Zhao Y, Liao W, Chan JC-W. Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sensing. 2019; 11(2):193. https://doi.org/10.3390/rs11020193
Chicago/Turabian StyleXue, Jize, Yongqiang Zhao, Wenzhi Liao, and Jonathan Cheung-Wai Chan. 2019. "Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction" Remote Sensing 11, no. 2: 193. https://doi.org/10.3390/rs11020193
APA StyleXue, J., Zhao, Y., Liao, W., & Chan, J. C.-W. (2019). Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sensing, 11(2), 193. https://doi.org/10.3390/rs11020193






