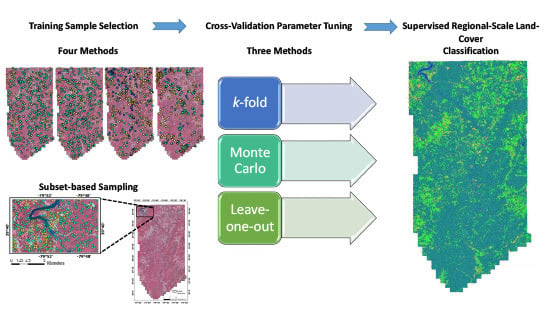
Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification
Abstract
1. Introduction
1.1. Background on Sample Selection in Remote Sensing
1.2. Background on Cross-Validation Tuning
1.3. Research Questions and Aims
- Which training sample selection method results in the highest classification accuracy for a supervised support vector machine (SVM) classification of a regional-scale HR remotely sensed dataset? The methods tested include both statistical (simple random, proportional stratified random, and disproportional stratified random) and non-statistical (deliberative) methods.
- Which cross-validation method provides the highest classification accuracy? Methods tested are k-fold, leave-one-out, and Monte Carlo.
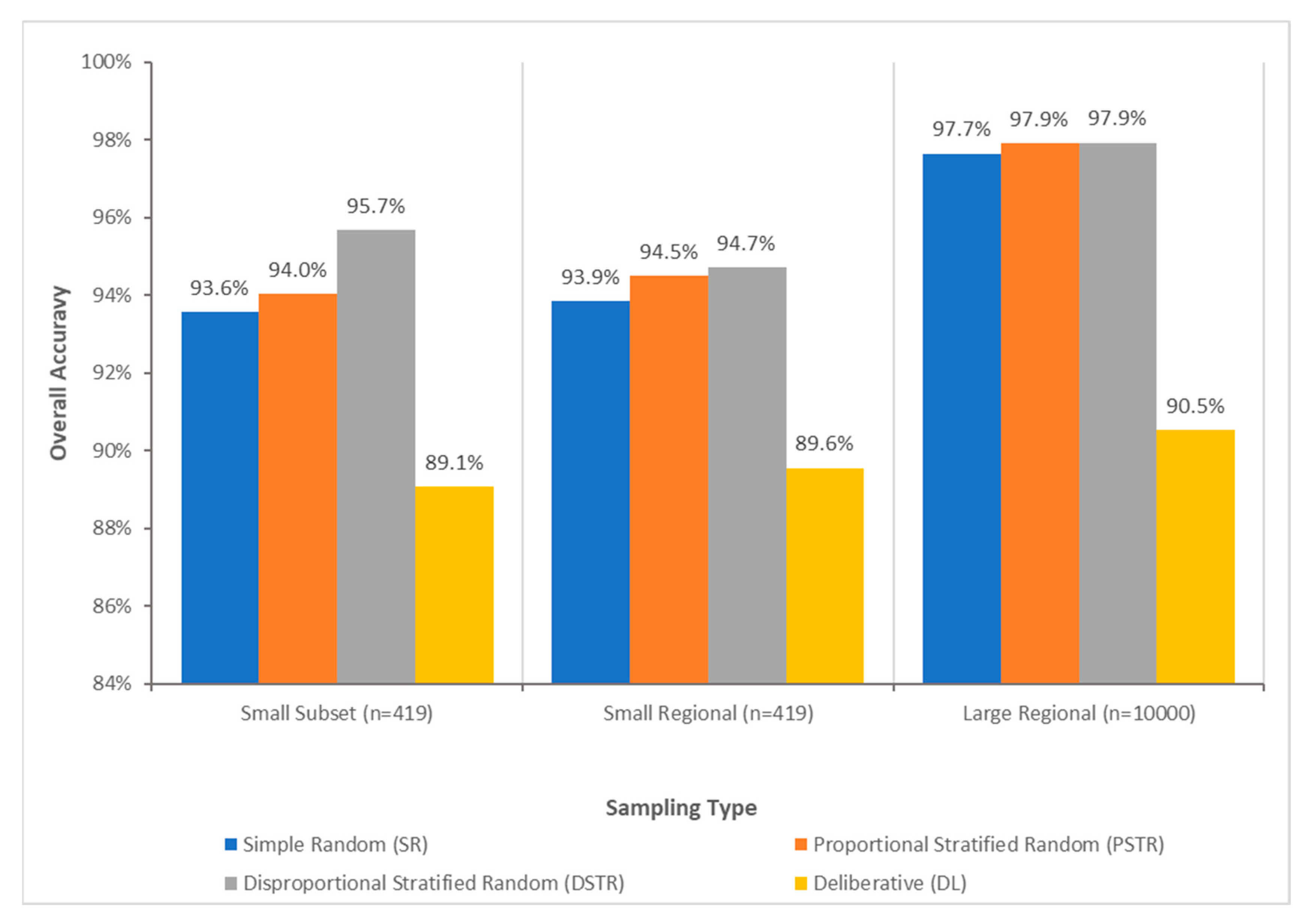
- What is the effect on classification accuracy for the different sampling and cross-validation methods when the samples are collected from a small localized region rather than from across the entire study area?
2. Materials and Methods
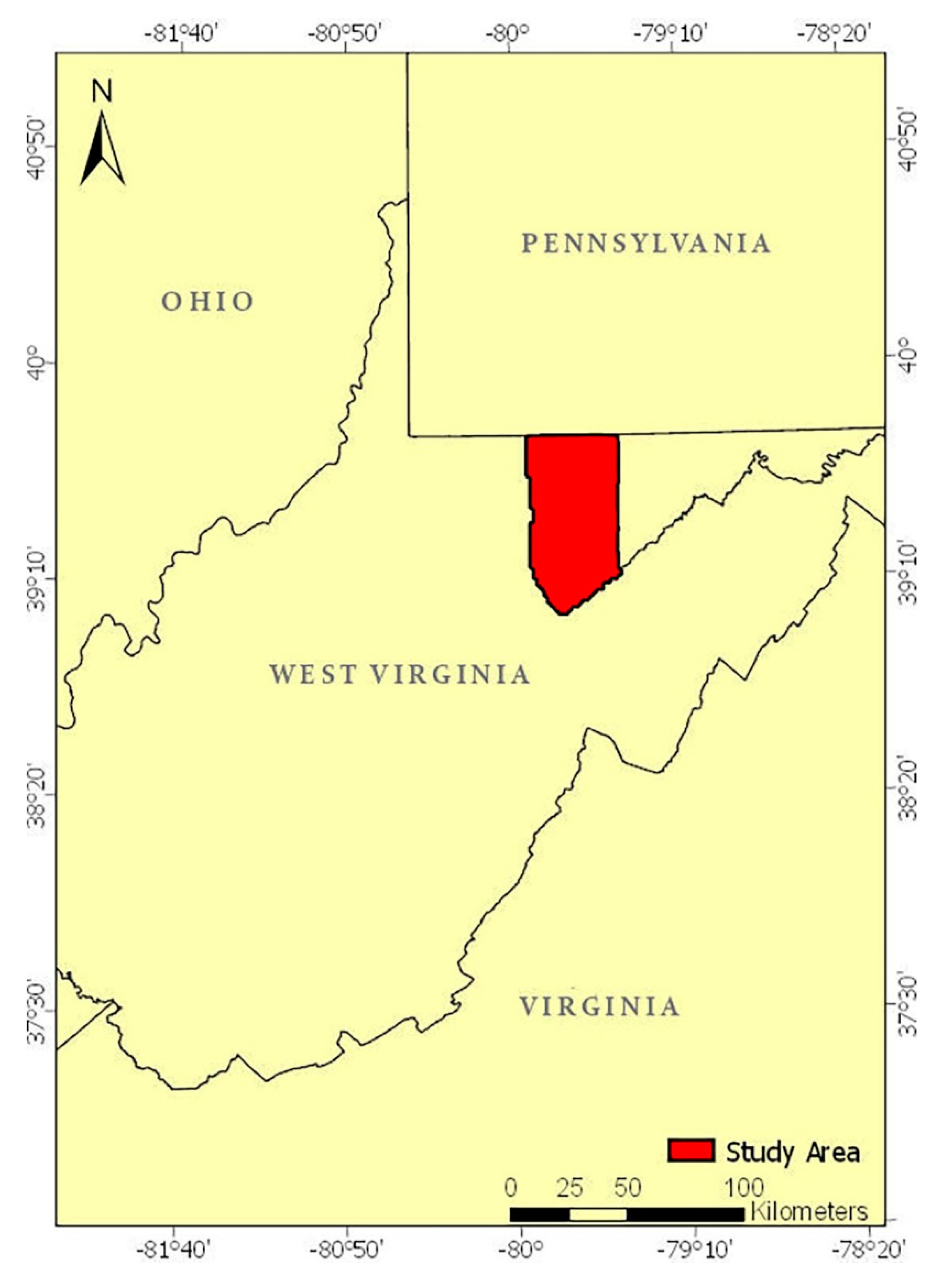
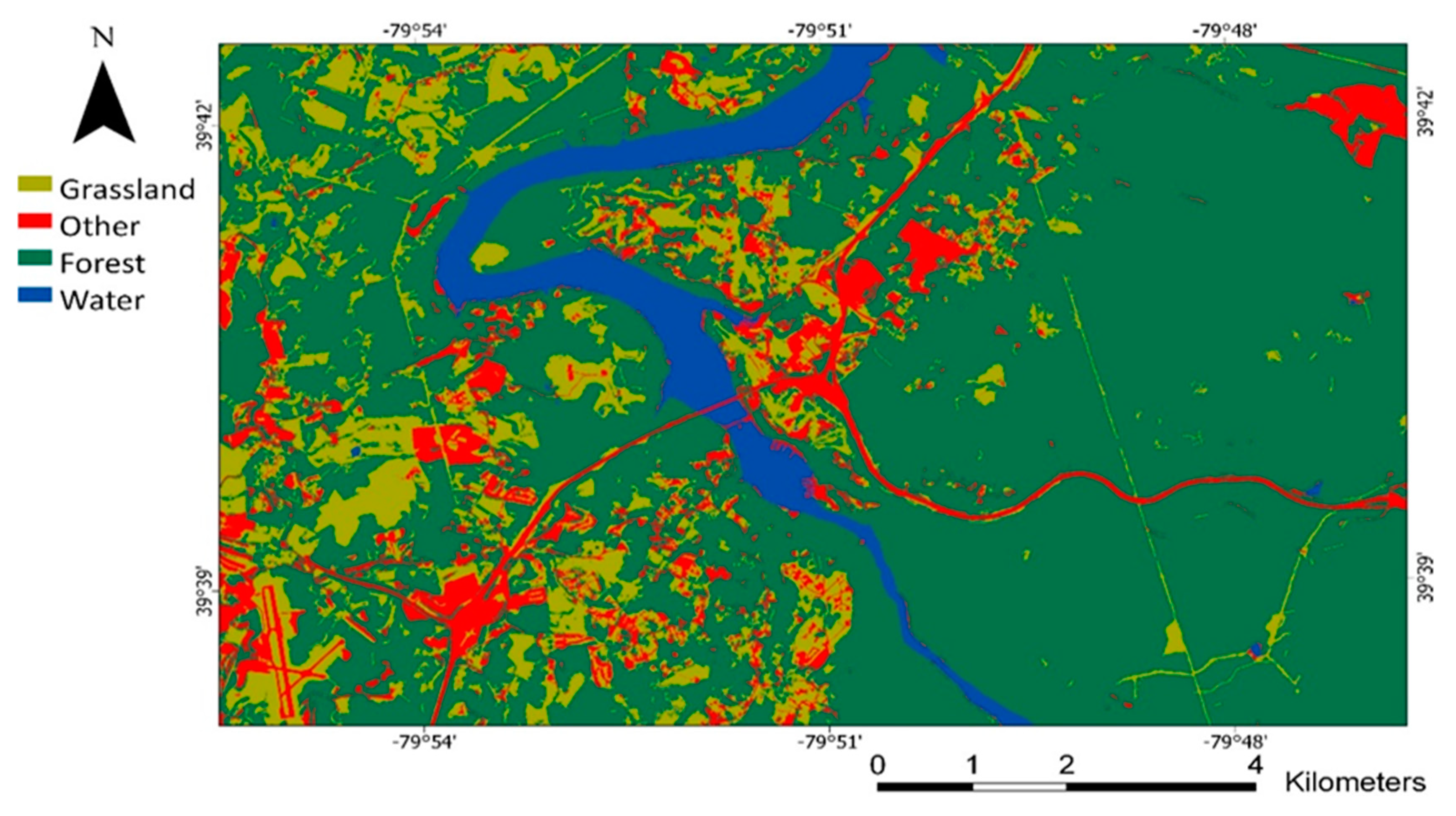
2.1. Study Area and Data
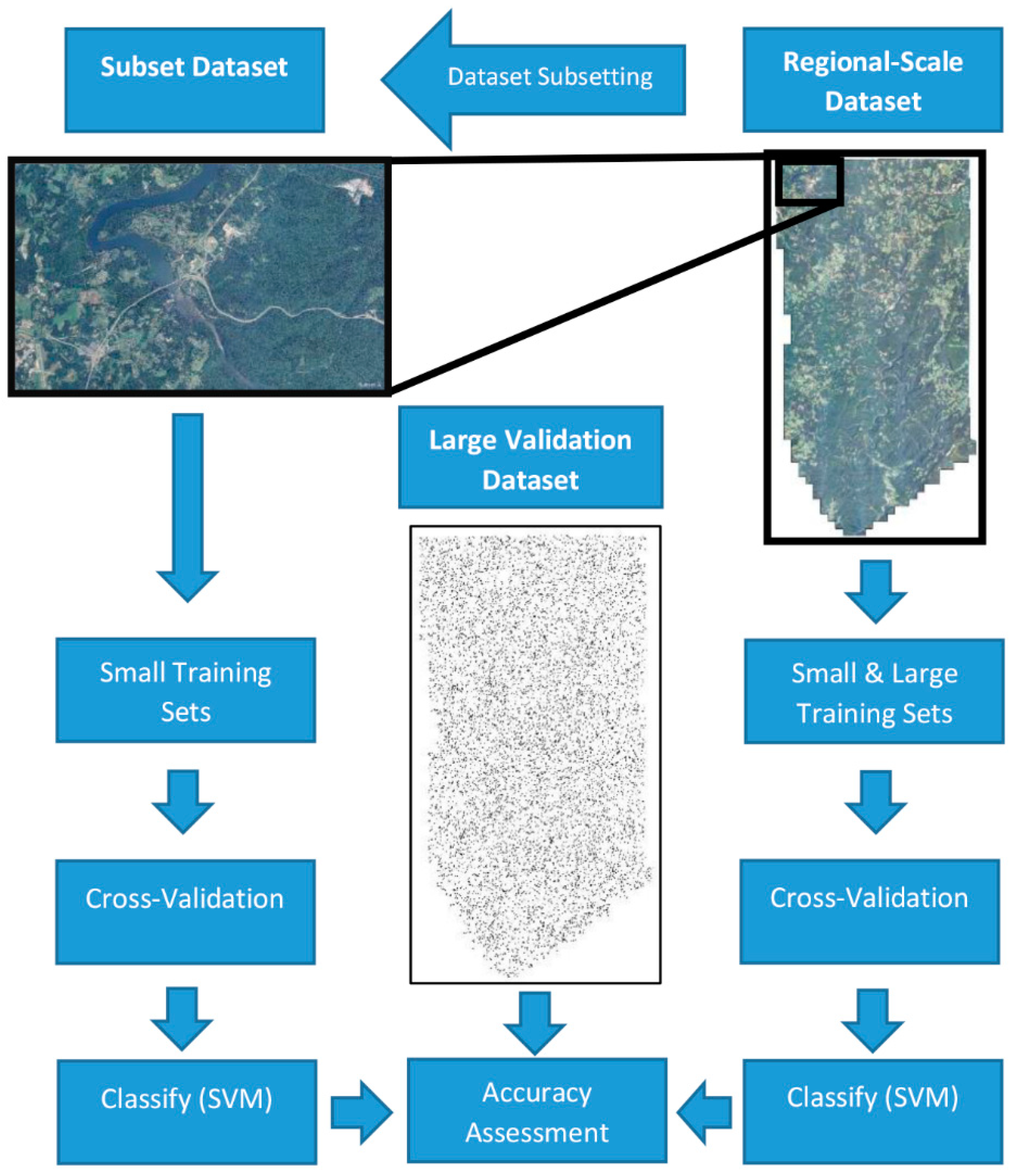
2.2. Experimental Design
2.3. Data Processing
2.4. Image Segmentation
2.5. Dataset Subsetting
2.6. Segment Attributes Used for Classification
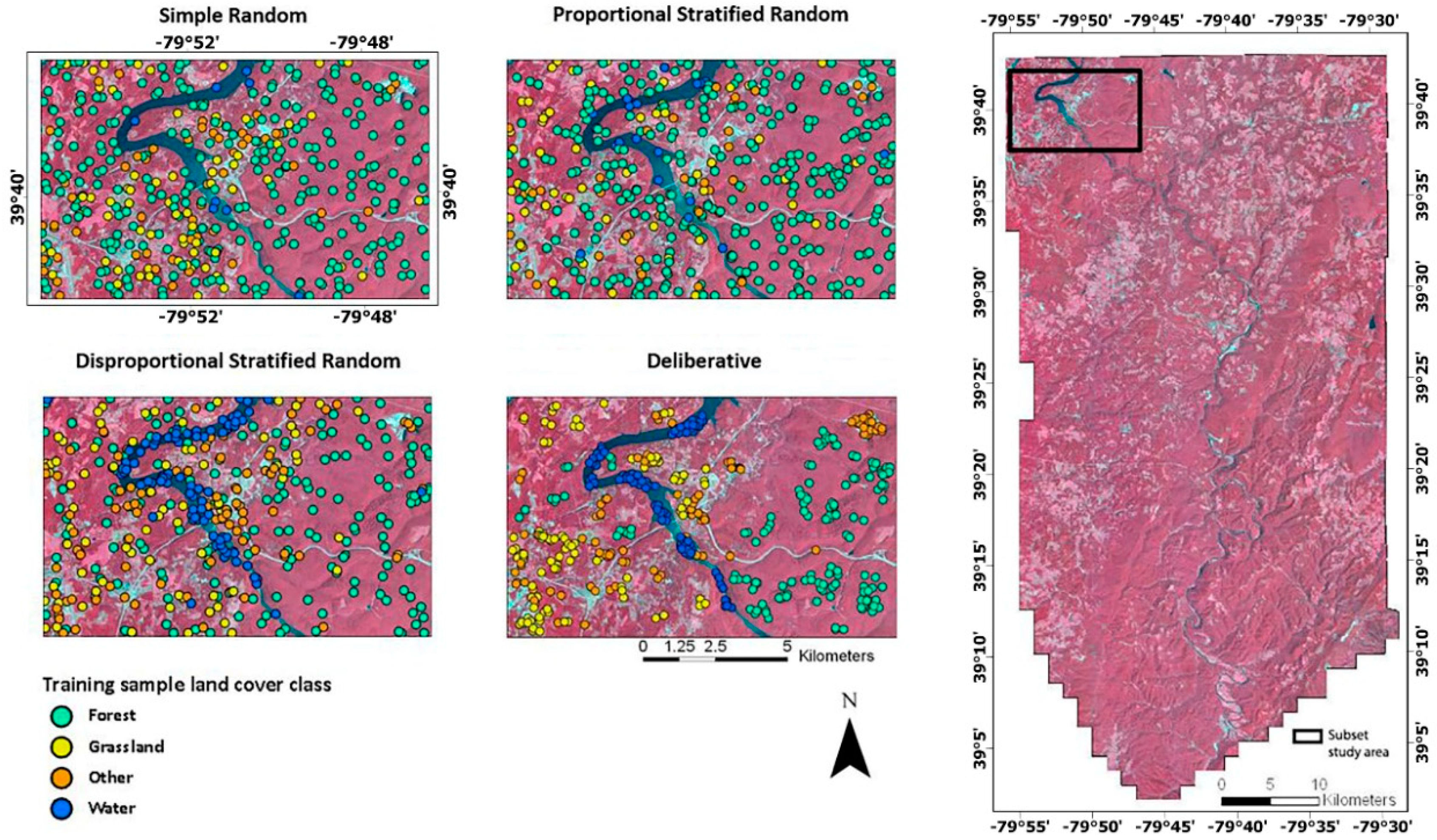
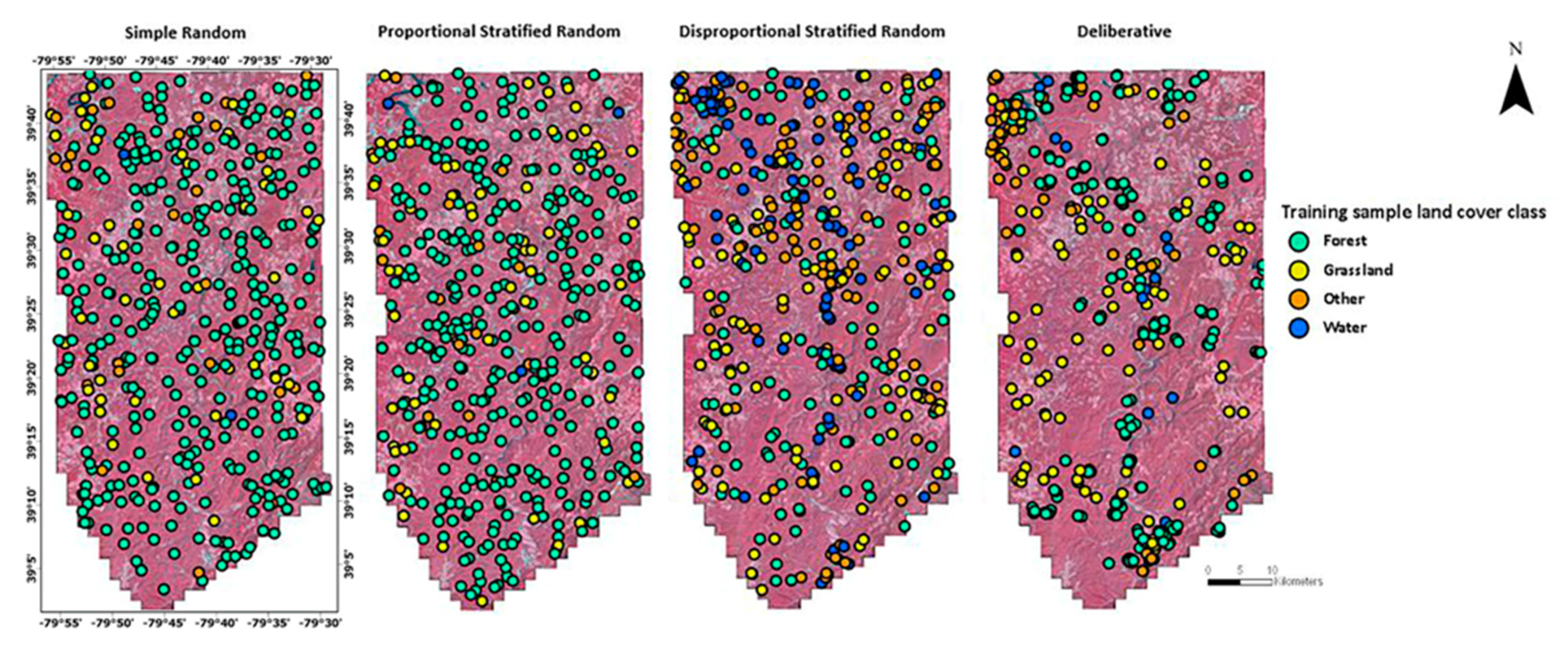
2.7. Sample Data Selection
2.7.1. Simple Random Sampling
2.7.2. Proportional Stratified Random Sampling
2.7.3. Disproportional Stratified Random Sampling
2.7.4. Deliberative Sampling
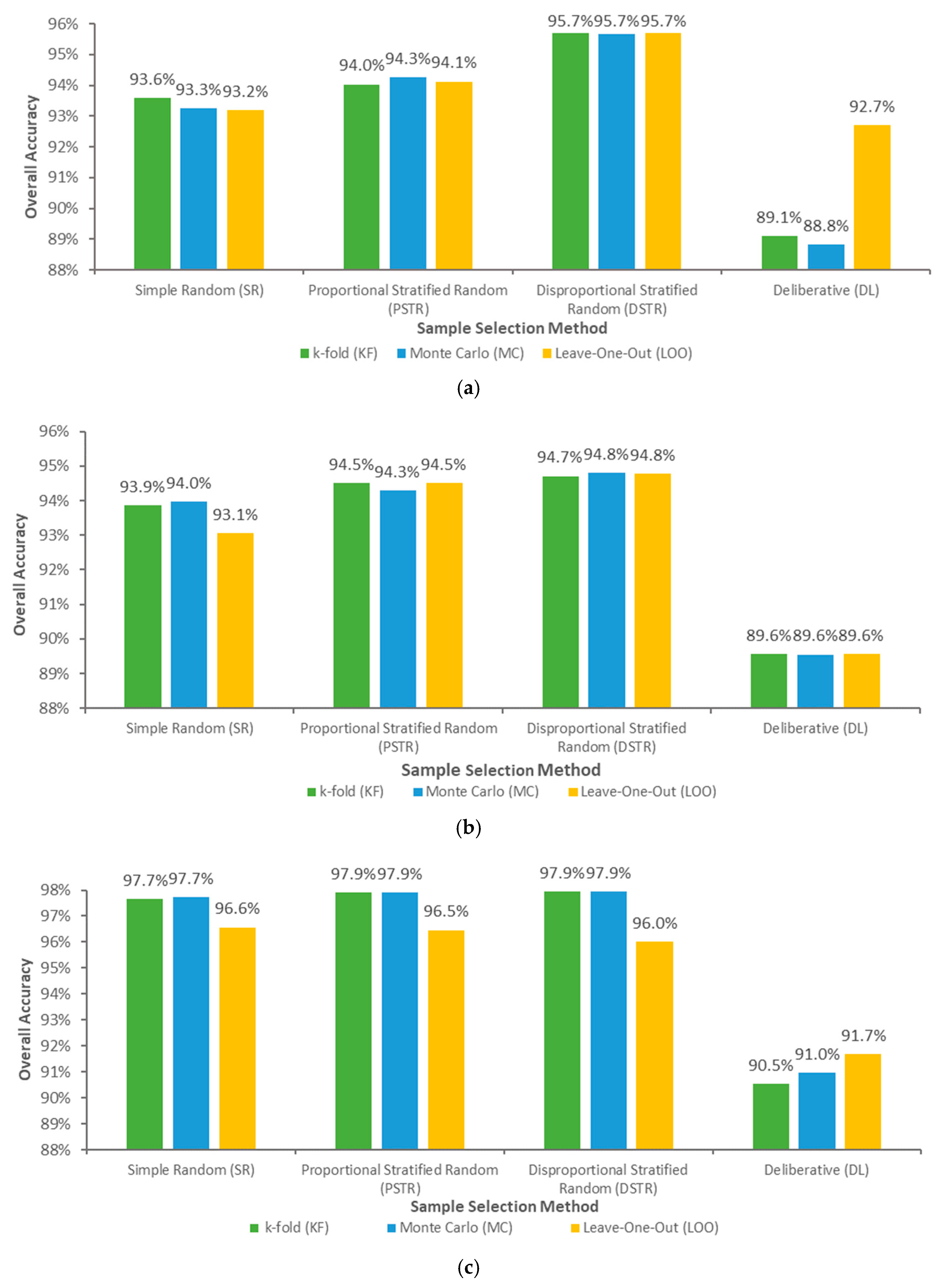
2.8. Cross-Validation Strategies
2.9. Supervised Classification
- SVM is a commonly used supervised classifier in remote sensing analyses [17].
- SVM is a non-parametric classifier, meaning it makes no assumption regarding the underlying data distribution. This may be advantageous for a small sample set [50].
- SVMs are able to perform well with relatively small training datasets when compared to other commonly used classifiers.
- SVMs are attractive for their ability to find a balance between accuracy and generalization [51].
2.10. Error Assessment
3. Results and Discussion
3.1. Performance of Sample Selection Methods
3.2. Performance of Cross-Validation Tuning Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernandez, J.; Corvalan, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, L.; Zhu, F.; Liu, F. Selecting Training Samples from Large-Scale Remote-Sensing Samples Using an Active Learning Algorithm. In Computational Intelligence and Intelligent Systems; Li, K., Li, J., Liu, Y., Castiglione, A., Eds.; Springer: Singapore, 2016; pp. 40–51. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Foody, G.M. Sample size determination for image classification accuracy assessment and comparison. Int. J. Remote Sens. 2009, 30, 5273–5291. [Google Scholar] [CrossRef]
- Jin, H.; Stehman, S.V.; Mountrakis, G. Assessing the impact of training sample selection of accuracy of an urban classification: A case study in Denver, Colorado. Int. J. Remote Sens. 2014, 35, 2067–2081. [Google Scholar] [CrossRef]
- Radoux, J.; Bogaert, P.; Fasbender, D.; Defourny, P. Thematic accuracy assessment of geographic object-based image classification. Int. J. Geogr. Inf. Sci. 2011, 25, 895–911. [Google Scholar] [CrossRef]
- Stehman, S.V. Impact of sample size allocation when using stratified random sampling to estimate accuracy and area of land-cover change. Remote Sens. Lett. 2012, 3, 111–120. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Ma, X.; Cheng, K.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Foody, G.M.; Pal, M.; Rocchini, D.; Garzon-Lopez, C.X.; Bastin, L. The Sensitivity of mapping Methods to Reference Data Quality: Training Supervised Image Classifications with Imperfect Reference Data. ISPRS Int. J. Geo-Inf. 2016, 5, 199. [Google Scholar] [CrossRef]
- Congalton, R.G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A.; Sanchez-Hernandez, C.; Boyd, D.S. Training Set Size Requirements for the Classification of a Specific Class. Remote Sens. Environ. 2006, 104, 1–14. [Google Scholar] [CrossRef]
- Mu, X.; Hu, M.; Song, W.; Ruan, G.; Ge, Y.; Wang, J.; Huang, S.; Yan, G. Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sens. 2015, 7, 16164–16182. [Google Scholar] [CrossRef]
- Chen, D.M.; Stow, D. The Effect of Training Strategies on Supervised Classification at Different Spatial Resolutions. Photogramm. Eng. Remote Sens. 2002, 68, 1155–1161. [Google Scholar]
- Chen, D.; Stow, D.A.; Gong, P. Examining the effect of spatial resolution and texture windows size on classification accuracy: An urban environment case. Int. J. Remote Sens. 2004, 25, 2177–2192. [Google Scholar] [CrossRef]
- Congalton, R.G. A comparison of sampling schemes used in generating error matrices for assessing the accuracy of maps generated from remotely sensed data. Photogramm. Eng. Remote Sens. 1988, 54, 593–600. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when the strata are different from the map classes. Int. J. Remote Sens. 2014, 35, 4923–4939. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Accuracy assessment. In The SAGE Handbook of Remote Sensing; Warner, T.A., Nellis, M.D., Foody, G.M., Eds.; Sage Publications Ltd.: London, UK, 2009; pp. 129–145. ISBN 9781412936163. [Google Scholar]
- Pal, M.; Foody, G.M. Evaluation of SVM, RVM and SMLR for accurate image classification with limited ground data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1344–1355. [Google Scholar] [CrossRef]
- Demir, B.; Minello, L.; Bruzzone, L. An Effective Strategy to Reduce the Labeling Cost in the Definition of Training Sets by Active Learning. IEEE Geosci. Remote Sens. Lett. 2014, 11, 79–83. [Google Scholar] [CrossRef]
- Wuttke, S.; Middlemann, W.; Stilla, U. Concept for a compound analysis in active learning remote sensing. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing, and Spatial Information Sciences, Munich, Germany, 25–27 March 2015; Volume XL-3(W2), pp. 273–279. [Google Scholar] [CrossRef]
- Babcock, C.; Finely, A.O.; Bradford, J.B.; Kolka, R.K.; Birdsey, R.A.; Ryan, M.G. LiDAR based prediction of forest biomass using hierarchial models with spatially varying coefficients. Remote Sens. Environ. 2015, 169, 113–127. [Google Scholar] [CrossRef]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar] [CrossRef]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Sharma, R.C.; Hara, K.; Hirayama, H. A Machine Learning and Cross-Validation Approach for the Discrimination of Vegetation Physiognomic Types Using Satellite Based Multispectral and Multitemporal Data. Scientifica 2017, 2017, 9806479. [Google Scholar] [CrossRef] [PubMed]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Picard, R.R.; Cook, R.D. Cross-Validation of Regression Models. J. Am. Stat. Assoc. 1984, 387, 575–583. [Google Scholar] [CrossRef]
- Braun, E.L. Deciduous Forests of Eastern North America; Hafner Publishing Company: New York, NY, USA, 1950. [Google Scholar]
- Maxwell, A.E.; Strager, M.P.; Warner, T.A.; Zegre, N.P.; Yuill, C.B. Comparison of NAIP orthophotography and RapidEye satellite imagery for mapping of mining and mine reclamation. GISci. Remote Sens. 2014, 51, 301–320. [Google Scholar] [CrossRef]
- WVU NRAC. Aerial Lidar Acquistion Report: Preston County and North Branch (Potomac) LIDAR *.LAS 1.2 Data Comprehensive and Bare Earth. West Virginia Department of Environmental Protection. Available online: http://wvgis.wvu.edu/lidar/data/WVDEP_2011_Deliverable4/WVDEP_deliverable_4_Project_Report.pdf (accessed on 1 December 2018).
- ESRI. ArcGIS Desktop: Release 10.5.1; Environmental Systems Research Institute: Redlands, CA, USA, 2017. [Google Scholar]
- Charaniya, A.P.; Manduchi, R.; Lodha, S.K. Supervised parametric classification of aerial LIDAR data. In Proceedings of the IEEE 2004 Conferences on Computer Vision and Pattern Recognition Workshop, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Kashani, A.G.; Olsen, M.; Parrish, C.; Wilson, N. A Review of LIDAR Radiometric Processing: From Ad Hoc Intensity correction to Rigorous Radiometric Calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef] [PubMed]
- Song, J.H.; Han, S.H.; Yu, K.Y.; Kim, Y.I. Assessing the possibility of land-cover classification using LIDAR intensity data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 259–262. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P.; Conley, J.F.; Sharp, A.L. Assessing machine learning algorithms and image- and LiDAR-derived variables for GEOBIA classification of mining and mine reclamation. Int. J. Remote Sens. 2015, 36, 954–978. [Google Scholar] [CrossRef]
- Beşol, B.; Alganci, U.; Sertel, E. The use of object based classification with nDSM to increase the accuracy of building detection. In Proceedings of the 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15–18 May 2017. [Google Scholar]
- Lear, R.F. NAIP Quality Samples. United States Department of Agriculture Aerial Photography Field Office. Available online: https://www.fsa.usda.gov/Internet/FSA_File/naip_quality_samples_pdf.pdf (accessed on 28 December 2018).
- Trimble. Trimble eCognition Suite 9.3.2; Trimble Germany GmbH: Munich, Germany, 2018. [Google Scholar]
- Petrie, G.; Toth, C.K. Airborne and Spaceborne Laser Profilers and Scanners. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution segmentation—An optimization approach for high quality multi-scale image segmentation. In Proceedings of the Angewandte Geographische Informations-Verarbeitung XII, Karlsruhe, Germany, 30 June 2000; pp. 12–23. [Google Scholar]
- Belgiu, M.; Drăgut, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef]
- Drăgut, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterization for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D. Multi-scale texture segmentation and classification of salt marsh using digital aerial imagery with very high spatial resolution. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Maguigan, M.; Rodgers, J.; Dash, P.; Meng, Q. Assessing Net Primary Production in Montane Wetlands from Proximal, Airborne, and Satellite Remote Sensing. Adv. Remote Sens. 2016, 5, 118–130. [Google Scholar] [CrossRef]
- Griffith, D.A. Establishing Qualitative Geographic Sample Size in the Presence of Spatial Autocorrelation. Ann. Assoc. Am. Geogr. 2013, 103, 1107–1122. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training. R package Version 6.0-71. 2016. Available online: https://CRAN.R-project.org/package=caret (accessed on 21 February 2018).
- Scheuenemeyer, J.H.; Drew, L.J. Statistics for Earth and Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 9780470650707. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Meyer, D. Support Vector Machines: The Interface to Libsvm in Package e1071. R Package Version 6.0-71. 2012. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 21 February 2018).
- Ulrich, J.M. Microbenchmark: Accurate Timing Functions. R Package Version 1.4-4. 2018. Available online: https://cran.r-project.org/web/packages/microbenchmark/microbenchmark.pdf (accessed on 21 February 2018).
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef]
- Foody, G.M. Thematic Map Comparison: Evaluating the Statistical Significance of Differences in Classification Accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Waske, B.; Benediktsson, J.A.; Sveinsson, J.R. Classifying Remote Sensing Data with Support Vector Machines and Imbalanced Training Data; CMS 2009, LNCS 5519; Benediktsson, J.A., Kittler, J., Roli, F., Eds.; Springer: Berlin/Heidleberg, Germany, 2009; pp. 375–384. [Google Scholar]
- Stehman, S.V. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]

| Attribute Type | Attributes | Number of Attributes |
|---|---|---|
| Spectral | Mean (Blue, Green, Intensity, NIR, Red, nDSM), Mode (Blue, Green, Intensity, NIR, Red, nDSM), Standard deviation (Blue, Green, Intensity, NIR, Red, nDSM), Skewness (Blue, Green, Intensity, NIR, Red, nDSM), Brightness | 25 |
| Geometric | Density, Roundness, Border length, Shape index, Area, Compactness, Volume, Rectangular fit, Asymmetry | 9 |
| Spectral Indices | Mean NDVI | 1 |
| Sample Selection Method | Number of Samples per Class | ||||
|---|---|---|---|---|---|
| Forest | Grass | Other | Water | Total # of Samples | |
| Small Subset Simple Random | 290 | 67 | 53 | 9 | 419 |
| Small Subset Proportional Stratified Random | 305 | 59 | 35 | 20 | 419 |
| Small Subset Disproportional Stratified Random | 209 | 84 | 84 | 42 | 419 |
| Small Subset Deliberative | 139 | 100 | 100 | 80 | 419 |
| Sample Selection Method | Number of Samples per Class | ||||
|---|---|---|---|---|---|
| Forest | Grass | Other | Water | Total # of Samples | |
| Small Regional Simple Random | 341 | 50 | 26 | 2 | 419 |
| Small Regional Proportional Stratified Random | 333 | 65 | 18 | 3 | 419 |
| Small Regional Disproportional Stratified Random | 209 | 84 | 84 | 42 | 419 |
| Small Regional Deliberative | 254 | 80 | 69 | 16 | 419 |
| Sample Name | Number of Samples per Class | ||||
|---|---|---|---|---|---|
| Forest | Grass | Other | Water | Total # of Samples | |
| Large Regional Simple Random | 8183 | 1178 | 600 | 39 | 10,000 |
| Large Regional Proportional Stratified Random | 7984 | 1553 | 408 | 55 | 10,000 |
| Large Regional Disproportional Stratified Random | 5000 | 2000 | 2000 | 1000 | 10,000 |
| Large Regional Deliberative | 6087 | 1897 | 1651 | 365 | 10,000 |
| Class | Proportion of Total Area Occupied | |
|---|---|---|
| Subset Dataset | Regional Dataset | |
| Forest | 72.73% | 79.84% |
| Grassland | 14.10% | 15.53% |
| Other | 8.34% | 4.08% |
| Water | 4.84% | 0.55% |
| Cross-Validation Method | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k-Fold (KF) | Monte Carlo (MC) | Leave-One-Out (LOO) | k-Fold (KF) | Monte Carlo (MC) | Leave-One-Out (LOO) | k-Fold (KF) | Monte Carlo (MC) | Leave-One-Out (LOO) | ||
| Small Subset-Trained Classification | Small Regional-Scale Trained Classification | Large Regional-Scale Trained Classification | ||||||||
| Sample Selection Method | Simple Random (SR) | Small-Subset-(SR-KF) | Small-Subset-(SR-MC) | Small-Subset-(SR-LOO) | Small-Regional-(SR-KF) | Small-Regional-(SR-MC) | Small-Regional-(SR-LOO) | Large-Regional-(SR-KF) | Large-Regional-(SR-MC) | Large-Regional-(SR-LOO) |
| Proportional Stratified Random (PSTR) | Small-Subset-(PSTR-KF) | Small-Subset-(PSTR-MC) | Small-Subset-(PSTR-LOO) | Small-Regional-(PSTR-KF) | Small-Regional-(PSTR-MC) | Small-Regional-(PSTR-LOO) | Large-Regional-(PSTR-KF) | Large-Regional-(PSTR-MC) | Large-Regional-(PSTR-LOO) | |
| Disproportional Stratified Random (DSTR) | Small-Subset-(DSTR-KF) | Small-Subset-(DSTR-MC) | Small-Subset-(DSTR-LOO) | Small-Regional-(DSTR-KF) | Small-Regional-(DSTR-MC) | Small-Regional-(DSTR-LOO) | Large-Regional-(DSTR-KF) | Large-Regional-(DSTR-MC) | Large-Regional-(DSTR-LOO) | |
| Deliberative (DL) | Small-Subset-(DL-KF) | Small-Subset-(DL-MC) | Small-Subset-(DL-LOO) | Small-Regional-(DL-KF) | Small-Regional-(DL-MC) | Small-Regional-(DL-LOO) | Large-Regional-(DL-KF) | Large-Regional-(DL-MC) | Large-Regional-(DL-LOO) | |
| Subset-SR-KF | Subset-PSTR-KF | Subset-DSTR-KF | Subset-DL-KF | Small-Regional-SR-KF | Small-Regional-PSTR-KF | Small-Regional-DSTR-KF | Small-Regional-DL-KF | Large-Regional-SR-KF | Large-Regional-PSTR-KF | Large-Regional-DSTR-KF | Large-Regional-DL-KF | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Subset-SR-KF | |
| 0.007 * | <0.001 * | <0.001 * | <0.001 * | 0.004 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Subset-PSTR-KF | ||
| <0.001 * | 0.043 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Subset-DSTR-KF | |||
| <0.001 * | <0.001 * | <0.001 * | 0.009 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Subset-DL-KF | ||||
| 0.013 * | 0.002 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Small-Regional-SR-KF | |||||
| 0.031 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Small-Regional-PSTR-KF | ||||||
| <0.001 * | <0.001 * | <0.001 * | <0.001 * | <0.001 * | Small-Regional-DSTR-KF | |||||||
| <0.001 * | <0.001 * | <0.001 * | <0.001 * | Small-Regional-DL-KF | ||||||||
| 0.108 | 0.113 | <0.001 * | Large-Regional-SR-KF | |||||||||
| 0.162 | <0.001 * | Large-Regional-PSTR-KF | ||||||||||
| <0.001 * | Large-Regional-DSTR-KF | |||||||||||
| Large-Regional-DL-KF |
| Reference Data (No. Objects) | |||||||
|---|---|---|---|---|---|---|---|
| Forest | Grassland | Other | Water | Total | User’s Accuracy | ||
| Classified data (No. objects) | Forest | 7238 | 31 | 4 | 0 | 7273 | 99.5% |
| Grassland | 699 | 1151 | 85 | 0 | 1935 | 59.5% | |
| Other | 136 | 73 | 479 | 28 | 716 | 66.9% | |
| Water | 12 | 1 | 22 | 41 | 76 | 53.9% | |
| Total | 8085 | 1256 | 590 | 69 | 10,000 | Overall accuracy: 89.1% | |
| Producer’s accuracy | 89.5% | 91.6% | 81.2% | 59.4% | |||
| Reference Data (No. Objects) | |||||||
|---|---|---|---|---|---|---|---|
| Forest | Grassland | Other | Water | Total | User’s Accuracy | ||
| Classified data (No. objects) | Forest | 7723 | 36 | 6 | 0 | 7265 | 99.4% |
| Grassland | 723 | 1133 | 80 | 0 | 1936 | 58.5% | |
| Other | 129 | 86 | 487 | 29 | 731 | 66.6% | |
| Water | 10 | 1 | 17 | 40 | 68 | 58.8% | |
| Total | 8085 | 1256 | 590 | 69 | 10,000 | Overall accuracy: 88.8% | |
| Producer’s accuracy | 89.3% | 90.2% | 82.5% | 58.0% | |||
| Reference Data (No. Objects) | |||||||
|---|---|---|---|---|---|---|---|
| Forest | Grassland | Other | Water | Total | User’s Accuracy | ||
| Classified data (No. objects) | Forest | 7728 | 174 | 5 | 0 | 7907 | 97.7% |
| Grassland | 176 | 1034 | 95 | 1 | 1306 | 79.2% | |
| Other | 176 | 48 | 466 | 26 | 716 | 65.1% | |
| Water | 5 | 0 | 24 | 42 | 71 | 59.2% | |
| Total | 8085 | 1256 | 590 | 69 | 10,000 | Overall accuracy: 92.7% | |
| Producer’s accuracy | 95.6% | 82.3% | 79.0% | 60.9% | |||
| Classification | Processing Time (seconds) |
|---|---|
| SVM-Subset-KF | 10 |
| SVM-Large-Regional-KF | 468 |
| SVM-Subset-MC | 17 |
| SVM-Large-Regional-MC | 876 |
| SVM-Subset-LOO | 313 |
| SVM-Large-Regional-LOO | 489,960 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
A. Ramezan, C.; A. Warner, T.; E. Maxwell, A. Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification. Remote Sens. 2019, 11, 185. https://doi.org/10.3390/rs11020185
A. Ramezan C, A. Warner T, E. Maxwell A. Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification. Remote Sensing. 2019; 11(2):185. https://doi.org/10.3390/rs11020185
Chicago/Turabian StyleA. Ramezan, Christopher, Timothy A. Warner, and Aaron E. Maxwell. 2019. "Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification" Remote Sensing 11, no. 2: 185. https://doi.org/10.3390/rs11020185
APA StyleA. Ramezan, C., A. Warner, T., & E. Maxwell, A. (2019). Evaluation of Sampling and Cross-Validation Tuning Strategies for Regional-Scale Machine Learning Classification. Remote Sensing, 11(2), 185. https://doi.org/10.3390/rs11020185