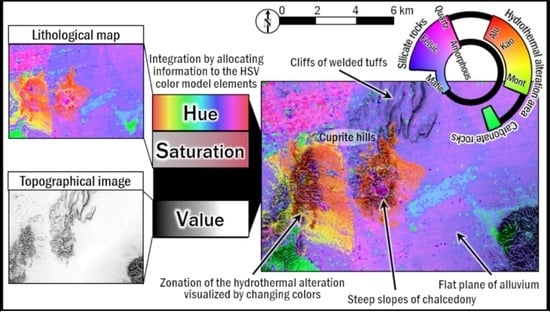
Integration and Visualization of Mineralogical and Topographical Information Derived from ASTER and DEM Data
Abstract
:1. Introduction
2. Methods and Materials
2.1. Fundamental Concept
2.2. Data and Test Sites
2.2.1. Data
2.2.2. Test Sites
2.3. Lithological Indices
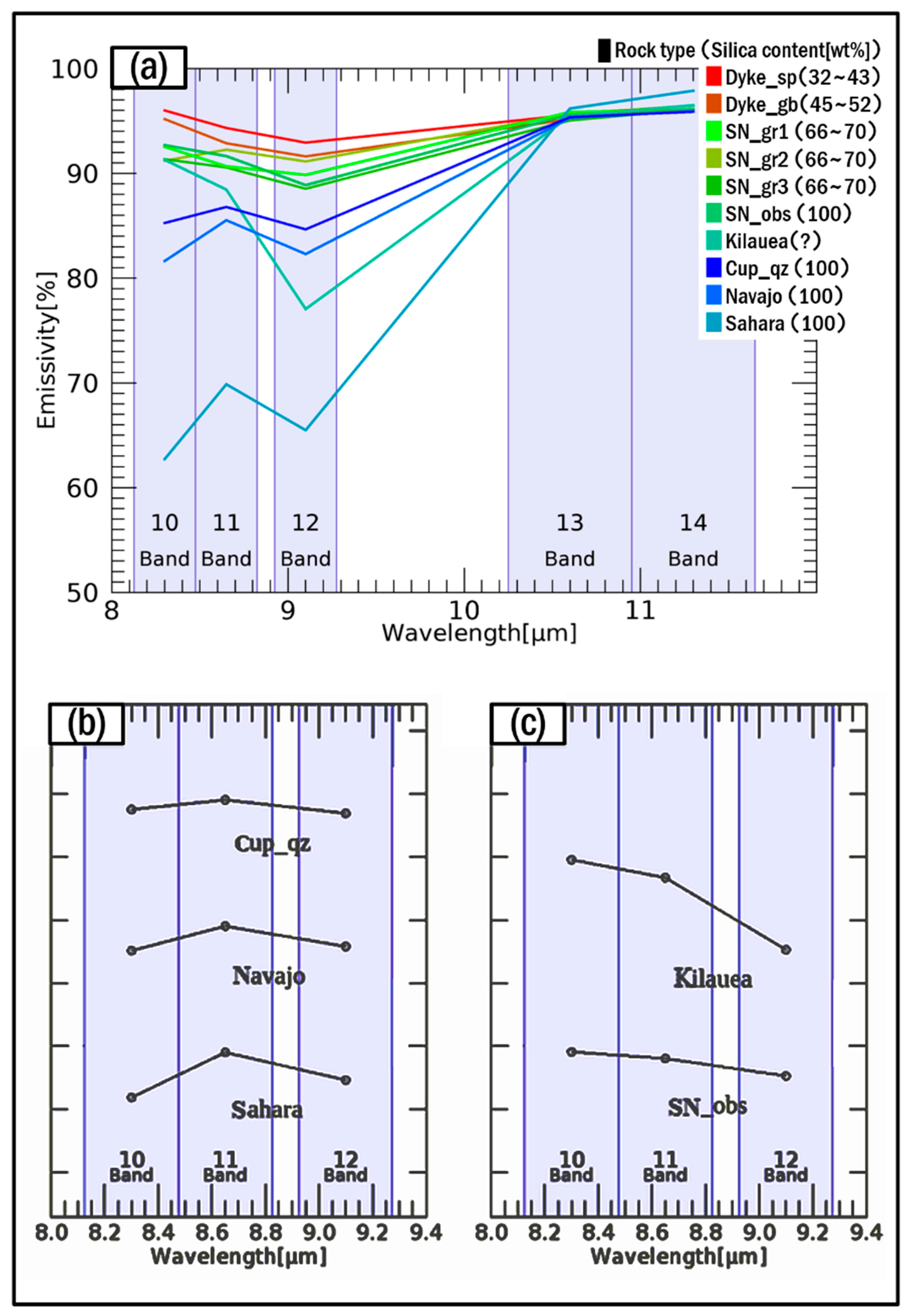
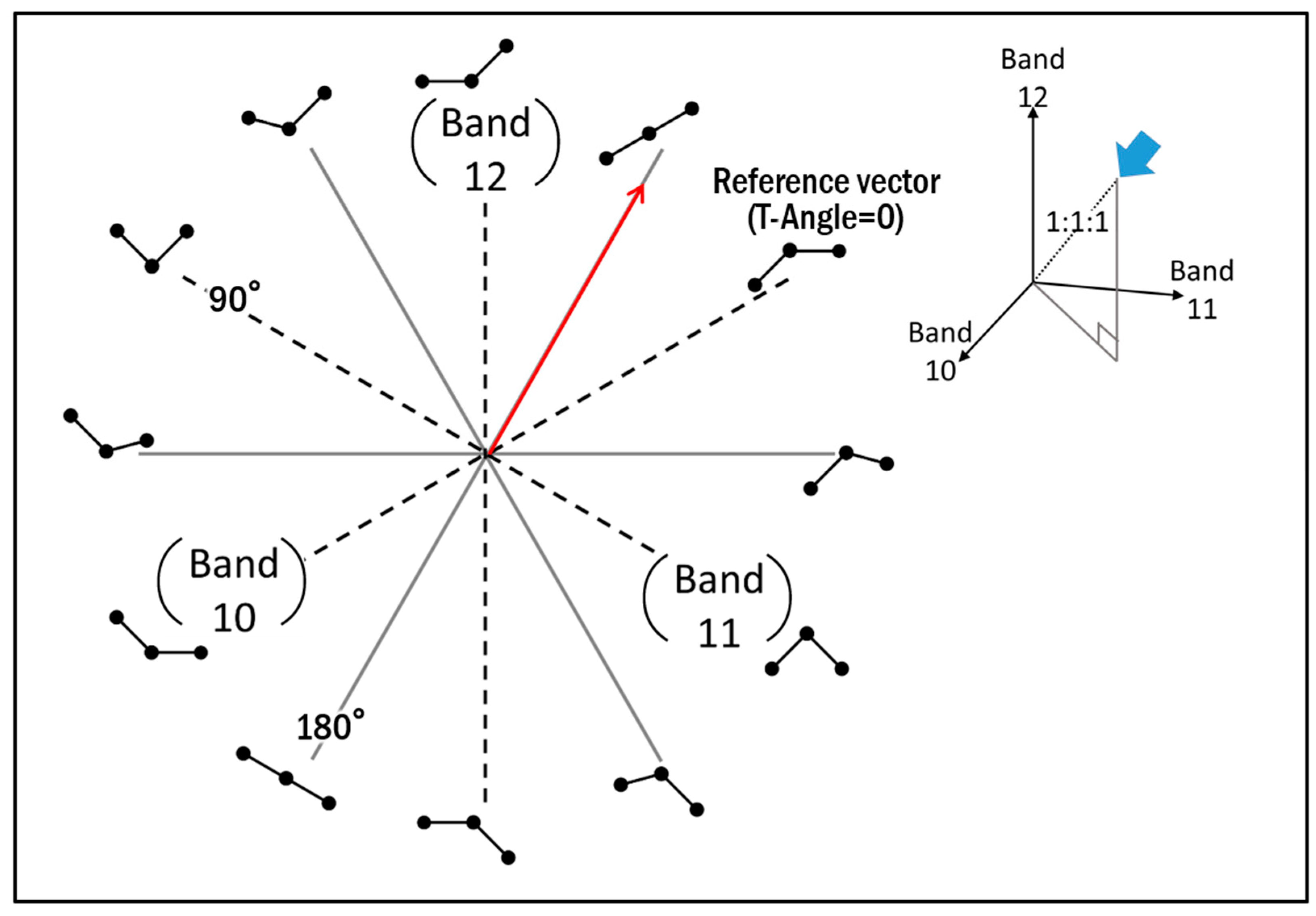
2.3.1. TIR Spectral Indices for Mapping Silicate Rocks
2.3.2. Delineating Carbonate Rocks
2.3.3. Delineating Hydrothermal Alteration Zones
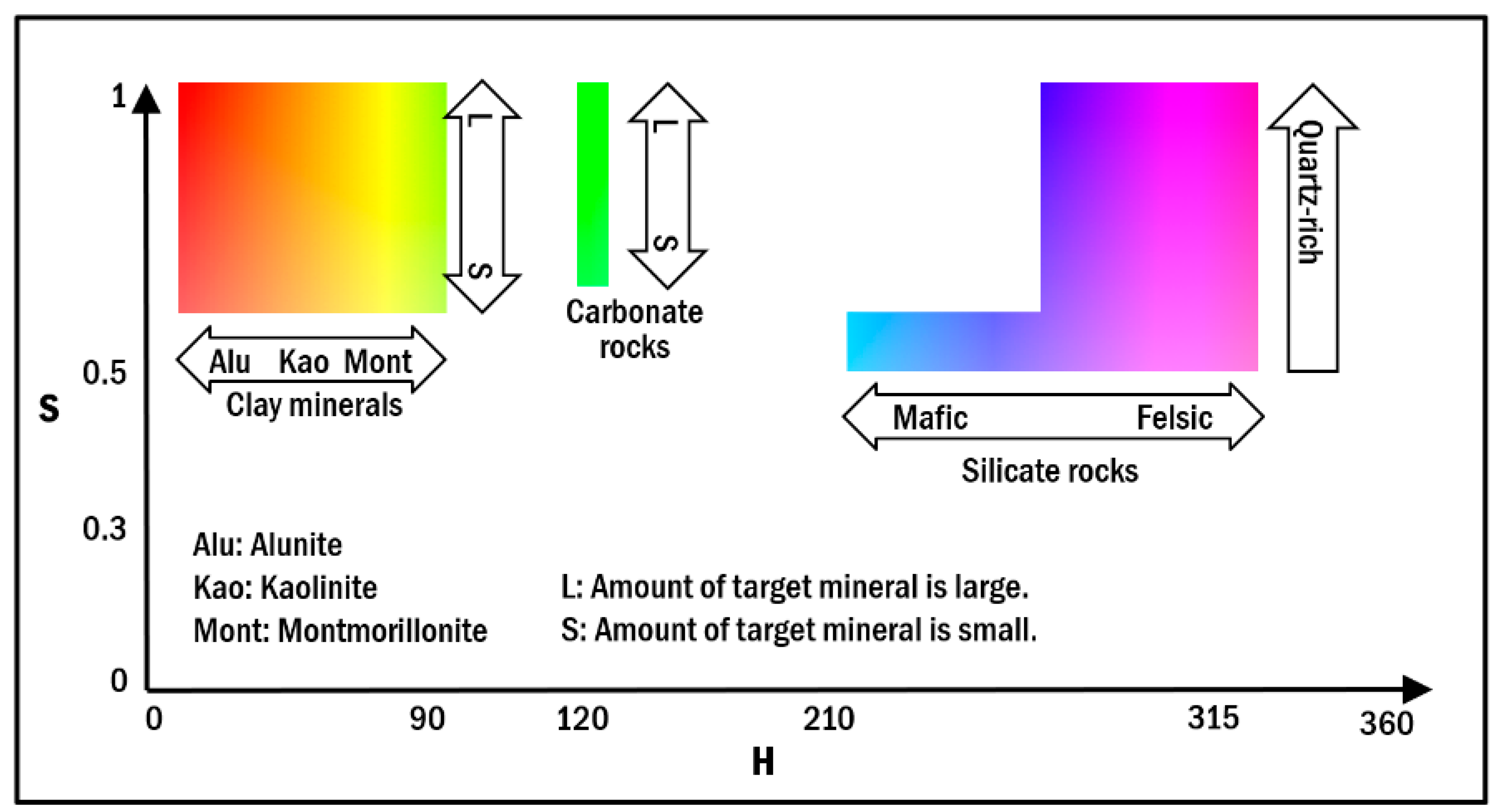
2.3.4. Allocation of Spectral Indices to the H and S Elements
2.4. DEM Visualization by the V Element
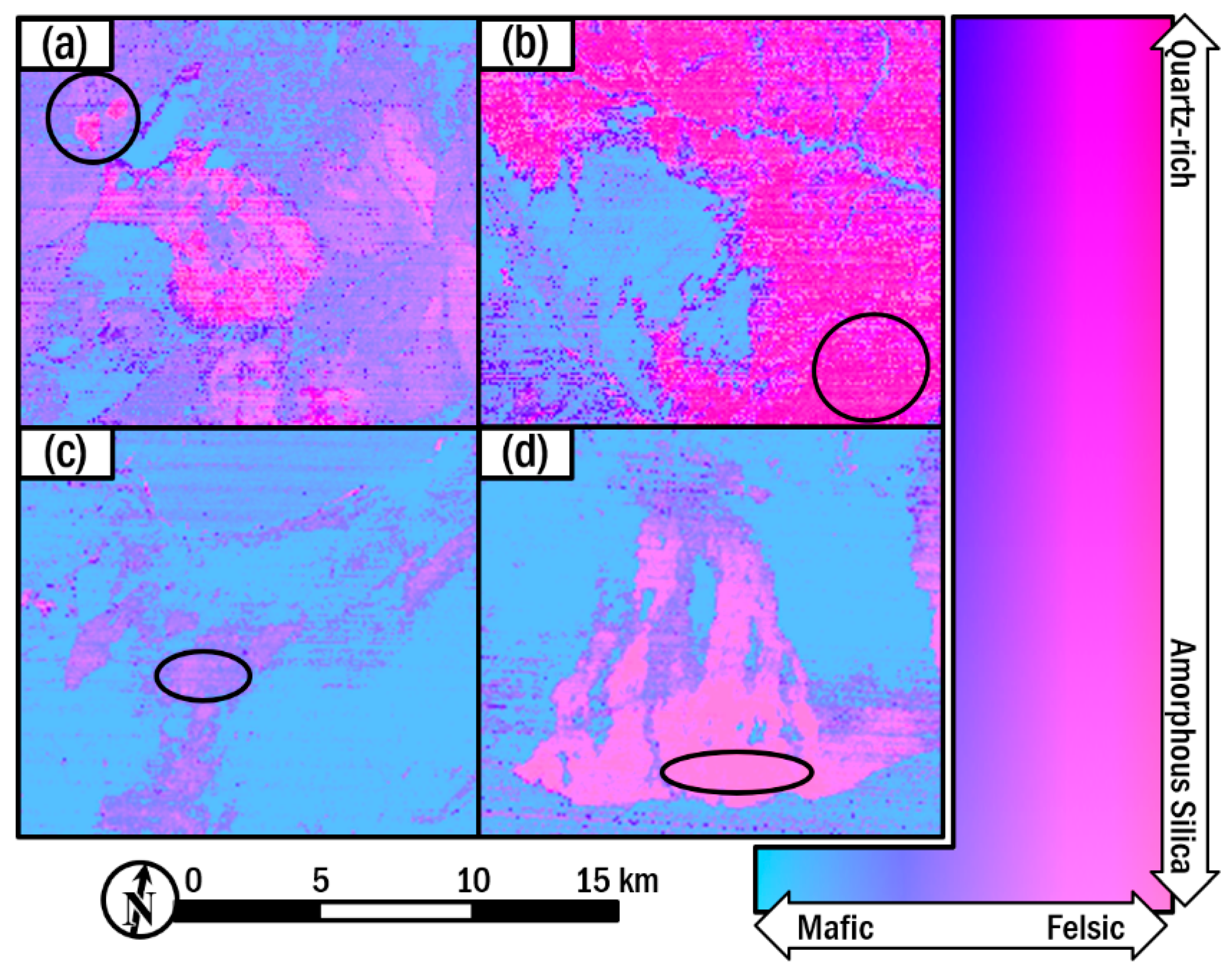
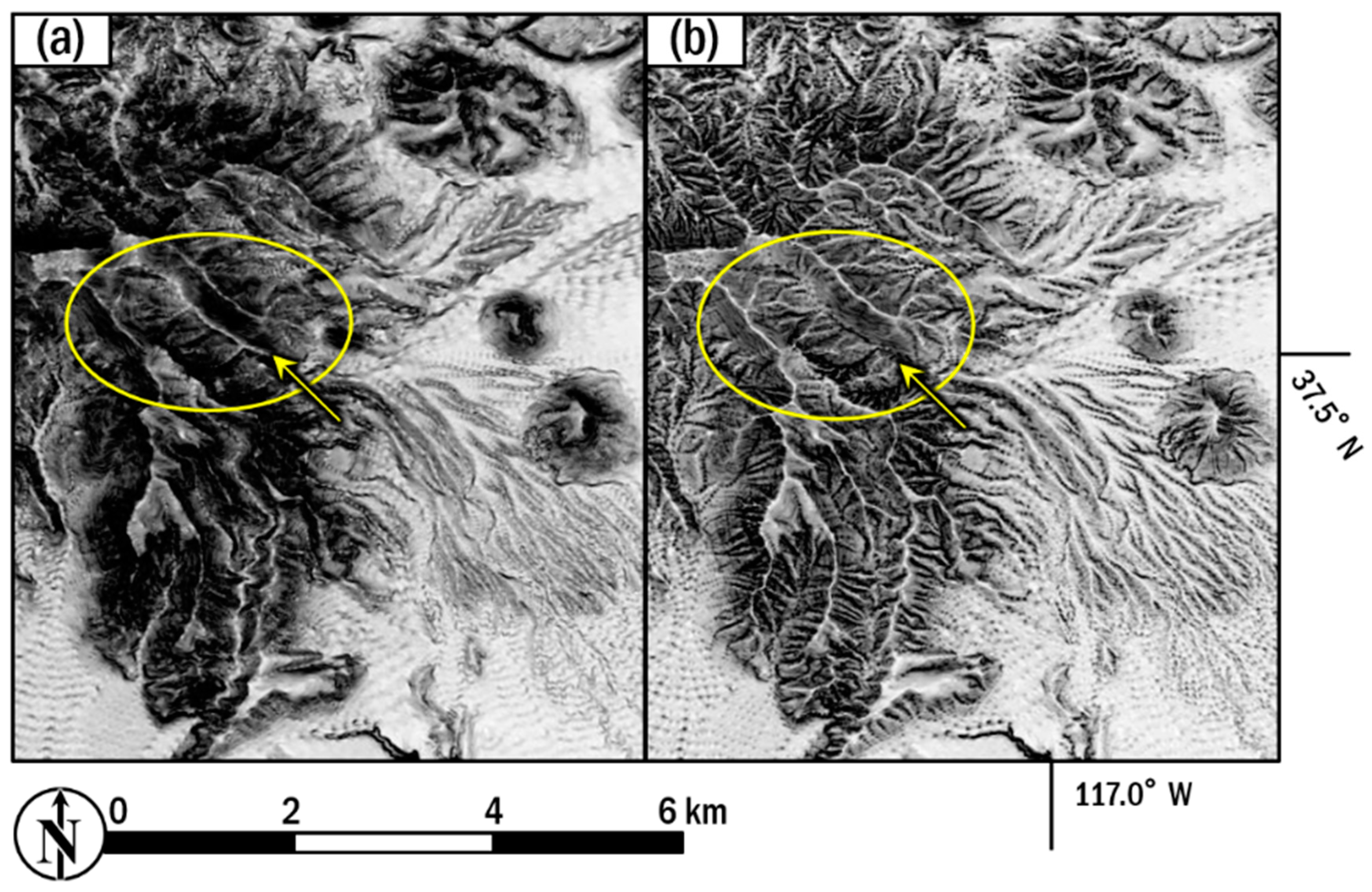
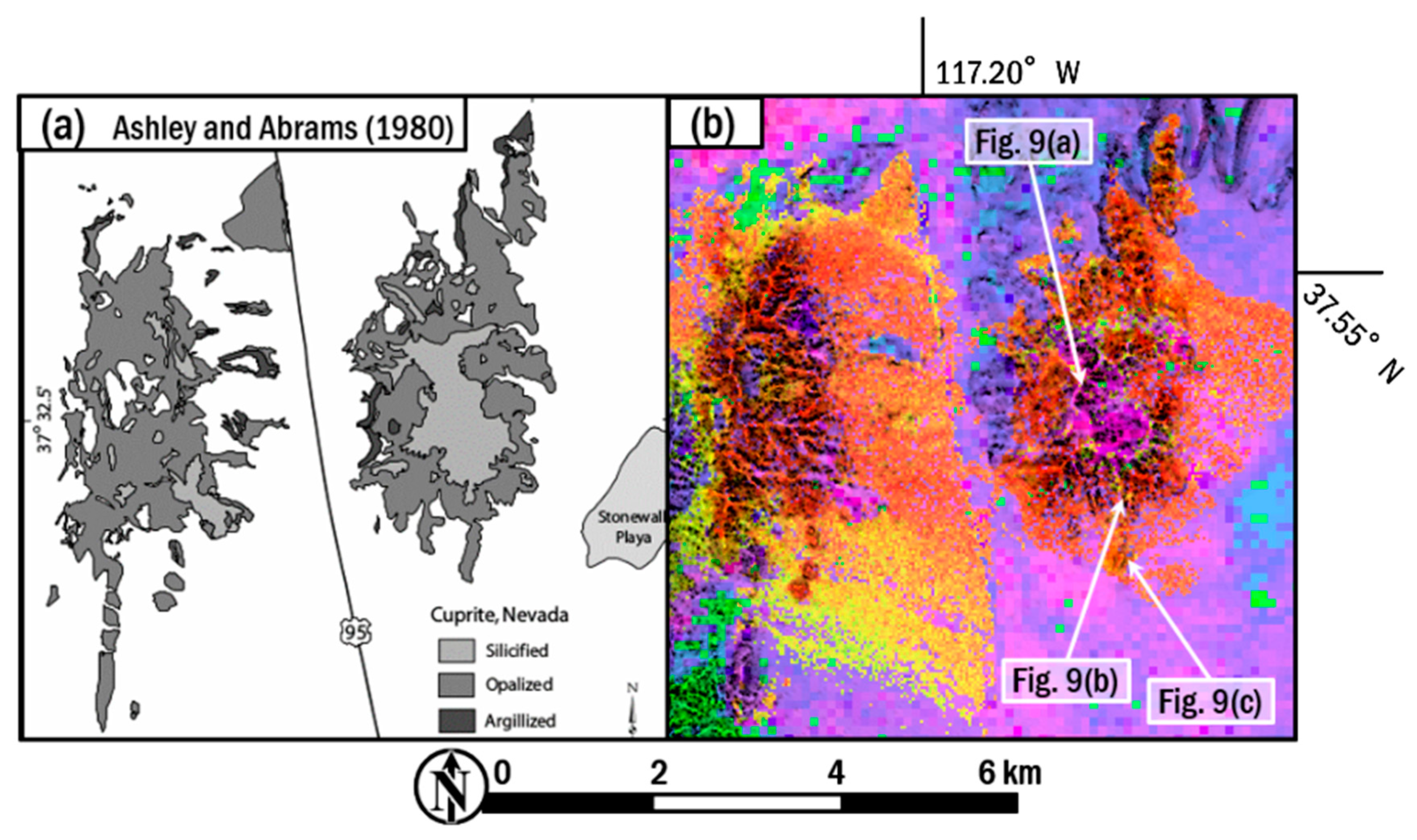
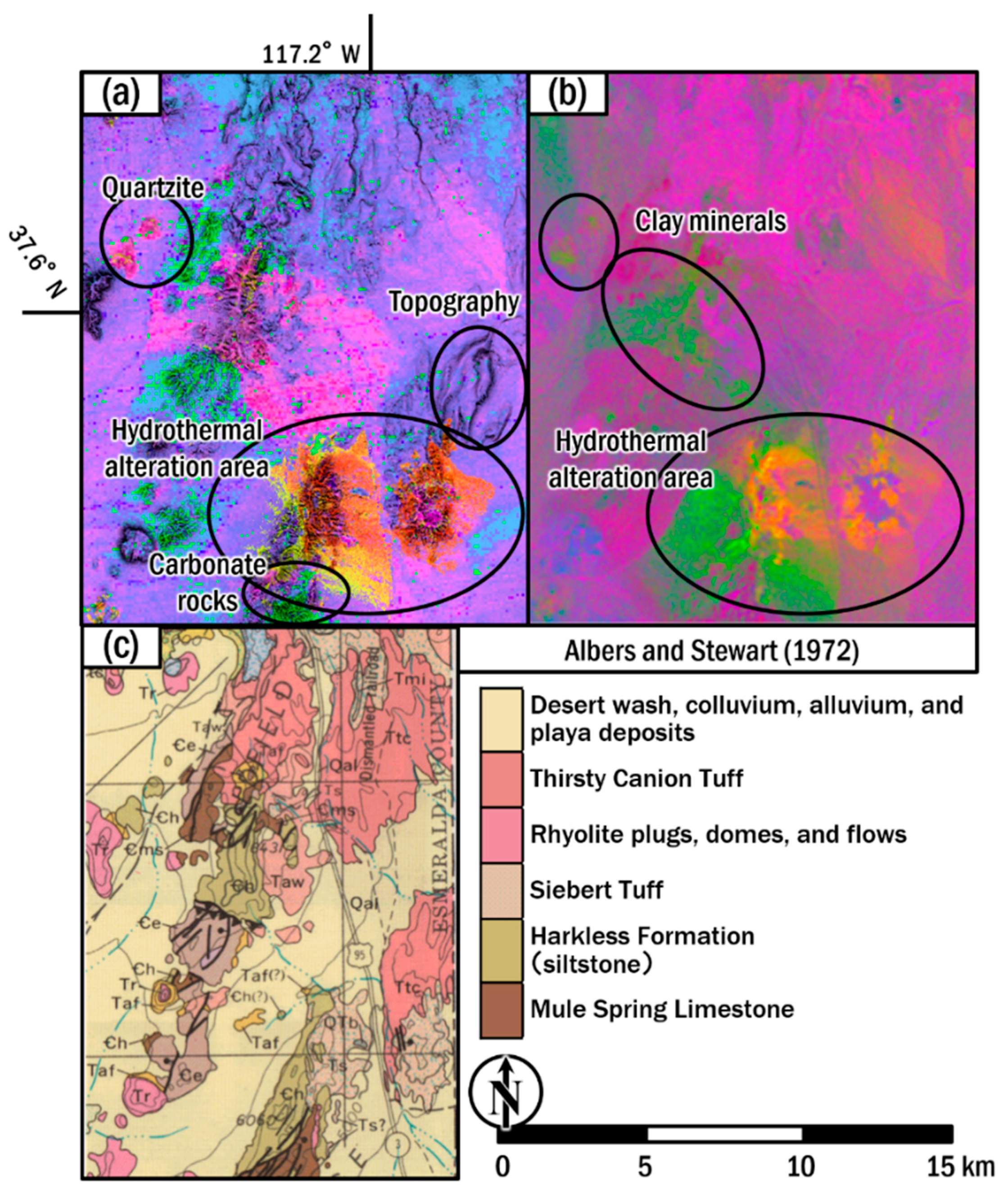
3. Results
4. Discussion
4.1. Integration Method
4.2. Lithological Indices and Geological Interpretation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; Smeth, J.B.D.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Kereszturi, G.; Schaefer, L.N.; Schleiffarth, W.K.; Procter, J.; Pullanagari, R.R.; Mead, S.; Kennedy, B. Integrating airborne hyperspectral imagery and LiDAR for volcano mapping and monitoring through image classification. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 323–339. [Google Scholar] [CrossRef]
- Rogge, D.; Rivard, B.; Segl, K.; Grant, B.; Feng, J. Mapping of NiCu–PGE ore hosting ultramafic rocks using airborne and simulated EnMAP hyperspectral imagery, Nunavik, Canada. Remote Sens. Environ. 2014, 152, 302–317. [Google Scholar] [CrossRef]
- Kruse, F.A. Mapping surface mineralogy using imaging spectrometry. Geomorphology 2012, 137, 41–56. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kahle, A.B.; Tsu, H.; Kawakami, T.; Pniel, M. Overview of Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). IEEE Trans. Geosci. Remote Sens. 1998, 36, 1062–1071. [Google Scholar] [CrossRef]
- Rowan, L.C.; Wetlaufer, P.H.; Goetz, A.F.H.; Billingsley, F.C.; Stewart, J.H. Discrimination of Rock Types and Detection of Hydrothermally Altered Areas in South-Central Nevada by the Use of Computer-Enhanced ERTS Images; Geological Survey Professional Paper; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1976; Volume 883, p. 35.
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image-processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Naito, C. Spectral indices for lithologic discrimination and mapping by using the ASTER SWIR bands. Int. J. Remote Sens. 2003, 24, 4311–4323. [Google Scholar] [CrossRef]
- Fatima, K.; Khattak, M.U.K.; Kausar, A.B.; Toqeer, M.; Haider, N.; Rehman, A.U. Minerals identification and mapping using ASTER satellite image. J. Appl. Remote Sens. 2017, 11, 46006. [Google Scholar] [CrossRef]
- Jakob, S.; Gloaguen, R.; Laukamp, C. Remote sensing-based exploration of structurally-related mineralizations around Mount Isa, Queensland, Australia. Remote Sens. 2016, 8, 358. [Google Scholar] [CrossRef]
- Zimmermann, R.; Brandmeier, M.; Andreani, L.; Mhopjeni, K.; Gloaguen, R. Remote sensing exploration of Nb-Ta-LREE-enriched carbonatite (Epembe/Namibia). Remote Sens. 2016, 8, 620. [Google Scholar] [CrossRef]
- Fujisada, H.; Urai, M.; Iwasaki, A. Technical methodology for ASTER global DEM. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3725–3736. [Google Scholar] [CrossRef]
- Takaku, I.; Tadono, T.; Tsutsui, K. Generation of high resolution global DSM from ALOS PRISM. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-4, 243–248. [Google Scholar] [CrossRef]
- Whelley, P.L.; Glaze, L.S.; Calder, E.S.; Harding, D.J. LiDAR-derived surface roughness texture mapping: Application to Mount St. Helens pumice plain deposit analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 426–438. [Google Scholar] [CrossRef]
- Kurata, K.; Yamaguchi, Y. Combining multiple lithological indices derived from ASTER data by using the HSV color model. J. Remote Sens. Soc. Jpn. 2018, 38, 163–173, (In Japanese with an English abstract). [Google Scholar]
- Smith, R.A. Color gamut transform pairs. ACM Siggraph Computer Graphics 1978, 3, 12–19. [Google Scholar] [CrossRef]
- Ninomiya, Y.; Fu, B. Quartz index, carbonate index and SiO2 content index defined for ASTER TIR data. J. Remote Sens. Soc. Jpn. 2002, 22, 50–61, (In Japanese with an English abstract). [Google Scholar]
- Gillespie, A.R.; Matsunaga, T.; Rokugawa, S.; Hook, S.J. Temperature and emissivity from Advanced Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Abrams, M.J.; Ashley, R.P.; Rowan, L.C.; Goetz, A.F.H.; Kahle, A.B. Mapping of hydrothermal alteration in the Cuprite mining district, Nevada using aircraft scanner images for the spectral region 0.46–2.36 μm. Geology 1977, 5, 713–718. [Google Scholar] [CrossRef]
- Ashley, R.P.; Abrams, M.J. Alteration Mapping Using Multispectral Images-Cuprite Mining District, Esmeralda County, Nevada; U.S. Geological Survey Open File Report; U.S. Geological Survey: Reston, VA, USA, 1980; pp. 80–367.
- Kahle, A.B.; Goetz, A.F.H. Mineralogic information from a new airborne thermal infrared multispectral scanner. Science 1983, 222, 24–27. [Google Scholar] [CrossRef]
- Swayze, G.A.; Clark, R.N.; Goetz, A.F.H.; Livo, K.E.; Breit, G.N.; Kruse, F.A.; Sutley, S.J.; Snee, L.W.; Lowers, H.A.; Post, J.L. Mapping advanced argillic alteration at Cuprite, Nevada using imaging spectroscopy. Econ. Geol. 2014, 109, 1179–1221. [Google Scholar] [CrossRef]
- Lyon, R.J.P. Analysis of rocks by spectral infrared emission (8 to 25 microns). Econ. Geol. 1965, 60, 715–736. [Google Scholar] [CrossRef]
- Kahle, A.B.; Gillespie, A.R.; Abbott, E.A.; Abrams, M.J.; Walter, R.E.; Hoover, G. Relative dating of Hawaiian lava flows using multispectral thermal infrared images: A new tool for geologic mapping of young volcanic terranes. J. Geophys. Res. 1988, 93, 15239–15251. [Google Scholar] [CrossRef]
- Jackson, R.D. Spectral indices in n-space. Remote Sens. Environ. 1983, 13, 409–421. [Google Scholar] [CrossRef]
- Balick, L.; Gillespie, A.; French, A.; Danilina, I.; Allard, J.-P.; Mushkin, A. Longwave thermal infrared spectral variability in individual rocks. IEEE Geosci. Remote Sens. Lett. 2009, 6, 52–56. [Google Scholar] [CrossRef]
- Yokoyama, R.; Shirasawa, M.; Kikuchi, Y. Representation of topographical features by openness. J. Jpn. Soc. Photogramm. Remote Sens. 1999, 38, 26–34, (In Japanese with an English abstract). [Google Scholar]
- Yajima, T.; Yamaguchi, Y. Application of inverted slope images generated from ASTER GDEM to geological mapping. In Proceedings of the 56th Spring Conference of the Remote Sensing Society of Japan, Ibaraki, Japan, 15–16 May 2014; pp. 57–58, (In Japanese with an English abstract). [Google Scholar]
- Guth, P.L. Slope and aspect calculations on gridded digital elevation models: Examples from a geomorphometric toolbox for personal computers. Z. Geomorphol. Suppl. 1995, 101, 31–52. [Google Scholar]
- Bedini, E.; van der Meer, F.; van Ruitenbeek, F. Use of HyMap imaging spectrometer data to map mineralogy in the Rodalquilar caldera, southeast Spain. Int. J. Remote Sens. 2009, 30, 327–348. [Google Scholar] [CrossRef]
- Ashley, R.P. Relation between Volcanism and Ore Deposition at Goldfield, Nevada; Nevada Bureau of Mines and Geology Report; Nevada Bureau of Mines and Geology: Reno, NV, USA, 1979; Volume 33, pp. 77–86. [Google Scholar]
- Hunt, G.R.; Salisbury, J.W.; Lenhoff, C.J. Visible and near-infrared spectra of minerals and rocks: VII. Acidic igneous rocks. Mod. Geol. 1973, 4, 217–224. [Google Scholar]
- Kalinowski, A.A.; Oliver, S. ASTER Processing Manual. Remote Sensing Applications; Internal Report; Geoscience Australia: Canberra, Australia, 2004. [Google Scholar]
- Cudahy, T. Australian Satellite ASTER Geoscience Product Notes, Version 1; No. EP-30-07-12-44; CSIRO ePublish: Canberra, Australia, 2012. [Google Scholar]
- Albers, P.J.; Stewart, H.J. Geology and Mineral Deposits of Esmeralda County, Nevada; Nevada Bureau of Mines and Geology: Reno, NV, USA, 1972; Volume 78, p. 88. [Google Scholar]
- Blakely, R.J.; John, D.A.; Box, S.; Berger, B.R.; Fleck, R.J.; Ashley, R.P.; Newport, G.R.; Heinemeyer, G.R. Crustal controls on magmatic-hydrothermal systems: A geophysical comparison of White River, Washington, with Goldfield, Nevada. Geosphere 2007, 3, 91–107. [Google Scholar] [CrossRef]

| Subsystem. | Band No. | Spectral Range | Spatial Resolution |
|---|---|---|---|
| VNIR | 1 | 0.52–0.60 | 15 m |
| 2 | 0.63–0.69 | ||
| 3N | 0.78–0.86 | ||
| 3B | 0.78–0.86 | ||
| SWIR | 4 | 1.600–1.700 | 30 m |
| 5 | 2.145–2.185 | ||
| 6 | 2.185–2.225 | ||
| 7 | 2.235–2.285 | ||
| 8 | 2.295–2.365 | ||
| 9 | 2.360–2.430 | ||
| TIR | 10 | 8.125–8.475 | 90 m |
| 11 | 8.475–8.825 | ||
| 12 | 8.925–9.275 | ||
| 13 | 10.25–10.95 | ||
| 14 | 10.95–11.65 |
| Sampling Area and Approximate Location | SiO2 (%) | Lithology | Minerals | Texture |
|---|---|---|---|---|
| Felsic Samples | ||||
| 1. Cup_qz (37°37′35″ N/117°16′58″ W) | ≒100 | Quartzite | Quartz | Well-sorted quartz grains |
| Quartzite in the northwest of Cuprite, Nevada, USA | ||||
| 2. Navajo (37°42′05″ N/111°22′35″ W) | ≒100 | Quartzose sandstone | Quartz | Well-sorted quartz grains |
| Navajo Sandstone in Utah, USA | ||||
| 3. Sahara (25°47′14″ N/25°21′07″ E) | ≒100 | Quartzose sediments | Quartz | Unconsolidated Well-sorted quartz grains |
| Sand dunes in western New Valley, Egypt | ||||
| 4. SN_obs (37°54′40″ N, 119°01′20″ W) | ≒100 | Obsidian | Glass | Amorphous |
| Obsidian on the hills in south side of Mono Lake, California, USA | ||||
| 5. Kilauea (19°16′55″ N, 155°21′08″ W) | ? | Amorphous silica on pahoehoe lava | Glass | Amorphous |
| Basalt lava with thin silica coating in Kilauea Volcano, Hawaii, USA | ||||
| 6. SN_gr1 (37°52′47″ N, 119°20′58″ W) | 66~70 | Granite | Quartz Feldspar | Crystalline |
| Granite of Lembert dome in Yosemite, California, USA | ||||
| 7. SN_gr2 (37°28′ 48″ N, 119°29′ 09″ W) | 66~70 | Granite | Quart Feldspar Biotite | Crystalline |
| Granite near Olmsted Point in Yosemite, California, USA | ||||
| 8. SN_gr3 (37°50′43″ N, 119°26′40″ W) | 66~70 | Granite | Quartz Feldspar Biotite | Crystalline |
| Granite in the North of Tenaya Lake in Yosemite, California, USA | ||||
| Mafic Samples | ||||
| 9. Dyke_gb (20°19′07″ S, 29°48′27″ E) Gabbro in southern in the southern Great Dyke, Midlands, Zimbabwe | 45~52 | Gabbro | Amphibole Pyroxene Plagioclase | Crystalline |
| 10. Dyke_sp (20°26′23″ S, 29°44′35″ E) Serpentinite in the southern Great Dyke, Midlands, Zimbabwe | 32~43 | Serpentinite | Serpentine | Crystalline |
| Sampling Area. | Average of T-Depth |
|---|---|
| Felsic Samples | |
| Cup_qz | 10.058 |
| Navajo | 12.464 |
| Sahara | 31.009 |
| SN_obs | 4.804 |
| Kilauea | 10.388 |
| SN_gr1 | 4.944 |
| SN_gr2 | 5.440 |
| SN_gr3 | 4.542 |
| Mafic Samples | |
| Dyke_gb | 2.394 |
| Dyke_sp | 1.387 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurata, K.; Yamaguchi, Y. Integration and Visualization of Mineralogical and Topographical Information Derived from ASTER and DEM Data. Remote Sens. 2019, 11, 162. https://doi.org/10.3390/rs11020162
Kurata K, Yamaguchi Y. Integration and Visualization of Mineralogical and Topographical Information Derived from ASTER and DEM Data. Remote Sensing. 2019; 11(2):162. https://doi.org/10.3390/rs11020162
Chicago/Turabian StyleKurata, Kana, and Yasushi Yamaguchi. 2019. "Integration and Visualization of Mineralogical and Topographical Information Derived from ASTER and DEM Data" Remote Sensing 11, no. 2: 162. https://doi.org/10.3390/rs11020162
APA StyleKurata, K., & Yamaguchi, Y. (2019). Integration and Visualization of Mineralogical and Topographical Information Derived from ASTER and DEM Data. Remote Sensing, 11(2), 162. https://doi.org/10.3390/rs11020162