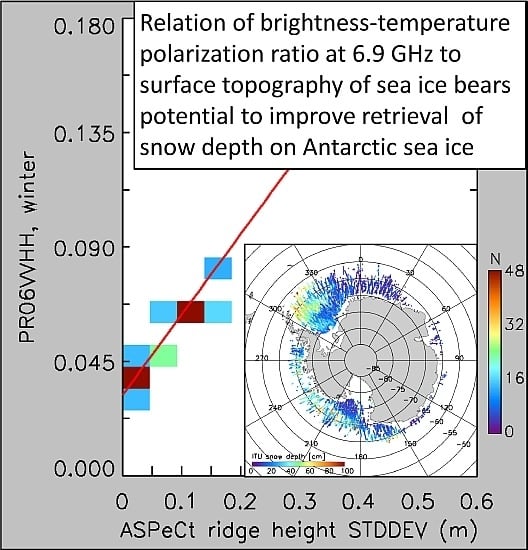
An Attempt to Improve Snow Depth Retrieval Using Satellite Microwave Radiometry for Rough Antarctic Sea Ice
Abstract
1. Introduction
2. Data
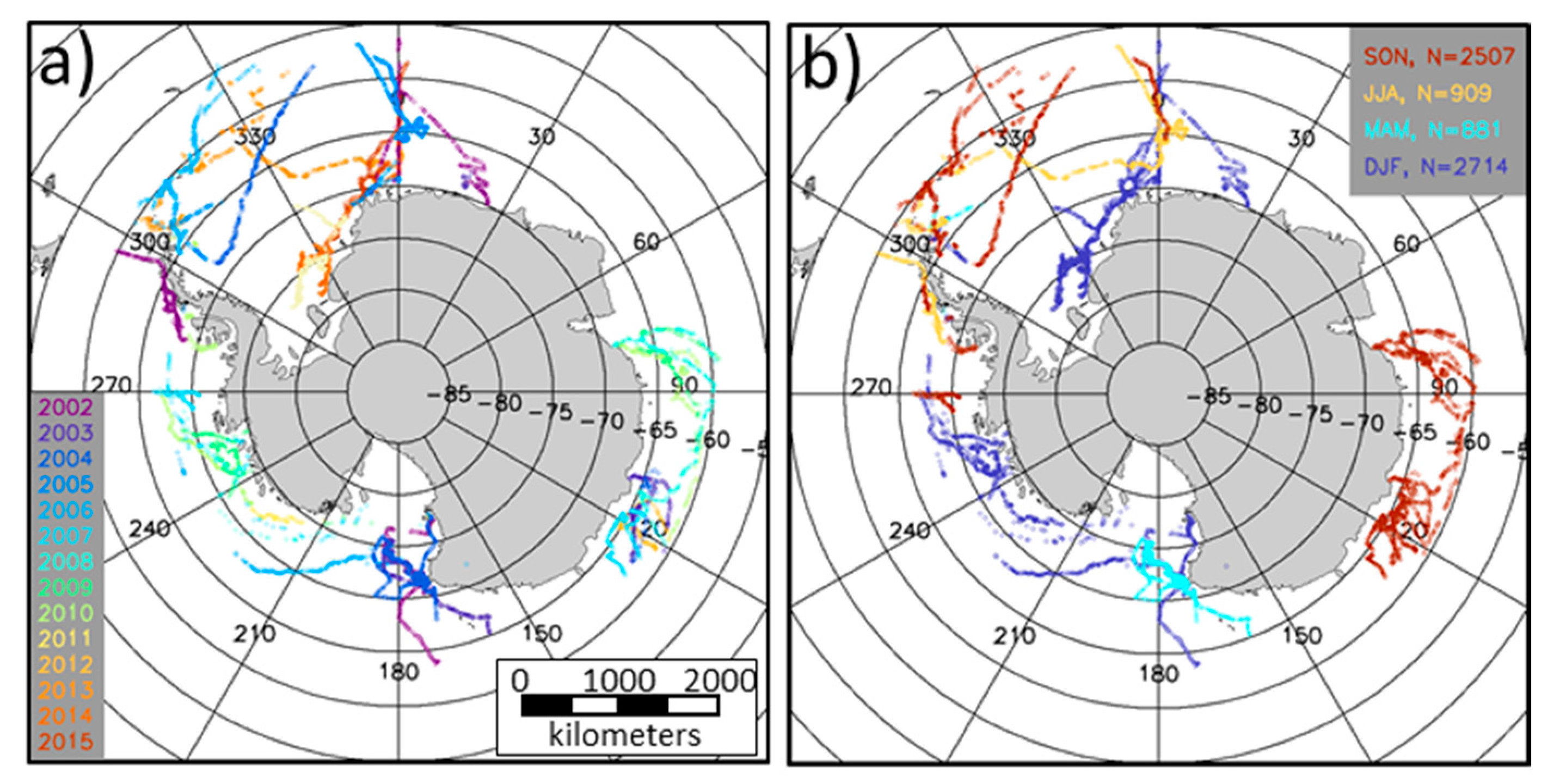
2.1. Ship-Based Observations
2.2. Brightness Temperatures
2.3. ICESat Surface Roughness
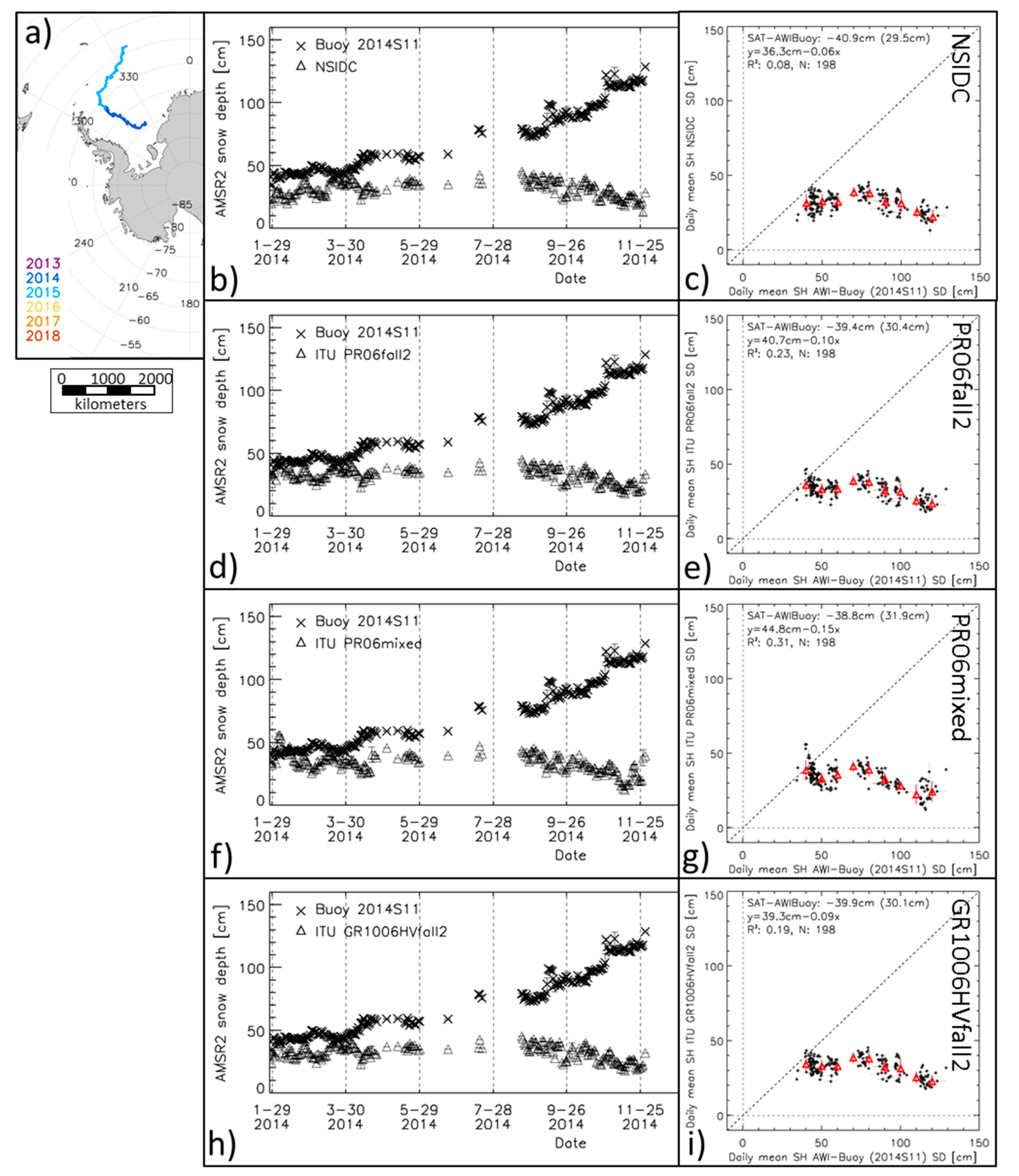
2.4. AWI Snow Buoy Data
3. Methodologies
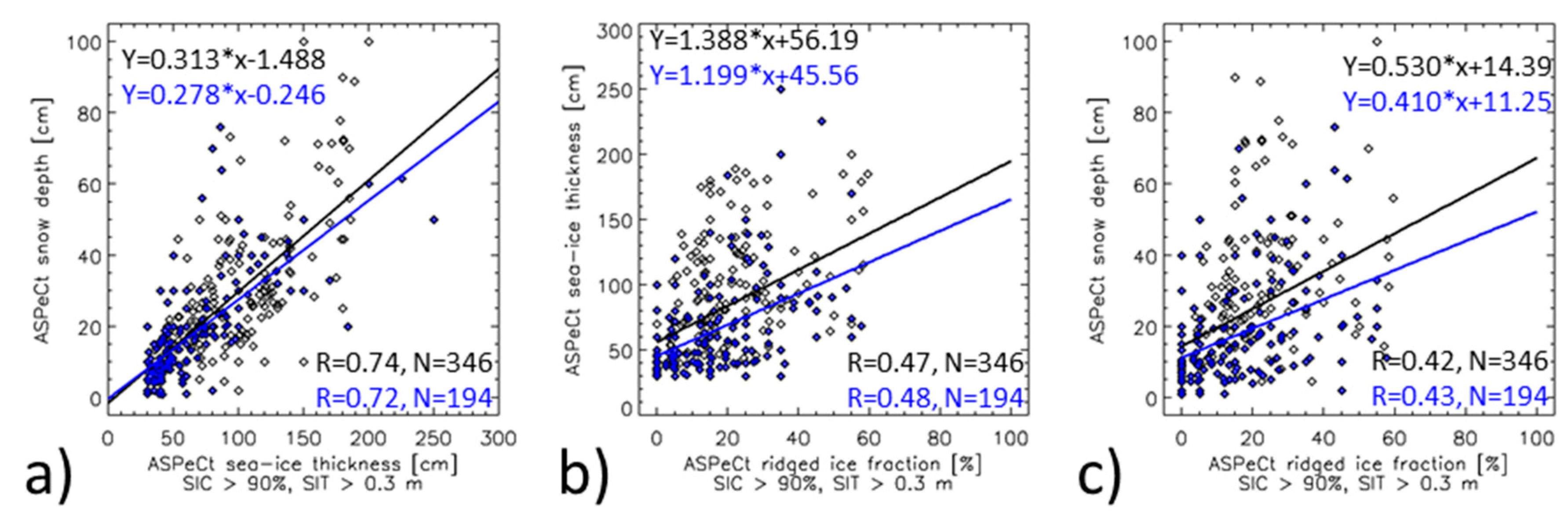
3.1. Quality Check of the Input Data and Confirmation of Recent Findings
3.2. Algorithm Development
4. Results
4.1. Snow Depths from Co-Located Data Sets
4.2. AMSR-E/AMSR2 Snow Depth Compared to Ship-Based Snow-Depth Observations
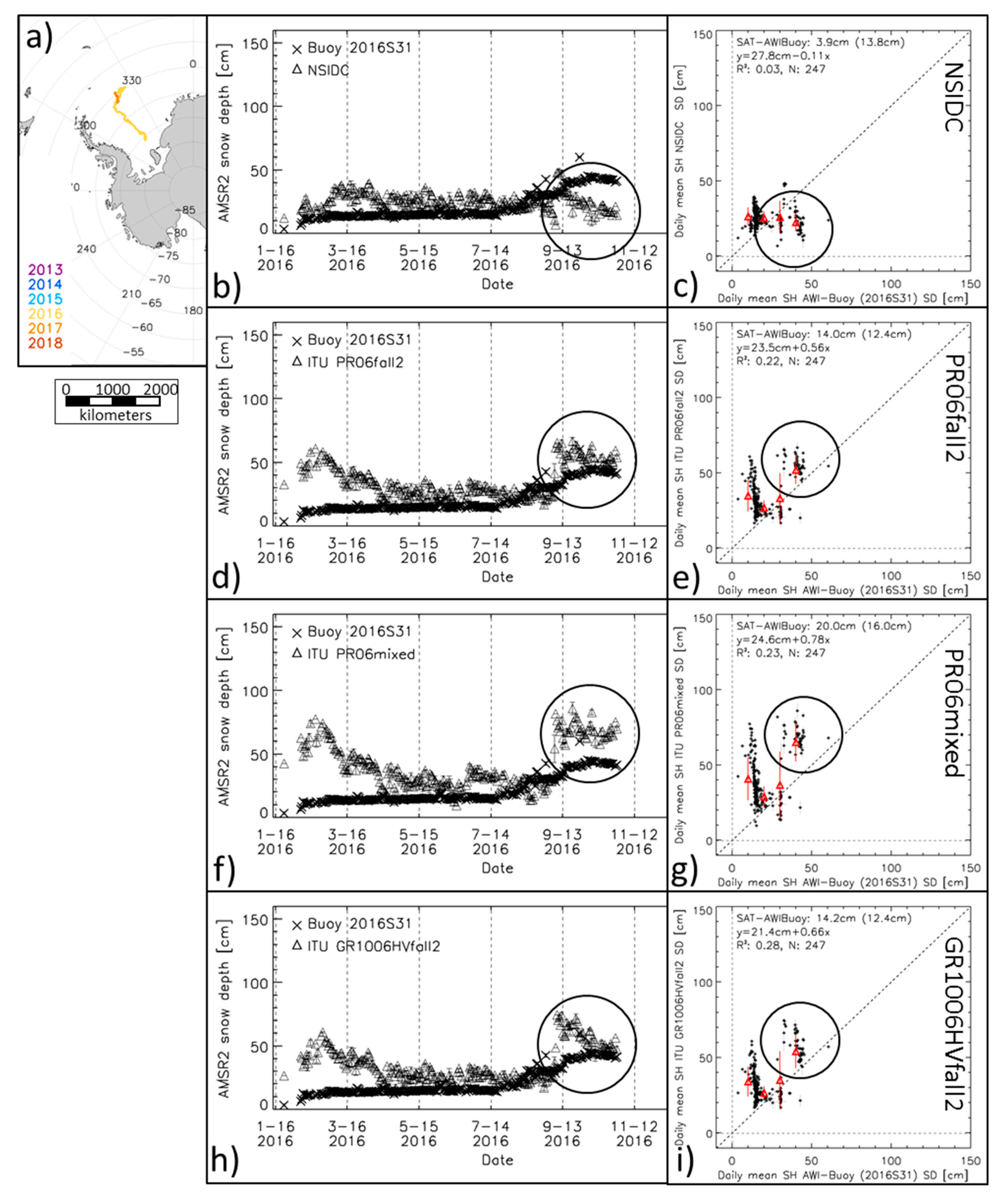
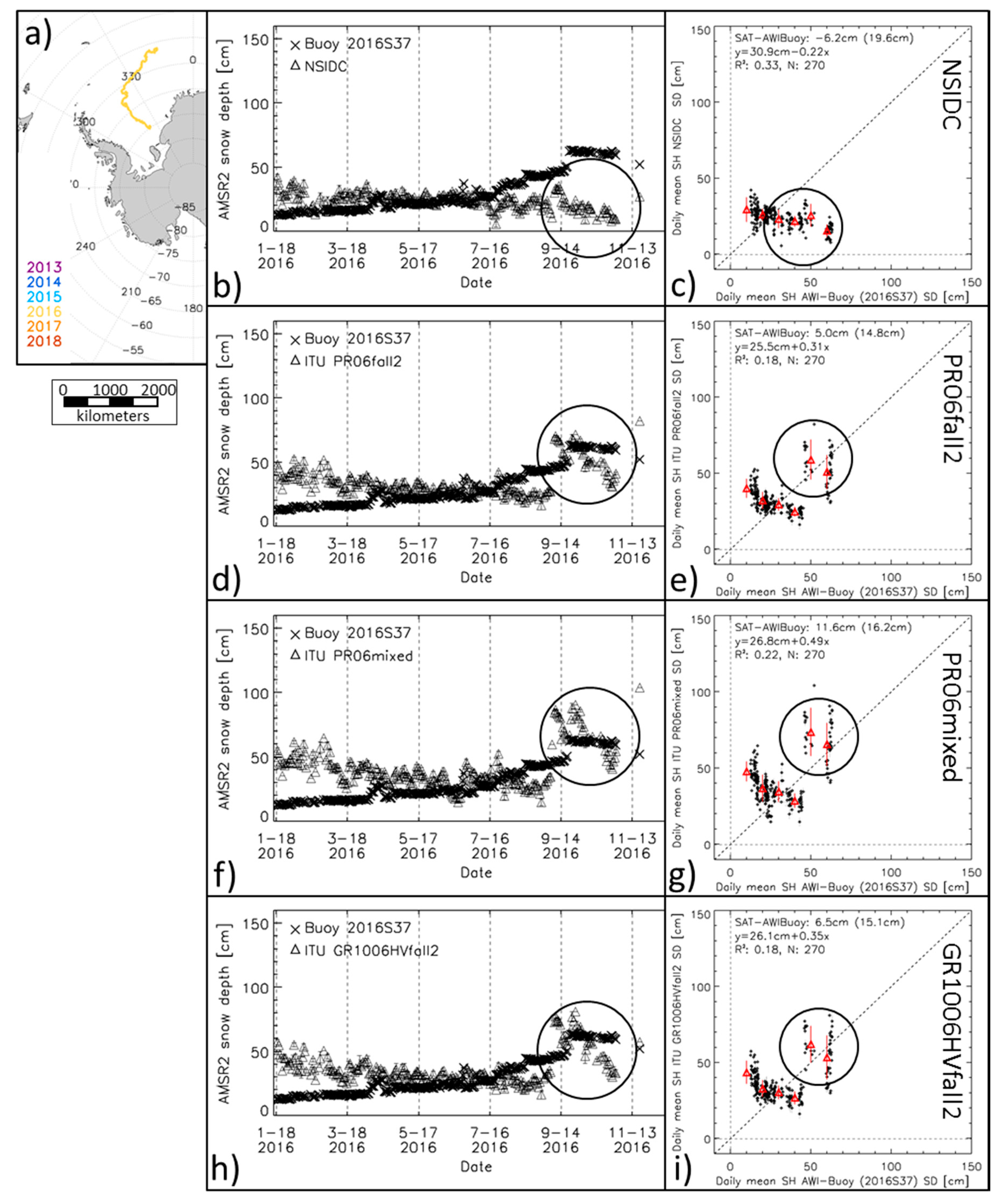
4.3. AMSR2 Snow Depth Compared to Buoy Snow-Depth Observations
5. Discussion
5.1. Differences in the Observations Themselves
5.2. Differences in the Scales
5.3. Discussion of the Inter-Comparison Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Comiso, J. Polar Oceans from Space, 1st ed.; Atmospheric and Oceanographic Sciences Library; Springer Science+Business Media: New York, NY, USA, 2010; Volume 41. [Google Scholar]
- Andreas, L.A. A theory for the scalar roughness and the scalar transfer coefficients over snow and sea ice. Bound. Lay. Meteorol. 1987, 38, 159–184. [Google Scholar] [CrossRef]
- Adolphs, U. Roughness variability of sea ice and snow cover thickness profiles in the Ross, Amundsen, and Bellingshausen Seas. J. Geophys. Res. 1999, 104, 13577–13591. [Google Scholar] [CrossRef]
- Maksym, T.; Markus, T. Antarctic sea ice thickness and snow-to-ice conversion from atmospheric reanalysis and passive microwave snow depth. J. Geophys. Res. 2008, 113, C02S12. [Google Scholar] [CrossRef]
- Granskog, M.A.; Rösel, A.; Dodd, P.A.; Divine, D.; Gerland, S.; Martma, T.; Leng, M.J. Snow contribution to first-year and second-year Arctic sea ice mass balance north of Svalbard. J. Geophys. Res. Oceans 2017, 122, 2539–2549. [Google Scholar] [CrossRef]
- Laxon, S.W.; Peacock, N.; Smith, D. High interannual variability of sea-ice thickness in the Arctic region. Nature 2003, 425, 947–950. [Google Scholar] [CrossRef] [PubMed]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea-ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef]
- Paul, S.; Hendricks, S.; Ricker, R.; Kern, S.; Rinne, E. Empirical parametrization of Envisat freeboard retrieval of Arctic and Antarctic sea ice based on CryoSat-2: Progress in the ESA Climate Change Initiative. Cryosphere 2018, 12, 2437–2460. [Google Scholar] [CrossRef]
- Giles, K.A.; Laxon, S.W.; Worby, A.P. Antarctic sea ice elevation from satellite radar altimetry. Geophys. Res. Lett. 2008, 35, L03503. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. ICESat over Arctic sea ice: Estimation of snow depth and thickness. J. Geophys. Res. Oceans 2008, 113, C08010. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F. Variability of Arctic sea ice thickness and volume from CryoSat-2. Philos. Trans. R. Soc. A 2015, 373, 20140157. [Google Scholar] [CrossRef]
- Kern, S.; Ozsoy-Cicek, B.; Worby, A.P. Antarctic sea ice thickness retrieval from ICESat: Inter-comparison of different approaches. Remote Sens. 2016, 8, 538. [Google Scholar] [CrossRef]
- Kwok, R.; Cunningham, G.F.; Zwally, H.J.; Yi, D. Ice, Cloud, and land Elevation Satellite (ICESat) over Arctic sea ice: Retrieval of freeboard. J. Geophys. Res. Oceans 2007, 112, C12013. [Google Scholar] [CrossRef]
- Ricker, R.; Hendricks, S.; Helm, V.; Skourup, H.; Davidson, M. Sensitivity of CryoSat-2 Arctic sea-ice freeboard and thickness on radar-waveform interpretation. Cryosphere 2014, 8, 1607–1622. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Markus, T.; Comiso, J.C. AMSR-E/Aqua daily L3 12.5 km Brightness Temperatures, Sea Ice Concentration, & Snow Depth Polar Grids; Version 3; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. Available online: https://doi.org/10.5067/AMSR-E/AE_SI12.003 (accessed on 26 April 2018).
- Markus, T.; Cavalieri, D.J. Snow depth distribution over sea ice in the southern ocean from satellite passive microwave data. In Antarctic Sea Ice: Physical Processes, Interactions and Variability; Jeffries, M.O., Ed.; AGU: Washington, DC, USA, 1998; Volume 74, pp. 19–39. [Google Scholar]
- Markus, T.; Cavalieri, D.J. Interannual and regional variability of Southern Ocean snow on sea ice. Ann. Glaciol. 2006, 44, 53–57. [Google Scholar] [CrossRef][Green Version]
- Cavalieri, D.J.; Markus, T.; Ivanoff, A.; Miller, J.A.; Brucker, L.; Sturm, M.; Maslanik, J.A.; Heinrichs, J.F.; Gasiewski, A.J.; Leuschen, C.; et al. A comparison of snow depth on sea ice retrievals using airborne altimters and AMSR-E simulator. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3027–3040. [Google Scholar] [CrossRef]
- Worby, A.P.; Markus, T.; Steer, A.D.; Lytle, V.I.; Massom, R.A. Evaluation of AMSR-E snow depth product over East Antarctic sea ice using in situ measurements and aerial photography. J. Geophys. Res. 2008, 113, C05S94. [Google Scholar] [CrossRef]
- Brucker, L.; Markus, T. Arctic-scale assessment of satellite passive microwave-derived snow depth on sea ice using Operation IceBridge airborne data. J. Geophys. Res. Oceans 2013, 118, 2892–2905. [Google Scholar] [CrossRef]
- Ozsoy-Cicek, B.; Kern, S.; Ackley, S.F.; Xie, H.; Tekeli, A.E. Intercomparisons of Antarctic sea ice types from visual ship, RADARSAT-1 SAR, Envisat ASAR, QuikSCAT, and AMSR-E satellite observations in the Bellingshausen Sea. Deep-Sea Res. Part II 2011, 58, 1092–1111. [Google Scholar] [CrossRef]
- Markus, T.; Massom, R.A.; Worby, A.P.; Lytle, V.I.; Kurtz, N.; Maksym, T. Freeboard, snow depth and sea-ice roughness in East Antarctica from in situ and multiple satellite data. Ann. Glaciol. 2011, 52, 242–248. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Markus, T.; Maslanik, J.A.; Cavalieri, D.J.; Gasiewski, A.J.; Heinrichs, J.F.; Holmgren, J.; Perovich, D.K.; Sturm, M. Impact of surface roughness on AMSR-E sea ice products. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3103–3117. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J.; Gasiewski, A.J.; Klein, M.; Maslanik, J.A.; Powell, D.C.; Stankov, B.B.; Stroeve, J.C.; Sturm, M. Microwave signatures of snow on sea ice: Observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3081–3090. [Google Scholar] [CrossRef]
- Kern, S.; Khvorostovsky, K.; Skourup, H.; Rinne, E.; Parsakhoo, Z.S.; Djepa, V.; Wadhams, P.; Sandven, S. The impact of snow depth, snow density and ice density on sea ice thickness retrieval from satellite radar altimetry: Results from the ESA-CCI Sea Ice ECV project round robin exercise. Cryosphere 2015, 9, 37–52. [Google Scholar] [CrossRef]
- Rösel, A.; Itkin, P.; King, J.; Divine, D.; Wang, C.; Granskog, M.A.; Krumpen, T.; Gerland, S. Thin sea ice, thick snow, and widespread negative freeboard observed during N-ICE2015 north of Svalbard. J. Geophys. Res. Oceans 2018, 123, 1156–1176. [Google Scholar] [CrossRef]
- Ozsoy-Cicek, B.; Ackley, S.F.; Xie, H.; Yi, D.; Zwally, J. Sea ice thickness retrieval algorithms based on in-situ surface elevation and thickness values for application to altimetry. J. Geophys. Res. Oceans 2013, 118, 3807–3822. [Google Scholar] [CrossRef]
- Kern, S.; Ozsoy-Cicek, B. Satellite remote sensing of snow depth on Antarctic sea ice: An inter-comparison of two empirical approaches. Remote Sens. 2016, 8, 450. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, L.; Liu, J.; Lu, H.; Wang, B. Data synergy between altimetry and L-Band passive microwave remote sensing for the retrieval of sea ice parameters-a theoretical study of methodology. Remote Sens. 2017, 9, 1079. [Google Scholar] [CrossRef]
- Guerreiro, K.; Fleury, S.; Zakharova, E.; Remy, F.; Kouraev, A. Potential for estimation of snow depth on Arctic sea ice from CryoSat-2 and SARAL/AltiKa missions. Remote Sens. Environ. 2016, 186, 339–349. [Google Scholar] [CrossRef]
- Rostosky, P.; Spreen, G.; Farrell, S.L.; Frost, T.; Heygster, G.; Melsheimer, C. Snow depth retrieval on Arctic sea ice from passive microwave radiometers-Improvements and extensions to multiyear ice using lower frequencies. J. Geophys. Res. Oceans 2018, 123, 7120–7138. [Google Scholar] [CrossRef]
- Maass, N.; Kaleschke, L.; Tian-Kunze, X.; Drusch, M. Snow thickness retrieval over thick Arctic sea ice using SMOS satellite data. Cryosphere 2013, 7, 1971–1989. [Google Scholar] [CrossRef]
- Maass, N.; Kaleschke, L.; Tian-Kunze, X.; Tonboe, R.T. Snow thickness retrieval from L-Band brightness temperatures: A model comparison. Ann. Glaciol. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Worby, A.P.; Geiger, C.A.; Paget, M.J.; Van Woert, M.L.; Ackley, S.F.; DeLiberty, T.L. The thickness distribution of Antarctic sea ice. J. Geophys. Res. 2008, 113, C05S92. [Google Scholar] [CrossRef]
- Worby, A.P.; Allison, I.A. Ship-Based Technique for Observing Antarctic Sea Ice: Part I: Observational Techniques and Results; Research Report No. 14; Antarctic Cooperative Research Centre: Hobart, Australia, 1999; Volume 14, 64p. [Google Scholar]
- Worby, A.P.; Dirita, V. A Technique for Making Ship-Based Observations of Antarctic Sea-Ice Thickness and Characteristics—Part II: User Operating Manual; Research Report No. 14; Antarctic Cooperative Research Centre: Hobart, Australia, 1999; Volume 14, 64p. [Google Scholar]
- Tekeli, A.E.; Kern, S.; Ackley, S.F.; Ozsoy-Cicek, B.; Xie, H. Summer Antarctic sea ice as seen by ASAR and AMSR-E and observed during two IPY field cruises: A case study. Ann. Glaciol. 2011, 52, 327–336. [Google Scholar] [CrossRef]
- Beitsch, A.; Kern, S.; Kaleschke, L. Comparison of SSM/I and AMSR-E sea ice concentrations with ASPeCt ship observations around Antarctica. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1985–1996. [Google Scholar] [CrossRef]
- Kern, S. Standardized Sea-Ice Parameters from Ship-Based Manual Visual Observations under the ASPeCt and ASSIST/IceWatch Protocols for 2002 through 2015; Version 1; Integrated Climate Data Center: Hamburg, Germany, 2019; Available online: https://icdc.cen.uni-hamburg.de/1/daten/cryosphere/seaiceparameter-shipobs/ (accessed on 12 April 2019).
- Pedersen, L.T.; Saldo, R.; Ivanova, N.; Kern, S.; Heygster, G.; Tonboe, R.T.; Huntemann, M.; Ozsoy, B.; Girard-Ardhuin, F.; Kaleschke, L. Reference Dataset for Sea Ice Concentration. 2019. Available online: https://figshare.com/articles/Reference_dataset_for_sea_ice_concentration/6626549 (accessed on 4 October 2019).
- Cavalieri, D.J.; Markus, T.; Comiso, J.C. AMSR-E/Aqua Daily L3 25 km Brightness Temperatures & Sea Ice Concentration Polar Grids; Version 3; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. Available online: https://doi.org/10.5067/AMSR-E/AE_SI25.003 (accessed on 26 April 2018).
- Markus, T.; Comiso, J.C.; Meier, W.N. AMSR-E/AMSR2 Unified L3 Daily 25 km Brightness Temperatures & Sea Ice Concentration Polar Grids; Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. Available online: https://doi.org/10.5067/TRUIAL3WPAUP (accessed on 18 May 2019).
- Meier, W.N.; Markus, T.; Comiso, J.C. AMSR-E/AMSR2 Unified L3 Daily 12.5 km Brightness Temperatures, Sea Ice Concentration, Motion & Snow Depth Polar Grids; Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. Available online: https://doi.org/10.5067/RA1MIJOYPK3P (accessed on 18 May 2019).
- Zwally, H.J.; Schutz, R.; Bentley, C.; Bufton, J.; Herring, T.; Minster, J.; Spinhirne, J.; Ross, T. GLAS/ICESat L2 Sea Ice Altimetry Data; Version 33; [Periods 2B to 3J]; National Snow and Ice Data Center: Boulder, CO, USA, 2011.
- Kern, S.; Spreen, G. Uncertainties in Antarctic sea-ice thickness retrieval from ICESat. Ann. Glaciol. 2015, 56, 107–119. [Google Scholar] [CrossRef]
- Nicolaus, M.; Arndt, S.; Hendricks, S.; Heygster, G.; Hoppmann, M.; Huntemann, M.; Katlein, C.; Langevin, D.; Rossmann, L.; König-Langlo, G. Snow depth and air temperature on sea ice derived from autonomous snow buoy measurements. In Proceedings of the ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Grosfeld, K.; Treffeisen, R.; Asseng, J.; Bartsch, A.; Bräuer, B.; Fritzsch, B.; Gerdes, R.; Hendricks, S.; Hiller, W.; Heygster, G.; et al. Online Sea-Ice Knowledge and Data Platform www.meereisportal.de; Alfred Wegener Institute, Helmholtz Center for Polar and Marine Research: Polarforschung, Bremerhaven, 2016; Volume 85, pp. 143–155. [Google Scholar] [CrossRef]
- Nicolaus, M.; Hoppmann, M.; Arndt, S.; Hendricks, S.; Katlein, C.; König-Langlo, G.; Nicolaus, A.; Rossmann, L.; Schiller, M.; Schwegmann, S.; et al. Snow Height and Air Temperature on Sea Ice from Snow Buoy Measurements; Alfred Wegener Institute, Helmholtz Center for Polar and Marine Research: Polarforschung, Bremerhaven, 2017. [Google Scholar] [CrossRef]
- Mei, M.J.; Maksym, T.; Singh, H. Estimating early-winter Antarctic sea ice thickness from deformed ice morphology. Cryosphere Disc. 2019. [Google Scholar] [CrossRef]
- Kwok, R.; Maksym, T. Snow depth of the Weddell and Bellingshausen sea ice covers from IceBridge surveys in 2010 and 2011: An examination. J. Geophys. Res. Oceans 2014, 119, 4141–4167. [Google Scholar] [CrossRef]
- Tonboe, R.T.; Pedersen, L.T. D2.1 Sea Ice Concentration Algorithm Theoretical Basis Document ATBD; SICCI-P2-ATBD(SIC), Issue 1.0; European Space Agency: Paris, France, 2017; 178p. [Google Scholar]
- Powell, D.C.; Markus, T.; Cavalieri, D.J.; Gasiewski, A.J.; Klein, M.; Maslanik, J.A.; Stroeve, J.C.; Sturm, M. Microwave signatures of snow on sea ice: Modelling. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3091–3102. [Google Scholar] [CrossRef]
- Farmer, D.L.; Eppler, D.T.; Lohanick, A.W. Passive microwave signatures of fractures and ridges in sea ice and 33.6 GHz (vertical polarization) as observed in aircraft images. J. Geophys. Res. 1995, 98, 4645–4665. [Google Scholar] [CrossRef]
- Maslanik, J.A.; Sturm, M.; Belmonte-Rivas, M.; Gasiewski, A.J.; Heinrichs, J.F.; Herzfeld, U.C.; Holmgren, J.; Klein, M.; Markus, T.; Perovich, D.K.; et al. Spatial variability of Barrow-area shore-fast sea ice and its relationships to passive microwave emissivity. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3021–3031. [Google Scholar] [CrossRef]
- Frost, T.; Heygster, G.; Kern, S. ANT D1.1 Passive Microwave Snow Depth on Antarctic Sea Ice Assessment; ESA-CCI Sea Ice ECV Project Report, SICCI-ANT-PMW-SDASS-11-14; European Space Agency: Paris, France, 2014; 166p, Available online: http://icdc.cen.uni-hamburg.de/1/projekte/esa-cci-sea-ice-ecv0.html (accessed on 4 October 2019).
- Kern, S.; Frost, T.; Heygster, G. ANT D1.3 Product User Guide (PUG) for Antarctic Snow Depth Product SD v1.1; ESA-CCI Sea Ice ECV Project Report, SICCI-ANT-SD-PUG-14-08; European Space Agency: Paris, France, 2014; 15p, Available online: http://icdc.cen.uni-hamburg.de/1/projekte/esa-cci-sea-ice-ecv0.html (accessed on 4 October 2019).
- Yi, D.; Zwally, H.J.; Robbins, J.W. ICESat observations of seasonal and interannual variations of sea-ice freeboard and estimated thickness in the Weddell Sea, Antarctica (2003–2009). Ann. Glaciol. 2011, 52, 43–51. [Google Scholar] [CrossRef]
- Grenfell, T.C.; Cavalieri, D.J.; Comiso, J.C.; Drinkwater, M.R.; Onstott, R.G.; Rubinstein, I.; Steffen, K.; Winebrenner, D.P. Considerations for microwave remote sensing of thin sea ice. In Microwave Remote Sensing of Sea Ice; Carsey, F.D., Ed.; American Geophysics Union: Washington, DC, USA, 1992; Volume 68, pp. 201–231. [Google Scholar]
- Massom, R.A.; Worby, A.; Lytle, V.; Markus, T.; Allison, I.; Scambos, T.; Enomoto, H.; Tateyama, K.; Haran, T.; Comiso, J.C.; et al. ARISE (Antarctic Remote Ice Sensing Experiment) in the East 2003: Validation of satellite-derived sea-ice data products. Ann. Glaciol. 2006, 44, 288–296. [Google Scholar] [CrossRef]
- Heil, P.; Massom, R.A.; Allison, I.; Worby, A.P.; Lytle, V.I. Role of off-shelf to on-shelf transitions for East Antarctic sea ice dynamics during spring 2003. J. Geophys. Res. 2009, 114, C09010. [Google Scholar] [CrossRef]
- Heil, P.; Stammerjohn, S.; Reid, P.; Massom, R.A.; Hutchings, J.K. SIPEX 2012: Extreme sea-ice and atmospheric conditions off East Antarctica. Deep Sea Res. Part II 2016, 131, 7–21. [Google Scholar] [CrossRef]
- Meiners, K. ASPeCt-Bio: Chlorophyll a in Antarctic Sea Ice from Historical Ice Core Dataset (2013, updated 2017). Australian Antarctic Data Centre—CAASM Metadata. Available online: https://data.aad.gov.au/metadata/records/ASPeCt-Bio (accessed on 24 September 2019).
- Tison, J.-L.; Maksym, T.; Lieser, J.; Carnat, G.; Sapart, C.; Ackley, S.; de Jong, J.; Vanderlindens, F.; Stammerjohn, S.; Delille, B. Physical and Biogeochemical Properties of Winter Sea Ice during PIPERS, Ross Sea. Abstract A-938-0055-00744. In Proceedings of the POLAR 2018—SCAR Open Science Conference, Davos, Switzerland, 19–23 June 2018. [Google Scholar]
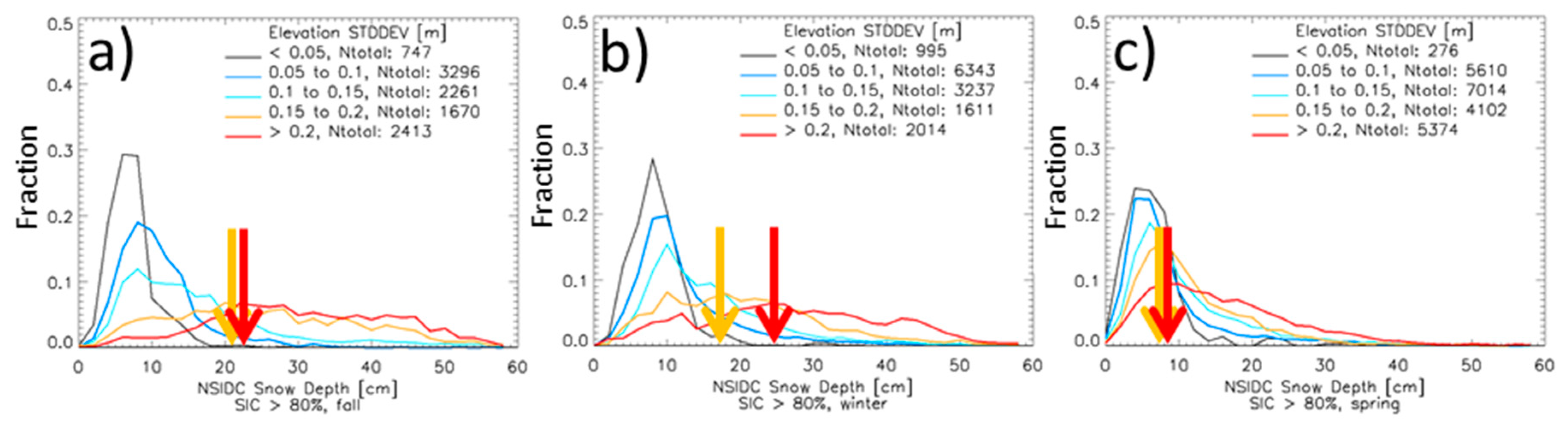
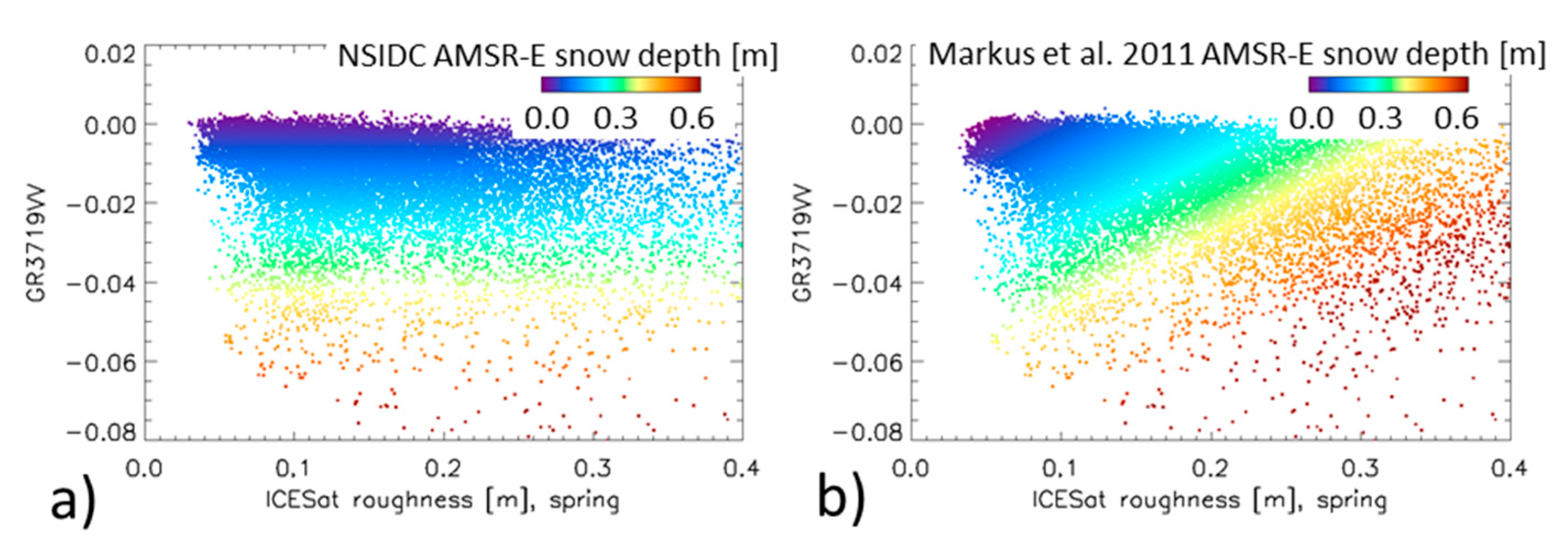
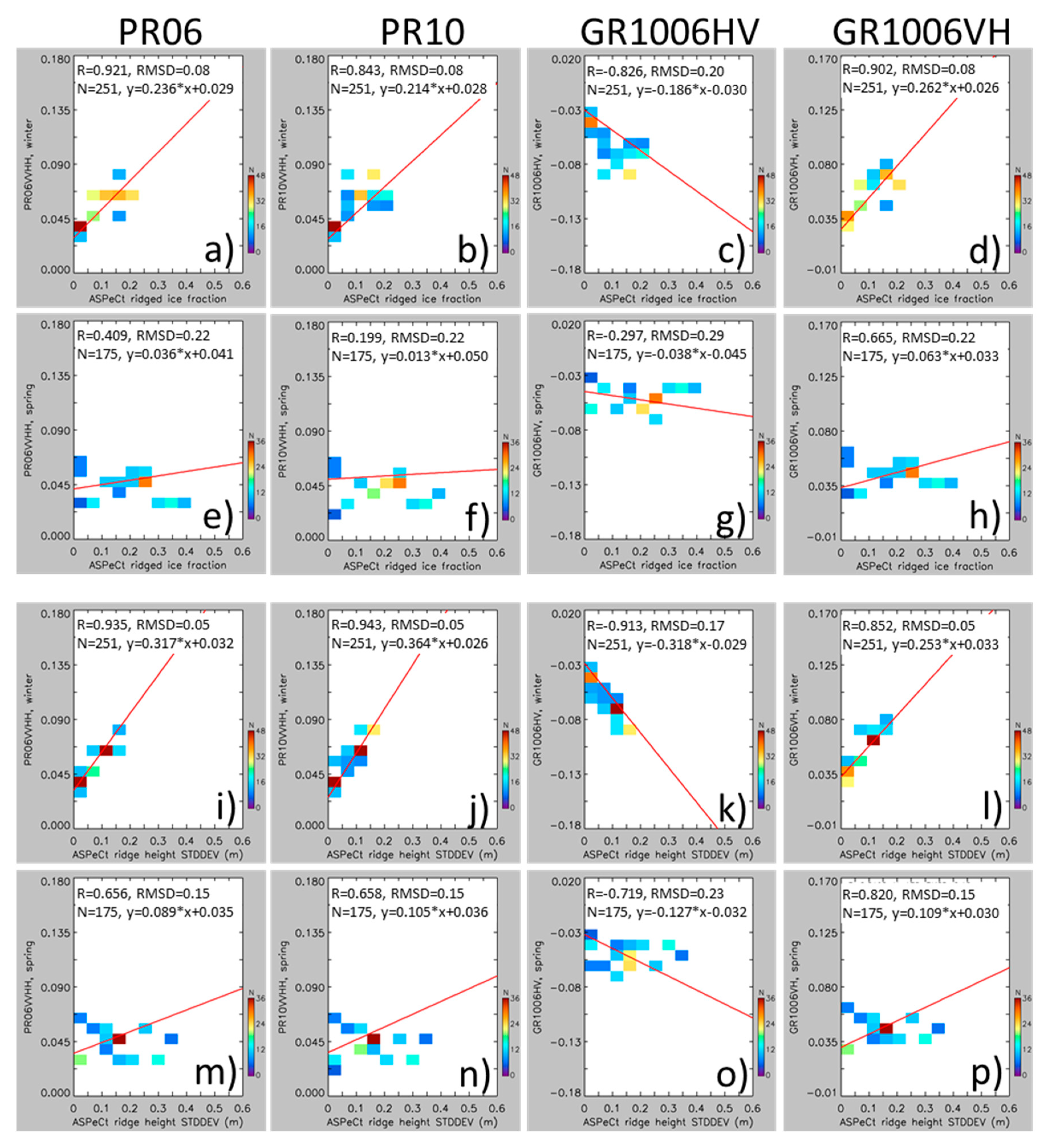

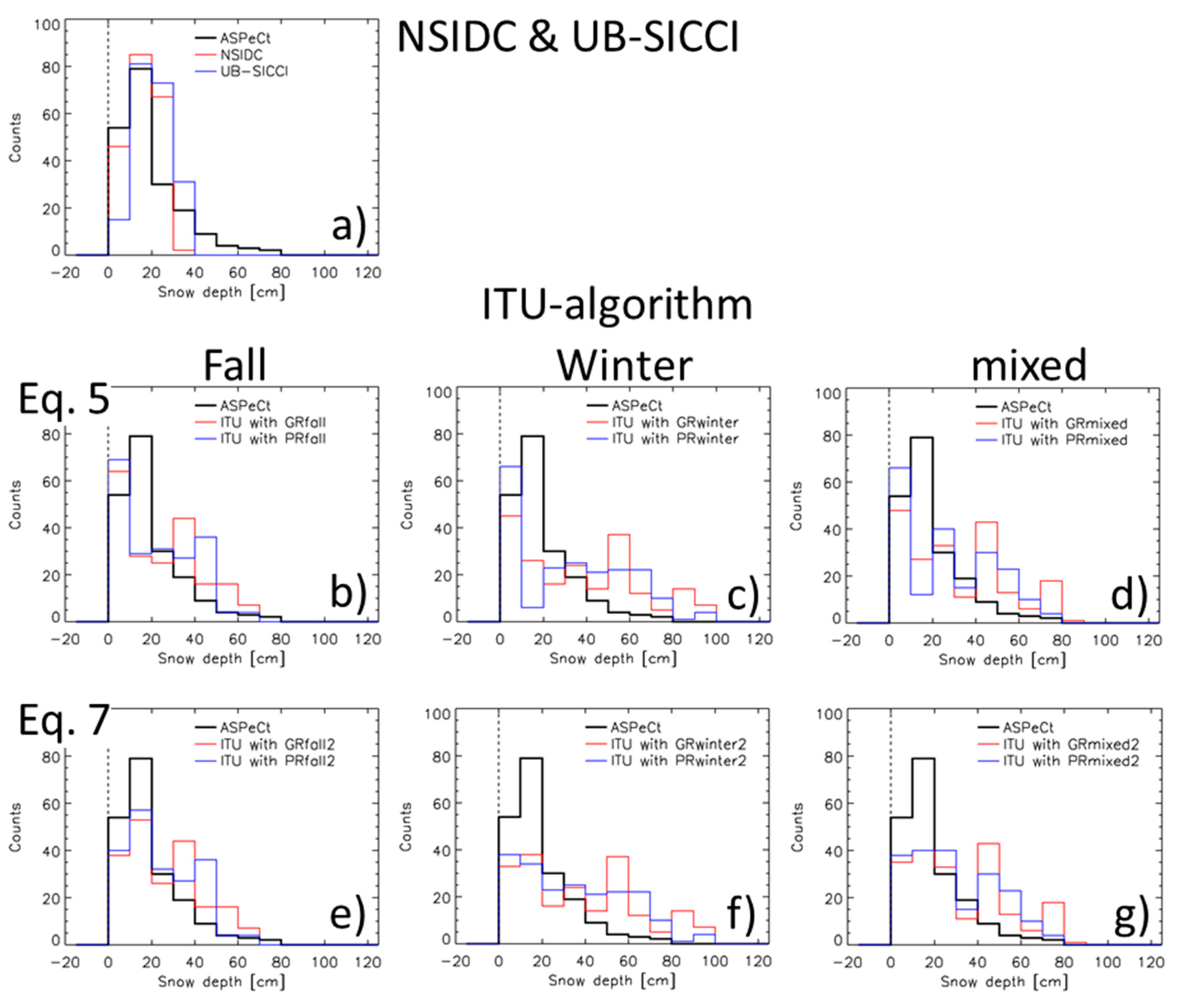
| Year | Spring (ON) | Fall (FM) | Winter (MJ) |
|---|---|---|---|
| 2003 | 25 September–17 November (ON03) | – | – |
| 2004 | 3 October–8 November (ON04) | 17 February–21 March (FM04) | 18 May–21 June (MJ04) |
| 2005 | 21 October–24 November (ON05) | 17 February–24 March (FM05) | 20 May–23 June (MJ05) |
| 2006 | 25 October–27 November (ON06) | 22 February–27 March (FM06) | 24 May–26 June (MJ06) |
| 2007 | 2 October–5 November (ON07) | 12 March–14 April (MA07) | – |
| 2008 | 3–18 October; 24 November–16 December (ND08) | 18 February–20 March (FM08) | – |
| 2009 | – | 8 March–10 April (MA09) | – |
| All Year | Fall | Winter | Spring | |
|---|---|---|---|---|
| GR1006HV | 0.366 | 0.721 | 0.476 | 0.195 |
| GR1006VH | 0.390 | 0.454 | 0.383 | 0.145 |
| PR06 | 0.400 | 0.732 | 0.552 | 0.000 |
| PR10 | 0.365 | 0.628 | 0.527 | 0.170 |
| Fall Coefficients | Winter Coefficients | Mixed Coefficients | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ASPeCt-AMSRX | R2 | ASPeCt-AMSRX | R2 | ASPeCt-AMSRX | R2 | |||||||
| Mean | Sdev | Median | Mean | Sdev | Median | Mean | Sdev | Median | ||||
| NSIDC | 1.1 | 14.4 | −2.5 | 0.16 | 1.1 | 14.4 | −2.5 | 0.16 | 1.1 | 14.4 | −2.5 | 0.16 |
| UB-SICCI | −2.8 | 14.7 | −6.3 | 0.16 | −2.8 | 14.7 | −6.3 | 0.16 | −2.8 | 14.7 | −6.3 | 0.16 |
| GR1006HV, Equation (5) | −6.8 | 21.0 | −6.6 | 0.19 | −19.8 | 28.7 | −19.3 | 0.19 | −13.3 | 24.7 | −13.4 | 0.19 |
| GR1006HV, Equation (7) | −8.8 | 19.6 | −8.1 | 0.18 | −21.2 | 27.2 | −19.3 | 0.18 | −14.9 | 23.3 | −14.2 | 0.18 |
| PR06, Equation (5) | −4.4 | 20.2 | −4.2 | 0.21 | −15.2 | 26.6 | −14.8 | 0.21 | −9.8 | 23.3 | −10.2 | 0.21 |
| PR06, Equation (7) | −7.1 | 18.5 | −6.7 | 0.19 | −17.4 | 24.7 | −17.1 | 0.20 | −12.2 | 21.4 | −10.8 | 0.20 |
| Season | Fall | Winter | Spring | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameters | ΔS | σS | R | ΔS | σS | R | ΔS | σS | R |
| NSIDC-Markus2011 | −6.5 | 8.4 | 0.92 | −3.8 | 7.6 | 0.90 | −9.1 | 8.7 | 0.75 |
| GR1006HVfall | |||||||||
| Markus2011-ITU, Equation (5) | −1.0 | 13.5 | 0.80 | −0.3 | 14.3 | 0.71 | 4.0 | 13.3 | 0.59 |
| As above but Equation (7) | −2.4 | 12.7 | 0.81 | −2.8 | 12.8 | 0.73 | 2.5 | 12.2 | 0.62 |
| NSIDC-ITU, Equation (5) | −7.6 | 12.4 | 0.89 | −4.2 | 12.2 | 0.87 | −5.1 | 9.7 | 0.88 |
| As above but Equation (7) | −8.0 | 11.0 | 0.90 | −6.7 | 10.2 | 0.88 | −6.5 | 8.3 | 0.90 |
| PR06fall | |||||||||
| Markus2011-ITU, Equation (5) | 2.3 | 12.7 | 0.80 | 3.4 | 12.5 | 0.73 | 4.8 | 13.3 | 0.54 |
| As above but Equation (7) | −0.1 | 11.5 | 0.81 | −0.1 | 10.9 | 0.76 | 3.1 | 11.9 | 0.59 |
| NSIDC-ITU, Equation (5) | −4.3 | 11.4 | 0.87 | −0.4 | 10.0 | 0.87 | −4.3 | 9.2 | 0.83 |
| As above but Equation (7) | −6.6 | 9.5 | 0.89 | −4.0 | 7.8 | 0.90 | −6.0 | 7.5 | 0.86 |
| PR06mixed | |||||||||
| Markus2011-ITU, Equation (5) | −2.8 | 16.0 | 0.77 | −0.1 | 15.5 | 0.69 | 0.2 | 15.8 | 0.50 |
| As above but Equation (7) | −4.6 | 14.6 | 0.77 | −3.1 | 13.7 | 0.71 | −1.1 | 14.5 | 0.53 |
| NSIDC-ITU, Equation (5) | −9.3 | 15.6 | 0.83 | −3.9 | 13.7 | 0.84 | −8.8 | 12.5 | 0.79 |
| As above but Equation (7) | −11.2 | 13.9 | 0.85 | −7.0 | 11.6 | 0.86 | −10.2 | 11.0 | 0.81 |
| Season | Fall → Winter | Winter → Spring |
|---|---|---|
| NSIDC | −4.2, −3.7 | −5.2, −4.9 |
| Markus2011 | −7.1, −6.5 | −0.1, +0.3 |
| ITU GR1006HVfall, Equation (5) | −7.1, −7.2 | −4.9, −4.0 |
| As above but Equation (7) | −6.1, −6.1 | −6.0, −5.0 |
| ITU PR06fall, Equation (5) | −7.6, −7.6 | −1.5, −1.1 |
| As above but Equation (7) | −6.6, −6.4 | −3.2, −1.9 |
| ITU PR06mixed, Equation (5) | −9.0, −9.2 | −0.5, 0.0 |
| As above but Equation (7) | −8.0, −8.0 | −2.1, −1.7 |
| All Year | Winter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
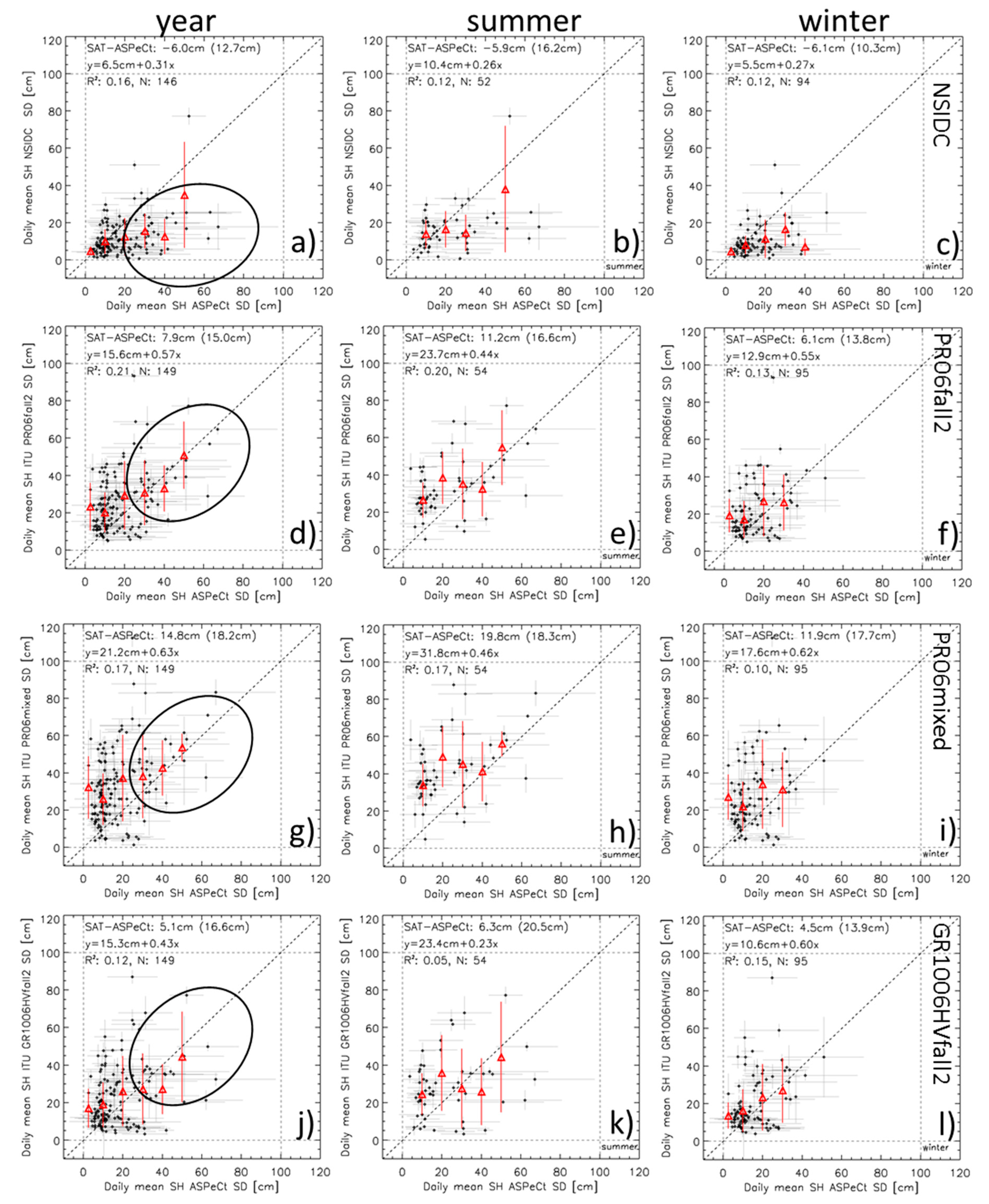
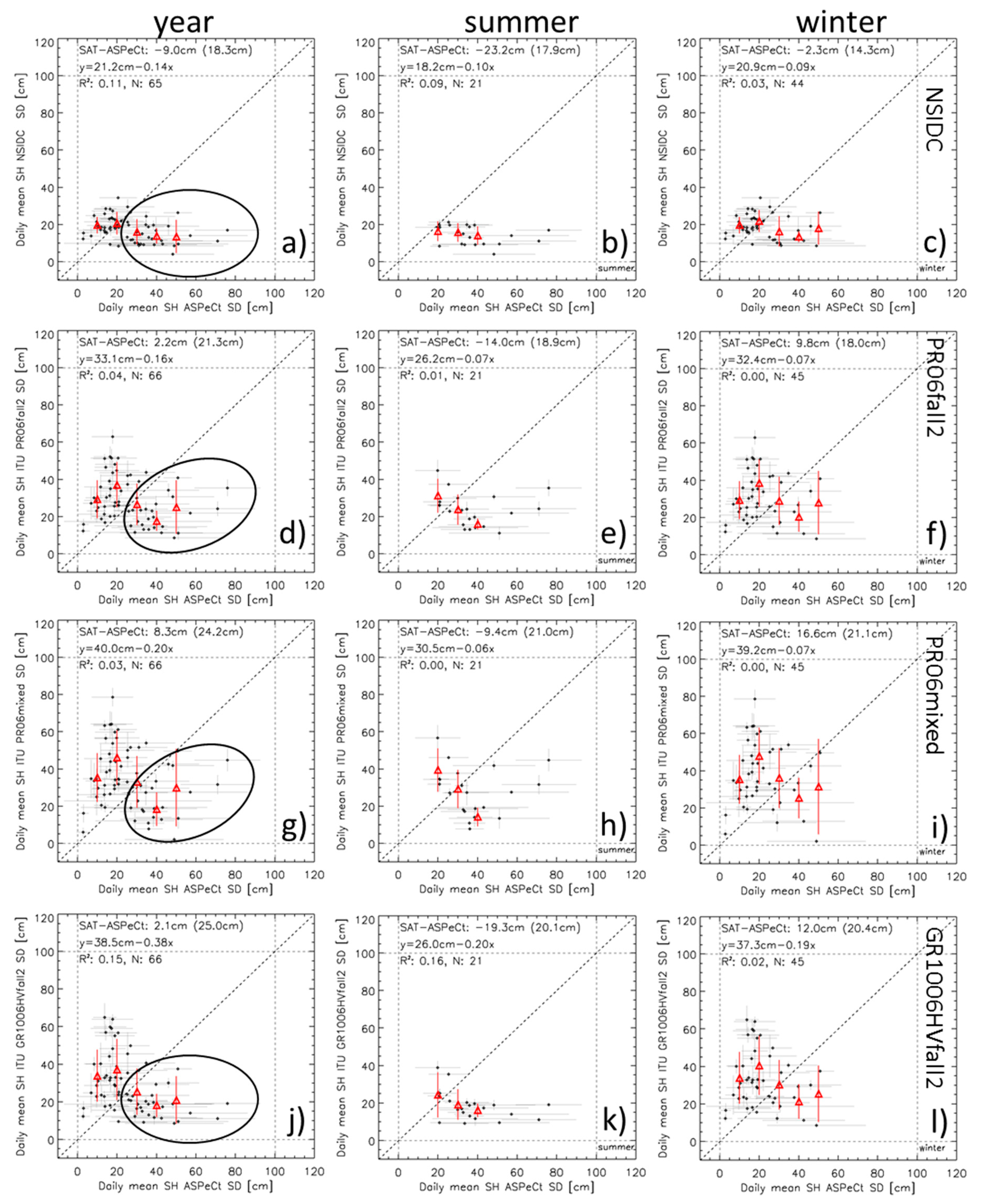
| Method, Nyear|Nwinter | SAT-ASPeCt [cm] Mean STDDEV | R2 | Slope | Intercept [cm] | SAT-ASPeCt [cm] Mean STDDEV | R2 | Slope | Intercept [cm] | ||
| NSIDC, 146|94 | −6.0 | 12.7 | 0.16 | 0.31 | 6.5 | −6.1 | 10.3 | 0.12 | 0.27 | 5.5 |
| UB-SICCI, 151|97 | −3.1 | 13.4 | 0.14 | 0.33 | 9.0 | −3.2 | 10.8 | 0.11 | 0.30 | 7.9 |
| PR06fall2, 149|95 | 7.9 | 15.0 | 0.21 | 0.57 | 15.6 | 6.1 | 13.8 | 0.14 | 0.55 | 12.9 |
| PR06mixed, 149|95 | 14.8 | 18.2 | 0.18 | 0.64 | 21.2 | 11.9 | 17.7 | 0.11 | 0.63 | 17.6 |
| GR1006HVfall2, 149|95 | 5.1 | 16.6 | 0.12 | 0.43 | 15.3 | 4.5 | 13.9 | 0.15 | 0.60 | 10.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kern, S.; Ozsoy, B. An Attempt to Improve Snow Depth Retrieval Using Satellite Microwave Radiometry for Rough Antarctic Sea Ice. Remote Sens. 2019, 11, 2323. https://doi.org/10.3390/rs11192323
Kern S, Ozsoy B. An Attempt to Improve Snow Depth Retrieval Using Satellite Microwave Radiometry for Rough Antarctic Sea Ice. Remote Sensing. 2019; 11(19):2323. https://doi.org/10.3390/rs11192323
Chicago/Turabian StyleKern, Stefan, and Burcu Ozsoy. 2019. "An Attempt to Improve Snow Depth Retrieval Using Satellite Microwave Radiometry for Rough Antarctic Sea Ice" Remote Sensing 11, no. 19: 2323. https://doi.org/10.3390/rs11192323
APA StyleKern, S., & Ozsoy, B. (2019). An Attempt to Improve Snow Depth Retrieval Using Satellite Microwave Radiometry for Rough Antarctic Sea Ice. Remote Sensing, 11(19), 2323. https://doi.org/10.3390/rs11192323