Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration
Abstract
1. Introduction
2. Methods
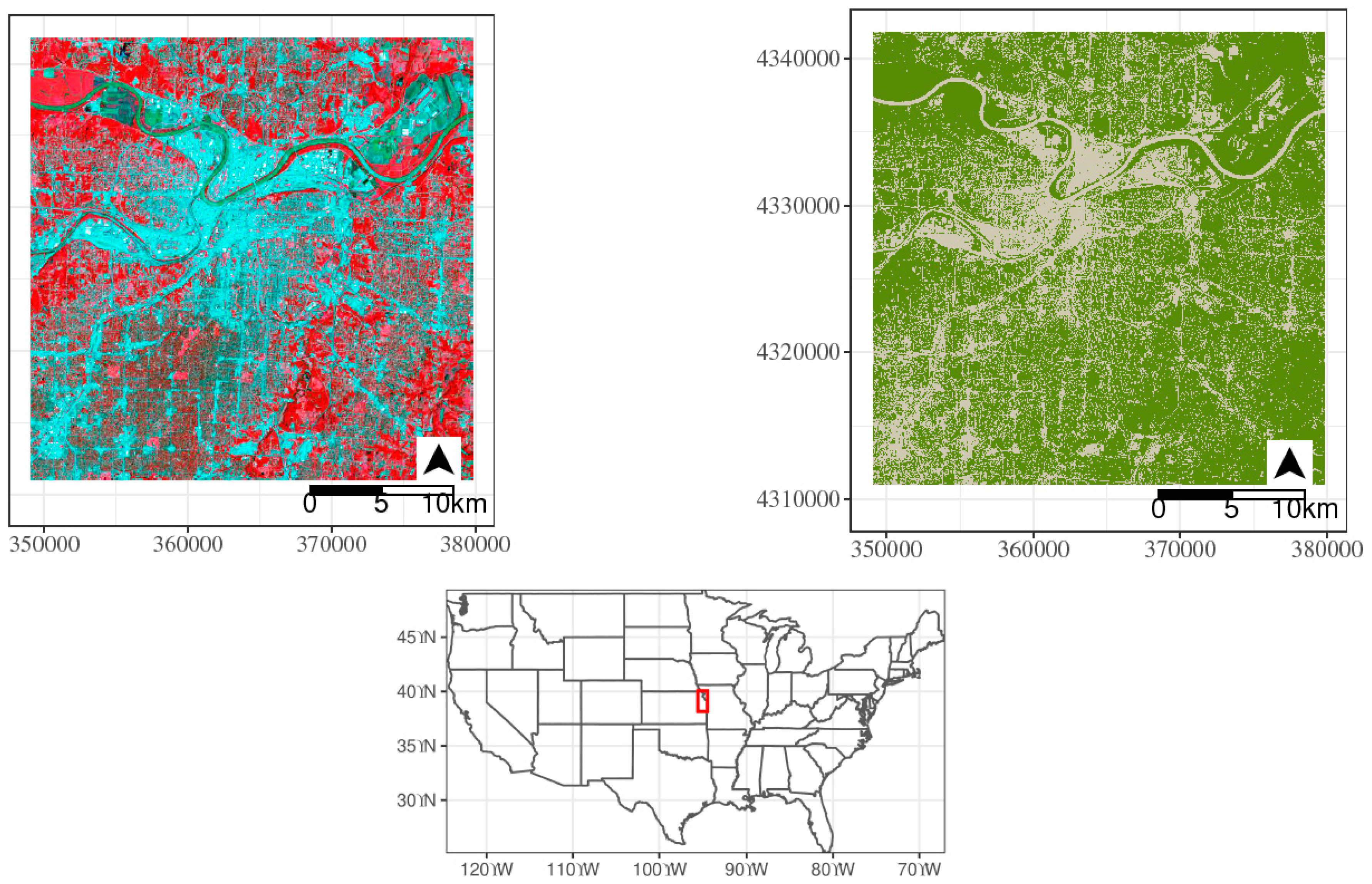
2.1. Study Area
2.2. Data and Preprocessing
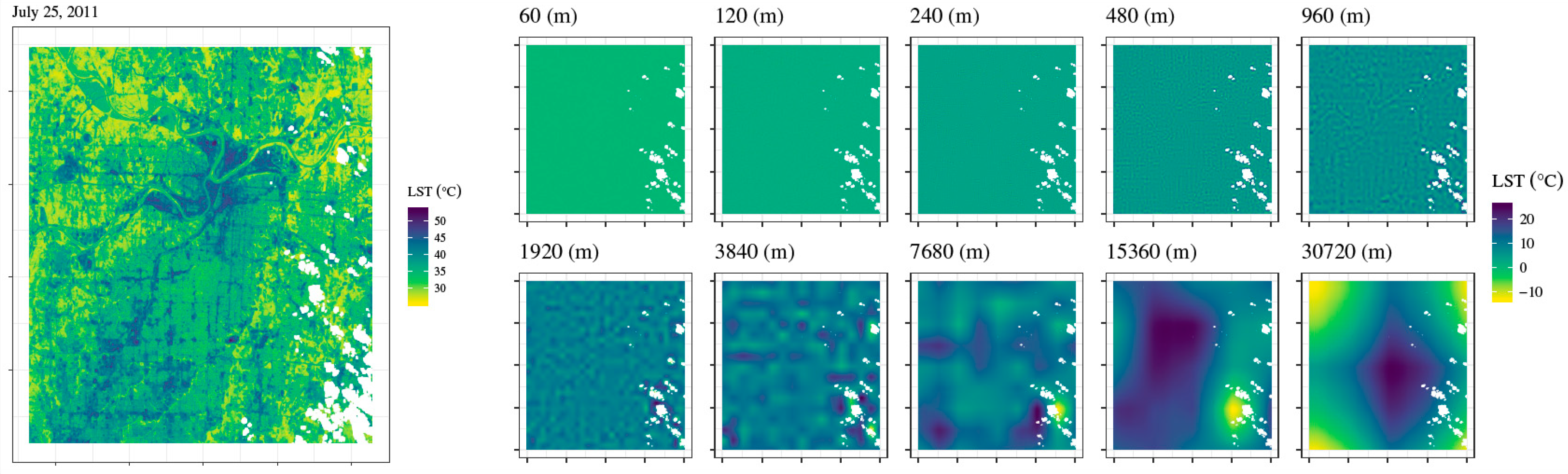
2.3. Land Surface Temperature Retrieval
2.4. Multi-Resolution Wavelet Analysis
2.5. Landscape Metrics Calculations
2.6. Statistical Analysis
3. Results
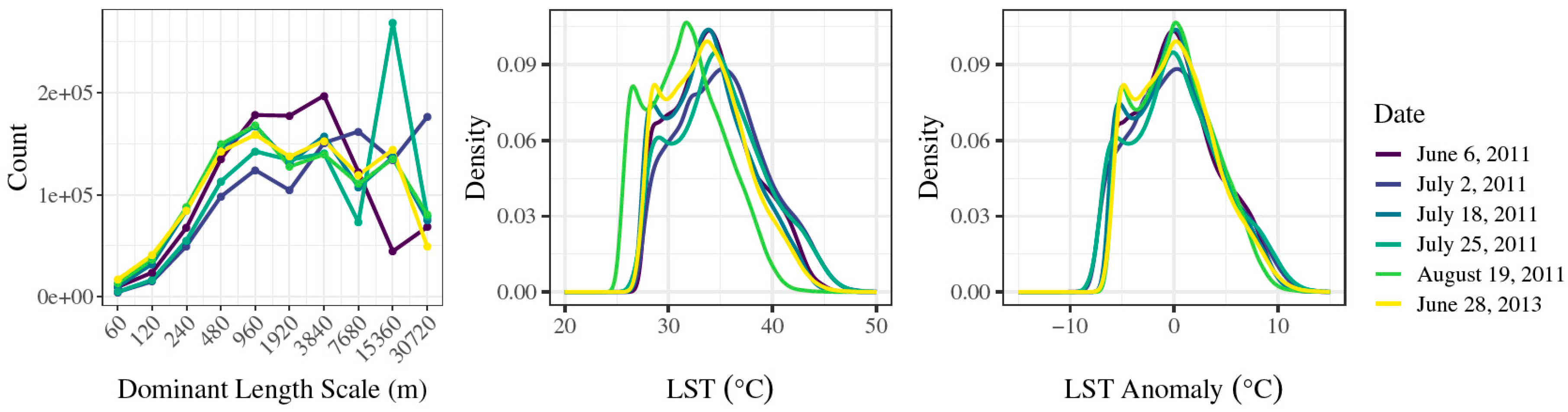
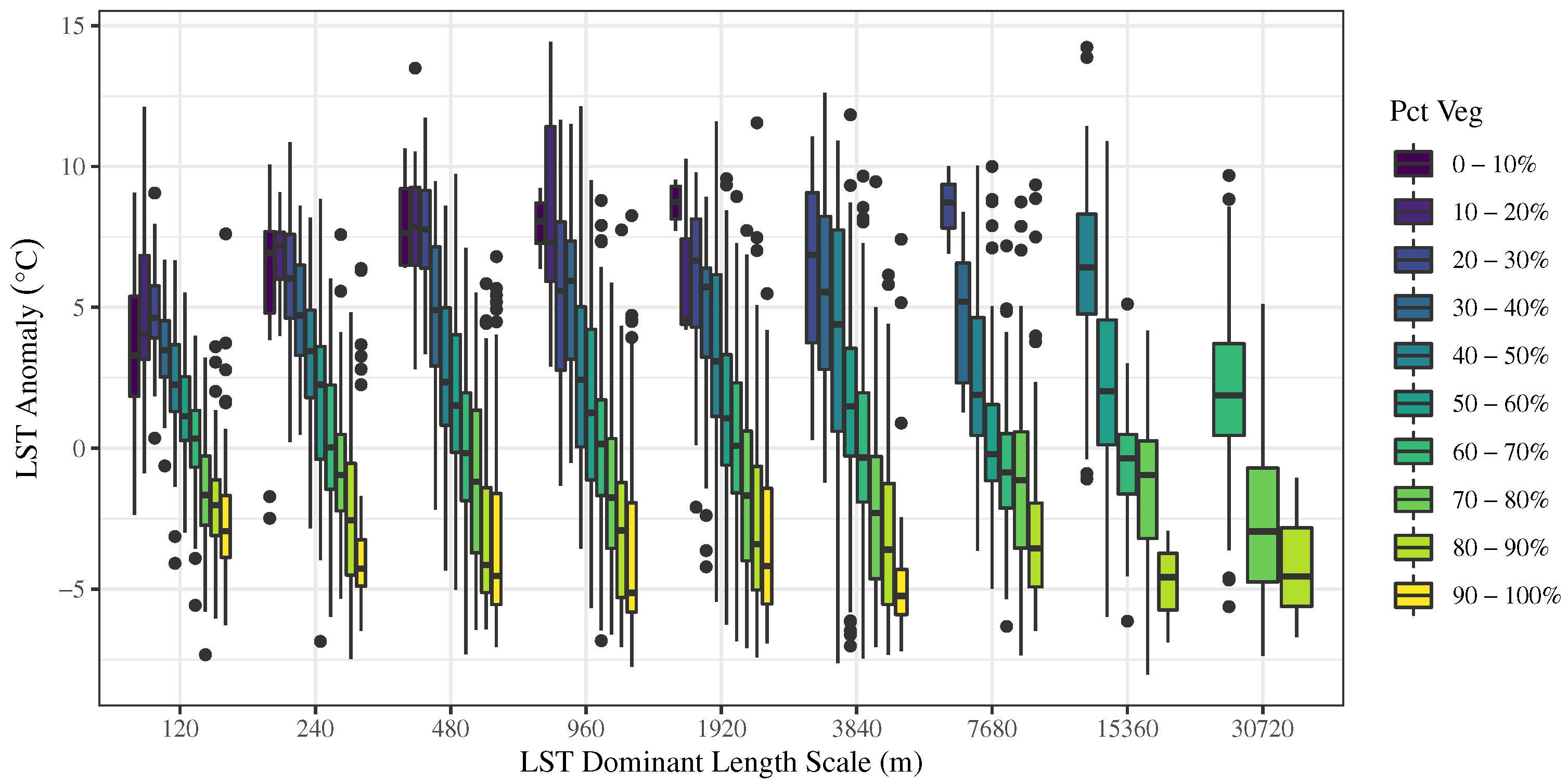
3.1. Variation of Dominant Length Scales and LST
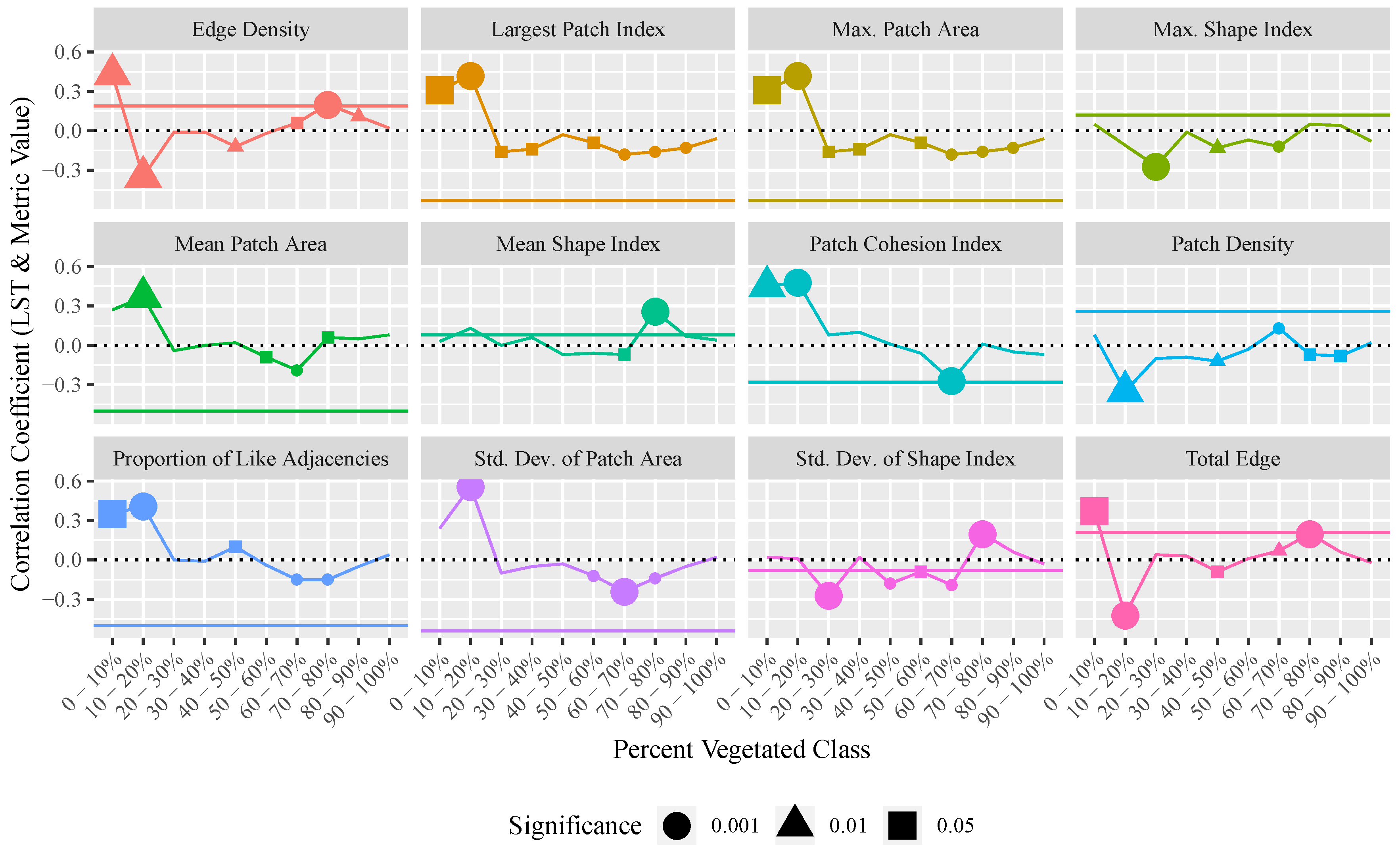
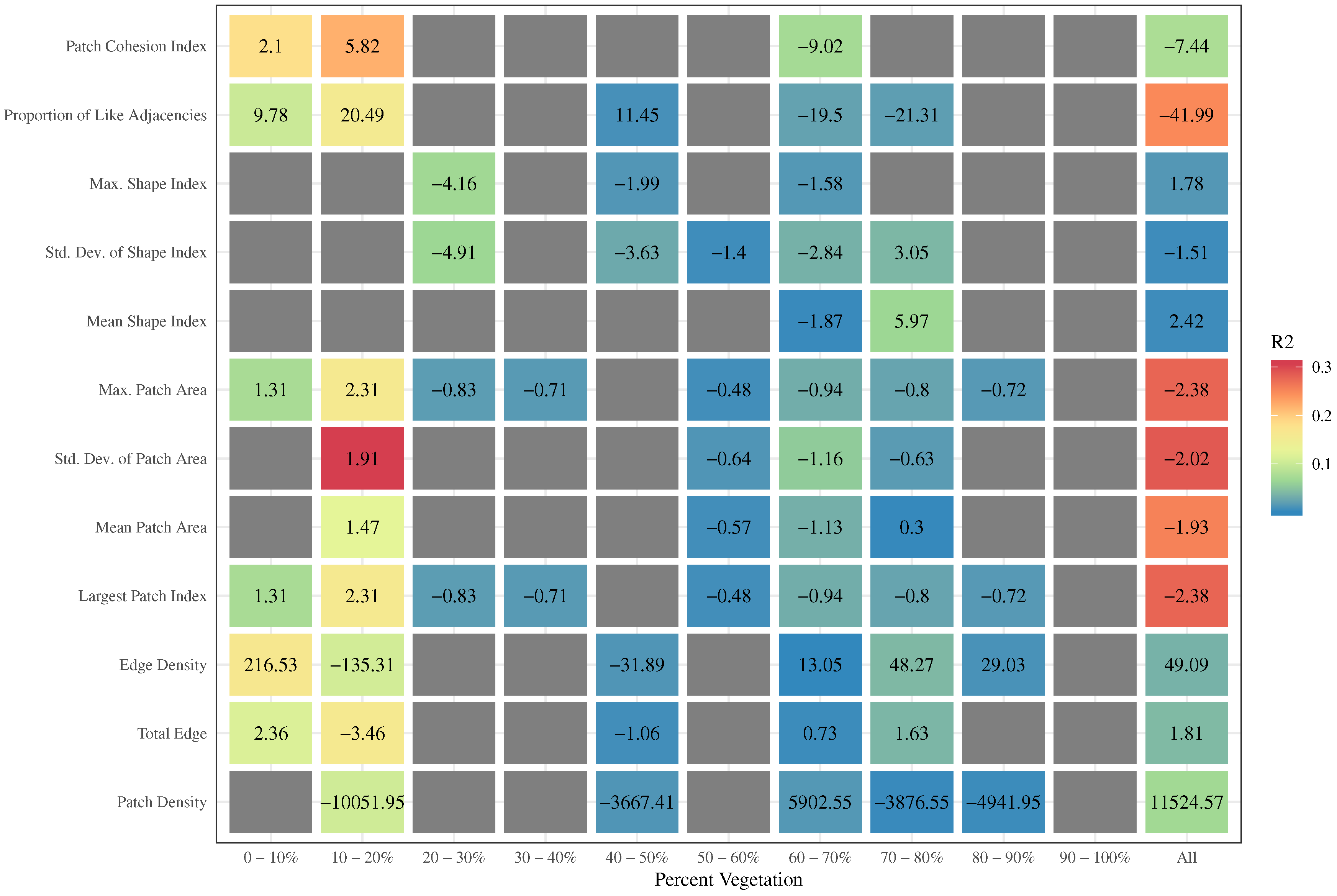
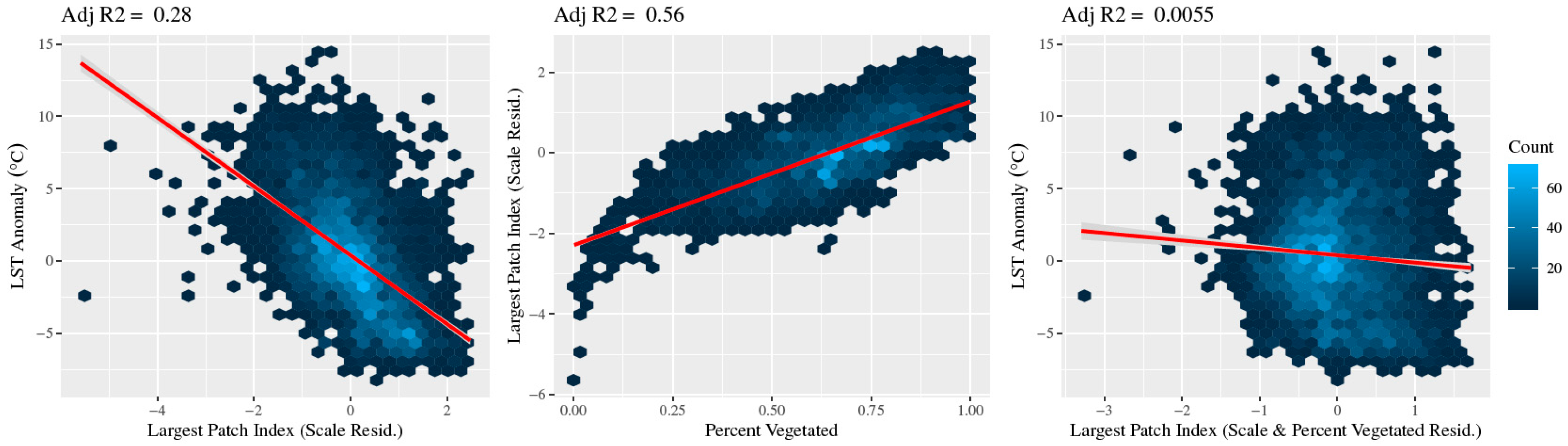
3.2. Relationship between Landscape Metrics and LST
4. Discussion
4.1. Methodological Implications for Urban Landscape Pattern Analysis
4.2. Percent of Vegetation Has a Consistent Negative Effect on LST, However the Contribution of the Spatial Configuration of Green Space Is Negligible
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- United Nations. World Urbanization Prospects: The 2014 Revision; Technical Report; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2014. [Google Scholar]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Alberti, M. Maintaining ecological integrity and sustaining ecosystem function in urban areas. Curr. Opin. Environ. Sustain. 2010, 2, 178–184. [Google Scholar] [CrossRef]
- Oke, T.R. The Heat Island of the Urban Boundary Layer: Characteristics, Causes and Effects. In Wind Climate in Cities of NATO ASI Series; Cermak, J.E., Davenport, A.G., Plate, E.J., Viegas, D.X., Eds.; Springer: Dordrecht, The Netherlands, 1995; Volume 277, pp. 81–107. [Google Scholar] [CrossRef]
- Weng, Q.H.; Liu, H.; Liang, B.Q.; Lu, D.S. The spatial variations of urban land surface temperatures: Pertinent factors, zoning effect, and seasonal variability. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2008, 1, 154–166. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. An evapotranspiration-interception model for urban areas. Water Resour. Res. 1991, 27, 1739–1755. [Google Scholar] [CrossRef]
- Hu, L.; Brunsell, N.A. The impact of temporal aggregation of land surface temperature data for surface urban heat island (SUHI) monitoring. Remote Sens. Environ. 2013, 134, 162–174. [Google Scholar] [CrossRef]
- Stone, B.; Vargo, J.; Habeeb, D. Managing climate change in cities: Will climate action plans work? Landsc. Urban Plan. 2012, 107, 263–271. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef]
- Luber, G.; McGeehin, M. Climate change and extreme heat events. Am. J. Prev. Med. 2008, 35, 429–435. [Google Scholar] [CrossRef] [PubMed]
- Patz, J.A.; Campbell-Lendrum, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Stott, P.A.; Stone, D.A.; Allen, M.R. Human contribution to the European heatwave of 2003. Nature 2004, 432, 610–614. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, Ü.; Sawut, M.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef]
- Weng, Q.; Liu, H.; Lu, D. Assessing the effects of land use and land cover patterns on thermal conditions using landscape metrics in city of Indianapolis, United States. Urban Ecosyst. 2007, 10, 203–219. [Google Scholar] [CrossRef]
- McGarigal, K. FRAGSTATS Help. 2015. Available online: https://www.umass.edu/landeco/research/fragstats/documents/fragstats.help.4.2.pdf (accessed on 10 August 2019).
- Huang, G.; Zhou, W.; Cadenasso, M.L. Is everyone hot in the city? Spatial pattern of land surface temperatures, land cover and neighborhood socioeconomic characteristics in Baltimore, MD. J. Environ. Manag. 2011, 92, 1753–1759. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2010, 25, 17–33. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S. Impacts of urban landscape patterns on urban thermal variations in Guangzhou, China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 65–71. [Google Scholar] [CrossRef]
- Wu, J. Urban sustainability: An inevitable goal of landscape research. Landsc. Ecol. 2010, 25, 1–4. [Google Scholar] [CrossRef]
- Leitao, A.B.; Ahern, J. Applying landscape ecological concepts and metrics in sustainable landscape planning. Landsc. Urban Plan. 2002, 59, 65–93. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Middel, A.; Harlan, S.L.; Brazel, A.J.; Turner, B.L., II. Remote sensing of the surface urban heat island and land architecture in Phoenix, Arizona: Combined effects of land composition and configuration and cadastral-demographic-economic factors. Remote Sens. Environ. 2016, 174, 233–243. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Stone, B.; Rodgers, M.O. Urban form and thermal efficiency: How the design of cities influences the urban heat island effect. J. Am. Plan. Assoc. 2001, 67, 186–198. [Google Scholar] [CrossRef]
- Grafius, D.R.; Corstanje, R.; Harris, J.A. Linking ecosystem services, urban form and green space configuration using multivariate landscape metric analysis. Landsc. Ecol. 2018, 33, 1–17. [Google Scholar] [CrossRef]
- Liu, J.; Dietz, T.; Carpenter, S.R.; Alberti, M.; Folke, C.; Moran, E.; Pell, A.N.; Deadman, P.; Kratz, T.; Lubchenco, J.; et al. Complexity of Coupled Human and Natural Systems. Science 2007, 317, 1513–1516. [Google Scholar] [CrossRef]
- Wu, J. Scale and Scaling: A Cross-Disciplinary Perspective. In Key Topics in Landscape Ecology; Cambridge University Press: Cambridge, UK, 2007; pp. 115–142. [Google Scholar]
- Wu, J. Key concepts and research topics in landscape ecology revisited: 30 years after the Allerton Park workshop. Landsc. Ecol. 2013, 28, 1–11. [Google Scholar] [CrossRef]
- Wu, J. Effects of changing scale on landscape pattern analysis: Scaling relations. Landsc. Ecol. 2004, 19, 125–138. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Guo, G.; Wu, Z.; Chen, Y. Complex mechanisms linking land surface temperature to greenspace spatial patterns: Evidence from four southeastern Chinese cities. Sci. Total Environ. 2019, 674, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Buyantuyev, A.; Wu, J.; Gries, C. Multiscale analysis of the urbanization pattern of the Phoenix metropolitan landscape of USA: Time, space and thematic resolution. Landsc. Urban Plan. 2010, 94, 206–217. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Gillies, R.R. Length scale analysis of surface energy fluxes derived from remote sensing. J. Hydrometeorol. 2003, 4, 1212–1219. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Stone, B.; Hess, J.J.; Frumkin, H. Urban form and extreme heat events: Are sprawling cities more vulnerable to climate change than compact cities? Environ. Health Perspect. 2010, 118, 1425–1428. [Google Scholar] [CrossRef]
- Ji, W. Landscape effects of urban sprawl: Spatial and temporal analyses using remote sensing images and landscape metrics. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1691–1694. [Google Scholar]
- Stone, B.; Norman, J.M. Land use planning and surface heat island formation: A parcel-based radiation flux approach. Atmos. Environ. 2006, 40, 3561–3573. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Scaling effect on the relationship between landscape pattern and land surface temperature: A case study of Indianapolis, United States. Photogramm. Eng. Remote Sens. 2009, 75, 291–304. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Relationship between land surface temperature and spatial pattern of greenspace: What are the effects of spatial resolution? Landsc. Urban Plan. 2013, 114, 1–8. [Google Scholar] [CrossRef]
- Mid-America Regional Council; Applied Ecological Services. Kansas City Natural Resource Inventory II: Beyond the Map Summary Report; Technical Report; Mid-America Regional Council: Kansas City, MO, USA, 2013. [Google Scholar]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Gillies, R.R. Incorporating surface emissivity into a thermal atmospheric correction. Photogramm. Eng. Remote Sens. 2002, 68, 1263–1269. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Landsat 8 (L8) Data Users Handbook, Version 3.0. Available online: https://www.usgs.gov/media/files/landsat-8-data-users-handbook (accessed on 7 June 2019).
- Zhou, Y.; Smith, S.J.; Elvidge, C.D.; Zhao, K.; Thomson, A.; Imhoff, M. A cluster-based method to map urban area from DMSP/OLS nightlights. Remote Sens. Environ. 2014, 147, 173–185. [Google Scholar] [CrossRef]
- Whitcher, B. Waveslim: Basic Wavelet Routines for One-, Two- and Three-Dimensional Signal Processing. 2015. Available online: https://cran.r-project.org/package=waveslim (accessed on 7 June 2019).
- Evans, J.S.; spatialEco. R Package Version 0.1.1-1. Available online: https://github.com/jeffreyevans/spatialEco (accessed on 7 June 2019).
- Hu, L.; Brunsell, N.A. A new perspective to assess the urban heat island through remotely sensed atmospheric profiles. Remote Sens. Environ. 2015, 158, 393–406. [Google Scholar] [CrossRef]
- Hoverter, S.P. Adapting to Urban Heat: A Tool Kit for Local Governments; Technical Report; Georgetown Climate Center: Washington, DC, USA, 2012. [Google Scholar]
- Cadenasso, M.L.; Pickett, S.T.A. Urban principles for ecological landscape design and management: Scientific fundamentals. Urban Ecol. 2008, 1, 1–16. [Google Scholar]
- Schmid, H.; Cleugh, H.; Grimmond, C.; Oke, T. Spatial variability of energy fluxes in suburban terrain. Bound. Lay. Meteorol. 1991, 54, 249–276. [Google Scholar] [CrossRef]
| Date | Sensor |
|---|---|
| 7 June 2011 | Landsat 5 |
| 2 July 2011 | Landsat 5 |
| 18 July 2011 | Landsat 5 |
| 25 July 2011 | Landsat 5 |
| 19 August 2011 | Landsat 5 |
| 28 June 2013 | Landsat 7 |
| Pattern Measure | Landscape Metric | Description | Equation |
|---|---|---|---|
| Composition | Proportion of landscape (PLAND) | Percent of landscape composed of vegetated surfaces. | |
| Patch size | Patch size distribution (AREA) | The statistical distribution of vegetated patch sizes, including the mean, minimum, maximum, and standard deviation. | |
| Fragmentation | Largest patch index (LPI) | Percentage of each dominant length scale extent comprised of the largest vegetated patch. | |
| Patch density (PD) | Number of vegetated patches divided by the area of the extent. | ||
| Total edge (TE) | Total perimeter length of all vegetated patches within an extent. | ||
| Edge density (ED) | Total perimeter length of all vegetated patches within an extent divided by the area of that extent. | ||
| Shape | Shape index distribution (SHAPE) | Statistical distribution of the shape index which provides a standardized measure of shape complexity calculated from the perimeters of the vegetated patches within each extent. A measure of disaggregation. | |
| Connectivity | Patch cohesion index (COHESION) | Measure of the physical connectedness of the vegetated patches within each dominant length scale extent which increases as patches become more aggregated. | |
| Proximity | Proportion of like adjacencies (PLADJ) | Degree of aggregation of vegetated patches. |
| Metric Scale | |
|---|---|
| Prop. of Landscape | 0.15 |
| Patch Density | −0.44 |
| Total Edge | 0.99 |
| Edge Density | −0.36 |
| Largest Patch Index | −0.80 |
| Mean Patch Area | 0.31 |
| Std. Dev. of Patch Area | 0.73 |
| Max. Patch Area | 0.94 |
| Mean Shape Index | 0.33 |
| Std. Dev. of Shape Index | 0.66 |
| Max. Shape Index | 0.94 |
| Prop. of Like Adjacencies | 0.37 |
| Patch Cohesion Index | 0.71 |
| Metric | Model | |
|---|---|---|
| Patch Density | y log(x) | 0.19 |
| Total Edge | log(y) log(x) | 0.98 |
| Edge Density | y log(x) | 0.13 |
| Largest Patch Index | log(y) log(x) | 0.64 |
| Mean Patch Area | log(y) log(x) | 0.10 |
| Std. Dev. of Patch Area | log(y) log(x) | 0.53 |
| Max. Patch Area | log(y) log(x) | 0.88 |
| Mean Shape Index | log(y) log(x) | 0.11 |
| Std. Dev. of Shape Index | y log(x) | 0.43 |
| Max. Shape Index | log(y) log(x) | 0.88 |
| Proportion of Like Adjacencies | y log(x) | 0.13 |
| Patch Cohesion Index | y log(x) | 0.51 |
| LST Metric | Metric Pct Veg | |
|---|---|---|
| Patch Density | 0.26 | −0.44 |
| Total Edge | 0.21 | −0.24 |
| Edge Density | 0.19 | −0.22 |
| Largest Patch Index | −0.53 | 0.75 |
| Mean Patch Area | −0.50 | 0.80 |
| Std. Dev. of Patch Area | −0.54 | 0.77 |
| Max. Patch Area | −0.53 | 0.75 |
| Mean Shape Index | 0.08 | −0.08 |
| Std. Dev. of Shape Index | −0.08 | 0.08 |
| Max. Shape Index | 0.12 | −0.26 |
| Proportion of Like Adjacencies | −0.50 | 0.80 |
| Patch Cohesion Index | −0.28 | 0.49 |
| Scale | LST Pct. Veg |
|---|---|
| 120 | −0.76 |
| 240 | −0.75 |
| 480 | −0.70 |
| 960 | −0.66 |
| 1920 | −0.61 |
| 3840 | −0.66 |
| 7680 | −0.57 |
| 15360 | −0.65 |
| 30720 | −0.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wesley, E.J.; Brunsell, N.A. Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration. Remote Sens. 2019, 11, 2322. https://doi.org/10.3390/rs11192322
Wesley EJ, Brunsell NA. Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration. Remote Sensing. 2019; 11(19):2322. https://doi.org/10.3390/rs11192322
Chicago/Turabian StyleWesley, Elizabeth Jane, and Nathaniel A. Brunsell. 2019. "Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration" Remote Sensing 11, no. 19: 2322. https://doi.org/10.3390/rs11192322
APA StyleWesley, E. J., & Brunsell, N. A. (2019). Greenspace Pattern and the Surface Urban Heat Island: A Biophysically-Based Approach to Investigating the Effects of Urban Landscape Configuration. Remote Sensing, 11(19), 2322. https://doi.org/10.3390/rs11192322





