Multiple-Object-Tracking Algorithm Based on Dense Trajectory Voting in Aerial Videos
Abstract
1. Introduction
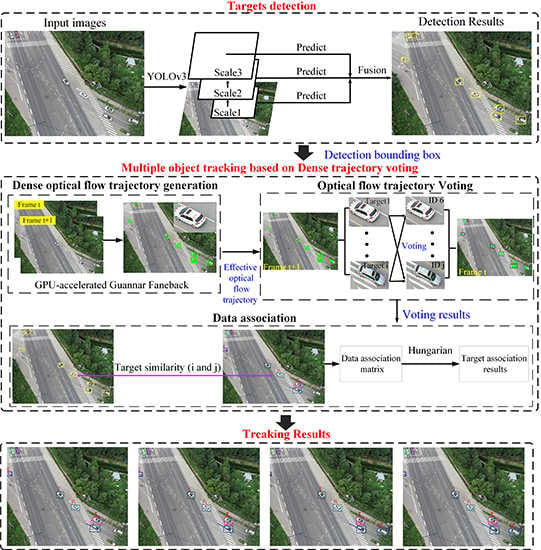
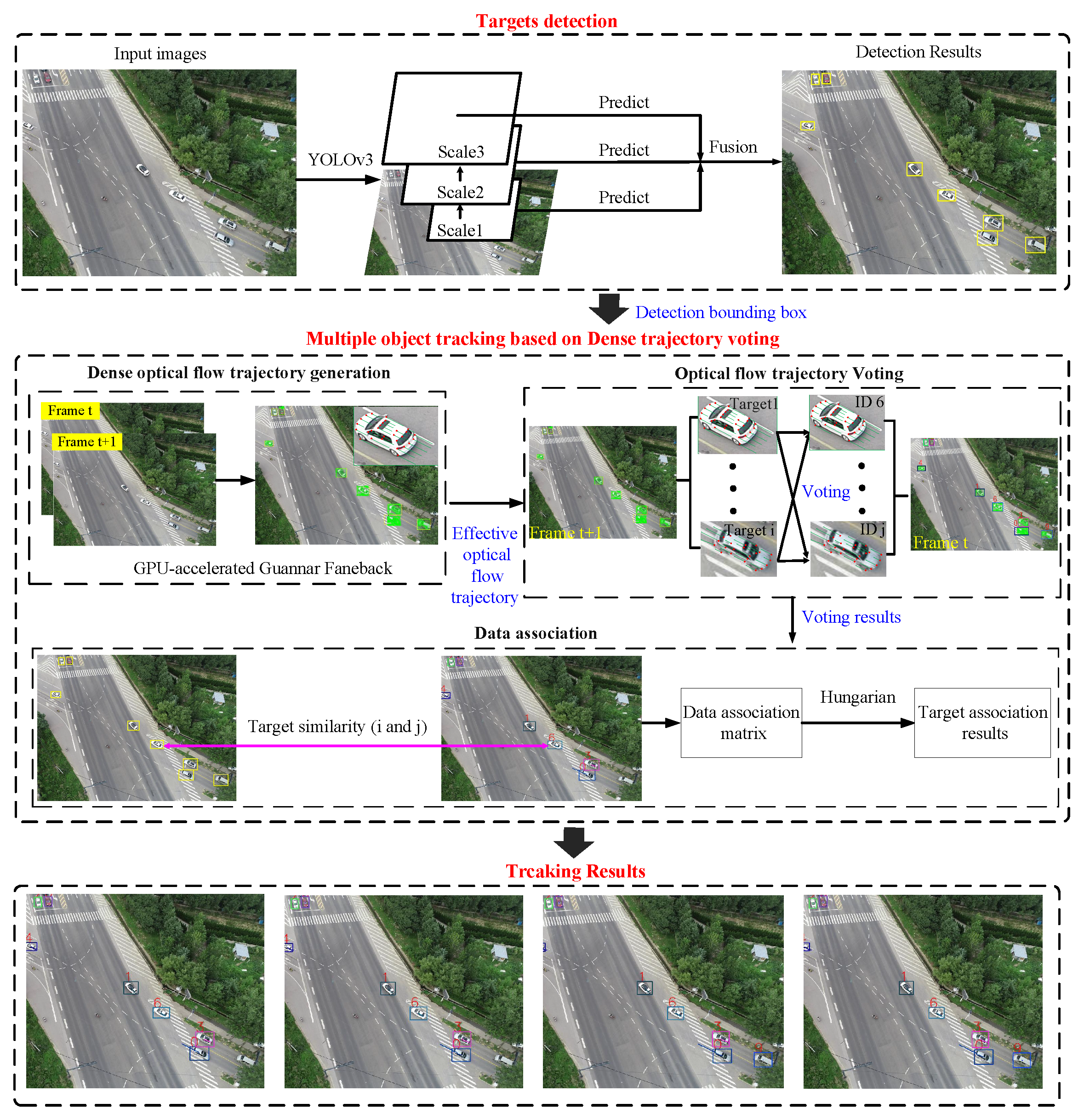
- First of all, we proposed a novel multiple-target-tracking algorithm which is based on dense-optical-flow-trajectory voting. The algorithm models the multiple-target-tracking problem as a voting problem of the dense-optical-flow trajectory to the target ID. In the method, we first generated the optical-flow trajectories of the target and performed ID voting on the optical-flow trajectories of each target. Then, voting results were used to measure the similarity of objects in adjacent frames, and tracking results were obtained by data association. Since the optical-flow trajectory of the target could accurately reflect the position change of the target with time, regardless of the appearance, shape, and size of the target, the algorithm could enhance tracking performance in the aerial video, even at a low frame rate.
- Second, we built a training dataset and a test dataset for deep-learning vehicle-detection in aerial videos. The training dataset contained many self-captured aerial images, and we used the LabelImg tool to label vehicle targets in these aerial images. The test dataset was collected by our UAV system and included four kinds of surveillance scenarios and multiple video frame rates. The UAV system was composed of DJI-MATRICE 100 and a monocular point-gray camera. Due to the different UAV shooting angles and heights, vehicle sizes in the images are various, and the background is complex. Based on this, we could generate the network model of the deep-learning algorithm and obtain good vehicle-detection results, which is the basis of multiple-target tracking.
- Finally, we conducted a large number of experiments on the test dataset to prove the effectiveness and robustness of the algorithm. The experiment results on aerial video with various environments and different frame rates show that our algorithm could obtain effective and robust tracking results in various complex environments, and the tracking effect was still robust when there were problems such as target adhesion, low frame rate, and small target size. In addition, we carried out qualitative and quantitative comparison experiments with three state-of-art tracking algorithms, which further proved that this algorithm could not only obtain good tracking results in aerial videos, but also had excellent performance under low frame rate conditions.
2. Proposed Method
2.1. Target Detection
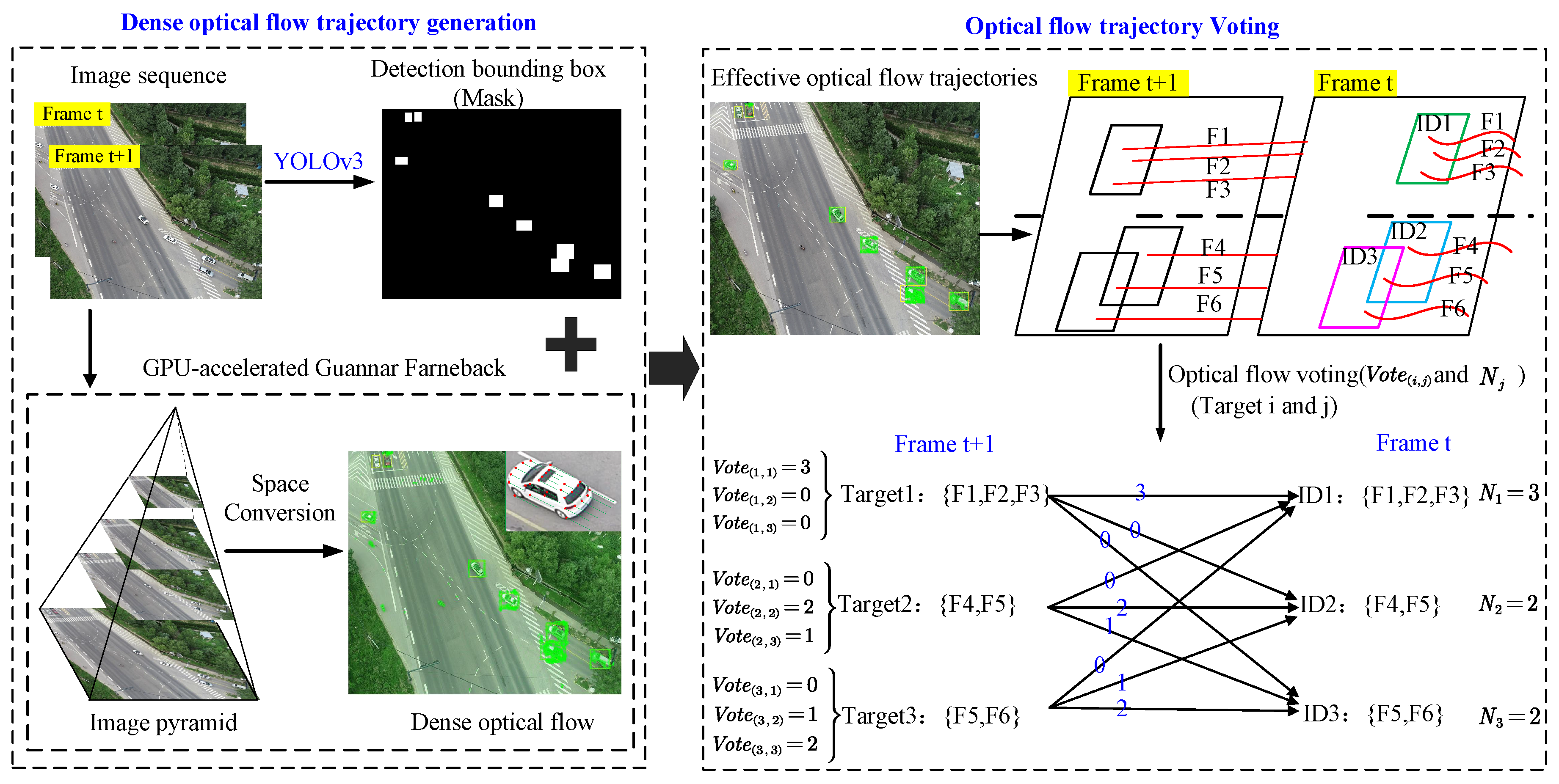
2.2. Dense-Optical-Flow-Trajectory Generation and Voting
2.3. Data-Association Based on Dense-Trajectory Voting
| Algorithm 1: Proposed multiple-target-tracking method. |
 |
3. Experiment Results
3.1. Self-Built Dataset of Aerial Images
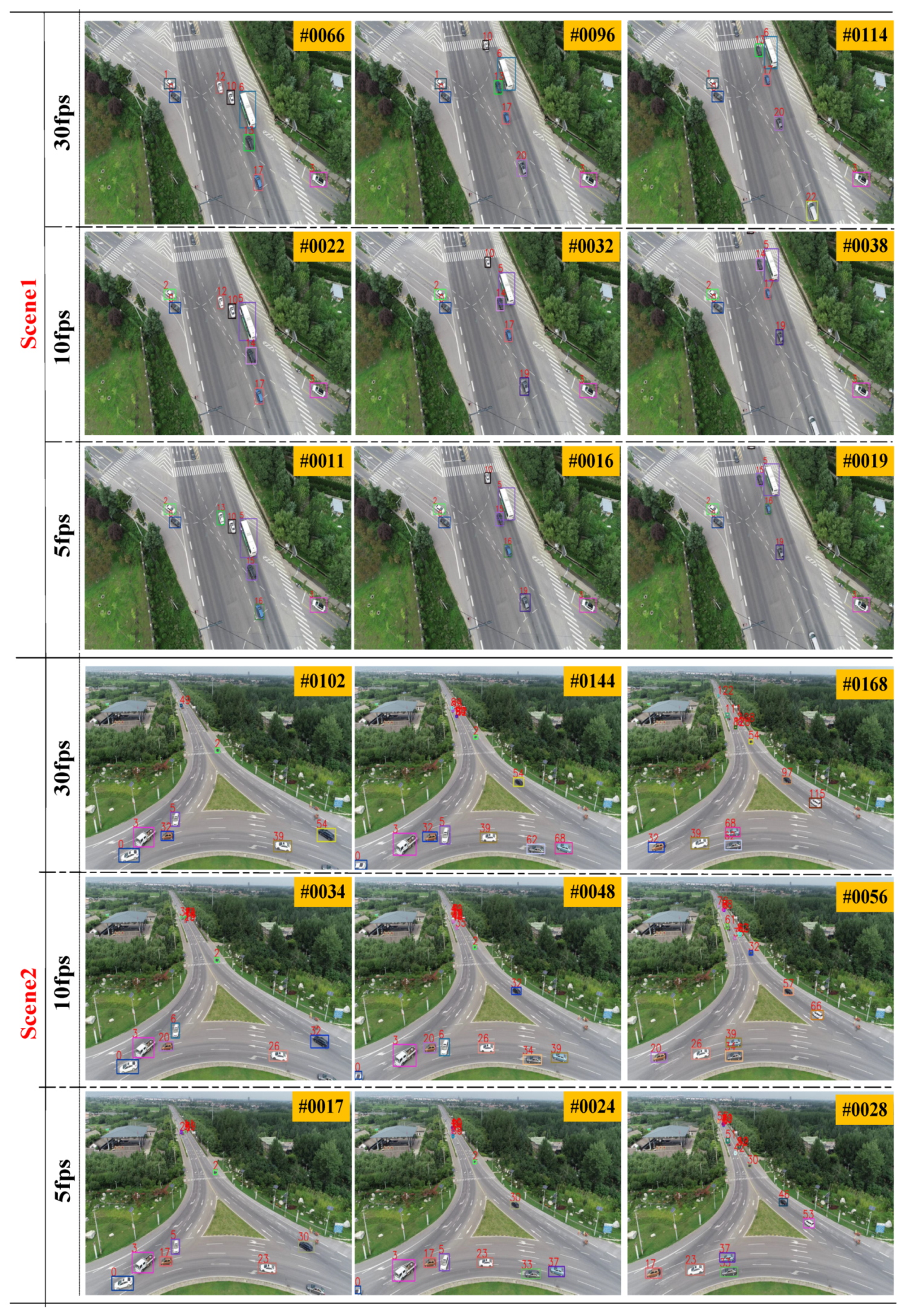
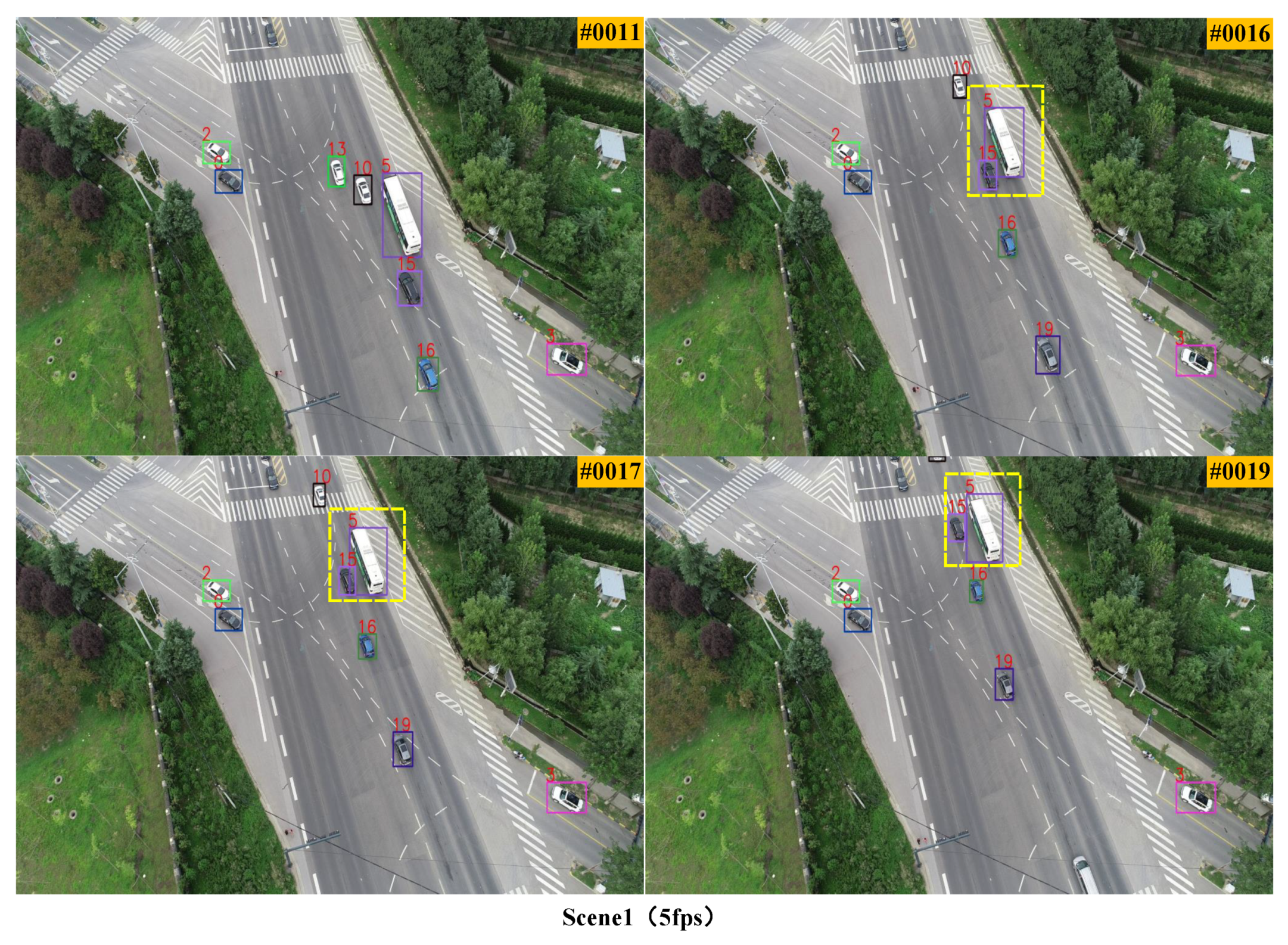
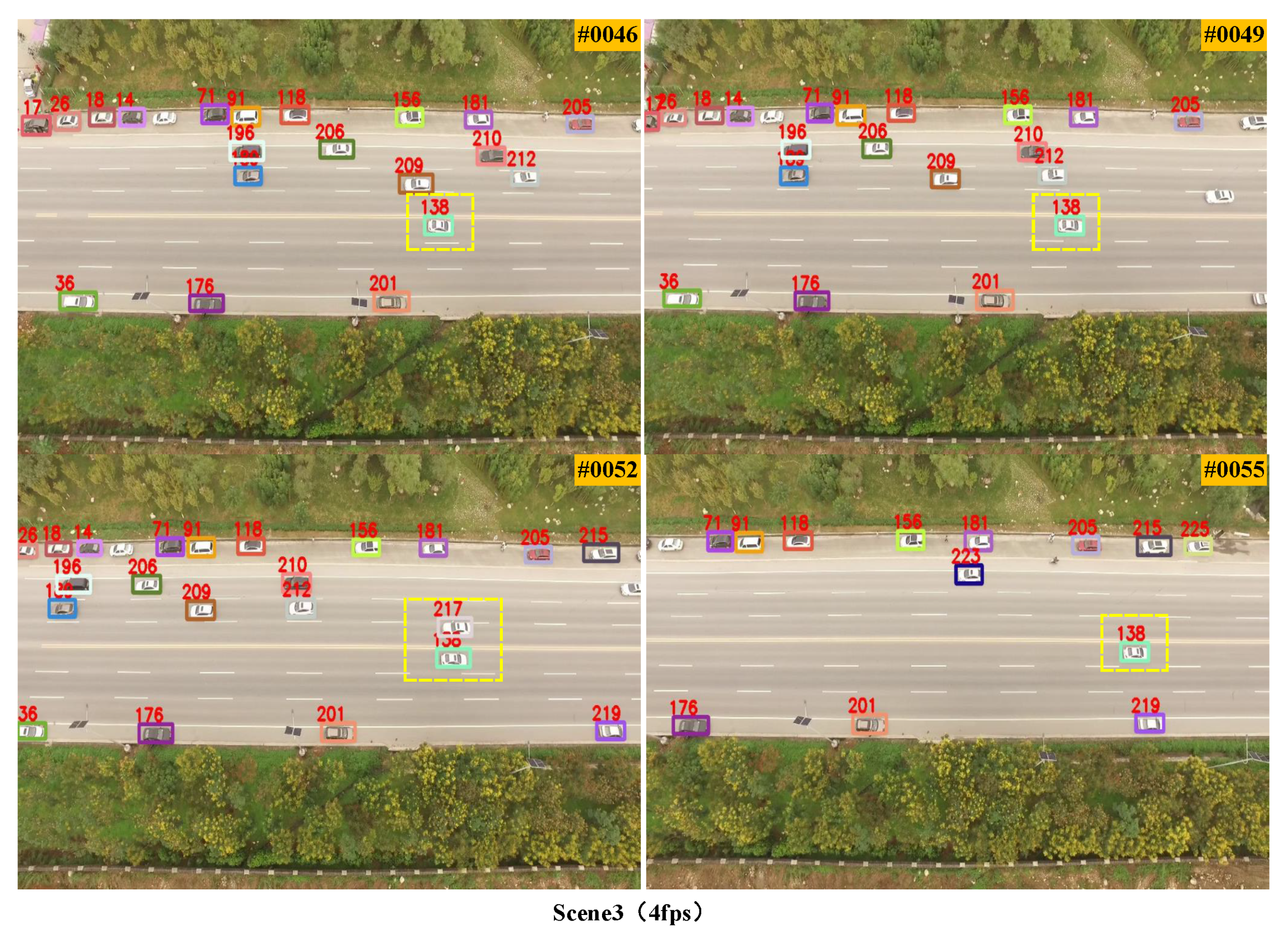
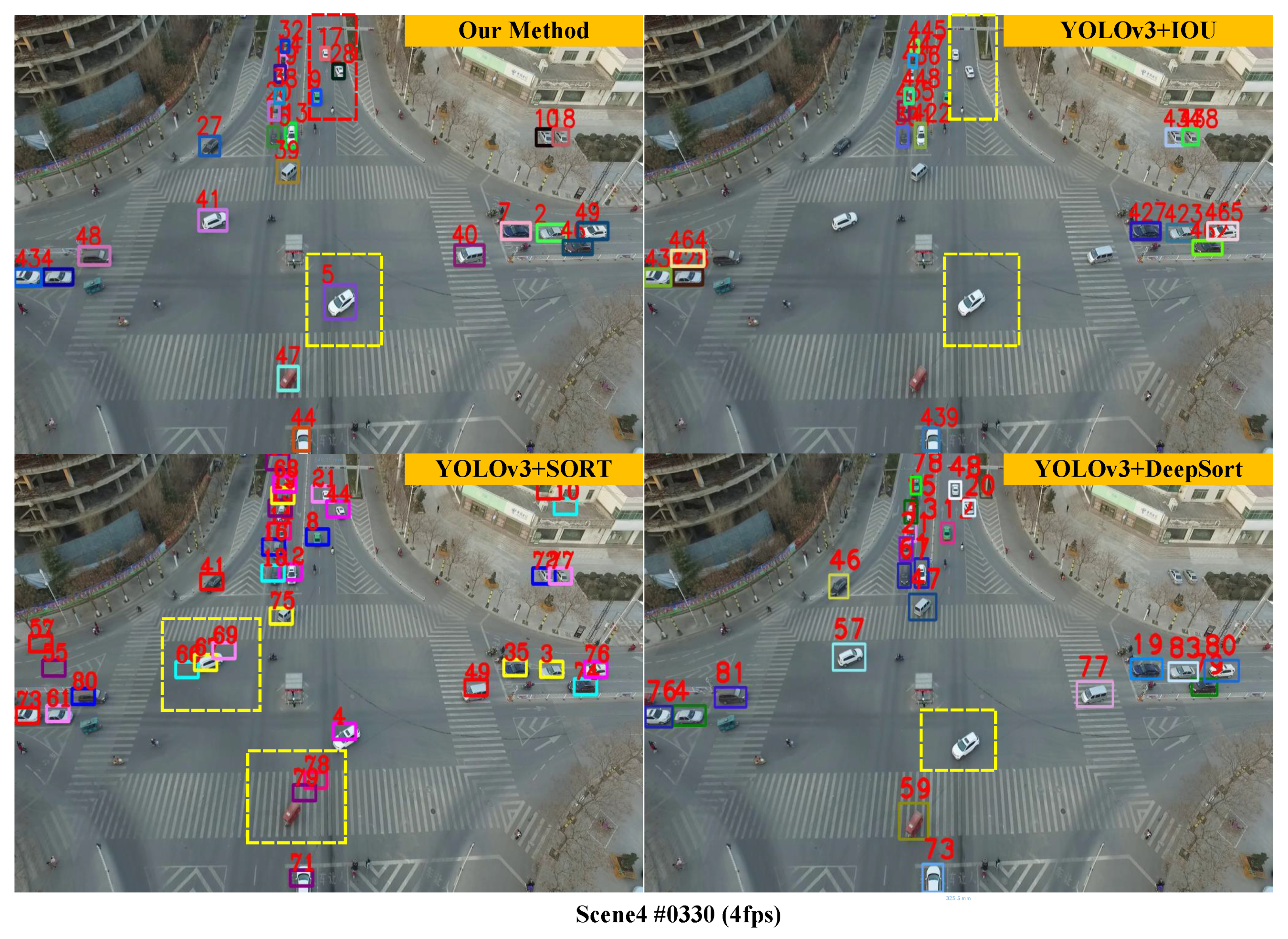
3.2. Qualitative Experiments at Different Frame Rates
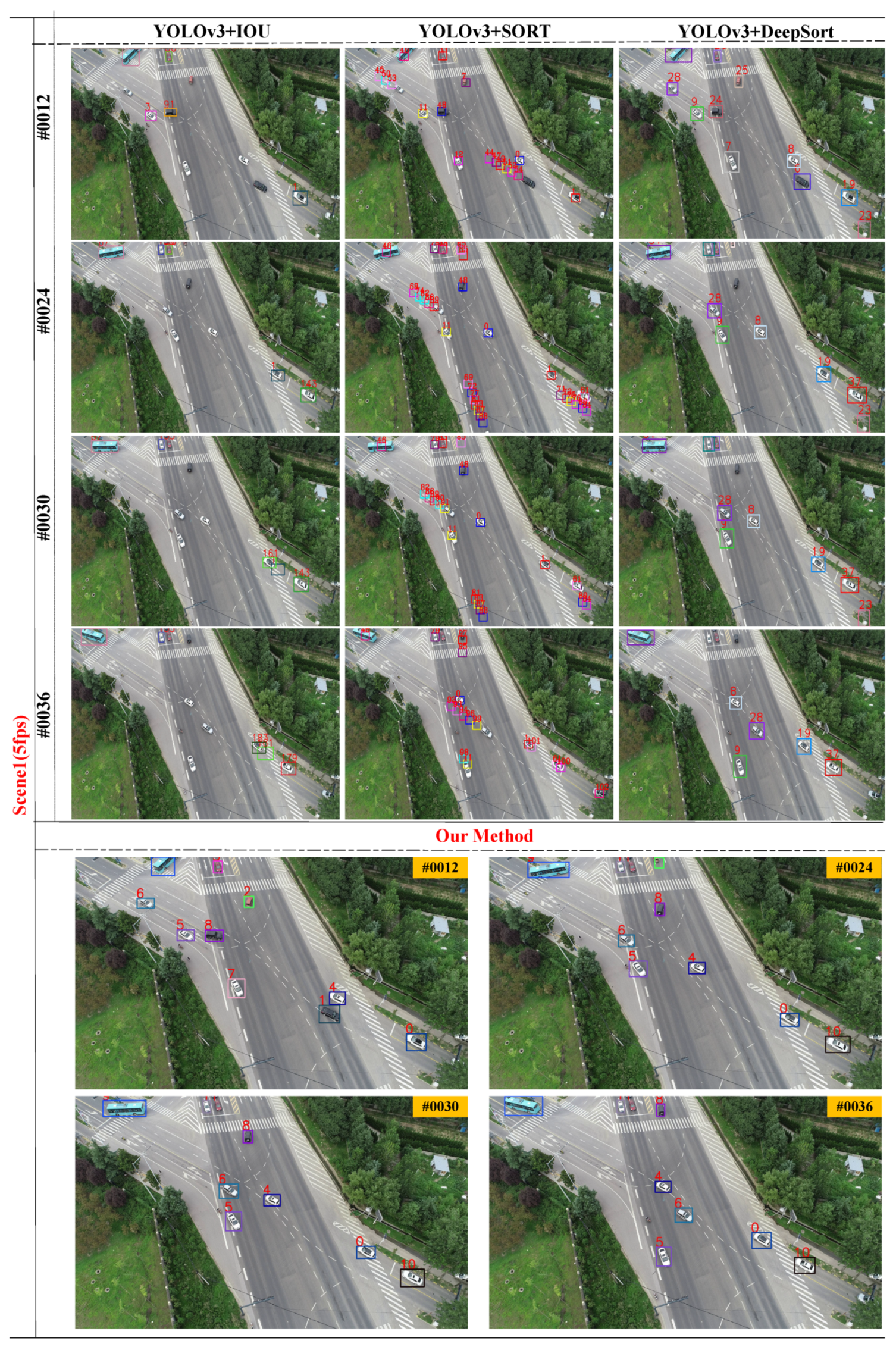
3.3. Qualitative and Quantitative Comparison Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kumar, R.; Sawhney, H.; Samarasekera, S.; Hsu, S.; Tao, H.; Guo, Y.; Hanna, K.; Pope, A.; Wildes, R.; Hirvonen, D. Aerial video surveillance and exploitation. Proc. IEEE 2001, 89, 1518–1539. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Zhang, F.; Xie, B.; Li, J.; Liu, L. Panoramic uav surveillance and recycling system based on structure-free camera array. IEEE Access 2019, 7, 25763–25778. [Google Scholar] [CrossRef]
- Ke, R.; Li, Z.; Kim, S.; Ash, J.; Cui, Z.; Wang, Y. Real-Time Bidirectional Traffic Flow Parameter Estimation From Aerial Videos. IEEE Trans. Intell. Transp. Syst. 2017, 18, 890–901. [Google Scholar] [CrossRef]
- Zhao, X.; Pu, F.; Wang, Z.; Chen, H.; Xu, Z. Detection, Tracking, and Geolocation of Moving Vehicle From UAV Using Monocular Camera. IEEE Access 2019, 7, 101160–101170. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, X.; Li, X.; Yan, P. Correlation-Based Tracking of Multiple Targets With Hierarchical Layered Structure. IEEE Trans. Cybern. 2018, 48, 90–102. [Google Scholar] [CrossRef] [PubMed]
- Bi, F.; Lei, M.; Wang, Y.; Huang, D. Remote Sensing Target Tracking in UAV Aerial Video Based on Saliency Enhanced MDnet. IEEE Access 2019, 7, 76731–76740. [Google Scholar] [CrossRef]
- Farmani, N.; Sun, L.; Pack, D.J. A Scalable Multitarget Tracking System for Cooperative Unmanned Aerial Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1947–1961. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Idrees, H.; Saleemi, I.; Ali, S.; Shah, M. Moving object detection and tracking in forward looking infra-red aerial imagery. In Machine Vision Beyond Visible Spectrum; Springer: Berlin/Heidelberg, Germany, 2011; pp. 221–252. [Google Scholar]
- Andres, B.; Kroeger, T.; Briggman, K.L.; Denk, W.; Korogod, N.; Knott, G.; Koethe, U.; Hamprecht, F.A. Globally Optimal Closed-Surface Segmentation for Connectomics. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 778–791. [Google Scholar]
- Uzkent, B.; Hoffman, M.J.; Vodacek, A. Real-Time Vehicle Tracking in Aerial Video Using Hyperspectral Features. In Proceedings of the Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1443–1451. [Google Scholar]
- Liu, X.; Yang, T.; Li, J. Real-Time Ground Vehicle Detection in Aerial Infrared Imagery Based on Convolutional Neural Network. Electronics 2018, 7, 78. [Google Scholar] [CrossRef]
- Ochs, P.; Malik, J.; Brox, T. Segmentation of Moving Objects by Long Term Video Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1187–1200. [Google Scholar] [CrossRef] [PubMed]
- Keuper, M.; Andres, B.; Brox, T. Motion Trajectory Segmentation via Minimum Cost Multicuts. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3271–3279. [Google Scholar]
- Li, J.; Dai, Y.; Li, C.; Shu, J.; Li, D.; Yang, T.; Lu, Z. Visual Detail Augmented Mapping for Small Aerial Target Detection. Remote. Sens. 2019, 11, 14. [Google Scholar] [CrossRef]
- Xiao, J.; Cheng, H.; Sawhney, H.; Han, F. Vehicle detection and tracking in wide field-of-view aerial video. In Proceedings of the Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 679–684. [Google Scholar]
- Szottka, I.; Butenuth, M. Tracking multiple vehicles in airborne image sequences of complex urban environments. In Proceedings of the Urban Remote Sensing Event, Munich, Germany, 11–13 April 2011; pp. 13–16. [Google Scholar]
- Wang, Y.; Zhang, Z.; Wang, Y. Moving Object Detection in Aerial Video. In Proceedings of the International Conference on Machine Learning and Applications, Boca Raton, FL, USA, 12–15 December 2012; pp. 446–450. [Google Scholar]
- Al-Kaff, A.; Gómez-Silva, M.J.; Moreno, F.M.; de la Escalera, A.; Armingol, J.M. An appearance-based tracking algorithm for aerial search and rescue purposes. Sensors 2019, 19, 652. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Pennisi, A.; Li, Z.; Zhang, Y.; Sahli, H. A Hierarchical Association Framework for Multi-Object Tracking in Airborne Videos. Remote. Sens. 2018, 10, 1347. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, X.; Xu, D.; Liu, F.; Wang, Y.; Wu, W. Robust visual detection—learning—tracking framework for autonomous aerial refueling of UAVs. IEEE Trans. Instrum. Meas. 2016, 65, 510–521. [Google Scholar] [CrossRef]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the 2016 IEEE International Conference on Image Processing, Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar]
- Wojke, N.; Bewley, A.; Paulus, D. Simple Online and Realtime Tracking with a Deep Association Metric. In Proceedings of the 2017 IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017; pp. 3645–3649. [Google Scholar]
- Wojke, N.; Bewley, A. Deep Cosine Metric Learning for Person Re-identification. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 748–756. [Google Scholar]
- Bochinski, E.; Eiselein, V.; Sikora, T. High-speed tracking-by-detection without using image information. In Proceedings of the IEEE International Conference on Advanced Video and Signal Based Surveillance, Lecce, Italy, 29 August–1 September 2017; pp. 1–6. [Google Scholar]
- Zhou, H.; Kong, H.; Wei, L.; Creighton, D.; Nahavandi, S. Efficient Road Detection and Tracking for Unmanned Aerial Vehicle. IEEE Trans. Intell. Transp. Syst. 2015, 16, 297–309. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. CoRR. 2018. Available online: http://xxx.lanl.gov/abs/1804.02767 (accessed on 1 March 2019).
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; 2015; pp. 91–99. Available online: https://papers.nips.cc/paper/5638-faster-r-cnn-towards-real-time-object-detection-with-region-proposal-networks.pdf (accessed on 1 March 2019).
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Tzutalin. LabelImg. Available online: https://github.com/tzutalin/labelImg (accessed on 1 March 2019).
- UA-DETRAC. Available online: http://detrac-db.rit.albany.edu/ (accessed on 1 March 2019).
- Hosang, J.; Benenson, R.; Schiele, B. Learning Non-maximum Suppression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6469–6477. [Google Scholar]
- Farneback, G. Two-Frame Motion Estimation Based on Polynomial Expansion. In Proceedings of the Scandinavian Conference on Image Analysis, Halmstad, Sweden, 29 June–2 July 2003; pp. 363–370. [Google Scholar]
- Bernardin, K.; Stiefelhagen, R. Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 2008, 246309. [Google Scholar] [CrossRef]






| Methods | Scene1 | Scene4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | FP | FN | IDs | MOTA(%) | Total | FP | FN | IDs | MOTA(%) | |
| YOLOv3+IOU [24] | 1888 | 72 | 824 | 56 | 49.57 | 2956 | 120 | 1010 | 314 | 51.15 |
| YOLOv3+SORT [21] | 1888 | 1448 | 74 | 214 | 8.05 | 2956 | 1302 | 84 | 106 | 49.52 |
| YOLOv3+DeepSort [22] | 1888 | 80 | 362 | 10 | 91.94 | 2956 | 10 | 60 | 20 | 96.95 |
| Our Method | 1888 | 2 | 14 | 4 | 98.94 | 2956 | 4 | 62 | 6 | 97.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Li, D.; Bai, Y.; Zhang, F.; Li, S.; Wang, M.; Zhang, Z.; Li, J. Multiple-Object-Tracking Algorithm Based on Dense Trajectory Voting in Aerial Videos. Remote Sens. 2019, 11, 2278. https://doi.org/10.3390/rs11192278
Yang T, Li D, Bai Y, Zhang F, Li S, Wang M, Zhang Z, Li J. Multiple-Object-Tracking Algorithm Based on Dense Trajectory Voting in Aerial Videos. Remote Sensing. 2019; 11(19):2278. https://doi.org/10.3390/rs11192278
Chicago/Turabian StyleYang, Tao, Dongdong Li, Yi Bai, Fangbing Zhang, Sen Li, Miao Wang, Zhuoyue Zhang, and Jing Li. 2019. "Multiple-Object-Tracking Algorithm Based on Dense Trajectory Voting in Aerial Videos" Remote Sensing 11, no. 19: 2278. https://doi.org/10.3390/rs11192278
APA StyleYang, T., Li, D., Bai, Y., Zhang, F., Li, S., Wang, M., Zhang, Z., & Li, J. (2019). Multiple-Object-Tracking Algorithm Based on Dense Trajectory Voting in Aerial Videos. Remote Sensing, 11(19), 2278. https://doi.org/10.3390/rs11192278