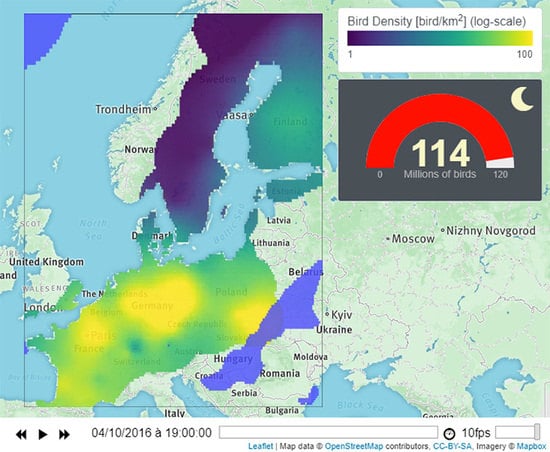
A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network
Abstract
1. Introduction
2. Materials and Methods
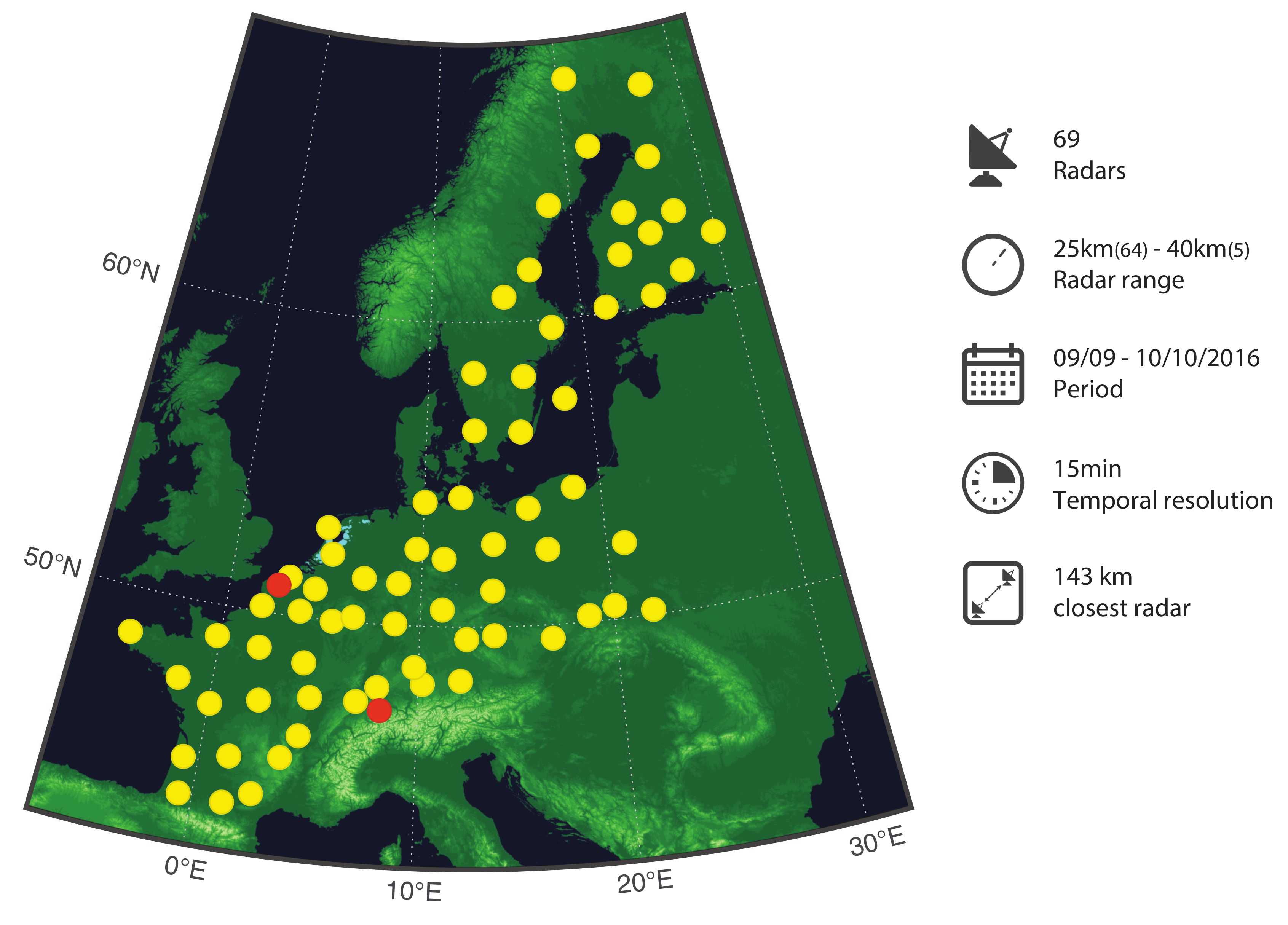
2.1. Weather Radar Dataset
2.2. Interpolation Approach
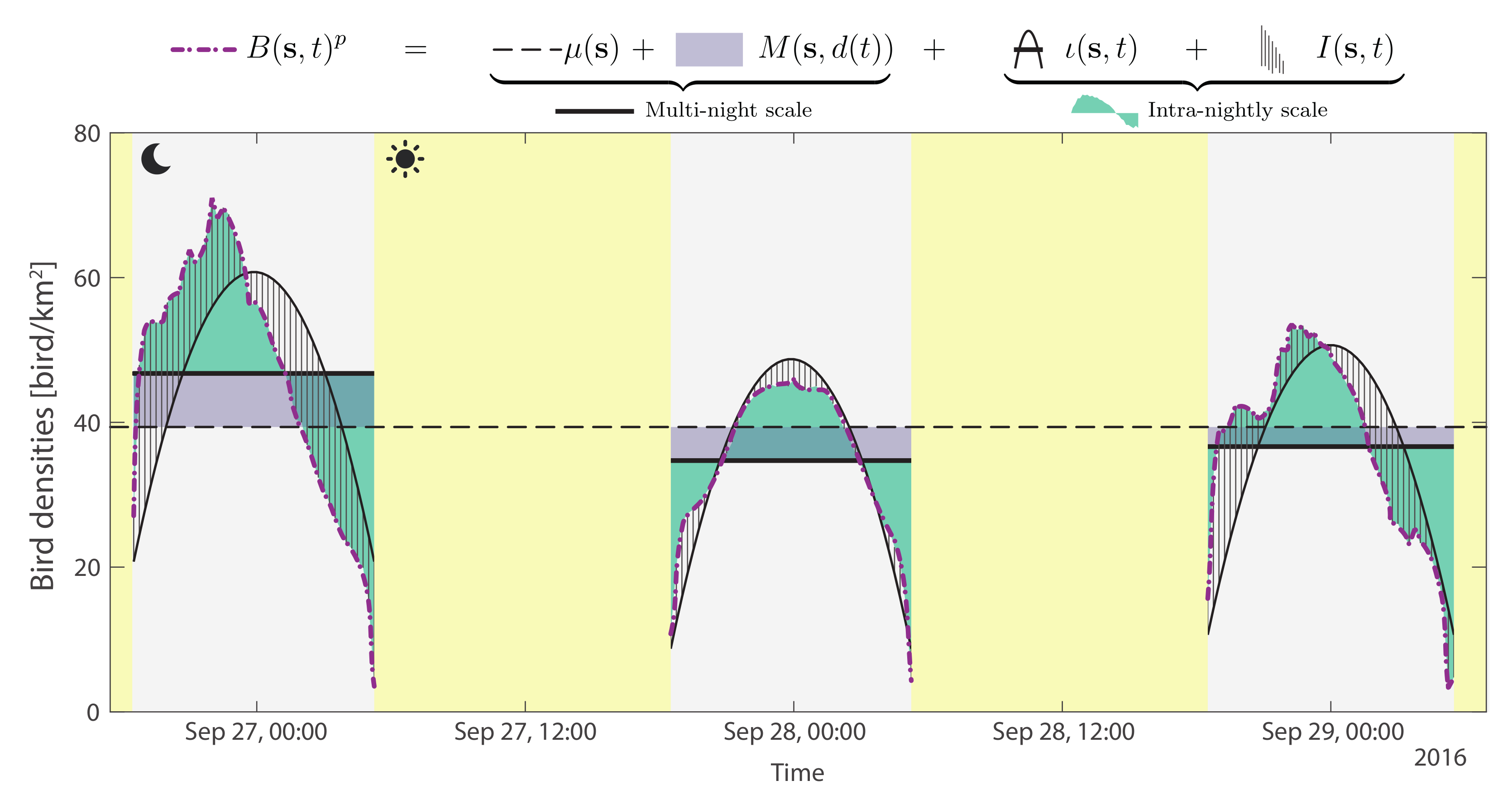
2.3. Geostatistical Model
2.3.1. Multi-Night Scale
2.3.2. Intra-Night Scale
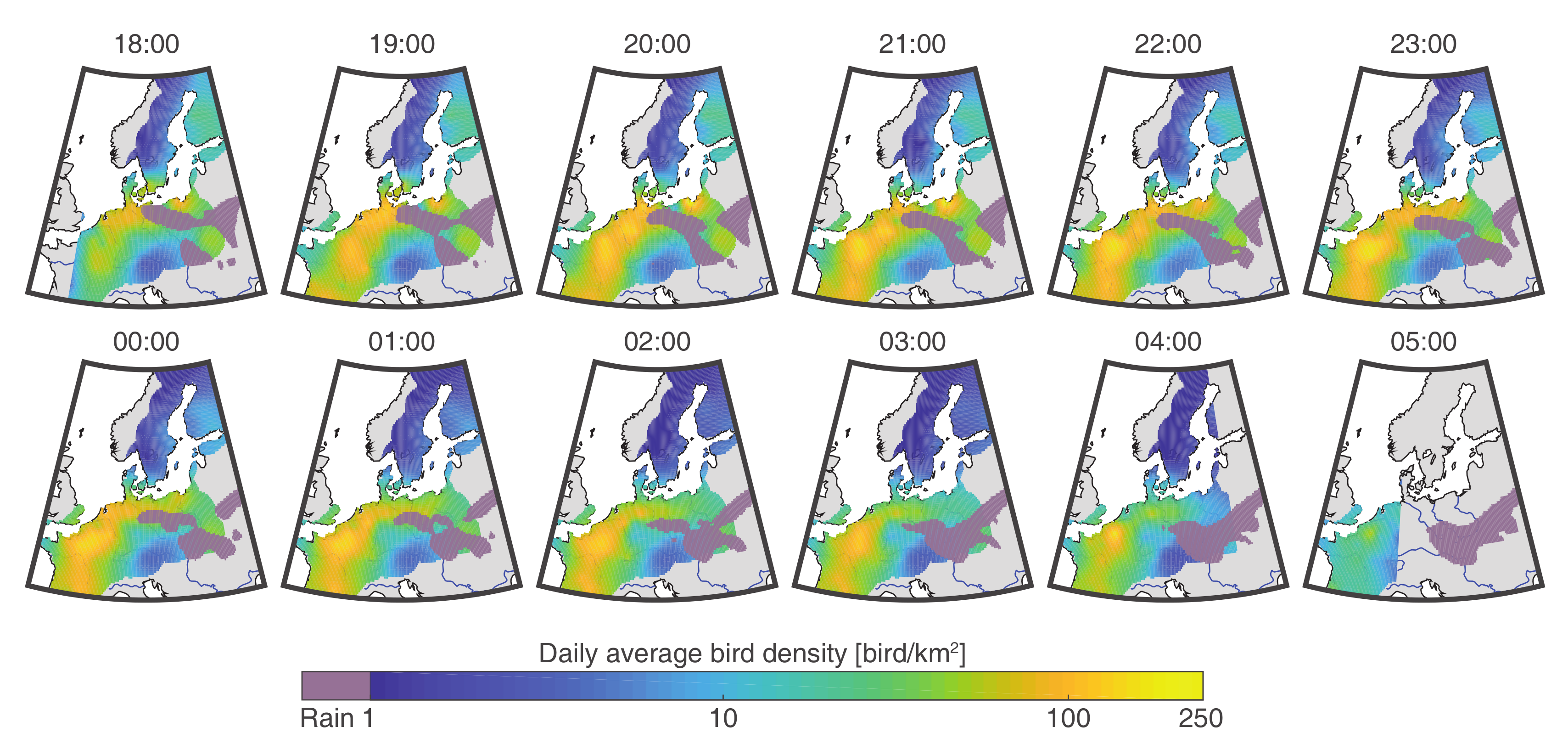
2.4. Bird Migration Mapping
2.4.1. Estimation
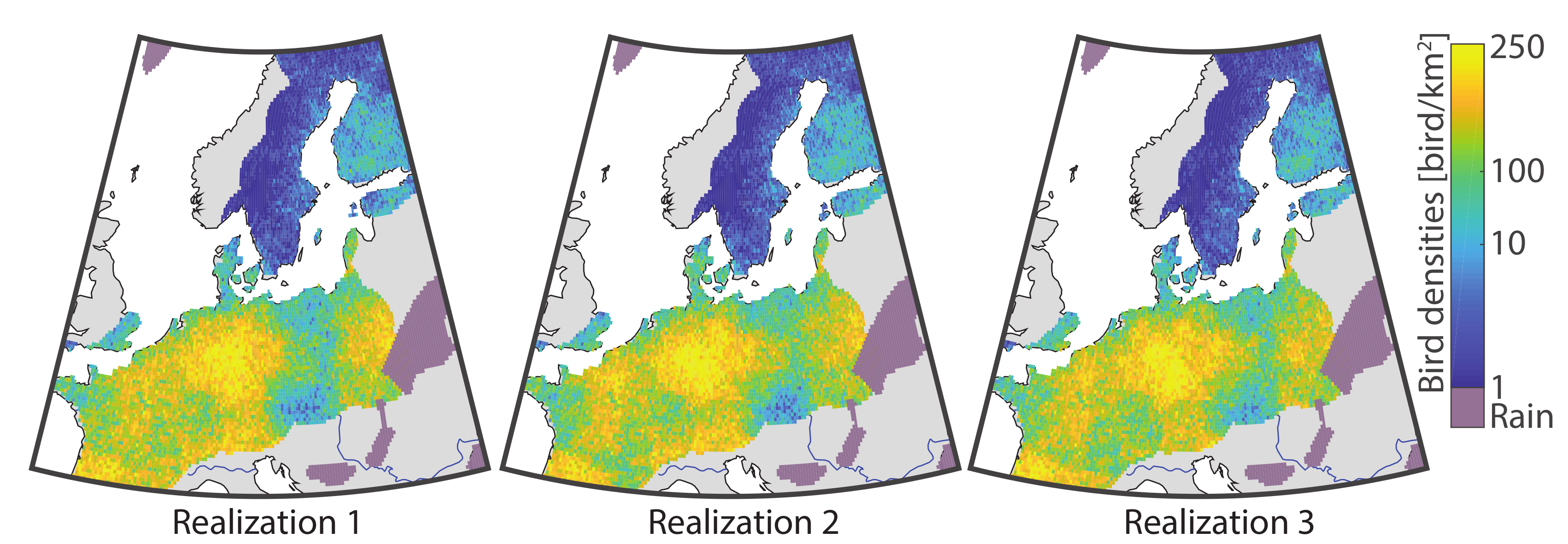
2.4.2. Simulation
2.5. Validation
2.5.1. Cross-Validation
2.5.2. Comparison with Dedicated Bird Radars
3. Results
3.1. Validation
3.1.1. Cross-Validation
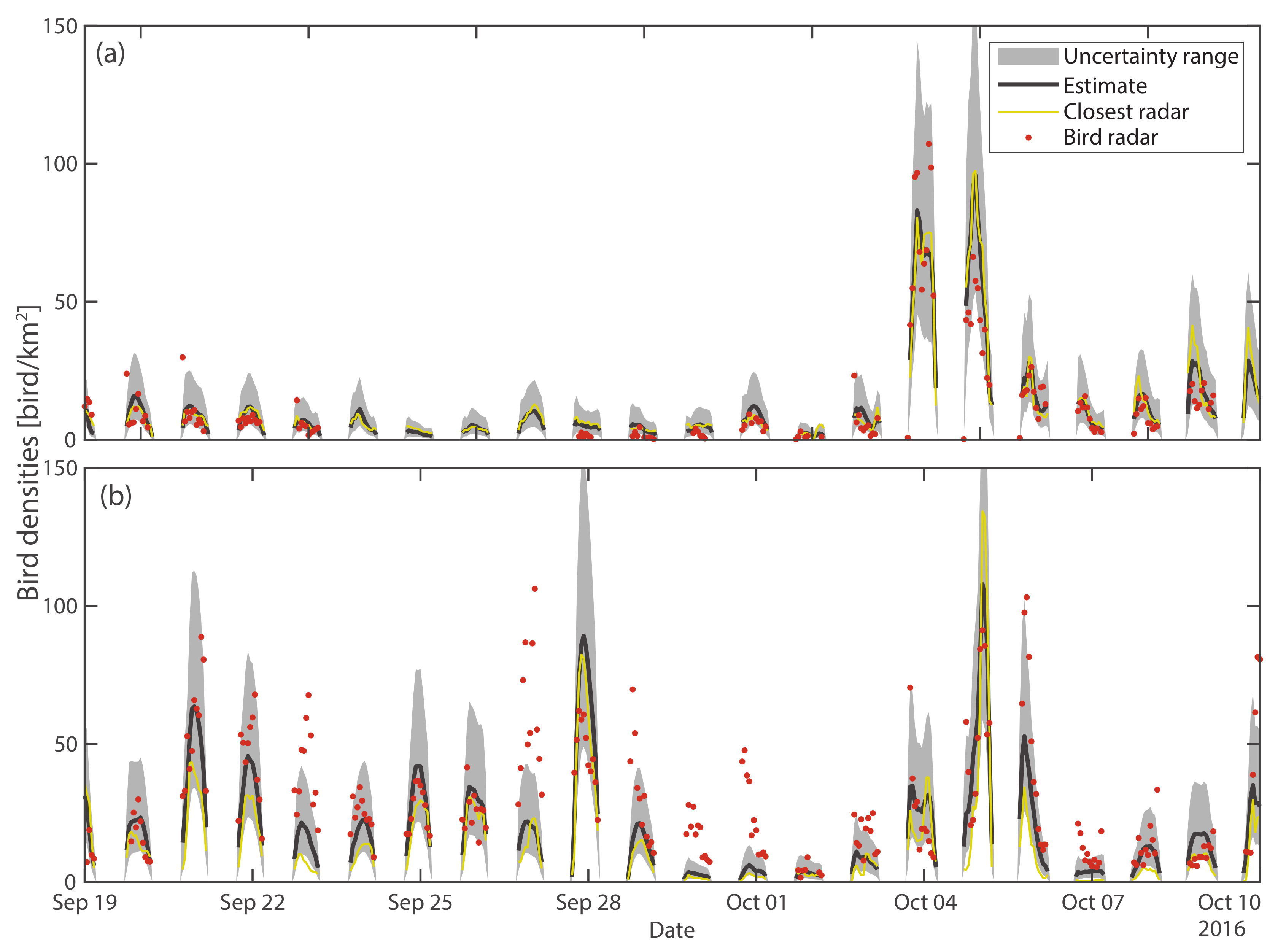
3.1.2. Comparison with Dedicated Bird Radars
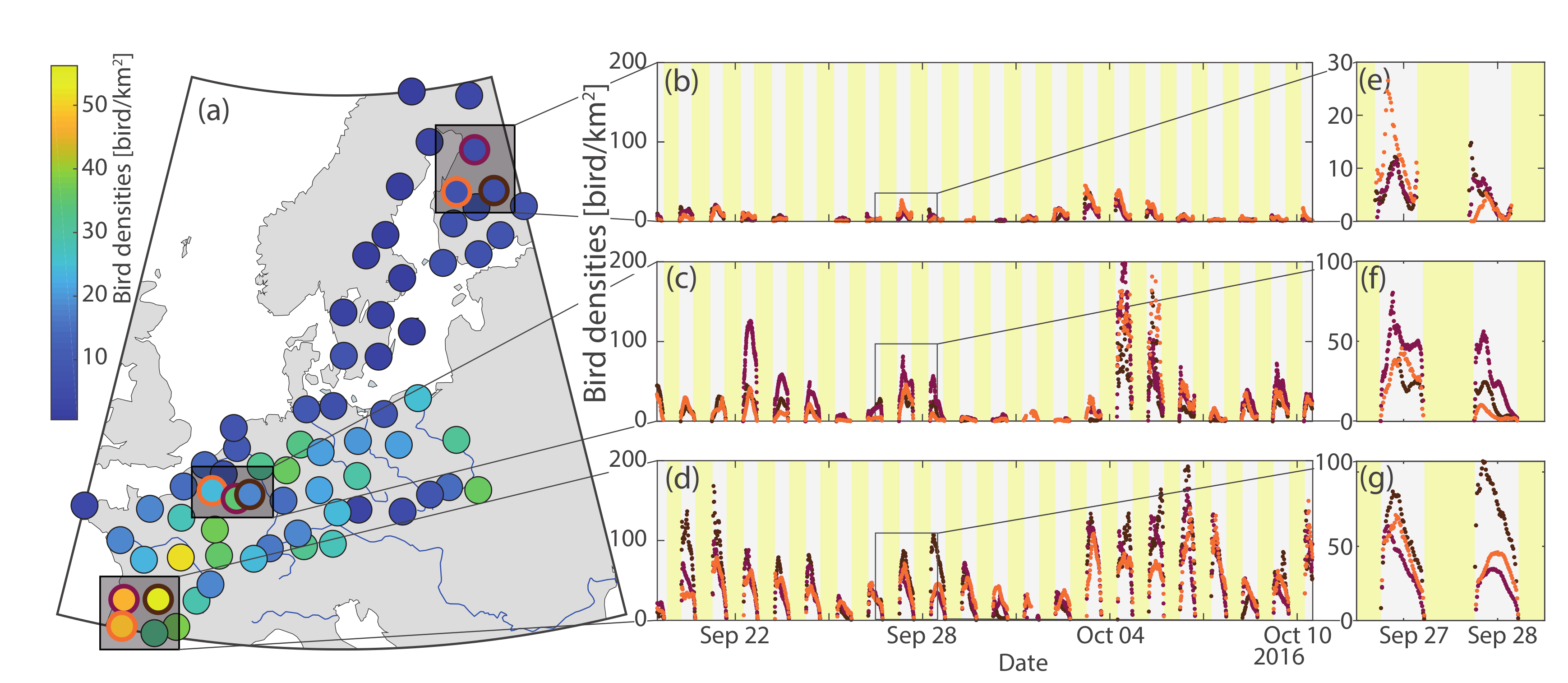
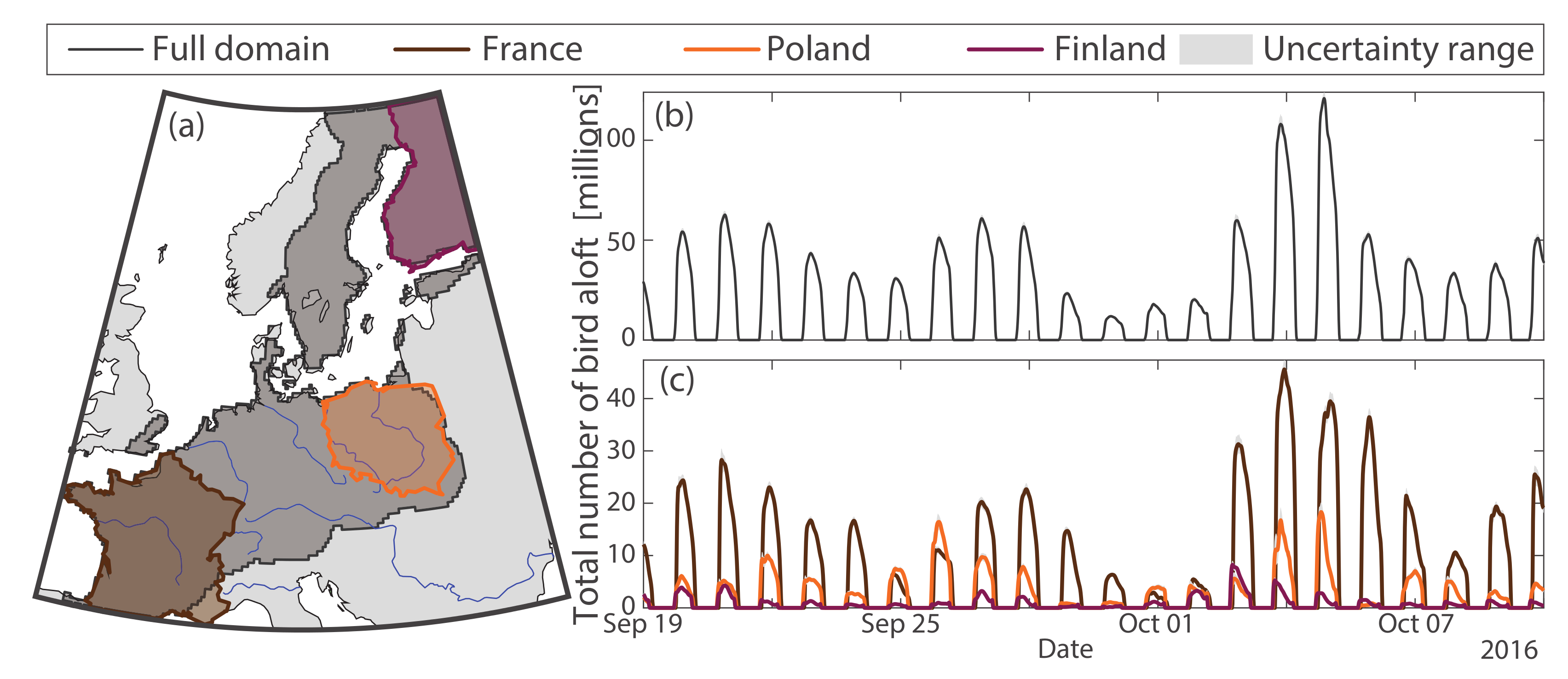
3.2. Application to Bird Migration Mapping
4. Discussion
4.1. Advantages and Limitations
4.2. Applications
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Data Preprocessing
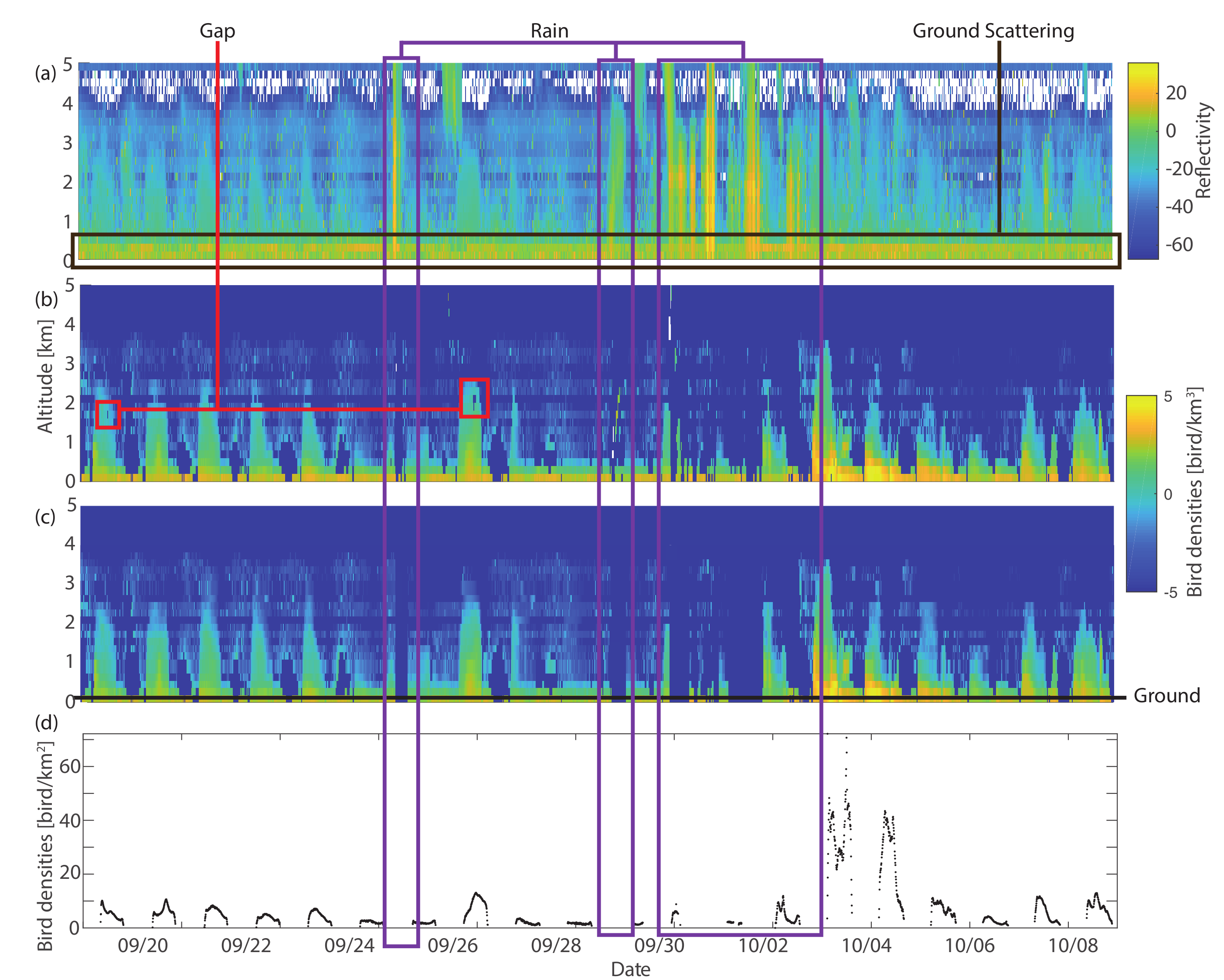
- Of the 84 radars contributing data during the study period, 11 radars are discarded because of their poor quality due to S-band radar type, poor processing, or large gaps (temporal or altitude cut). The same radars were removed in [21]. In addition, the four radars from Bulgaria and Portugal were excluded because of their geographic isolation.
- The full vertical profile was discarded when rain was present at any altitude bin (purple rectangle in Figure A1). A dedicated MATLAB GUI was used to visualize the data and manually set bird densities to “not-a-number” in such cases.
- Zones of high bird densities can sometimes be incorrectly eliminated in the raw data (red rectangle in Figure A1). To address this, reference [21] excluded problematic time or height ranges from the data. Here, in order to keep as much data as possible, the data was manually edited to replace erroneous data either with “not-a-number”, or by cubic interpolation using the dedicated MATLAB GUI.
- Due to ground scattering (brown rectangle in Figure A1), the lower altitude layers are sometimes contaminated by errors or excluded in the raw data. We vertically interpolated bird density by copying the first layer without error into to the lower ones. This approach is relatively conservative as bird migration intensity usually decreases with height in the absence of obstacles, and more so in autumn [39].
- The vertical profiles were vertically integrated from the radar ground level (black line in Figure A1c) and up to 5000 m asl.
- The data recorded during daytime are excluded. Daytime is defined for each radar by the civil dawn and dusk (sun 6° below horizon).
- Finally, the data of 10 radars with high temporal resolution (5–10 min) was downsampled to 15 min to preserve a balanced representation of each radar.
Appendix B. Model Parametrisation
| Power transformation | p = 0.133 |
| Spatial trend | w0 = 2.566, wlat = −0.024 |
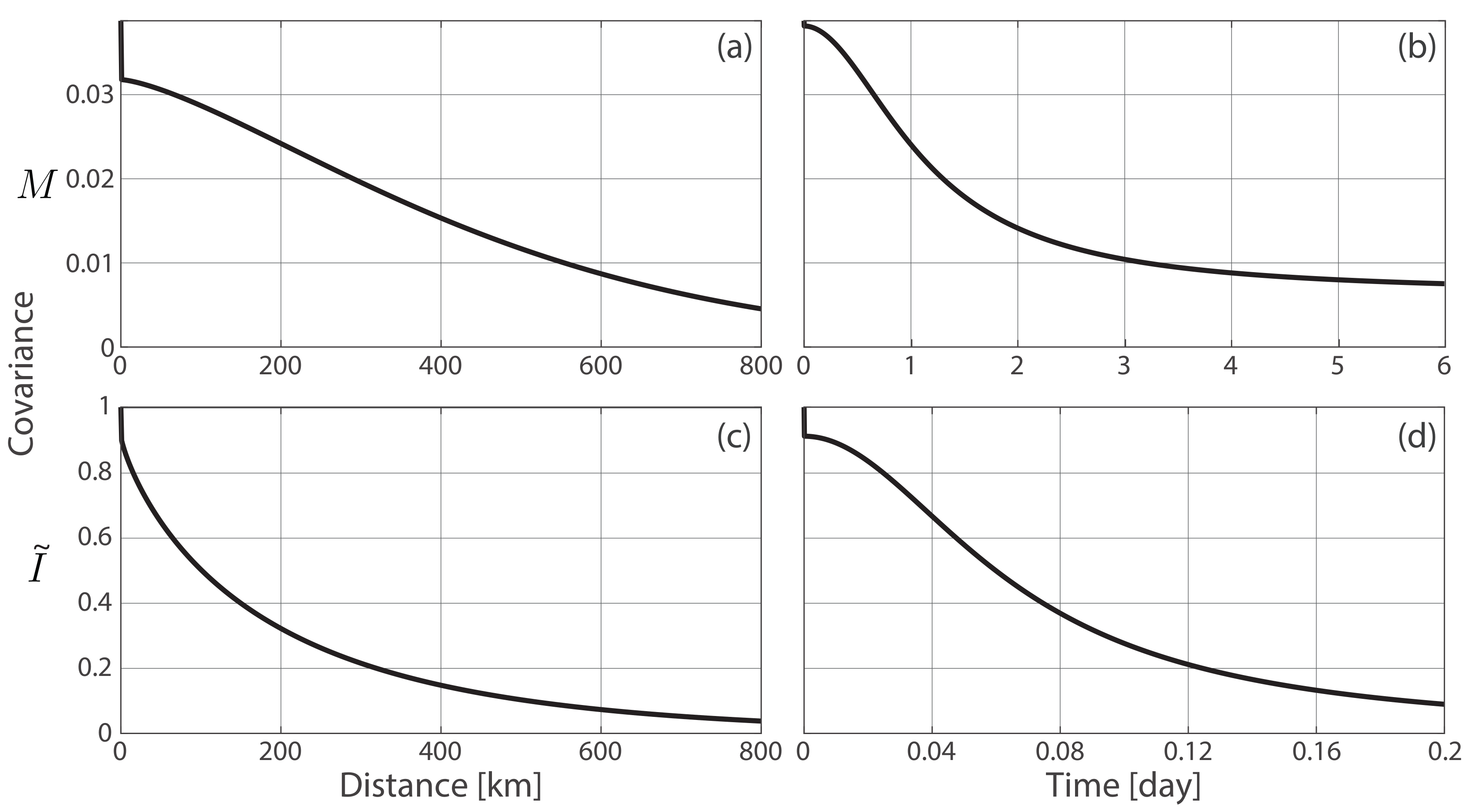
| Covariance ofM | C0 = 0.006, Cg = 0.032, rt = 1.24, rs = 500, α = 0.98, γ = 0.71, β = 0.95 |
| Curve | a = [0.04,−0.10, 0.07, 0.27,−1.29, −0.59, 2.86, 0.44, −1.92] |
| Curve variance | b = [0.00, 0.00, 0.02, 0.04,−0.17, −0.17, 0.62, 0.26, −0.93, −0.12, 0.49] |
| Covariance ofI | C0 = 0.009, Cg = 0.91, rt = 0.07, rs = 190, α = 1, γ = 0.4, β = 1 |
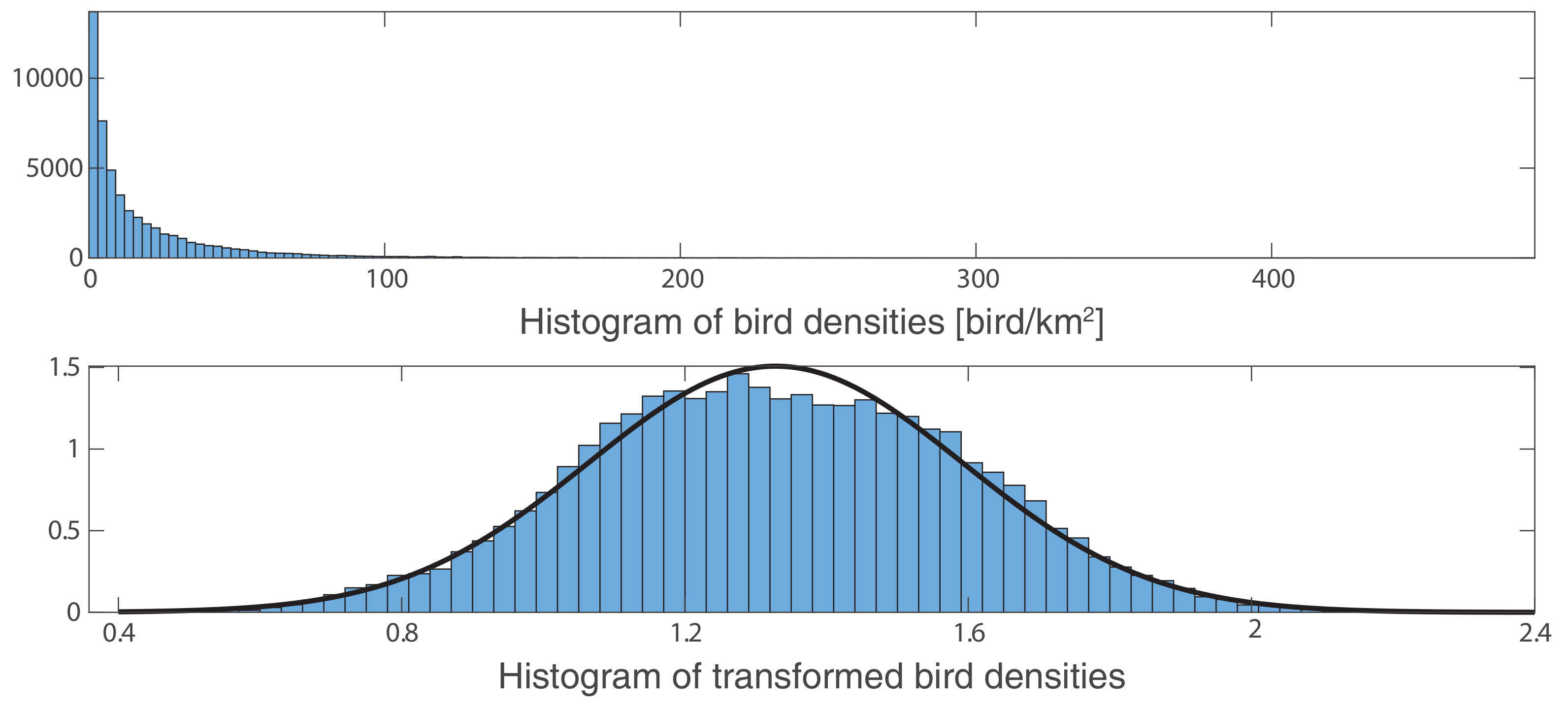
Appendix B.1. Power Transform p
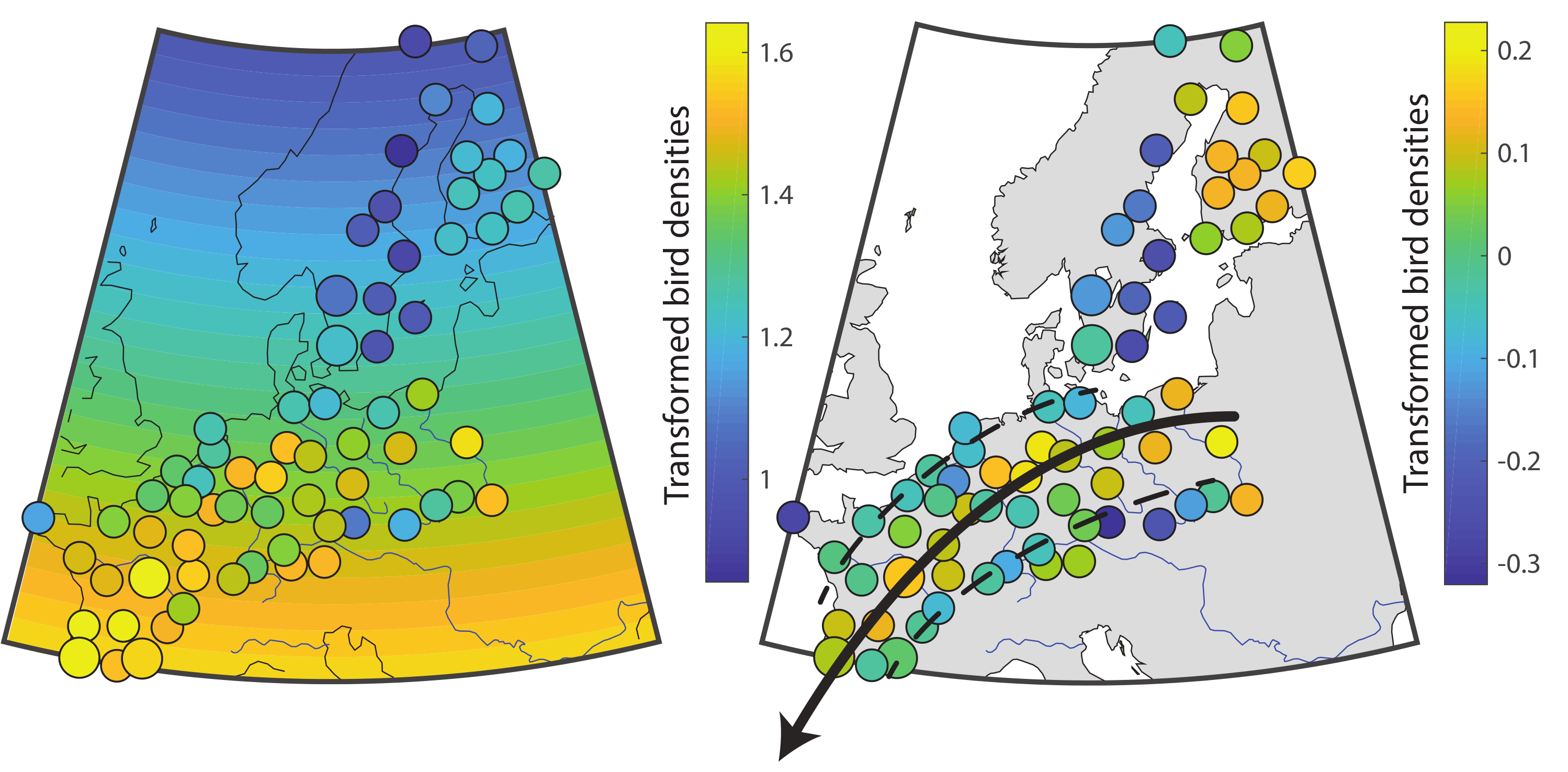
Appendix B.2. Spatial Trend μ
Appendix B.3. Curve Trend ι and Variance σ I
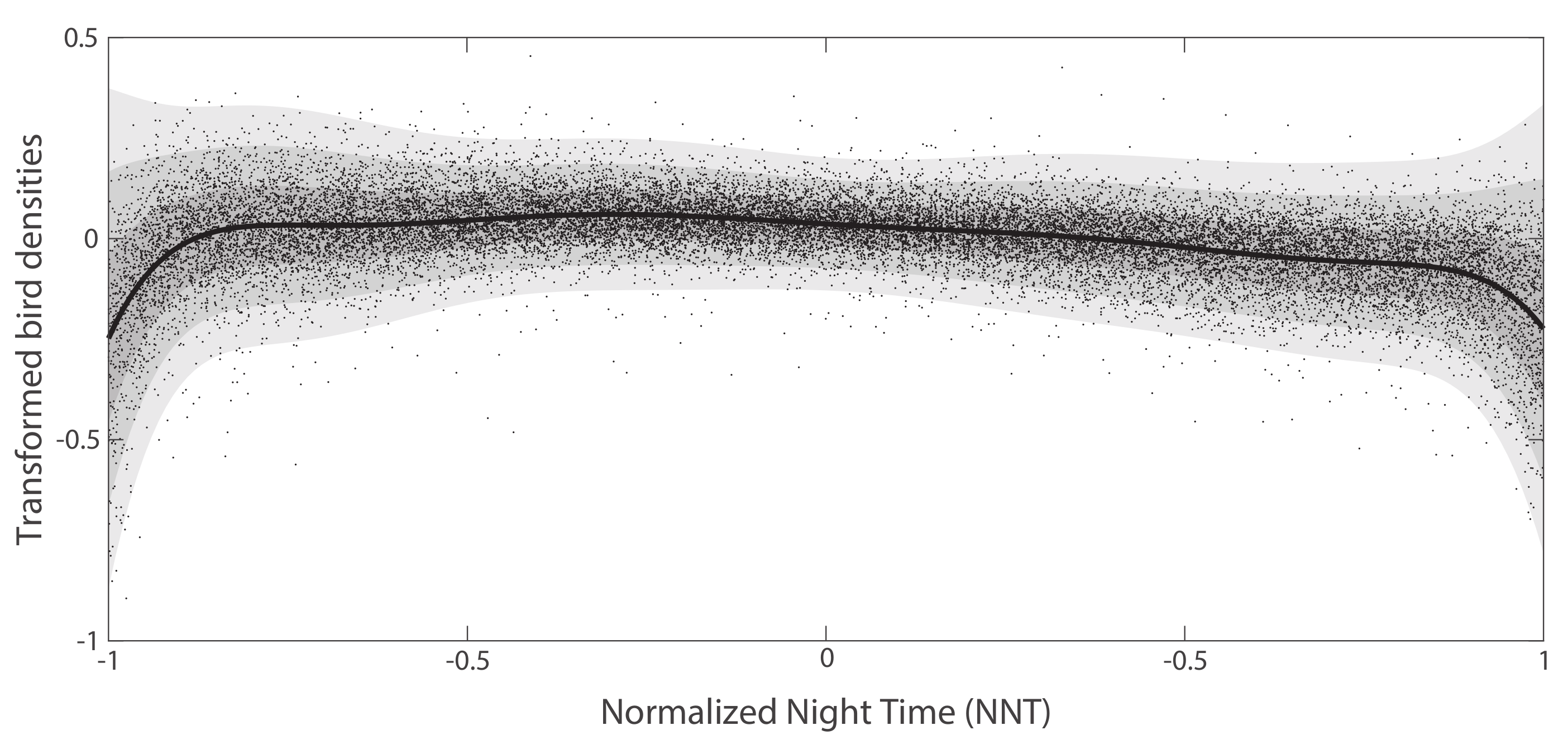
Appendix B.4. Covariance Functions of M and I
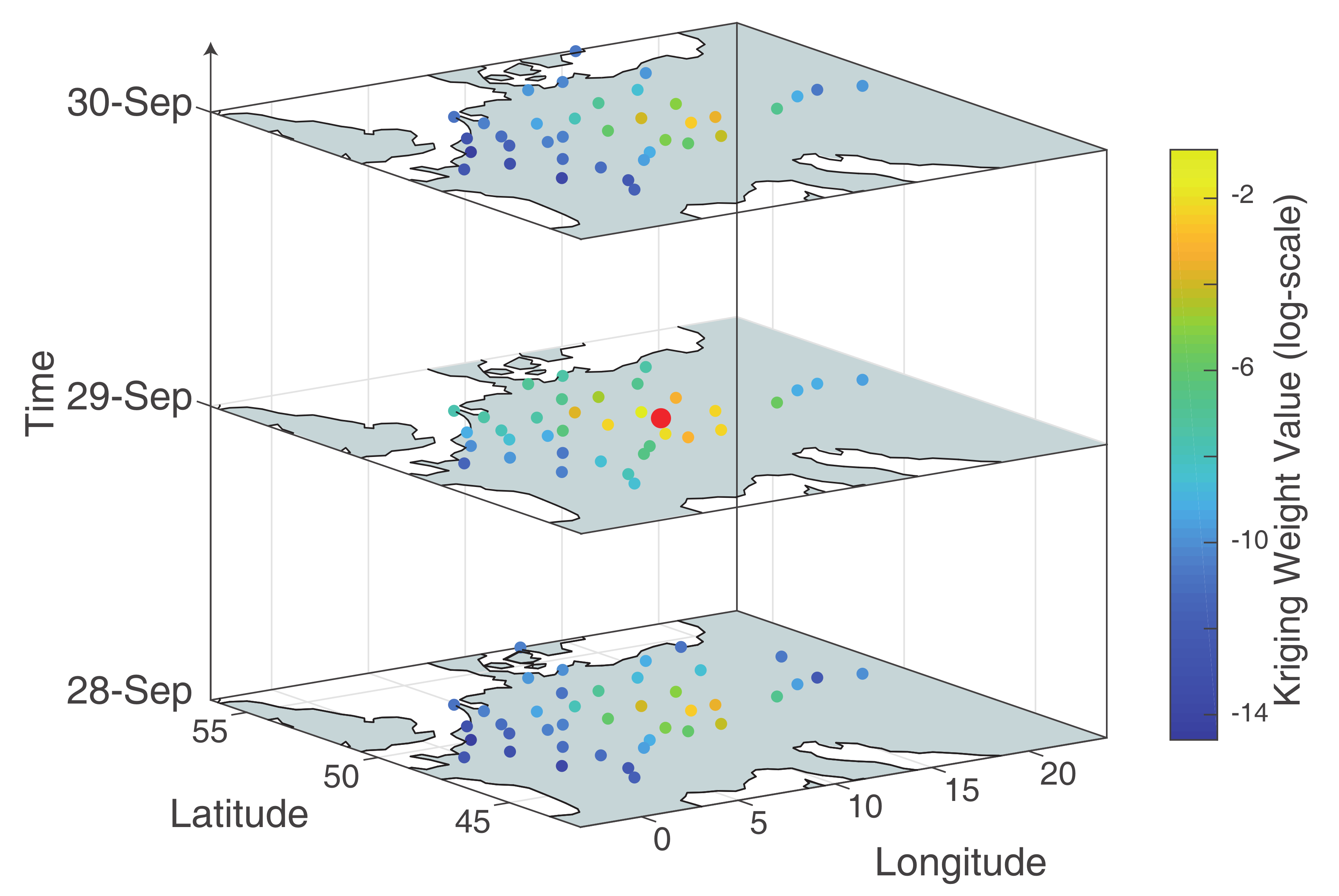
Appendix C. Kriging
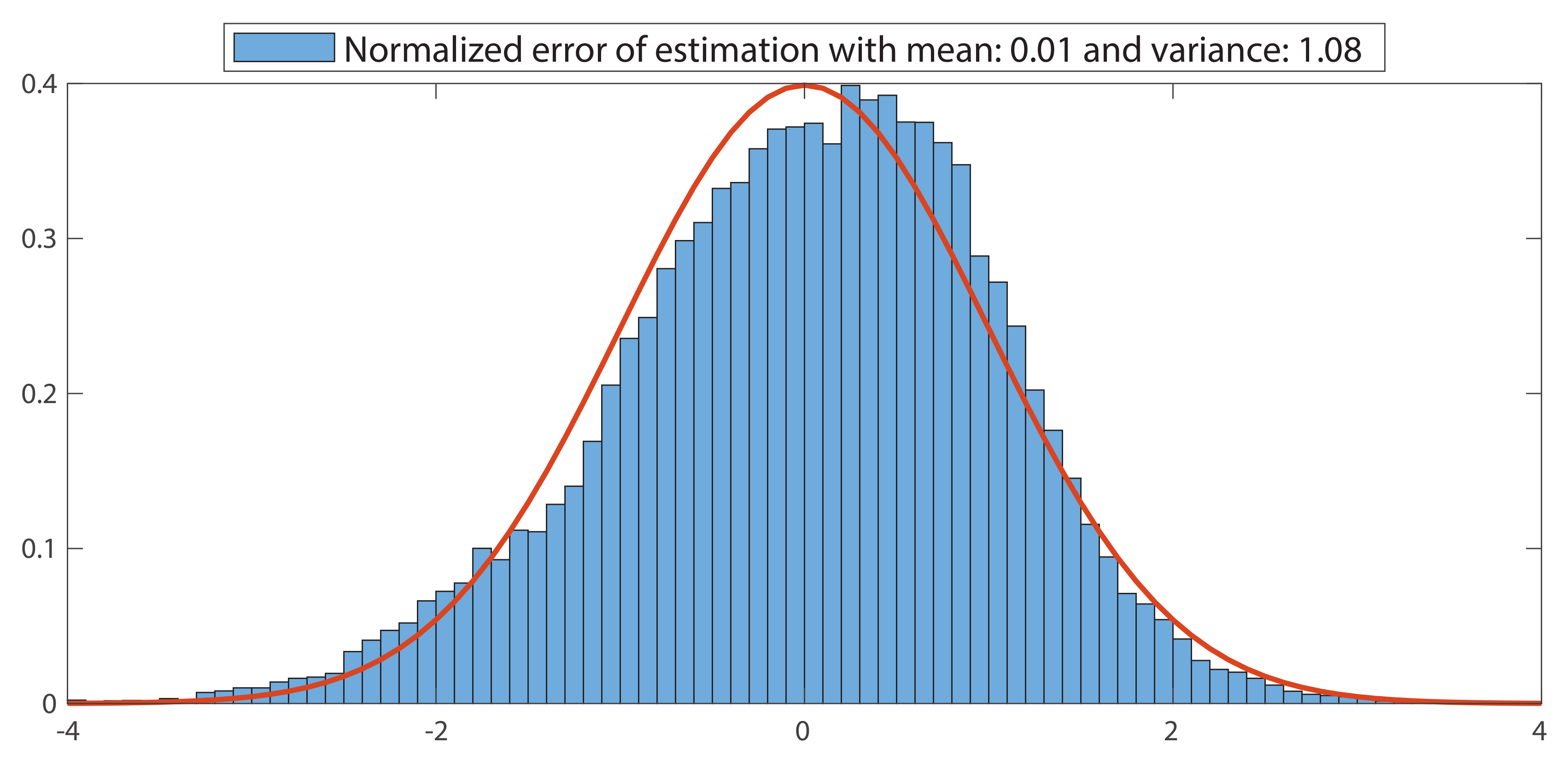
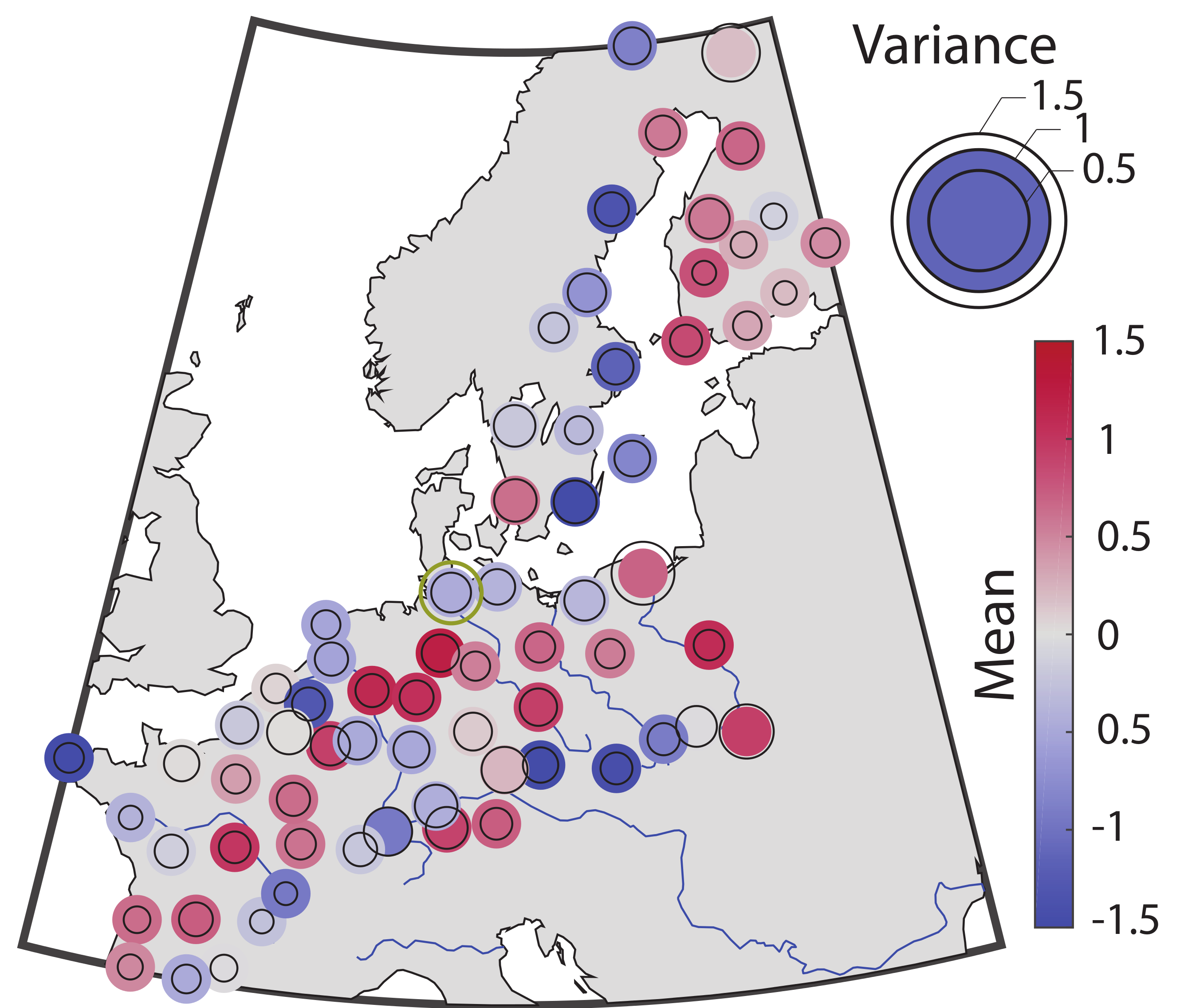
Appendix D. Cross-Validation
Appendix E. Manual for Website Interface
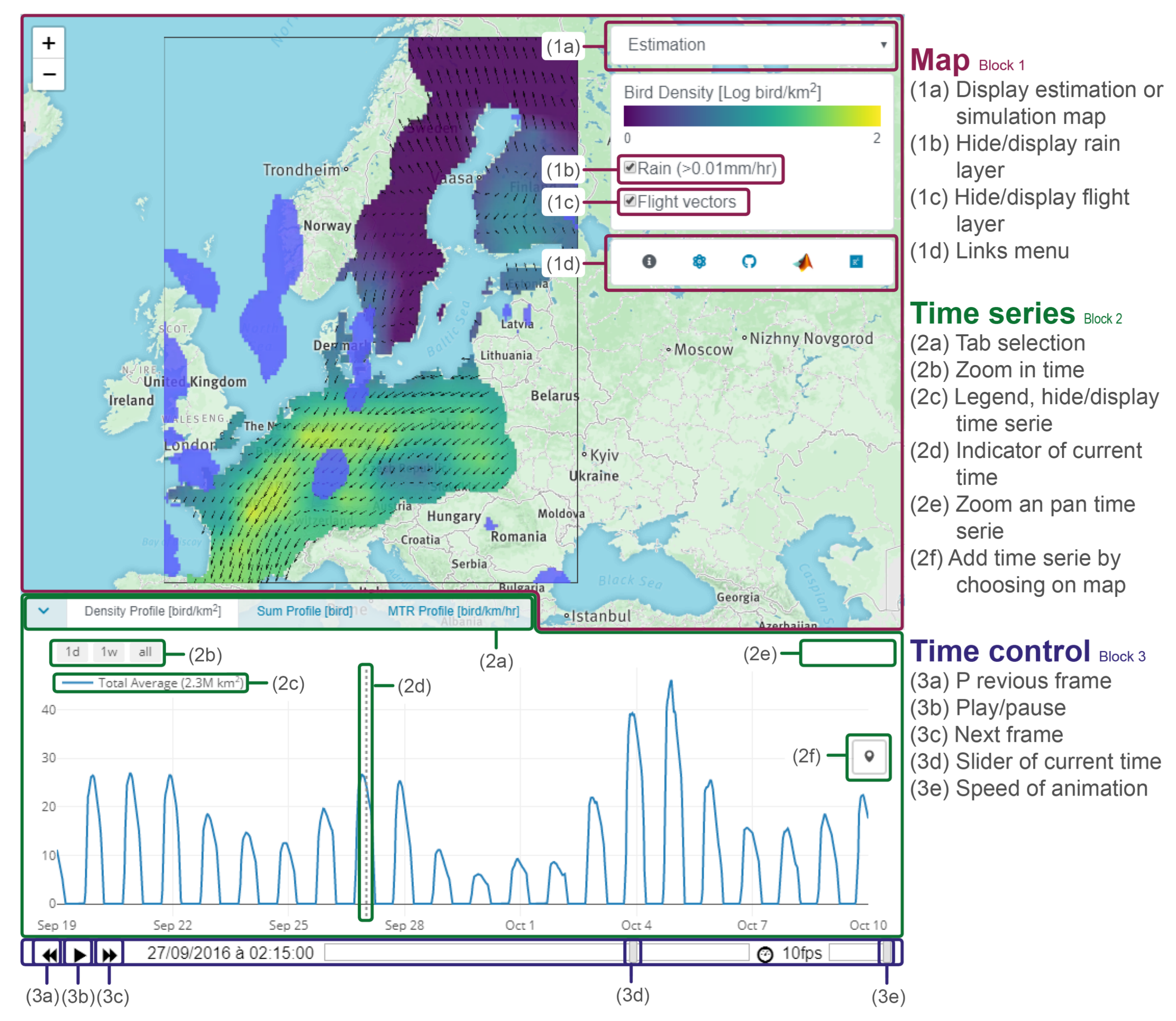
Appendix E.1. Block 1: Interactive Map
- The first layer illustrates bird densities in a log-color scale. This layer can display either the estimation map or a single simulation map. Users can choose using the drop-down menu (1a).
- The second layer displays the rain in light-blue. The layer can be hidden/displayed using the checkbox (1b).
- The third layer corresponds to bird flight speed and direction, visualized by black arrows. The checkbox (1c) allows users to display/hide this layer. Finally, the menu (1d) provides a link to (1) documentation, (2) model description, (3) Github repository, (4) MATLAB livescript, and (5) Researchgate page.
Appendix E.2. Block 2: Time Series
- Densities profile shows the bird densities [bird/km2] at a specific location.
- Sum profile shows the total number of birds [bird] over an area.
- MTR profile shows the mean traffic rate (MTR) [bird/km/h] perpendicular to a transect.
Appendix E.3. Block 3: Time Control
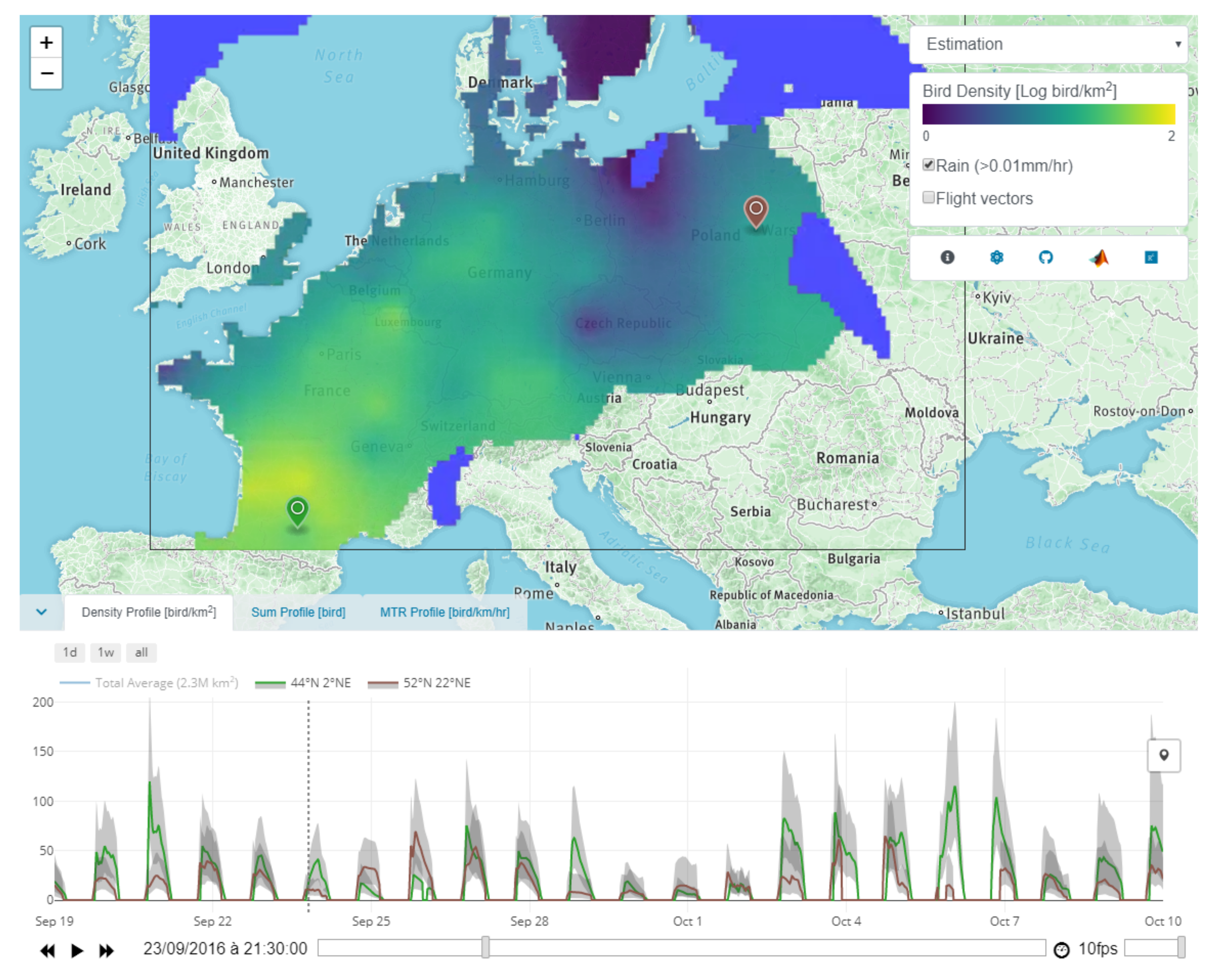
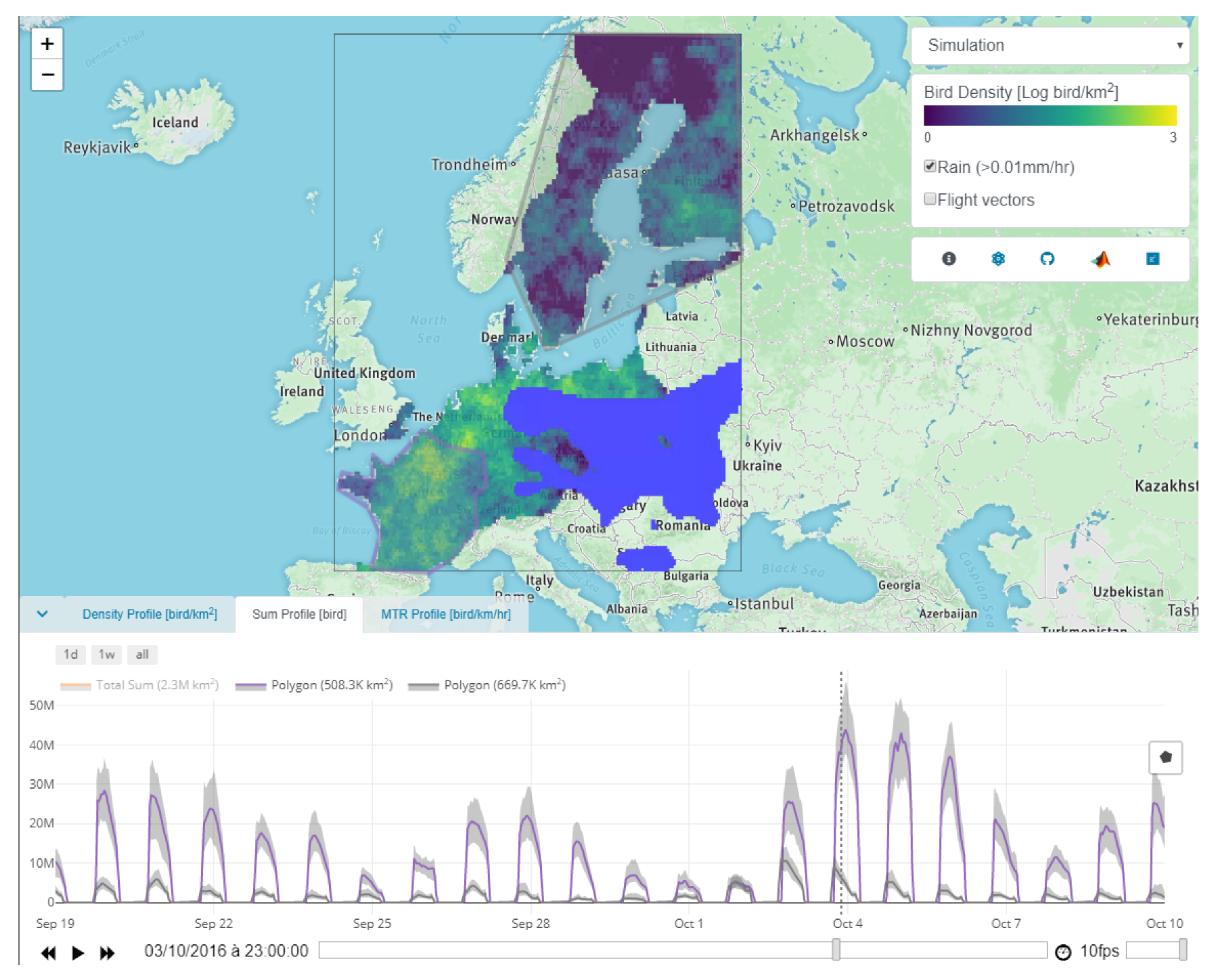
Appendix E.4. API
Appendix E.5. Examples
References and Note
- Hahn, S.; Bauer, S.; Liechti, F. The natural link between Europe and Africa—2.1 billion birds on migration. Oikos 2009, 118, 624–626. [Google Scholar] [CrossRef]
- Dokter, A.M.; Farnsworth, A.; Fink, D.; Ruiz-Gutierrez, V.; Hochachka, W.M.; la Sorte, F.A.; Robinson, O.J.; Rosenberg, K.V.; Kelling, S. Seasonal abundance and survival of North America’s migratory avifauna determined by weather radar. Nat. Ecol. Evol. 2018, 2, 1603. [Google Scholar] [CrossRef] [PubMed]
- Bauer, S.; Hoye, B.J. Migratory animals couple biodiversity and ecosystem functioning worldwide. Science 2014, 344. [Google Scholar] [CrossRef] [PubMed]
- Runge, C.A.; Martin, T.G.; Possingham, H.P.; Willis, S.G.; Fuller, R.A. Conserving mobile species. Front. Ecol. Environ. 2014, 12, 395–402. [Google Scholar] [CrossRef]
- Sanderson, F.J.; Donald, P.F.; Pain, D.J.; Burfield, I.J.; van Bommel, F.P. Long-term population declines in Afro-Palearctic migrant birds. Biol. Conserv. 2006, 131, 93–105. [Google Scholar] [CrossRef]
- Vickery, J.A.; Smith, K.W.; Pain, D.J.; Gregory, R.D.; Škorpilová, J.; Bairlein, F.; Ewing, S.R. The decline of Afro-Palaearctic migrants and an assessment of potential causes. Ibis 2013, 156, 1–22. [Google Scholar] [CrossRef]
- Diehl, R.H. The airspace is habitat. Trends Ecol. Evol. 2013, 28, 377–379. [Google Scholar] [CrossRef]
- La Sorte, F.A.; Horton, K.G.; Nilsson, C.; Dokter, A.M. Projected changes in wind assistance under climate change for nocturnally migrating bird populations. Glob. Chang. Biol. 2019, 25, 589–601. [Google Scholar] [CrossRef]
- Van Doren, B.M.; Horton, K.G.; Dokter, A.M.; Klinck, H.; Elbin, S.B.; Farnsworth, A. High-intensity urban light installation dramatically alters nocturnal bird migration. Proc. Natl. Acad. Sci. USA 2017, 114, 11175–11180. [Google Scholar] [CrossRef]
- Winger, B.M.; Weeks, B.C.; Farnsworth, A.; Jones, A.W.; Hennen, M.; Willard, D.E. Nocturnal flight-calling behaviour predicts vulnerability to artificial light in migratory birds. Proc. Biol. Sci. 2019, 286, 20190364. [Google Scholar] [CrossRef]
- Aschwanden, J.; Stark, H.; Peter, D.; Steuri, T.; Schmid, B.; Liechti, F. Bird collisions at wind turbines in a mountainous area related to bird movement intensities measured by radar. Biol. Conserv. 2018, 220, 228–236. [Google Scholar] [CrossRef]
- van Gasteren, H.; Krijgsveld, K.L.; Klauke, N.; Leshem, Y.; Metz, I.C.; Skakuj, M.; Sorbi, S.; Schekler, I.; Shamoun-Baranes, J. Aeroecology meets aviation safety: early warning systems in Europe and the Middle East prevent collisions between birds and aircraft. Ecography 2019, 42, 899–911. [Google Scholar] [CrossRef]
- Loss, S.R.; Will, T.; Marra, P.P. Direct Mortality of Birds from Anthropogenic Causes. Annu. Rev. Ecol. Evol. Syst. 2015, 46, 99–120. [Google Scholar] [CrossRef]
- Winkler, R. Avifaune. In Avifaune de Suisse; Nos Oiseaux, 1999; Volume 3. [Google Scholar]
- Drake, A.V.; Bruderer, B. Aeroecological Observation Methods. In Aeroecology; Chilson, P.B., Frick, W.F., Kelly, J.F., Liechti, F., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 201–237. [Google Scholar] [CrossRef]
- Gauthreaux, S.A.; Belser, C.G.; van Blaricom, D. Using a Network of WSR-88D Weather Surveillance Radars to Define Patterns of Bird Migration at Large Spatial Scales. In Avian Migration; Springer: Berlin/Heidelberg, Germany, 2003; pp. 335–346. [Google Scholar] [CrossRef]
- Shamoun-Baranes, J.; Alves, J.A.; Bauer, S.; Dokter, A.M.; Hüppop, O.; Koistinen, J.; Leijnse, H.; Liechti, F.; van Gasteren, H.; Chapman, J.W. Continental-scale radar monitoring of the aerial movements of animals. Mov. Ecol. 2014, 2, 4–9. [Google Scholar] [CrossRef]
- Bauer, S.; Chapman, J.W.; Reynolds, D.R.; Alves, J.A.; Dokter, A.M.; Menz, M.M.; Sapir, N.; Ciach, M.; Pettersson, L.B.; Kelly, J.F.; et al. From Agricultural Benefits to Aviation Safety: Realizing the Potential of Continent-Wide Radar Networks. BioScience 2017, 67, 912–918. [Google Scholar] [CrossRef]
- Van Doren, B.M.; Horton, K.G. A continental system for forecasting bird migration. Science 2018, 361, 1115–1118. [Google Scholar] [CrossRef]
- Huuskonen, A.; Saltikoff, E.; Holleman, I. The operational weather radar network in Europe. Bull. Am. Meteorol. Soc. 2014, 95, 897–907. [Google Scholar] [CrossRef]
- Nilsson, C.; Dokter, A.M.; Verlinden, L.; Shamoun-Baranes, J.; Schmid, B.; Desmet, P.; Bauer, S.; Chapman, J.; Alves, J.A.; Stepanian, P.M.; et al. Revealing patterns of nocturnal migration using the European weather radar network. Ecography 2019, 42, 876–886. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service (C3S). ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Available online: https://climate.copernicus.eu/climate-reanalysis (accessed on 20 February 2018).
- Chilès, J.P.; Delfiner, P. Geostatistics; Wiley Series in Probability and Statistics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1999; Volume 497. [Google Scholar] [CrossRef]
- Lantuéjoul, C. Geostatistical Simulation; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Gneiting, T. Nonseparable, stationary covariance functions for space time data. J. Am. Stat. Assoc. 2002, 97, 590–600. [Google Scholar] [CrossRef]
- Bruderer, B.; Liechti, F. Variation in density and height distribution of nocturnal migration in the south of israel. Isr. J. Zool. 1995, 41, 477–487. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997; p. 483. [Google Scholar]
- Gómez-Hernández, J.J.; Cassiraga, E.F. Theory and Practice of Sequential Simulation; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994; pp. 111–124. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: New York, NY, USA, 1992; p. 147. [Google Scholar]
- Schmid, B.; Zaugg, S.; Votier, S.C.; Chapman, J.W.; Boos, M.; Liechti, F. Size matters in quantitative radar monitoring of animal migration: Estimating monitored volume from wingbeat frequency. Ecography 2019, 42, 931–941. [Google Scholar] [CrossRef]
- Nilsson, C.; Dokter, A.M.; Schmid, B.; Scacco, M.; Verlinden, L.; Bäckman, J.; Haase, G.; Dell’Omo, G.; Chapman, J.W.; Leijnse, H.; et al. Field validation of radar systems for monitoring bird migration. J. Appl. Ecol. 2018, 55, 2552–2564. [Google Scholar] [CrossRef]
- Erni, B.; Liechti, F.; Underhill, L.G.; Bruderer, B. Wind and rain govern the intensity of nocturnal bird migration in central Europe-a log-linear regression analysis. Ardea 2002, 90, 155–166. [Google Scholar]
- Van Belle, J.; Shamoun-Baranes, J.; van Loon, E.; Bouten, W. An operational model predicting autumn bird migration intensities for flight safety. J. Appl. Ecol. 2007, 44, 864–874. [Google Scholar] [CrossRef]
- Lin, T.; Winner, K.; Bernstein, G.; Mittal, A.; Dokter, A.M.; Horton, K.G.; Nilsson, C.; van Doren, B.M.; Farnsworth, A.; la Sorte, F.A.; et al. MistNet: Measuring historical bird migration in the US using archived weather radar data and convolutional neural networks. Methods Ecol. Evol. 2019. [Google Scholar] [CrossRef]
- Angell, R.; Sheldon, D.R. Inferring Latent Velocities from Weather Radar Data Using Gaussian Processes; Number Nips; Neural Information Processing Systems (NIPS); Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Montréal, QC, Canada, 2018; pp. 8984–8993. [Google Scholar]
- Nussbaumer, R.; Benoit, L.; Mariethoz, G.; Liechti, F.; Bauer, S.; Schmid, B.; Interpolated Maps of Bird Density and Flight Vector over Europe [Data Set]. Zenodo. 2019. Available online: https://zenodo.org/record/3243465 (accessed on 17 June 2019).
- Nussbaumer, R.; Benoit, L.; Schmid, B.; Vertical Profiles and Integrated Time Series of Bird Density and Flight Speed Vector (19–10 October 2016) [Data Set]. Zenodo. 2019. Available online: https://zenodo.org/record/3243396 (accessed on 17 June 2019).
- Bruderer, B.; Peter, D.; Korner-Nievergelt, F. Vertical distribution of bird migration between the Baltic Sea and the Sahara. J. Ornithol. 2018, 159, 315–336. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nussbaumer, R.; Benoit, L.; Mariethoz, G.; Liechti, F.; Bauer, S.; Schmid, B. A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network. Remote Sens. 2019, 11, 2233. https://doi.org/10.3390/rs11192233
Nussbaumer R, Benoit L, Mariethoz G, Liechti F, Bauer S, Schmid B. A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network. Remote Sensing. 2019; 11(19):2233. https://doi.org/10.3390/rs11192233
Chicago/Turabian StyleNussbaumer, Raphaël, Lionel Benoit, Grégoire Mariethoz, Felix Liechti, Silke Bauer, and Baptiste Schmid. 2019. "A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network" Remote Sensing 11, no. 19: 2233. https://doi.org/10.3390/rs11192233
APA StyleNussbaumer, R., Benoit, L., Mariethoz, G., Liechti, F., Bauer, S., & Schmid, B. (2019). A Geostatistical Approach to Estimate High Resolution Nocturnal Bird Migration Densities from a Weather Radar Network. Remote Sensing, 11(19), 2233. https://doi.org/10.3390/rs11192233