How Does Scale Effect Influence Spring Vegetation Phenology Estimated from Satellite-Derived Vegetation Indexes?
Abstract
:1. Introduction
2. Theoretical Analyses of the Scale Effect of VI on GUD Detection by Using Two-Endmember Scenarios
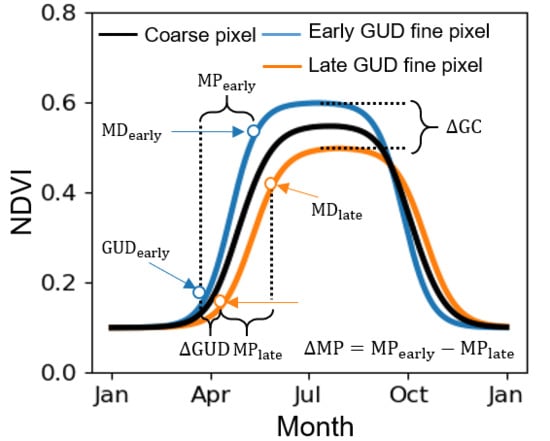
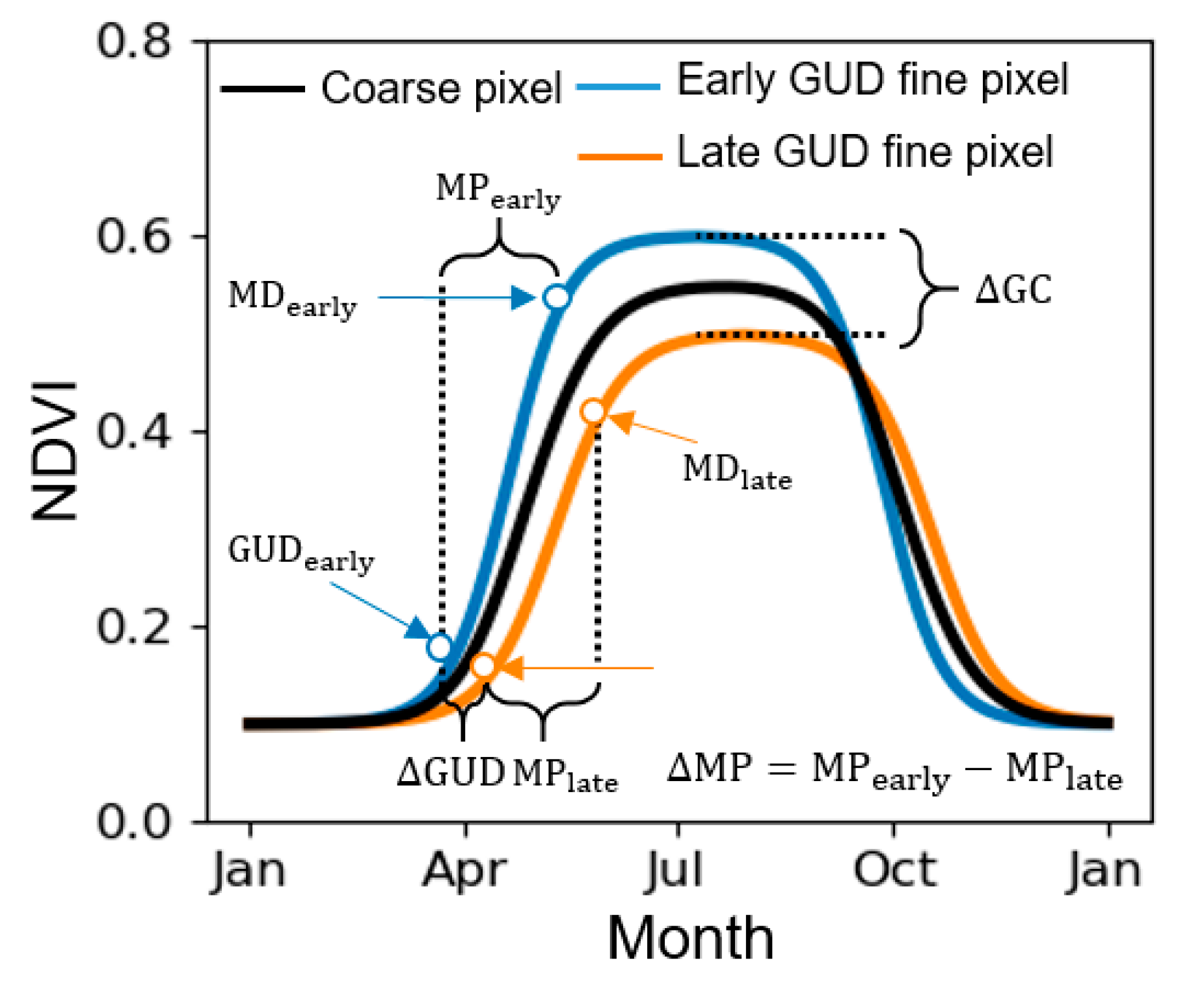
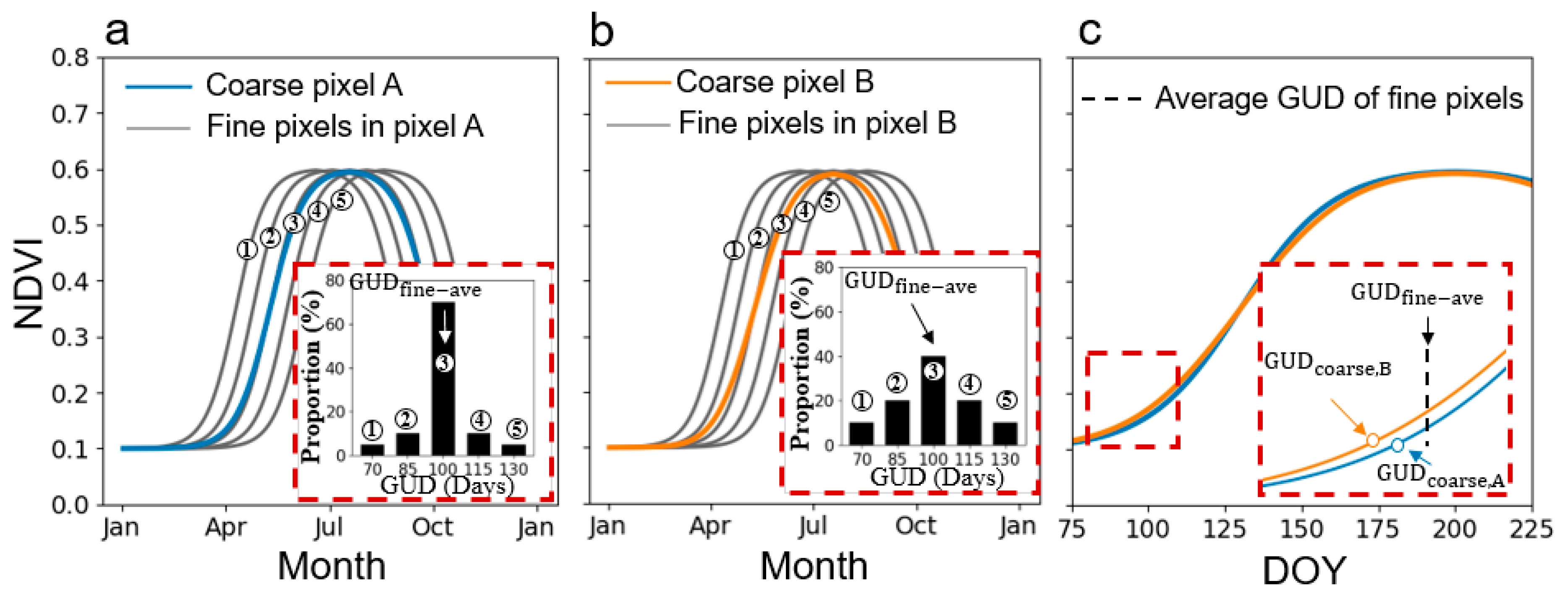
2.1. Defining GUD in VI Time-Series
2.2. Defining the Scale Effect of VI on GUD Estimation
2.3. Factors Influencing the Scale Effect on GUD Estimation
2.4. Form of Function f in Equation (9)
3. Experimental Design
3.1. Simulation Experiments Based on PhenoCam Sites Data
3.1.1. Phenology Observations
3.1.2. Testing the Two-Endmember Model
3.1.3. Testing the Multi-Endmember Model Based on SIMMAP Simulated Data
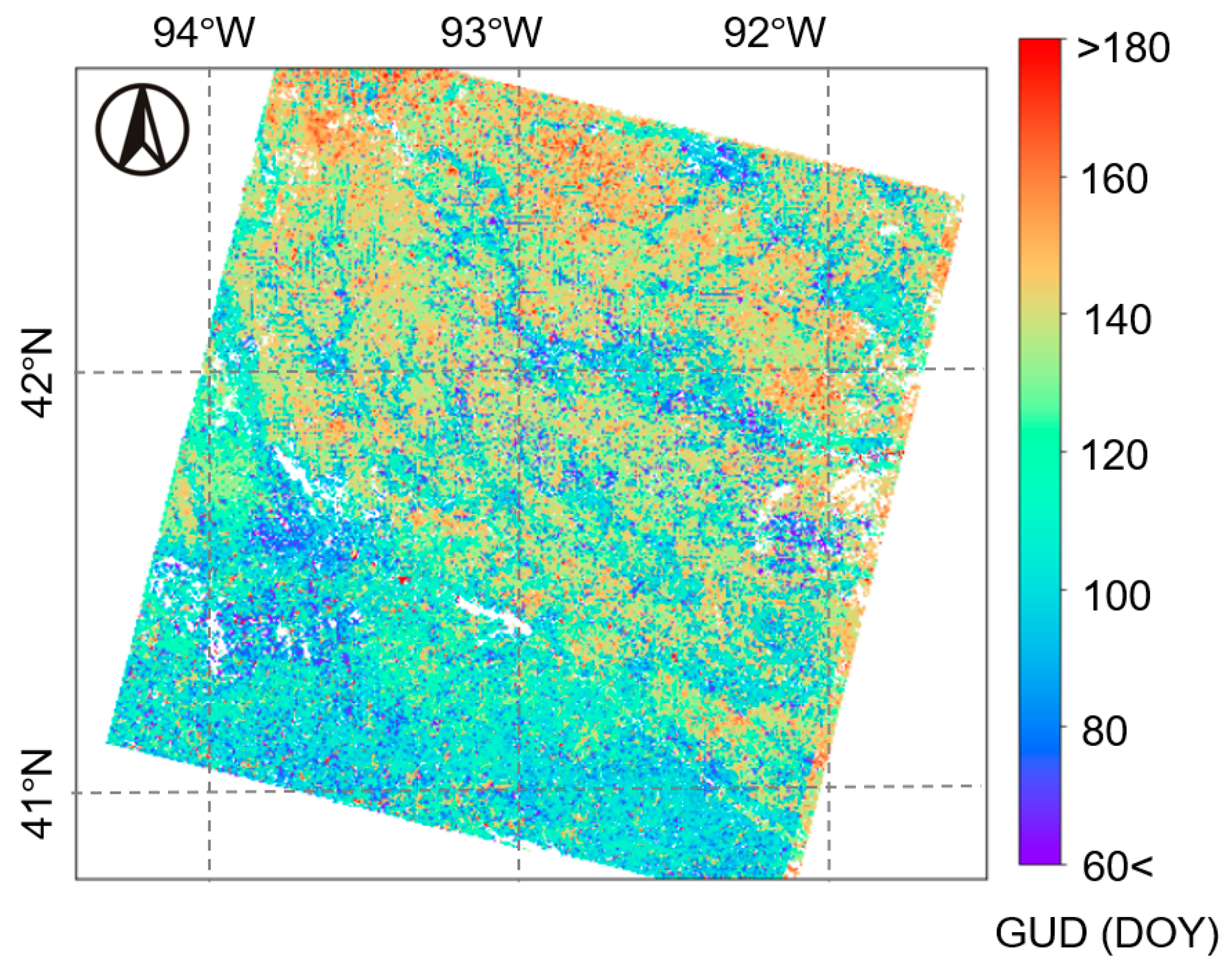
3.2. Testing the Multi-Endmember Model Based on Landsat-MODIS Fused EVI2 Data
4. Results
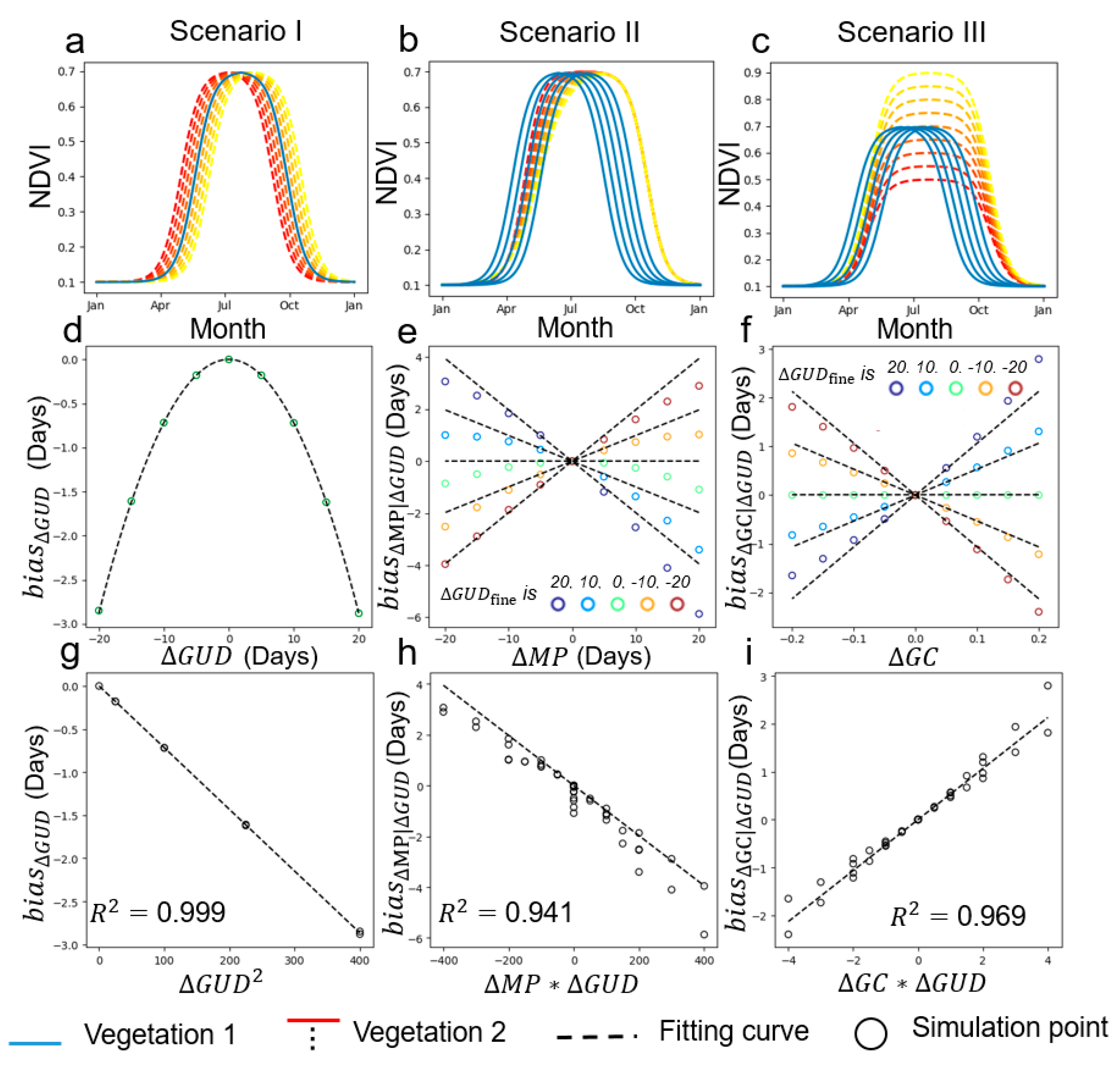
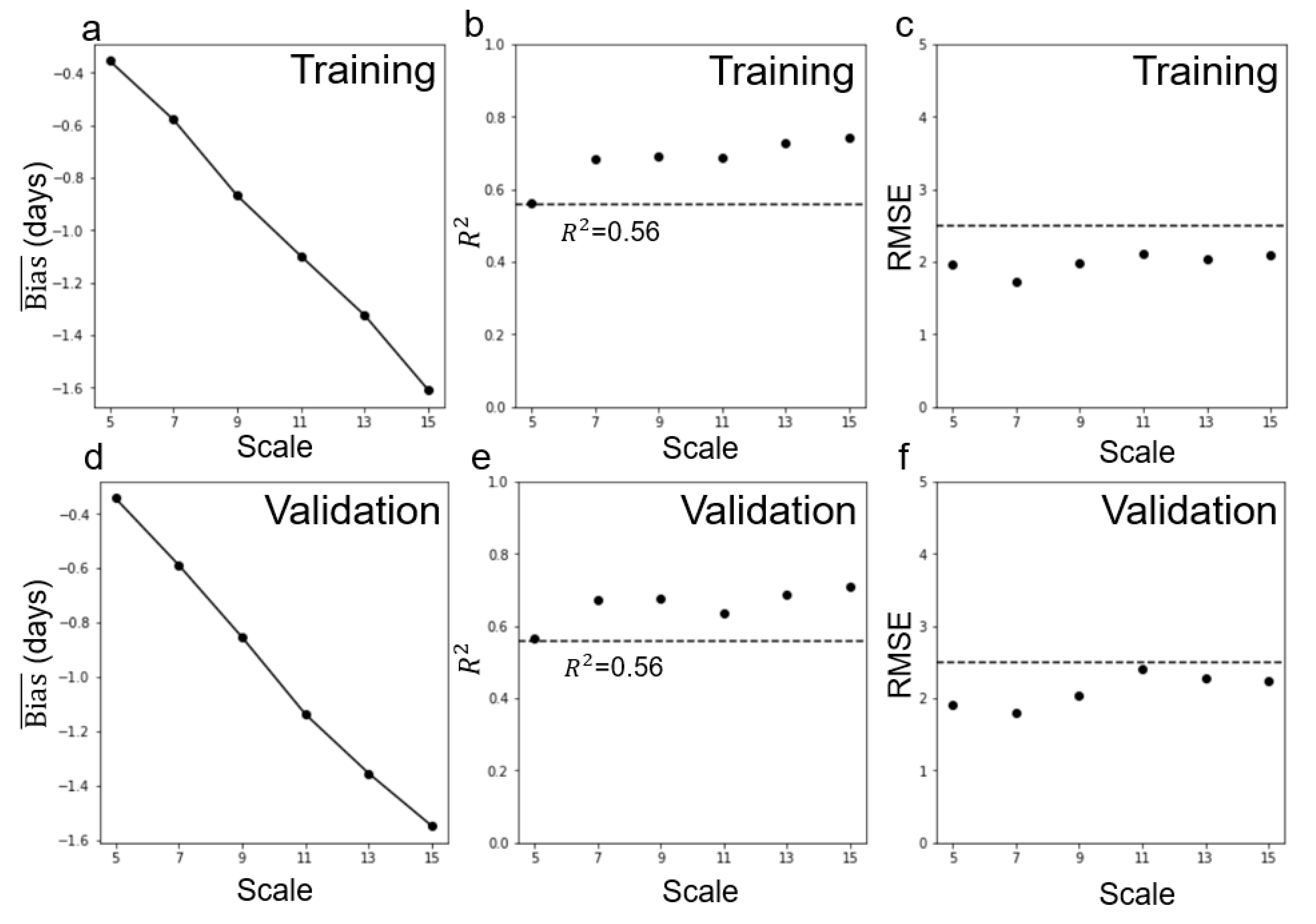
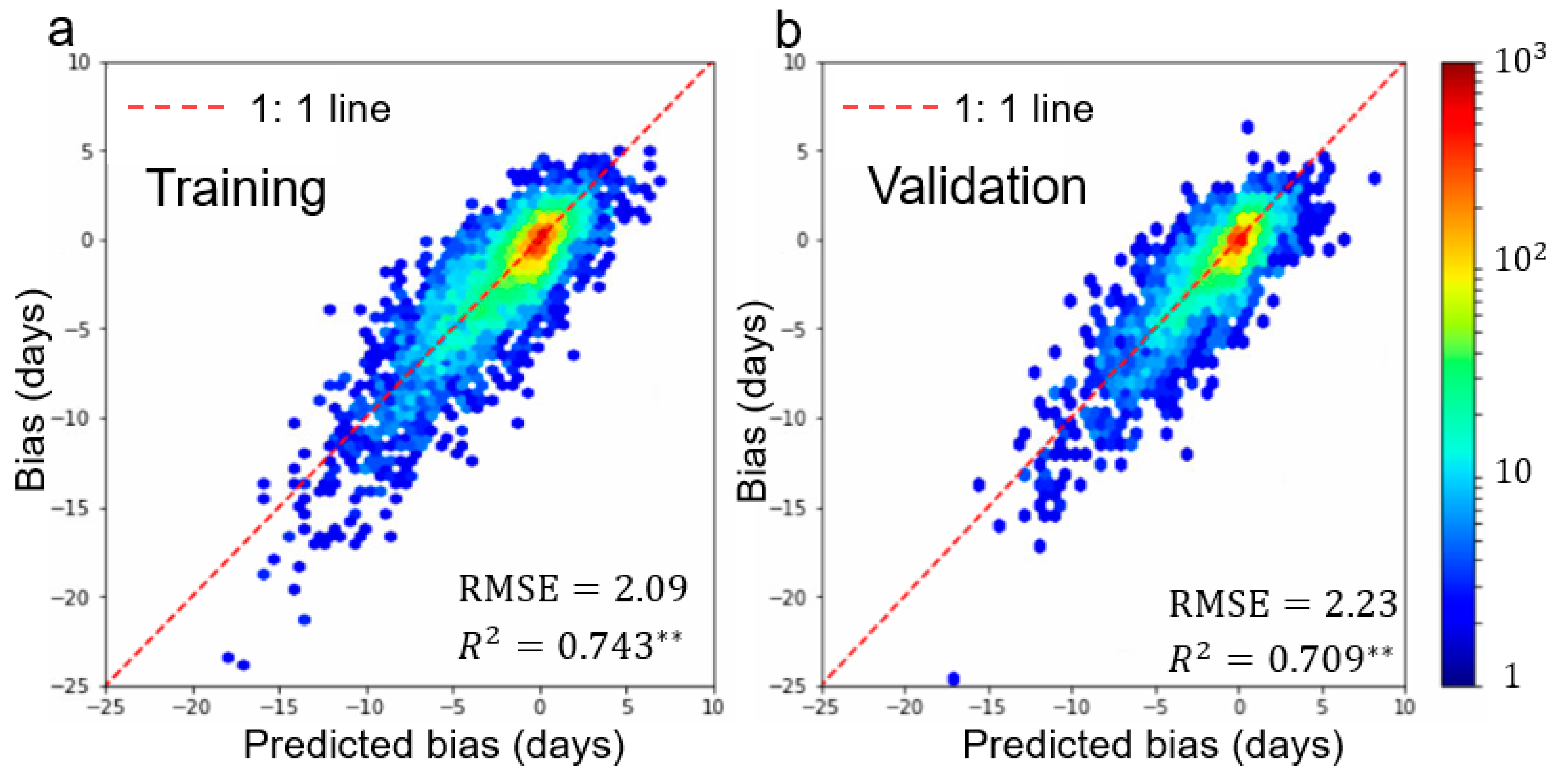
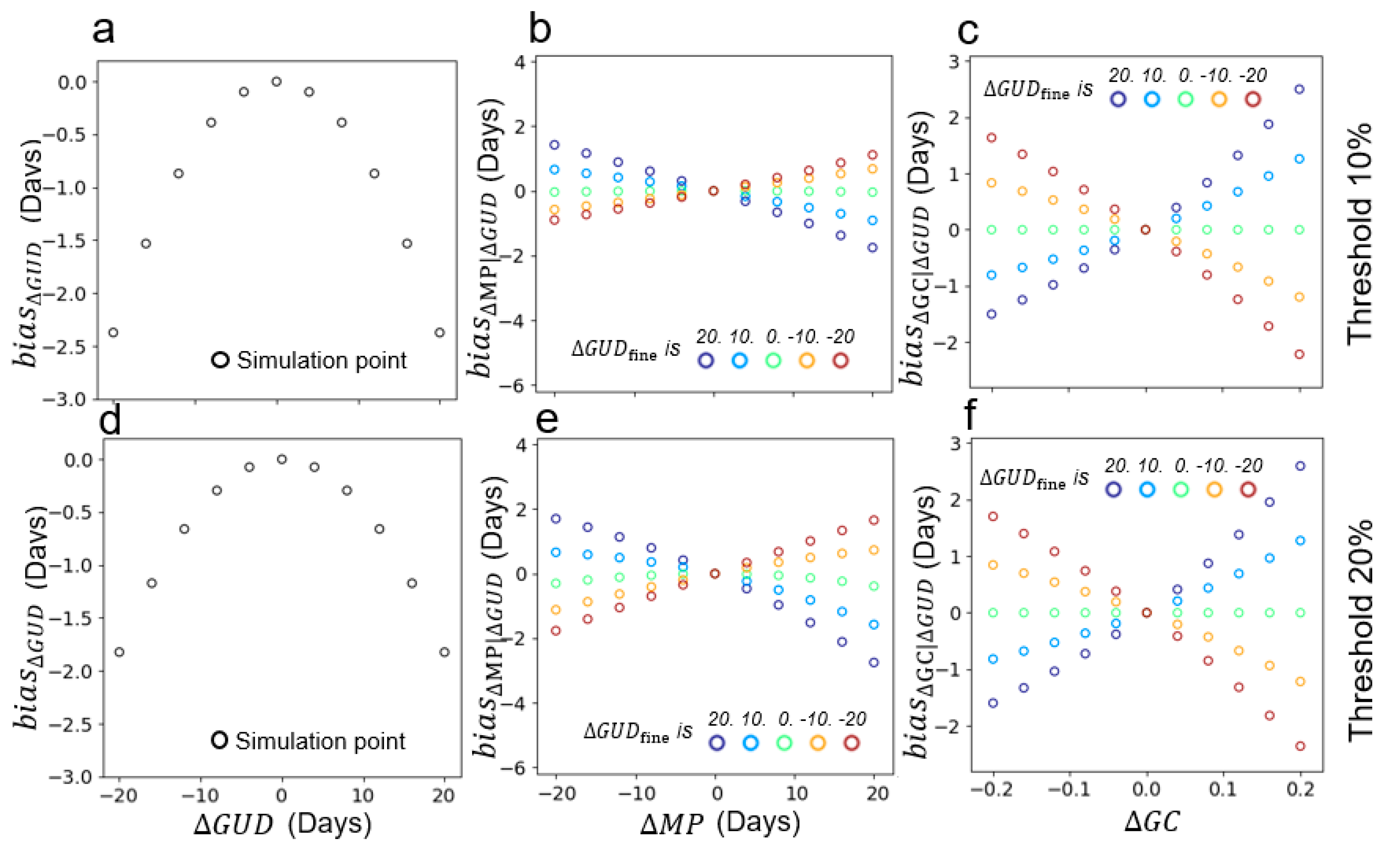
4.1. Performance of the Two-Endmember Model
4.2. Performance of Multi-Endmember Model Based on SIMMAP Simulated Data
4.3. Performance of Multi-Endmember Model Based on MODIS-Landsat Fused EVI2 Data
5. Discussion
5.1. Conceptual Explanations of the Scale Effect
5.2. Implications and Limitations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Badeck, F.W.; Bondeau, A.; Bottcher, K.; Doktor, D.; Lucht, W.; Schaber, J.; Sitch, S. Responses of spring phenology to climate change. New Phytol. 2004, 162, 295–309. [Google Scholar] [CrossRef]
- Ganguly, S.; Friedl, M.A.; Tan, B.; Zhang, X.; Verma, M. Land surface phenology from MODIS: Characterization of the Collection 5 global land cover dynamics product. Remote Sens. Environ. 2010, 114, 1805–1816. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, L.; Dong, Y. Comparisons of Global Land Surface Seasonality and Phenology Derived from AVHRR, MODIS and VIIRS Data: Phenology from AVHRR, MODIS and VIIRS. J. Geophys. Res. Biogeosci. 2017, 122, 1506–1525. [Google Scholar] [CrossRef]
- Shen, M.; Zhang, G.; Nan, C.; Wang, S.; Kong, W.; Piao, S. Increasing altitudinal gradient of spring vegetation phenology during the last decade on the Qinghai–Tibetan Plateau. Agric. For. Meteorol. 2014, 89–190, 71–80. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Gao, F.; Liu, Y.; Schaaf, C.; Friedl, M.; Yu, Y.; Jayavelu, S.; Gray, J.; Liu, L. Exploration of scaling effects on coarse resolution land surface phenology. Remote Sens. Environ. 2017, 190, 318–330. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Zhang, X.; Zhang, B.; Liu, L.; Liu, X.; Huete, A.R.; Huang, W.; Wang, S.; Luo, S.; Zhang, X.; et al. Scaling effects on spring phenology detections from MODIS data at multiple spatial resolutions over the contiguous United States. ISPRS J. Photogramm. Remote Sens. 2017, 132, 185–198. [Google Scholar] [CrossRef]
- Peng, D.; Chaoyang, W.; Xiaoyang, Z.; Yu, L.; Huete, A.R.; Wang, F.; Luo, S.; Liu, X.; Zhang, H. Scaling up spring phenology derived from remote sensing images. Agric. For. Meteorol. 2018, 256–257, 207–219. [Google Scholar] [CrossRef]
- Duchemin, B.T.; Goubier, J.; Courrier, G. Monitoring phenological key stages and cycle duration of temporate deciduous forest ecosystems with NOAA/AVHRR data. Remote Sens. Environ. 1999, 67, 68–82. [Google Scholar] [CrossRef]
- Schwartz, M.; Reed, B. Surface phenology and satellite sensor-derived onset of greenness: An initial comparison. Int. J. Remote Sens. 1999, 20, 3451–3457. [Google Scholar] [CrossRef]
- Wang, H.; Liu, D.; Lin, H.; Montenegro, A.; Zhu, X. NDVI and vegetation phenology dynamics under the influence of sunshine duration on the Tibetan plateau. Int. J. Climatol. 2015, 35, 687–698. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.; Chen, J.; Wang, C.; Shen, M. The mixed pixel effect in land surface phenology: A simulation study. Remote Sens. Environ. 2018, 211, 338–344. [Google Scholar] [CrossRef]
- Fisher, J.I.; Mustard, J.F. Cross-scalar satellite phenology from ground, Landsat, and MODIS data. Remote Sens. Environ. 2007, 109, 261–273. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Friedl, M.A.; Davis, F.W.; Michaelsen, J.; Moritz, M.A. Scaling and uncertainty in the relationship between the NDVI and land surface biophysical variables: An analysis using a scene simulation model and data from FIFE. Remote Sens. Environ. 1995, 54, 233–246. [Google Scholar] [CrossRef]
- Aman, A.; Randriamanantena, H.P.; Podaire, A.; Frouin, R. Upscale integration of normalized difference vegetation index: The problem of spatial heterogeneity. IEEE Trans. Geosci. Remote Sens. 1992, 30, 326–338. [Google Scholar] [CrossRef]
- Kerdiles, H.; Grondona, M.O. NOAA-AVHRR NDVI decomposition and subpixel classification using linear mixing in the Argentinean Pampa. Int. J. Remote Sens. 1995, 16, 1303–1325. [Google Scholar] [CrossRef]
- Shang, R.; Liu, R.; Xu, M.; Liu, Y.; Zuo, L.; Ge, Q. xThe relationship between threshold-based and inflexion-based approaches for extraction of land surface phenology. Remote Sens. Environ. 2017, 199, 167–170. [Google Scholar] [CrossRef]
- Doktor, D.; Bondeau, A.; Koslowski, D.; Badeck, F.W. Influence of heterogeneous landscapes on computed green-up dates based on daily AVHRR NDVI observations. Remote Sens. Environ. 2009, 113, 2618–2632. [Google Scholar] [CrossRef]
- Richardson, A.D.; Hufkens, K.; Milliman, T.; Aubrecht, D.M.; Chen, M.; Gray, J.M.; Johnston, M.R.; Keenan, T.F.; Klosterman, S.T.; Kosmala, M. Tracking vegetation phenology across diverse North American biomes using PhenoCam imagery. Sci. Data 2018, 5, 180028. [Google Scholar] [CrossRef]
- Soudani, K.; Maire, G.L.; Dufrêne, E.; François, C.; Delpierre, N.; Ulrich, E.; Cecchini, S. Evaluation of the onset of green-up in temperate deciduous broadleaf forests derived from Moderate Resolution Imaging Spectroradiometer (MODIS) data. Remote Sens. Environ. 2008, 112, 2643–2655. [Google Scholar] [CrossRef]
- Keenan, T.F.; Darby, B.; Felts, E.; Sonnentag, O.; Friedl, M.A.; Hufkens, K.; O’Keef, J.; Klosterman, S.; Munger, J.W.; Toome, M.; et al. Tracking forest phenology and seasonal physiology using digital repeat photography: A critical assessment. Ecol. Appl. A Publ. Ecol. Soc. Am. 2016, 24, 1478–1489. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Wu, J.; Tang, Y.; Shi, P.; Black, T.A.; Zhu, K. A snow-free vegetation index for improved monitoring of vegetation spring green-up date in deciduous ecosystems. Remote Sens. Environ. 2017, 196, 1–12. [Google Scholar] [CrossRef]
- Saura, S.; Martínez-Millán, J. Landscape patterns simulation with a modified random clusters method. Landsc. Ecol. 2000, 15, 661–678. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Liang, L.A.; Schwartz, M.D.; Fei, S.L. Validating satellite phenology through intensive ground observation and landscape scaling in a mixed seasonal forest. Remote Sens. Environ. 2011, 115, 143–157. [Google Scholar] [CrossRef]
- Chuine, I.; Morin, X.; Bugmann, H. Warming, Photoperiods, and Tree Phenology. Science 2010, 329, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Shen, M.; Zhou, J.; Chen, J. Modeling vegetation green-up dates across the Tibetan Plateau by including both seasonal and daily temperature and precipitation. Agric. For. Meteorol. 2018, 249, 176–186. [Google Scholar] [CrossRef]
- Cong, N.; Shen, M.; Piao, S.; Chen, X.; An, S.; Yang, W.; Fu, Y.H.; Meng, F.; Wang, T. Little change in heat requirement for vegetation green-up on the Tibetan Plateau over the warming period of 1998–2012. Agric. For. Meteorol. 2017, 232, 650–658. [Google Scholar] [CrossRef]
- Murray, M.; Cannell, M.; Smith, R. Date of budburst of 15 tree species in Britain following climatic warming. J. Appl. Ecol. 1989, 26, 693–700. [Google Scholar] [CrossRef]
- Wang, C.; Tang, Y.; Chen, J. Plant phenological synchrony increases under rapid within-spring warming. Sci. Rep. 2016, 6, 25460. [Google Scholar] [CrossRef] [Green Version]
- Shen, M.; Cong, N.; Cao, R. Temperature sensitivity as an explanation of the latitudinal pattern of green-up date trend in Northern Hemisphere vegetation during 1982–2008. Int. J. Climatol. 2015, 35, 3707–3712. [Google Scholar] [CrossRef]
- Cao, R.; Chen, J.; Shen, M.; Tang, Y. An improved logistic method for detecting spring vegetation phenology in grasslands from MODIS EVI time-series data. Agric. For. Meteorol. 2015, 200, 9–20. [Google Scholar] [CrossRef]
- Huete, A.R.; Jackson, R.D. Soil and atmosphere influences on the spectra of partial canopies. Remote Sens. Environ. 1988, 25, 89–105. [Google Scholar] [CrossRef]
- Ding, Y.; Zheng, X.; Kai, Z.; Xin, X.; Liu, H. Quantifying the Impact of NDVIsoil Determination Methods and NDVIsoil Variability on the Estimation of Fractional Vegetation Cover in Northeast China. Remote Sens. 2016, 8, 29. [Google Scholar] [CrossRef]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A simple method to improve the quality of NDVI time-series data by integrating spatiotemporal information with the Savitzky-Golay filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar] [CrossRef]
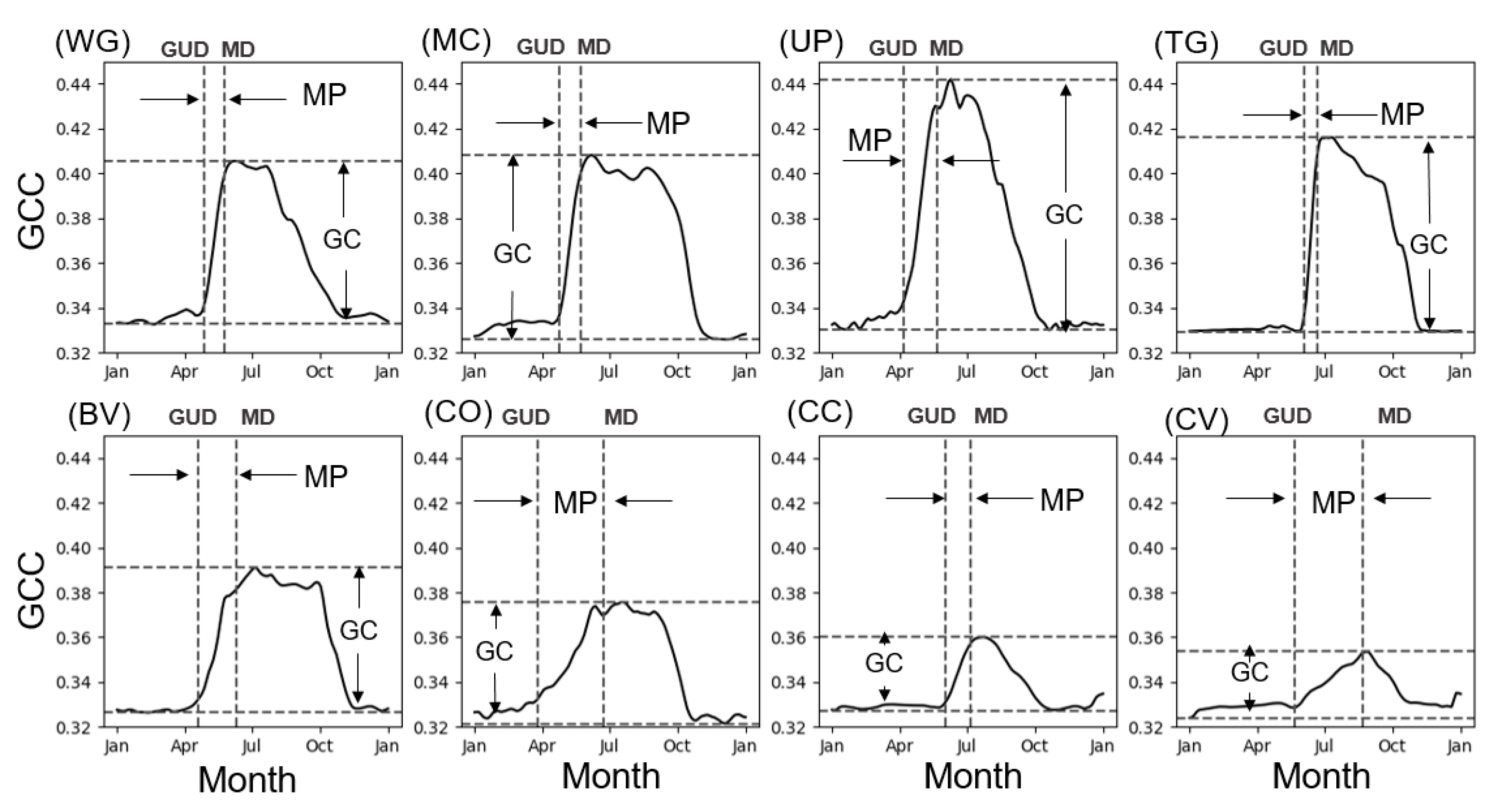





| Site ID | Site Name | Type | Year | Longitude | Latitude | GUD | MP | GC |
|---|---|---|---|---|---|---|---|---|
| WG | uiefswitchgrass | SG | 2014 | −88.197 | 40.064 | 118.2 | 28.0 | 0.073 |
| MC | uiefmiscanthus | MC | 2012 | −88.198 | 40.063 | 116.2 | 28.2 | 0.082 |
| UP | uiefprairie | GR | 2011 | −88.197 | 40.064 | 98.1 | 45 | 0.112 |
| TG | torgnon-ld | DN | 2013 | 7.561 | 45.824 | 156.0 | 16.9 | 0.087 |
| BV | bitterootvalley | DB | 2014 | −114.091 | 46.507 | 110.3 | 51.8 | 0.065 |
| CO | canadaOBS | MX | 2012 | −105.118 | 53.987 | 86.4 | 88.1 | 0.054 |
| CC | contactcreek | SH | 2012 | −155.923 | 58.208 | 154.6 | 32.7 | 0.033 |
| CV | coville | TN | 2011 | −155.563 | 58.803 | 141.7 | 92.3 | 0.030 |
| Type | Scale | ||||||
|---|---|---|---|---|---|---|---|
| Standardized | Unstandardized | Standardized | Unstandardized | Standardized | Unstandardized | ||
| Simulation data (p = 0.5) | 3 | −0.76 | −0.035 | −0.61 | −0.031 | 0.29 | 14.5 |
| 4 | −0.73 | −0.035 | −0.60 | −0.030 | 0.30 | 14.6 | |
| 5 | −0.72 | −0.035 | −0.60 | −0.030 | 0.31 | 14.7 | |
| 6 | −0.72 | −0.035 | −0.62 | −0.029 | 0.30 | 15.0 | |
| 7 | −0.72 | −0.036 | −0.61 | −0.030 | 0.30 | 14.8 | |
| 8 | −0.71 | −0.037 | −0.60 | −0.032 | 0.32 | 13.6 | |
| 9 | −0.73 | −0.036 | −0.63 | −0.030 | 0.33 | 14.7 | |
| 10 | −0.72 | −0.035 | −0.62 | −0.029 | 0.33 | 14.9 | |
| 12 | −0.75 | −0.036 | −0.65 | −0.029 | 0.31 | 15.0 | |
| 15 | −0.75 | −0.036 | −0.64 | −0.029 | 0.34 | 15.2 | |
| 17 | −0.78 | −0.037 | −0.64 | −0.029 | 0.33 | 14.4 | |
| 20 | −0.90 | −0.036 | −0.78 | −0.029 | 0.28 | 14.8 | |
| Landsat-MODIS fused data | 5 | −1.68 | −0.037 | −1.36 | −0.032 | 0.23 | 1.61 |
| 7 | −1.84 | −0.039 | −1.45 | −0.033 | 0.27 | 1.69 | |
| 9 | −1.72 | −0.039 | −1.29 | −0.033 | 0.25 | 1.71 | |
| 11 | −1.67 | −0.038 | −1.24 | −0.032 | 0.24 | 1.58 | |
| 13 | −1.71 | −0.039 | −1.25 | −0.033 | 0.25 | 1.69 | |
| 15 | −1.70 | −0.040 | −1.23 | −0.034 | 0.26 | 1.78 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Cao, R.; Shen, M.; Chen, J.; Wang, J.; Zhang, X. How Does Scale Effect Influence Spring Vegetation Phenology Estimated from Satellite-Derived Vegetation Indexes? Remote Sens. 2019, 11, 2137. https://doi.org/10.3390/rs11182137
Liu L, Cao R, Shen M, Chen J, Wang J, Zhang X. How Does Scale Effect Influence Spring Vegetation Phenology Estimated from Satellite-Derived Vegetation Indexes? Remote Sensing. 2019; 11(18):2137. https://doi.org/10.3390/rs11182137
Chicago/Turabian StyleLiu, Licong, Ruyin Cao, Miaogen Shen, Jin Chen, Jianmin Wang, and Xiaoyang Zhang. 2019. "How Does Scale Effect Influence Spring Vegetation Phenology Estimated from Satellite-Derived Vegetation Indexes?" Remote Sensing 11, no. 18: 2137. https://doi.org/10.3390/rs11182137
APA StyleLiu, L., Cao, R., Shen, M., Chen, J., Wang, J., & Zhang, X. (2019). How Does Scale Effect Influence Spring Vegetation Phenology Estimated from Satellite-Derived Vegetation Indexes? Remote Sensing, 11(18), 2137. https://doi.org/10.3390/rs11182137