Coupled Biospheric Synchrony of the Coastal Temperate Ecosystem in Northern Patagonia: A Remote Sensing Analysis
Abstract
1. Introduction
2. Methodology
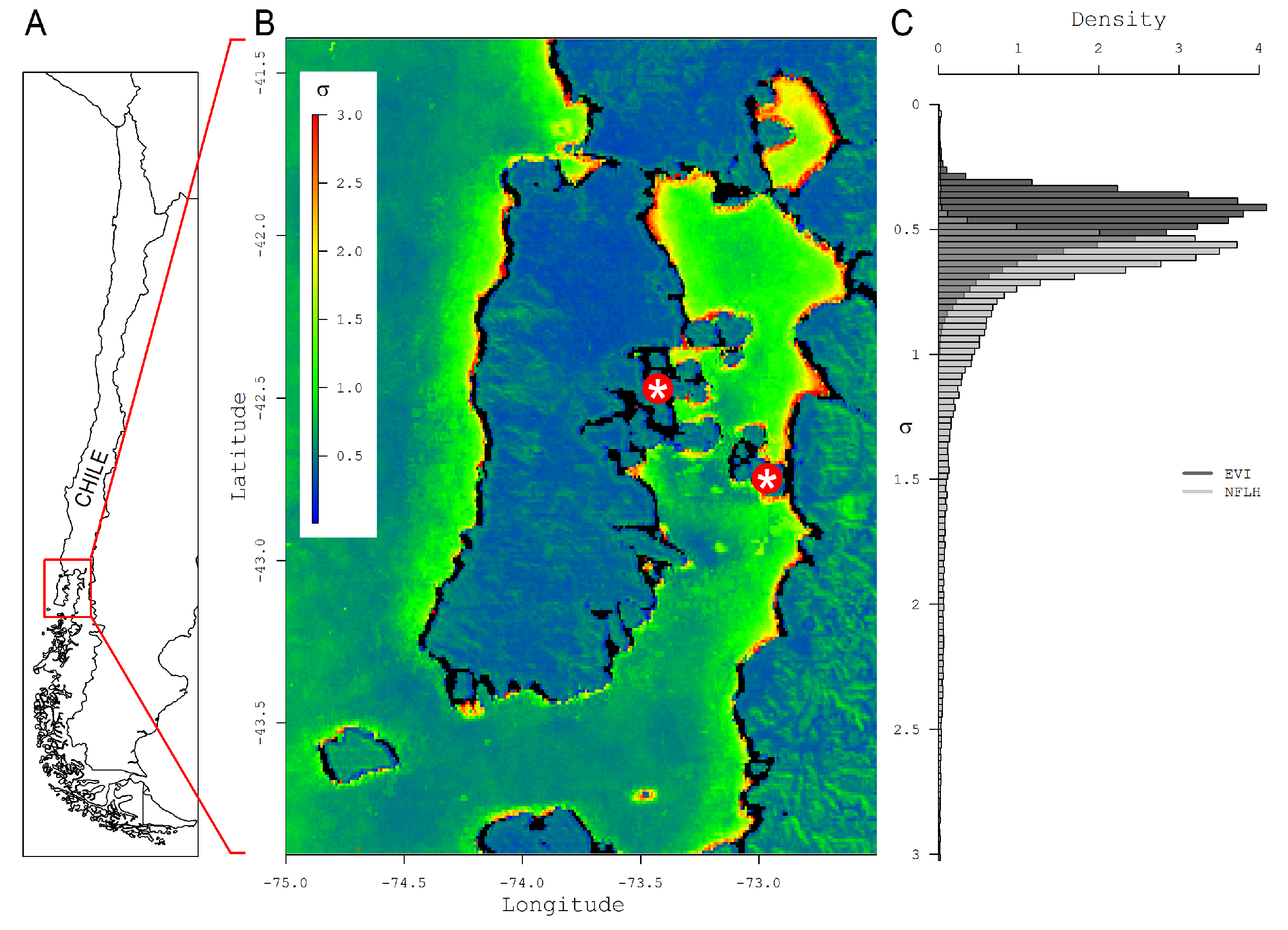
2.1. Study Area
2.2. Satellite Data
2.3. Climate Indices
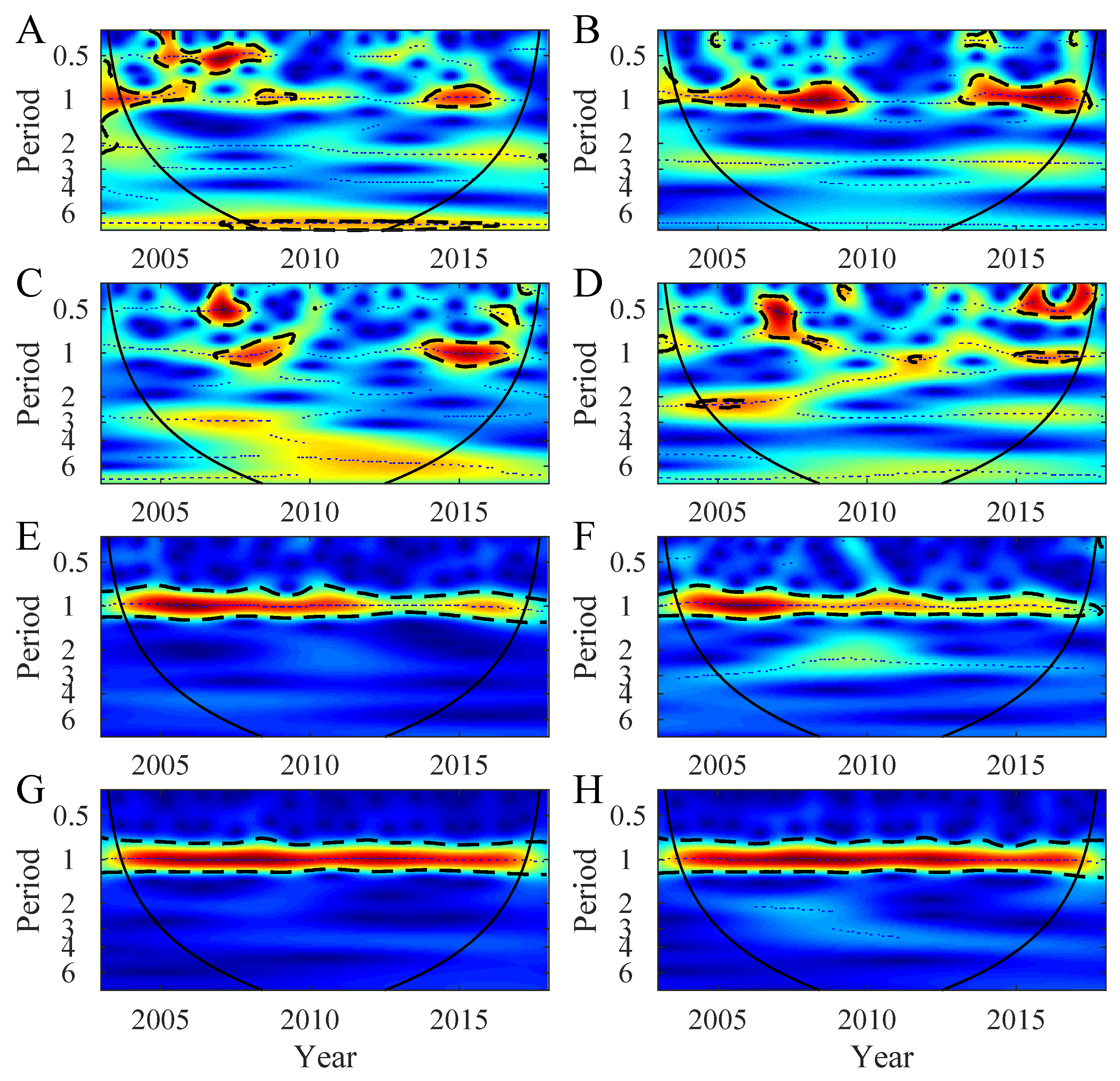
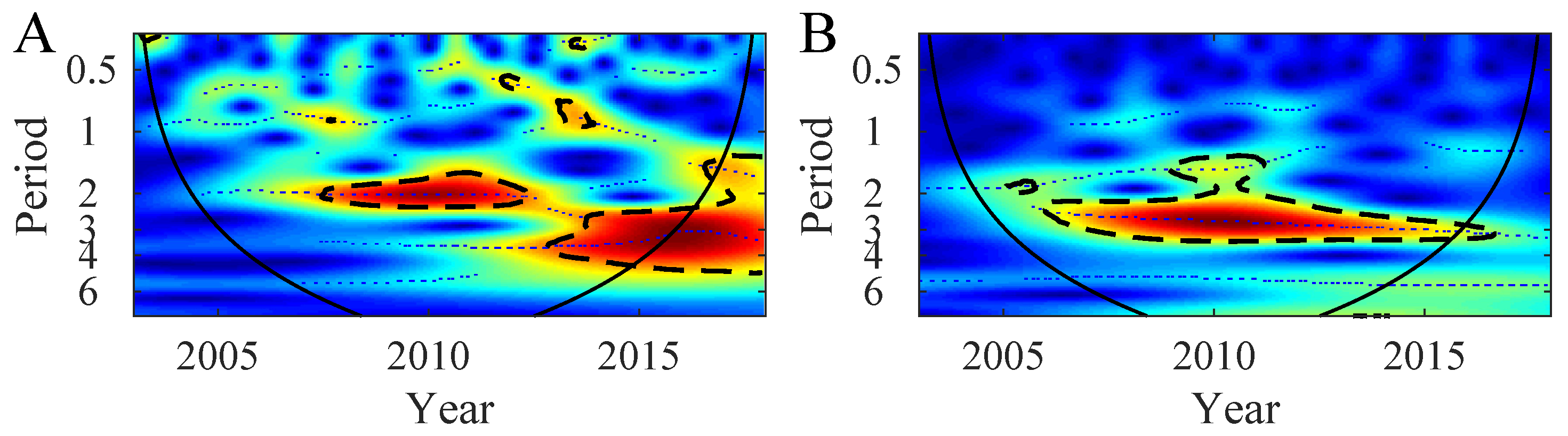
2.4. Wavelet Analysis
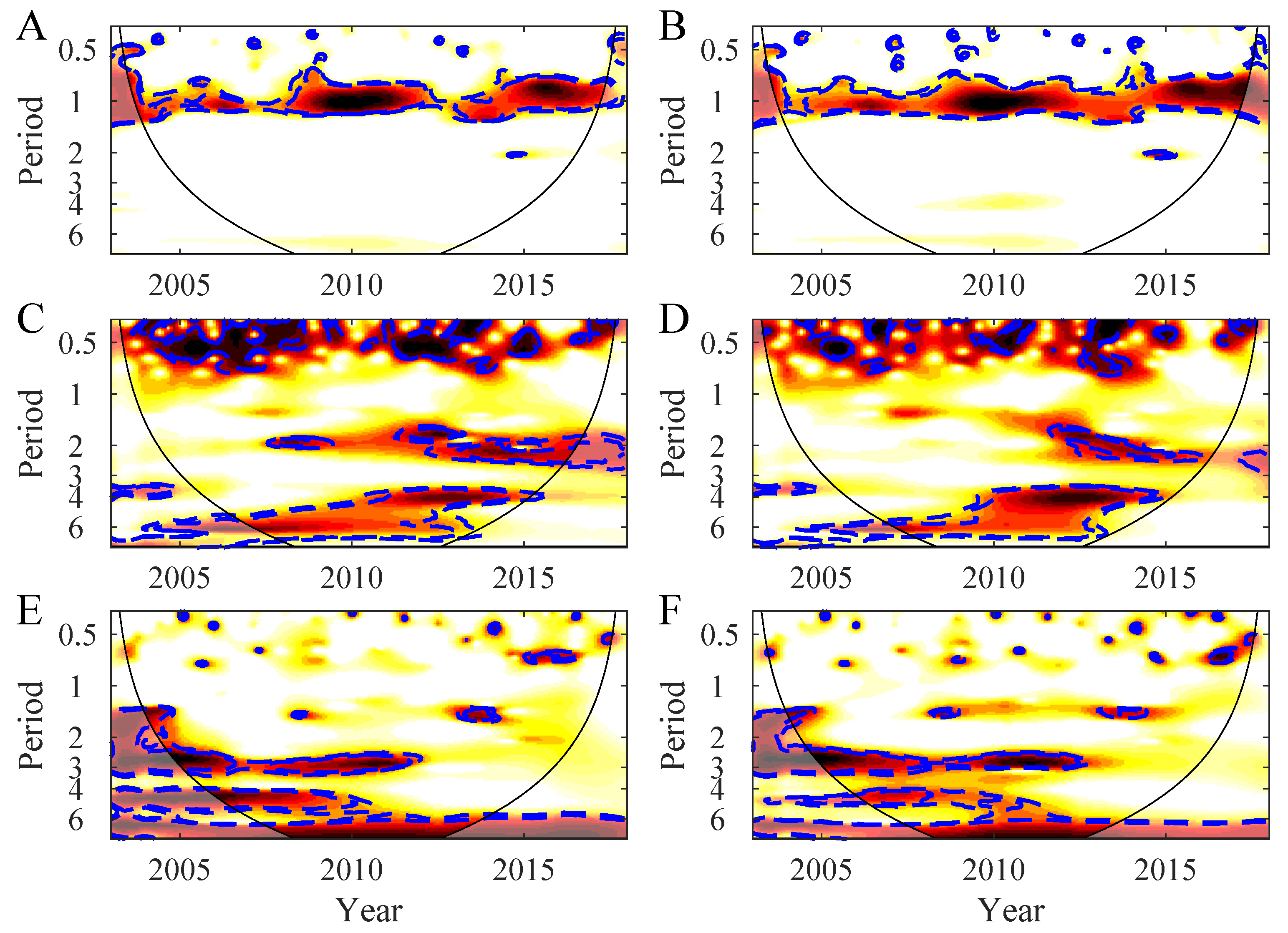
2.5. Coherence and Synchrony Analysis
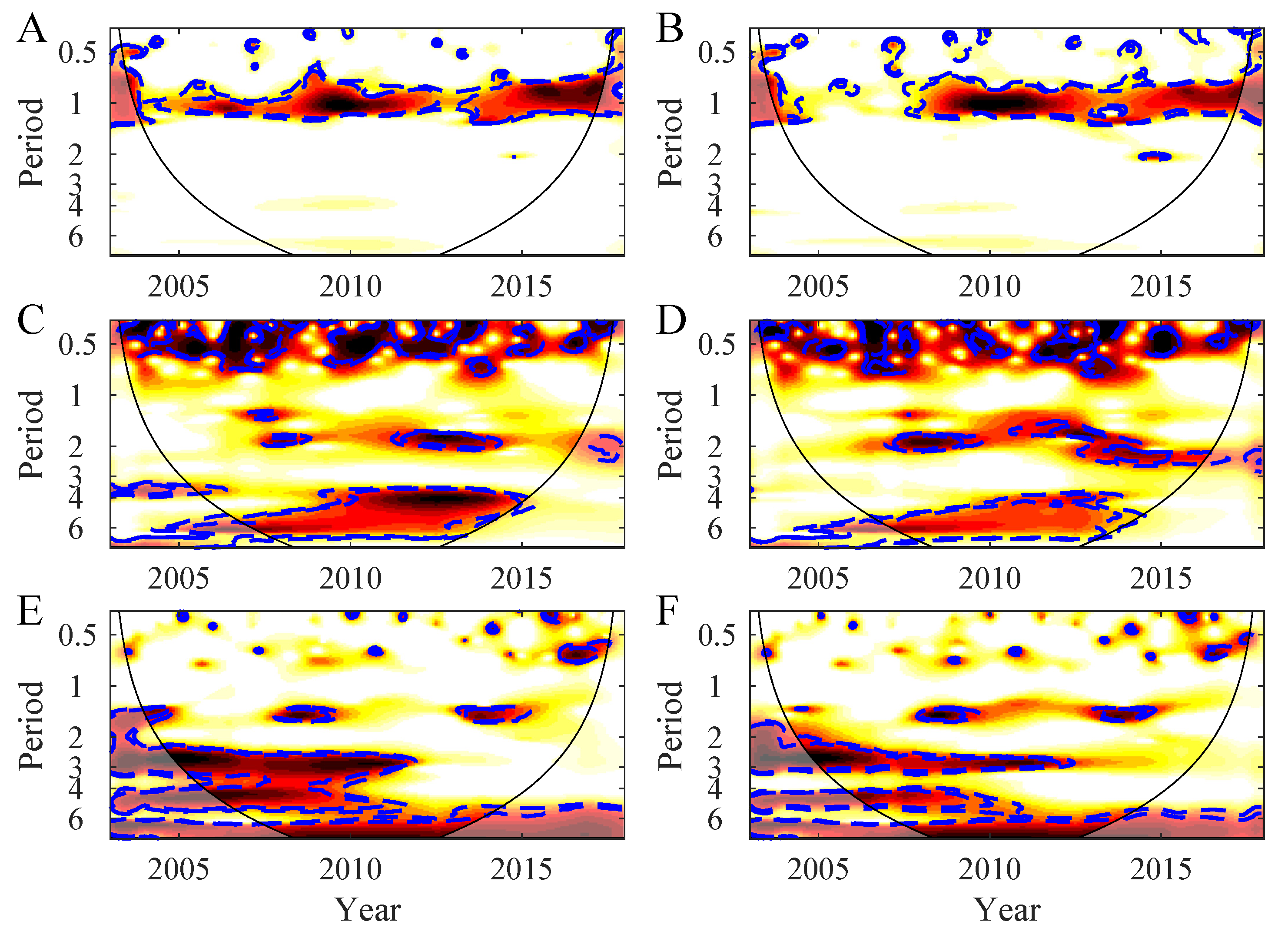
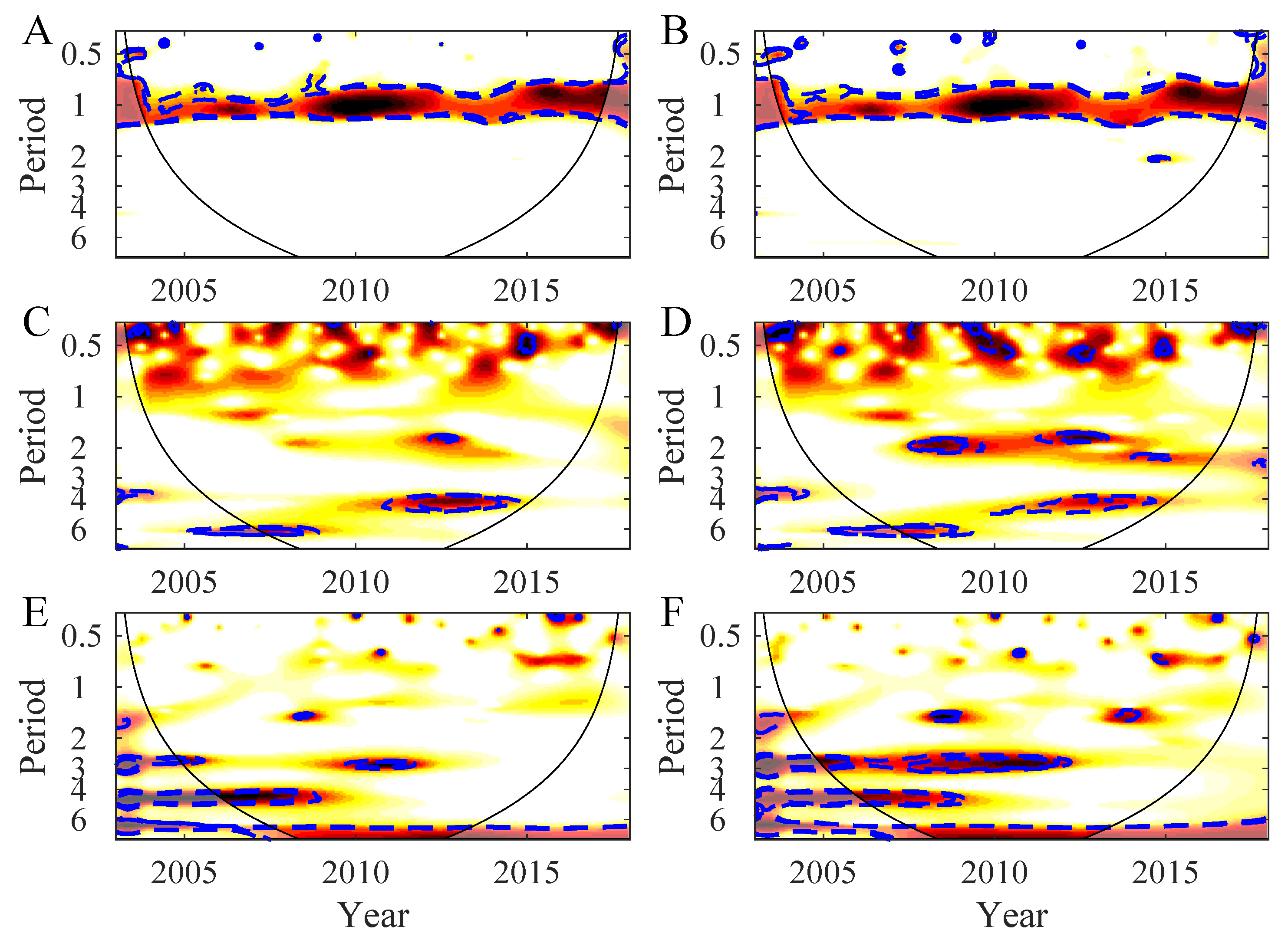
3. Results
3.1. Temporal Variability in the Northern Patagonia Ecosystem
3.2. Synchrony in the Northern Patagonia Ecosystem
4. Discussion
5. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thuiller, W.; Lavorel, S.; Araújo, M.B.; Sykes, M.T.; Prentice, I.C. Climate change threats to plant diversity in Europe. Proc. Natl. Acad. Sci. USA 2005, 102, 8245–8250. [Google Scholar] [CrossRef] [PubMed]
- Defriez, E.J.; Reuman, D.C. A global geography of synchrony for terrestrial vegetation. Glob. Ecol. Biogeogr. 2017, 26, 878–888. [Google Scholar] [CrossRef]
- Bradley, N.L.; Leopold, A.C.; Ross, J.; Huffaker, W. Phenological changes reflect climate change in Wisconsin. Proc. Natl. Acad. Sci. USA 1999, 96, 9701–9704. [Google Scholar] [CrossRef] [PubMed]
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389. [Google Scholar] [CrossRef] [PubMed]
- Edwards, M.; Richardson, A.J. Impact of climate change on marine pelagic phenology and trophic mismatch. Nature 2004, 430, 881. [Google Scholar] [CrossRef] [PubMed]
- Grøtan, V.; SÆther, B.E.; Engen, S.; Solberg, E.J.; Linnell, J.D.; Andersen, R.; Brøseth, H.; Lund, E. Climate causes large-scale spatial synchrony in population fluctuations of a temperate herbivore. Ecology 2005, 86, 1472–1482. [Google Scholar] [CrossRef]
- Kent, A.D.; Yannarell, A.C.; Rusak, J.A.; Triplett, E.W.; McMahon, K.D. Synchrony in aquatic microbial community dynamics. Isme J. 2007, 1, 38. [Google Scholar] [CrossRef]
- Walter, J.A.; Sheppard, L.W.; Anderson, T.L.; Kastens, J.H.; Bjørnstad, O.N.; Liebhold, A.M.; Reuman, D.C. The geography of spatial synchrony. Ecol. Lett. 2017, 20, 801–814. [Google Scholar] [CrossRef]
- Cazelles, B.; Chavez, M.; McMichael, A.J.; Hales, S. Nonstationary influence of El Niño on the synchronous dengue epidemics in Thailand. PLoS Med. 2005, 2, e106. [Google Scholar] [CrossRef]
- Navarrete, S.A.; Broitman, B.R.; Menge, B.A. Interhemispheric comparison of recruitment to intertidal communities: pattern persistence and scales of variation. Ecology 2008, 89, 1308–1322. [Google Scholar] [CrossRef]
- Defriez, E.J.; Sheppard, L.W.; Reid, P.C.; Reuman, D.C. Climate change-related regime shifts have altered spatial synchrony of plankton dynamics in the North Sea. Glob. Chang. Biol. 2016, 22, 2069–2080. [Google Scholar] [CrossRef] [PubMed]
- Edeline, E.; Groth, A.; Cazelles, B.; Claessen, D.; Winfield, I.J.; Ohlberger, J.; Vøllestad, L.A.; Stenseth, N.C.; Ghil, M. Pathogens trigger top-down climate forcing on ecosystem dynamics. Oecologia 2016, 181, 519–532. [Google Scholar] [CrossRef] [PubMed]
- Buttay, L.; Cazelles, B.; Miranda, A.; Casas, G.; Nogueira, E.; González-Quirós, R. Environmental multi-scale effects on zooplankton inter-specific synchrony. Limnol. Oceanogr. 2017, 62, 1355–1365. [Google Scholar] [CrossRef]
- Defriez, E.J.; Reuman, D.C. A global geography of synchrony for marine phytoplankton. Glob. Ecol. Biogeogr. 2017, 26, 867–877. [Google Scholar] [CrossRef]
- Koenig, W.D. Global patterns of environmental synchrony and the Moran effect. Ecography 2002, 25, 283–288. [Google Scholar] [CrossRef]
- Lara, C.; Saldías, G.S.; Tapia, F.J.; Iriarte, J.L.; Broitman, B.R. Interannual variability in temporal patterns of chlorophyll–a and their potential influence on the supply of mussel larvae to inner waters in northern Patagonia (41–44∘S). J. Mar. Syst. 2016, 155, 11–18. [Google Scholar] [CrossRef]
- García-Reyes, M.; Lamont, T.; Sydeman, W.J.; Black, B.A.; Rykaczewski, R.R.; Thompson, S.A.; Bograd, S.J. A comparison of modes of upwelling-favorable wind variability in the Benguela and California current ecosystems. J. Mar. Syst. 2018, 188, 17–26. [Google Scholar] [CrossRef]
- Leibold, M.A.; Chase, J.M.; Ernest, S.M. Community assembly and the functioning of ecosystems: How metacommunity processes alter ecosystems attributes. Ecology 2017, 98, 909–919. [Google Scholar] [CrossRef]
- Fram, J.P.; Stewart, H.L.; Brzezinski, M.A.; Gaylord, B.; Reed, D.C.; Williams, S.L.; MacIntyre, S. Physical pathways and utilization of nitrate supply to the giant kelp, Macrocystis pyrifera. Limnol. Oceanogr. 2008, 53, 1589–1603. [Google Scholar] [CrossRef]
- Johnstone, J.A.; Dawson, T.E. Climatic context and ecological implications of summer fog decline in the coast redwood region. Proc. Natl. Acad. Sci. USA 2010, 107, 4533–4538. [Google Scholar] [CrossRef]
- Subramaniam, A.; Yager, P.; Carpenter, E.; Mahaffey, C.; Björkman, K.; Cooley, S.; Kustka, A.; Montoya, J.; Sañudo-Wilhelmy, S.; Shipe, R. Amazon River enhances diazotrophy and carbon sequestration in the tropical North Atlantic Ocean. Proc. Natl. Acad. Sci. USA 2008, 105, 10460–10465. [Google Scholar] [CrossRef] [PubMed]
- Iriarte, J.L.; González, H.E.; Nahuelhual, L. Patagonian fjord ecosystems in southern Chile as a highly vulnerable region: Problems and needs. AMBIO 2010, 39, 463–466. [Google Scholar] [CrossRef] [PubMed]
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-scale control on the Patagonian climate. J. Clim. 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Narváez, D.A.; Vargas, C.A.; Cuevas, L.A.; García-Loyola, S.A.; Lara, C.; Segura, C.; Tapia, F.J.; Broitman, B.R. Dominant scales of subtidal variability in coastal hydrography of the Northern Chilean Patagonia. J. Mar. Syst. 2019, 193, 59–73. [Google Scholar] [CrossRef]
- Iriarte, J.; González, H.; Liu, K.; Rivas, C.; Valenzuela, C. Spatial and temporal variability of chlorophyll and primary productivity in surface waters of southern Chile (41.5–43∘S). Estuar. Coast. Shelf Sci. 2007, 74, 471–480. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. The State of World Fisheries and Aquaculture; Report, opportunities and challenges; FAO: Rome, Italy, 2007; Volume 4, pp. 40–41. [Google Scholar]
- Adger, W.N.; Hughes, T.P.; Folke, C.; Carpenter, S.R.; Rockström, J. Social-ecological resilience to coastal disasters. Science 2005, 309, 1036–1039. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.B. Ecological extinction and evolution in the brave new ocean. Proc. Natl. Acad. Sci. USA 2008, 105, 11458–11465. [Google Scholar] [CrossRef] [PubMed]
- León-Muñoz, J.; Urbina, M.A.; Garreaud, R.; Iriarte, J.L. Hydroclimatic conditions trigger record harmful algal bloom in western Patagonia (summer 2016). Sci. Rep. 2018, 8, 1330. [Google Scholar] [CrossRef] [PubMed]
- McCabe, R.M.; Hickey, B.M.; Kudela, R.M.; Lefebvre, K.A.; Adams, N.G.; Bill, B.D.; Gulland, F.; Thomson, R.E.; Cochlan, W.P.; Trainer, V.L. An unprecedented coastwide toxic algal bloom linked to anomalous ocean conditions. Geophys. Res. Lett. 2016, 43, 46–58. [Google Scholar] [CrossRef]
- Echeverría, C.; Newton, A.C.; Lara, A.; Benayas, J.M.R.; Coomes, D.A. Impacts of forest fragmentation on species composition and forest structure in the temperate landscape of Southern Chile. Glob. Ecol. Biogeogr. 2007, 16, 426–439. [Google Scholar] [CrossRef]
- Nahuelhual, L.; Carmona, A.; Aguayo, M.; Echeverria, C. Land use change and ecosystem services provision: A case study of recreation and ecotourism opportunities in southern Chile. Landsc. Ecol. 2014, 29, 329–344. [Google Scholar] [CrossRef]
- Holt, T.V.; Moreno, C.A.; Binford, M.W.; Portier, K.M.; Mulsow, S.; Frazer, T.K. Influence of landscape change on nearshore fisheries in southern Chile. Glob. Chang. Biol. 2012, 18, 2147–2160. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Barrena, J.; Nahuelhual, L.; Báez, A.; Schiappacasse, I.; Cerda, C. Valuing cultural ecosystem services: Agricultural heritage in Chiloé island, Southern Chile. Ecosyst. Serv. 2014, 7, 66–75. [Google Scholar] [CrossRef]
- Sanderson, J.; Sunquist, M.E.; Iriarte, A.W. Natural history and landscape-use of guignas (Oncifelis guigna) on Isla Grande de Chiloé, Chile. J. Mammal. 2002, 83, 608–613. [Google Scholar] [CrossRef]
- Fernández, F.J.; Ponce, R.D.; Vásquez-Lavin, F.; Figueroa, Y.; Gelcich, S.; Dresdner, J. Exploring typologies of artisanal mussel seed producers in Southern Chile. Ocean Coast. Manag. 2018, 158, 24–31. [Google Scholar] [CrossRef]
- Smith-Ramírez, C. The Chilean coastal range: a vanishing center of biodiversity and endemism in South American temperate rainforests. Biodivers. Conserv. 2004, 13, 373–393. [Google Scholar] [CrossRef]
- Lara, C.; Saldías, G.S.; Paredes, A.L.; Cazelles, B.; Broitman, B.R. Temporal variability of MODIS Phenological Indices in the Temperate Rainforest of Northern Patagonia. Remote Sens. 2018, 10, 956. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250 m SIN Grid V006; NASA EOSDIS Land Process DAAC: Sioux Falls, SD, USA, 2015.
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Esaias, W.E.; Abbott, M.R.; Barton, I.; Brown, O.B.; Campbell, J.W.; Carder, K.L.; Clark, D.K.; Evans, R.H.; Hoge, F.E.; Gordon, H.R. An overview of MODIS capabilities for ocean science observations. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1250–1265. [Google Scholar] [CrossRef]
- Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Atmos. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [PubMed]
- Behrenfeld, M.J.; Westberry, T.K.; Boss, E.S.; O’Malley, R.T.; Siegel, D.A.; Wiggert, J.D.; Franz, B.; McLain, C.; Feldman, G.; Doney, S.C. Satellite-detected fluorescence reveals global physiology of ocean phytoplankton. Biogeosciences 2009, 6, 779. [Google Scholar] [CrossRef]
- Kilpatrick, K.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.; Minnett, P.J.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- Gillett, N.P.; Kell, T.D.; Jones, P. Regional climate impacts of the Southern Annular Mode. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Stammerjohn, S.; Martinson, D.; Smith, R.; Yuan, X.; Rind, D. Trends in Antarctic annual sea ice retreat and advance and their relation to El Niño–Southern Oscillation and Southern Annular Mode variability. J. Geophys. Res-Oceans. 2008, 113. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Jones, P.D. An extension of the Tahiti–Darwin southern oscillation index. Mon. Weather Rev. 1987, 115, 2161–2165. [Google Scholar]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet analysis of ecological time series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef]
- Cazelles, B.; Chavez, M.; de Magny, G.C.; Guégan, J.F.; Hales, S. Time-dependent spectral analysis of epidemiological time-series with wavelets. J. R. Soc. Interface 2007, 4, 625–636. [Google Scholar] [CrossRef]
- Ng, E.K.; Chan, J.C. Geophysical applications of partial wavelet coherence and multiple wavelet coherence. J. Atmos. Ocean. Technol. 2012, 29, 1845–1853. [Google Scholar] [CrossRef]
- Medkour, T.; Walden, A.T.; Burgess, A. Graphical modelling for brain connectivity via partial coherence. J. Neurosci. Meth. 2009, 180, 374–383. [Google Scholar] [CrossRef]
- Cazelles, B.; Cazelles, K.; Chavez, M. Wavelet analysis in ecology and epidemiology: Impact of statistical tests. J. R. Soc. Interface 2014, 11, 20130585. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American Carbon Program Site Synthesis. Glob. Chang. Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D. Complex seasonal patterns of primary producers at the land–sea interface. Ecol. Lett. 2008, 11, 1294–1303. [Google Scholar] [CrossRef] [PubMed]
- Keogan, K.; Daunt, F.; Wanless, S.; Phillips, R.A.; Walling, C.A.; Agnew, P.; Ainley, D.G.; Anker-Nilssen, T.; Ballard, G.; Barrett, R.T. Global phenological insensitivity to shifting ocean temperatures among seabirds. Nat. Clim. Chang. 2018, 8, 313. [Google Scholar] [CrossRef]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37. [Google Scholar] [CrossRef] [PubMed]
- Carmona, M.R.; Aravena, J.C.; Bustamante-Sanchez, M.A.; Celis-Diez, J.L.; Charrier, A.; Díaz, I.A.; Díaz-Forestier, J.; Díaz, M.F.; Gaxiola, A.; Gutiérrez, A.G. Estación Biológica Senda Darwin: Investigación ecológica de largo plazo en la interfase ciencia-sociedad. Rev. Chil. Hist. Nat. 2010, 83, 113–142. [Google Scholar] [CrossRef]
- Bustamante-Sánchez, M.A.; Armesto, J.J.; Halpern, C.B. Biotic and abiotic controls on tree colonization in three early successional communities of Chiloé Island, Chile. J. Ecol. 2011, 99, 288–299. [Google Scholar] [CrossRef]
- Strub, P.T.; James, C.; Montecino, V.; Rutllant, J.A.; Blanco, J.L. Ocean circulation along the southern Chile transition region (38∘–46∘S): Mean, seasonal and interannual variability, with a focus on 2014–2016. Prog. Oceanogr. 2019, 172, 159–198. [Google Scholar] [CrossRef]
- Iriarte, J.; León-Muñoz, J.; Marcé, R.; Clément, A.; Lara, C. Influence of seasonal freshwater streamflow regimes on phytoplankton blooms in a Patagonian fjord. New Zealand J. Mar. Freshw. Res. 2017, 51, 304–315. [Google Scholar] [CrossRef]
- Garreaud, R. Record-breaking climate anomalies lead to severe drought and environmental disruption in western Patagonia in 2016. Clim. Res. 2018, 74, 217–229. [Google Scholar] [CrossRef]
- Oliva, R.D.P.; Vasquez-Lavín, F.; San Martin, V.A.; Hernández, J.I.; Vargas, C.A.; Gonzalez, P.S.; Gelcich, S. Ocean Acidification, Consumers’ Preferences, and Market Adaptation Strategies in the Mussel Aquaculture Industry. Ecol. Econ. 2019, 158, 42–50. [Google Scholar] [CrossRef]
- Marshall, A.G.; Hendon, H.H.; Wang, G. On the role of anomalous ocean surface temperatures for promoting the record Madden-Julian Oscillation in March 2015. Geophys. Res. Lett. 2016, 43, 472–481. [Google Scholar] [CrossRef]
- Alvarez, M.S.; Vera, C.S.; Kiladis, G.N.; Liebmann, B. Influence of the Madden Julian Oscillation on precipitation and surface air temperature in South America. Clim. Dynam. 2016, 46, 245–262. [Google Scholar] [CrossRef]
- Boisier, J.P.; Rondanelli, R.; Garreaud, R.D.; Muñoz, F. Anthropogenic and natural contributions to the Southeast Pacific precipitation decline and recent megadrought in central Chile. Geophys. Res. Lett. 2016, 43, 413–421. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Alvarez-Garreton, C.; Barichivich, J.; Boisier, J.P.; Christie, D.; Galleguillos, M.; LeQuesne, C.; McPhee, J.; Zambrano-Bigiarini, M. The 2010–2015 megadrought in central Chile: impacts on regional hydroclimate and vegetation. Hydrol. Earth Syst. Sci. 2017, 21, 6307–6327. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara, C.; Cazelles, B.; Saldías, G.S.; Flores, R.P.; Paredes, Á.L.; Broitman, B.R. Coupled Biospheric Synchrony of the Coastal Temperate Ecosystem in Northern Patagonia: A Remote Sensing Analysis. Remote Sens. 2019, 11, 2092. https://doi.org/10.3390/rs11182092
Lara C, Cazelles B, Saldías GS, Flores RP, Paredes ÁL, Broitman BR. Coupled Biospheric Synchrony of the Coastal Temperate Ecosystem in Northern Patagonia: A Remote Sensing Analysis. Remote Sensing. 2019; 11(18):2092. https://doi.org/10.3390/rs11182092
Chicago/Turabian StyleLara, Carlos, Bernard Cazelles, Gonzalo S. Saldías, Raúl P. Flores, Álvaro L. Paredes, and Bernardo R. Broitman. 2019. "Coupled Biospheric Synchrony of the Coastal Temperate Ecosystem in Northern Patagonia: A Remote Sensing Analysis" Remote Sensing 11, no. 18: 2092. https://doi.org/10.3390/rs11182092
APA StyleLara, C., Cazelles, B., Saldías, G. S., Flores, R. P., Paredes, Á. L., & Broitman, B. R. (2019). Coupled Biospheric Synchrony of the Coastal Temperate Ecosystem in Northern Patagonia: A Remote Sensing Analysis. Remote Sensing, 11(18), 2092. https://doi.org/10.3390/rs11182092






