Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data
Abstract
1. Introduction
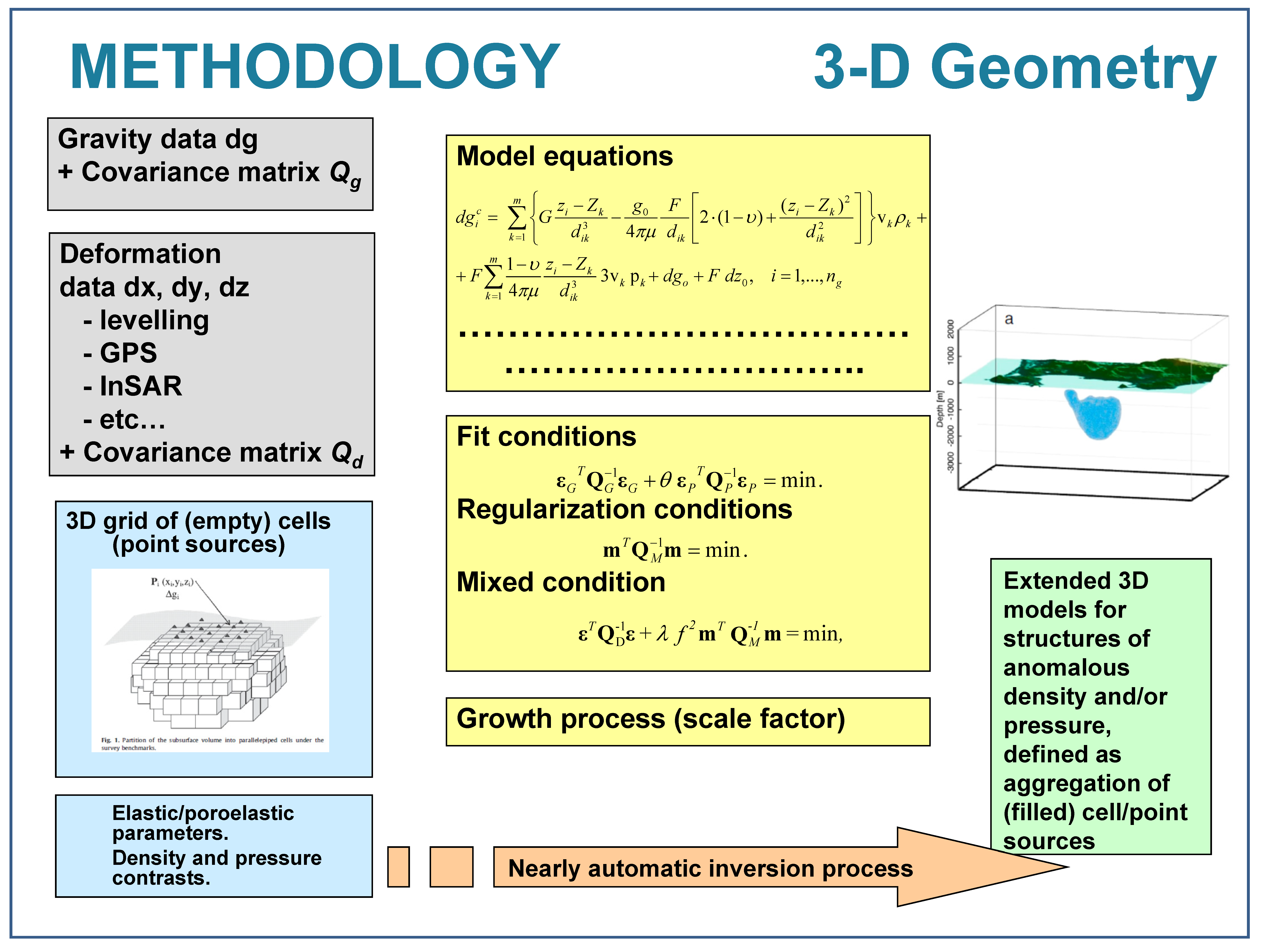
2. Inversion Approach for Deformation and Gravity Changes
2.1. System of Nonlinear Equations
- Free-air effects, corresponding to the relocation of the benchmarks, due to elevation changes according a free-air vertical gravity gradient (about −290 μGal/m for Campi Flegrei); this effect can be included in the model fit using modeled or observed elevation changes;
- Newtonian effects due to density changes within the original boundaries of the deep bodies;
- Newtonian effects due to mass relocation or change of volume;
- Effects due to mass uplift in the surface corresponding to elevation changes. These effects can be obtained using another vertical gravity gradient, depending on the regional terrain density (similar to the Bouguer correction [57,58,59,60]). Effects 1 and 4 depend on the surface elevation changes and can be combined by using a combined gravity gradient F (about −210 μGal/m);
- Water table effects which correspond to very local and shallow perturbations;
2.2. Misfit Conditions
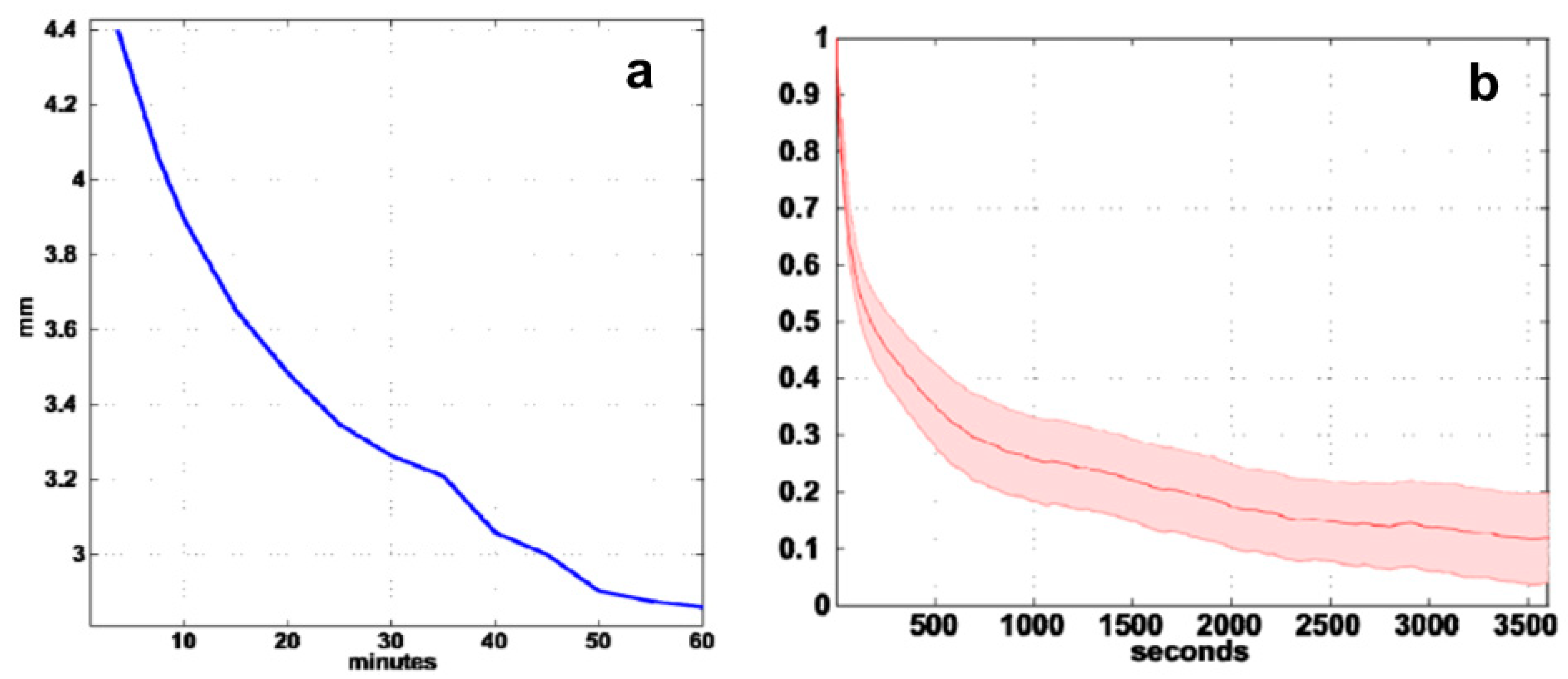
2.3. Exploration Approach for Solving the System
3. Application Results
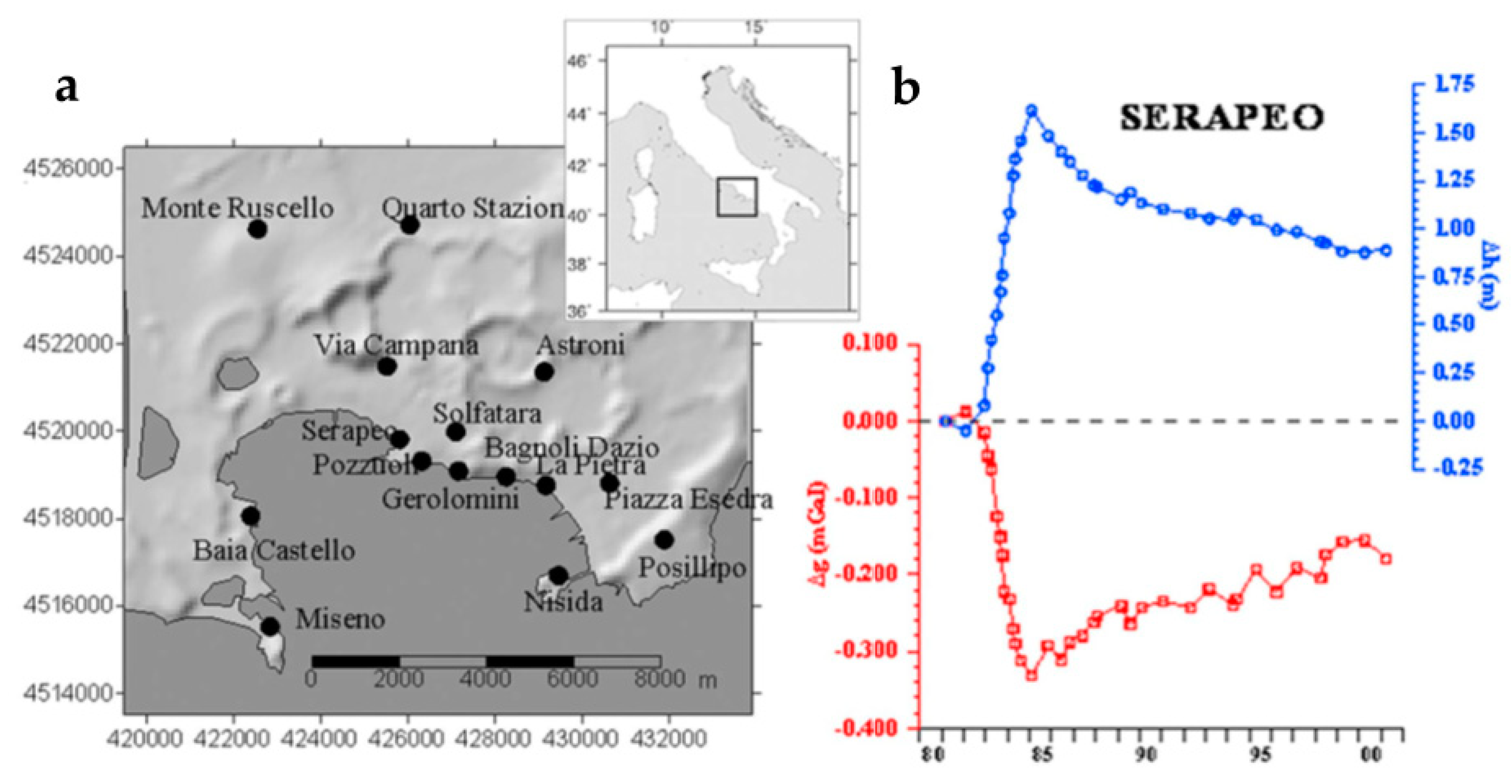
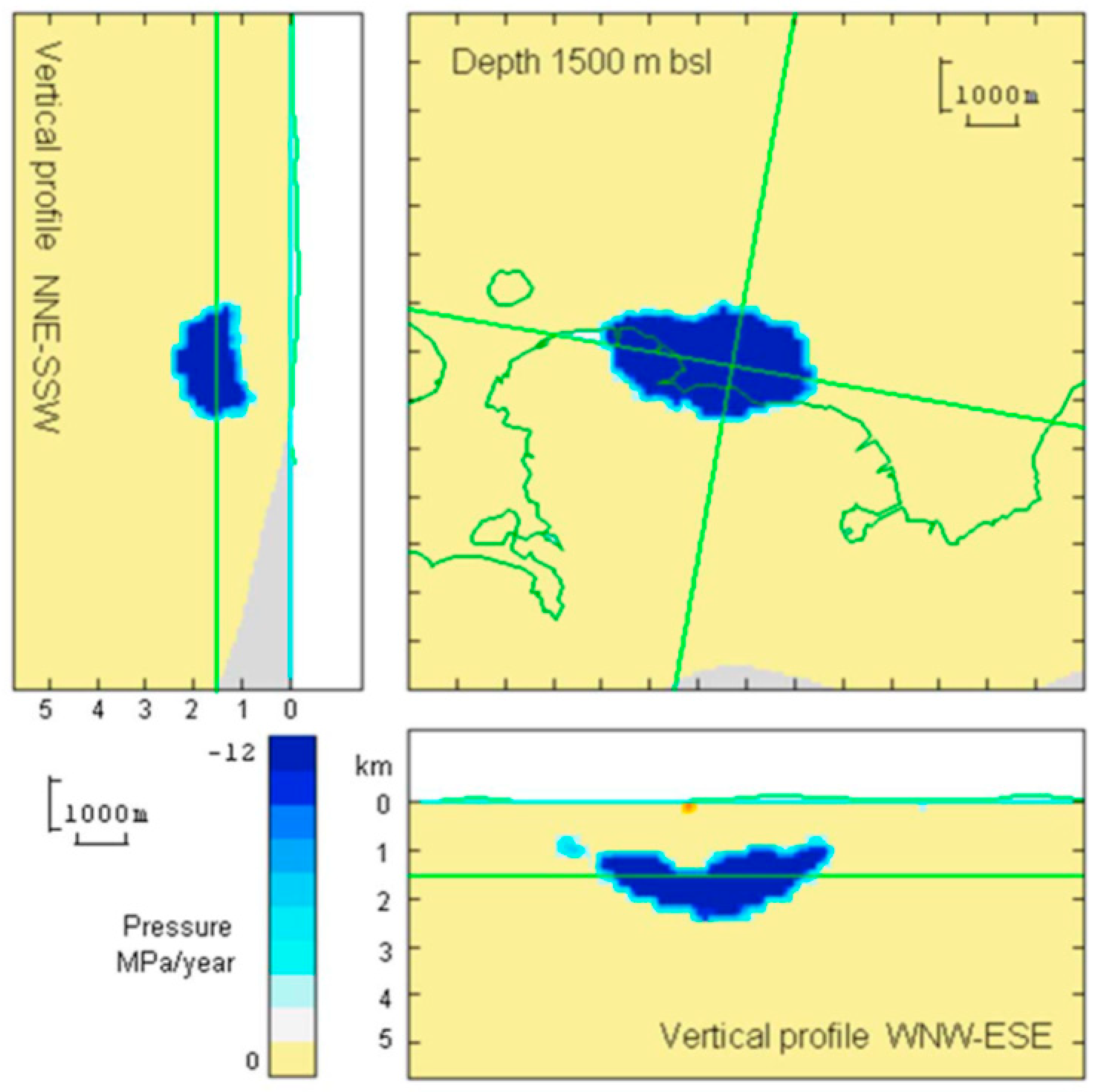
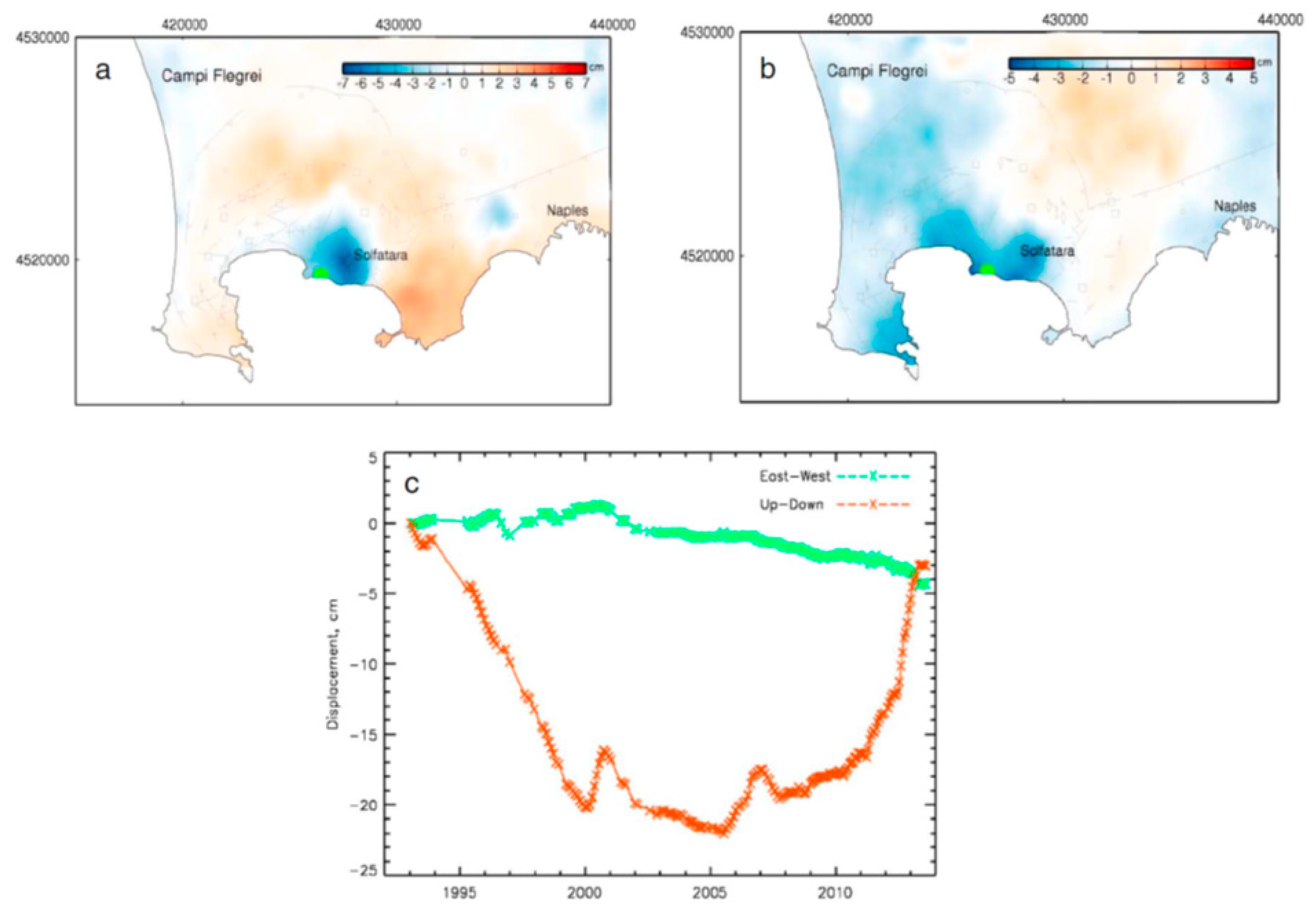
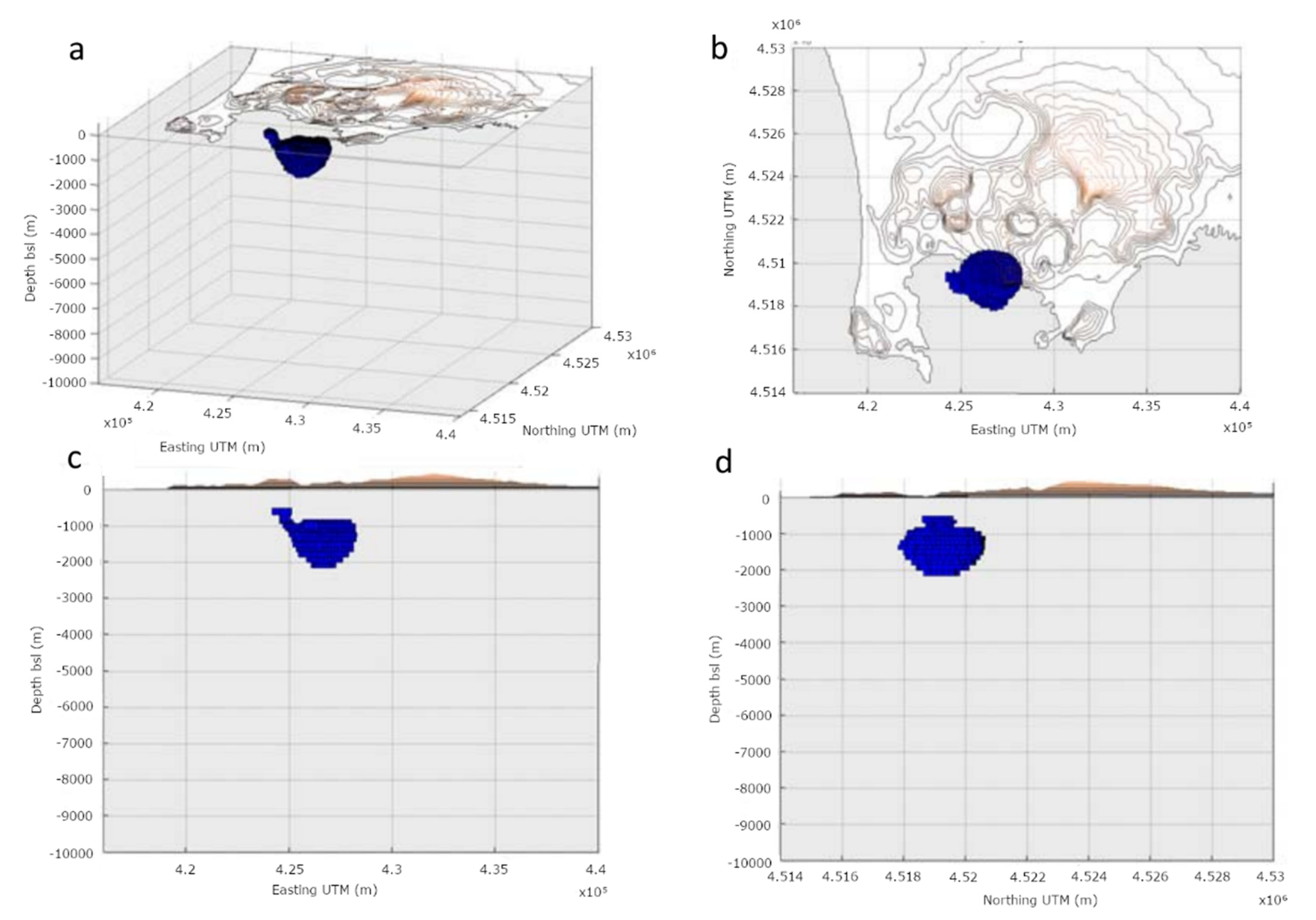
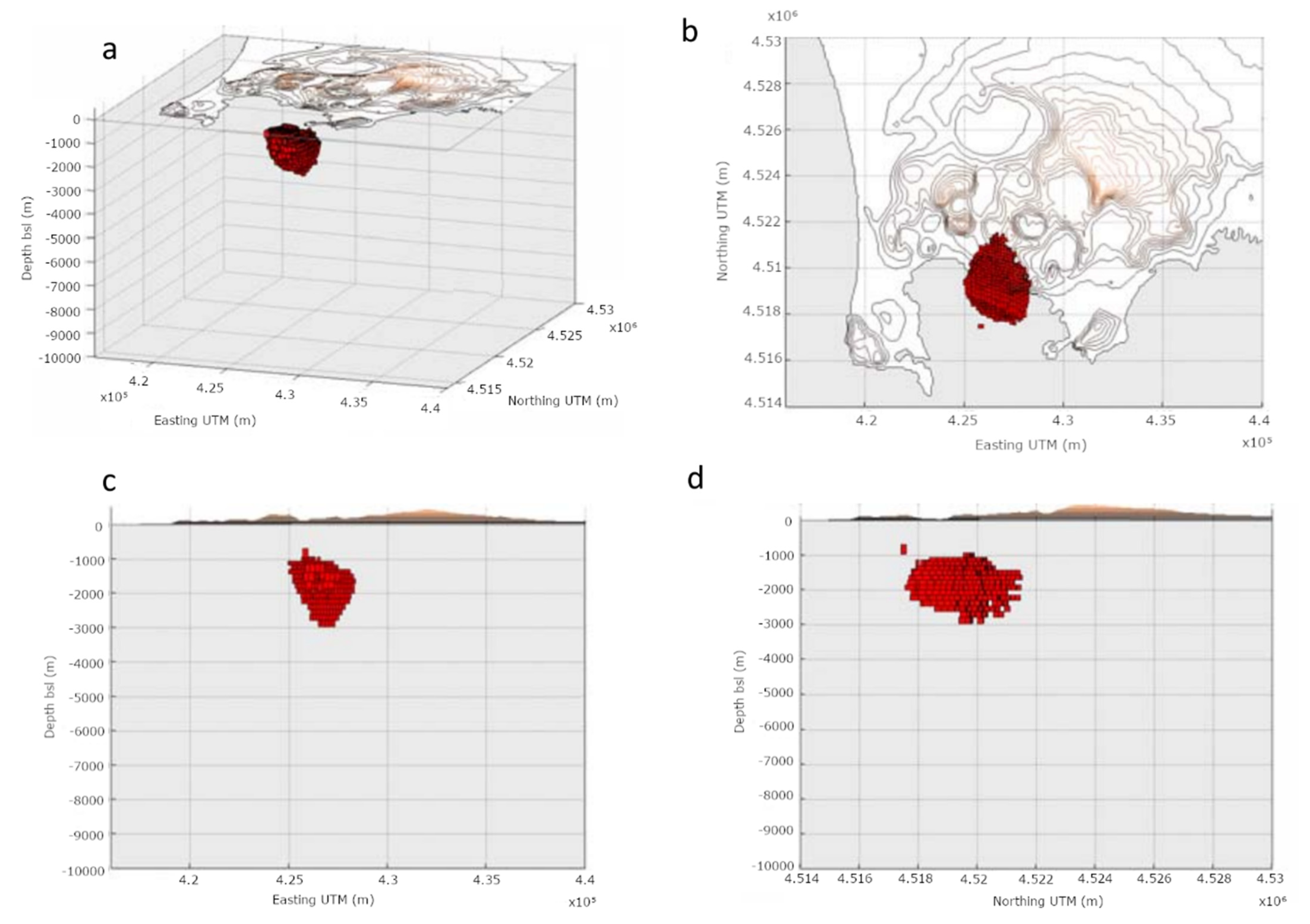
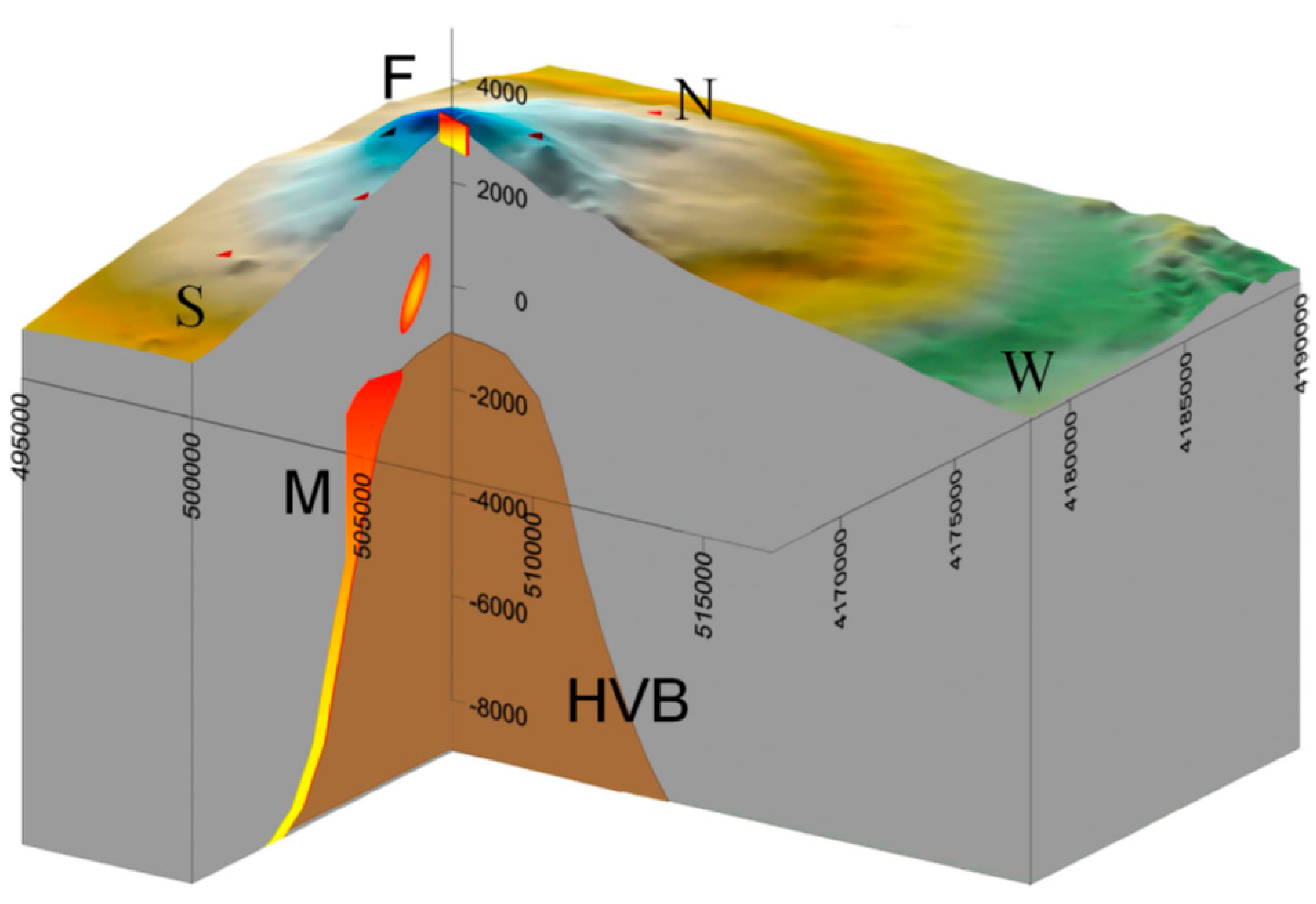
3.1. Modeling of Campi Flegrei Unrest 1992–2000 Using Deformation and Gravity Changes
Discussion
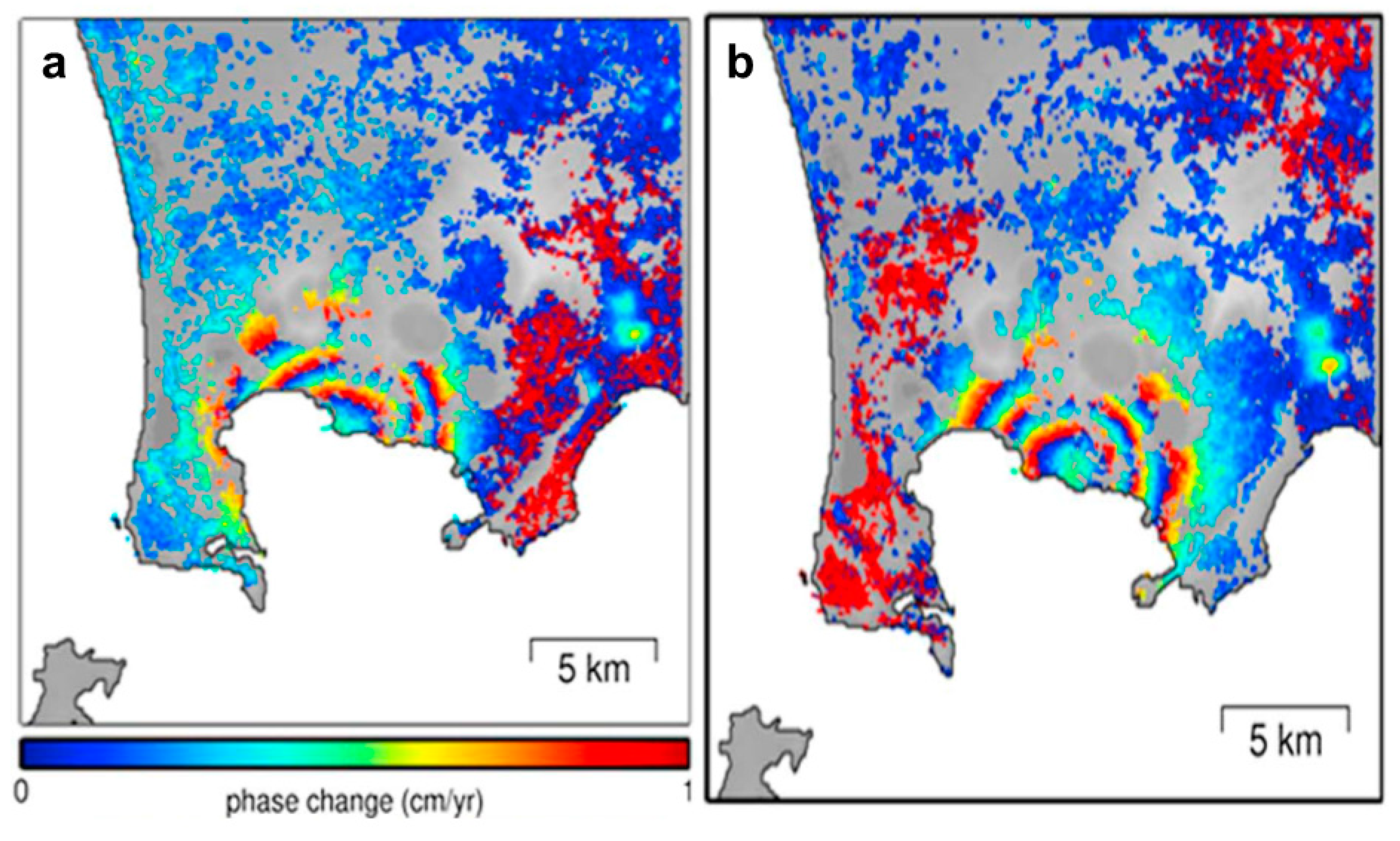
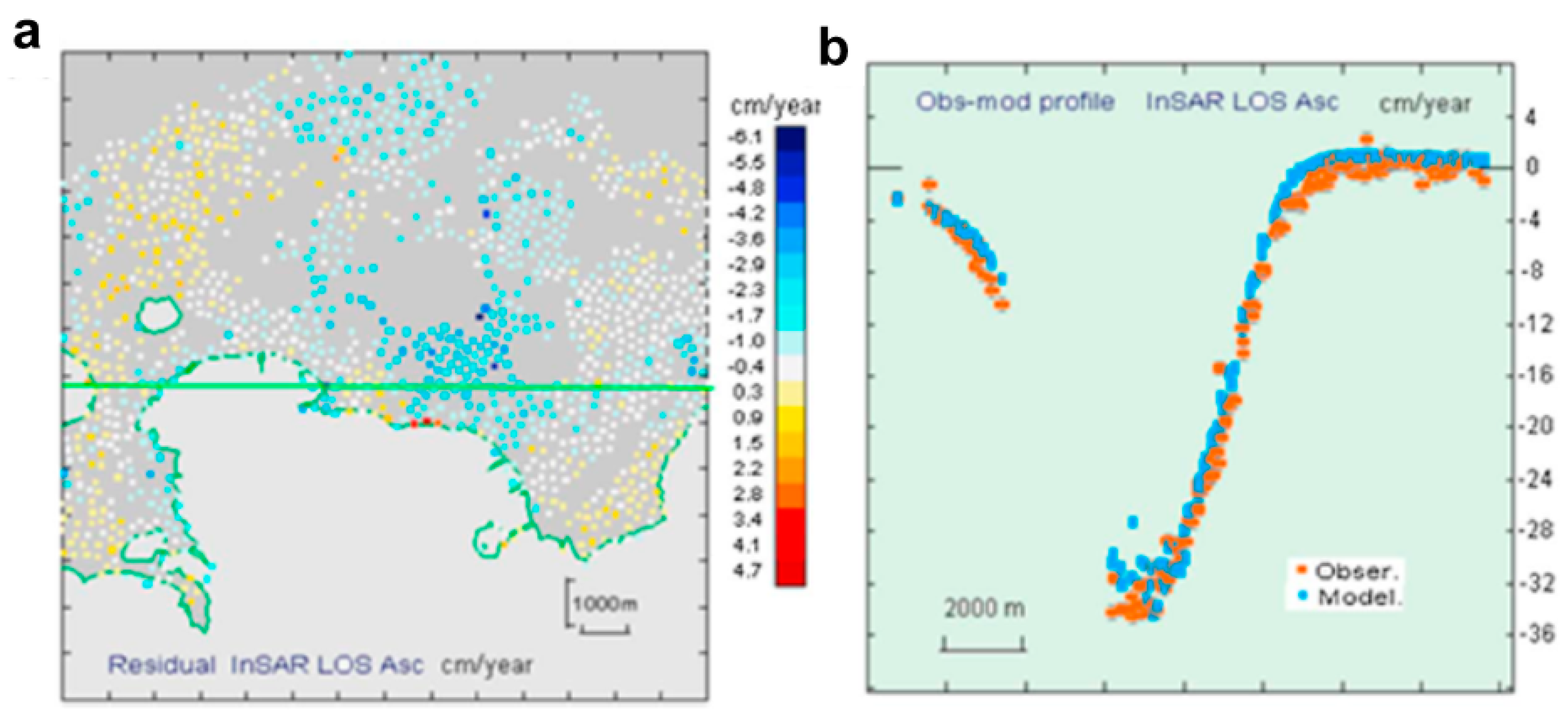
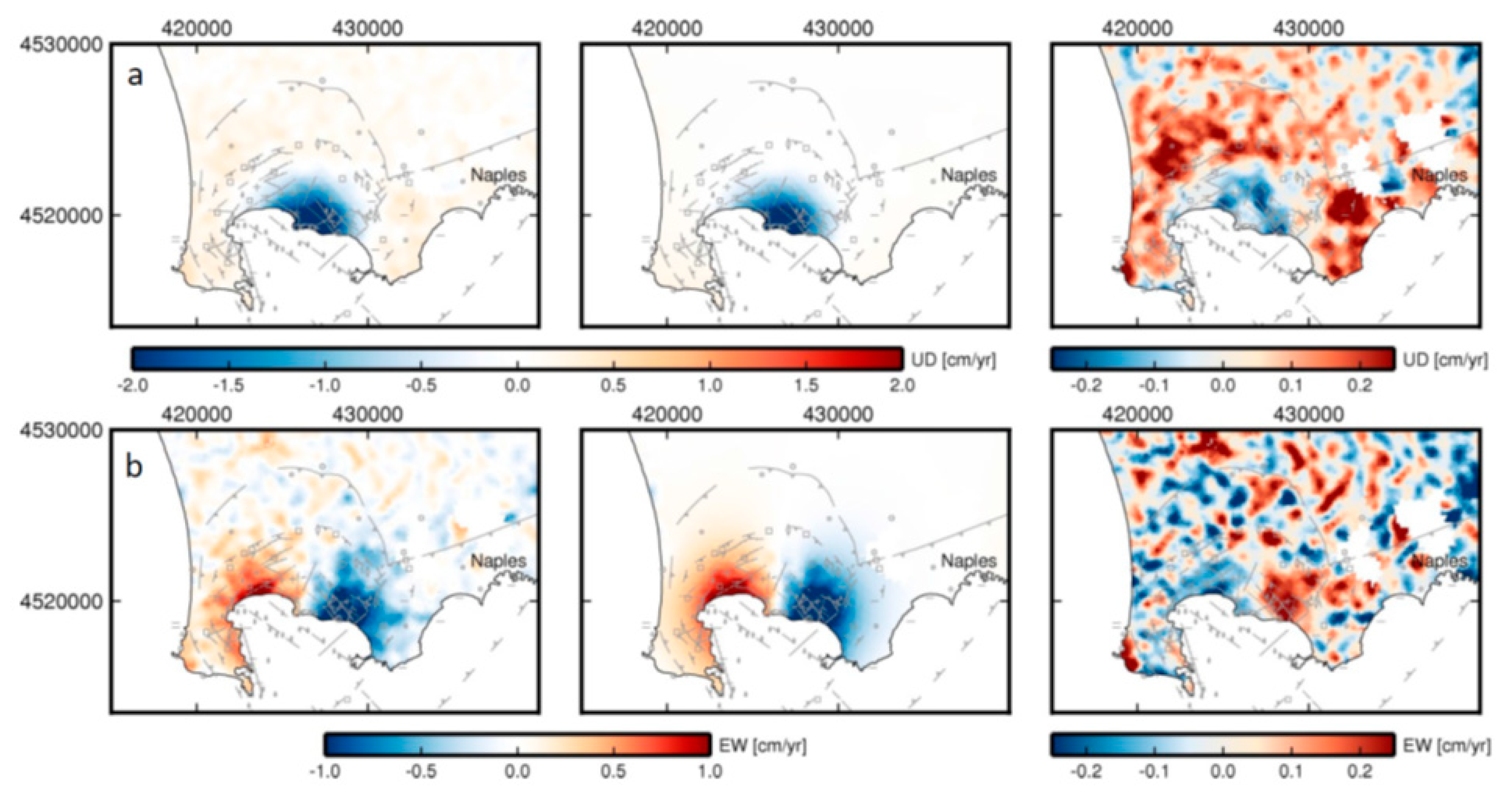
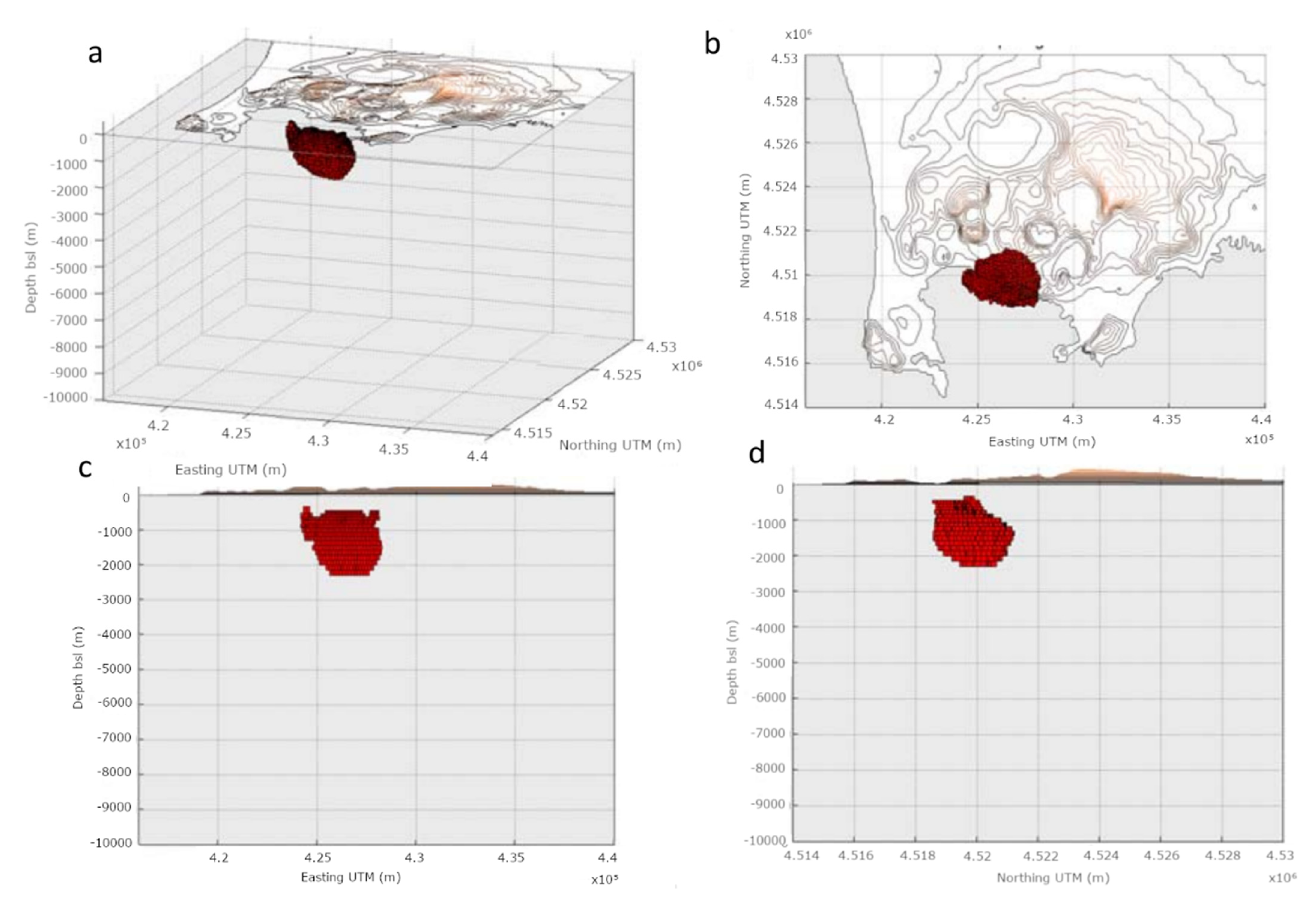
3.2. Modeling of Campi Flegrei Unrest 1993–2013 Using Only Displacement Data
Discussion
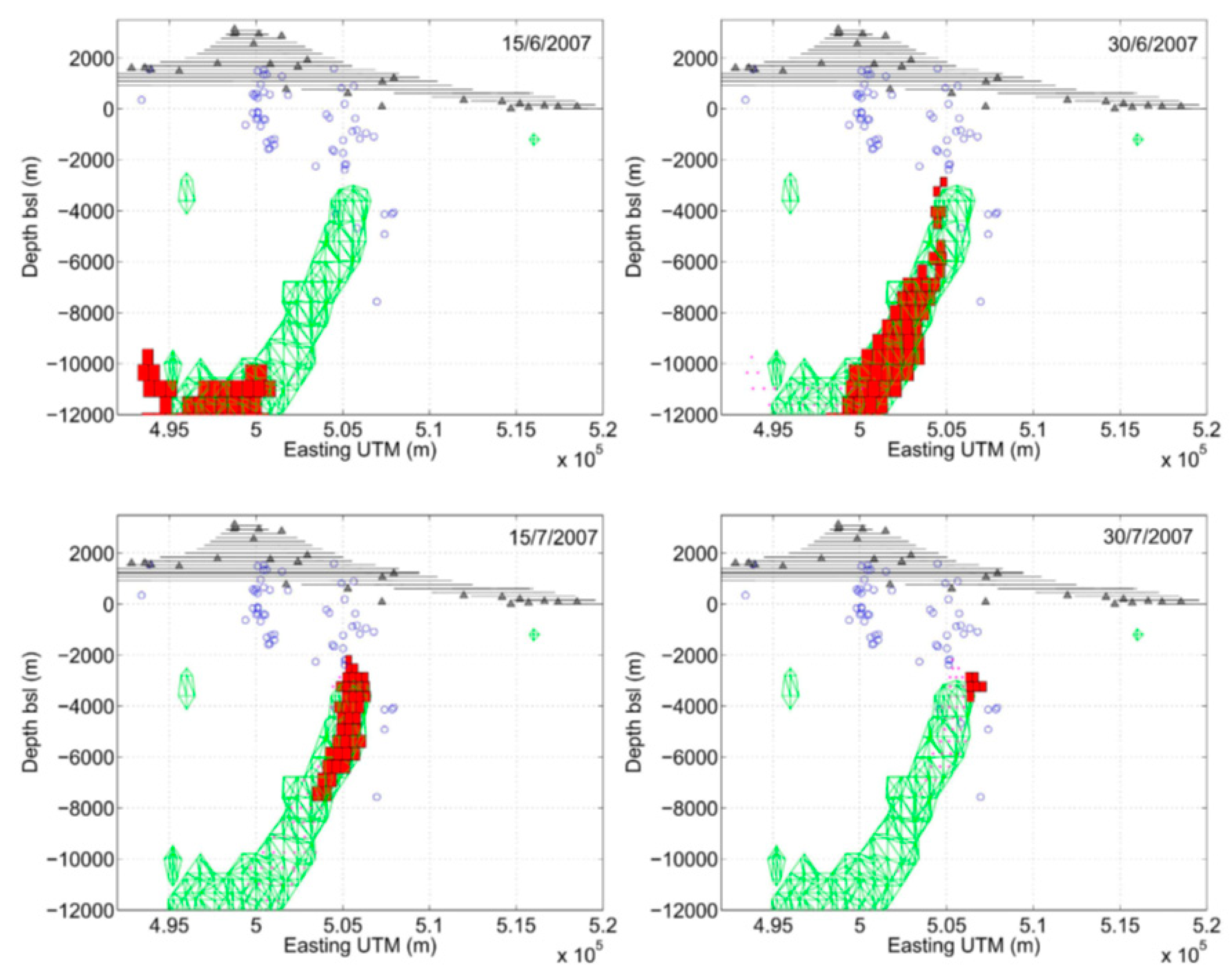
3.3. Real Time Tracking of Magmatic Intrusions During Volcanic Crisis: 2008 May Etna Eruption
3.3.1. Results
3.3.2. Discussion
3.4. Land Subsidence Associated with Overexploitation of Aquifers: Lorca, Spain
Discussion and Inversion of the 3D Displacement Field
4. General Summary
- (a)
- It permits simultaneous inversion of the 1D to 3D displacement data coming from different techniques, including terrestrial and space data (GNSS, DInSAR, leveling, etc.);
- (b)
- Non-planar, non-gridded, inexact data can be used;
- (c)
- It allows for objective modelling of two causative structures: Pressure and mass anomalies bodies;
- (d)
- Simple analytical and well-known expressions are used for direct calculation for mass and pressure cells and their aggregation;
- (e)
- This methodology works in a fully 3D context;
- (f)
- There is not additional a priori requirements on the geometry and types of the causative sources;
- (g)
- The method automatically determines the type and number, modeling the geometry, of the causative source structures;
- (h)
- A free geometry of the causative structures is described by aggregation of small elemental cells. Surface deformation can be computed by adding the influence of the small considered prisms. Given that the used direct models are linear and the entire subsurface is assumed to be isotropic, superposition is allowable. Using this assumption, these linear equations permit the computation of surface deformation based on the superposition of many prismatic blocks within a compacting reservoir of any geometric shape [5]. The effect of each cell is computed using point sources [1,5].
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Camacho, A.G.; González, P.J.; Fernández, J.; Berrino, G. Simultaneous inversion of surface deformation and gravity changes by means of extended bodies with a free geometry: Application to deforming calderas. J. Geophys. Res. 2011, 116, B10401. [Google Scholar] [CrossRef]
- Dzurisin, D. Volcano Deformation: Geodetic Monitoring Techniques; Springer-Praxis Books in Geophysical Sciences. Praxis Publishing Ltd.: Chichester, UK, 2007; p. 441. [Google Scholar]
- Herring, T. Treatise on Geophysics, Geodesy, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2009; Volume 3, p. 446. [Google Scholar]
- Fernández, J.; Pepe, A.; Poland, M.P.; Sigmundsson, F. Volcano geodesy: Recent developments and future challenges. J. Volcanol. Geotherm. Res. 2017, 344, 1–12. [Google Scholar] [CrossRef]
- Fernández, J.; Prieto, J.F.; Escayo, J.; Camacho, A.G.; Luzón, F.; Tiampo, K.F.; Palano, M.; Abajo, T.; Pérez, E.; Velasco, J.; et al. Modeling the two-and three-dimensional displacement field in Lorca, Spain, subsidence and the global implications. Sci. Rep. 2018, 8, 14782. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yu, M.; Xu, Q.; Sawada, K.; Moriguchi, S.; Yashima, A.; Liu, C.; Xue, L. InSAR-derived digital elevation models for terrain change analysis of earthquake-triggered flow-like kandslides bases on ALOS/PALSAR imagery. Environ. Earth Sci. 2015, 73, 7661–7668. [Google Scholar] [CrossRef]
- Yu, M.; Huang, Y.; Zhou, J.; Mao, L. Modeling of landslide topography based on micro-unmanned aerial vehicle photography and structure-from-motion. Environ. Earth Sci. 2017, 76, 520. [Google Scholar] [CrossRef]
- Biggs, J.; Ebmeier, S.K.; Aspinall, W.P.; Lu, Z.; Pritchard, M.E.; Sparks, R.S.J.; Mather, T.A. Global link between deformation and volcanic eruption quantified by satellite imagery. Nat. Commun. 2014, 5, 3471. [Google Scholar] [CrossRef] [PubMed]
- Biggs, J.; Pritchard, M.E. Global volcano monitoring: What does it mean when volcanoes deform? Elements 2017, 13, 17–22. [Google Scholar] [CrossRef]
- Tralli, D.M.; Blom, R.G.; Zlotnicki, V.; Donnellan, A.; Evans, D.L. Satellite remote sensing of earthquake, volcano, flood, landslide and coastal inundation hazards. ISPRS J. Photogramm. Remote Sens. 2005, 59, 185–198. [Google Scholar] [CrossRef]
- Bilham, R. The seismic future of cities. Bull. Earthq. Eng. 2009, 7, 839–887. [Google Scholar] [CrossRef]
- González, P.J. Medida y Caracterización de Deformaciones Usando Técnicas Geodésicas y de Teledetección. Aplicación en Volcanología y Sismotectónica. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2010. (In Spanish). [Google Scholar]
- Fernández, J.; González, P.J.; Camacho, A.G.; Prieto, J.F.; Bru, G. An overview of geodetic volcano research in the Canary Islands. Pure Appl. Geophys. 2015, 172, 3189–3228. [Google Scholar] [CrossRef]
- Terranova, C.; Ventura, G.; Vilardo, G. Multiple causes of ground deformation in the Napoli metropolitan area (Italy) from integrated persistent scatterers DinSAR, geological, hydrological, and urban infrastructure data. Earth-Sci. Rev. 2015, 146, 105–119. [Google Scholar] [CrossRef]
- Sparks, R.S.J.; Biggs, J.; Neuberg, J.W. Monitoring volcanoes. Science 2012, 335, 1310–1311. [Google Scholar] [CrossRef] [PubMed]
- Sigmundsson, F.; Hreinsdóttir, S.; Hooper, A.; Árnadóttir, T.; Pedersen, R.; Roberts, M.J.; Óskarsson, N.; Auriac, A.; Decriem, J.; Einarsson, P.; et al. Intrusion triggering of the 2010 Eyjafjallajökull explosive eruption. Nature 2010, 468, 426–430. [Google Scholar] [CrossRef] [PubMed]
- Cannavò, F.; Camacho, A.G.; González, P.J.; Mattia, M.; Puglisi, G.; Fernández, J. Real time tracking of magmatic intrusions by means of ground deformation modeling during volcanic crises. Sci. Rep. 2015, 5, 10970. [Google Scholar] [CrossRef] [PubMed]
- Galloway, D.; Jones, D.R.; Ingebritsen, S. Land Subsidence in the United States; US Geological Survey Circular: Reston, VA, USA, 1999. [Google Scholar]
- Dokka, R.K. Modern-day tectonic subsidence in coastal Louisiana. Geology 2006, 34, 281–284. [Google Scholar] [CrossRef]
- Amelung, F.; Galloway, D.L.; Bell, J.W.; Zebker, H.A.; Laczniak, R.J. Sensing the ups and downs of Las Vegas: InSAR reveals structural control of land subsidence and aquifer-system deformation. Geology 1999, 27, 483–486. [Google Scholar] [CrossRef]
- González, P.J.; Fernández, J. Drought-driven transient aquifer compaction imaged using multitemporal satellite radar interferometry. Geology 2011, 39, 551–554. [Google Scholar] [CrossRef]
- Boní, R.; Herrera, G.; Meisina, C.; Notti, D.; Béjar-Pizarro, M.; Zucca, F.; González, P.J.; Palano, M.; Tomás, R.; Fernández, J.; et al. Twenty-year advanced DInSAR analysis of severe land subsidence: The Alto Guadalentín basin (Spain) case study. Eng. Geol. 2015, 198, 40–52. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Tiampo, K.F.; Feng, W. Fast subsidence in downtown of Seattle observed with satellite radar. Remote Sens. Appl. Soc. Environ. 2016, 4, 179–187. [Google Scholar] [CrossRef]
- Bru, G.; González, P.J.; Mateos, R.M.; Roldán, F.J.; Herrera, G.; Béjar-Pizarro, M.; Fernández, J. A-DInSAR monitoring of landslide and subsidence activity: A case of urban damage in arcos de la frontera, Spain. Remote Sens. 2017, 9, 787. [Google Scholar] [CrossRef]
- Gourmelen, N.; Amelung, F.; Casu, F.; Manzo, M.; Lanari, R. Mining-related ground deformation in Crescent Valley, Nevada: Implications for sparse GPS networks. Geophys. Res. Lett. 2007, 34, L09309. [Google Scholar] [CrossRef]
- Ma, C.; Cheng, X.; Yang, Y.; Zhang, X.; Guo, Z.; Zou, Y. Investigation on mining subsidence based on multi-temporal InSAR and time-series analysis of the small baseline subset—case study of working faces 22201-1/2 in Bu’ertai mine, shendong coalfield. Remote Sens. 2016, 8, 951. [Google Scholar] [CrossRef]
- Lisowski, M. Analytical volcano deformation source parameters in volcano deformation: New geodetic monitoring techniques. In Volcano Deformation: Geodetic Monitoring Techniques; Dzurisin, D., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; pp. 279–304. [Google Scholar]
- Segall, P. Earthquake and Volcano Deformation; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2010; p. 432. ISBN 978-0-691-13302-7. [Google Scholar]
- Rymer, H.; Williams-Jones, G. Volcanic eruption prediction: Magma chamber physics from gravity and deformation measurements. Geophys. Res. Lett. 2000, 27, 16–2389. [Google Scholar] [CrossRef]
- Fernández, J.; Tiampo, K.F.; Jentzsch, G.; Charco, M.; Rundle, J.B. Inflation or deflation? New results for Mayon volcano applying elastic-gravitational modeling. Geophys. Res. Lett. 2001, 28, 2349–2352. [Google Scholar] [CrossRef]
- Masterlark, T. Magma intrusion and deformation predictions: Sensitivities to the Mogi assumptions. J. Geophys. Res. 2007, 112, B06419. [Google Scholar] [CrossRef]
- Long, S.M.; Grosfils, E.B. Modeling the effect of layered volcanic material on magma reservoir failure and associated deformation, with application to Long Valley caldera, California. J. Volcanol. Geotherm. Res. 2009, 186, 349–360. [Google Scholar] [CrossRef]
- Castaldo, R.; Gola, G.; Santilano, A.; De Novellis, V.; Pepe, S.; Manzo, M.; Manzella, A.; Tizzani, P. The role of thermo-rheological properties of the crust beneath Ischia island (Southern Italy) in the modulation of the ground deformation pattern. J. Volcanol. Geotherm. Res. 2017, 344, 154–173. [Google Scholar] [CrossRef]
- Trasatti, E.; Giunchi, C.; Agostinetti, N.P. Numerical inversion of deformation caused by pressure sources: Application to Mount Etna (Italy). Geophys. J. Int. 2008, 172, 873–884. [Google Scholar] [CrossRef]
- Battaglia, M.; Gottsmann, J.; Carbone, D.; Fernández, J. 4D volcano gravimetry. Geophysics 2008, 73, WA3–WA18. [Google Scholar] [CrossRef]
- Carbone, D.; Poland, M.P.; Diament, M.; Grecco, F. The added value of 4D microgravimetry to the understanding of how volcanoes work. Earth Sci. Rev. 2017, 169, 146–179. [Google Scholar] [CrossRef]
- Charco, M.; Fernández, J.; Luzón, F.; Rundle, J.B. On the relative importance of selfgravitation and elasticity in modeling volcanic ground deformation and gravity changes. J. Geophys. Res. 2006, 111, B03404. [Google Scholar] [CrossRef]
- Johnson, D.J.; Eggers, A.A.; Bagnardi, M.; Battaglia, M.; Poland, M.P.; Miklius, A. Shallow magma accumulation at Kīlauea Volcano, Hawaii, revealed by microgravity surveys. Geology 2010, 38, 1139–1142. [Google Scholar] [CrossRef]
- Bagnardi, M.; Poland, M.P.; Carbone, D.; Baker, S.; Battaglia, M.; Amelung, F. Gravity changes and deformation at Kīlauea Volcano, Hawaii, associated with summit eruptive activity, 2009–2012. J. Geophys. Res. 2014, 119, 7288–7305. [Google Scholar] [CrossRef]
- Currenti, G. Numerical evidence enabling reconciliation of gravity and height changes in volcanic areas. Geophys. J. Int. 2014, 197, 164–173. [Google Scholar] [CrossRef]
- Charco, M.; Camacho, A.G.; Tiampo, K.F.; Fernández, J. Spatiotemporal gravity changes on volcanoes: Assessing the importance of topography. Geophys. Res. Lett. 2009, 36, L08306. [Google Scholar] [CrossRef]
- Fokker, P.A.; Wassing, B.B.T.; van Leijen, F.J.; Hanssen, R.F.; Nieuwland, D.A. Application of an ensemble smoother with multiple data assimilation to the Bergermeer gas field, using PS-InSAR. Geomech. Energy Environ. 2016, 5, 16–28. [Google Scholar] [CrossRef]
- Vasco, D.W.; Wicks, C.; Karasaki, K.; Marques, O. Geodetic imaging: Reservoir monitoring using satellite interferometry. Geophys. J. Int. 2002, 149, 555–571. [Google Scholar] [CrossRef]
- Tiampo, K.F.; Ouegnin, F.-A.; Valluri, S.; Samsonov, S.; Fernández, J.; Kapp, G. An elliptical model for deformation due to groundwater fluctuations. Pure Appl. Geophys. 2012, 169, 1443–1456. [Google Scholar] [CrossRef]
- Geertsma, J. Land subsidence above compacting oil and gas reservoirs. J. Pet. Technol. 1973, 25, 734–744. [Google Scholar] [CrossRef]
- Geertsma, J.; Van Opstal, G. A numerical technique for predicting subsidence above compacting reservoirs based on the nucleus of strain concept. Verh. Kon. Ned. Geol. Mijnbouwk 1973, 28, 63–78. [Google Scholar]
- Segall, P. Stress and subsidence resulting from subsurface fluid withdrawal in the epicentral region of the 1983 Coalinga Earthquake. J. Geophys. Res. 1985, 90, 6801–6816. [Google Scholar] [CrossRef]
- Vasco, D.W.; Karasaki, K.; Doughty, C. Using surface deformation to image reservoir dynamics. Geophysics 2000, 65, 132–147. [Google Scholar] [CrossRef]
- Walsh, J.B. Subsidence above a planar reservoir. J. Geophys. Res. Solid Earth 2002, 107, 2202. [Google Scholar] [CrossRef]
- Brown, N.J.; Woods, A.W.; Neufeld, J.A.; Richardson, C. Constraining Surface Deformation Predictions Resulting From Coal Seam Gas Extraction; Geoscience Australia: Symonston, Australia, 2014. [Google Scholar] [CrossRef]
- González, P.J.; Tiampo, K.F.; Palano, M.; Cannavó, F.; Fernández, J. The 2011 Lorca earthquake slip distribution controlled by groundwater crustal unloading. Nat. Geosci. 2012, 5, 821–825. [Google Scholar] [CrossRef]
- Charco, M.; Galán del Sastre, P. Efficient inversion of 3D finite element models of volcano deformation. Geophys. J. Int. 2014, 196, 1441–1454. [Google Scholar] [CrossRef][Green Version]
- Samsonov, S.V.; Tiampo, K.F.; Camacho, A.G.; Fernández, J.; González, P.J. Spatiotemporal analysis and interpretation of 1993–2013 ground deformation at Campi Flegrei, Italy, observed by advanced DInSAR. Geophys. Res. Lett. 2014, 41, 6101–6108. [Google Scholar] [CrossRef]
- Camacho, A.G.; Fernández, J.; Cannavò, F. PAF: A software tool to estimate free-geometry extended bodies of anomalous pressure from surface deformation data. Comput. Geosci. 2018, 111, 235–243. [Google Scholar] [CrossRef]
- Camacho, A.G.; Montesinos, F.G.; Vieira, R. A 3-D gravity inversion by means of growing bodies. Geophysics 2000, 65, 95–191. [Google Scholar] [CrossRef]
- Davis, R.O.; Selvadurai, A.P.S. Elasticity and Geomechanics; Cambridge University Press: Cambridge, UK, 1996; p. 201. [Google Scholar]
- Saleh, B. Underground deformation measurements using new quarts instruments. In Proceedings of the 95th Annual CIG Geomatics Conference, Can. Inst. of Geomatics, Ottawa, ON, Canada, 8–23 July 2002. [Google Scholar]
- Rundle, J.B. Gravity changes and the Palmdale uplift. Geophys. Res. Lett. 1978, 5, 41–44. [Google Scholar] [CrossRef]
- Walsh, J.B.; Rice, J.R. Local changes in gravity resulting from deformation. J. Geophys. Res. 1979, 84, 165–170. [Google Scholar] [CrossRef]
- Currenti, G.; Del Negro, C.; Ganci, G. Modelling of ground deformation and gravity fields using finite element method: An application to Etna volcano. Geophys. J. Int. 2007, 169, 775–786. [Google Scholar] [CrossRef]
- Williams, C.A.; Wadge, G. The effects of topography on magma chamber deformation models: Application to Mt. Etna and radar interferometry. Geophys. Res. Lett. 1998, 25, 1549–1552. [Google Scholar] [CrossRef]
- Battaglia, M.; Hill, D.P. Analytical modeling of gravity changes and crustal deformation at volcanoes: The Long Valley caldera, California, case study. Tectonophysics 2009, 471, 45–57. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Tiede, C.; Tiampo, K.F.; Fernández, J.; Gerstenecker, C. Deeper understanding of non-linear geodetic data inversion using a quantitative sensitivity analysis. Nonlinear Processes Geophys. 2005, 12, 373–379. [Google Scholar] [CrossRef]
- Farquharson, C.G.; Oldenbourg, D.W. Non-linear inversion using general measures of data misfit and model structure. Geophys. J. Int. 1998, 134, 213–227. [Google Scholar] [CrossRef]
- Bertete-Aguirre, H.; Cherkaev, E.; Oristaglio, M. Non-smooth gravity problem with total variation penalization functional. Geophys. J. Int. 2002, 149, 499–507. [Google Scholar] [CrossRef]
- Camacho, A.G.; Nunes, J.C.; Ortiz, E.; França, Z.; Vieira, R. Gravimetric determination of an intrusive complex under the Island of Faial (Azores): Some methodological improvements. Geophys. J. Int. 2007, 171, 478–494. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory; Elsevier: Amsterdam, The Netherlands, 1987; p. 613. [Google Scholar]
- Camacho, A.G.; Montesinos, F.G.; Vieira, R. A 3-D gravity inversion tool based on exploration of model possibilities. Comput. Geosci. 2002, 28, 191–204. [Google Scholar] [CrossRef]
- Gottsmann, J.; Camacho, A.G.; Marti, J.; Wooller, L.; Fernández, J.; Garcia, A.; Rymer, H. Shallow structure beneath the central volcanic complex of tenerife from new gravity data: Implications for its evolution and recent reactivation. Phys. Earth Planet. Inter. 2008, 168, 212–230. [Google Scholar] [CrossRef]
- Corrado, G.; Guerra, I.; Lo Bascio, A.; Luongo, G.; Rampoldi, R. Inflation and microearthquake activity of Phlegraean Fields, Italy. Bull. Volcanol. 1976, 40, 1–20. [Google Scholar] [CrossRef]
- Berrino, G.; Corrado, G.; Luongo, G.; Toro, B. Ground deformation and gravity changes accompanying the 1982 Pozzuoli Uplift. Bull. Volcanol. 1984, 47, 187–200. [Google Scholar] [CrossRef]
- Orsi, G.; Civetta, L.; Del Gaudio, C.; De Vita, S.; Di Vito, M.A.; Isaia, R.; Petrazzuoli, S.M.; Ricciardi, G.P.; Ricco, C. Short-term ground deformation and seismicity in the resurgent Campi Flegrei caldera (Italy): An example of active block-resurgence in a densely populated area. J. Volcanol. Geotherm. Res. 1999, 91, 415–451. [Google Scholar] [CrossRef]
- Gottsmann, J.; Berrino, G.; Rymer, H.; William-Jones, G. Hazard assessment during caldera unrest at the Campi Flegrei, Italy: A contribution from gravity-height gradients. Earth Planet. Sci. Lett. 2003, 211, 295–309. [Google Scholar] [CrossRef]
- Berrino, G. Gravity changes induced by height-mass variations at the Campi Flegrei caldera. J. Volcanol. Geotherm. Res. 1994, 61, 293–309. [Google Scholar] [CrossRef]
- Manconi, A.; Walter, T.R.; Manzo, M.; Zeni, G.; Tizzani, P.; Sansosti, E.; Lanari, R. On the effects of 3-D mechanical heterogeneities at Campi Flegrei caldera, southern Italy. J. Geophys. Res. 2010, 115, B08405. [Google Scholar] [CrossRef]
- Lanari, R.; Berardino, P.; Borgström, S.; Del Gaudio, C.; De Martino, P.; Fornaro, G.; Guarino, S.; Ricciardi, G.P.; Sansosti, E.; Lundgren, P. The use of IFSAR and classical geodetic techniques for caldera unrest episodes: Application to the Campi Flegrei uplift event of 2000. J. Volcanol. Geotherm. Res. 2004, 133, 247–260. [Google Scholar] [CrossRef]
- Casu, F.; Manzo, M.; Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Gottsmann, J.; Rymer, H.; Berrino, G. Unrest at the campi flegrei caldera (Italy): A critical evaluation of source parameters from geodetic data inversion. J. Volcanol. Geotherm. Res. 2006, 150, 132–145. [Google Scholar] [CrossRef]
- Berrino, G.; Rymer, H.; Brown, G.C.; Corrado, G. Gravity height correlations for unrest calderas. J. Volcanol. Geotherm. Res. 1992, 53, 11–26. [Google Scholar] [CrossRef]
- Talwani, P.; Acree, S. Pore pressure diffusion and the mechanism of reservoir-induced seismicity. Pure Appl. Geophys. 1984, 122, 947–965. [Google Scholar] [CrossRef]
- Todesco, M.; Berrino, G. Modeling hydrothermal fluid circulation and gravity signals at the Phlegraean Fields caldera. Earth Planet. Sci. Lett. 2005, 240, 328–338. [Google Scholar] [CrossRef]
- Berrino, G.; Corrado, G.; Riccardi, U. Sea gravity data in the Gulf of Naples: A contribution to delineating the Phlegraean Volcanic District. J. Volcanol. Geotherm. Res. 2008, 175, 241–252. [Google Scholar] [CrossRef]
- Gottsmann, J.; Folch, A.; Rymer, H. Unrest at Campi Flegrei: A contribution to the magmatic versus hydrothermal debate from inverse and finite element modeling. J. Geophys. Res. 2006, 111, B07203. [Google Scholar] [CrossRef]
- Battaglia, M.; Obrizzo, F.; Pingue, F.; De Natale, G. Evidence for fluid migration as the source of deformation at Campi Flegrei caldera (Italy). Geophys. Res. Lett. 2006, 33, L01307. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Rem. Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Usai, S. A least squares database approach for SAR interferometric data. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef]
- Samsonov, S.; van der Koij, M.; Tiampo, K. A simultaneous inversion for deformation rates and topographic errors of DInSAR data utilizing linear least square inversion technique. Comput. Geosci. 2011, 37, 1083–1091. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Rem. Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N. Multidimensional time series analysis of ground deformation from multiple InSAR data sets applied to Virunga volcanic province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N.; Smets, B. Ground deformation associated with post-mining activity at the French-German border revealed by novel InSAR time series method. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 142–154. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N.; González, P.; Tiampo, K.; Ertolahti, L.; Clague, J.J. Rapidly accelerating subsidence in the Greater Vancouver region from two decades of ERS-ENVISAT-RADARSAT-2 DInSAR measurements. Rem. Sens. Environ. 2014, 143, 180–191. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Sabbetta, I. Paired deformation sources of the Campi Flegrei caldera (Italy) required by recent (1980–2010) deformation history. J. Geophys. Res. Solid Earth 2014, 119, 858–879. [Google Scholar] [CrossRef]
- Chiodini, G.; Caliro, S.; De Martino, P.; Avino, R.; Gherardi, F. Early signals of new volcanic unrest at Campi Flegrei caldera? Insights from geochemical data and physical simulations. Geology 2012, 40, 943–946. [Google Scholar] [CrossRef]
- Aloisi, M.; Bonaccorso, A.; Cannavò, F.; Gambino, S.; Mattia, M.; Puglisi, G.; Boschi, E. A new dyke intrusion style for the Mount Etna May 2008 eruption modelled through continuous tilt and GPS data. Terr. Nova 2009, 21, 316–321. [Google Scholar] [CrossRef]
- Palano, M.; Rossi, M.; Cannavò, F.; Bruno, V.; Marco, A.; Daniele, P.; Mario, P.; Siligato, G.; Mattia, M. Etn@ref: A geodetic reference frame for Mt. Etna GPS networks. Ann. Geophys. 2010, 53, 49–57. [Google Scholar]
- Bonaccorso, A.; Bonforte, A.; Currenti, G.; Del Negro, C.; Di Stefano, A.; Greco, F. Magma storage, eruptive activity and flank instability: Inferences from ground deformation and gravity changes during the 1993-2000 recharging of Mt. Etna volcano. J. Volcanol. Geotherm. Res. 2011, 200, 245–254. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, D.R.; Yohai, V.J. Robust Statistics: Theory and Methods; John Wiley & Sons Ltd.: Chichester, UK, 2006; p. 436. [Google Scholar]
- Patané, D.; De Gori, P.; Chiarabba, C.; Bonaccorso, A. Magma ascent and the pressurization of Mount Etna’s volcanic system. Science 2003, 290, 2061–2063. [Google Scholar] [CrossRef]
- Aloisi, M.; Mattia, M.; Monaco, C.; Pulvirenti, F. Magma, faults, and gravitational loading at Mount Etna: The 2002–2003 eruptive period. J. Geophys. Res. 2011, 116, B05203. [Google Scholar] [CrossRef]
- D’Auria, L.; Giudicepietro, F.; Martini, M.; Lanari, R. The 4D imaging of the source of ground deformation at Campi Flegrei caldera (southern Italy). J. Geophys. Res. 2012, 117, B08209. [Google Scholar] [CrossRef]
- Fernández, J.; Rundle, J.B. Gravity changes and deformation due to a magmatic intrusion in a two-layered crustal model. J. Geophys. Res. 1994, 99, 2737–2746. [Google Scholar] [CrossRef]
- Rundle, J.B. Viscoelastic-gravitational deformation by a rectangular thrust fault in a layered Earth. J. Geophys. Res. 1982, 87, 7787–7796. [Google Scholar] [CrossRef]
- AEMET, Agencia Estatal de Meteorología. Available online: www.aemet.es/es/datos_abiertos/ AEMET_OpenData (accessed on 15 January 2018).
- Bourgois, J.; Mauffret, A.; Ammar, A.; Demnati, A. Multichannel seismic data imaging of inversion tectonics of the Alboran Ridge (western Mediterranean Sea). Geo Marine Lett. 1992, 12, 117–122. [Google Scholar] [CrossRef]
- Martínez-Díaz, J.J. Stress field variation related to fault interaction in a reverse oblique-slip fault: The Alhama de Murcia fault, Betic Cordillera, Spain. Tectonophysics 2002, 356, 291–305. [Google Scholar] [CrossRef]
- Palano, M.; González, P.J.; Fernández, J. Strain and stress fields along the Gibraltar Orogenic Arc: Constraints on active geodynamics. Gondwana Res. 2013, 23, 1071–1088. [Google Scholar] [CrossRef]
- Cerón, J.C.; Pulido-Bosch, A. Groundwater problems resulting from CO 2 pollution and overexploitation in Alto Guadalentín aquifer (Murcia, Spain). Environ. Geol. 1996, 28, 223–228. [Google Scholar] [CrossRef]
- Confederación Hidrográfica del Segura. Plan especial de actuación en situaciones de alerta y eventual Sequía. Tech. Rep. 2006, 298. [Google Scholar]
- IGN. Instituto Geográfico Nacional. Available online: http://www.ign.es/ (accessed on 15 January 2018).
- Tomás, R.; Herrera, G.; Lopez-Sanchez, J.; Vicente-Guijalba, F.; Cuenca, A.; Mallorqui, J.J. Study of the land subsidence in Orihuela City (SE Spain) using PSI data: Distribution, evolution and correlation with conditioning and triggering factors. Eng. Geol. 2010, 115, 105–121. [Google Scholar] [CrossRef]
- Herrera, G.; Tomás, R.; Monells, D.; Centolanza, G.; Mallorquí, J.J.; Vicente, F.; Navarro, V.D.; Lopez-Sanchez, J.M.; Sanabria, M.; Cano, M.; et al. Analysis of subsidence using TerraSAR-X data: Murcia case study. Eng. Geol. 2010, 116, 284–295. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Li, X.; Wang, R.; Chen, B.; Dai, Z.; Teatini, P. Land subsidence due to groundwater withdrawal in the northern Beijing plain, China. Eng. Geol. 2015, 193, 243–255. [Google Scholar] [CrossRef]
- Pacheco-Martínez, J.; Cabral-Cano, E.; Wdowinski, S.; Hernández-Marín, M.; Ortiz-Lozano, J.A.; Zermeño-de-León, M.E. Application of InSAR and gravimetry for land subsidence hazard zoning in Aguascalientes, Mexico. Remote Sens. 2015, 7, 17035–17050. [Google Scholar] [CrossRef]
- Solari, L.; Ciampalini, A.; Raspini, F.; Bianchini, S.; Moretti, S. PSInSAR analysis in the Pisa urban area (Italy): A case study of subsidence related to stratigraphical factors and urbanization. Remote Sens. 2016, 8, 120. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote sensing of ground deformation for monitoring groundwater management practices: Application to the Santa Clara Valley during the 2012–2015 California drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Y.; Zeng, R.; Yang, Z.; Chen, X.; Zhao, F.; Meng, X. Detection of land subsidence associated with land creation and rapid urbanization in the Chinese Loess Plateau using time series InSAR: A case study of Lanzhou New district. Remote Sens. 2018, 10, 270. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; p. 308. [Google Scholar] [CrossRef]
- Samieie-Esfahany, S.; Hanssen, R.F.; van Thienen-Visser, K.; Muntendam-Bos, A.; Systems, S. On the effect of horizontal deformation on InSAR subsidence estimates. In Proceedings of the Fringe Workshop, Frascati, Italy, 30 November–4 December 2009. [Google Scholar]
- Mora, O.; Ordoqui, P.; Iglesias, R.; Blanco, P. Earthquake rapid mapping using ascending and descending Sentinel-1 TOPSAR interferograms. Procedia Comput. Sci. 2016, 100, 1135–1140. [Google Scholar] [CrossRef]
- Blanco-Sánchez, P.; Mallorquí, J.J.; Duque, S.; Monells, D. The coherent pixels technique (CPT): An advanced DInSAR technique for nonlinear deformation monitoring. Pure Appl. Geophys. 2008, 165, 1167–1193. [Google Scholar] [CrossRef]
- Ezquerro, P.; Guardiola-Albert, C.; Herrera, G.; Fernández-Merodo, J.A.; Béjar-Pizarro, M.; Bonì, R. Groundwater and subsidence modeling combining geological and multi-satellite SAR data over the alto guadalentín aquifer (SE Spain). Geofluids 2017, 1–17. [Google Scholar] [CrossRef]
- Pascal, K.; Neuberg, J.; Rivalta, I. On precisely modelling surface deformation due to interacting magma chambers and dykes. Geophys. J. Int. 2014, 196, 253–278. [Google Scholar] [CrossRef]
- European Plate Observing System. Available online: https://www.epos-ip.org/ (accessed on 25 July 2019).
- Okada, Y. Surface deformation due to shear and tensile faults in a halfspace. Bull. Seismol. Soc. Amer. 1985, 75, 1135–1154. [Google Scholar]
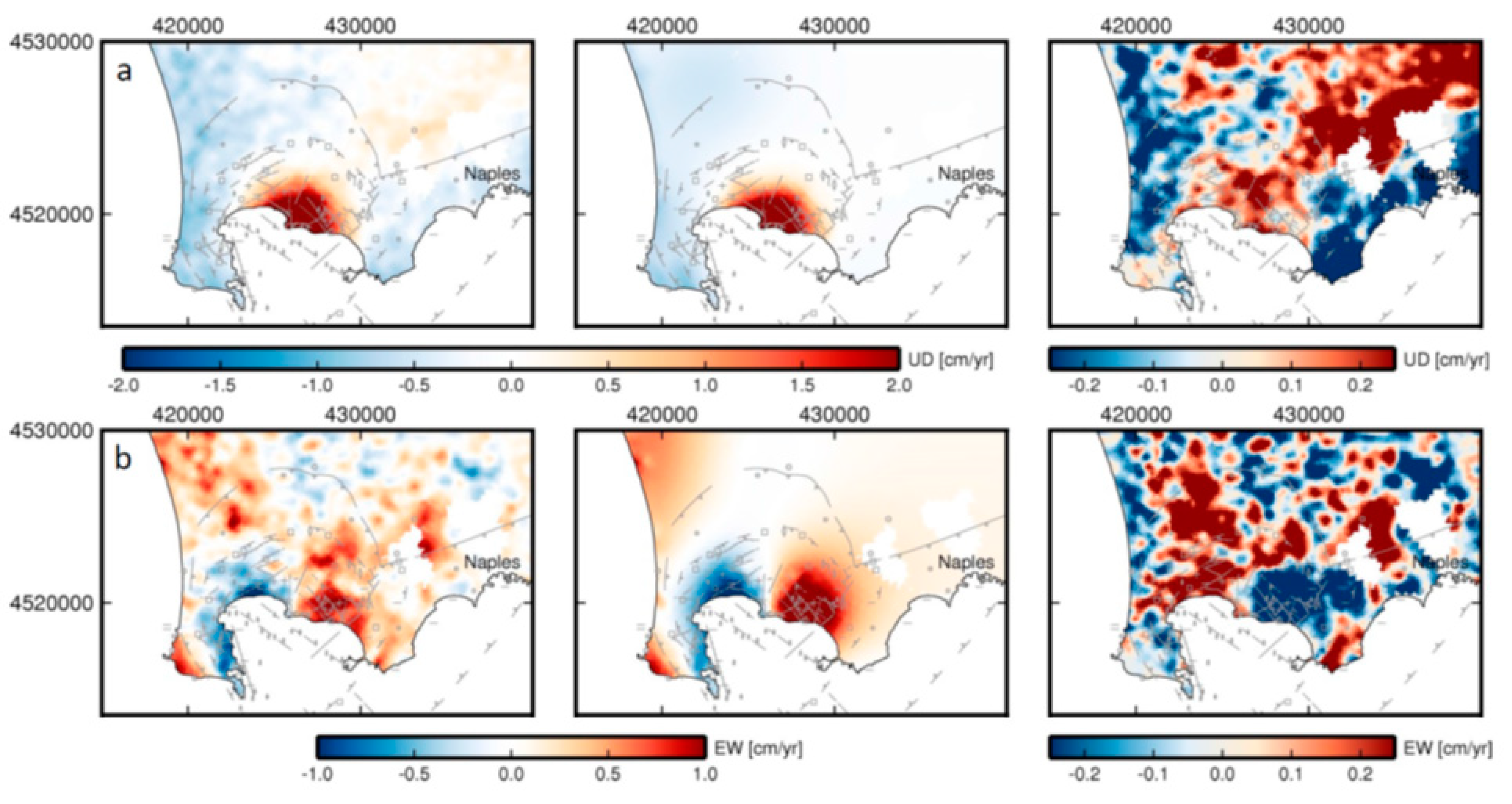

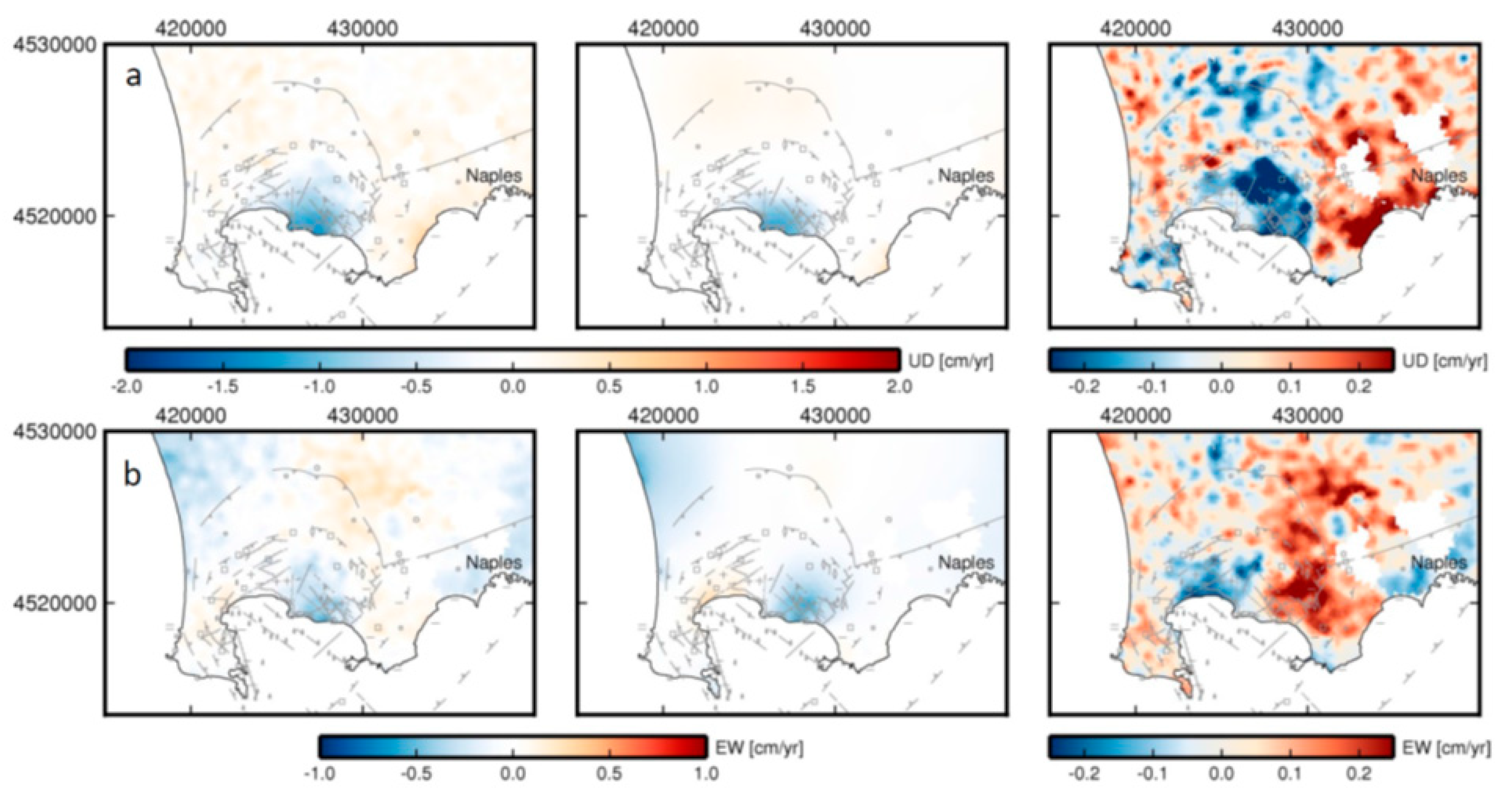
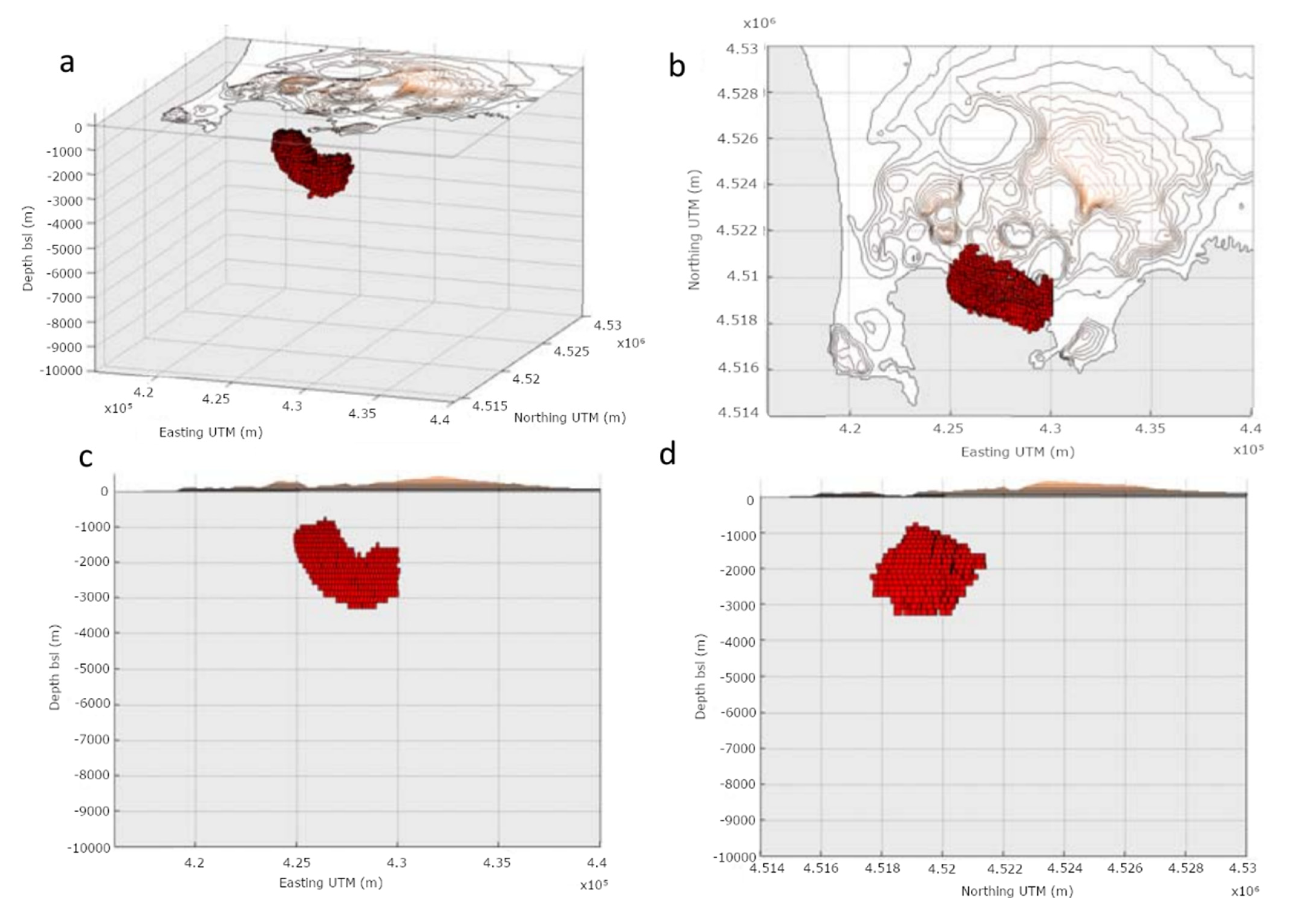
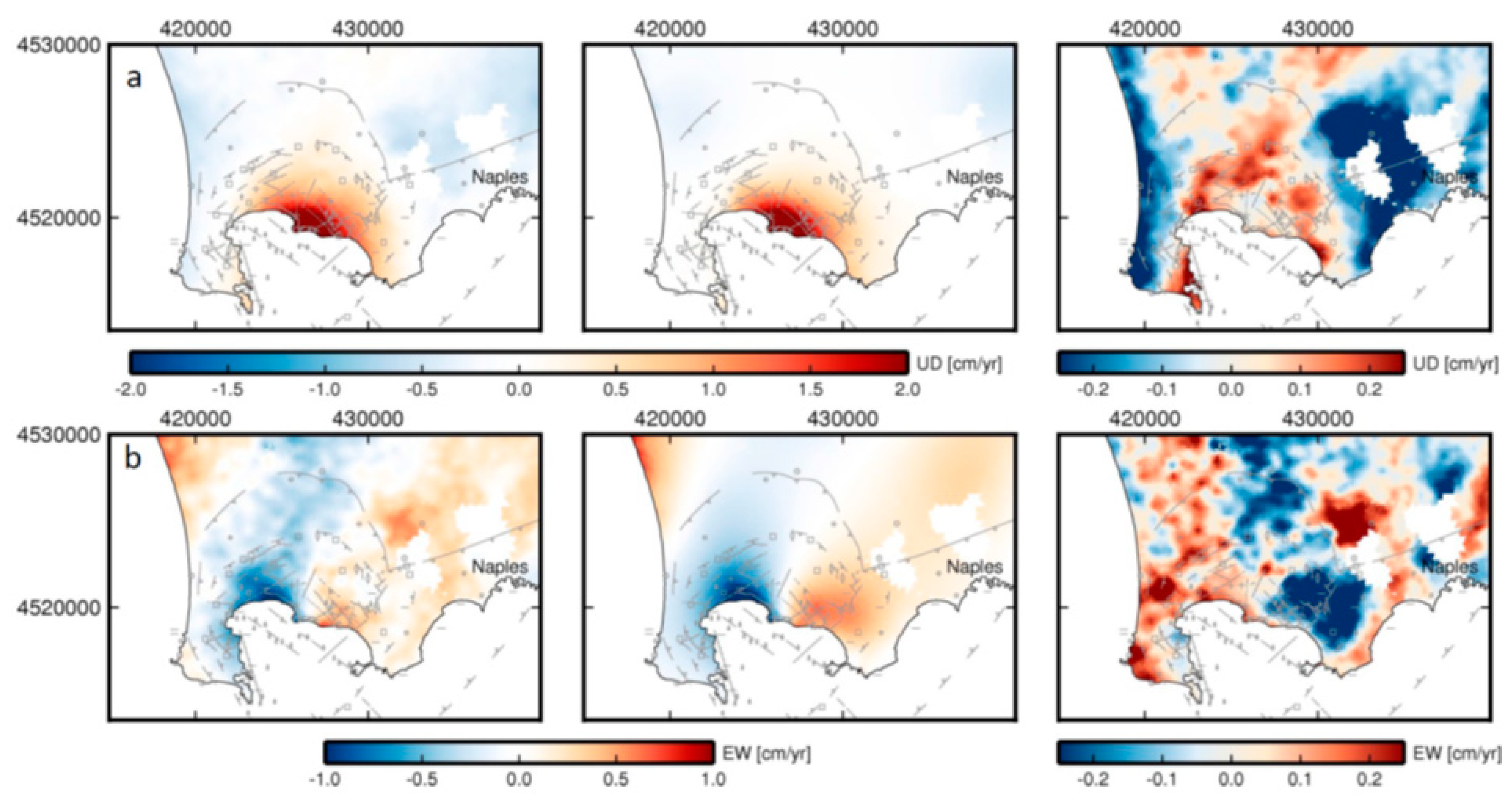





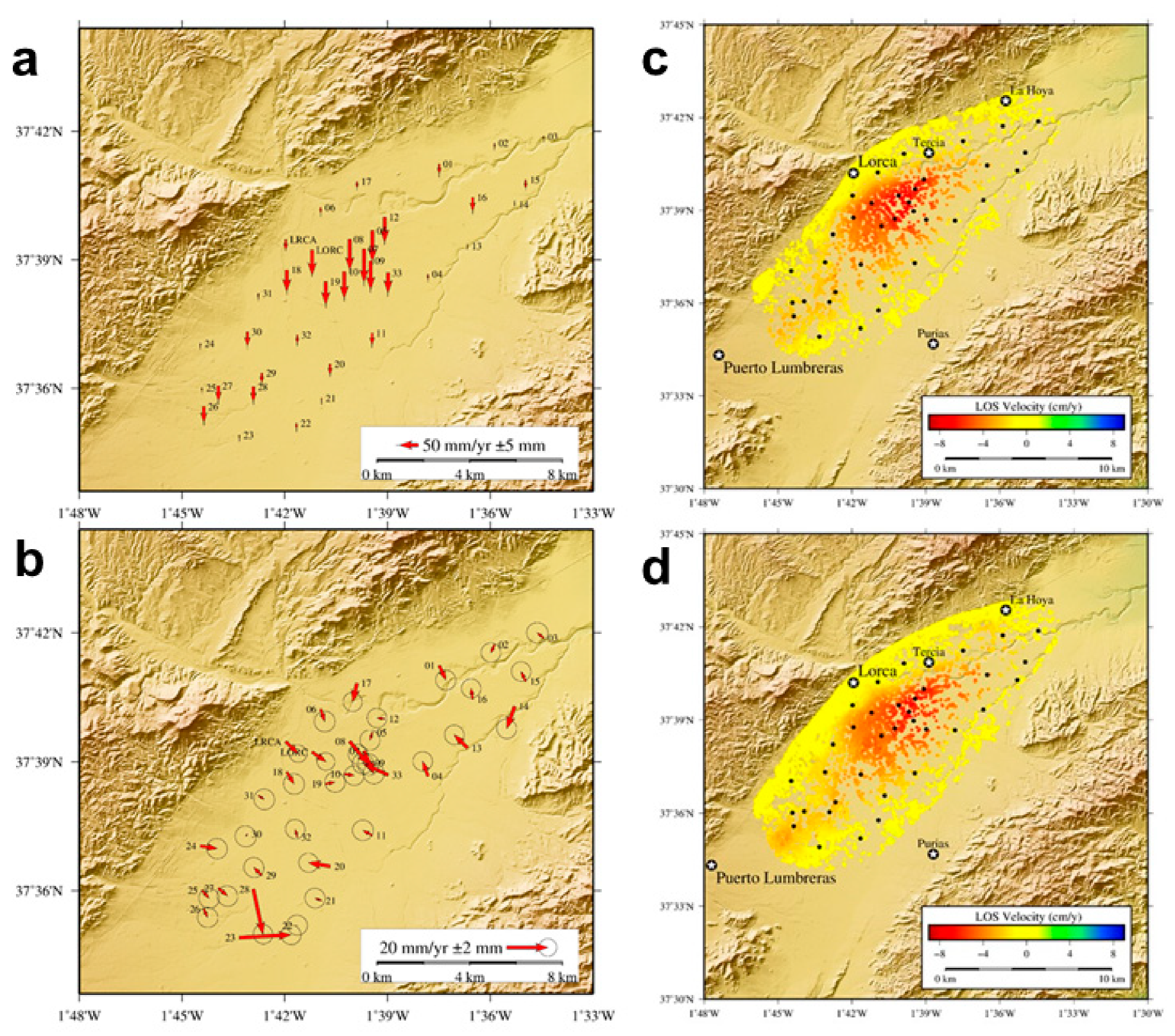
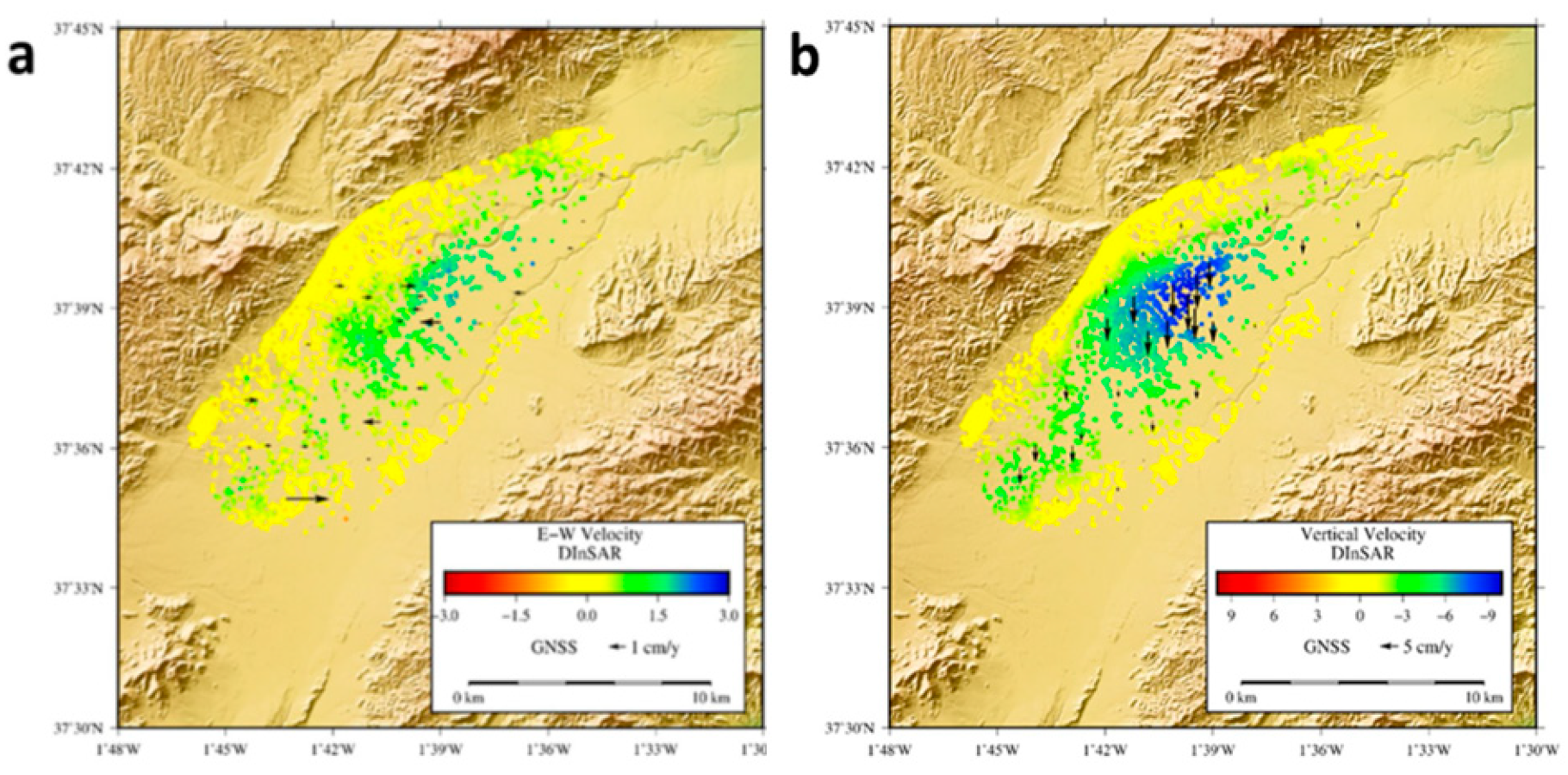
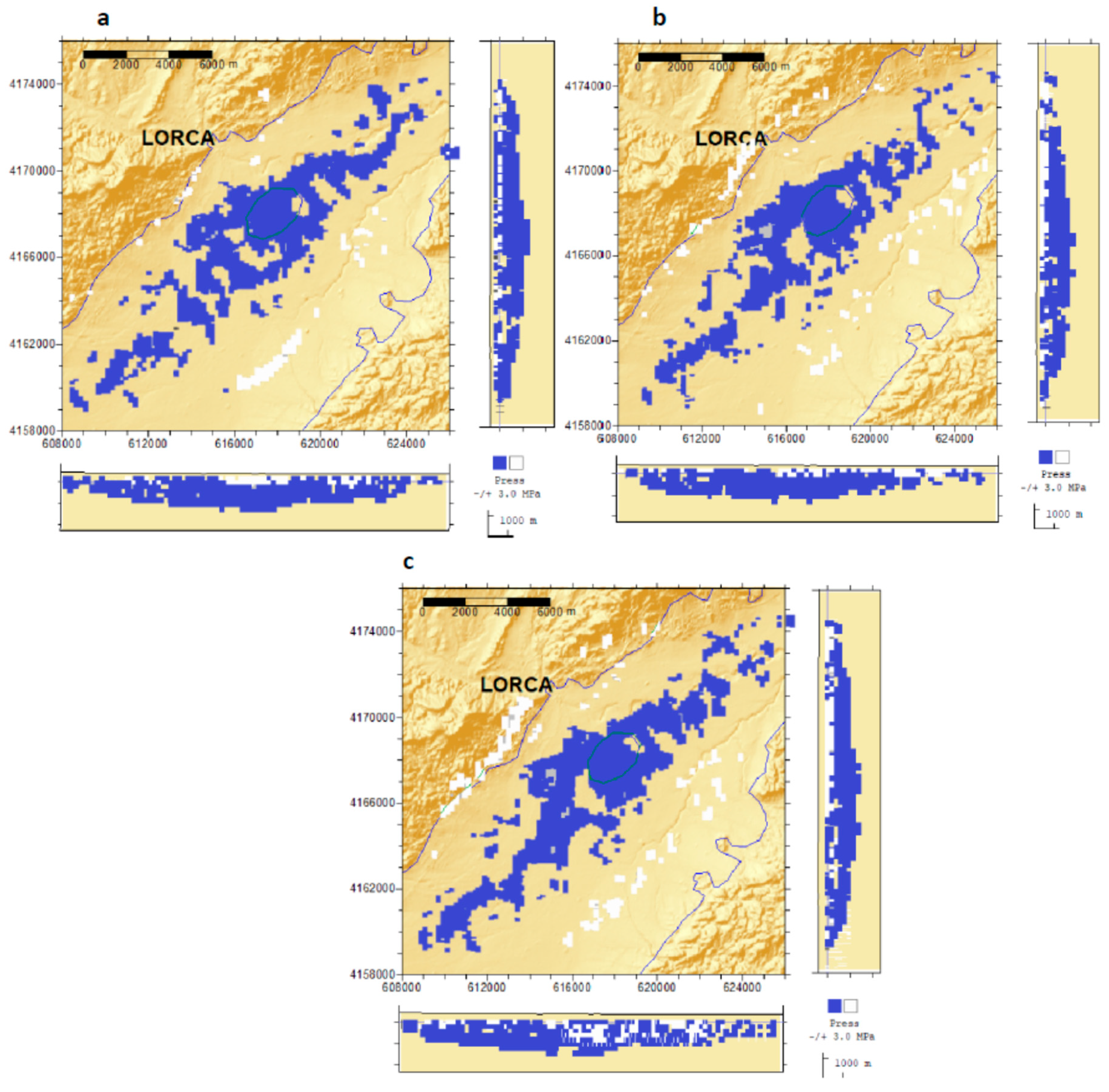
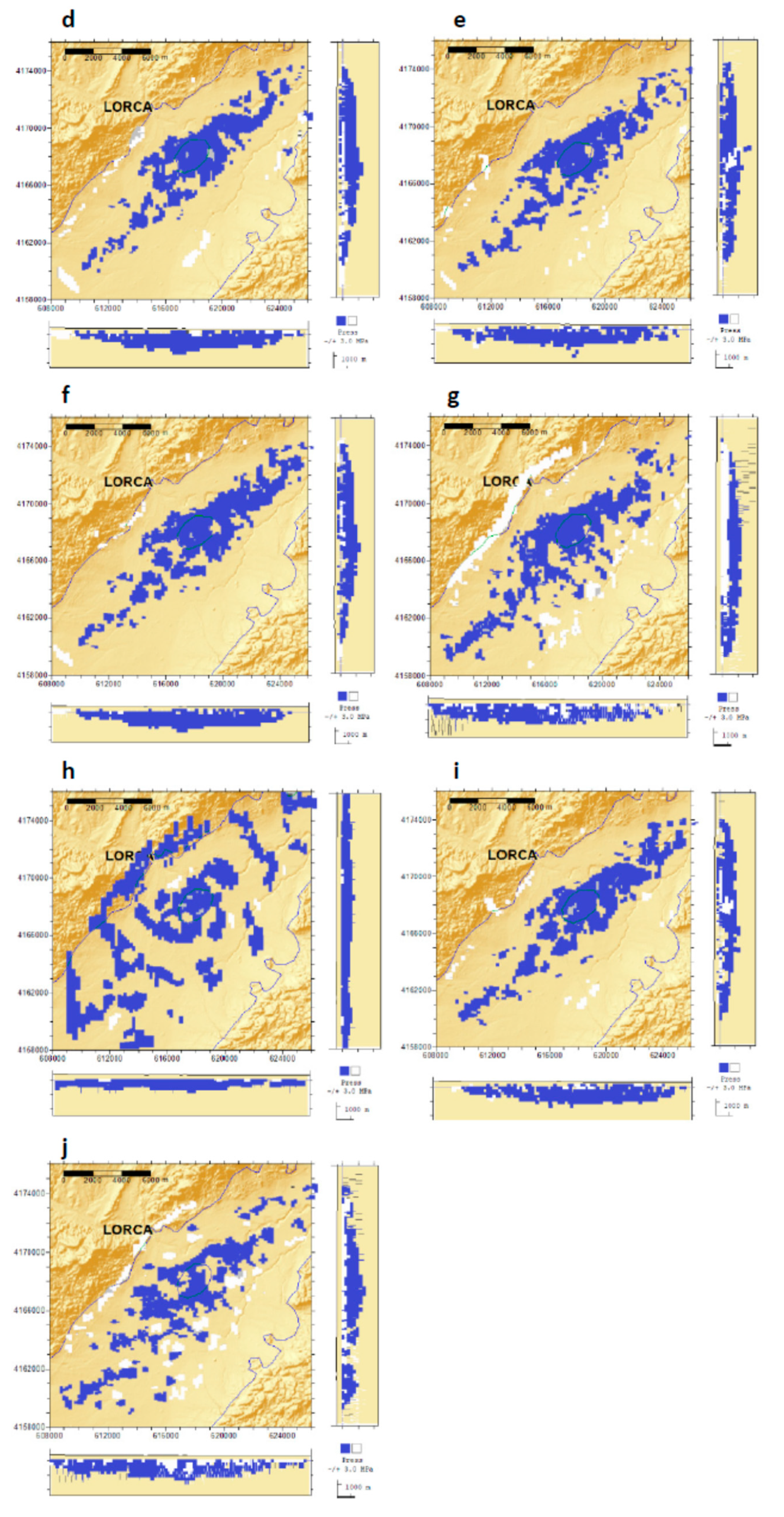
| DInSAR Data Set | Orbit | Coverage Period b | θ | Φ | N | M |
|---|---|---|---|---|---|---|
| ERS, track 129 | asc | 10/1/1993–17/9/2008 | 344.1 | 23.2 | 90 | 215 |
| ERS, track 036 | dsc | 8/6/1992–25/12/2008 | 194.1 | 23.2 | 84 | 164 |
| Envisat, track 129 | asc | 13/11/2002–16/12/2009 | 344.0 | 22.8 | 46 | 120 |
| Envisat, track 036 | dsc | 5/6/2003–21/10/2010 | 195.9 | 22.8 | 60 | 158 |
| R2, S3 | asc | 19/1/2009–2/8/2013 | 348.7 | 35.1 | 42 | 166 |
| R2, S3 | dsc | 27/12/2008–3/8/2013 | 190.4 | 35.1 | 53 | 290 |
| R2, F6 | asc | 29/12/2008–5/8/2013 | 351.0 | 48.3 | 50 | 158 |
| Time Period (Years) | X Location UTM (m) | Y Location UTM (m) | Depth (m bsl) | Pressure (MPa × 109/yr) | Volume (km3/yr) |
|---|---|---|---|---|---|
| (±50) | (±50) | (±60) | (±0.05) | (±0.7) | |
| 1993–1999 | 426573 | 4519313 | 1372 | −0.37 | 6.2 |
| 1999–2000 | 426419 | 4519781 | 1434 | +0.51 | 8.5 |
| 2000–2005 | 426469 | 4519501 | 1874 | −0.13 | 2.2 |
| 2005–2007 | 427388 | 4519326 | 2126 | +0.69 | 11.4 |
| 2007–2007 | 426184 | 4519238 | 1683 | −0.47 | 7.9 |
| 2007–2013 | 426669 | 4519315 | 1819 | +0.49 | 8.2 |
| CASE | Intensity MPa×Km3 | Misfit (cm) | Mean Model Intensity(MPa × Km3) | Pres. (MPa) | Vol. (Km3) | Displacement Components Considered | Nº of Data Used |
|---|---|---|---|---|---|---|---|
| A | −41 | 0.36 | −42.7±3.8 (9%) [−40±1.4 (4%)] | −3 | 14.2 [13.3] | 1D | 1505 |
| B | −39 | 0.31 | 1203 | ||||
| C | −48 | 0.19 | 1572 | ||||
| D | −32 | 0.30 | −33.9 ± 1.9 (6%) [−32.5 ± 1.1 (3%)] | −3 | 11.3 [10.8] | 2D | 1505 |
| E | −31 | 0.28 | 1203 | ||||
| F | −33 | 0.32 | 2708 | ||||
| G | −37 | 0.45 | 3144 | ||||
| H | −34 | 0.94 | 3D | 108 | |||
| I | −34 | 0.43 | 2D + 3D | 2816 | |||
| J | −36 | 0.63 | 3252 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camacho, A.G.; Fernández, J. Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data. Remote Sens. 2019, 11, 2042. https://doi.org/10.3390/rs11172042
Camacho AG, Fernández J. Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data. Remote Sensing. 2019; 11(17):2042. https://doi.org/10.3390/rs11172042
Chicago/Turabian StyleCamacho, Antonio G., and José Fernández. 2019. "Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data" Remote Sensing 11, no. 17: 2042. https://doi.org/10.3390/rs11172042
APA StyleCamacho, A. G., & Fernández, J. (2019). Modeling 3D Free-geometry Volumetric Sources Associated to Geological and Anthropogenic Hazards from Space and Terrestrial Geodetic Data. Remote Sensing, 11(17), 2042. https://doi.org/10.3390/rs11172042






