An Action Plan Towards Fiducial Reference Measurements for Satellite Altimetry
Abstract
1. Introduction
2. The FRM Problem at Issue
- We start by accepting that there is a “true” measure for the parameter calibrating the altimeter and its uncertainty and which both describe the satellite behavior.
- We recognize that there is no such a thing as an “absolute” measure of satellite performance given certain resources. There are certainly good, bad, or moderate measures for the calibrating parameter and its uncertainty but not perfect ones. A remedy for all the trouble and problems in satellite altimetry is not likely to be achieved in this FRM4ALT work.
- We find that there are many kinds of measures and procedures to accomplish this task. In measuring the different degree of information, we try to identify the sources of failure and the weakness of each contributing factor (errors) in the final altimeter performance, to gain a deeper understanding of their limitations for practical applications and given certain resources.
3. The Need behind the FRM Principle
4. Expected Products and Services with FRM
- Define a realistic strategy for long-term altimetry data records, derived by the existing Cal/Val practices.
- Provide a long-term data record of calibrated and quality-controlled observations and sensors to allow the creation of consistent, accurate, and stable monitoring signals for sea and water levels by altimetry.
- Support a rigorous treatment and a trustworthy assessment for uncertainties in altimetry calibration, as well as for observations of the altimeter themselves.
- Quantitatively understand and characterize, in time and space, the measurement system of the altimeter, its bias, offsets, and drifts.
- Determine altimeter’s corrections with certainty, but also to reveal and report their underlying uncertainty with confidence.
- Standardize practices for reporting uncertainties for sea level observation with altimetry by defining basic principles and requirements in calibration for a consistent description of uncertainty resources (constituents, properties, relationships between error contributing constituents, and so on) and to establish a common terminology, definitions and procedures.
- Provide a Cal/Val common ground to state that the applied calibration method and/or associated uncertainties are at first accepted, and secondly are also appropriate for a specific application in altimetry.
- Help assess whether a data set is compliant with predefined standards that quantify where these observations are suitable for a particular purpose. It is essential that their reference “yardstick” measurement is not ambiguous and allows the full capture of data quality.
- Make us capable of reproducing altimetry data products at any time in the future with certainty. If measurements and procedures for altimetry calibration are kept to an FRM standard, then we would be able to reproduce them and understand how measurements were made, which corrections were applied to the instruments, the processing and algorithms, and what changes occurred during observations.
- Support us in keeping a record of the altimeter data and error provenance and processing.
- Provide users with these FRM tools to better understand the assumptions and limitations of altimeter observations, and judge safely their applicability for the intended use.
- Provide a target for development of an altimetric system, and thus to steer the process of new mission design, system design, and algorithm development.
- Provide proper and good quality documentation and practical guidelines for those unfamiliar with the altimetry data, but also for the data providers to better manage data production, storage, updating, and reuse.
5. Technologies and Services to Reach FRM
- Decide and describe clearly the reference measurements for Cal/Val: Reference data and standards have to be established at the Cal/Val sites. These could encompass, for example, atomic clocks, diverse instrumentation, previous measurement data, manufacturer’s specifications, instrument characterization results, external sources, and handbooks. It is imperative to understand how reference measurements are established to ensure the traceability of results and propagation of uncertainties. The way these are to be implemented has to be clearly decided before any set up. Establish the way other instrument observations are traced and related to that reference standard (Traceability Principle).
- Follow FRM operational practice for Cal/Val: The performance and operational practice of the Cal/Val sites used for satellite altimetry have to be assessed in terms of long-term stability, homogeneity, consistency, and traceability to SI units. This is translated as all observations, measurements and uncertainties have to be related with reference measurements.
- Control the quality for data and sensors: Data quality and the estimation of uncertainty for the Cal/Val results in satellite altimetry have to be revamped following practical guidelines, procedures, protocols and best practices for fiducial reference measurements. These are also necessary steps for up-scaling a Cal/Val infrastructure. These practical steps could indicatively and briefly include:
- Evaluating the impact in the process of calibration prior to the installation of new instruments and changes to them.
- Exercising an overlap period for new and old observing systems, always.
- Maintaining seamless (no-gaps) functioning of station operations and of observations.
- Carefully planning the conversion of the present research calibration systems to long-term operations.
- Always carrying out instrument characterization before deployment. Preferring to exercise calibration and characterization of sensors by National Metrology Institutes or the like.
- Putting into use redundant and complimentary observing systems of different types, makes, and diverse measuring principles, and also processing and procedures implemented.
- Maintaining a “master” baseline instrument onsite where all other devices are compared against it on a regular basis (i.e., every 6 months or sooner). This “master” instrument should be calibrated at Metrology Labs. Departures from the ideal should be recorded and reported.
- Addressing the key operational issues: Continuity, homogeneity, overlap, redundancy, stability, sustainability, and also sensor calibration and characterization, data interpretation, uncertainty traceability, measurement, and Cal/Val product archiving.
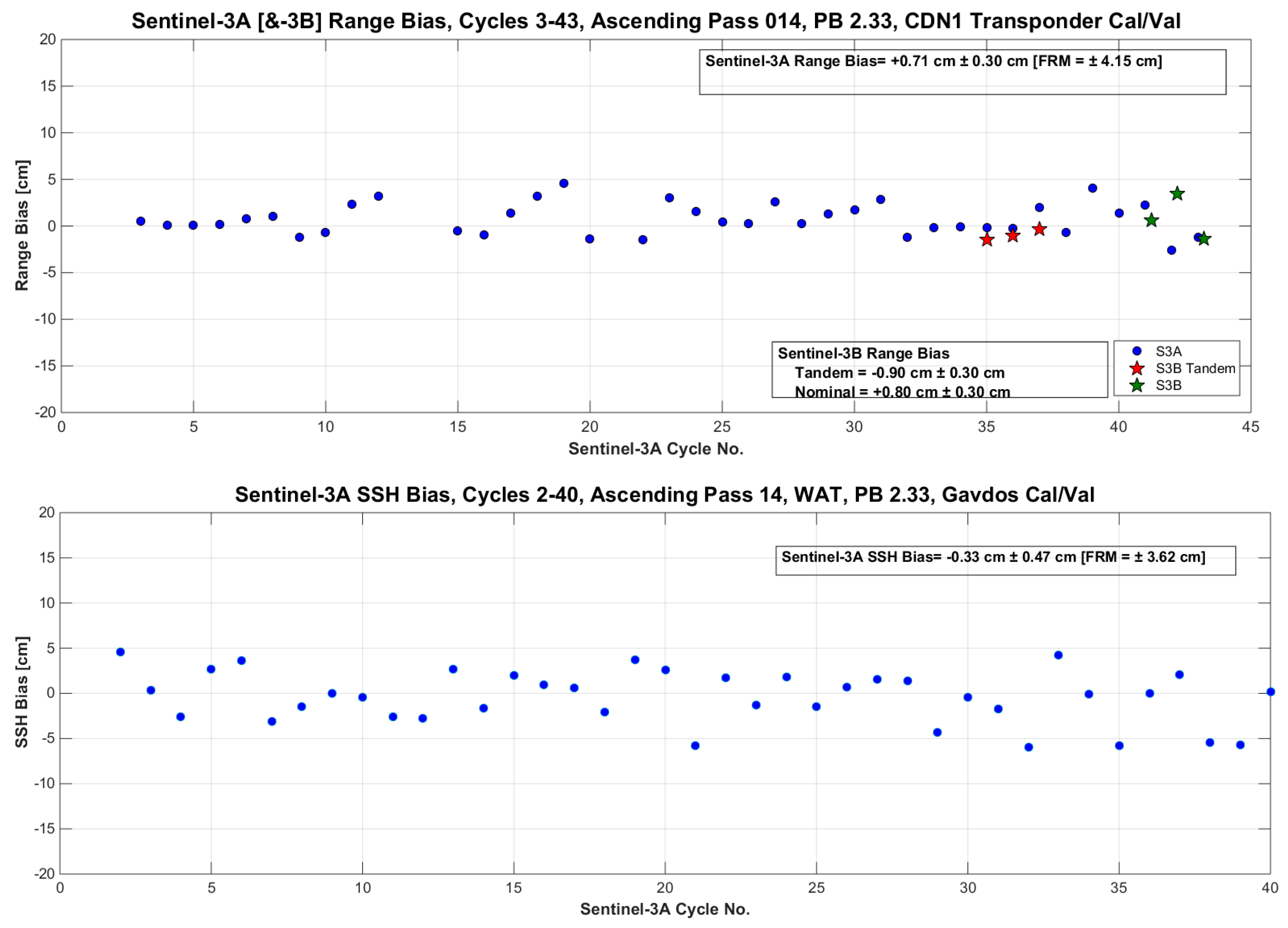
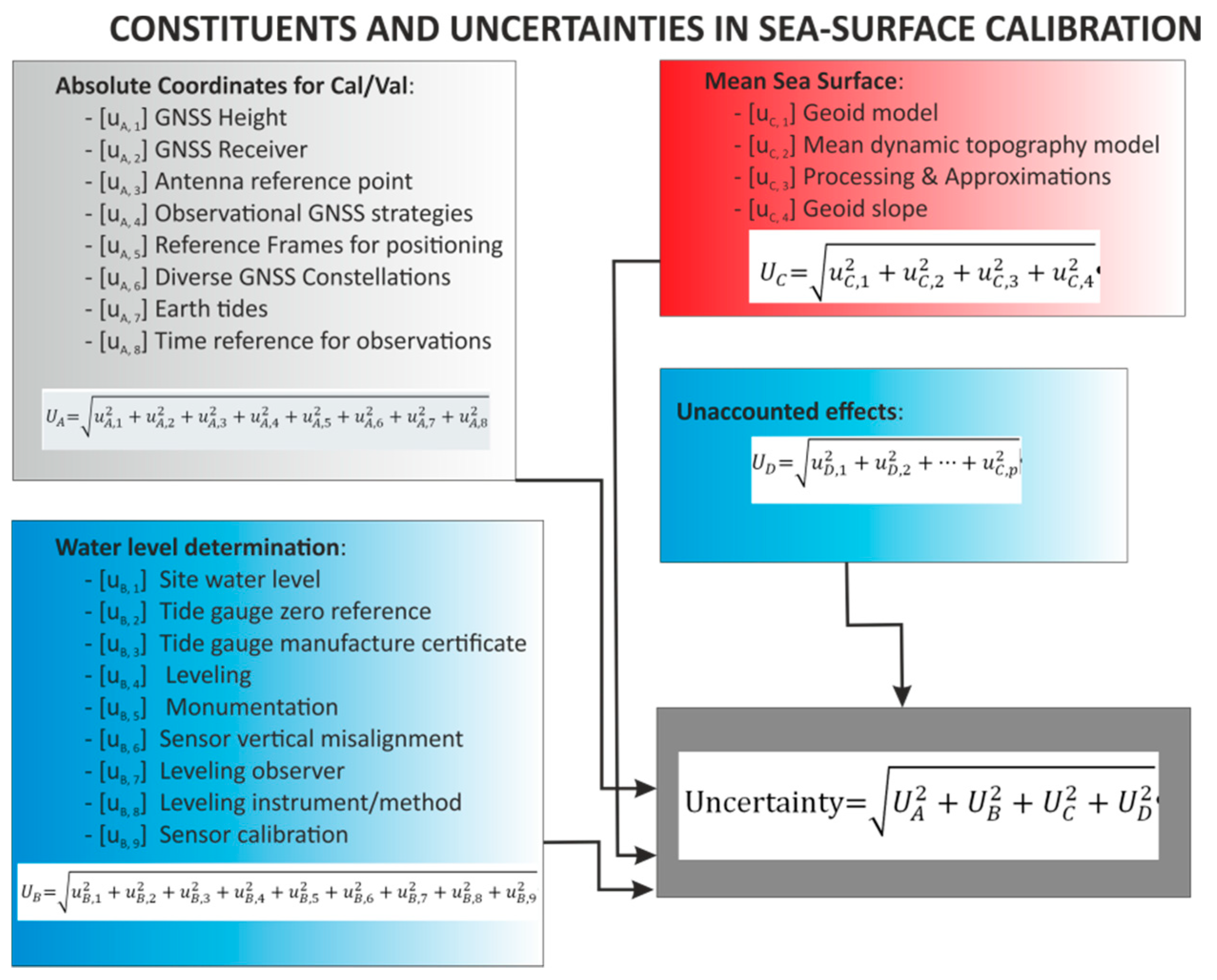
- Characterize uncertainty: Describe formally the scientific methodology for getting Cal/Val results and outline how uncertainties are computed in a traceable way. Without depending or being contingent upon other Cal/Val activities, existence, operation, etc., evaluate how instrumentation, models, reference surfaces, processes are implemented and how they affect final Cal/Val results. This step should be carried out with the aim of getting correct information about the reference measurements employed at the Cal/Val site.Uncertainties arise as a result of many aspects and can be generally grouped into the following categories: (a) Instrument measurement uncertainty, (b) retrieval/algorithm uncertainty, (c) application uncertainty and (d) unknown uncertainties. For each category, standard practice requires an uncertainty budget to be derived, including all aspects leading to a quantification of a root-sum-square (RSS) estimate of uncertainty. This is a challenging exercise but nevertheless, for climate and satellite calibration/validation activities, it is a requirement.Establishing an uncertainty budget for FRM is a fundamental step that drives a better understanding of the various components of FRM uncertainty: Quite often an instrument engineer will learn much about an instrument and its fitness for purpose by attempting the derivation of a full instrument uncertainty budget—potentially leading to innovation and improvement in design. But the real driver is to remember that, if reliable and well defined uncertainties can be provided with each FRM field equipment, then these measurements can uniquely provide an SI traceable measurement on a per-measurement basis when matched to satellite measurements—without the need for many observations to reduce the random error (for example, see Figure 8 for sea-surface uncertainty budget estimation).The estimation of uncertainty for each error constituent could be assessed either following the “Guide to the expression of uncertainty in measurement” [16], or applying the scale estimators presented in Table 1, or based on measurements documented with SI traceability (e.g., via round-robin intercalibration of instruments) using metrology standards.
- Exercise an external review of the calibration procedures and results. This external review should be made with multiple independent data sets arising from different and independent procedures and instrumentation and, in particular, not involved in the making of a particular instrument and product/model. For example, diverse satellite positioning systems such as GPS, Galileo, GLONASS, DORIS, Satellite Laser Ranging, various tide gauges of different measuring principles, various makes accompanied by an external and independent characterization, and so on. An external review should be applied regularly (e.g., annually to check seasonal characteristics of errors and uncertainties, for example). Such an external evaluation should also include a scrutinization of all the FRM documents applied in altimetry calibration. Independence is the essential element in this external review.
6. Review of Components in Cal/Val to Achieve FRM Quality
7. Components Influencing Cal/Val Results
7.1. Constituents in Sea-Surface Calibration
7.1.1. Absolute Coordinates of the Reference Cal/Val Site
- Site location: The site has to be chosen close to the sea, not far from the calibrating region, but also on stable ground. This ground motion has to be taken into account into the subsequent processing, but also be monitored not only with the operational GNSS receivers but tied to stable control benchmarks in the vicinity. It has to be also in proximity with water level instruments, accessible remotely, secure, etc. The site has to have good satellite visibility and be established on proper monumentation based on international standards and specifications [29]. A study on the stability of GNSS monumentation revealed that different types of monuments may affect the horizontal and vertical accuracy of the GNSS positioning by several mm/yr [30]. The stability of four different GNSS monuments were evaluated in [31] and movements in excess of 6 mm were detected. Temperature variations and solar radiation were the main sources of these movements. The authors state that simple shielding of the GNSS monument will significantly suppress the impact of these error sources.
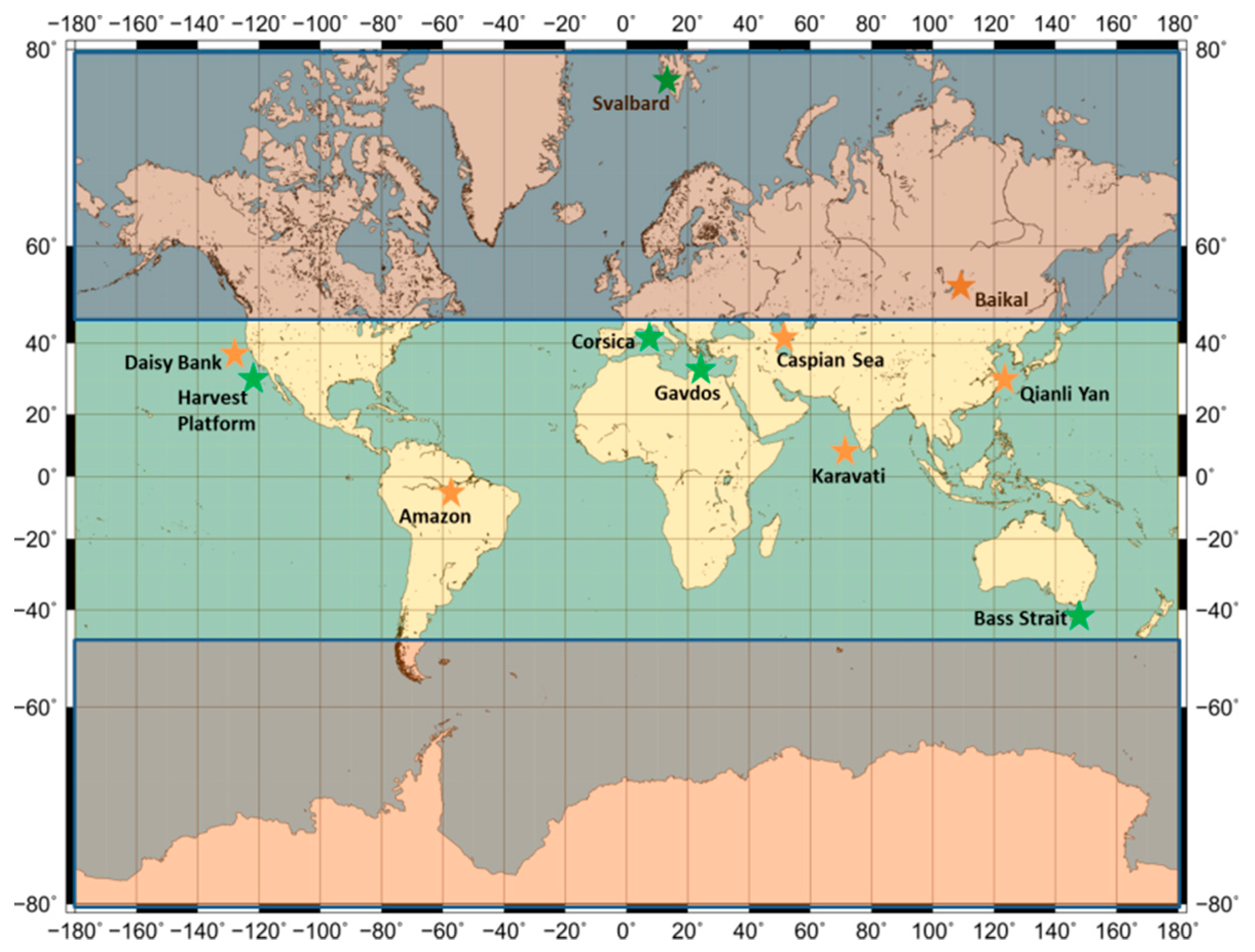
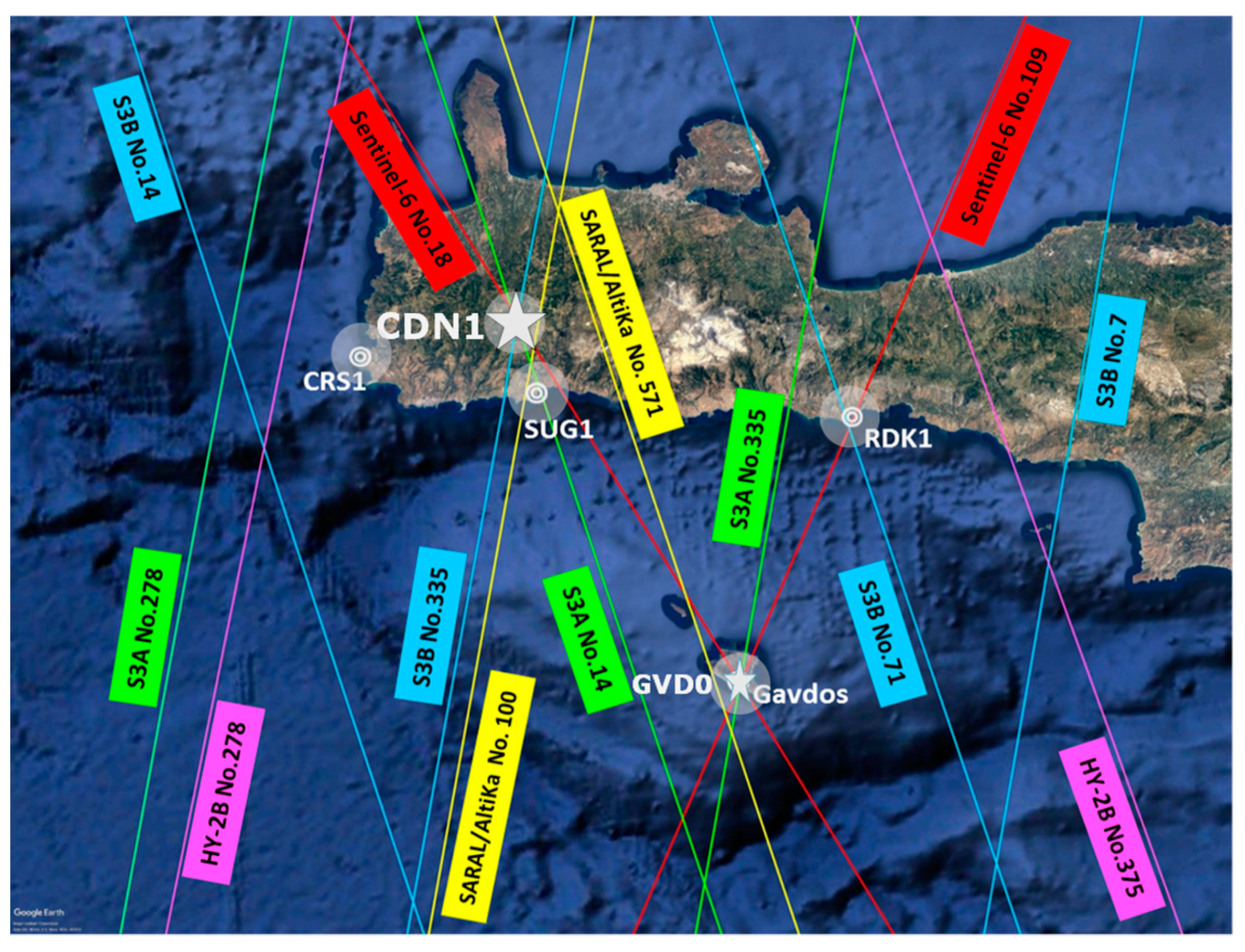
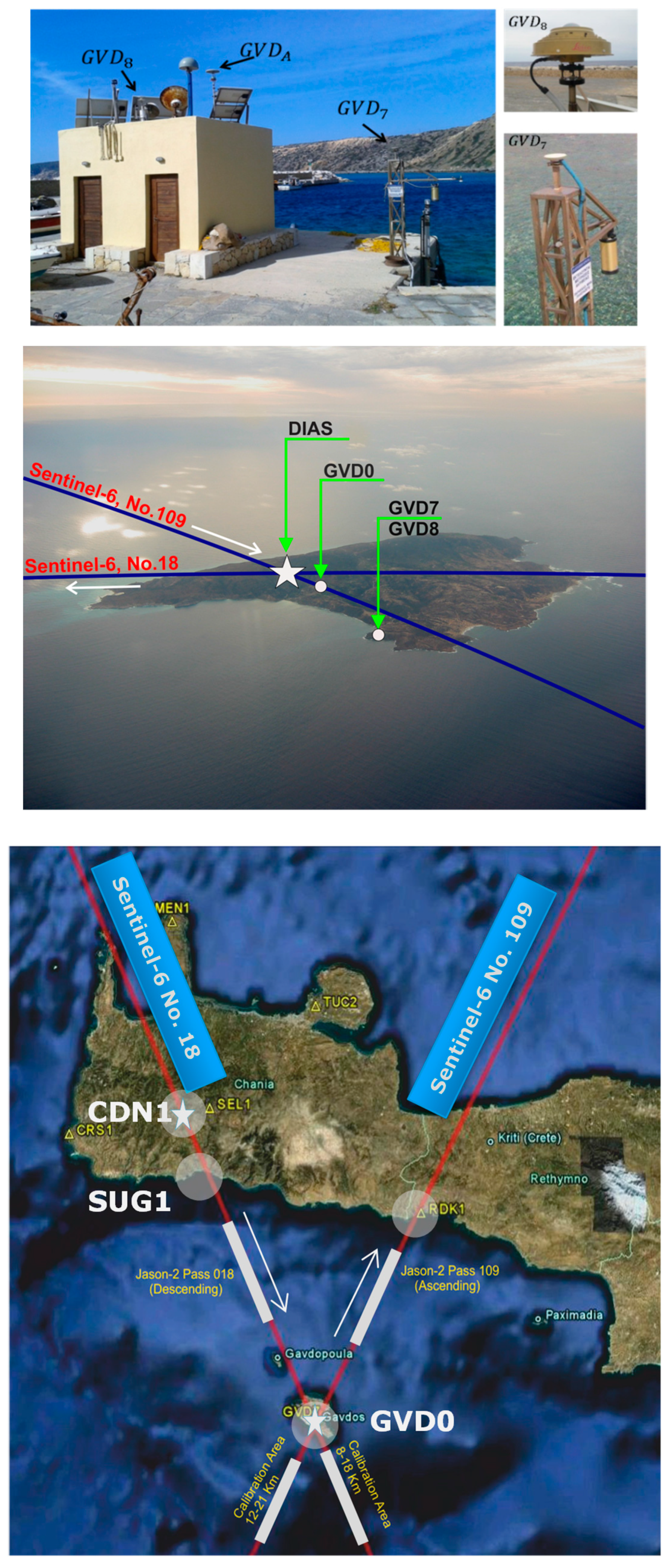
- Diverse GNSS constellations: As we would like to have an objective determination for the absolute coordinate values of the Cal/Val site, various GNSS constellations (GPS, Galileo, DORIS, GLONASS, BeiDou, etc.) have to be observed. That will help us to establish coordinate values using diverse positioning systems based on various measuring techniques, as well as reference systems to arrive at the same coordinates with confidence. For example, in Gavdos Cal/Val site, the existence of an alternative positioning system, that of a DORIS, along with the permanent GVD0 site of GPS (Figure 11), permitted us to verify coordinates but also determine atmospheric delays securely and reliably [32]. This procedure leads to data redundancy, consistency, and efficiency (As of 2014, the International DORIS Service has decided to decommission this DORIS site, named GAVB, in Gavdos.).
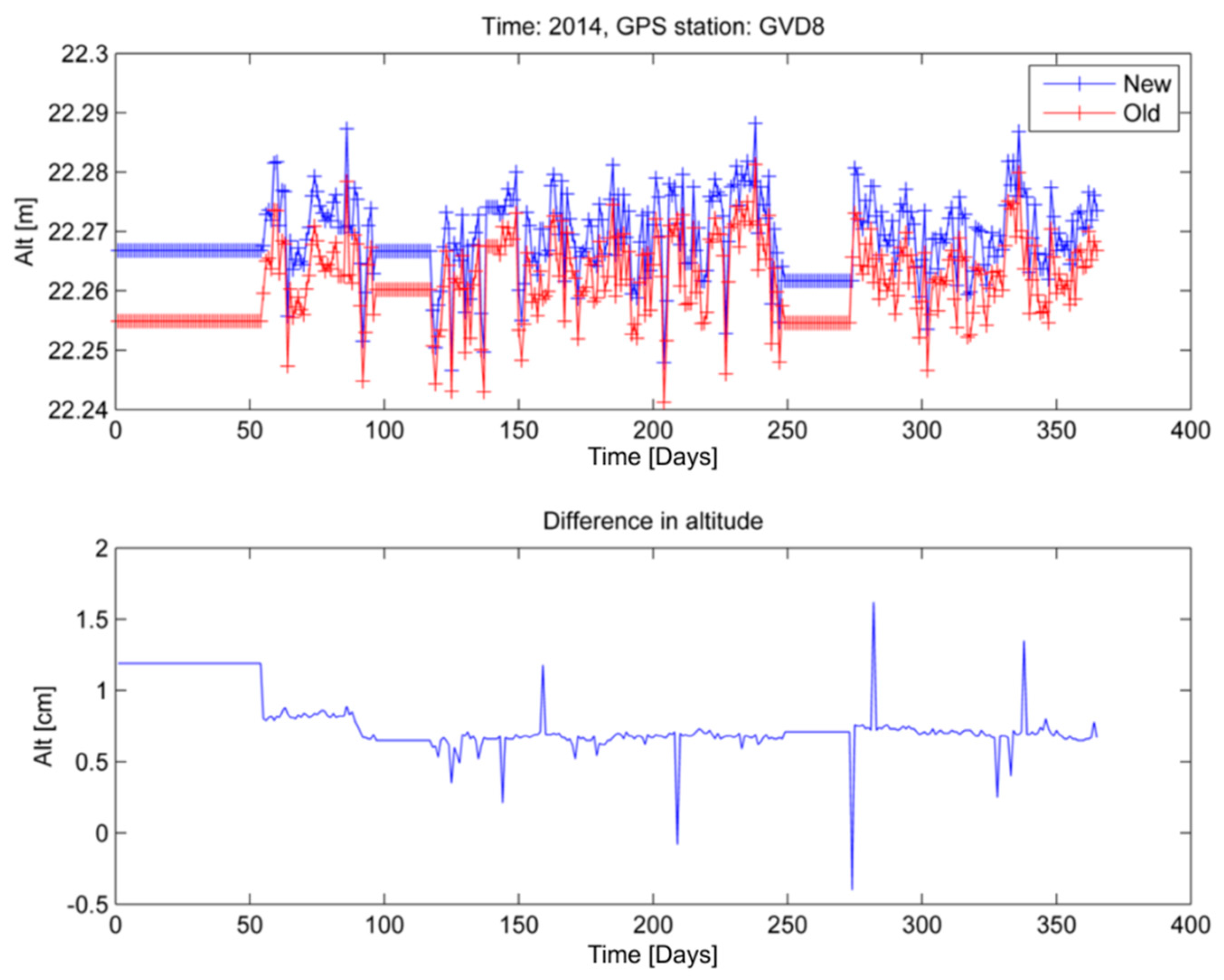
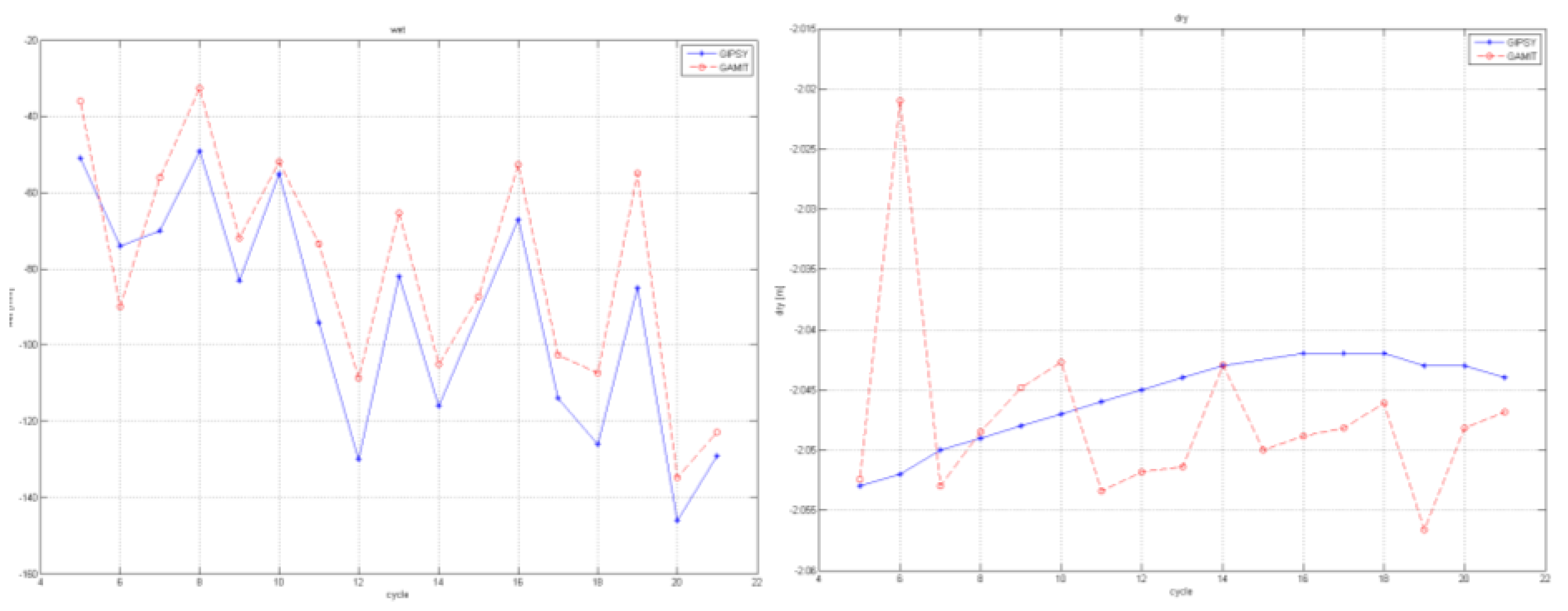
- GNSS hardware: Various GNSS receiver manufacturers apply different measuring principles for tracking satellite signals. For instance, Novatel receiver technology uses code-correlating techniques, while the Septentrio receiver implements the squaring signal technique (Z-tracking). Antennas constitute a major source of uncertainty, particularly in height, if not properly measured and characterized. Since April 2011, the igs08.atx antenna calibration model is used in the routine IGS data analysis. That is actually a mean of robot calibrations to correct for the offset and phase center variations of the GNSS receiver antennas. Although these values result in sufficient accuracy in typical GNSS positioning, individual antenna calibration has to be carried out in applications (such as satellite altimetry) where millimeter accuracy in the vertical component is the ultimate target. The impact of individual GNSS antenna calibration on geodetic positioning has been investigated by [33]. They reported that an antenna calibration (mean of individual calibrations of eight antennas of the same type and make) may differ up to 10 mm with respect to each individual calibration.Two main methods exist for GNSS antenna individual calibration: Robot calibration and anechoic chamber. The former depends on the institute that performs the calibration. For example, the absolute antenna calibration based on the robotic system at the Geo++ (Germany Lab) rotates the antenna around the nominated phase center of the antenna (fixed in space) using five rotation axes. On the other hand, the NOAA’s National Geodetic Survey (USA) robotic system is constrained to resolve about the fixed robot axis as there are only two rotation axes [34] (see Figure 12).The anechoic chamber calibration on a GNSS antenna involves monitoring its performance using a simulated signal while the antenna rotates for the determination of the azimuth-dependent antenna phase center. According to [35], the position offsets can reach 3 mm in the horizontal component and 7 mm in the vertical component when different individual calibration methods are employed. Moreover, [36] reported that the difference between Geo++ and UniBonn anechoic chamber individual calibration for the Leica AR25.R3 antenna and for the GPS L2 frequency is of the order of ±1 mm. They also conclude that in order to reach sub-mm accuracy in absolute GNSS positioning, the impact of the near-field multipath has to be resolved at the chamber, at the robot calibration laboratories but also in-situ.Field (or relative) antenna calibration involves the in-situ calibration of a GNSS antenna against a reference one at the same site, at a consistent height, and on flat terrain with no reflectors, other than the ground. This methodology tries to evaluate how well the individual GNSS antenna calibration values are valid in the field.Let us take an example for the impact of absolute GNSS antenna characterization on satellite altimetry Cal/Val. For several years in Gavdos, two GPS stations were providing heights for the same location by scientific software processing but disagreed by 1.7 cm. Individual calibration of the GNSS antenna installed at the GVD8 site (Leica AR25.R3, in Gavdos Island) was performed by Geo++ in Germany in 2016. It was discovered that an offset of 7 mm had to be applied to that AR25 antenna (Figure 13).Also, different types of GNSS geodetic antennas are implemented when tracking satellite signals. These could be choke ring with ground plane, with radome, software multipath reduction, etc. Preference is given to special multipath-limiting antennas (i.e., choke ring or multi-beam).
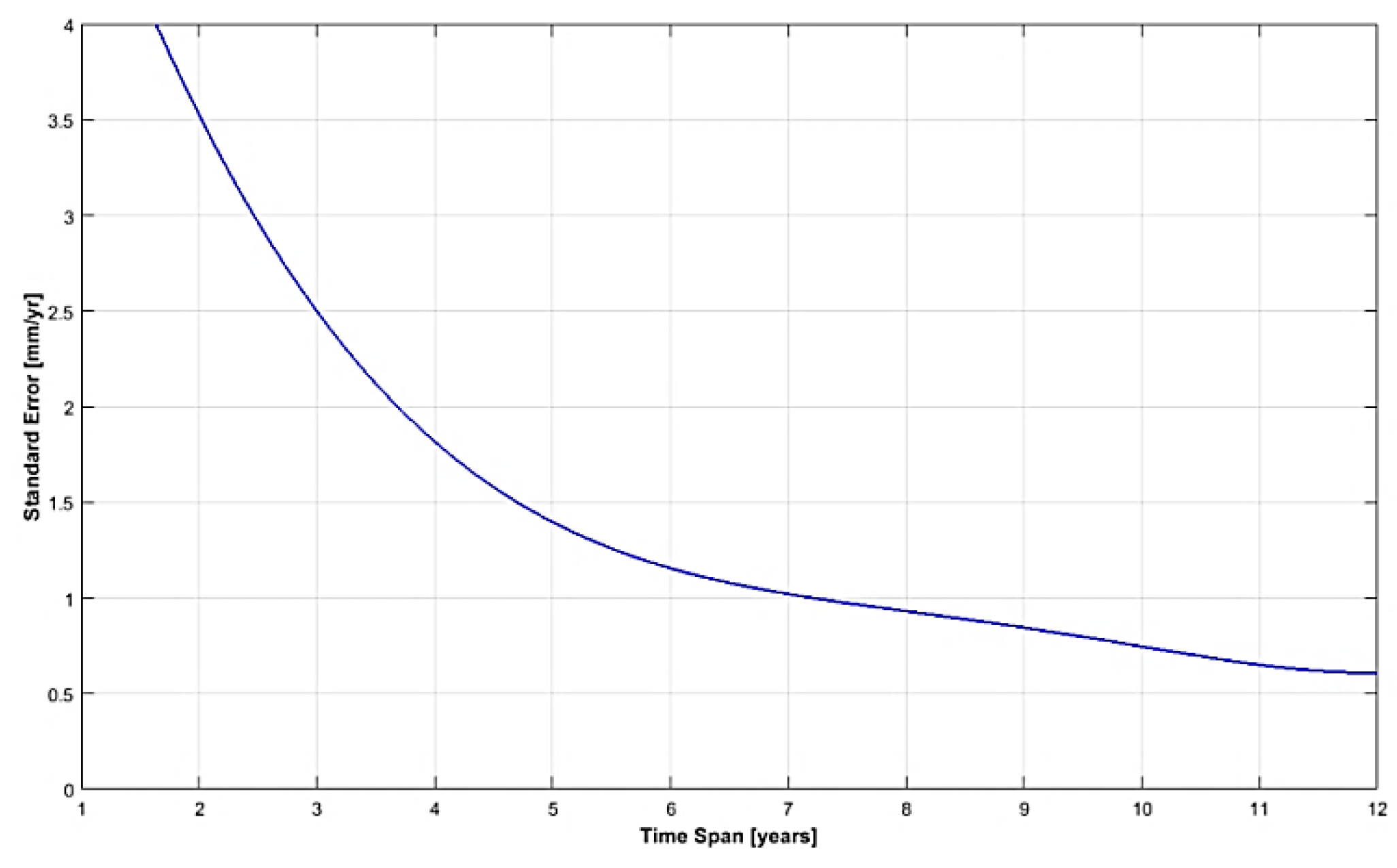
- Observation strategies for GNSS: As a general rule, sampling rates of 30 sec is implemented in the geodetic-type receivers, and daily observation files are produced for further processing. A cut off angle of zero degrees in satellite elevation is generally applied as well as no pseudo-range code smoothing for satellite tracking. A minimum observation length (i.e., 2–3 years) has to be decided to attain the goal of the FRM accuracy requirement.
- Reference frames for site positioning: Several reference coordinate systems are applied by various GNSS systems. For instance, GPS uses the WGS84 reference system, GLONASS applies the PZ-90, BeiDoU uses a Chinese system, though site coordinates are mainly tied to international terrestrial reference frames (ITRF) (Table 2). All these various reference systems have to be converted to that of the satellite altimeter system (primarily in the past the TOPEX/Poseidon or T/P ellipsoid) to support compatible calibration values in altimetry.According to [38], the estimated accuracy of the ITRF2014 origin is at the level of less than 3 mm (epoch 2010.0) and less than 0.2 mm/yr in time evolution. Accordingly, the scale and scale rate differences between the ITRF2008 and ITRF2014 are 1.37 (± 0.10) parts per billion (ppb) at epoch 2010.0 and 0.02 (± 0.02) ppb/yr.
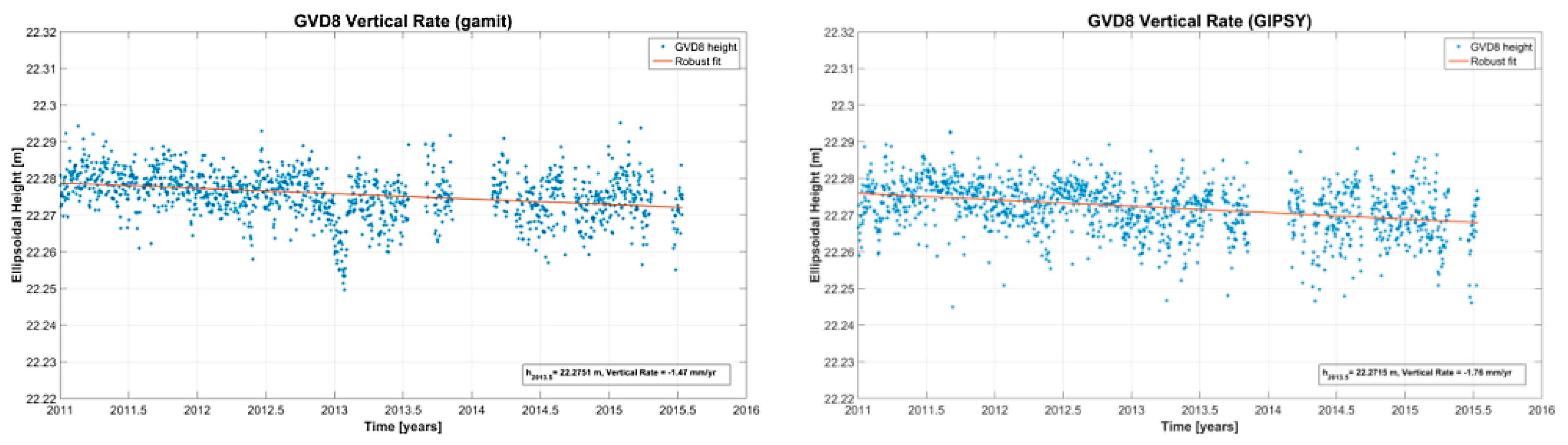
- Processing of GNSS Observations. Different software applies different processing techniques. For example, GAMIT (and or Bernese) software uses relative positioning based on double differences of GPS observations, and final site coordinates are established by tying the results to a set of about 300 global permanent GPS sites. On the contrary, GIPSY software applies the precise point positioning technique and final coordinates are with respect to satellite orbits. GIPSY is capable of processing not only GPS, but also GLONASS data and, more recently, BeiDou in its current release of Gipsy X (2016). A reduction of observations is also made by applying diverse models by GNSS processing software for earth tides, atmospheric loading, and atmospheric models for the ionosphere and troposphere, etc. To illustrate the impact of different processing on solutions, we present some height results produced by GAMIT and GIPSY (Figure 15).
- Earth tides: Computation of earth tides for the final determination of site coordinates is an essential constituent for achieving FRM status and should be examined in detail.
- Time reference for GNSS observations: All observations have to be recorded in and tied to a common reference system for the parameter “time”. For instance, GPS observations are commonly made using the GPS system time, while GLONASS uses UTC (Russia) time with leap seconds applied, and DORIS puts into use the international atomic time TAI.
7.1.2. Absolute Coordinates of the Reference Cal/Val Site
- Site location: The site has to be protected against waves, local sea level effects, but at the same time, be at a location to sense and feel the open sea conditions and dynamics where satellite calibration is taking place. The site has to be impervious to any human activities and close to the satellite ground pass. The site has to be continuously monitored for any vertical ground motion. It has to be not far from the calibrating region in the open sea where the satellite measurements are uncontaminated by land. As tide gauges commonly require frequent maintenance, the site has to be easily accessible by the respective personnel throughout the year. Such site should also allow installations of different tide gauge models, makes and types with diverse observations techniques (stilling well, dock for installing radar, unobstructed from boat berthing, power, communications, etc.).
- Conditions and Settings: Some tide gauges, such as acoustic ones, require protective and controlled measuring tubes to operate properly. Others may need a stilling well, connected to the sea, to measure water level. Nonetheless, a response delay in tide measurements may be present in measuring the water level in the stilling well, but also a subsequent issue on altimeter calibration results. All environmental conditions have to be continuously monitored as they influence altimetry observations. The setting up of certain tide gauges, for example the radar type, requires horizontal alignment of their measuring sensor but also to be established at an offset (eccentric) position in the harbor to be able to measure water level unobstructed (from any obstacles or structures). Any metallic support structures have to be monitored for any thermal expansion, particularly in regions of high temperature variations over seasons. Mains power lines, communication links, and certain water channels to the measuring location should be available on the site. Any systematic differences of water level between what is observed at harbor, where tide gauges are operating, and the satellite ground track has to be monitored periodically. Any local oceanographic conditions prevailing inside the harbor have to be known.
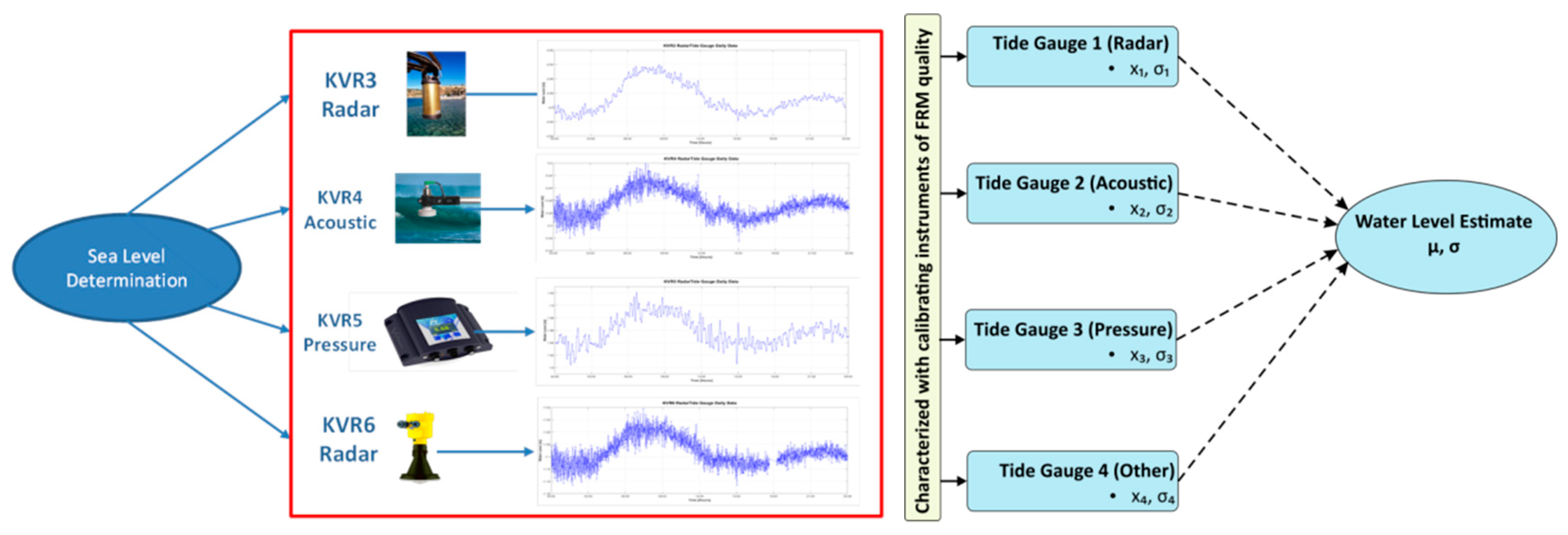
- Tide gauges: Tide gauge instrumentation constitutes a fundamental element in altimeter calibration. The water level has to be determined reliably and objectively and within FRM standards. Different types of instruments (e.g., acoustic, radar, pressure, floating) have to be set up on an FRM site to impartially determine the water level at the time of the satellite pass. They should also complement each other’s observations in case of data loss to insure continuity of service. All tide gauges should be accompanied by their site logs.To ensure that water level sensors (e.g., microwave radars, lasers, pressure sensors, float/stilling well sensors, acoustic) produce accurate observations, rigorous calibrations, characterizations and checks must be performed [39]. We summarize a few of those primary points here:
- Manufacturers of tide gauges (should) provide calibrations traceable to international standards as part of their standard product services. Fundamental standards such as length, temperature, and pressure will suffice when conducting calibration checks on most water level sensors.
- Real-time water level observations should have two features: Accurate time and accurate elevation relative to a known reference.
- For altimetry calibration, measurement changes or sensor drifts should be monitored in real time with quality checks and extensive statistical analysis, as it is difficult for post recovery of missing and/or faulty observations.
- Calibration activities must be tailored to match Cal/Val requirements, but also available resources. Calibration cost and effort increase dramatically as accuracy requirements increase.
- Calibration and characterization inspections should take place before instrument installation in a controlled environment, but also after its installation at the Cal/Val site. The time intervals between these calibration checks rely on the instrument measuring principle. Pressure tide gauges, for example, require maintenance and characterization every 6 months at most, while microwave radar sensors may not need a check after several years, although they do not work properly in large waves.
- It is strongly recommended that external calibration inspections of water level sensor measurements should be performed at least once a year at the Cal/Val site.
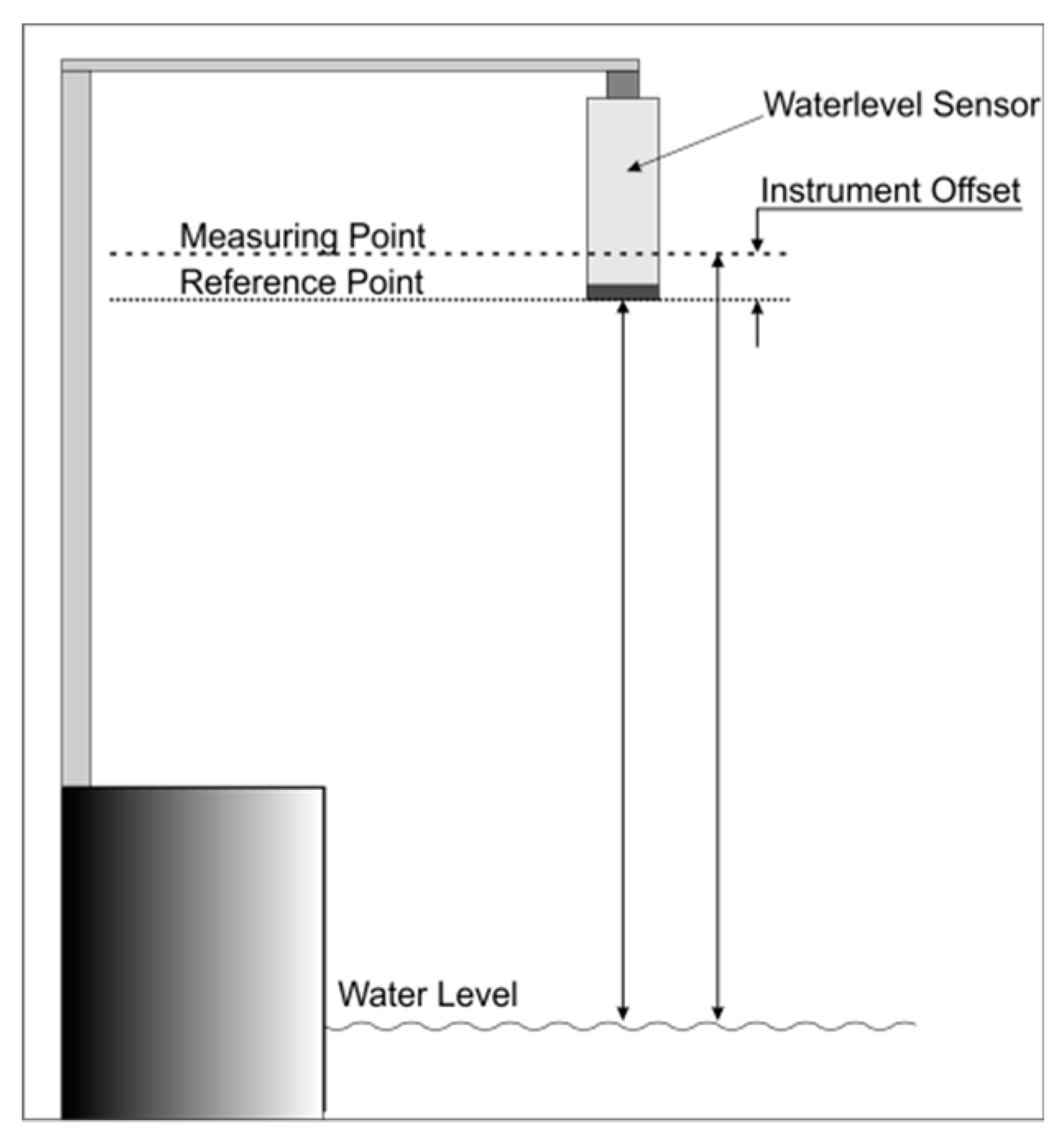
Local reference surfaces: Establishment of local surfaces for water surface is dependent upon the zero-reference point for measurement, as well as its offset, for each tide gauge and upon levelling between the tide gauge and the GNSS stations, operating nearby. The zero-reference measuring point of certain tide gauges has been observed to change over time although manufacturers may have supplied a constant value. This zero-point reference and its offset should be monitored periodically at the Cal/Val site (Figure 16).For an in-situ calibration in the field, it is advisable to consider water level readings from one tide gauge as a reference standard. This reference sensor might be operating and/or deployed periodically (for example annually) at the Cal/Val site.In the case of a continuous operating sensor, the time series of water levels is statistically investigated in depth. All tide gauges are compared and finally one is selected as reference sensor which fulfills certain criteria. The Van de Casteele test [40] could be then applied to all time series as a simple and efficient way to reveal errors which may have contaminated sea level data. However, this test provides only a qualitative indicator of the errors involved in sea level measurement but it cannot identify sources of error. Ways to quantify sources of error are given in [25,41]. These investigations recommend that field experiments and long-term comparisons among tide gauges is a necessity to reach, for example, the requirements of 1-cm accuracy prescribed by the Global Sea Level Observing System (GLOSS), let alone to attain the higher accuracy requirement of the Cal/Val for altimetry.The case of periodic deployment of a reference sensor involves the setting up of an additional tide gauge at the Cal/Val site and then to examine its data in contrast with the continuously operating sensors. It is recommended that the reference sensor should measure water level with better accuracy than all the rest. In any case, any differences and discrepancies observed may provide an upper limit of the uncertainty for the water level measurements at the Cal/Val site. Practical ways and custom-made structures are presented in [42] for laboratory and field characterization of radar tide gauges. - Measuring strategies and data storage: Various measuring strategies with different tide gauges result in a realistic value for water level. The way the final water level value is measured by each instrument has to be definitely known. For example, many tide gauges produce values by averaging a number of certain individual observations (such as 60 measurements) before they produce it.The sampling rate for the tide gauges is dependent upon tides prevailing in the area and the distance from the calibrating region in open sea. Sampling rates of tide gauges have to be set in such a way to meet the specific Cal/Val requirements. Data loggers have to keep records on a standard time reference (i.e., UTC time) and support the establishment of standard time tagging for all observations at the Cal/Val site. All tide gauge observations should be connected to a universal data logger which keeps timing through external sources such as GPS, external clocks, and the internet. Real-time quality control and assurance for observations as well as data transfer has to be secured at all times for the calibration process. Drifts in clocks and observations have been occasionally observed at tide gauges. Clock performance has to be monitored continuously.Eleven groups of quality control tests are suggested by the Integrated Ocean Observing System [39] to evaluate the quality of water level measurements. These involve (1) the Timing/Gap Test, (2) the Syntax Test, (3) the Location Test, (4) the Gross Range Test, (5) the Climatology Test, (6) the Spike Test, (7) the Rate of Change Test, (8) the Flat Line Test, (9) the Multivariate Test, (10) the Attenuated Signal Test, and (11) the Neighbor or Forecast test. Details on these tests can be found in [39].
7.1.3. Control Ties and Ground Monitoring at the Cal/Val Site
- Geodetic Control Ties: A number of control ties are commonly established and monumented around the Cal/Val site to secure the fundamental reference point used for calibration. Ties could be either benchmarks designating heights or geodetic control points with precise coordinates. Benchmarks are used for securing height differences in order to make the recovery of the fundamental control point possible as well as monitoring any ground vertical motion. Points have to be evenly and uniformly distributed around the Cal/Val site, but carefully set up on stable ground nearby. The minimum number should be no less than five (5) and their maximum distance no more than 100 m from the fundamental Cal/Val reference mark. The way these points are established and marked is usually described in national control survey documents and well established international standards as regards accuracy, designation, name, marking, security, etc.
- Ground deformation monitoring: The structure, the equipment and the facility should be monitored continuously for any land motion, particularly vertical, as this effect modifies altimeter calibration results. Based on the Cal/Val requirements, heights should be monitored every 6 months with uncertainties of ±1 mm. The same procedures would apply for connecting the GNSS height with the tide gauge instrumentation. Provision should be made to allow visibility of the leveling instruments between the fundamental control point of the Cal/Val and the respective benchmarks around the site.
7.1.4. Geoid and MDT Models around the Cal/Val Site
7.1.5. Geophysical Parameters
7.1.6. Atmospheric Delays in Altimeter Signals
7.1.7. Unaccounted Effects
7.2. Constituents in Transponder Calibration
7.2.1. Time Reference in Transponder Cal/Val
7.2.2. Transponder Data Processing
8. Conclusions
- (1)
- Choose “Reference Measurements” for Cal/Val: These could contain, for example,
- (a)
- The selection of a standard reference time and coordinate system for Cal/Val.
- (b)
- The institution of fundamental metrology standards and the tracing of all measurements and sources of uncertainties so trust is built in them.
- (c)
- The establishment of a standardized way on how instruments are to be characterized and calibrated before putting them into use in the field.
- (d)
- The establishment of the way ground-based sensor observations and uncertainties are traced and related to a reference standard (e.g., speed of light, atomic time).
- (2)
- Follow an operational practice that meets FRM standards: Access performance and operational practice in Cal/Val in terms of long-term stability, homogeneity, consistency, and traceability to SI units.
- (3)
- Control quality for data and sensors: Define error constituents, document all analytical procedures and practical steps to be followed for all FRM Cal/Val sites for describing and reporting uncertainty budgets for altimetry calibration. Describe regular maintenance standards, following agreed protocols and characterization procedures. Establish a procedure for consolidated approach to data formatting, archiving and distribution. Be prepared for the future of satellite altimetry Cal/Val, as new sites are to be ready to accommodate new measuring techniques.
- (4)
- Exercise an external review for procedures and results. This external review should be made with multiple independent data sets arising from different and independent procedures and instrumentation and specifically not involved in the making of a particular instrument and product/model. An external review should be applied regularly (e.g., annually to check seasonal characteristics of errors and uncertainties, for example). Such an external evaluation should also include a close and thorough inspection of all the FRM documents applied in altimetry calibration. Independence is the essential element in this external review. Examples of how uncertainties are calculated based on FRM for the sea-surface and the transponder calibration of satellite altimeters are given in Table 3 (see also [7]).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beckley, B.D.; Callahan, P.S.; Handcock, D.W., III; Mitchum, G.T.; Ray, R.D. On the “Cal-Mode” Correction to TOPEX Satellite Altimetry and Its Effect on the Global Mean Sea Level Time Series. J. Geophys. Res. Ocean 2017, 122, 8371–8384. [Google Scholar] [CrossRef]
- WCRP Global Sea Level Budget Group. Global sea-level budget 1993–present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar] [CrossRef]
- Donlon, C. Fiducial Reference Measurements for Altimetry (FRM4ALT). In Proceedings of the Presented at the International Review Workshop on Satellite Altimetry Cal/Val Activities & Applications, Chania, Greece, 23–26 April 2018; Available online: https://goo.gl/Yn23pQ (accessed on 12 June 2019).
- Mertikas, S.P.; Donlon, C.; Cullen, R.; Tripolitsiotis, A. Scientific and Operational Roadmap for Fiducial Reference Measurements in Satellite Altimetry Calibration & Validation. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Hollmann, R.; Merchant, C.J.; Saunders, R.; Downy, C.; Buchwitz, M.; Cazenave, A.; Chuvieco, E.; Defourny, P.; de Leeuw, G.; Forsberg, R.; et al. The ESA Climate Change Initiative: Satellite Data records for Essential Climate Variables. Bull. Am. Meteorol. Soc. 2013, 94, 1541–1552. [Google Scholar] [CrossRef]
- Loew, A.; Bell, W.; Bulgin, C.E.; Burdanowitz, J.; Callbet, X.; Donner, R.V.; Ghent, D.; Gruber, A.; Kaminski, T.; Kinzel, J.; et al. Validation practices for satellite-based Earth observation data across communities. Rev. Geophys. 2017, 55, 779–817. [Google Scholar] [CrossRef]
- Mertikas, S.; Donlon, C.; Féménias, P.; Mavrocordatos, C.; Galanakis, D.; Tripolitsiotis, A.; Frantzis, X.; Kokolakis, C.; Tziavos, I.N.; Vergos, G.; et al. Absolute Calibration of the European Sentinel-3A Surface Topography Mission over the Permanent Facility for Altimetry Calibration in west Crete, Greece. Remote Sens. 2018, 10, 1808. [Google Scholar] [CrossRef]
- Bureau International des Poids et Mesures. The International System of Units (SI); BIPM: Paris, France, 2019. [Google Scholar]
- Bonnefond, P.; Exertier, P.; Laurain, O.; Jan, G. Absolute calibration of Jason-1 and Jason-2 altimeters in Corsica during formation flight phase. Mar. Geod. 2010, 33, 80–90. [Google Scholar] [CrossRef]
- Haines, B.J.; Desai, S.; Born, G. The Harvest Experiment: Calibration of the climate data record from TOPEX/Poseidon, Jason-1 and the Ocean Surface Topography Mission. Mar. Geod. 2010, 33, 91–113. [Google Scholar] [CrossRef]
- Watson, C.; White, N.; Church, J.; Burgette, R.; Tregoning, P.; Coleman, R. Absolute calibration in Bass Strait, Australia: TOPEX, Jason-1 and OSTM/Jason-2. Mar. Geod. 2011, 34, 242–260. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Donlon, C.; Féménias, P.; Mavrocordatos, C.; Galanakis, D.; Tripolitsiotis, A.; Frantzis, X.; Tziavos, I.N.; Vergos, G.; Guinle, T. Fifteen Years of Cal/Val Service to Reference Altimetry Missions: Calibration of Satellite Altimetry at the Permanent Facilities in Gavdos and Crete, Greece. Remote Sens. 2018, 10, 1557. [Google Scholar] [CrossRef]
- AVISO. Ocean Surface Topography Science Team Meeting Final Report. 2018. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/OSTST/2018/OSTST_2018_Meeting_Report_Final.pdf (accessed on 14 August 2019).
- Huber, P.J.; Rochetti, E.M. Robust Statistics, 2nd ed.; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Hogg, R.V.; McKean, J.W.; Craig, A.T. Introduction to Mathematical Statistics, 8th ed.; Pearson Educated Limited: Harlow, UK, 2018. [Google Scholar]
- JCGM/WG. Evaluation of Measurement Data—An Introduction to the “Guide to the Expression of Uncertainty in Measurement” and Related Documents; Bureau International des Poids et Mesures: Paris, France, 2009. [Google Scholar]
- Mertikas, S.P.; Donlon, C.; Femenias, P.; Cullen, R.; Galanakis, D.; Frantzis, X.; Tripolitsiotis, A. Fiducial Reference Measurements for Satellite Altimetry Calibration: The Constituents. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Parkinson, C.L. Satellite Contributions to Climate Change Studies. In Proceedings of the American Philosophical Society, Philadelphia, PA, USA, 28 April 2017. [Google Scholar]
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-change–driven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef]
- Meltzner, A.J.; Switzer, A.D.; Horton, E.P.; Ashe, E.; Qiu, Q.; Hill, D.F.; Bradley, S.L.; Kopp, R.E.; Hill, E.M.; Majewski, J.M.; et al. Half-metre sea-level fluctuations on centennial timescales from mid-Holocene corals of Southeast Asia. Nat. Commun. 2017, 8, 14387. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.L.; Haines, B.J. The challenges in long-term altimetry calibration for addressing the problem of global sea level change. J. Adv. Space Res. 2012, 8, 1284–1300. [Google Scholar] [CrossRef]
- Müller, R. Calibration and verification of remote sensing instruments and observations. Remote Sens. 2014, 6, 5692–5695. [Google Scholar] [CrossRef]
- Mertikas, S.P. Description of accuracy using conventional and robust estimates of scale. Mar. Geod. 1994, 17, 251–269. [Google Scholar] [CrossRef]
- IOC/UNESCO. Manual on sea level measurement and interpretation, vol. IV: An Update to 2006. In IOC Manuals and Guides No.14, vol. IV; JCOMM Technical Report No.31, WMO/TD. No. 1339; UNESCO: Paris, France, 2006. [Google Scholar]
- Miquez, B.; Testut, L.; Wöppelmann, G. Performance of modern tide gauges: Towards the mm-level accuracy. Adv. Span. Phys. Oceanogr. 2012, 76, 221–228. [Google Scholar]
- WMO. Guide to Meteorological Instruments and Methods of Observation; World Meteorological Organization: Geneva, Switzerland, 2008. [Google Scholar]
- UNAVCO Knowledge Base. 23 November 2015. Available online: https://goo.gl/RJ4OHZ (accessed on 14 March 2019).
- NOAA. Guidelines for New and Existing Continuously Operating Reference Stations (CORS); National Geodetic Survey, National Ocean Survey, NOAA: Silver Spring, MD, USA, 2013.
- IGS. Monumentation Recommendations. International GNSS Service. 25 May 2017. Available online: http://kb.igs.org/hc/en-us/articles/202094816-Monumentation-Recommendations (accessed on 13 June 2019).
- Blume, F.; Berglund, H.; Feaux, K.; Austin, K.; Dittman, T.; Walls, C.; Mattioli, G. Stability of GNSS monumentation: Analysis of co-located monuments in the Plate Boundary Observatory. In Proceedings of the America Geophysical Union, Fall Meeting, San Francisco, CA, USA, 9–13 December 2013. [Google Scholar]
- Haas, R.; Bergstrand, S.; Lehner, W. Evaluation of GNSS monument stability. In Reference Frames for Applications in Geosciences, International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Willis, P.; Mertikas, S.; Argus, D.F.; Bock, O. DORIS and GPS monitoring of the Gavdos calibration site in Crete. Adv. Space Res. 2013, 51, 1438–1447. [Google Scholar] [CrossRef]
- Baire, Q.; Pottiaux, E.; Bruyninx, C.; Defraigne, P.; Aerts, W.; Legrand, J.; Bergeot, N.; Chevalier, J.M. Impact of individual GNSS Antenna Calibration used in the EPN on positioning. In Proceedings of the EUREF Symposium, Paris, France, 6–8 June 2012. [Google Scholar]
- Riddell, A.; Moore, M.; Hu, G. Geoscience Australia’s GNSS Antenna Calibration Facility: Initial Results. In Proceedings of the IGNSS Symposium, Miami, Australia, 14–16 July 2015. [Google Scholar]
- Baire, Q.; Bruyninx, C.; Legrand, J.; Pottiaux, E.; Aerts, W.; Defraigne, P.; Bergeot, N.; Chavalier, J.M. Influence of difference GPS receiver antenna calibration models on geodetic positioning. GPS Solut. 2014, 18, 529–539. [Google Scholar] [CrossRef]
- Aerts, W.; Baire, Q.; Bruyninx, C.; Legrand, J. On the Error Sources in Absolute Individual Antenna Calibrations. In Proceedings of the EGU General Assembly, Vienna, Austria, 9 April 2013. [Google Scholar]
- Snay, R.; Cline, M.; Dillinger, W.; Foote, R.; Hilla, S.; Kass, W.; Ray, J.; Rohde, J.; Sella, G.; Soler, T. Using global positioning system-derived crustal velocities to estimate rates of absolute sea level change from North American tide gauge records. J. Geophys. Res. 2007, 112, B04409. [Google Scholar] [CrossRef]
- Altamini, Z.; Rebischung, P.; Metivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Integrated Ocean Observing System. Manual for Real-Time Quality Control of Water Level Data; IOOS: Silver Spring, MD, USA, 2016.
- Miquez, B.M.; Testut, L.; Woppelmann, G. The Van de Casteele test Revisited: An efficient approach to tide gauge error characterization. J. Atm. Ocean. Technol. 2008, 25, 1238–1244. [Google Scholar] [CrossRef]
- Perez, B.; Payo, A.; Lopez, D.; Woodworth, P.L.; Alvarez Fanjul, E. Overlapping sea level time series measured using different technologies: An example from the REDMAR Spanish network. Nat. Hazards Earth Syst. Sci. 2014, 14, 589–610. [Google Scholar] [CrossRef]
- IOC. Manual on Sea Level, Measurement and Interpretation, Radar Gauges, Volume V; Woodworth, P., Aarup, T., Andre, G., Donato, V., Enet, S., Edwing, R., Heitsenrether, R., Farre, R., Fierro, J., Gaete, J., et al., Eds.; UNESCO JCOMM Technical Report No.89; UNESCO: Paris, France, 2016. [Google Scholar]
- Themens, D.R.; Jayachandran, P.T.; Langley, R.B.; Macdougall, J.W.; Nicolls, M.J. Determining receiver biases in GPS-derived total electron content in the aurora oval and polar cap region using ionosonde measurements. GPS Solut. 2013, 17, 357–369. [Google Scholar] [CrossRef]
- Münch, S.W. Atmospheric Water Vapour Sensing by Means of Differential Absorption Spectrometry Using Solar and Lunar Radiation. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2014. [Google Scholar]
- Matsakis, D.; Levine, J.; Lombardi, M. Metrological and legal traceability of time signals. In Proceedings of the 49th Annual PTTI Meeting, Reston, VA, USA, 29 January–1 February 2018; pp. 59–71. [Google Scholar]







| Scale Estimators | Statistical Definition | Remarks |
|---|---|---|
| Sample Standard Deviation | = | = sample size, observation value, sample average, |
| Trimmed Standard Deviation | = Trimming proportion, ith ordered value, = location estimate, , | |
| Mean Absolute Deviation | ||
| Median Absolute Deviation | = 0.6745 = factor for normality | |
| Fourth spread or Pseudo-sigma | are the sample 75th and 25th quantiles, are the standard Gaussian quantiles | |
| Gaussian Skip Scale | k= 2, = expected ith ordered Gaussian variables, = Biweight estimate of location, = weighting function, = Normalized deviations, c = tuning constant, S = estimate of scale (i.e., MAD) | |
| Huber’s M-estimator | , , , . | ) = first derivative of function, = scale estimate for the mth iteration, = Location estimate for the mth iteration, |
| Bi-weight A-estimators of Scale (Asymptotic Estimators) | = Median, | |
| Wave A-estimators of Scale | = Median Absolute Deviation, = Tuning constant (=2.1) | |
| Modified Wave A-estimators of Scale | = Tuning constant (=2.1) | |
| Gini’s Scale Estimator | Average of absolute differences for each pair of observations. |
| Altimeter | On-board Positioning System | Terrestrial Reference | Reference Ellipsoid |
|---|---|---|---|
| Jason series | GPS DORIS | WGS84 ITRF | T/P Ellipsoid |
| Sentinel-3 | GPS DORIS | WGS84 ITRF | WGS84 |
| CryoSat-2 | GPS DORIS | WGS84 ITRF | WGS84 |
| ICESat-2 | GPS | WGS84 | WGS84 |
| SARAL/AltiKa | DORIS | ITRF | T/P Ellipsoid |
| HY-2A | GPS DORIS | WGS84 ITRF | T/P Ellipsoid |
| Cal/Val Constituent (Sea Surface) | Uncertainty Estimate | Standard Uncertainty (Confidence 68%) | Cal/Val Constituent (Transponder) | Uncertainty Estimate | Standard Uncertainty (Confidence 68%) |
|---|---|---|---|---|---|
| GNSS Height | 0.11 mm | ± 0.11 mm | Measured Range | 3.00 mm | ± 1.73 mm |
| GNSS Receiver | 6.00 mm | ± 3.46 mm | Transponder Internal Delay | 30.00 mm | ± 15.00 mm |
| GNSS Antenna Reference Point | 2.00 mm | ± 2.00 mm | Dry Tropospheric Delay | 2.00 mm | ± 1.15 mm |
| Water Level | 1.30 mm | ± 1.30 mm | Wet Tropospheric Delay | 14 mm | ± 8.08 mm |
| Tide-Gauge Zero Reference | 0.15 mm | ± 0.15 mm | Ionospheric Delay | 4.00 mm | ± 2.31 mm |
| Tide-Gauge Vertical Alignment | 2.40 mm | ± 1.39 mm | Geophysical Corrections | 20.00 mm | ± 11.55 mm |
| Tide-Gauge Sensor Certificate | 5.50 mm | ± 5.50 mm | Satellite Orbit Height | 50.00 mm | ± 28.87 mm |
| Leveling | 0.11 mm | ± 0.11 mm | Pseudo-Doppler Correction | 2.00 mm | ± 2.00 mm |
| Monumentation | 1.10 mm | ± 0.64 mm | GNSS Instrument | 6.00 mm | ± 3.46 mm |
| Vertical Misalignment | 1.00 mm | ± 0.60 mm | GNSS Antenna Reference Point | 2.00 mm | ± 2.00 mm |
| Leveling Observer | 1.00 mm | ± 0.60 mm | GNSS Repeatability | 0.14 mm | ± 0.14 mm |
| Leveling Instrument/Method | 1.00 mm | ± 0.60 mm | Transponder Leveling | 0.16 mm | ± 0.16 mm |
| Tide Pole Reading During Calibration | 1.00 mm | ± 0.60 mm | Leveling Instrument/Method | 1.00 mm | ± 1.00 mm |
| Mean Sea Surface (Mean Dynamic Topography and Geoid) | 33.0 mm | ± 33.00 mm | Processing and Approximations | 30.00 mm | ± 17.32 mm |
| Processing and Approximations | 0.5 mm | ± 0.29 mm | Orbit Interpolations | 0.30 mm | ± 0.17 mm |
| Geoid Slope | 10.0 mm | ± 5.77 mm | Unaccounted Effects | 20.00 mm | ± 11.55 mm |
| Unaccounted Effects | 20.0 mm | ± 11.55 mm | |||
| Root-Sum-Squared Uncertainty | ± 36.16 mm | Root-Sum-Squared Uncertainty | ± 41.49 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mertikas, S.P.; Donlon, C.; Vuilleumier, P.; Cullen, R.; Féménias, P.; Tripolitsiotis, A. An Action Plan Towards Fiducial Reference Measurements for Satellite Altimetry. Remote Sens. 2019, 11, 1993. https://doi.org/10.3390/rs11171993
Mertikas SP, Donlon C, Vuilleumier P, Cullen R, Féménias P, Tripolitsiotis A. An Action Plan Towards Fiducial Reference Measurements for Satellite Altimetry. Remote Sensing. 2019; 11(17):1993. https://doi.org/10.3390/rs11171993
Chicago/Turabian StyleMertikas, Stelios P., Craig Donlon, Pierrik Vuilleumier, Robert Cullen, Pierre Féménias, and Achilles Tripolitsiotis. 2019. "An Action Plan Towards Fiducial Reference Measurements for Satellite Altimetry" Remote Sensing 11, no. 17: 1993. https://doi.org/10.3390/rs11171993
APA StyleMertikas, S. P., Donlon, C., Vuilleumier, P., Cullen, R., Féménias, P., & Tripolitsiotis, A. (2019). An Action Plan Towards Fiducial Reference Measurements for Satellite Altimetry. Remote Sensing, 11(17), 1993. https://doi.org/10.3390/rs11171993






