CLARREO Pathfinder/VIIRS Intercalibration: Quantifying the Polarization Effects on Reflectance and the Intercalibration Uncertainty
Abstract
1. Introduction
CLARREO Pathfinder and VIIRS Missions
2. Materials and Methods
2.1. Intercalibration Procedure
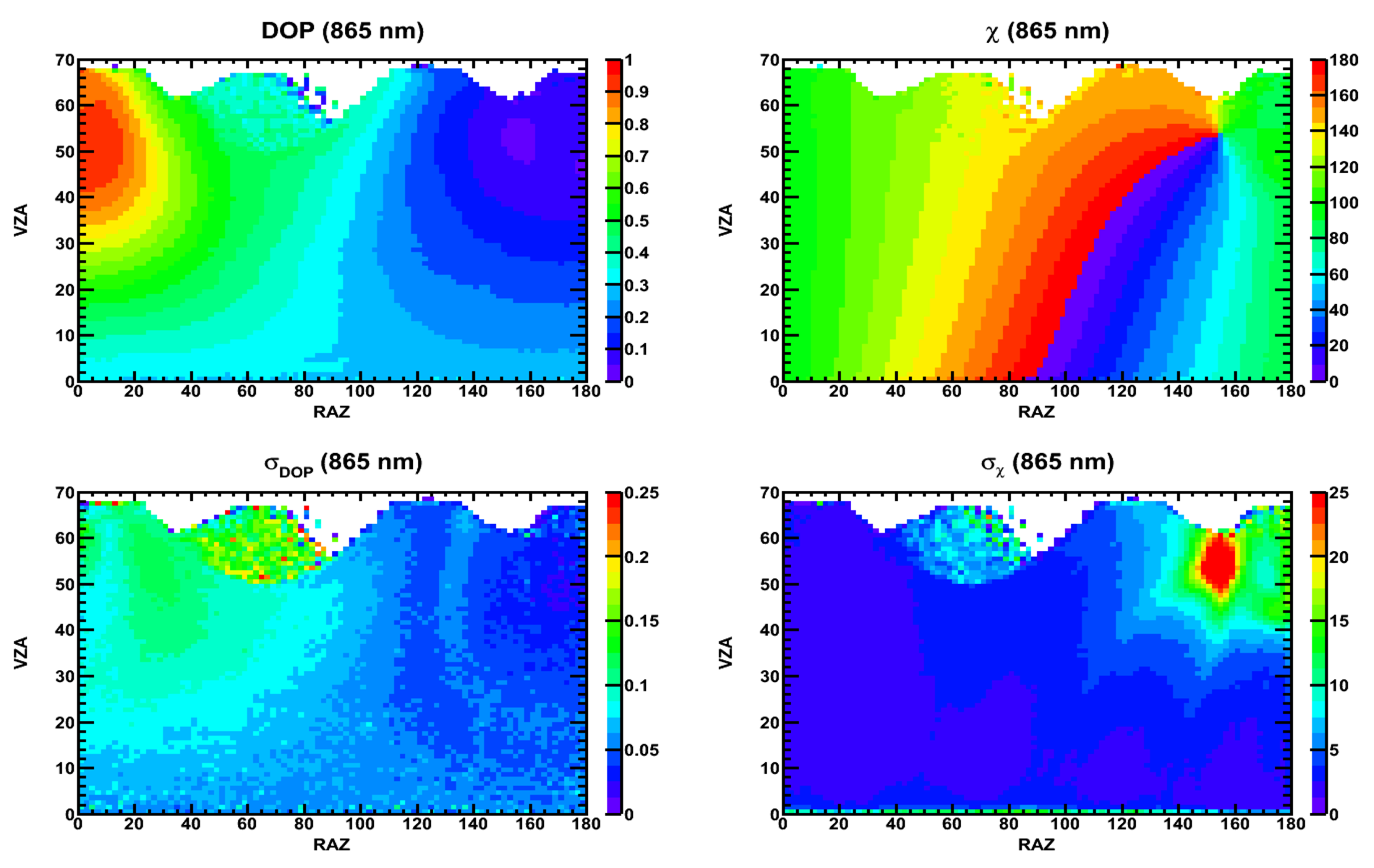
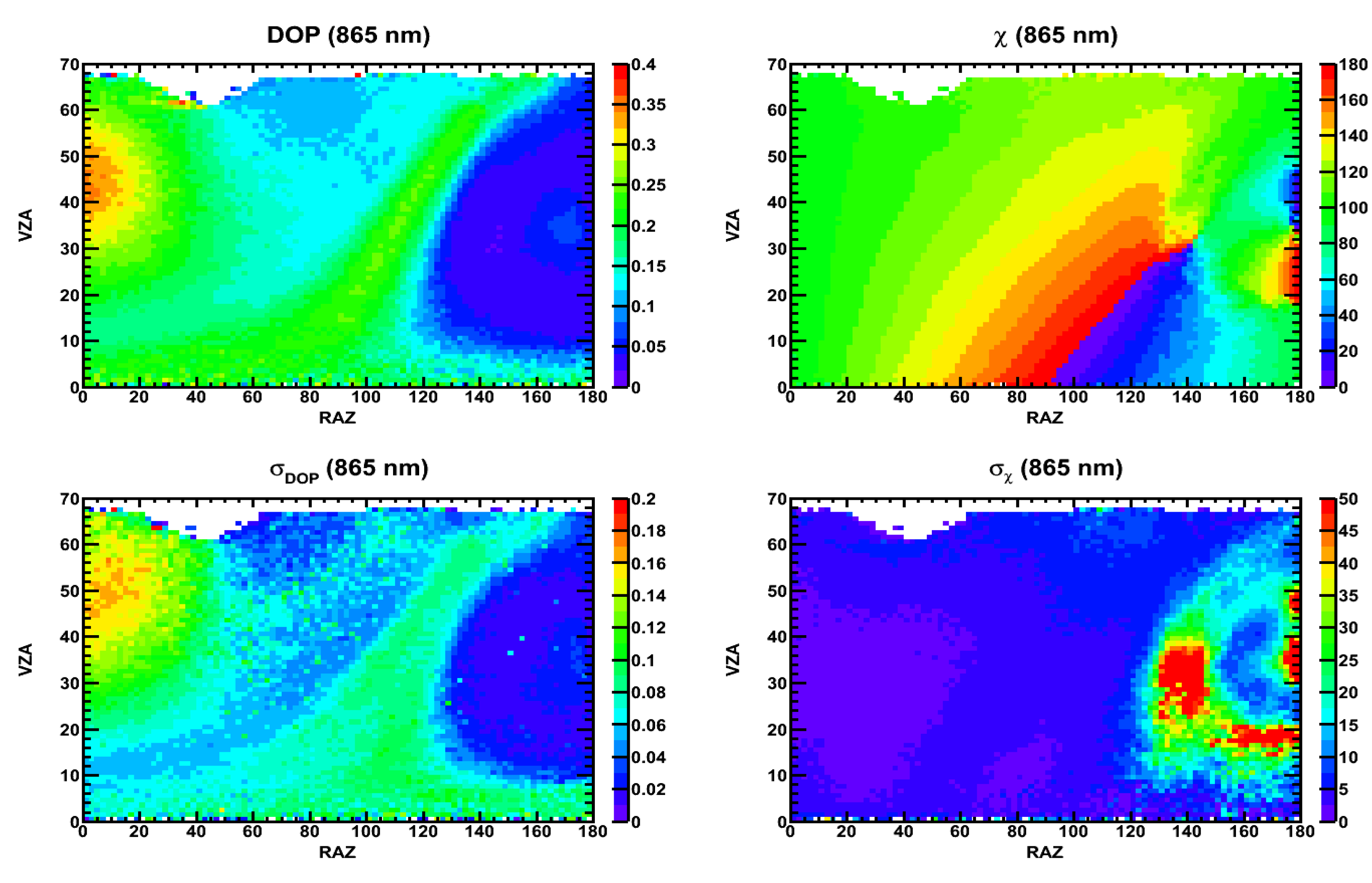
2.2. Polarization and Polarization Distribution Models
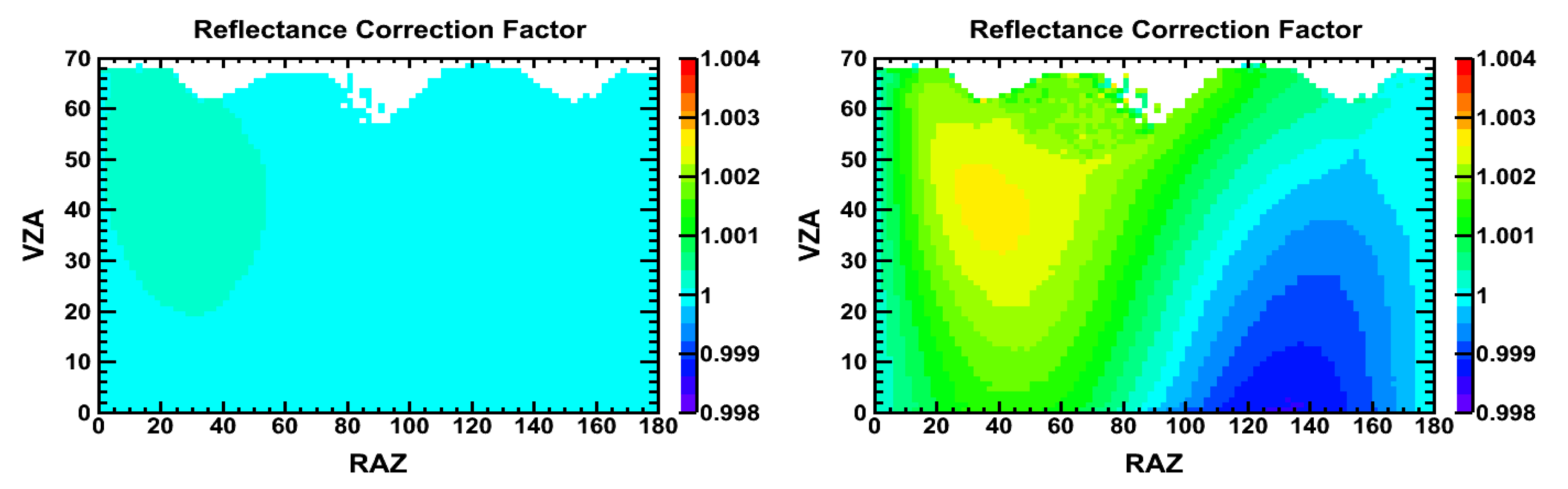
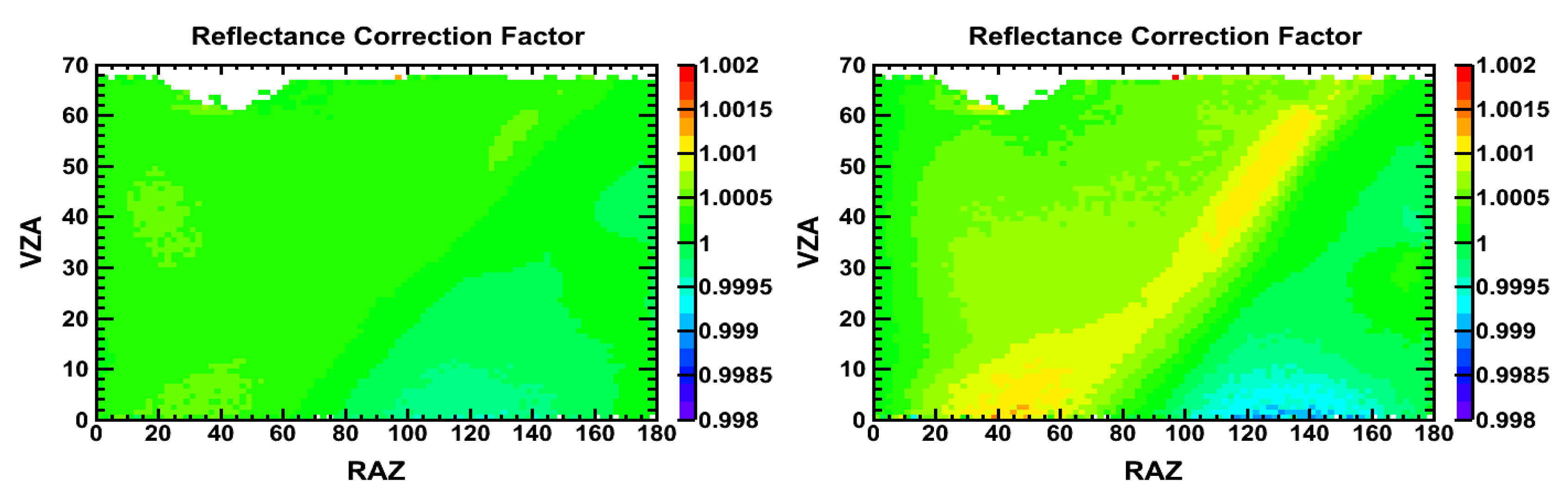
2.3. Polarization Correction and Uncertainty for a Single-Imager Reflectance Measurement
2.4. Polarization Contribution to the Overall Uncertainty in Reflectance after the Reference Detector/Target Imager Intercalibration
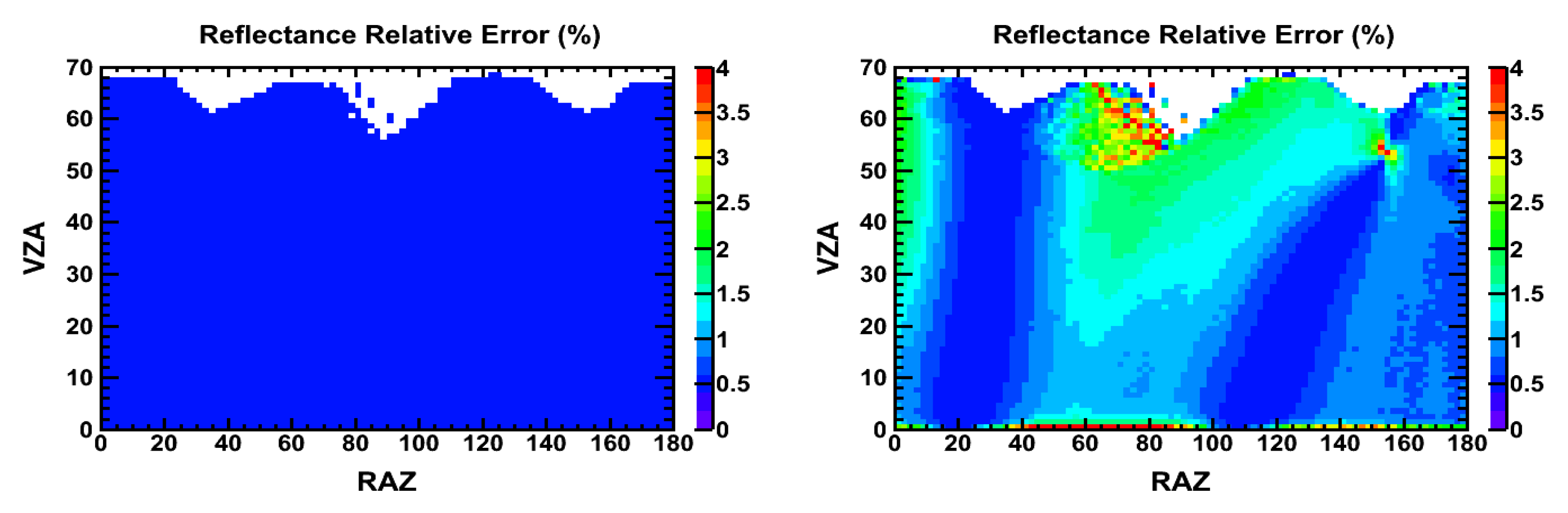
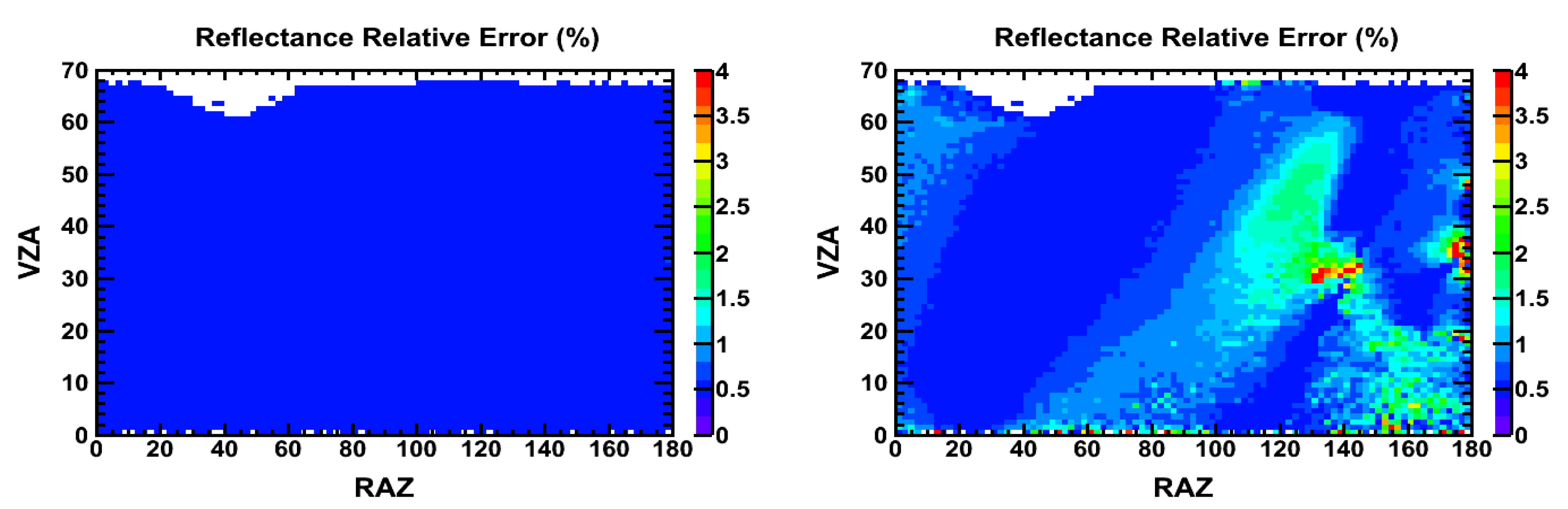
3. Results
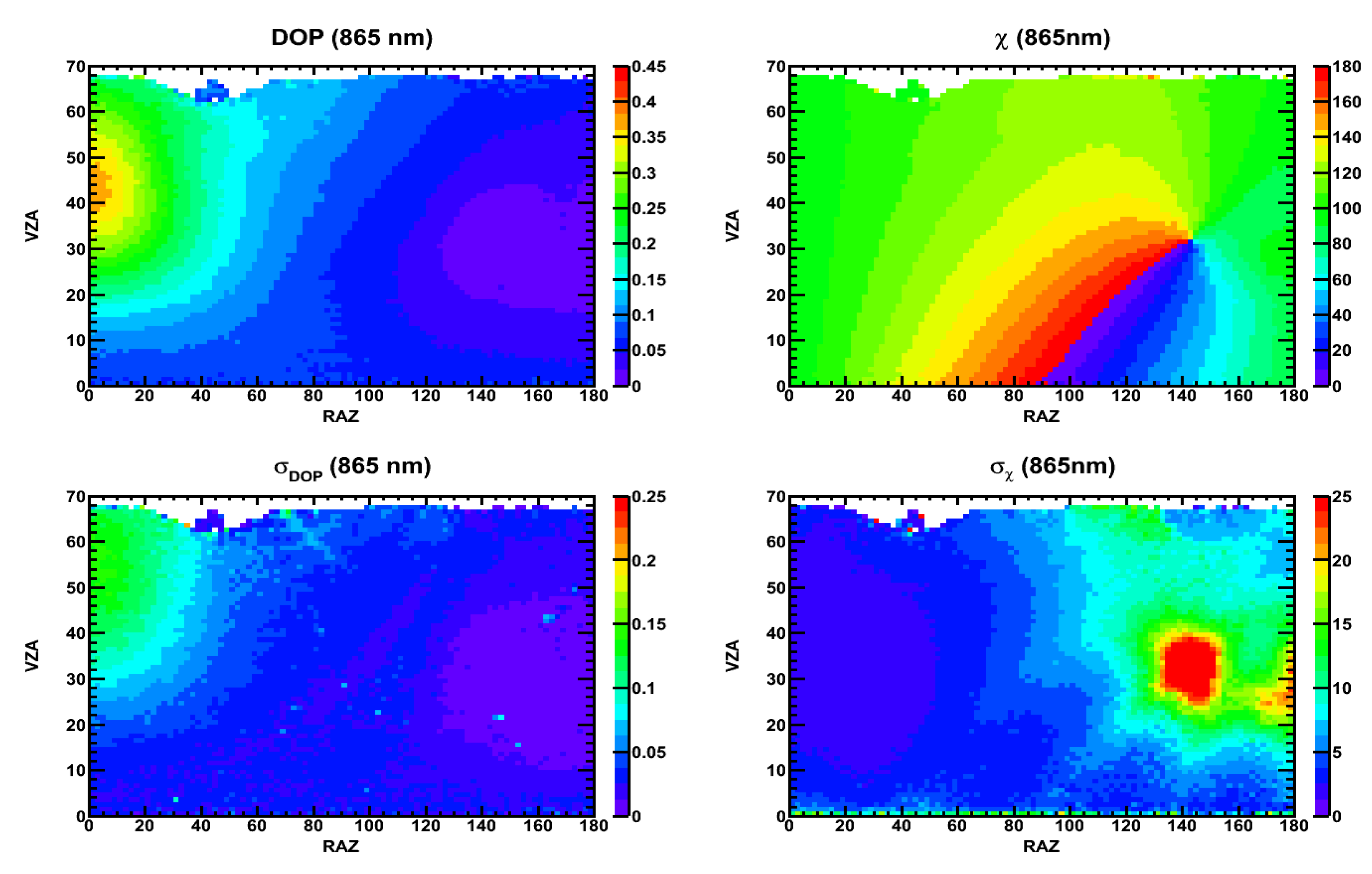
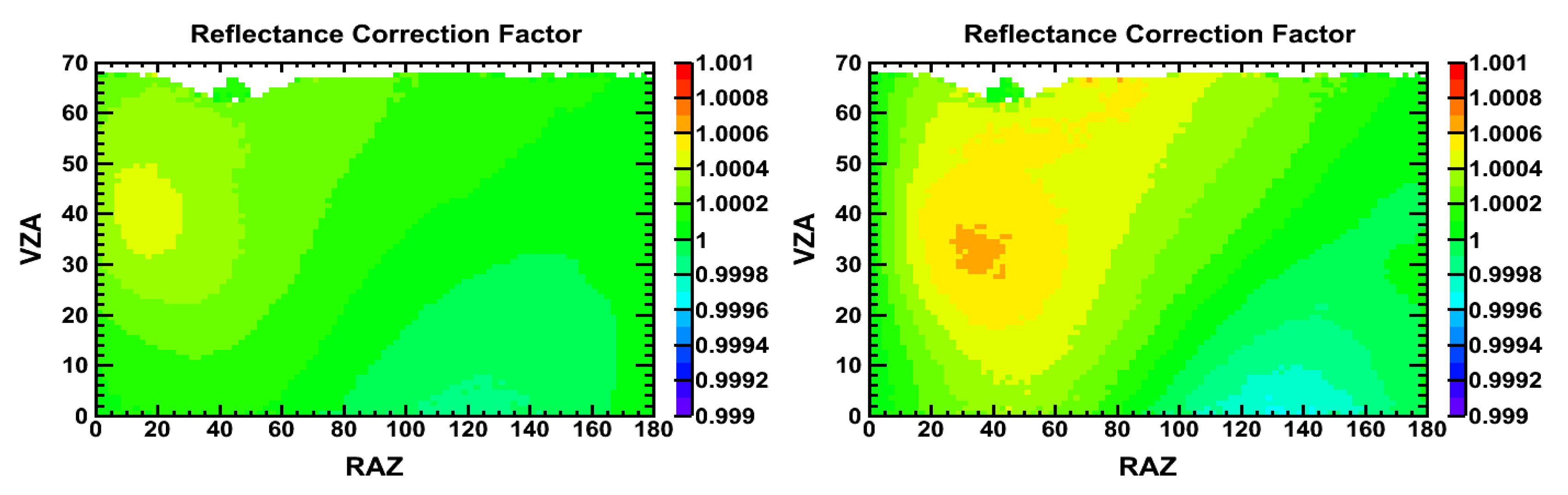
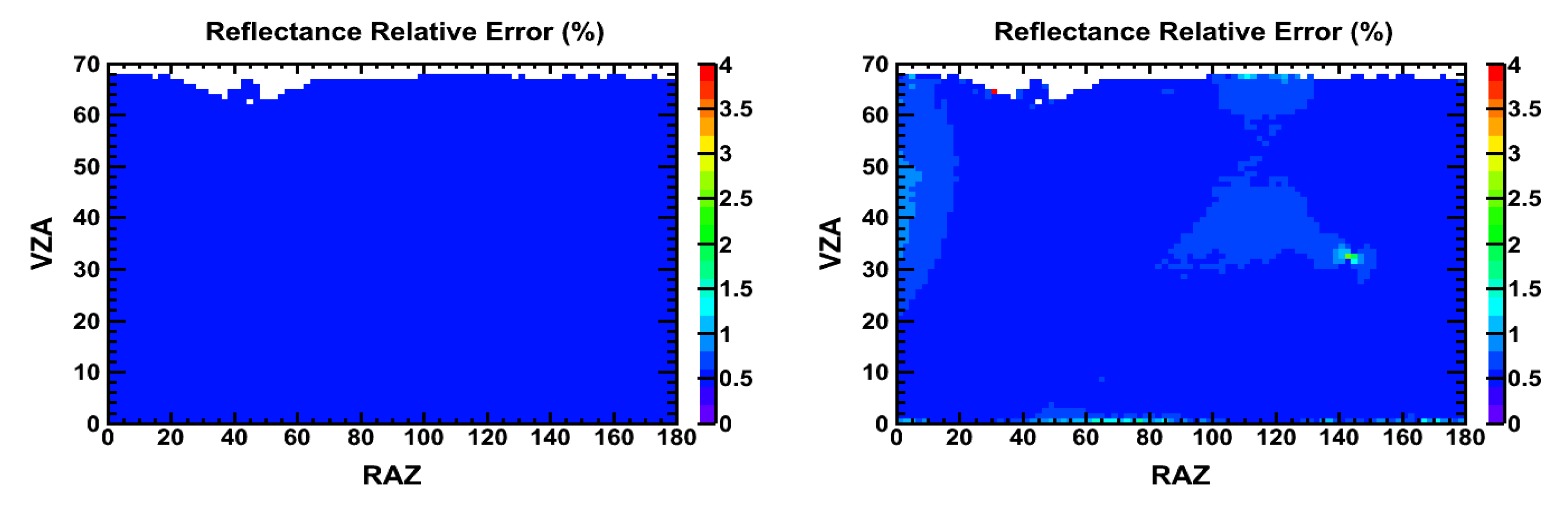
3.1. Clear-Sky Ocean
3.2. Overcast Ocean: Water Clouds
3.3. Overcast Ocean: Ice Clouds
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADRTM | Adding-Doubling Radiative Transfer Model |
| AOD | Aerosol Optical Depth |
| CERES | Clouds and the Earth’s Radiant Energy System |
| CLARREO | Climate Absolute Radiance and Refractivity Observatory |
| COT | Cloud Optical Thickness |
| CPF | Climate Absolute Radiance and Refractivity Observatory (CLARREO) Pathfinder |
| HAM | Half-Angle Mirror |
| IGBP | International Geosphere-Biosphere Programme index |
| ISS | International Space Station |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| RAZ | Relative Azimuth |
| RSB | Reflective Solar Band |
| RTA | Rotating Telescope Assembly |
| PARASOL | Polarization and Anisotropy of Reflectances for Atmospheric Sciences coupled |
| with Observations from a Lidar | |
| PDM | Polarization Distribution Model |
| POLDER | Polarization and Directionality of the Earth’s Reflectances |
| SZA | Solar Zenith Angle |
| SI | Sysème Internationale d’Unités |
| VIIRS | Visible/Infrared Imaging Radiometer Suite |
| VZA | Viewing Zenith Angle |
Appendix A. Deriving the Polarization Correction Factor
Appendix B. Deriving the Reflectance Uncertainty due to Polarization
References
- Wielicki, B.A.; Young, D.F.; Mlynczak, M.G. Achieving climate change absolute accuracy in orbit. Bull. Am. Meteorol. Soc. 2013, 94, 1519–1539. [Google Scholar] [CrossRef]
- Pathfinder Mission for Climate Absolute Radiance and Refractivity Observatory (CLARREO). CLARREO Pathfinder Mission Team Report. 2016. Available online: https://clarreo.larc.nasa.gov/pdf/CLARREO_Pathfinder_Report.pdf (accessed on 14 August 2019).
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B.; Smith, G.L.; Cooper, J.E. Clouds and Earth Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Lee, T.E.; Miller, S.D.; Turk, F.J.; Schueler, C.; Julian, R.; Deyo, S.; Dills, P.; Wang, S. The NPOESS VIIRS Day/Night Visible Sensor. Bull. Am. Meteorol. Soc. 2006, 87, 191–200. [Google Scholar] [CrossRef]
- Cao, C.; Deluccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite (VIIRS) onboard the Suomi national polar-orbiting partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, X.; Waluschka, E.; Wang, M. Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite polarization sensitivity analysis. Appl. Opt. 2016, 27, 7645–7658. [Google Scholar] [CrossRef] [PubMed]
- Roithmayr, C.M.; Lukashin, C.; Speth, P.W.; Kopp, G.; Thome, K.; Wielicki, B.A.; Young, D.F. CLARREO Approach for Reference Intercalibration of Reflected Solar Sensors: On-Orbit Data Matching and Sampling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6762–6774. [Google Scholar] [CrossRef]
- Lukashin, C.; Wielicki, B.A.; Young, D.F.; Thome, K.J.; Jin, Z.; Sun, W. Uncertainty Estimates for Imager Reference Inter-Calibration With CLARREO Reflected Solar Spectrometer. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1425–1436. [Google Scholar] [CrossRef]
- Coulson, K.L. Polarisation and Intensity of Light in the Atmosphere; A Deepak Publishing: Hampton, VA, USA, 1988; p. 596. [Google Scholar]
- Collett, E. Field Guide to Polarization; SPIE Field Guides; Greivenkamp, J.E., Ed.; SPIE: Bellingham, WA, USA, 2005; Volume FG05. [Google Scholar]
- Deschamps, P.-Y.; Breon, F.-M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.-C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Sun, W.; Lukashin, C. Modeling polarized solar radiation from the ocean-atmosphere system for CLARREO inter-calibration applications. Atmos. Chem. Phys. 2013, 13, 10303–10324. [Google Scholar] [CrossRef]
- Goldin, D.; Lukashin, C. Empirical Polarization Distribution Models for CLARREO-Imager Intercalibration. J. Atmospheric Ocean. Technol. 2016, 33, 439–451. [Google Scholar] [CrossRef]
- Sun, J.-Q.; Xiong, X. MODIS Polarization-Sensitivity Analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2875–2885. [Google Scholar]
- Bréon, F.-M. PARASOL Level-1 Product Data Format and User Manual; Ed. 1, Rev. 4. 2006. Available online: http://www.icare.univ-lille1.fr/projects_data/parasol/docs/Parasol_Level-1_format_latest.pdf (accessed on 14 August 2019).
- Bréon, F.-M. PARASOL level-2 Product Data Format and User Manual; Ed. 2, Rev. 1. 2011. Available online: http://www.icare.univ-lille1.fr/projects_data/parasol/docs/Parasol_Level-2_format_latest.pdf (accessed on 14 August 2019).
- Bartholomé, E.; Belward, A.S. GLC2000: A new approach to global land cover mapping from Earth observation data. Int. J. Remote Sens. 2005, 26, 1959–1977. [Google Scholar] [CrossRef]
- Fougnie, B.; Bracco, G.; Lafrance, B.; Ruffel, C.; Hagolle, O.; Tinel, C. PARASOL in-flight calibration and performance. Appl. Opt. 2007, 46, 5436–5451. [Google Scholar] [CrossRef] [PubMed]
| Constraint | Value/Range |
|---|---|
| Surface type: IGBP index [17] | 17 |
| POLDER band (nm) | 865 |
| SZA | |
| Wind speed (m/s) | |
| Aerosol Optical Depth (AOD) |
| Constraint | Value/Range |
|---|---|
| Surface type: IGBP index [17] | 17 |
| POLDER band (nm) | 865 |
| SZA (degrees) | |
| Cloud Fraction | |
| COT | |
| Water cloud mask | 1 |
| Constraint | Value/Range |
|---|---|
| Surface type: IGBP index [17] | 17 |
| POLDER band (nm) | 865 |
| SZA | |
| Cloud fraction | |
| COT | |
| Ice cloud mask | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldin, D.; Xiong, X.; Shea, Y.; Lukashin, C. CLARREO Pathfinder/VIIRS Intercalibration: Quantifying the Polarization Effects on Reflectance and the Intercalibration Uncertainty. Remote Sens. 2019, 11, 1914. https://doi.org/10.3390/rs11161914
Goldin D, Xiong X, Shea Y, Lukashin C. CLARREO Pathfinder/VIIRS Intercalibration: Quantifying the Polarization Effects on Reflectance and the Intercalibration Uncertainty. Remote Sensing. 2019; 11(16):1914. https://doi.org/10.3390/rs11161914
Chicago/Turabian StyleGoldin, Daniel, Xiaoxiong Xiong, Yolanda Shea, and Constantine Lukashin. 2019. "CLARREO Pathfinder/VIIRS Intercalibration: Quantifying the Polarization Effects on Reflectance and the Intercalibration Uncertainty" Remote Sensing 11, no. 16: 1914. https://doi.org/10.3390/rs11161914
APA StyleGoldin, D., Xiong, X., Shea, Y., & Lukashin, C. (2019). CLARREO Pathfinder/VIIRS Intercalibration: Quantifying the Polarization Effects on Reflectance and the Intercalibration Uncertainty. Remote Sensing, 11(16), 1914. https://doi.org/10.3390/rs11161914