Accurate Geo-Referencing of Trees with No or Inaccurate Terrestrial Location Devices
Abstract
1. Introduction
2. Methods
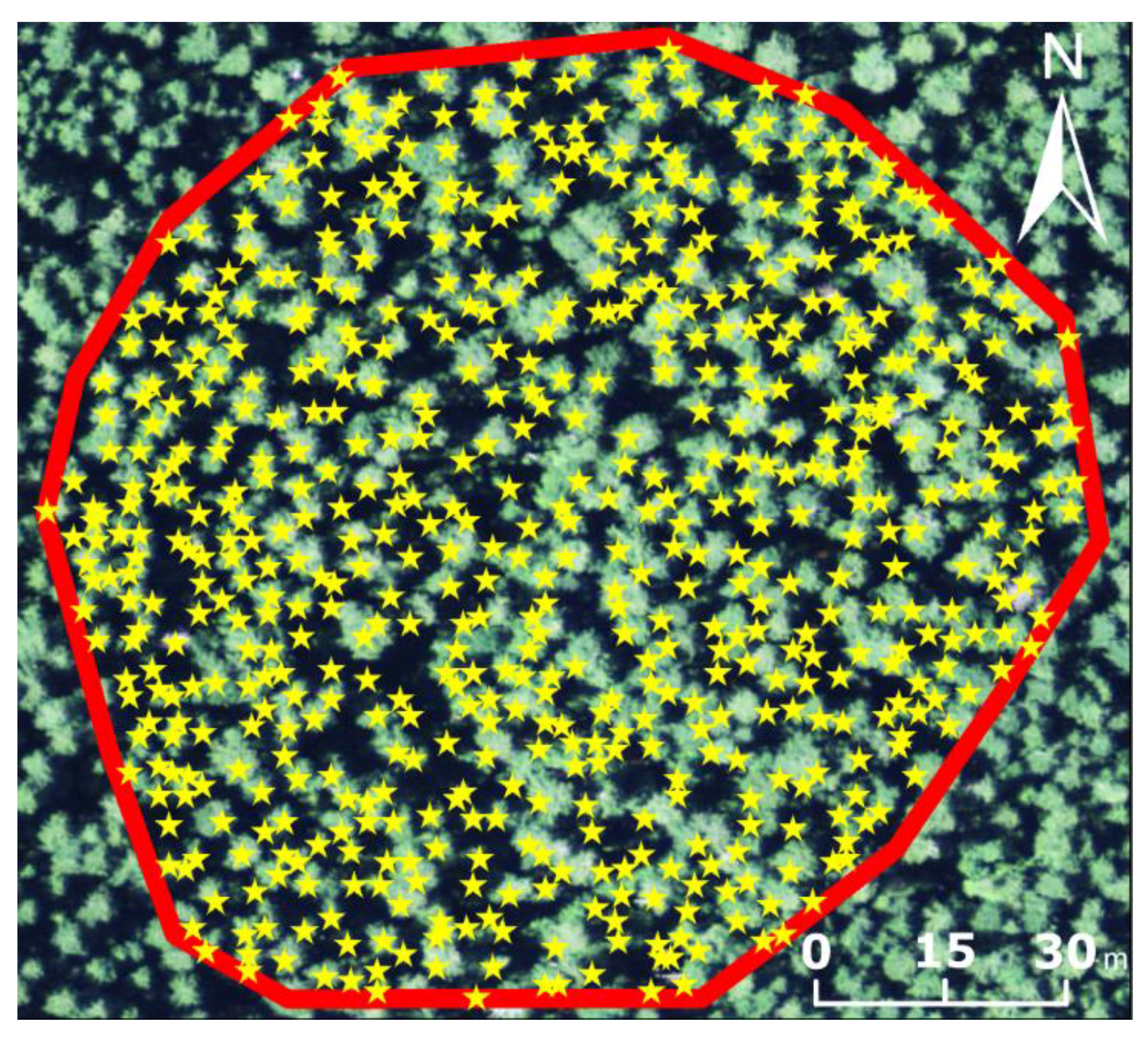
2.1. Study Area
2.2. Procedure
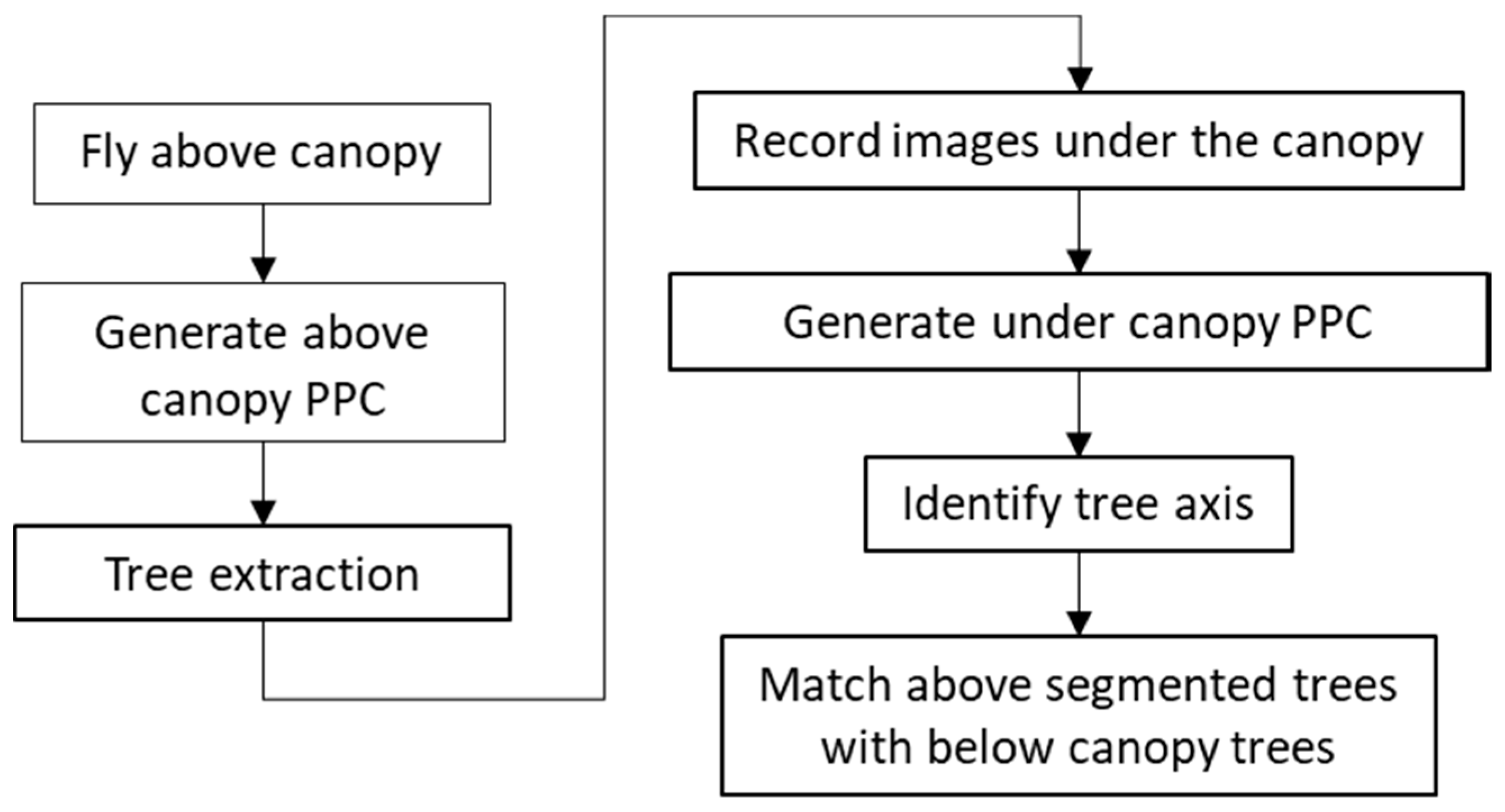
2.2.1. Tree Segmentation from the Above Canopy Acquired Point Clouds
2.2.2. Generation of Point Clouds from below Canopy Images
2.2.3. Identify the Relative Coordinates of the Trees from below Canopy Point Cloud
2.2.4. Match the Inaccurate or Unreferenced Trees with the Georeferenced Trees
- Step 1
- Input the location of the trees, as seen from below, , and as seen from above,
- Step 2
- Compute feature descriptors for the location of the trees seen from above
- Step 3
- Start a recursive procedure with a preset number of iterations
- Step3-1
- Compute feature descriptors for the relative location of the trees seen from below
- Step3-2
- Estimate the initial correspondences based on the feature descriptors of two-point sets locating the trees, one from above and one from below
- Step3-3
- Solve the transformation f, , which warps the set of points representing the trees seen from below (the model point set) to the set of points representing the trees seen from above (the target point set). The Γ is a positive defined matrix Γ: Rd × Rd → Rd×d and is a random subset of points to have nonzero coefficients in the expansion of the solution of f. The solution of f is found using the following steps:
- Step3-3a
- Input the annealing rate γ, and the parameters that control the smoothness of the transformation f, β and λ. Ma et al. [43] argued that the method is robust to parameter changes, therefore we have chosen the values recommended by Ma et al., namely γ = 0.5, β = 0.8 and λ = 0.1.
- Step3-3b
- Construct the Gram matrix Γ and matrix U, where
- Step3-3c
- Initialize C and σ2 whereσ2 is the variance of the point correspondence, computed as yi − f(xi)d is the dimension of the coefficient ci from the C, the coefficient matrix m × d used in conjunction with the Gram matrix: C = (c1, …, cm)
- Step3-3d
- Start deterministic annealing [55] aimed at minimization of the functionwhere CT is the transpose of C, and tr is the trace of the matrix CTΓCusing the quasi-Newton algorithm with C as the old value and the gradient ,
- Step3-3d-I:
- update C ← arg minC L2E(C, σ2)
- Step3-3d-II:
- anneal σ2 = γ σ2
- Step3-3e
- Select the solution of obtained by minimizing L2E
- Step3-4
- update the location of the trees seen from below (model point set)
- Step 4
- Stop when the preset number of iterations is reached
- Step 5
- The georeferenced trees seen from below have the location
2.2.5. Robustness of Tree Georeferencing to Missing and Erroneous Positioned Trees
3. Results
3.1. Geo-Referencing Trees Using Real Data
Initial Geo-Referencing
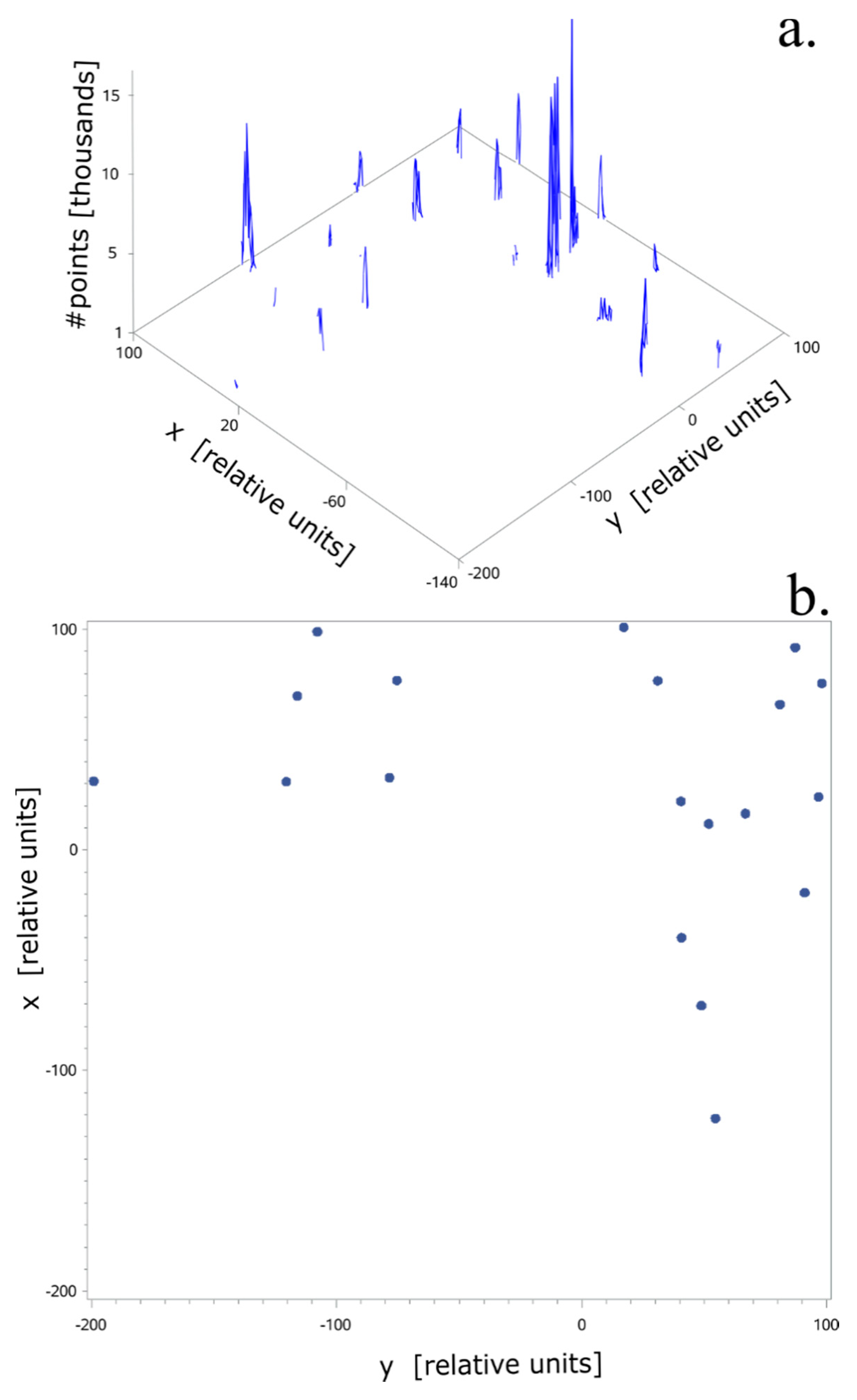
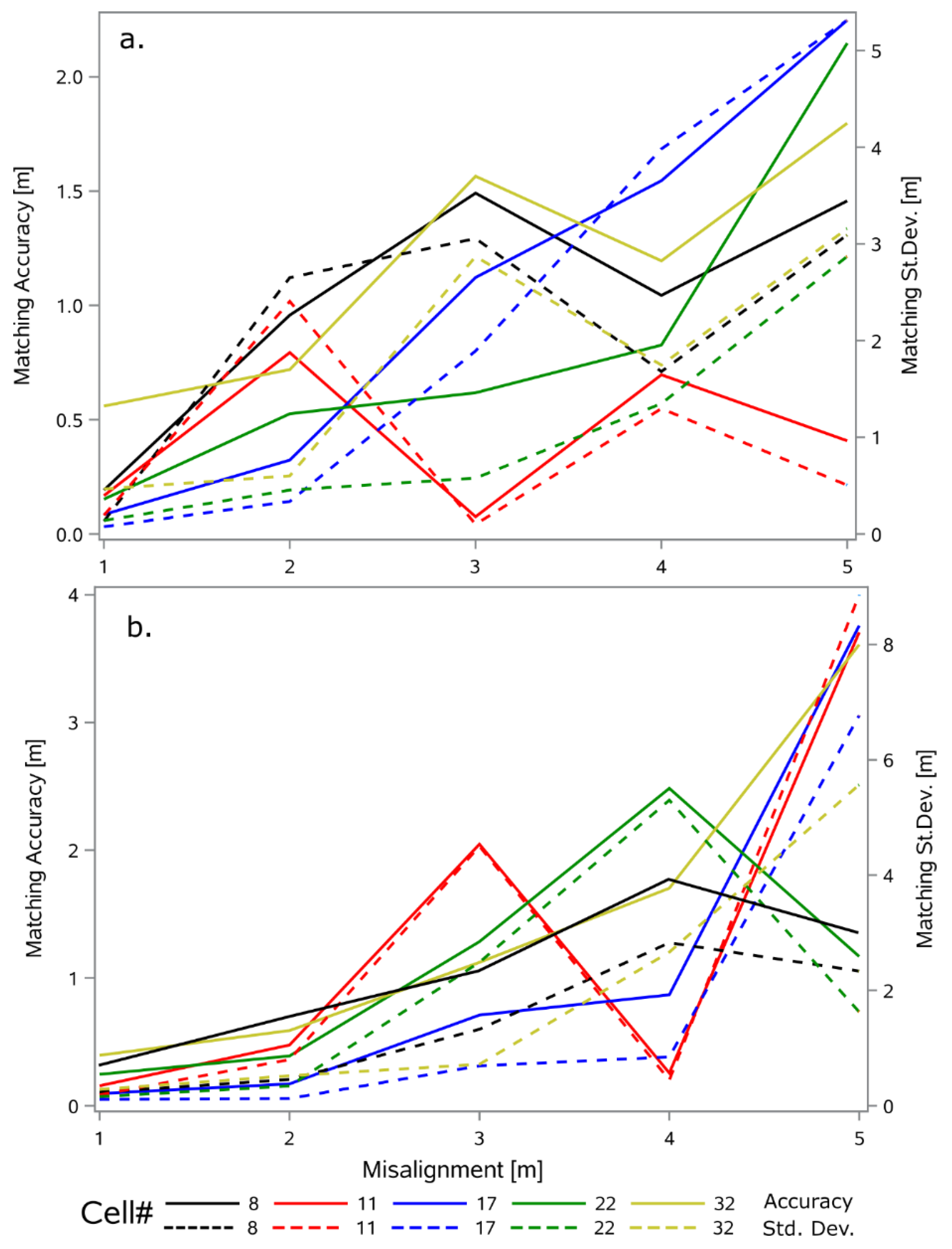
3.2. Accuracy of the Georeferencing Procedure Using Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kershaw, J.A.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; Wiley Blackwell: Hoboken, NJ, USA, 2017; p. 613. [Google Scholar]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; Wiley-Blackwell: Chichester, UK, 2011; Volume 430, p. 415. [Google Scholar]
- Popescu, S.; Wynne, R.H.; Nelson, R.H. Using lidar for measuring individual trees in the forest: An algorithm for estimating the crown diameter. Can. J. For. Res. 2003, 29, 564–577. [Google Scholar]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar]
- Strimbu, V.F.; Strimbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne lidar data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Wells, L. A Vision System for Automatic Dendrometry and Forest Mapping. Ph.D. Thesis, Oregon State University, Crovallis, OR, USA, 2018. [Google Scholar]
- Azizi, Z.; Najafi, A.; Sadeghian, S. Forest road detection using lidar data. J. For. Res. 2014, 25, 975–980. [Google Scholar] [CrossRef]
- White, R.A.; Dietterick, B.C.; Mastin, T.; Strohman, R. Forest roads mapped using lidar in steep forested terrain. Remote Sens. 2010, 2, 1120–1141. [Google Scholar] [CrossRef]
- Fritz, A.; Kattenborn, T.; Koch, B. Uav-based photogrammetric point clouds—Tree stem mapping in open stands in comparison to terrestrial laser scanner point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 141–146. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Liljedahl, A.K.; Dafflon, B.; Ulrich, C.; Peterson, J.E.; Gusmeroli, A.; Hubbard, S.S. Mapping snow depth within a tundra ecosystem using multiscale observations and bayesian methods. Cryosphere 2017, 11, 857–875. [Google Scholar] [CrossRef]
- Pierzchała, M.; Talbot, B.; Astrup, R. Measuring wheel ruts with close-range photogrammetry. For. Int. J. For. Res. 2016, 89, 383–391. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial lidar: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Fang, R.; Strimbu, B. Stem measurements and taper modeling using photogrammetric point clouds. Remote Sens. 2017, 9, 716. [Google Scholar] [CrossRef]
- Forsman, M.; Börlin, N.; Holmgren, J. Estimation of tree stem attributes using terrestrial photogrammetry with a camera rig. Forests 2016, 7, 61. [Google Scholar] [CrossRef]
- Means, J.E.; Helm, M.E. Height Growth and Site Index Curves for Douglas-Fir on Dry Sites in the Willamette National Forest; US Forest Service Pacific Northwest Forest and Range Experiment Station: Corvallis, OR, USA, 1985; p. 24.
- Ullman, S. The interpretation of structure from motion. Proc. R. Soc. Lond. B 1979, 203, 405–426. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Oliensis, J. A critique of structure-from-motion algorithms. Comput. Vis. Image Underst. 2000, 80, 172–214. [Google Scholar] [CrossRef]
- Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in the Geosciences; John Wiley & Sons: Chichester, UK, 2016; p. 197. [Google Scholar]
- Agisoft. Agisoft Photoscan Professional, 1.3.4 ed.; Agisoft: St. Petersburg, Russia, 2017. [Google Scholar]
- Fang, R.; Strimbu, B.M. Photogrammetric point cloud trees. Math. Comput. For. Nat. Resour. Sci. 2017, 9, 30–33. [Google Scholar]
- De Conto, T.; Olofsson, K.; Görgens, E.B.; Rodriguez, L.C.E.; Almeida, G. Performance of stem denoising and stem modelling algorithms on single tree point clouds from terrestrial laser scanning. Comput. Electron. Agric. 2017, 143, 165–176. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer stacking: A novel algorithm for individual forest tree segmentation from lidar point clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Applied Imagery. Quick Terrain Modeler, 8.0.6 ed.; Applied Imagery: Silver Spring, MD, USA, 2017. [Google Scholar]
- Soininen, A. Terrascan; Terrasolid: Helsinki, Finland, 2019. [Google Scholar]
- Isenburg, M. Lastools; Rapidlasso GmbH: Gilching, Germany, 2017. [Google Scholar]
- Ferrell, S. Pdal, 1.4 ed.; LIDAR Widgets: Mesa, AZ, USA, 2017. [Google Scholar]
- Maturbons, B. Sensitivity of Forest Structure and Biomass Estimation to Data Processing Algorithms; Oregon State University: Corvallis, OR, USA, 2018. [Google Scholar]
- Strimbu, V.F. Trex—Tree Extraction Algorithm, 022 ed.; Louisiana Tech University: Ruston, LA, USA, 2015. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Vanrell, M.; Lumbreras, F.; Pujol, A.; Baldrich, R.; Llados, J.; Villanueva, J.J. Colour normalisation based on background information. In Proceedings of the 2001 International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; Volume 871, pp. 874–877. [Google Scholar]
- Sánchez, J.M.; Binefa, X. Color normalization for digital video processing. In Advances in Visual Information Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 189–199. [Google Scholar]
- Youn, E.; Jeong, M.K. Class dependent feature scaling method using naive bayes classifier for text datamining. Pattern Recognit. Lett. 2009, 30, 477–485. [Google Scholar] [CrossRef]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis, 3rd ed.; John Wiley and Sons: New York NY, USA, 2012; p. 800. [Google Scholar]
- Jobson, J.D. Applied Multivariate Data Analysis: Categorical and Multivariate Methods; Springer: New York, NY, USA, 1992. [Google Scholar]
- SAS Institute. Sas, 9.4 ed.; SAS Institute: Cary, NC, USA, 2017. [Google Scholar]
- Bing, J.; Vemuri, B.C. A robust algorithm for point set registration using mixture of gaussians. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 1242, pp. 1246–1251. [Google Scholar]
- Fitzgibbon, A.W. Robust registration of 2d and 3d point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Holz, D.; Ichim, A.E.; Tombari, F.; Rusu, R.B.; Behnke, S. Registration with the point cloud library: A modular framework for aligning in 3-D. IEEE Robot. Autom. Mag. 2015, 22, 110–124. [Google Scholar] [CrossRef]
- Hill, D.L.G.; Hawkes, D.J.; Crossman, J.E.; Gleeson, M.J.; Cox, T.C.S.; Bracey, E.E.C.M.L.; Strong, A.J.; Graves, P. Registration of mr and ct images for skull base surgery using point-like anatomical features. Br. J. Radiol. 1991, 64, 1030–1035. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Zhao, J.; Tian, J.; Tu, Z.; Yuille, A.L. Robust estimation of nonrigid transformation for point set registration. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2147–2154. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-d shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Doermann, D. Robust point matching for nonrigid shapes by preserving local neighborhood structures. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 643–649. [Google Scholar] [CrossRef] [PubMed]
- Munkres, J. Algorithms for the assignment and transportation problems. J. Soc. Ind. Appl. Math. 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Krejov, P.; Bowden, R. Multi-touchless: Real-time fingertip detection and tracking using geodesic maxima. In Proceedings of the 2013 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG), Shanghai, China, 22–26 April 2013; pp. 1–7. [Google Scholar]
- Abraham, J.; Kwan, P.; Gao, J. Fingerprint matching using a hybrid shape and orientation descriptor. In State of the Art in Biometrics; Yang, J., Nanni, L., Eds.; Intech: London, UK, 2011. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, G.; Jiang, J.; Shen, D. Robust anatomical correspondence detection by hierarchical sparse graph matching. IEEE Trans. Med. Imaging 2013, 32, 268–277. [Google Scholar] [CrossRef]
- Yang, C.; Feinen, C.; Tiebe, O.; Shirahama, K.; Grzegorzek, M. Shape-based object matching using point context. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval, Shanghai, China, 23–26 June 2015; ACM: New York, NY, USA, 2015; pp. 519–522. [Google Scholar]
- Mladen, N. Measuring similarity of graph nodes by neighbor matching. Intell. Data Anal. 2012, 16, 865–878. [Google Scholar]
- Chui, H.; Rangarajan, A. A new algorithm for non-rigid point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2000), Hilton Head Island, SC, USA, 15 June 2000; Volume 42, pp. 44–51. [Google Scholar]
- The MathWorks Inc. Matlab; The MathWorks Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Rose, K.; Gurewitz, E.; Fox, G. A deterministic annealing approach to clustering. Pattern Recognit. Lett. 1990, 11, 589–594. [Google Scholar] [CrossRef]
- Martínez-Carricondo, P.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Mesas-Carrascosa, F.J.; García-Ferrer, A.; Pérez-Porras, F.J. Assessment of UAV-photogrammetric mapping accuracy based on variation of ground control points. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 1–10. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Surovy, P.; Kuzelka, K. Accuracy of structure from motion models in comparison with terrestrial laser scanner for the analysis of dbh and height influence on error behaviour. J. For. Sci. 2016, 62, 357–365. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyypp, J.; Honkavaara, E.; Liu, J. Forest data collection using terrestrial image-based point clouds from a handheld camera compared to terrestrial and personal laser scanning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5117–5132. [Google Scholar] [CrossRef]
- Weng, J.; Huang, T.S.; Ahuja, N. Motion and structure from two perspective views: Algorithms, error analysis, and error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 451–476. [Google Scholar] [CrossRef]
- Smith, R.C.; Cheeseman, P. On the representation and estimation of spatial uncertainty. Int. J. Robot. Res. 1986, 5, 56–68. [Google Scholar] [CrossRef]
- Leonard, J.J.; Durrant-Whyte, H.F. Simultaneous map building and localization for an autonomous mobile robot. In Proceedings of the IROS ’91: IEEE/RSJ International Workshop on Intelligent Robots and Systems’ 91, Osaka, Japan, 3–5 November 1991; Volume 1443, pp. 1442–1447. [Google Scholar]
- Kümmerle, R.; Steder, B.; Dornhege, C.; Ruhnke, M.; Grisetti, G.; Stachniss, C.; Kleiner, A. On measuring the accuracy of slam algorithms. Auton. Robot. 2009, 27, 387. [Google Scholar] [CrossRef]
- Akhter, I.; Sheikh, Y.; Khan, S.; Kanade, T. Trajectory space: A dual representation for nonrigid structure from motion. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1442–1456. [Google Scholar] [CrossRef]
- Nikolov, I.; Madsen, C. Benchmarking close-range structure from motion 3d reconstruction software under varying capturing conditions. In Digital Heritage. Progress in Cultural Heritage: Documentation, Preservation, and Protection: 6th International Conference, Euromed 2016, Nicosia, Cyprus, 31 October–5 November, 2016; Proceedings, Part I; Ioannides, M., Fink, E., Moropoulou, A., Hagedorn-Saupe, M., Fresa, A., Liestøl, G., Rajcic, V., Grussenmeyer, P., Eds.; Springer: Cham, Switzerland, 2016; pp. 15–26. [Google Scholar]
- Feduck, C.; McDermid, G.; Castilla, G. Detection of coniferous seedlings in UAV imagery. Forests 2018, 9, 432. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping Forest Type and Tree Species on a Regional Scale Using Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.C.; Lawing, A.M.; Eriksson, M.; Strimbu, B.M.; Bürkner, P.C. Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures. Remote Sens. 2018, 10, 39. [Google Scholar] [CrossRef]





| Grid Cell | # Trees Inside 2500 m2 Cell | #Trees from GoPro Images Inside 900 m2 Cell | Accuracy [m] | #Trees from Nikon Images Inside 900 m2 Cell | Accuracy [m] |
|---|---|---|---|---|---|
| 8 | 24 | 8 | 1.06 | 7 | 1.08 |
| 11 | 21 | 8 | 1.01 | 9 | 0.98 |
| 17 | 21 | 7 | 1.12 | 8 | 1.05 |
| 22 | 24 | 8 | 1.11 | 7 | 1.15 |
| 32 | 27 | 11 | 1.05 | 9 | 1.10 |
| Accuracy | - | - | 1.07 | - | 1.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strimbu, B.M.; Qi, C.; Sessions, J. Accurate Geo-Referencing of Trees with No or Inaccurate Terrestrial Location Devices. Remote Sens. 2019, 11, 1877. https://doi.org/10.3390/rs11161877
Strimbu BM, Qi C, Sessions J. Accurate Geo-Referencing of Trees with No or Inaccurate Terrestrial Location Devices. Remote Sensing. 2019; 11(16):1877. https://doi.org/10.3390/rs11161877
Chicago/Turabian StyleStrimbu, Bogdan M., Chu Qi, and John Sessions. 2019. "Accurate Geo-Referencing of Trees with No or Inaccurate Terrestrial Location Devices" Remote Sensing 11, no. 16: 1877. https://doi.org/10.3390/rs11161877
APA StyleStrimbu, B. M., Qi, C., & Sessions, J. (2019). Accurate Geo-Referencing of Trees with No or Inaccurate Terrestrial Location Devices. Remote Sensing, 11(16), 1877. https://doi.org/10.3390/rs11161877







