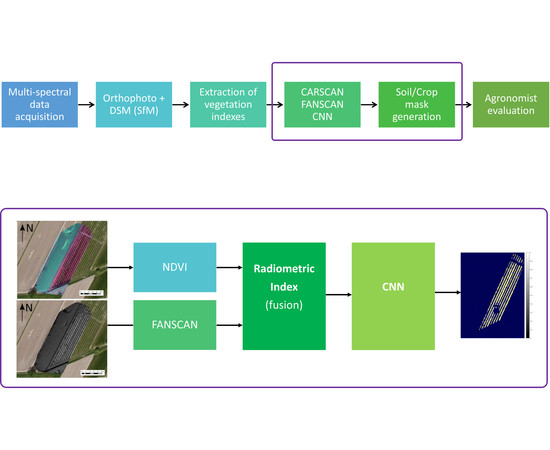
Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data
Abstract
1. Introduction
2. DSM Segmentation Methodology
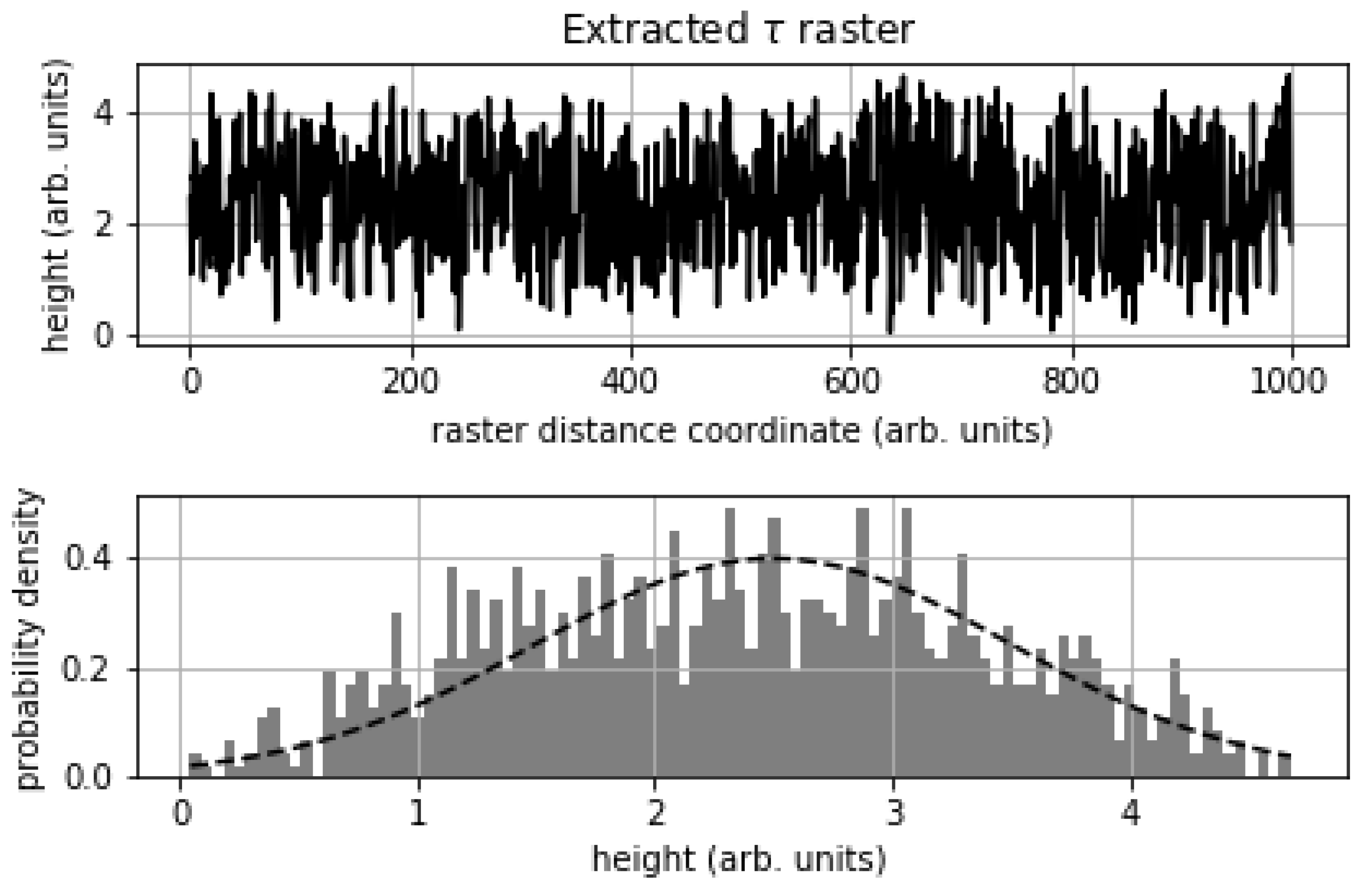
2.1. One Dimensional Rasterization
2.2. Derivation of the DSM/NDVI Index
2.3. Control Dataset
2.3.1. Noise Benchmarking Dataset
2.3.2. Real Flight Dataset
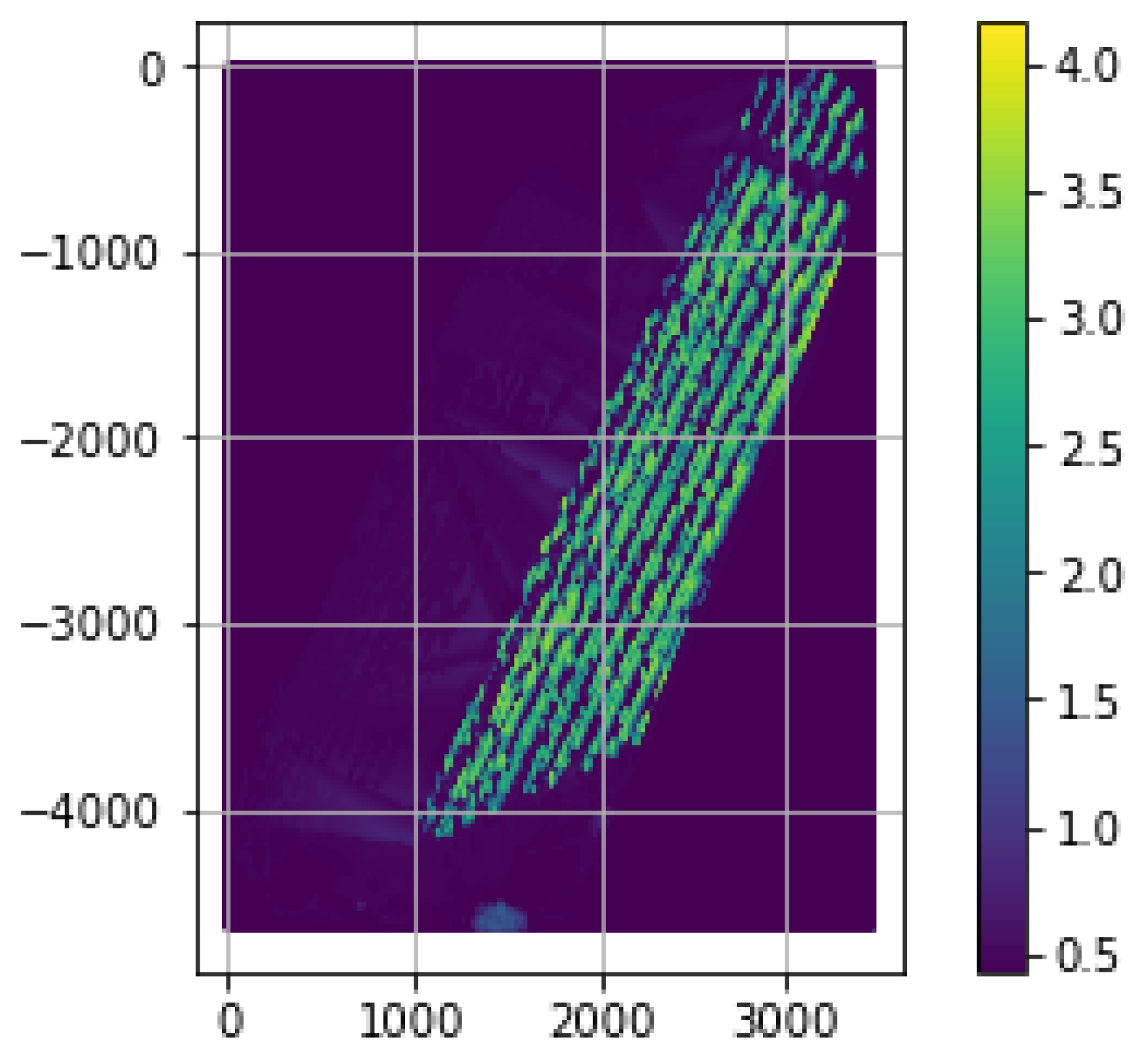
3. Results, Algorithms and Verification
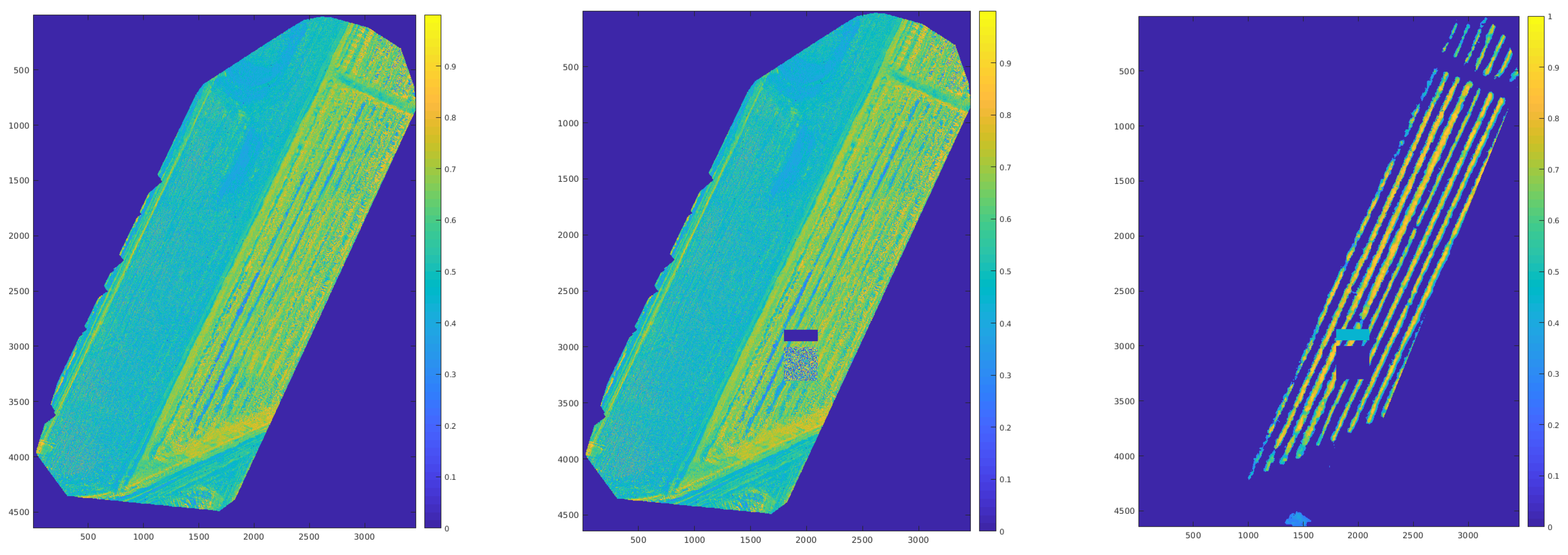
3.1. Work with the CARSCAN Algorithm
3.2. Work with the FANSCAN Algorithm
3.3. CARSCAN: Cartesian Grid Soil Field Extraction
| Algorithm 1 Pseudo code description of a Cartesian soil field extraction. Input = discretized horizontal image slices . Output = and fields. |
|
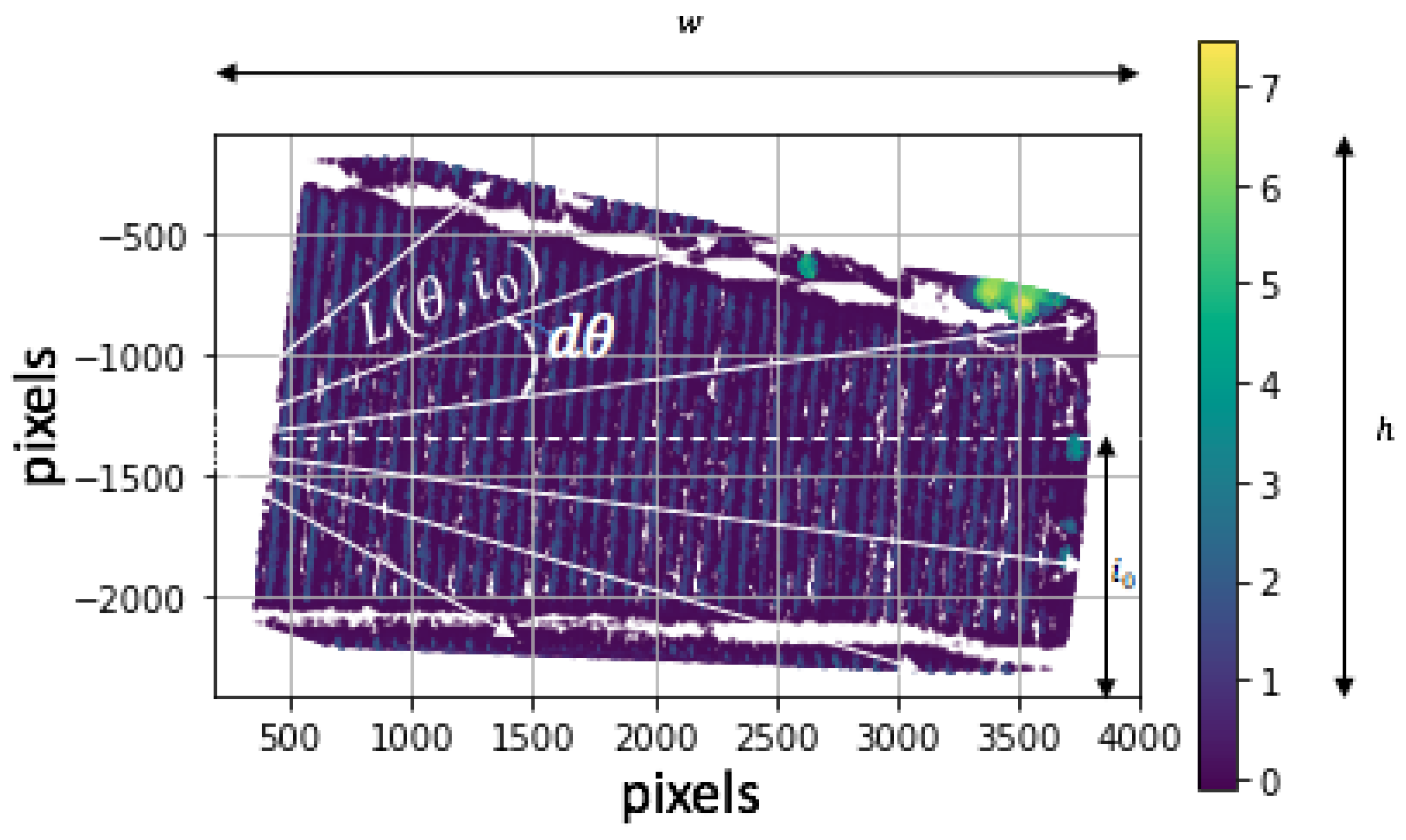
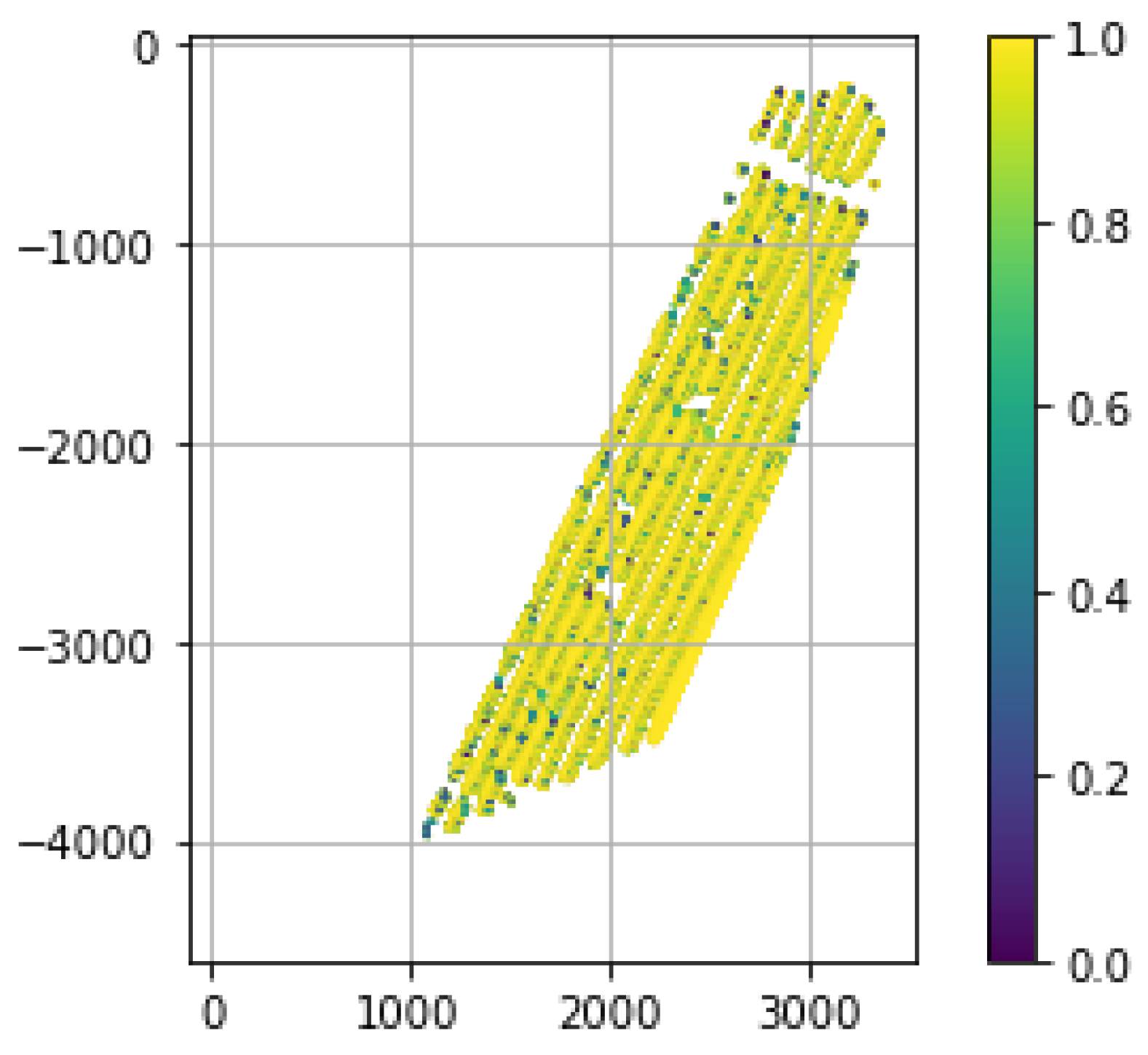
3.4. FANSCAN: Moving Radial Soil Field Extraction
| Algorithm 2 Pseudo code description of FANSCAN. Input = discretized radial image slices . Output = raw raster point field. | |||
| 1: | procedureFANSCAN(image,slices) | ||
| 2: | |||
| 3: | |||
| 4: | ▹ | ||
| 5: | vertical scan ath: | ||
| 6: | for do | ||
| 7: | ▹ | ||
| 8: | raster scan at θ: | ||
| 9: | for do | ||
| 10: | |||
| 11: | |||
| 12: | for do | ||
| 13: | |||
| 14: | end for | ||
| 15: | end for | ||
| 16: | end for | ||
| 17: | end procedure | ||
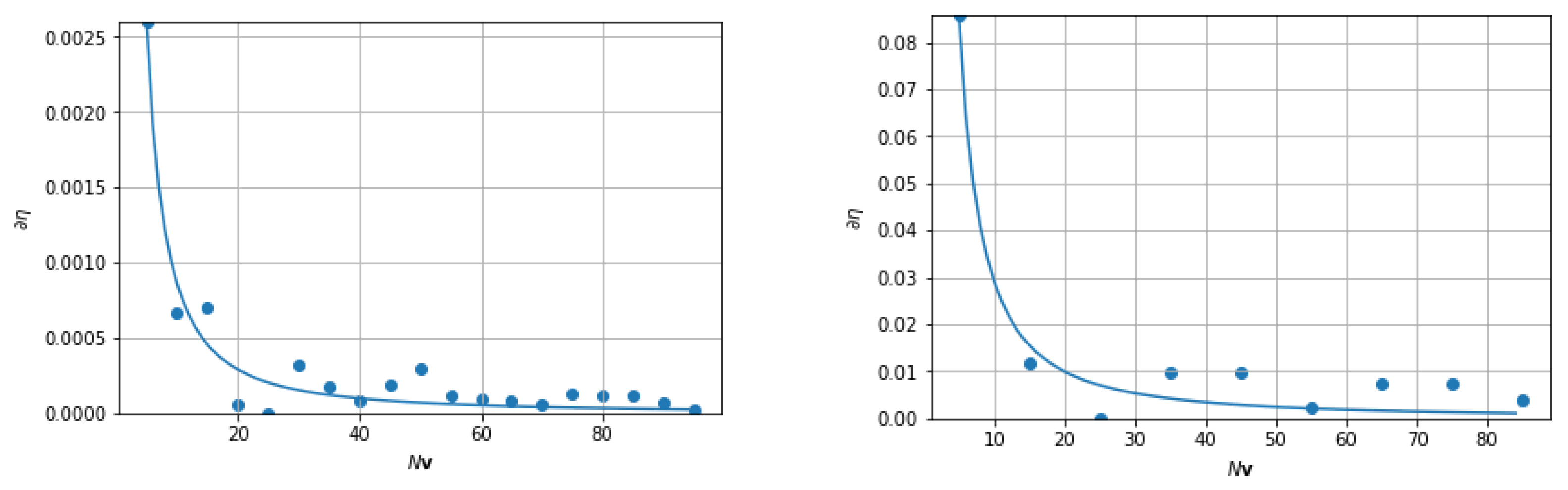
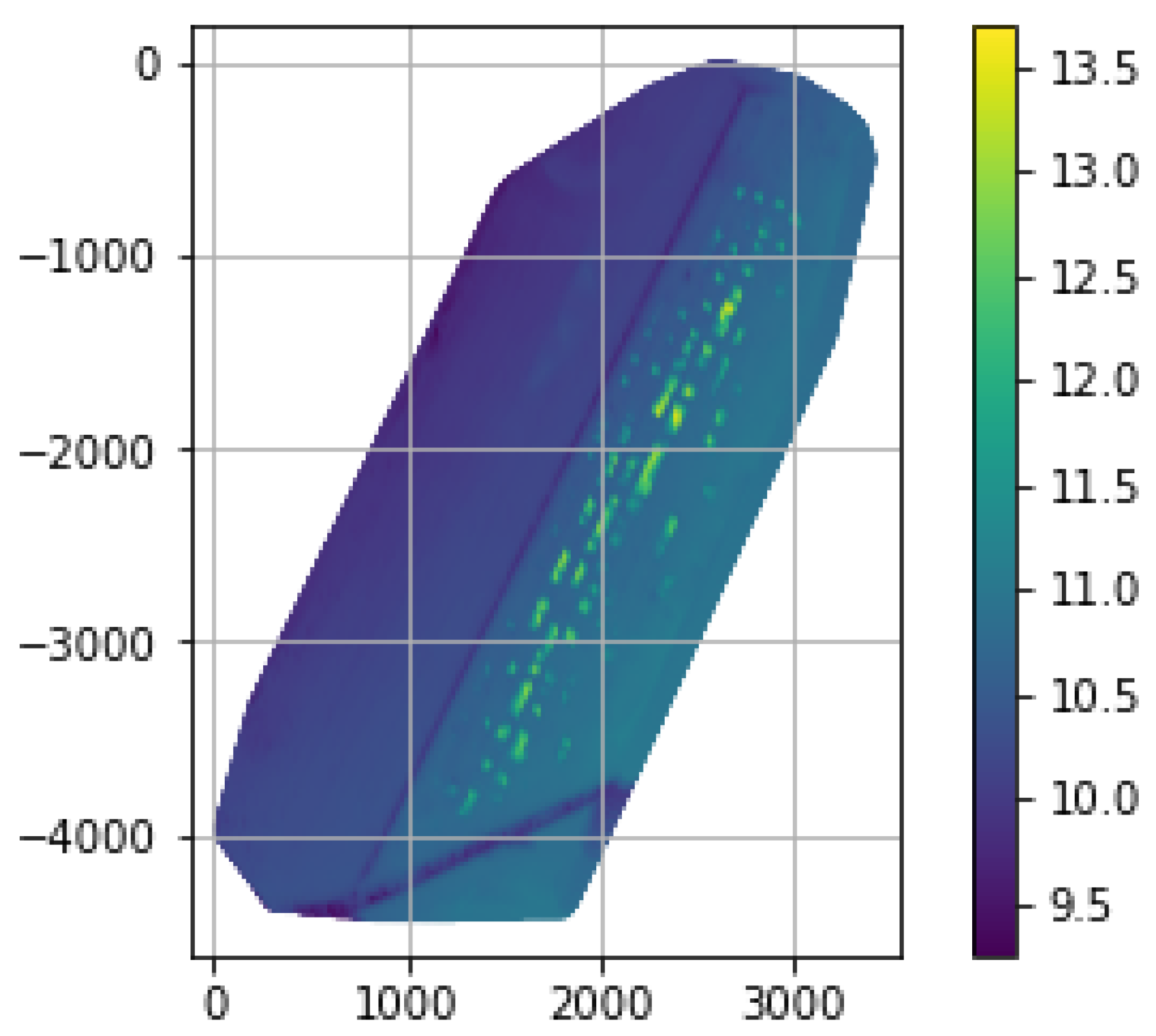
3.5. Convergence Properties for FANSCAN
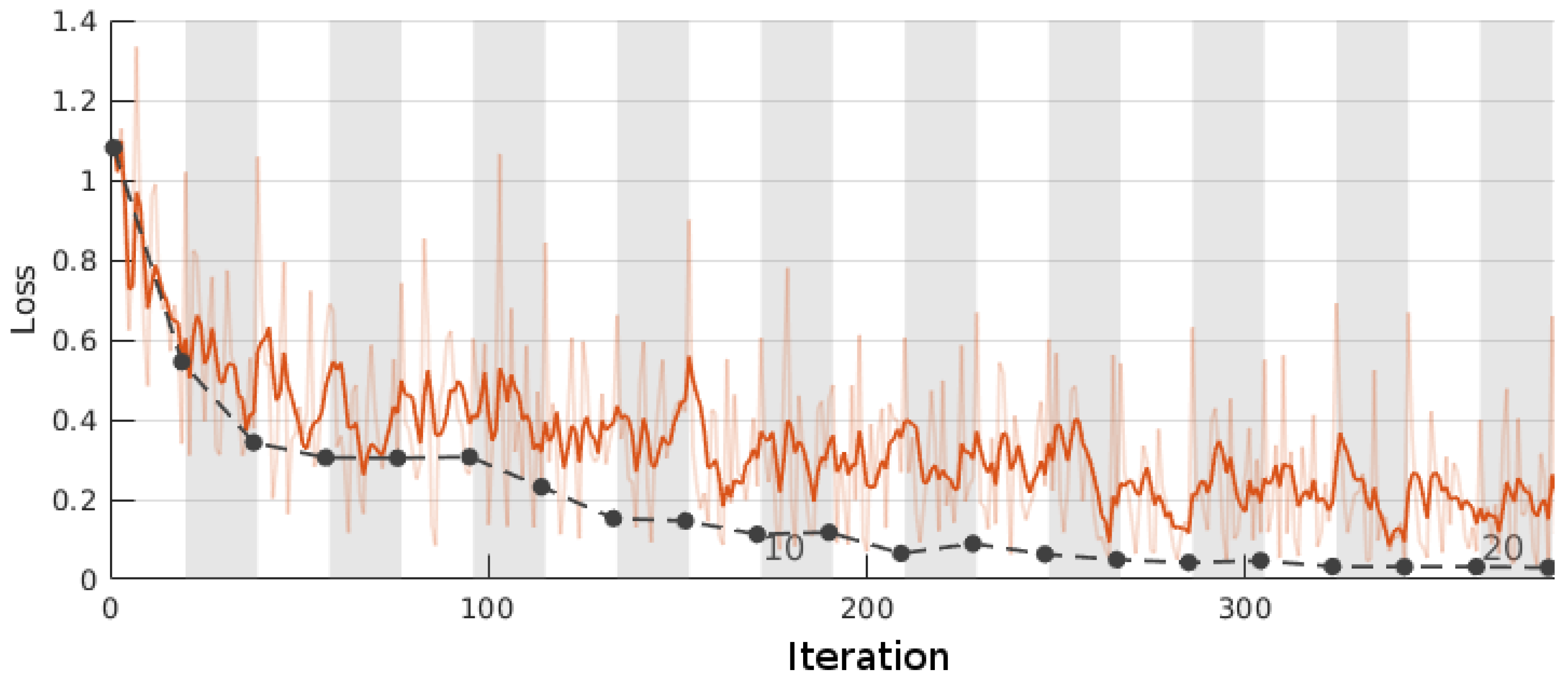
3.6. Convolutional Neural Network: A DSM/NDVI Strategy
4. Discussion
4.1. Convergence in Fourier Space
4.2. Radial Raster Geometry: An Achilles Heel
4.3. The DSM/Radiometric Approach to Canopy Segmentation
5. Conclusions
- increase the automation of the segmentation process,
- make the segmentation of soil from crop using a more robust radiometric index,
- increase the information content of the methodology in a natural way.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schenatto, K.; de Souza, E.; Bazzi, C.; Gavioli, A.; Betzek, N.; Beneduzzi, H. Normalization of data for delineating management zones. Comput. Electron. Agric. 2017, 143, 238–248. [Google Scholar] [CrossRef]
- Hedley, C. The role of precision agriculture for improved nutrient management on farms. J. Sci. Food Agric. 2015, 95, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Prasad, R.; Shriver, J.; Zhuang, Q. Crop model- and satellite imagery-based recommendation tool for variable rate N fertilizer application for the US Corn system. Precis. Agric. 2017, 18, 779–800. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Torres-Olivares, J.; Roman-Rangel, E.; Cervantes, S.; Juarez-Lopez, P.; Hermosillo-Valadez, J.; Rendón-Mancha, J.M. Fig Plant Segmentation from Aerial Images Using a Deep Convolutional Encoder-Decoder Network. Remote Sens. 2019, 11, 1157. [Google Scholar] [CrossRef]
- Sa, I.; Popović, M.; Khanna, R.; Chen, Z.; Lottes, P.; Liebisch, F.; Nieto, J.; Stachniss, C.; Walter, A.; Siegwart, R. WeedMap: A Large-Scale Semantic Weed Mapping Framework Using Aerial Multispectral Imaging and Deep Neural Network for Precision Farming. Remote Sens. 2018, 10, 1423. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.; Nguy-Robertson, A.; Arkebauer, T.; Wardlow, B.; Suyker, A.; Verma, S.; Shibayama, M. An alternative method using digital cameras for continuous monitoring of crop status. Agric. For. Meteorol. 2012, 154–155, 113–126. [Google Scholar] [CrossRef]
- Meyer, G.E. Machine vision identification of plants. In Recent Trends for Enhancing the Diversity and Quality of Soybean Products; InTech: London, UK, 2011. [Google Scholar]
- Onyango, C.M.; Marchant, J.A. Physics-based colour image segmentation for scenes containing vegetation and soil. Image Vis. Comput. 2001, 19, 523–538. [Google Scholar] [CrossRef]
- Sogaard, H. Weed Classification by Active Shape Models. Biosyst. Eng. 2005, 91, 271–281. [Google Scholar] [CrossRef]
- Abbasgholipour, M.; Omid, M.; Keyhani, A.; Mohtasebi, S. Color image segmentation with genetic algorithm in a raisin sorting system based on machine vision in variable conditions. Expert Syst. Appl. 2011, 38, 3671–3678. [Google Scholar] [CrossRef]
- Omid, M.; Khojastehnazhand, M.; Tabatabaeefar, A. Estimating volume and mass of citrus fruits by image processing technique. J. Food Eng. 2010, 100, 315–321. [Google Scholar] [CrossRef]
- Omid, M.; Ghojabeige, F.; Delshad, M.; Ahmadi, H. Energy use pattern and benchmarking of selected greenhouses in Iran using data envelopment analysis. Energy Convers. Manag. 2011, 52, 153–162. [Google Scholar] [CrossRef]
- Pang, J.; Bai, Z.Y.; Lai, J.C.; Li, S.K. Automatic segmentation of crop leaf spot disease images by integrating local threshold and seeded region growing. In Proceedings of the 2011 International Conference on Image Analysis and Signal Processing, Hubei, China, 21–23 October 2011; pp. 590–594. [Google Scholar] [CrossRef]
- Pugoy, R.A.D.; Mariano, V.Y. Automated rice leaf disease detection using color image analysis. In Proceedings of the Third International Conference on Digital Image Processing (ICDIP 2011), Chengdu, China, 15–17 April 2011; p. 80090F. [Google Scholar]
- De Benedetto, D.; Castrignanò, A.; Rinaldi, M.; Ruggieri, S.; Santoro, F.; Figorito, B.; Gualano, S.; Diacono, M.; Tamborrino, R. An approach for delineating homogeneous zones by using multi-sensor data. Geoderma 2013, 199, 117–127. [Google Scholar] [CrossRef]
- Yang, C.; Odvody, G.; Fernandez, C.; Landivar, J.; Minzenmayer, R.; Nichols, R. Evaluating unsupervised and supervised image classification methods for mapping cotton root rot. Precis. Agric. 2015, 16, 201–215. [Google Scholar] [CrossRef]
- Delenne, C.; Rabatel, G.; Deshayes, M. An Automatized Frequency Analysis for Vine Plot Detection and Delineation in Remote Sensing. IEEE Geosci. Remote. Sens. Lett. 2008, 5, 341–345. [Google Scholar] [CrossRef]
- Comba, L.; Gay, P.; Primicerio, J.; Ricauda Aimonino, D. Vineyard detection from unmanned aerial systems images. Comput. Electron. Agric. 2015, 114, 78–87. [Google Scholar] [CrossRef]
- Mancini, A.; Frontoni, E.; Zingaretti, P.; Longhi, S. High-resolution mapping of river and estuary areas by using unmanned aerial and surface platforms. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems, ICUAS 2015, Denver, CO, USA, 9–12 June 2015; pp. 534–542. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Cereda, S. A Comparison of Different Neural Networks for Agricultural Image Segmentation. MSc. Thesis, Politecnico di Milano, Milano, Italy, 2017. [Google Scholar]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the CVPR 2009. IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Sturari, M.; Frontoni, E.; Pierdicca, R.; Mancini, A.; Malinverni, E.S.; Tassetti, A.N.; Zingaretti, P. Integrating elevation data and multispectral high-resolution images for an improved hybrid Land Use/Land Cover mapping. Eur. J. Remote Sens. 2017, 50, 1–17. [Google Scholar] [CrossRef]
- Bittner, K.; Körner, M.; Fraundorfer, F.; Reinartz, P. Multi-Task cGAN for Simultaneous Spaceborne DSM Refinement and Roof-Type Classification. Remote Sens. 2019, 11, 1262. [Google Scholar] [CrossRef]
- Milioto, A.; Lottes, P.; Stachniss, C. Real-time Semantic Segmentation of Crop and Weed for Precision Agriculture Robots Leveraging Background Knowledge in CNNs. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018. [Google Scholar]

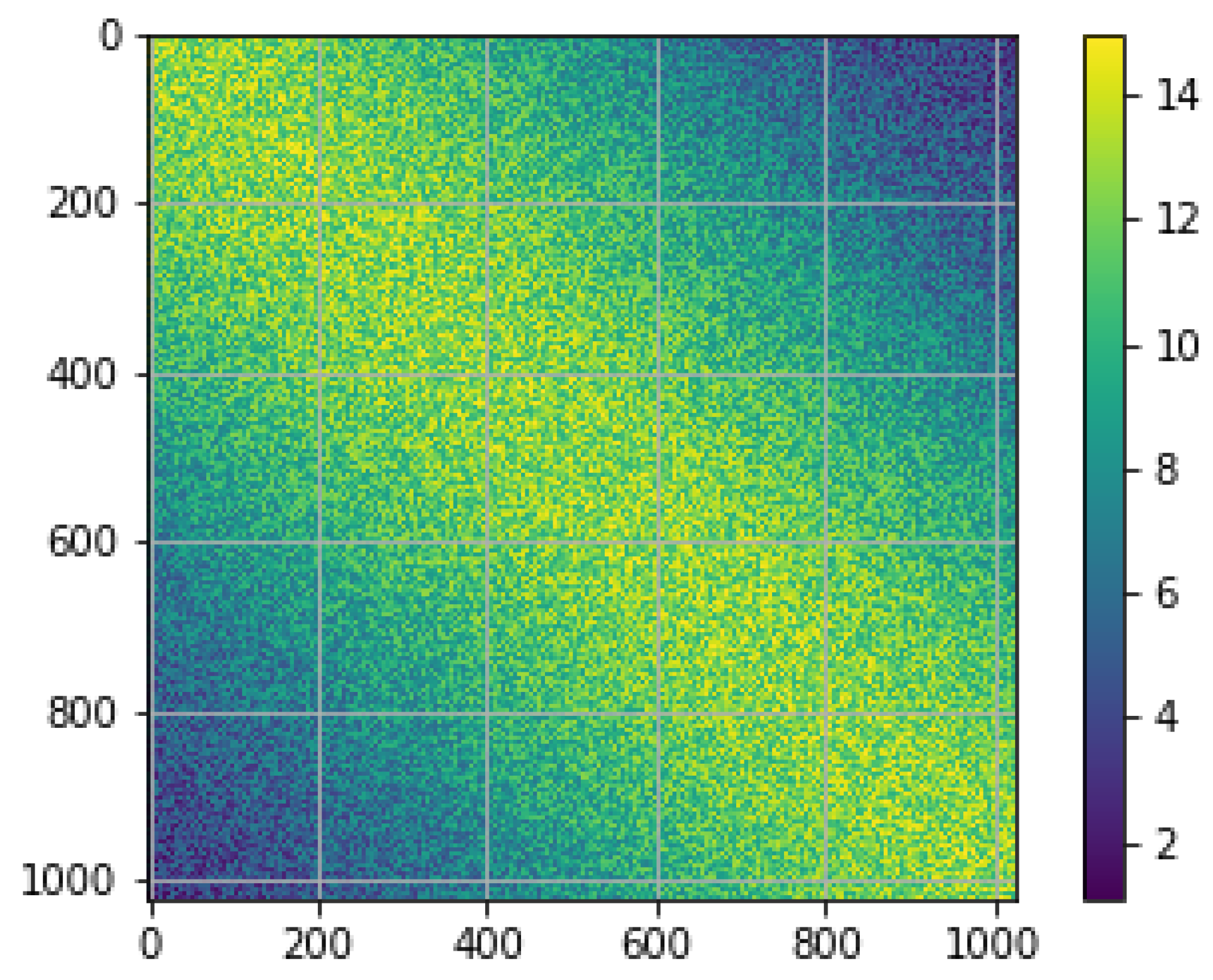


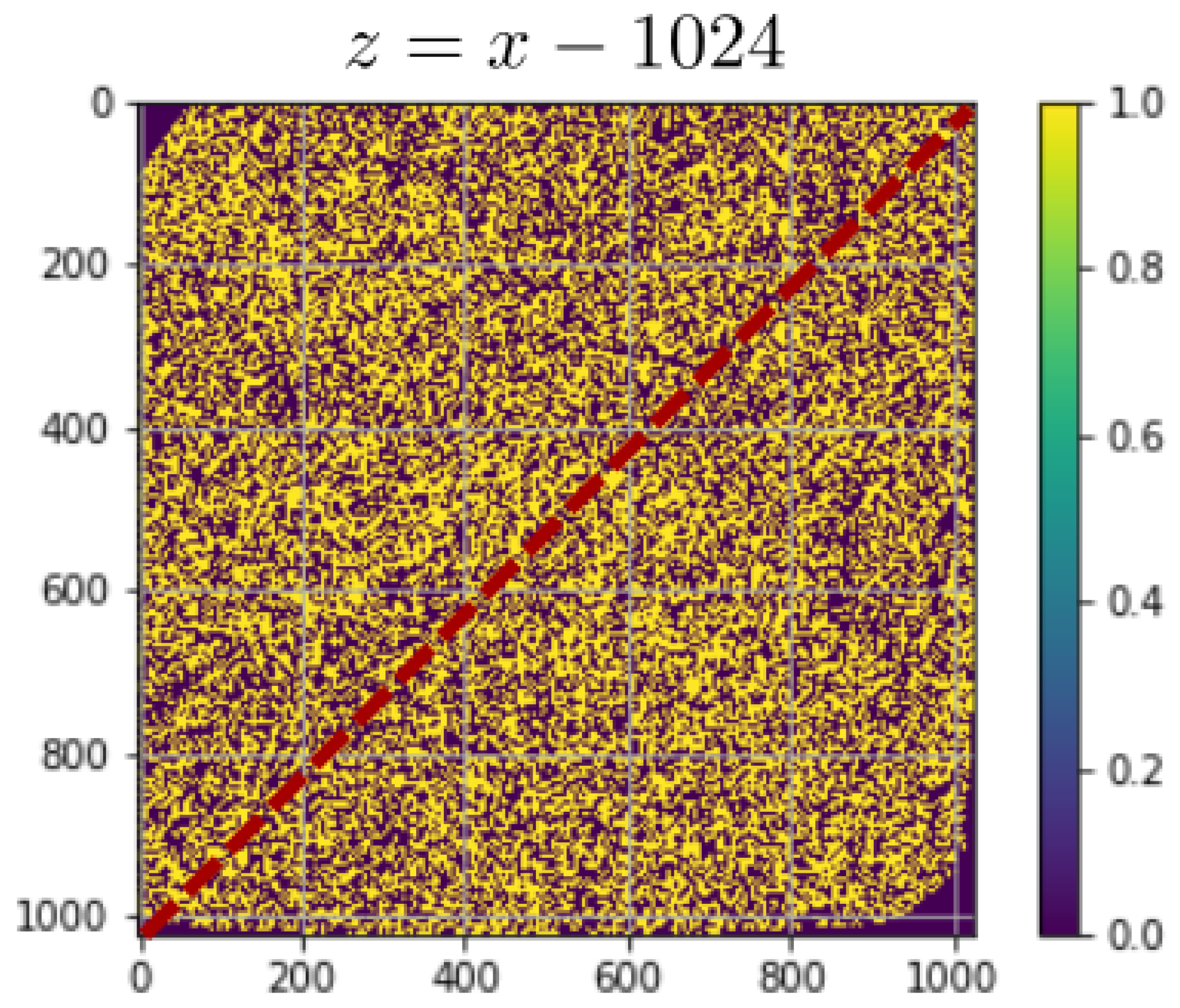
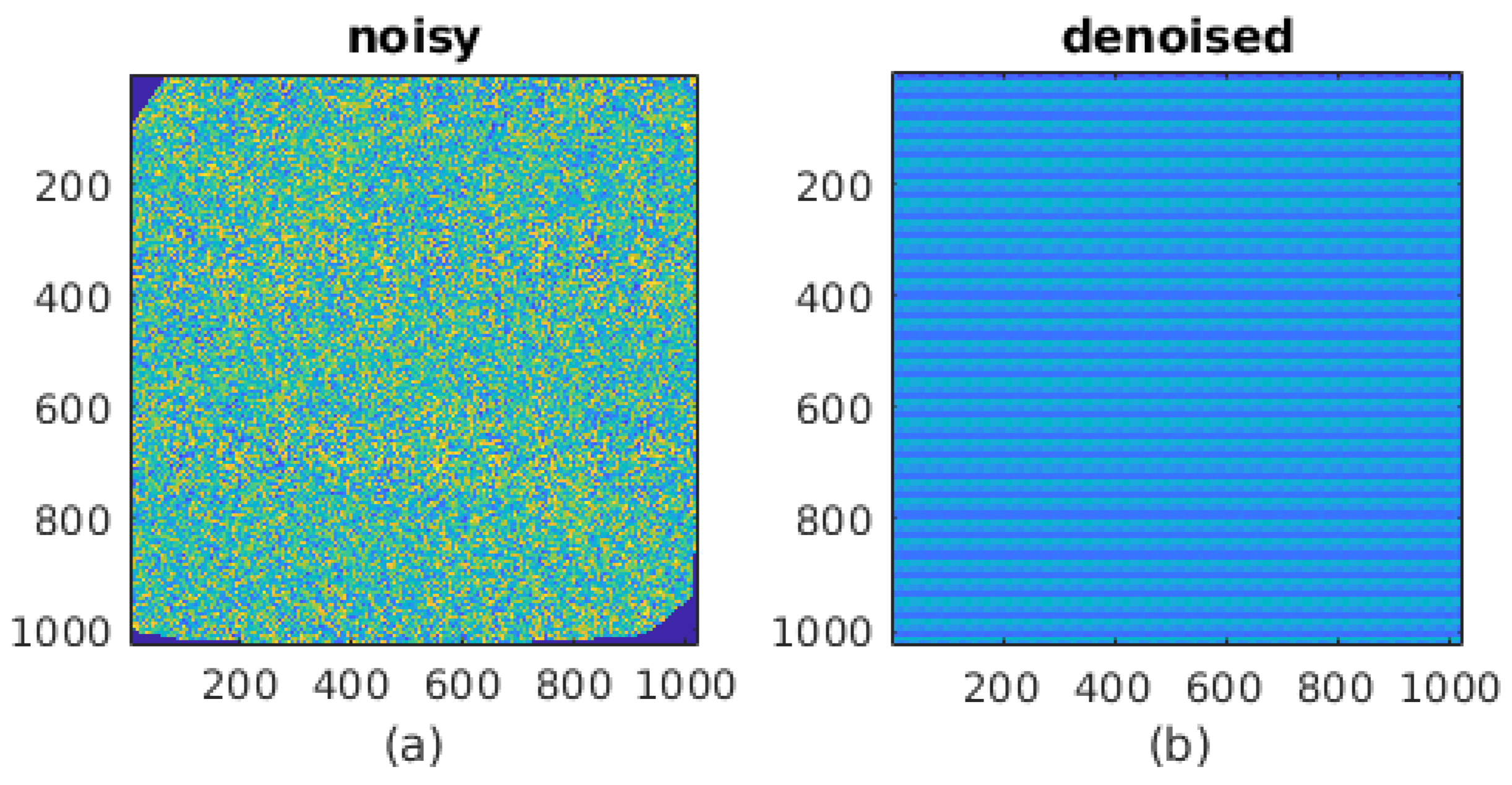


| Noisy | De-Noised | Ground Truth | |
|---|---|---|---|
| mu (arb. Units) | 2.3149 | 1.2364 | 2.5 |
| sigma | 1.0741 | 0.5069 | 0 |
| PSNR (dB) | 7.21 | 5.28 | ∞ |
| PSNR (corrected dB) | 7.21 | 13.32 | ∞ |
| # | Layer | Class | Description |
|---|---|---|---|
| 1 | ‘imageinput’ | Image Input | 28 × 28 × 1 images with ‘zerocenter’ normalization |
| 2 | ‘conv_1’ | Convolution | 16 3 × 3 × 1 conv with stride [1 1] and padding [1 1 1 1] |
| 3 | ‘relu_1’ | ReLU | ReLU |
| 4 | ‘maxpool_1’ | Max Pooling | 2 × 2 max pooling with stride [2 2] and padding [0 0 0 0] |
| 5 | ‘conv_2’ | Convolution | 32 3 × 3 × 16 conv with stride [1 1] and padding [1 1 1 1] |
| 6 | ‘relu_2’ | ReLU | ReLU |
| 7 | ‘maxpool_2’ | Max Pooling | 2 × 2 max pooling with stride [2 2] and padding [0 0 0 0] |
| 8 | ‘conv_3’ | Convolution | 64 3 × 3 × 32 conv with stride [1 1] and padding [1 1 1 1] |
| 9 | ‘relu_3’ | ReLU | ReLU |
| 10 | ‘fc’ | Fully Connected Softmax | 3 fully connected layer |
| 11 | ‘softmax’ | Softmax | softmax |
| 12 | ‘classoutput’ | Classification Output | crossentropyex with ‘0’, ‘1’, and 1 other classes |
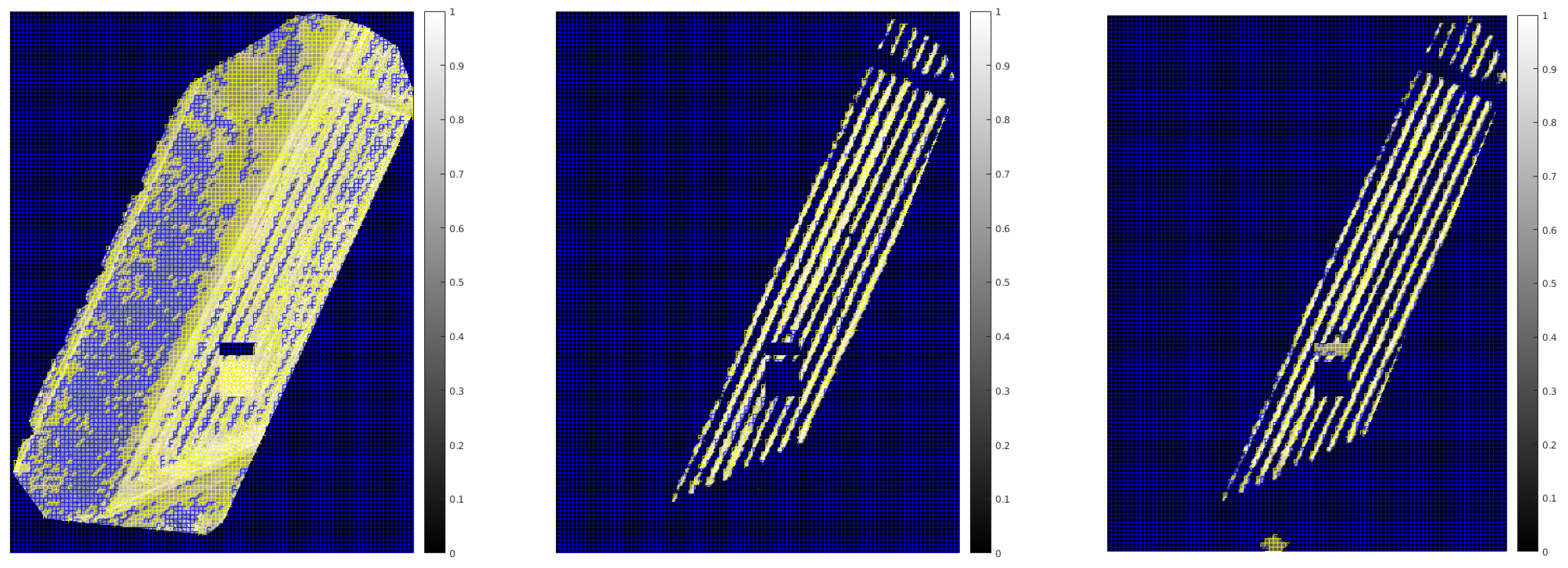
| Without Artifacts (Tiles) | With Artifacts (Tiles) | Gain % | Ground Truth Tiles | |
|---|---|---|---|---|
| Left | 4054 | 4024 | 20 | 154 |
| Centre | 1244 | 1113 | 85 | 154 |
| Right | 1397 | 1050 | 225 | 154 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyson, J.; Mancini, A.; Frontoni, E.; Zingaretti, P. Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data. Remote Sens. 2019, 11, 1859. https://doi.org/10.3390/rs11161859
Dyson J, Mancini A, Frontoni E, Zingaretti P. Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data. Remote Sensing. 2019; 11(16):1859. https://doi.org/10.3390/rs11161859
Chicago/Turabian StyleDyson, Jack, Adriano Mancini, Emanuele Frontoni, and Primo Zingaretti. 2019. "Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data" Remote Sensing 11, no. 16: 1859. https://doi.org/10.3390/rs11161859
APA StyleDyson, J., Mancini, A., Frontoni, E., & Zingaretti, P. (2019). Deep Learning for Soil and Crop Segmentation from Remotely Sensed Data. Remote Sensing, 11(16), 1859. https://doi.org/10.3390/rs11161859