Random Noise Suppression of Magnetic Resonance Sounding Data with Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation
Abstract
1. Introduction
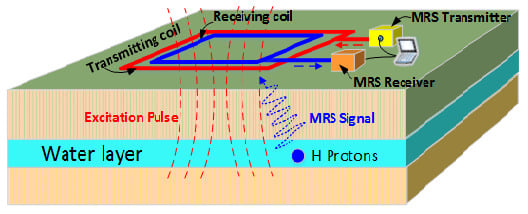
2. MRS Signal Analysis and the Classical Stacking Method
2.1. MRS Signal Analysis
2.2. Classic Stacking Method
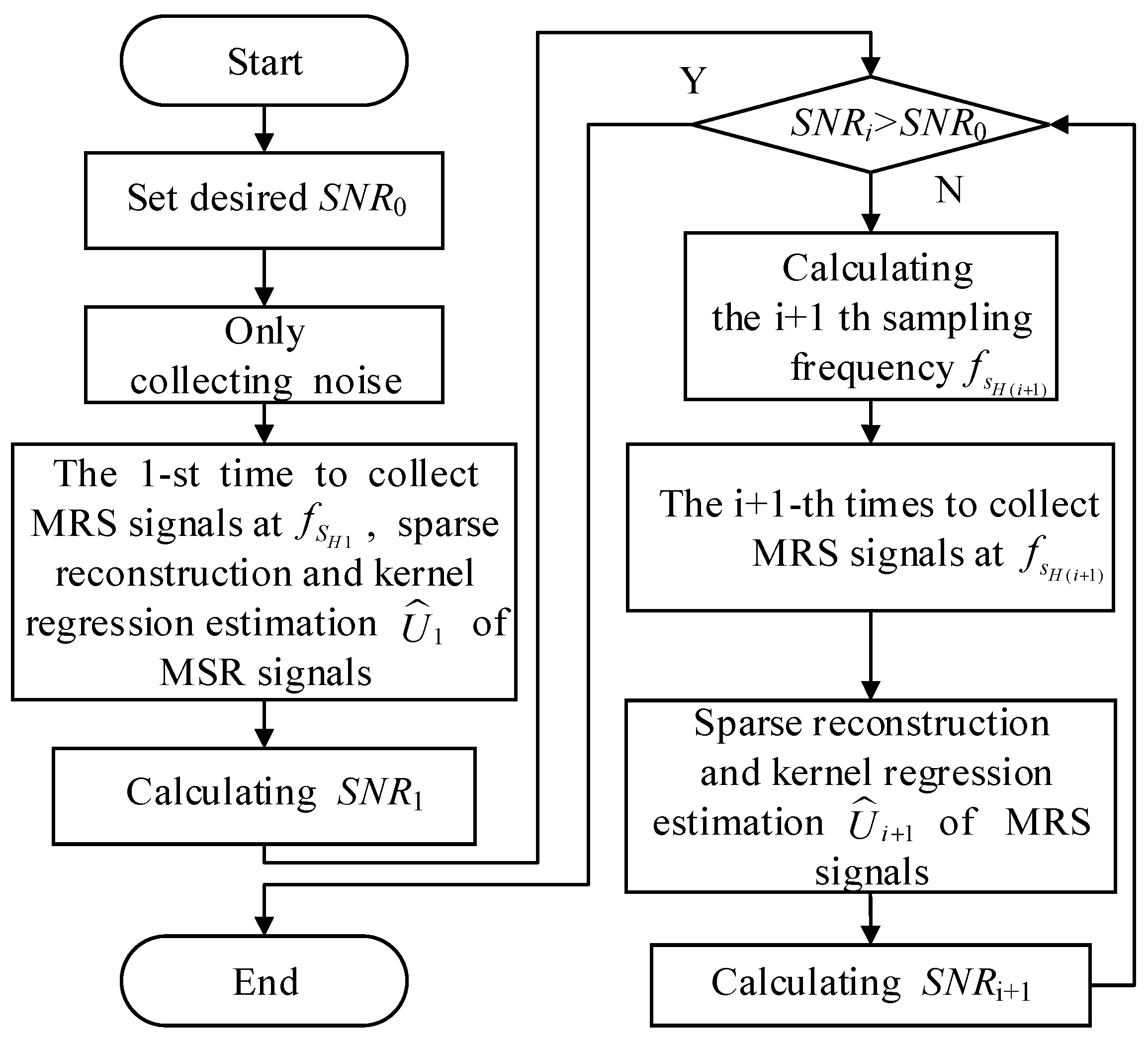
3. Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation
3.1. Overall Approach of ISSR-KRE for Suppressing Random Noise
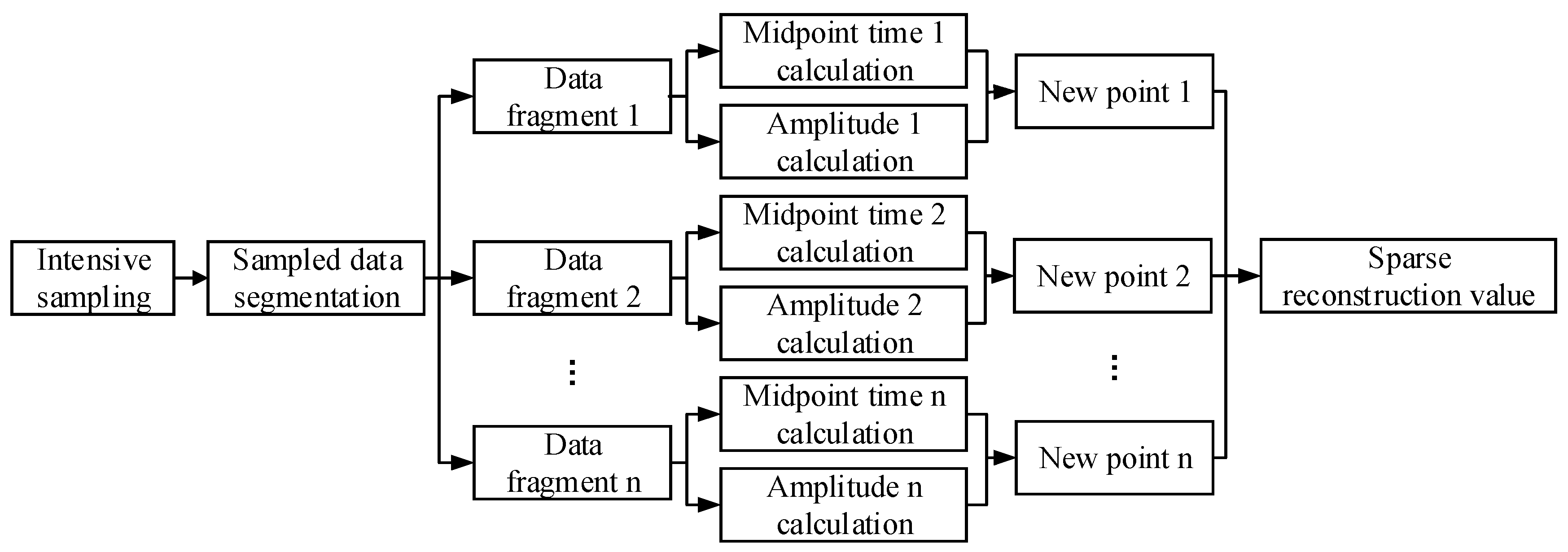
3.2. Intensive Sampling Sparse Reconstruction for Suppressing Random Noise
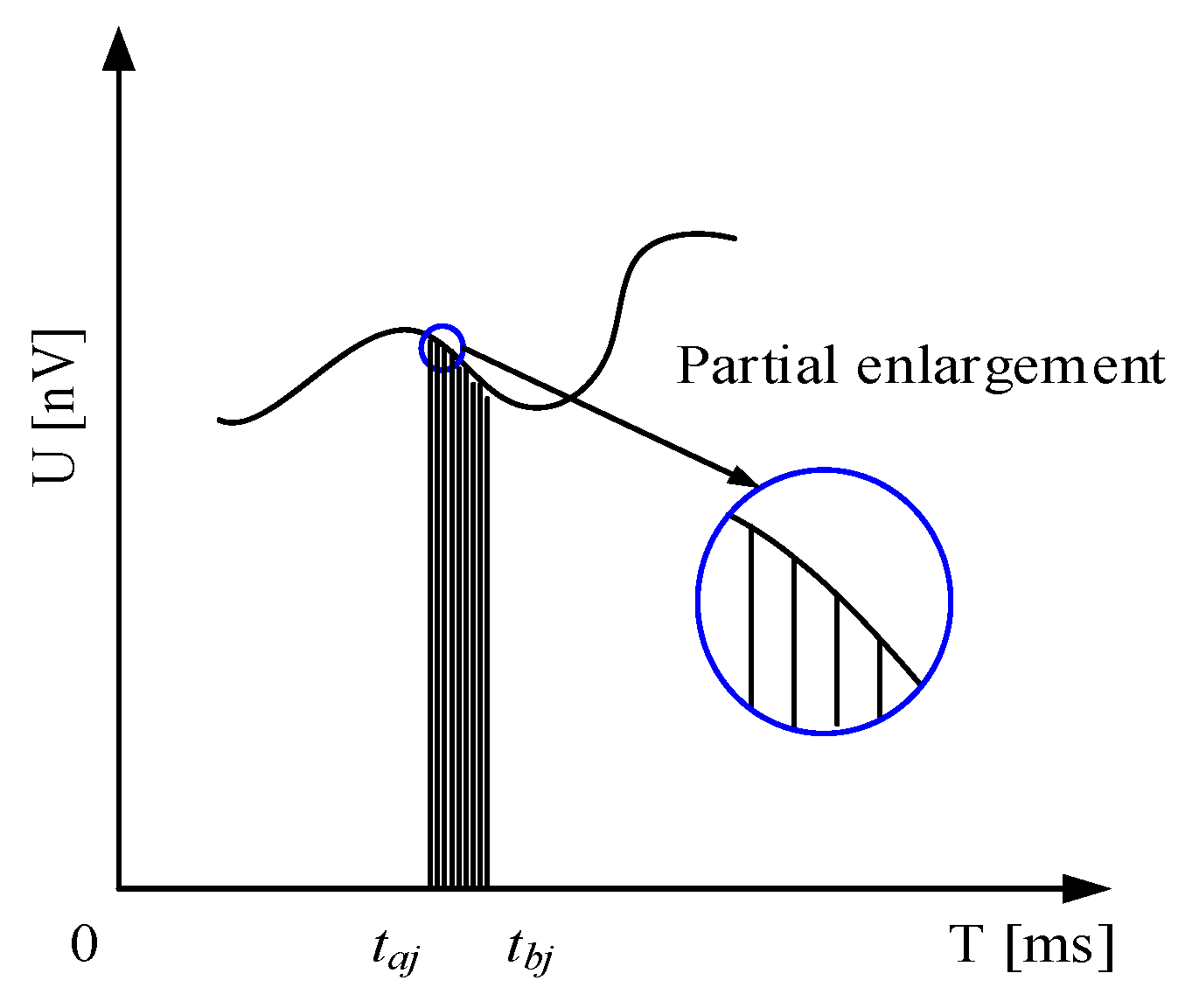
3.2.1. Basic Frequency of Sparse Reconstruction
3.2.2. ISSR Implementation Process
3.2.3. Rectangular Sparse Reconstruction
3.2.4. Trapezoidal Sparse Reconstruction
3.2.5. Simpson Sparse Reconstruction
3.3. Kernel Regression Estimation for Suppressing Random Noise
4. Numerical Simulations
4.1. Simulations of Intensive Sampling Sparse Reconstruction for Random Noise Suppression
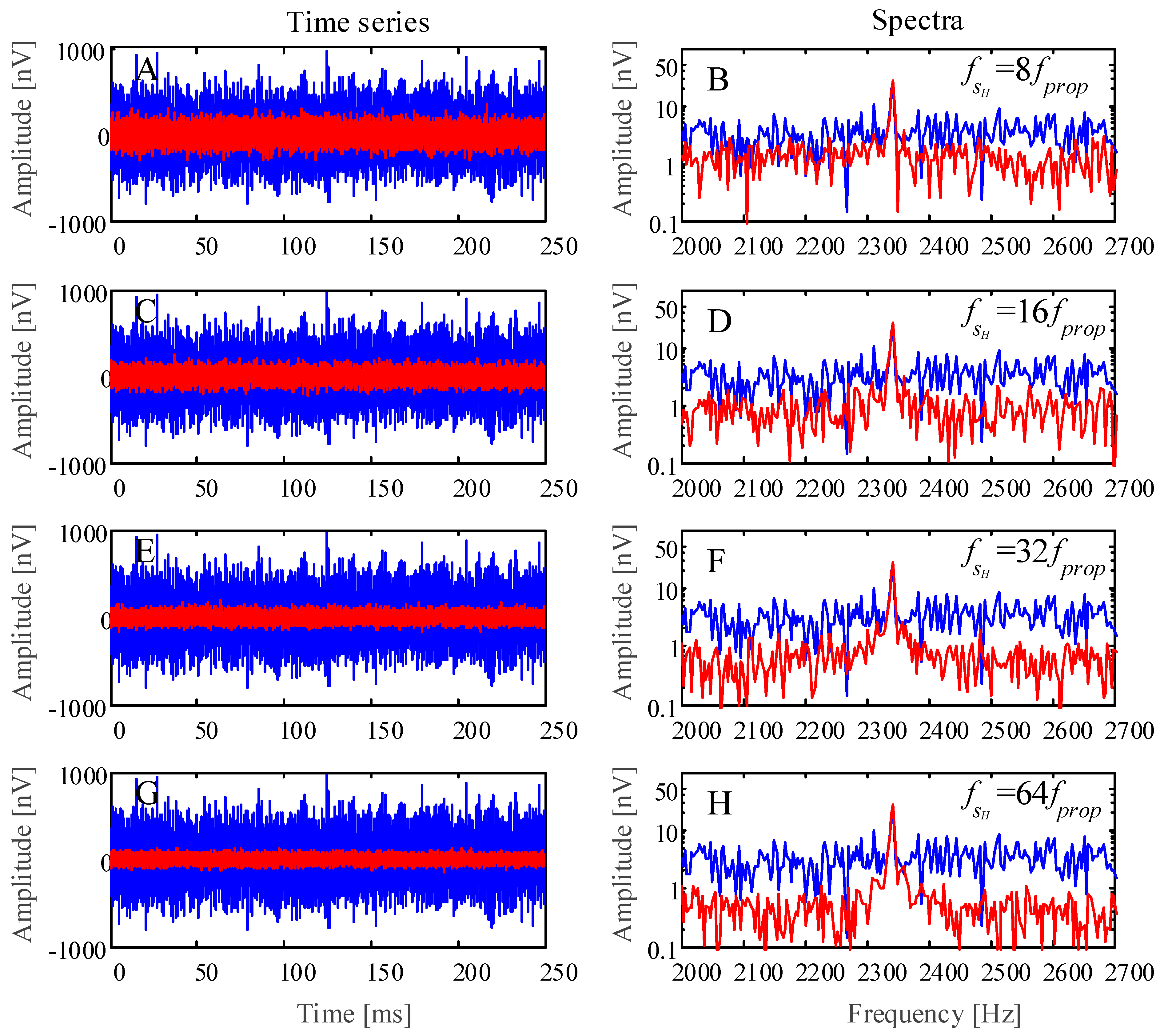
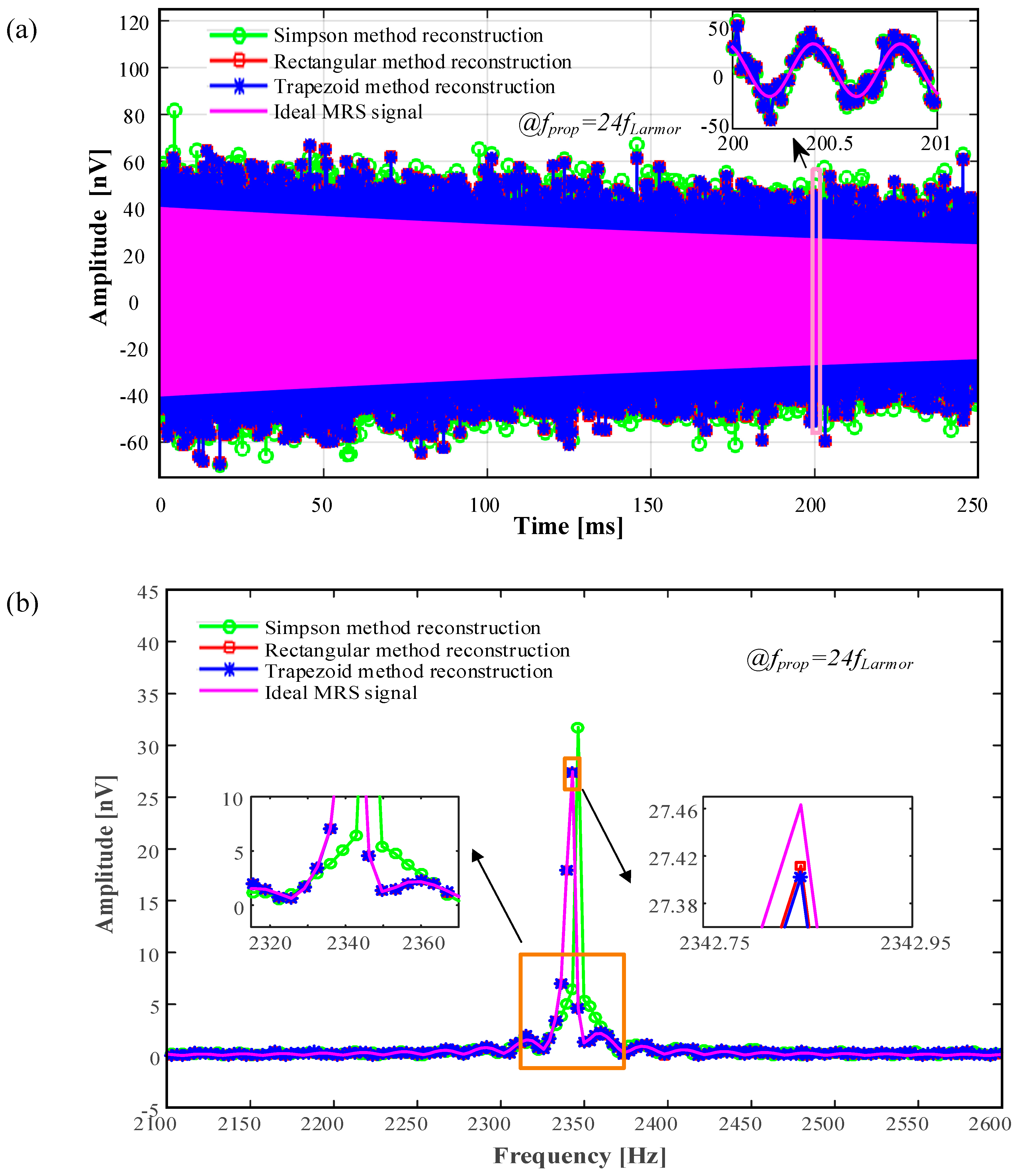
4.1.1. Sparse Reconstruction Simulation
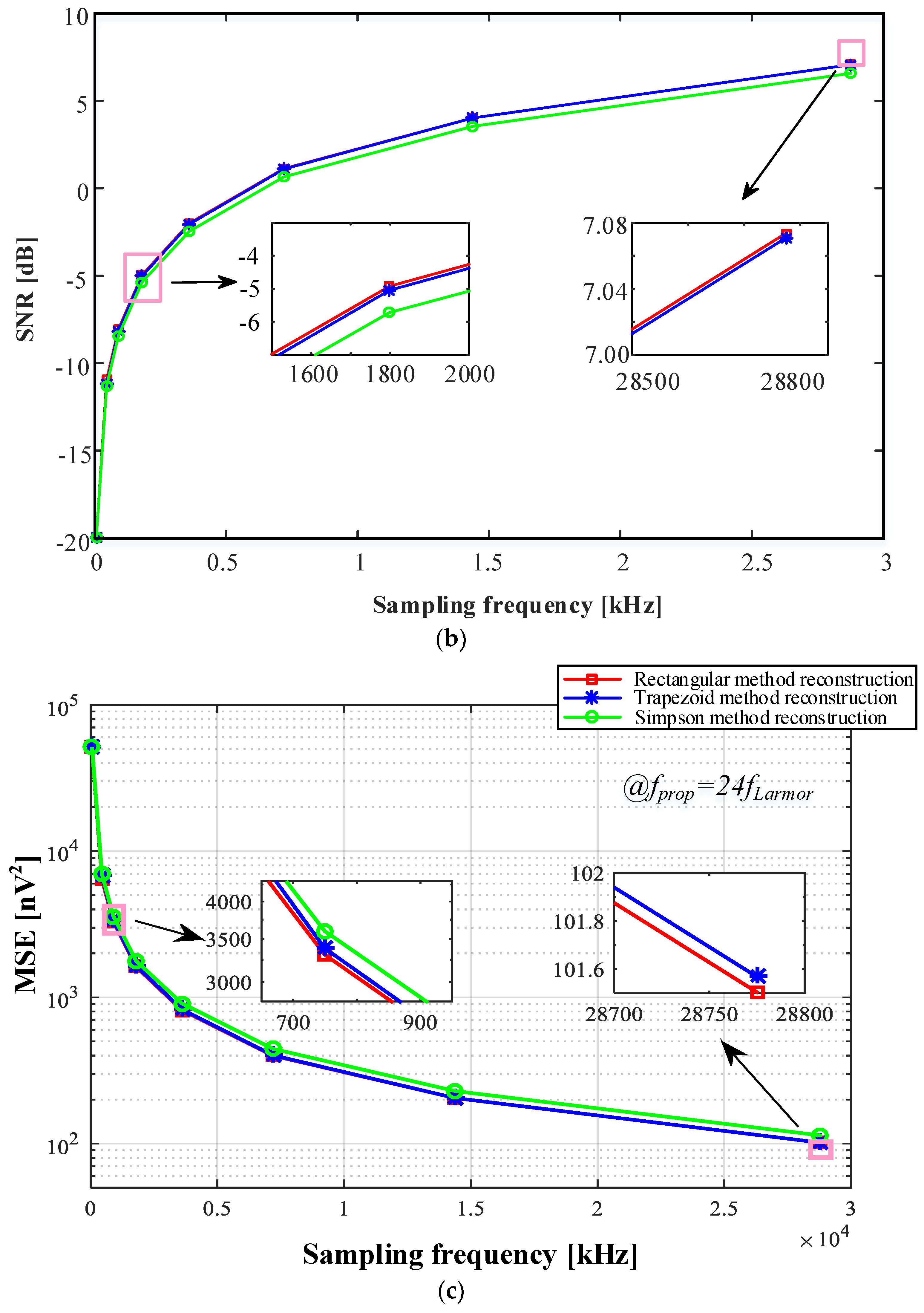
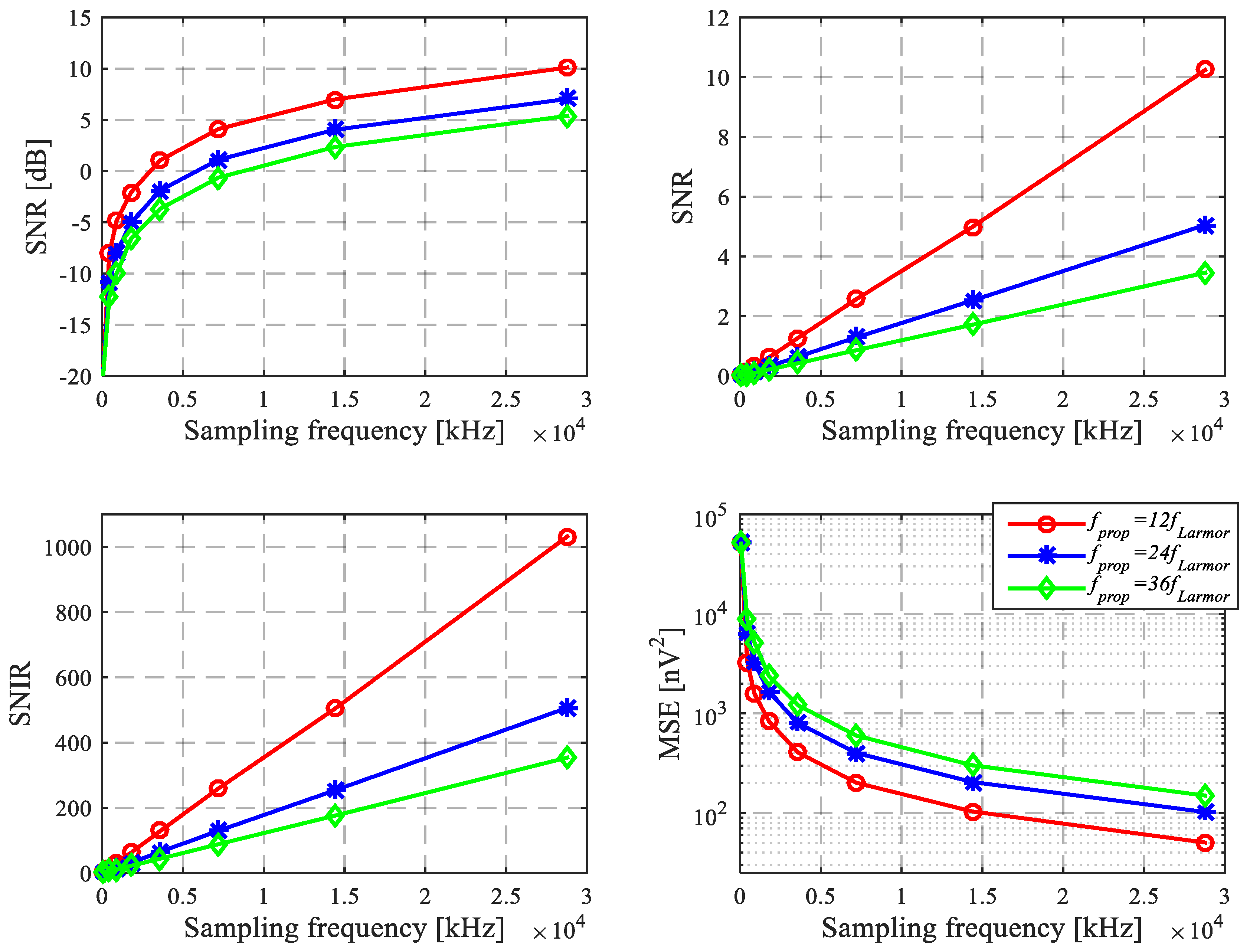
4.1.2. Comparison of Three Sparse Reconstructions
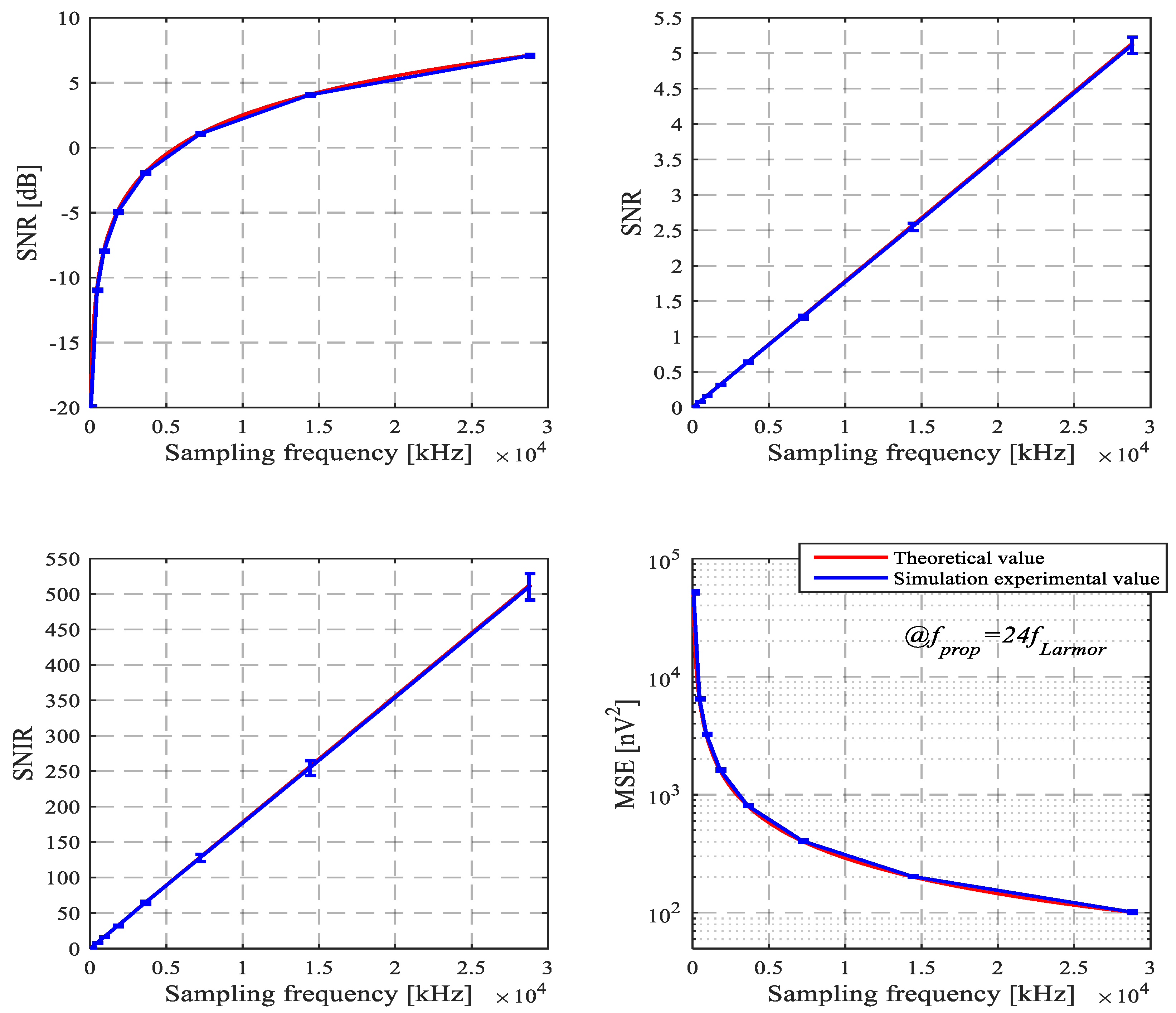
Comparison of SNR, SNIR and MSE
Waveform Comparison
Different Effect on Sparse Reconstruction
4.2. Comparison of Intensive Sampling Sparse Reconstruction and Classical Stacking Method
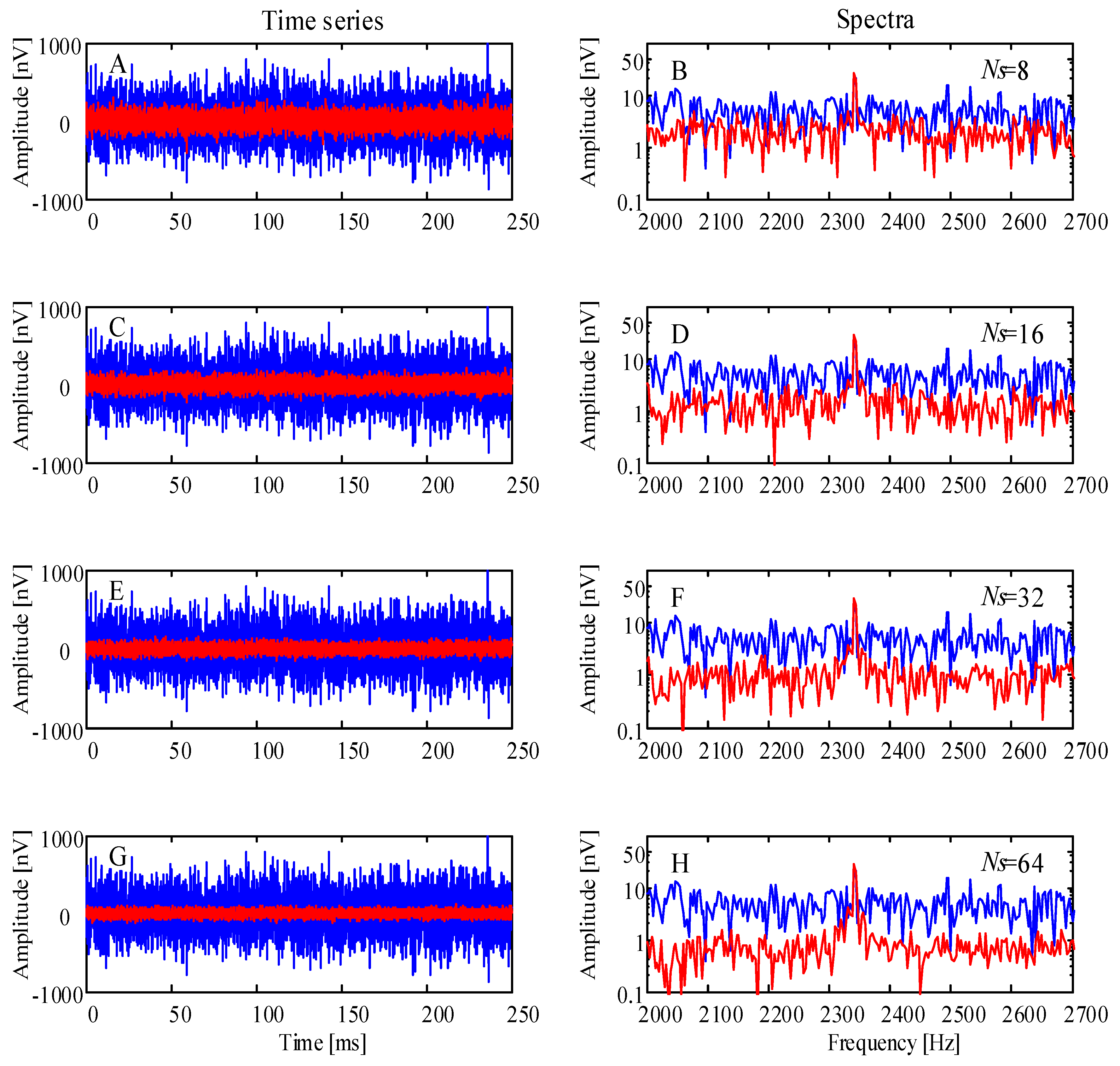
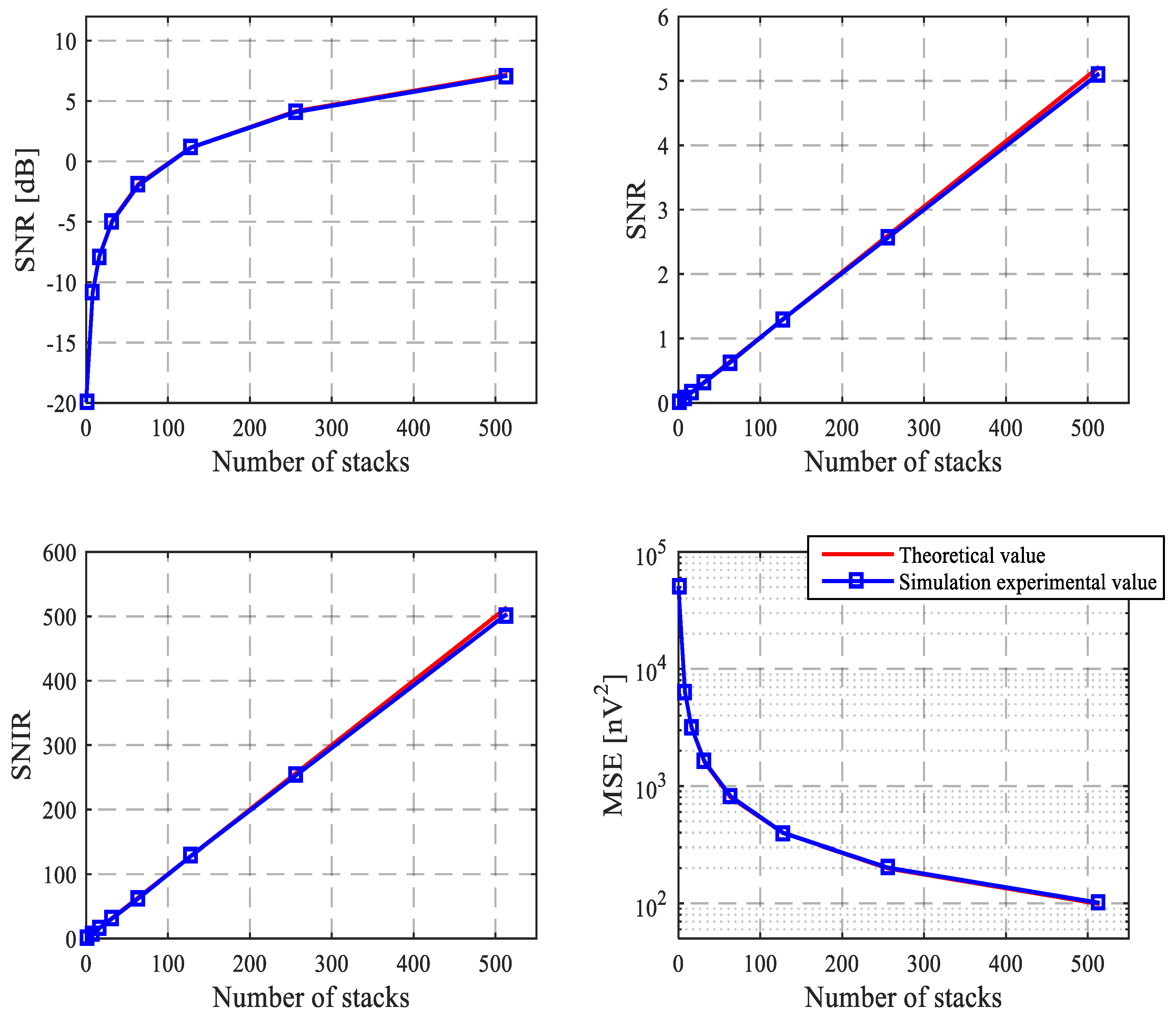
4.2.1. Simulations of Classical Stacking for Random Noise Suppression
4.2.2. Comparison of Intensive Sampling Sparse Reconstruction and Classical Stacking Method
4.3. Simulation of Kernel Regression Estimation
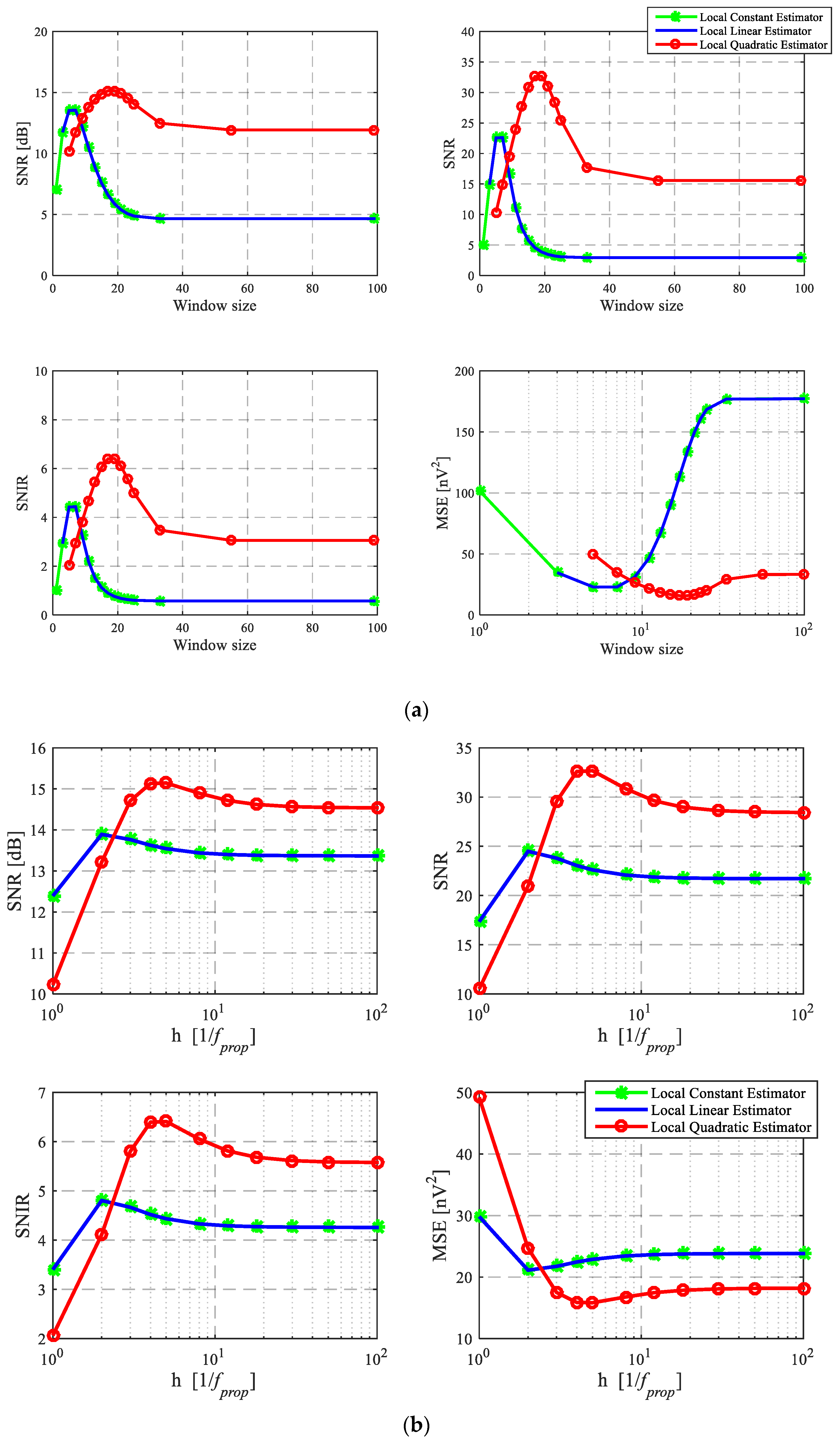
4.3.1. Window Size and Smoothing Factor Effect on the Estimation Result
Window Size Effect
Smoothing Factor Effect
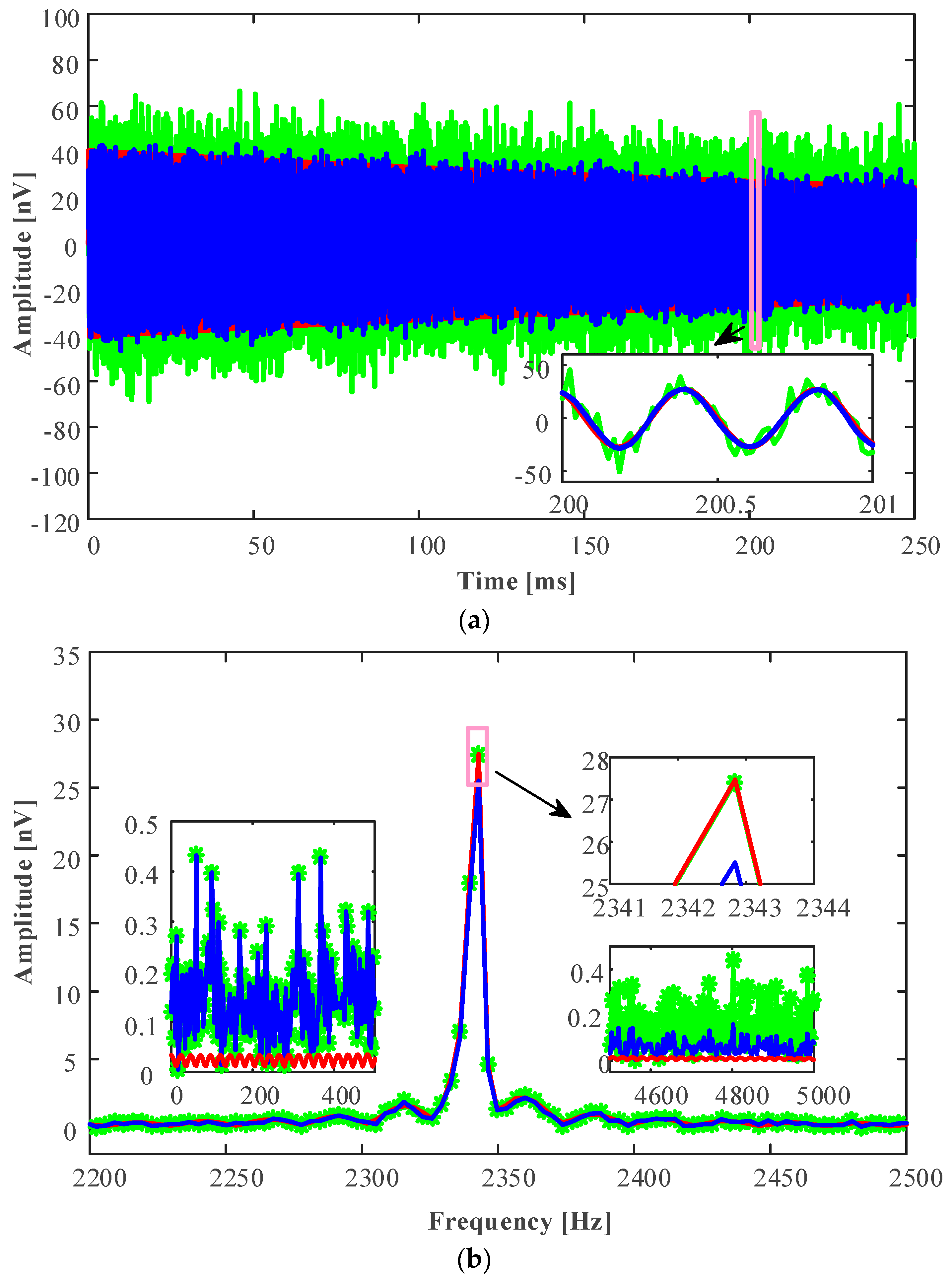
4.3.2. Waveform Comparison of Kernel Regression Estimation
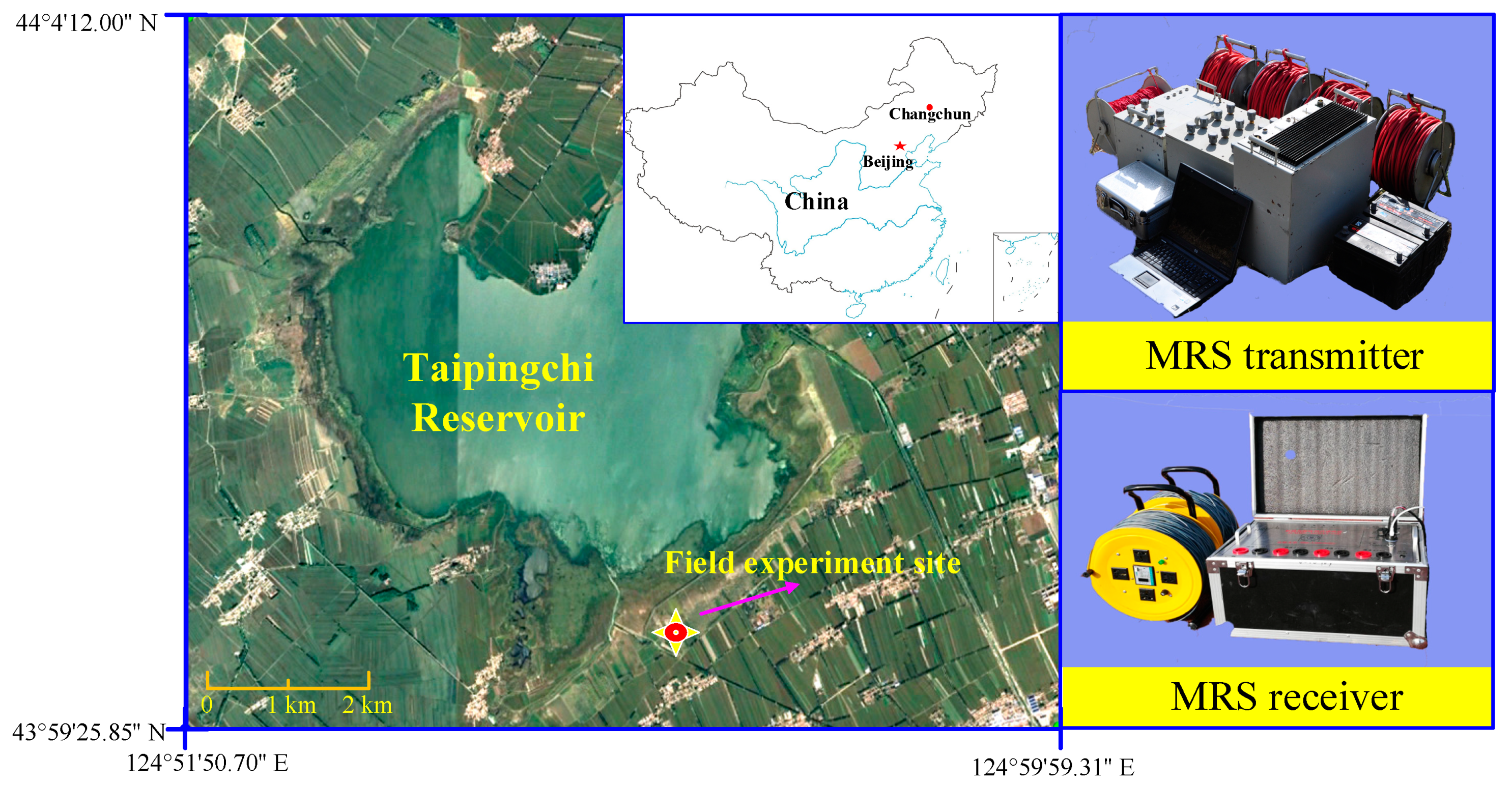
5. Field Experiments
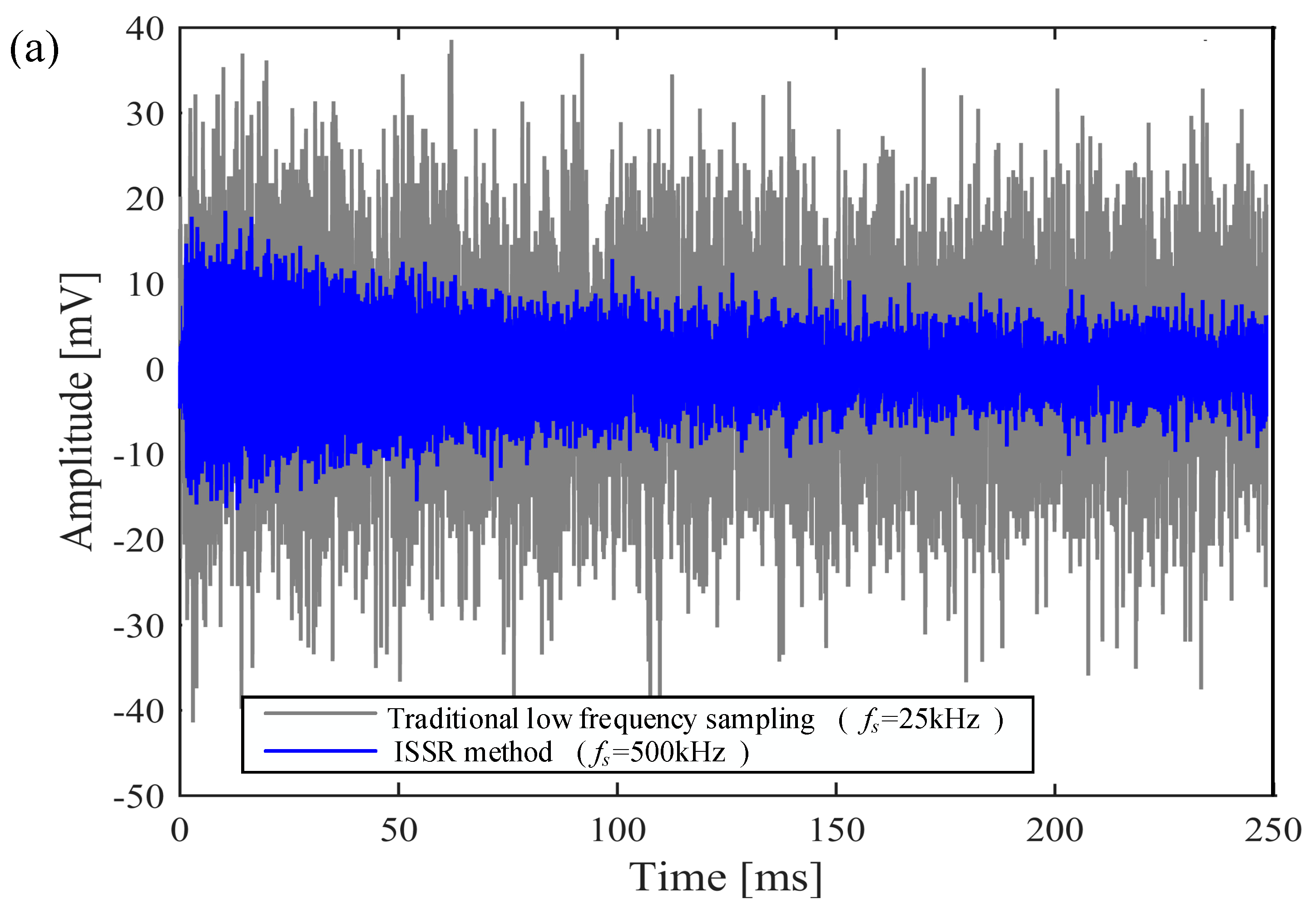
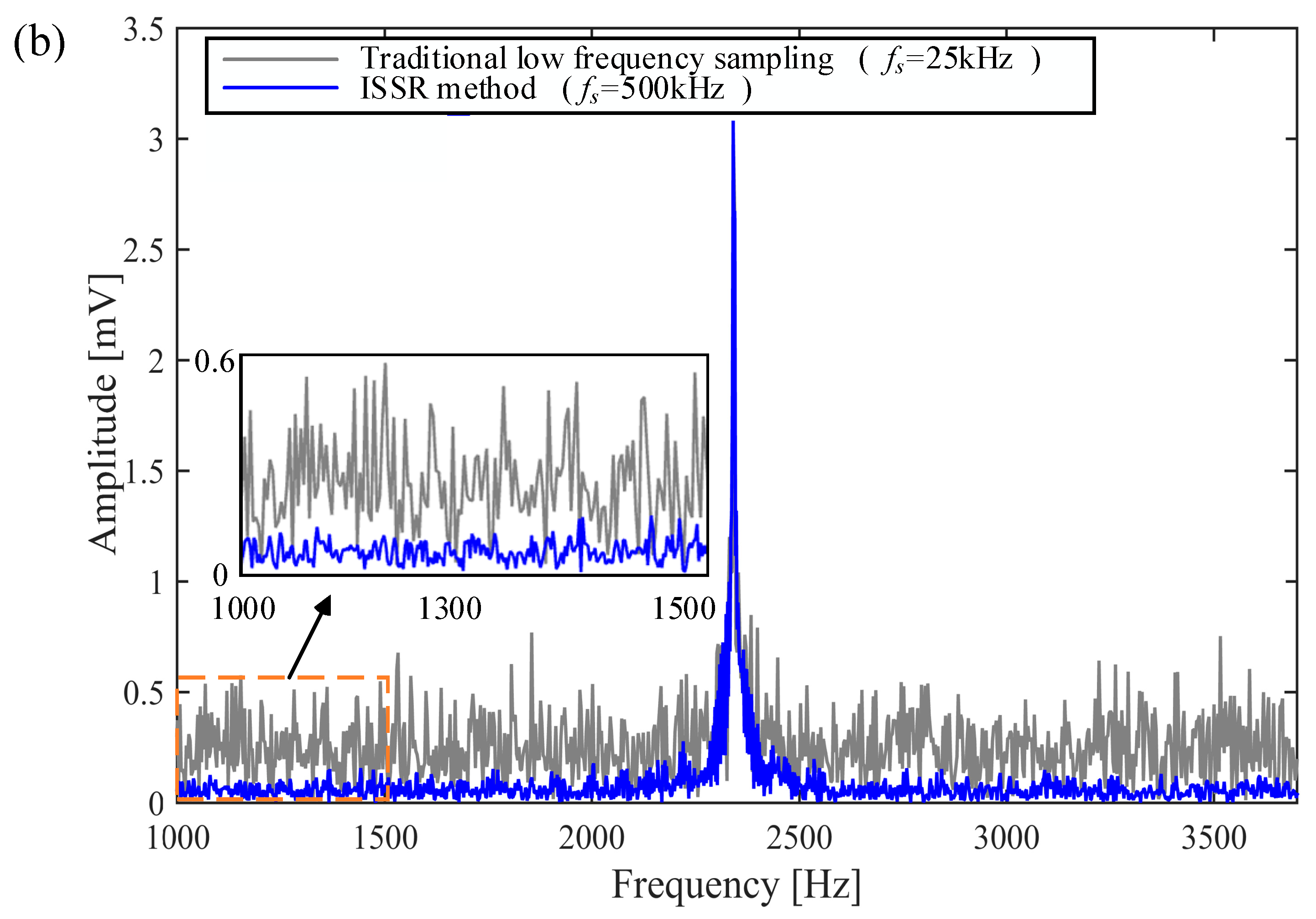
5.1. Laboratory Experiment
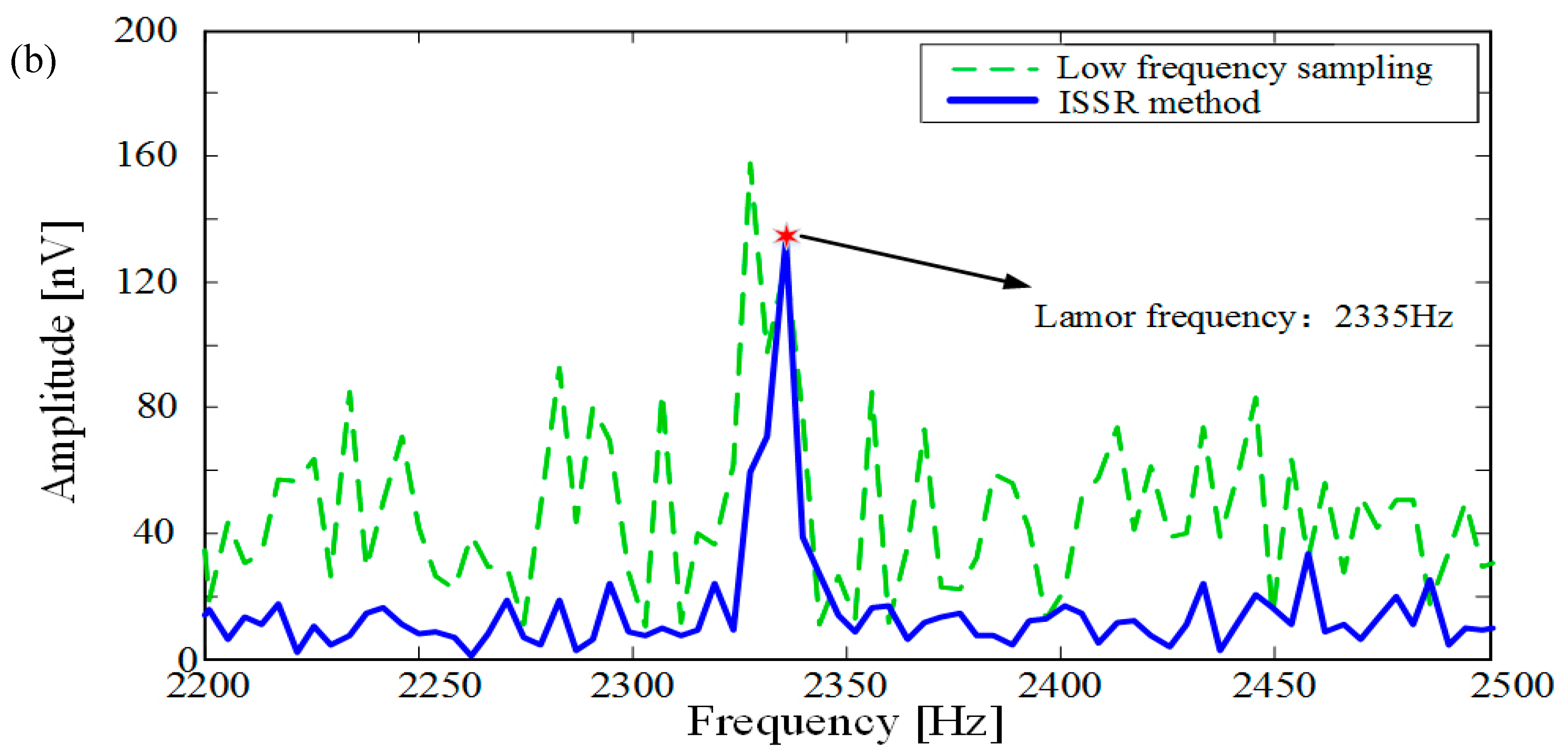
5.2. Processing Experiment of Noisy MRS Data
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Sparse Reconstruction
References
- Hertrich, M.; Braun, M.; Gunther, T.; Green, A.G.; Yaramanci, U. Surface nuclear magnetic resonance tomography. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3752–3759. [Google Scholar] [CrossRef]
- Legchenko, A.; Valla, P. Removal of power-line harmonics from proton magnetic resonance measurements. J. Appl. Geophys. 2003, 53, 10–120. [Google Scholar] [CrossRef]
- Liu, L.; Grombacher, D.; Auken, E.; Larsen, J.J. Removal of Co-Frequency Powerline Harmonics from Multichannel Surface NMR Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 53–57. [Google Scholar] [CrossRef]
- Chen, H.M.; Wang, H.C.; Chai, J.W.; Chen, C.C.C.; Xue, B.; Wang, L.; Yu, C.; Wang, Y.; Song, M.; Chang, C.I. A Hyperspectral Imaging Approach to White Matter Hyperintensities Detection in Brain Magnetic Resonance Images. Remote Sens. 2017, 9, 1174. [Google Scholar] [CrossRef]
- Powers, J.M.; Ioachim, G.; Stroman, P.W. Ten Key Insights into the Use of Spinal Cord fMRI. Brain Sci. 2018, 8, 173. [Google Scholar] [CrossRef] [PubMed]
- Legchenko, A.; Descloitres, M.; Bost, A.; Ruiz, L.; Reddy, M.; Girard, J.F.; Sekhar, M.; Kumar, M.S.M.; Braun, J.J. Resolution of MRS applied to the characterization of hard-rock aquifers. Groundwater 2006, 44, 547–554. [Google Scholar] [CrossRef] [PubMed]
- Walsh, D.O. Multi-channel surface NMR instrumentation and software for 1D/2D groundwater investigations. J. Appl. Geophys. 2008, 66, 140–150. [Google Scholar] [CrossRef]
- Qin, S.; Ma, Z.; Jiang, C.; Lin, J.; Xue, Y.; Shang, X.; Li, Z. Response Characteristics and Experimental Study of Underground Magnetic Resonance Sounding Using a Small-Coil Sensor. Sensors 2017, 17, 2127. [Google Scholar] [CrossRef]
- Valois, R.; Vouillamoz, J.M.; Lun, S.; Arnout, L. Mapping groundwater reserves in northwestern Cambodia with the combined use of data from lithologs and time-domain-electromagnetic and magnetic-resonance soundings. Hydrogeol. J. 2018, 26, 1187–1200. [Google Scholar] [CrossRef]
- Parsekian, A.D.; Creighton, A.L.; Jones, B.M.; Arp, C.D. Surface nuclear magnetic resonance observations of permafrost thaw below floating, bedfast and transitional ice lakes. Geophysics 2019, 84, EN33–EN45. [Google Scholar] [CrossRef]
- Garambois, S.; Legchenko, A.; Vincent, C.; Thibert, E. Ground-penetrating radar and surface nuclear magnetic resonance monitoring of an englacial water-filled cavity in the polythermal glacier of Tete Rousse. Geophysics 2016, 81, WA131–WA146. [Google Scholar] [CrossRef]
- Shang, X.; Jiang, C.; Ma, Z.; Qin, S. Combined System of Magnetic Resonance Sounding and Time-Domain Electromagnetic Method for Water-Induced Disaster Detection in Tunnels. Sensors 2018, 18, 3508. [Google Scholar] [CrossRef] [PubMed]
- Falzone, S.; Keating, K. Algorithms for removing surface water signals from surface nuclear magnetic resonance infiltration surveys. Geophysics 2016, 81, WB97–WB107. [Google Scholar] [CrossRef]
- Ghanati, R.; Hafizi, M.K.; Fallahsafari, M. Surface nuclear magnetic resonance signals recovery by integration of a non-linear decomposition method with statistical analysis. Geophys. Prospect. 2016, 64, 489–504. [Google Scholar] [CrossRef]
- Liu, L.; Grombacher, D.; Auken, E.; Larsen, J.J. Complex envelope retrieval for surface nuclear magnetic resonance data using spectral analysis. Geophys. J. Int. 2019, 217, 894–905. [Google Scholar] [CrossRef]
- Jiang, C.; Lin, J.; Duan, Q.; Sun, S.; Tian, B. Statistical stacking and adaptive notch filter to remove high-level electromagnetic noise from MRS measurements. Near Surf. Geophys. 2011, 9, 459–468. [Google Scholar] [CrossRef]
- Larsen, J.J. Model-based subtraction of spikes from surface nuclear magnetic resonance data. Geophysics 2016, 81, WB1–WB8. [Google Scholar] [CrossRef]
- Larsen, J.; Dalgaard, E.; Auken, E. Noise cancelling of MRS signals combining model-based removal of powerline harmonics and multichannel Wiener filtering. Geophys. J. Int. 2014, 196, 828–836. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, C.; Mueller-Petke, M. An alternative approach to handling co-frequency harmonics in surface nuclear magnetic resonance data. Geophys. J. Int. 2018, 215, 1962–1973. [Google Scholar] [CrossRef]
- Dalgaard, E.; Christiansen, P.; Larsen, J.J.; Auken, E. A temporal and spatial analysis of anthropogenic noise sources affecting SNMR. J. Appl. Geophys. 2014, 110, 34–42. [Google Scholar] [CrossRef]
- Legchenko, A.; Valla, P. Processing of surface proton magnetic resonance signals using non-linear fitting. J. Appl. Geophys. 1998, 39, 77–83. [Google Scholar] [CrossRef]
- Dalgaard, E.; Auken, E.; Larsen, J.J. Adaptive noise cancelling of multichannel magnetic resonance sounding signals. Geophys. J. Int. 2012, 191, 88–100. [Google Scholar] [CrossRef]
- Ghanati, R.; Hafizi, M.K.; Mahmoudvand, R.; Fallahsafari, M. Filtering and parameter estimation of surface-NMR data using singular spectrum analysis. J. Appl. Geophys. 2016, 130, 118–130. [Google Scholar] [CrossRef]
- Lin, T.; Zhang, Y.; Yi, X.; Fan, T.; Wan, L. Time-frequency peak filtering for random noise attenuation of magnetic resonance sounding signal. Geophys. J. Int. 2018, 213, 727–738. [Google Scholar] [CrossRef]
- Trushkin, D.V.; Shushakov, O.A.; Legchenko, A. The potential of a noise-reducing antenna for surface NMR groundwater surveys in the Earth’s magnetic field. Geophys. Prospect. 1994, 42, 855–862. [Google Scholar] [CrossRef]
- Behroozmand, A.A.; Auken, E.; Fiandaca, G.; Rejkjaer, S. Increasing the resolution and the signal-to-noise ratio of magnetic resonance sounding data using a central loop configuration. Geophys. J. Int. 2016, 205, 243–256. [Google Scholar] [CrossRef]
- Karine, A.; Toumi, A.; Khenchaf, A.; El Hassouni, M. Radar Target Recognition Using Salient Keypoint Descriptors and Multitask Sparse Representation. Remote Sens. 2018, 10, 843. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, Z.; Zhang, L.; Lu, Q.; Wang, K. Application of Mathematical Morphological Filtering to Improve the Resolution of Chang’E-3 Lunar Penetrating Radar Data. Remote Sens. 2019, 11, 524. [Google Scholar] [CrossRef]
- Takeda, H.; Farsiu, S.; Milanfar, P. Kernel Regression for Image Processing and Reconstruction. IEEE Trans. Image Process. 2007, 16, 349–366. [Google Scholar] [CrossRef]
- Legchenko, A. Magnetic Resonance Imaging for Groundwater; ISTE Ltd: London, UK, 2013. [Google Scholar]
- Legchenko, A.; Valla, P. A review of the basic principles for proton magnetic resonance sounding measurements. J. Appl. Geophys. 2002, 50, 3–19. [Google Scholar] [CrossRef]
- Li, Q.; Wang, N.; Yi, D. Numerical Analysis, 5th ed.; Tsinghua University Press: Beijing, China, 2008; pp. 97–135. [Google Scholar]
- Sheng, Z.; Xie, S.; Pan, C. Probability Theory and Mathematical Statistics, 4th ed.; Higher Education Press: Beijing, China, 2008; pp. 76–83. [Google Scholar]


| 0.2519 | 0.0999 | 0.0610 | 0.0487 | 0.0253 | 0.0032 | 0.0027 | |
| 0.3419 | 0.3650 | 0.3974 | 0.4625 | 0.4689 | 0.4814 | 0.4970 |
| 1 | 8 | 16 | 32 | 64 | |
|---|---|---|---|---|---|
| −20 | −10.9502 | −7.8772 | −4.9493 | −1.9423 | |
| 1 | 7.8387 | 15.9964 | 32.3185 | 63.2067 |
| −20 | −10.9537 | −7.8869 | −4.9097 | −1.9680 | |
| 1 | 7.7996 | 15.8032 | 31.3668 | 61.7511 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Zhang, J.; Yu, Z.; Zhao, F.; Sun, Y. Random Noise Suppression of Magnetic Resonance Sounding Data with Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation. Remote Sens. 2019, 11, 1829. https://doi.org/10.3390/rs11151829
Yao X, Zhang J, Yu Z, Zhao F, Sun Y. Random Noise Suppression of Magnetic Resonance Sounding Data with Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation. Remote Sensing. 2019; 11(15):1829. https://doi.org/10.3390/rs11151829
Chicago/Turabian StyleYao, Xiaokang, Jianmin Zhang, Zhenyang Yu, Fa Zhao, and Yong Sun. 2019. "Random Noise Suppression of Magnetic Resonance Sounding Data with Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation" Remote Sensing 11, no. 15: 1829. https://doi.org/10.3390/rs11151829
APA StyleYao, X., Zhang, J., Yu, Z., Zhao, F., & Sun, Y. (2019). Random Noise Suppression of Magnetic Resonance Sounding Data with Intensive Sampling Sparse Reconstruction and Kernel Regression Estimation. Remote Sensing, 11(15), 1829. https://doi.org/10.3390/rs11151829