Passive Bistatic Ground-Based Synthetic Aperture Radar: Concept, System, and Experiment Results
Abstract
1. Introduction
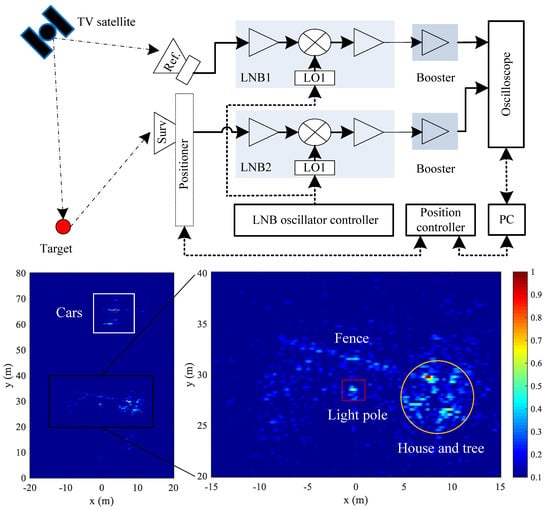
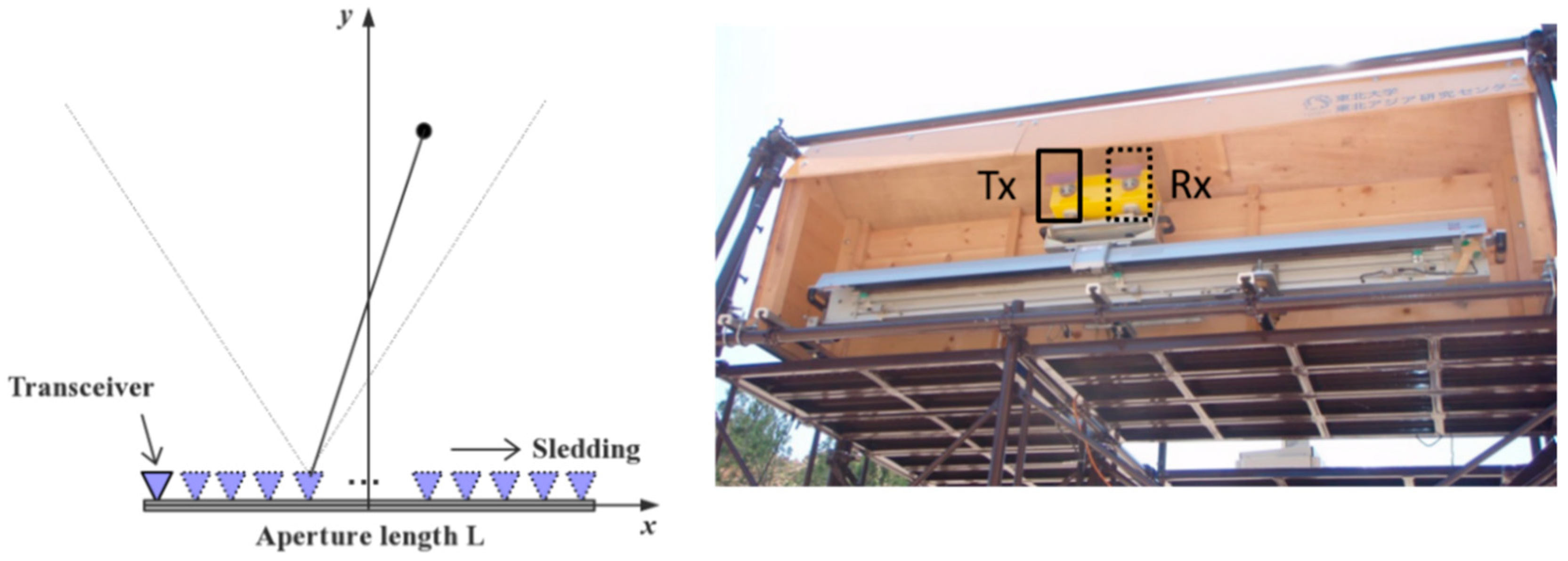
2. System Overview
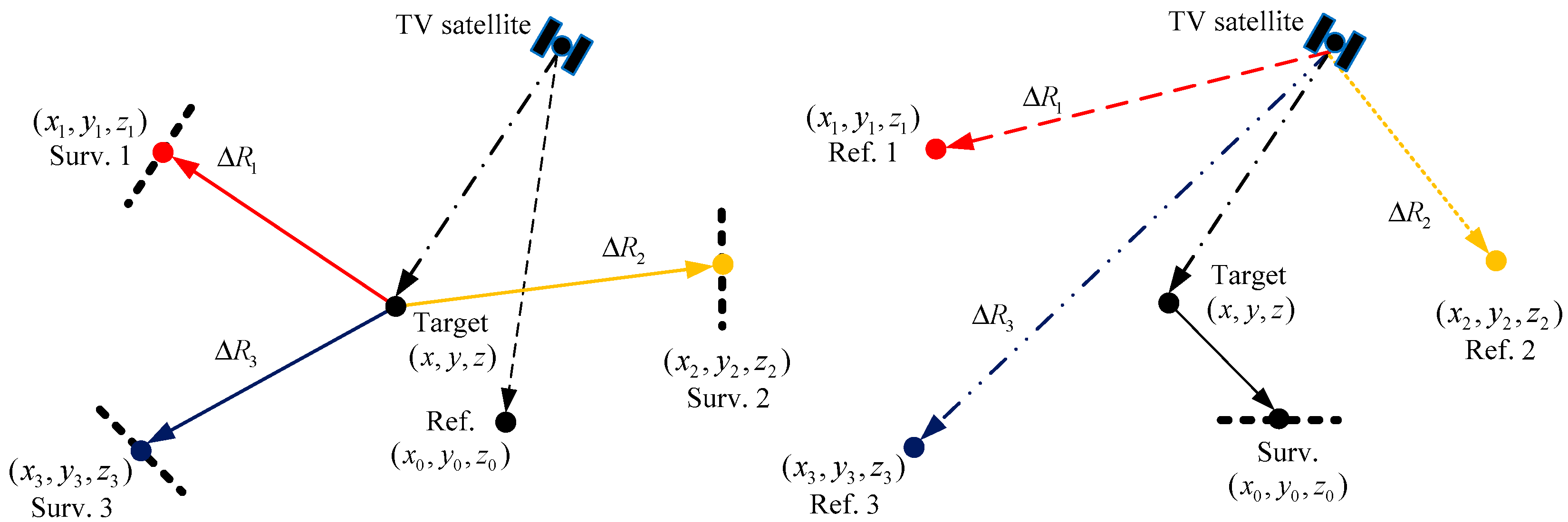
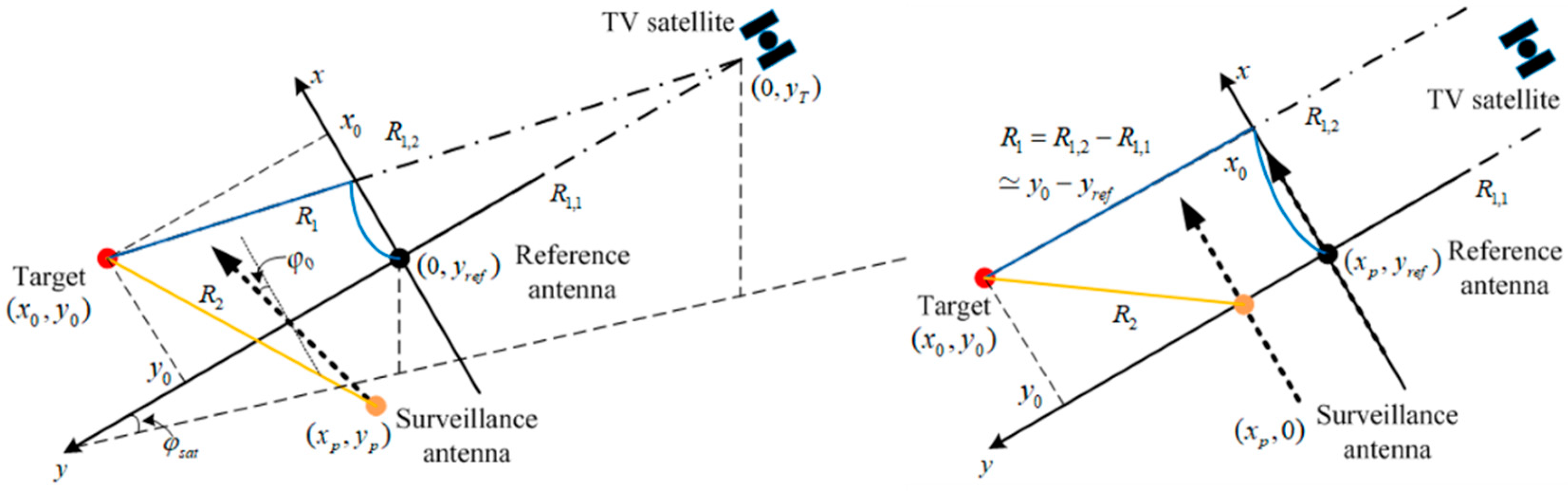
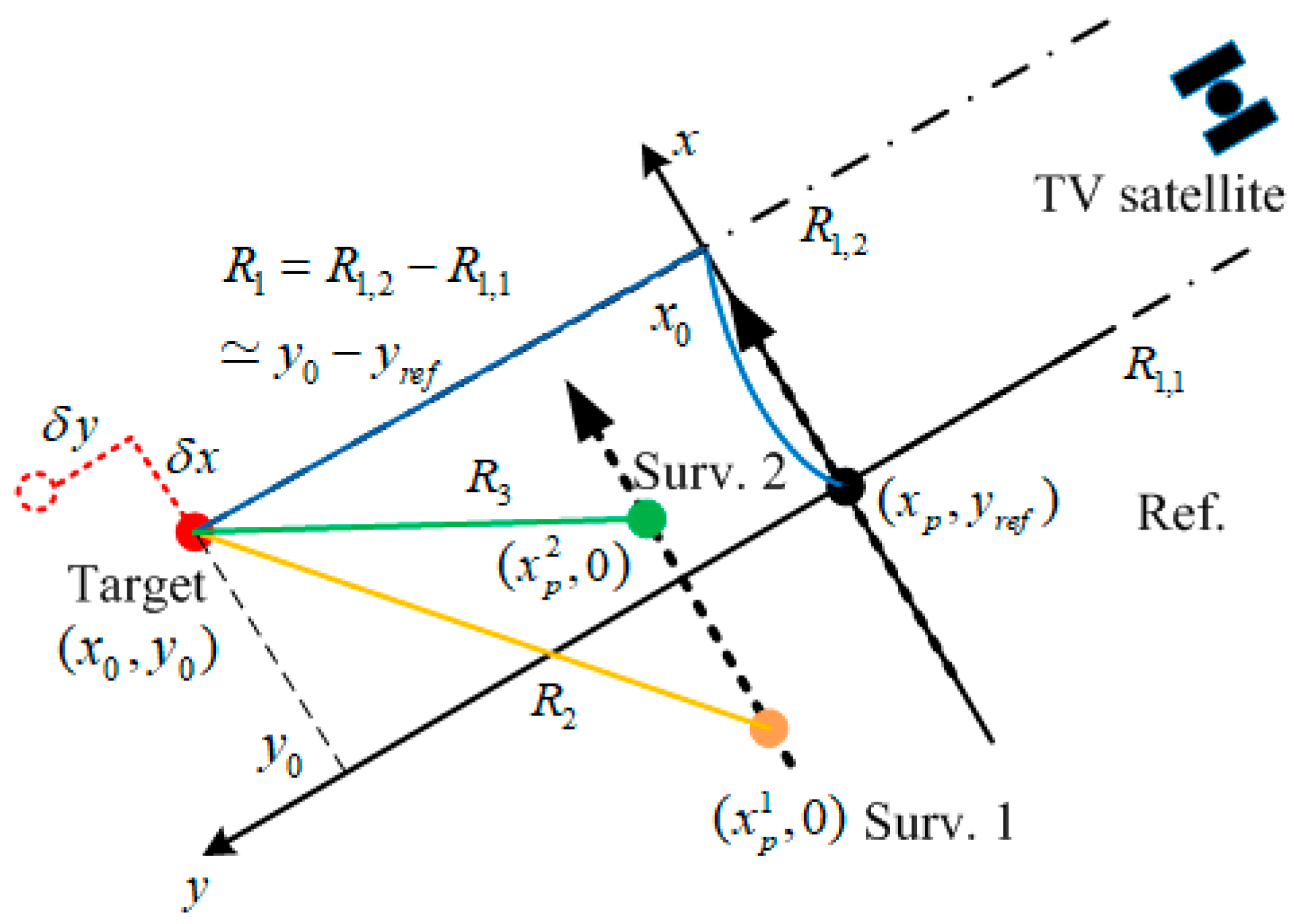
2.1. PB-GB-SAR Concept
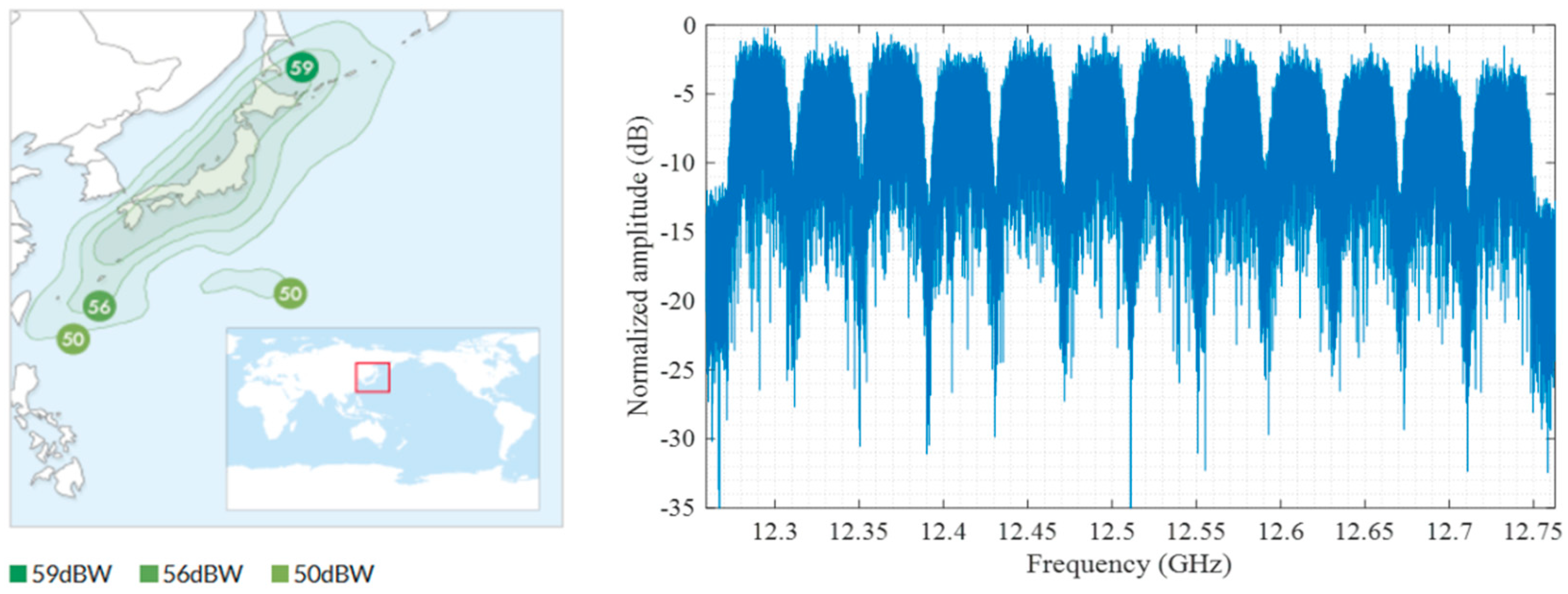
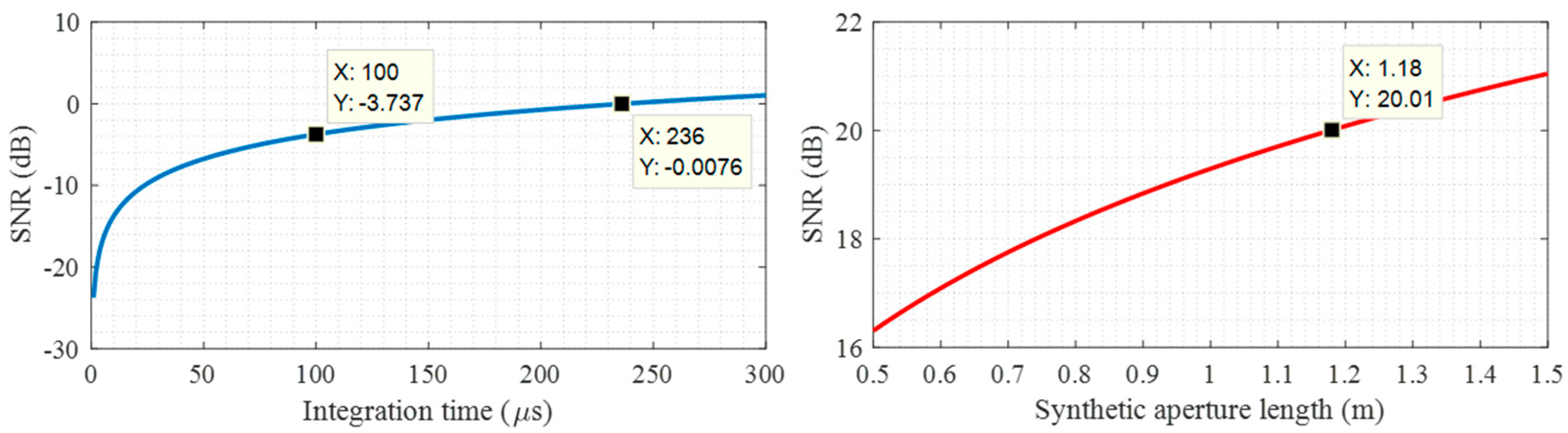
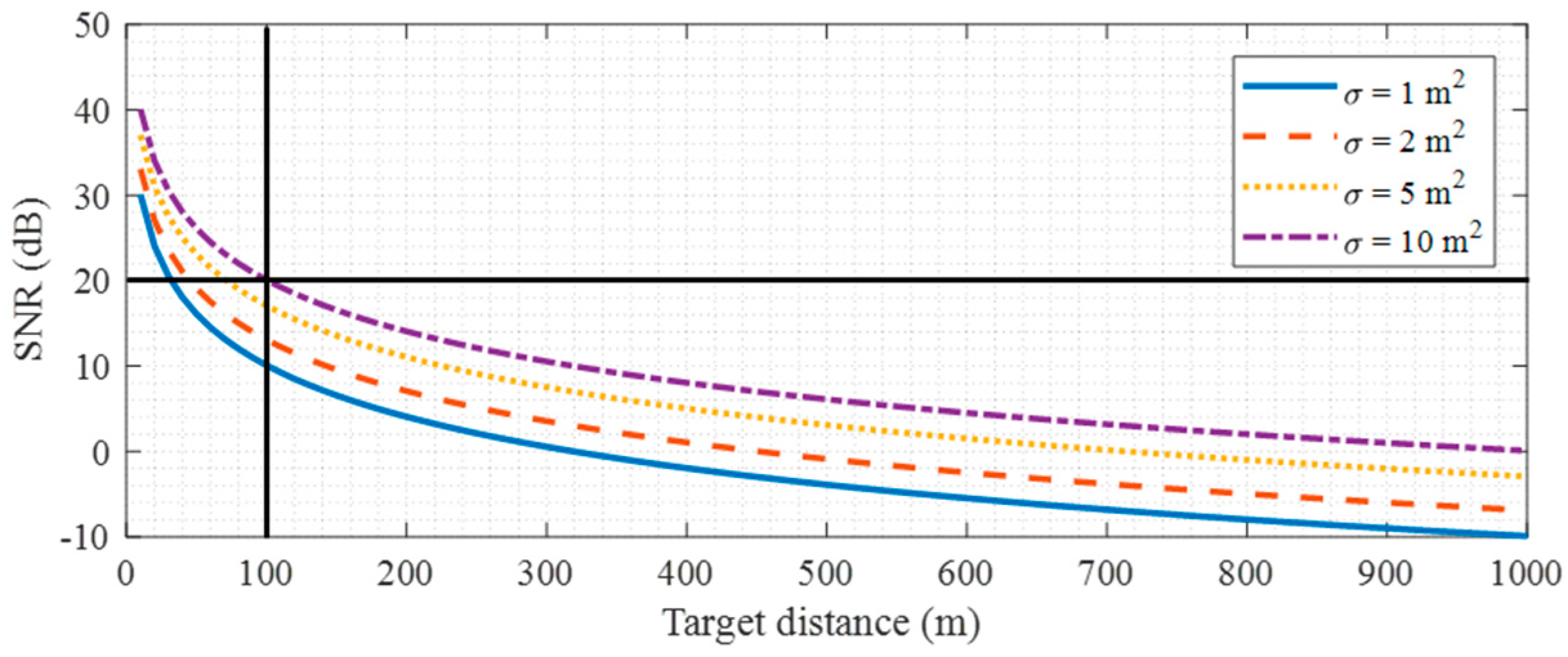
2.2. Link Budget Analysis
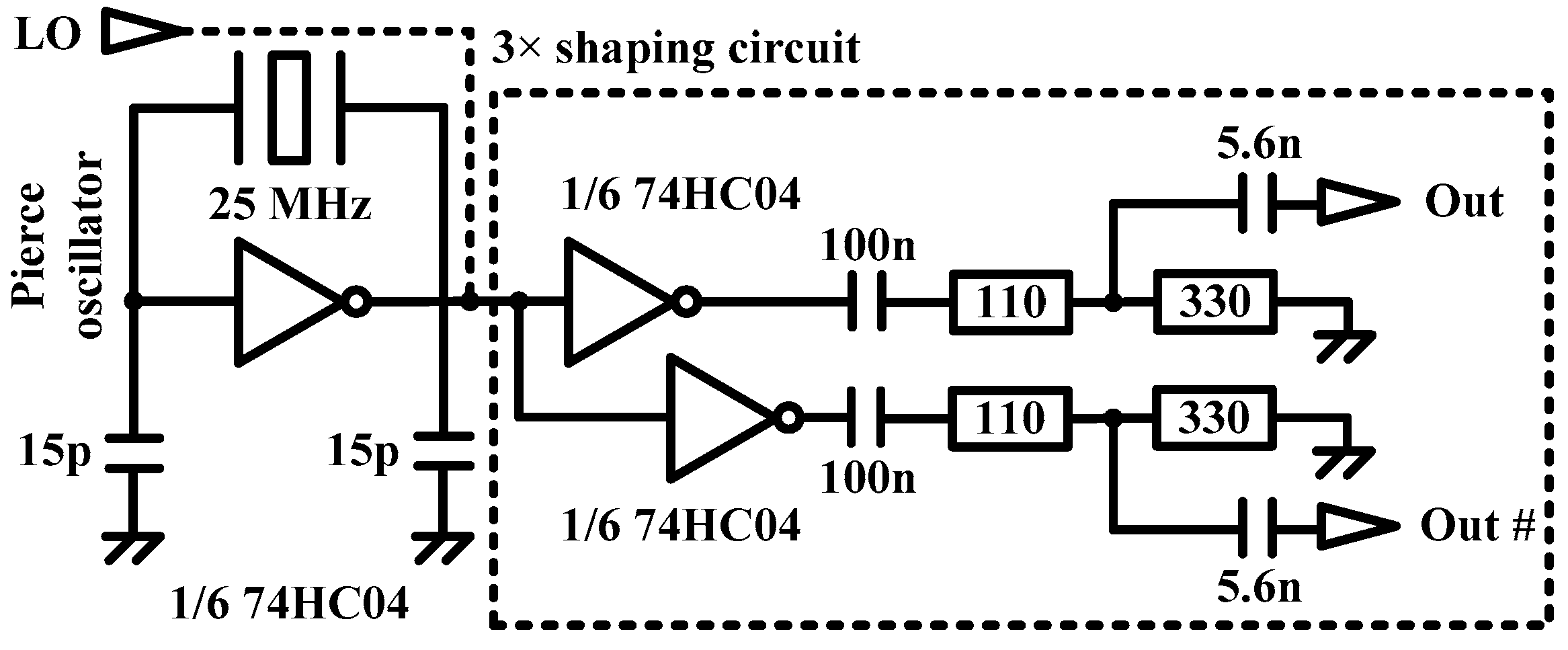
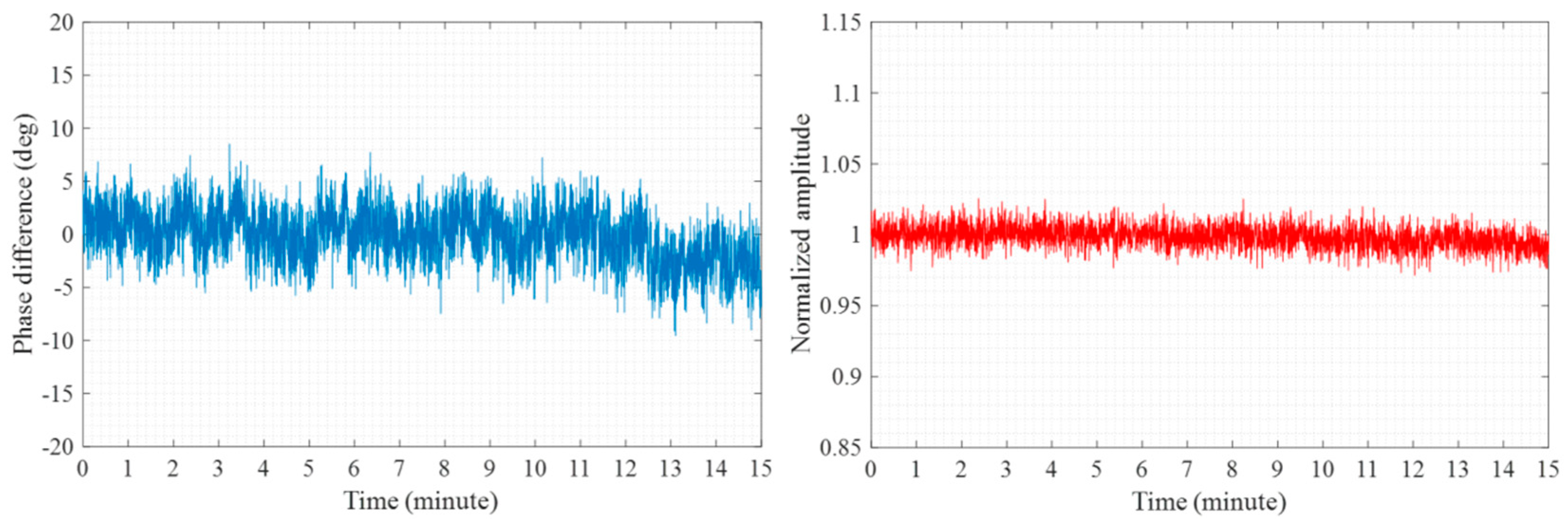
2.3. LNB Synchronization
3. Signal Processing
3.1. Signal Model
3.2. Imaging and Displacement Estimation
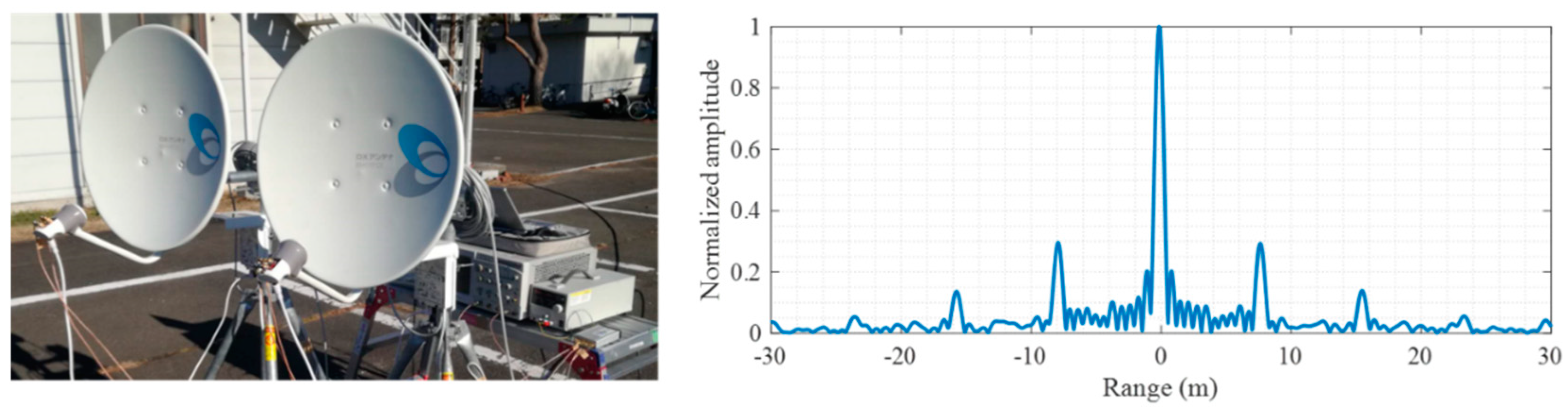
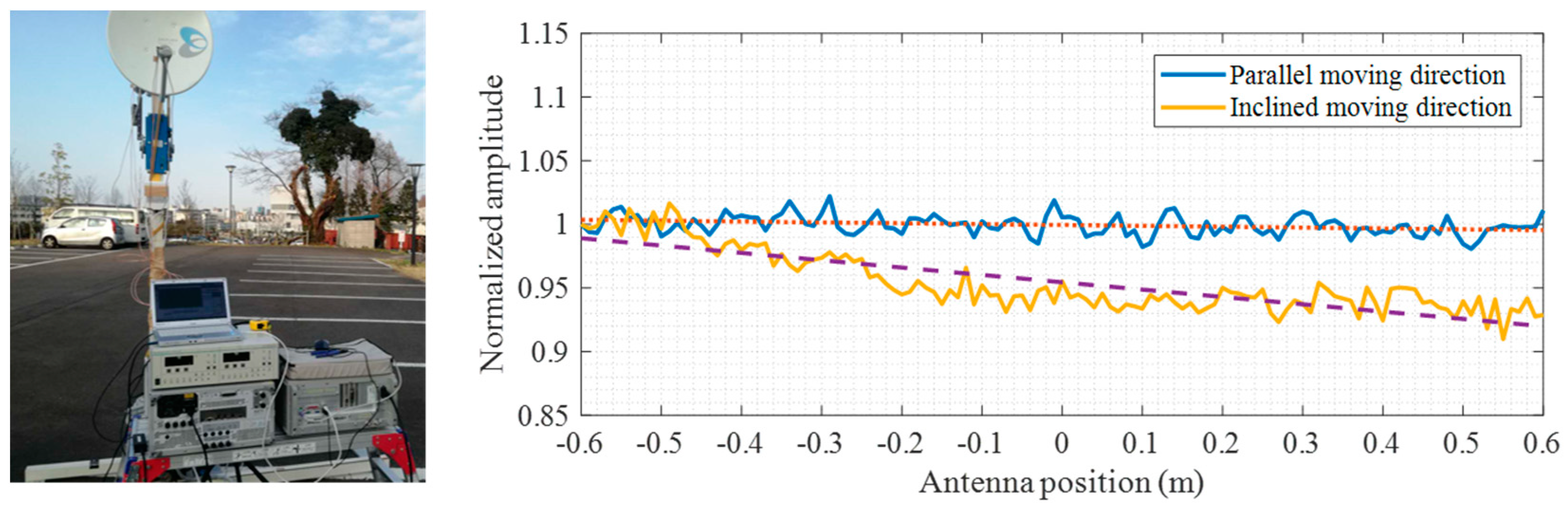
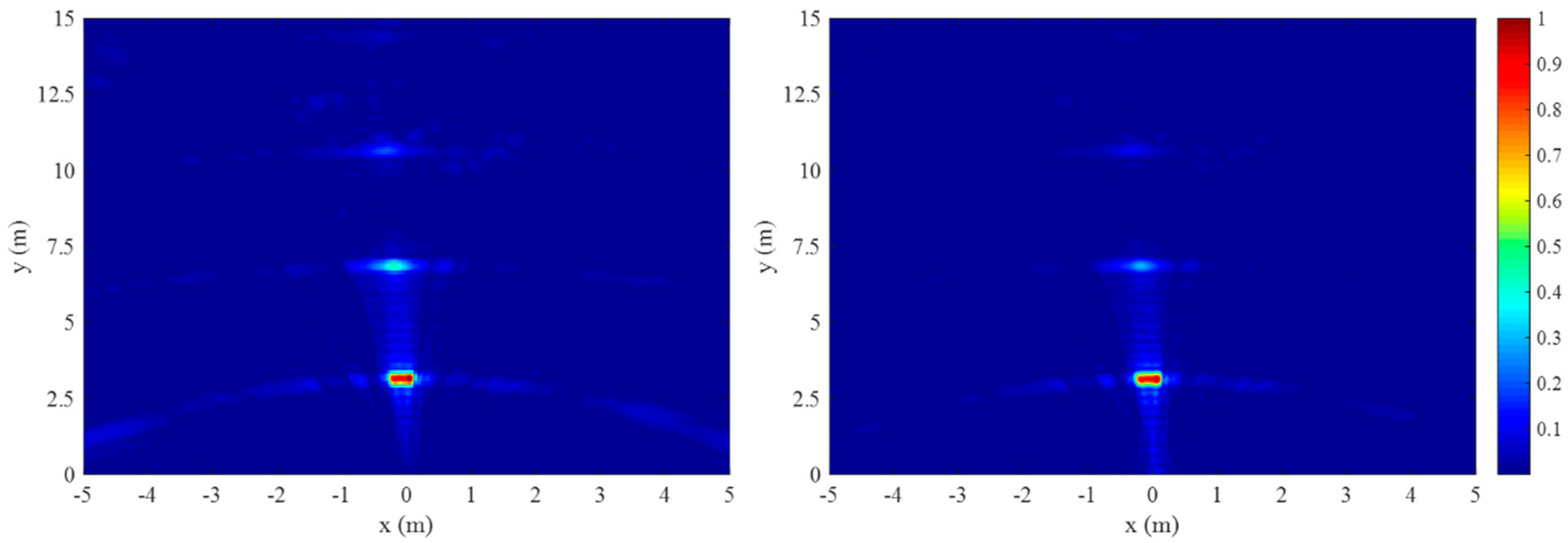
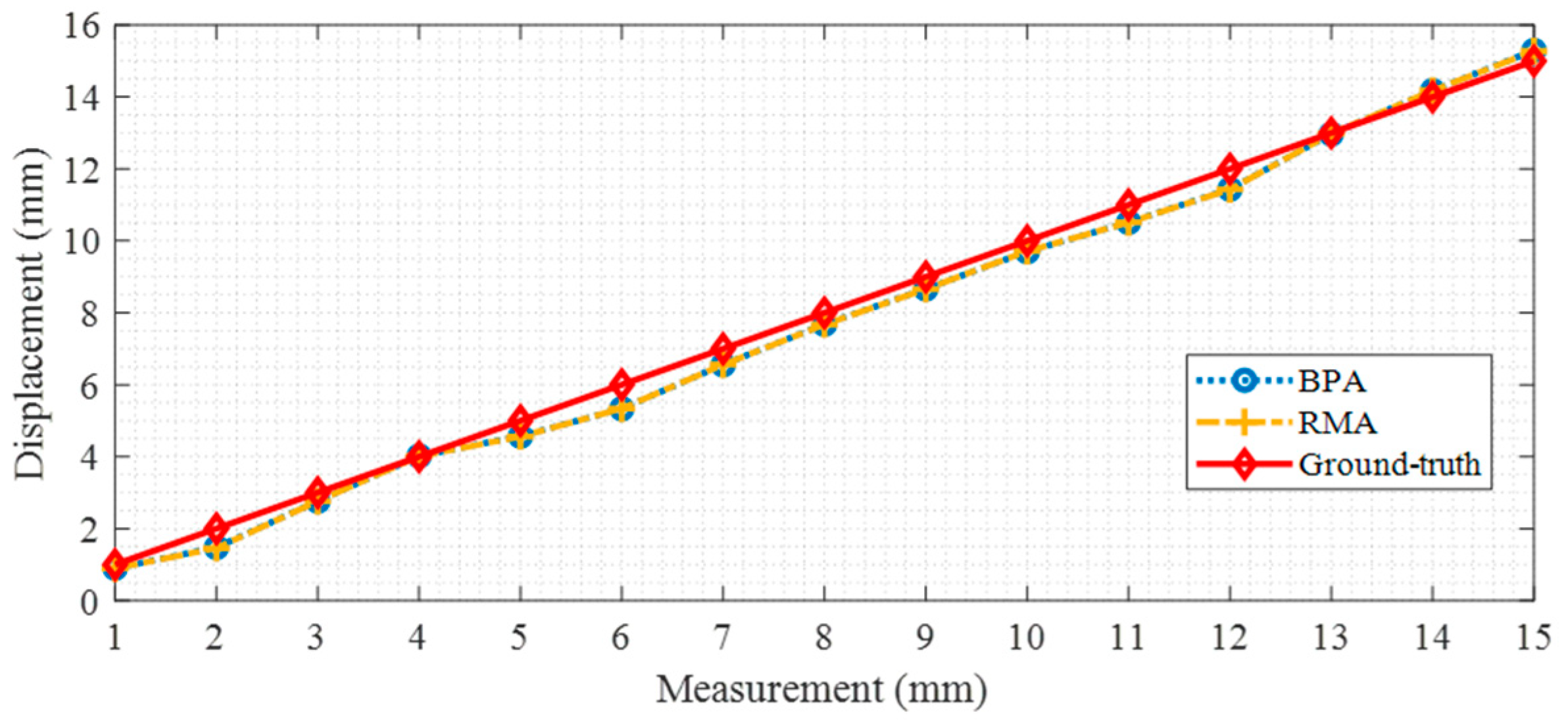
4. Experiment Results
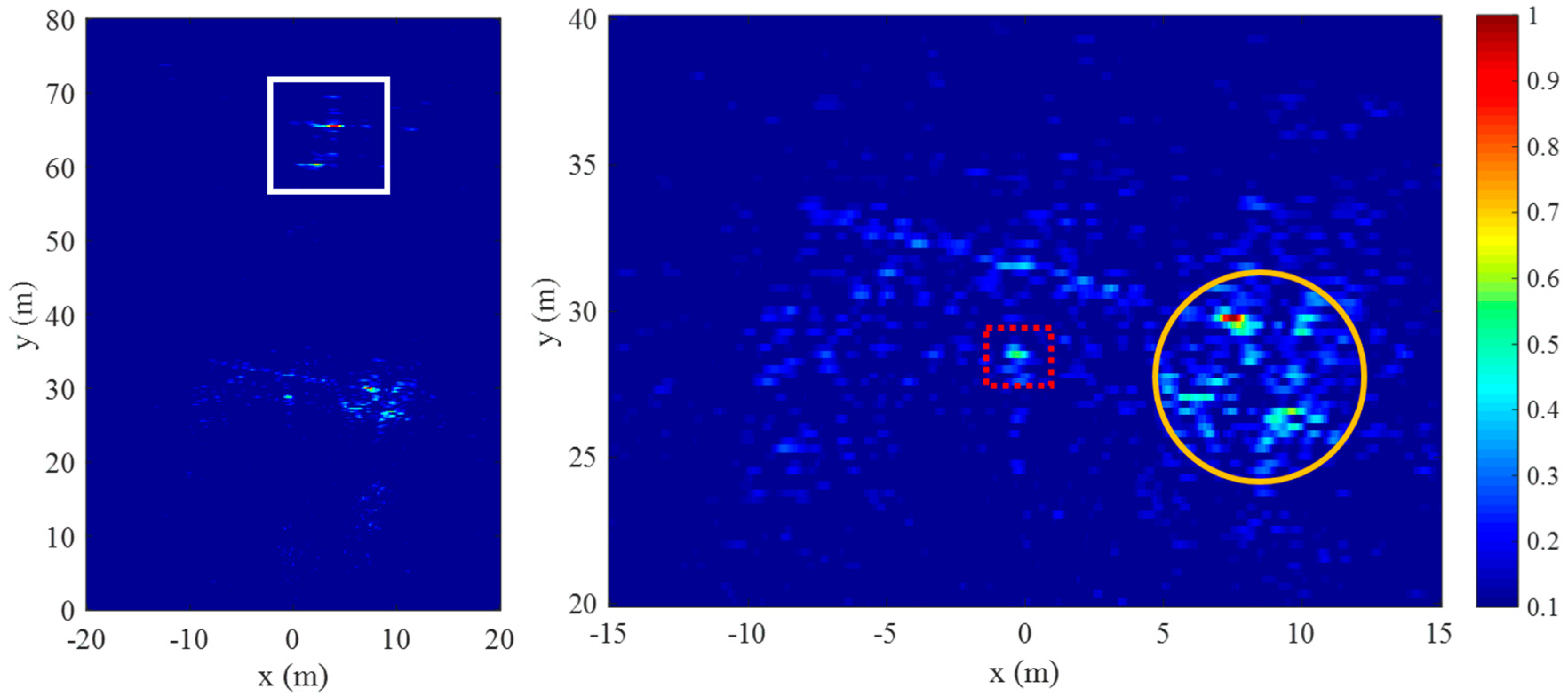
5. Discussions
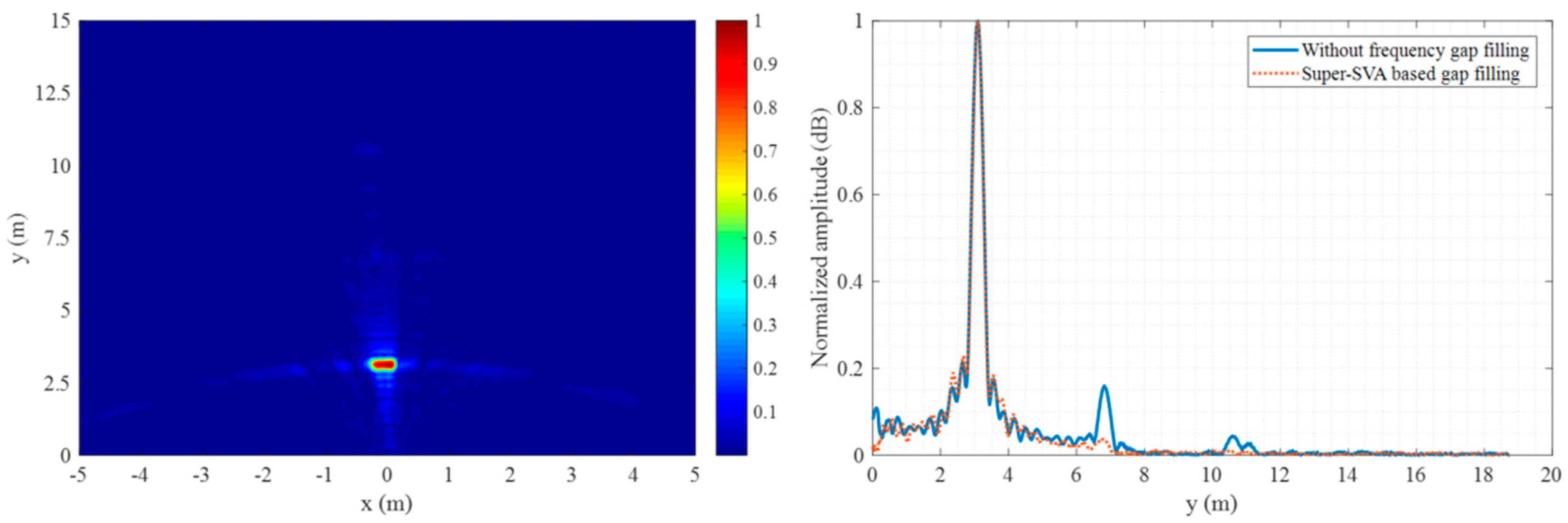
5.1. Artifact Suppression
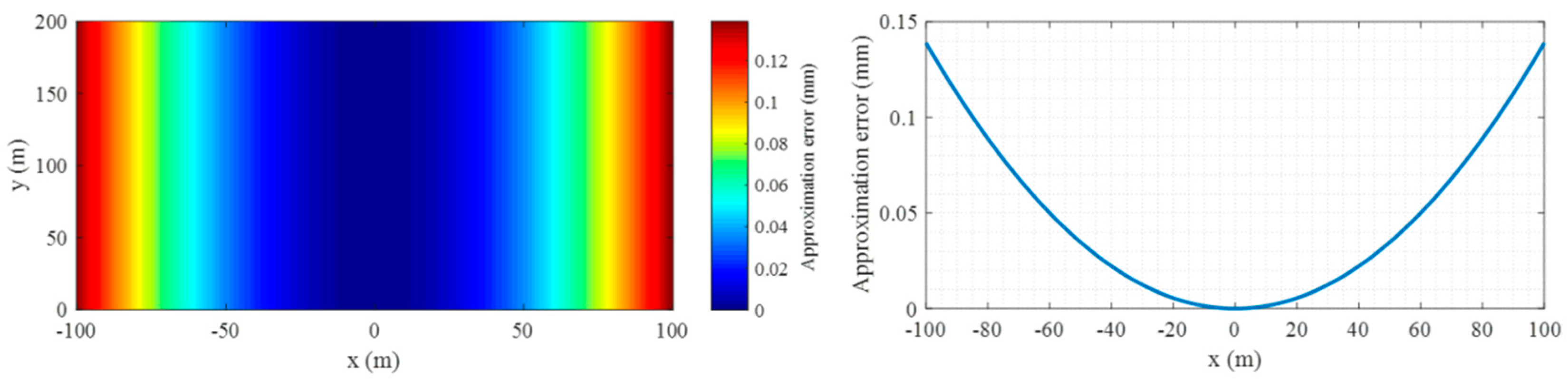
5.2. Improvement Directions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monserrat, O.; Crosetto, M.; Luzi, G. A review of ground-based SAR interferometry for deformation measurement. ISPRS J. Photogramm. Remote Sens. 2014, 93, 40–48. [Google Scholar] [CrossRef]
- Di Pasquale, A.; Nico, G.; Pitullo, A.; Prezioso, G. Monitoring strategies of Earth dams by ground-based radar interferometry: How to extract useful information for seismic risk assessment. Sensors 2018, 18, 244. [Google Scholar] [CrossRef] [PubMed]
- Pieraccini, M.; Miccinesi, L. Ground-based radar interferometry: A bibliographic review. Remote Sens. 2019, 11, 1029. [Google Scholar] [CrossRef]
- Takahashi, K.; Matsumoto, M.; Sato, M. Continuous observation of natural-disaster-affected areas using ground-based SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1286–1294. [Google Scholar] [CrossRef]
- Pieraccini, M.; Rojhani, N.; Miccinesi, L. Compressive sensing for ground based synthetic aperture radar. Remote Sens. 2018, 10, 1960. [Google Scholar] [CrossRef]
- Feng, W.; Nico, G.; Sato, M. GB-SAR interferometry based on dimension-reduced compressive sensing and multiple measurement vectors model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 70–74. [Google Scholar] [CrossRef]
- Nico, G.; Cifarelli, G.; Miccoli, G.; Soccodato, F.; Feng, W.; Sato, M.; Miliziano, S.; Marini, M. Measurement of pier deformation patterns by ground-based SAR interferometry: Application to a bollard pull trial. IEEE J. Ocean. Eng. 2018, 43, 822–829. [Google Scholar] [CrossRef]
- Anghel, A.; Tudose, M.; Cacoveanu, R.; Datcu, M.; Nico, G.; Masci, O.; Dongyang, A.; Tian, W.; Hu, C.; Ding, Z.; et al. Compact ground-based interferometric synthetic aperture radar: Short-range structural monitoring. IEEE Signal Process. Mag. 2019, 36, 42–52. [Google Scholar] [CrossRef]
- Hu, C.; Wang, J.; Tian, W.; Zeng, T.; Wang, R. Design and imaging of ground-based multiple-input multiple-output synthetic aperture radar (MIMO SAR) with non-collinear arrays. Sensors 2017, 17, 598. [Google Scholar] [CrossRef]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO radar and ground based SAR imaging systems: Equivalent approaches for remote sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 425–435. [Google Scholar] [CrossRef]
- Feng, W.; Yi, L.; Sato, M. Near range radar imaging based on block sparsity and cross-correlation fusion algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2079–2089. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. An interferometric MIMO radar for bridge monitoring. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.-M.; Nico, G. Three-dimensional ground based imaging radar based on C-band cross-MIMO array and tensor compressive sensing. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Zeng, T.; Mao, C.; Hu, C.; Yang, X.; Tian, W. Multi-static MIMO-SAR three dimensional deformation measurement system. In Proceedings of the IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 297–301. [Google Scholar]
- Pieraccini, M.; Miccinesi, L.; Rojhani, N. A GB-SAR operating in monostatic and bistatic modalities for retrieving the displacement vector. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1494–1498. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. Cross-pol transponder with frequency shifter for bistatic ground-based synthetic aperture radar. Remote Sens. 2018, 10, 1364. [Google Scholar] [CrossRef]
- Hu, C.; Deng, Y.; Wang, R.; Tian, W.; Zeng, T. Two-dimensional deformation measurement based on multiple aperture interferometry in GB-SAR. IEEE Geosci. Remote Sens. Lett. 2017, 14, 208–212. [Google Scholar] [CrossRef]
- Feng, W.; Nico, G.; Guo, J.; Wang, S.; Sato, M. Estimation of displacement vector by linear MIMO arrays with reduced phase gain and antenna position error influences. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 29 July–2 August 2019. [Google Scholar]
- Luzi, G.; Dematteis, N. Ku band terrestrial radar observations by means of circular polarized antennas. Remote Sens. 2019, 11, 270. [Google Scholar] [CrossRef]
- Iglesias, R.; Aguasca, A.; Fabregas, X.; Mallorqui, J.J.; Monells, D.; López-Martínez, C.; Pipia, L. Ground-based polarimetric SAR interferometry for the monitoring of terrain displacement phenomena—Part I: Theoretical Description. IEEE J. Sel. Top. Appl. Earth Obs. 2014, 8, 980–993. [Google Scholar] [CrossRef]
- Iglesias, R.; Aguasca, A.; Fabregas, X.; Mallorqui, J.J.; Monells, D.; López-Martínez, C.; Pipia, L. Ground-based polarimetric SAR interferometry for the monitoring of terrain displacement phenomena—Part II: Applications. IEEE J. Sel. Top. Appl. Earth Obs. 2014, 8, 994–1007. [Google Scholar] [CrossRef]
- Griffiths, H.D.; Baker, C.J. An Introduction to Passive Radar; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Kuschel, H.; Cristallini, D.; Olsen, K.E. Tutorial: Passive radar tutorial. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 2–19. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.M.; Cherniak, G.; Sato, M. Batch compressive sensing for passive radar range-Doppler map generation. IEEE Trans. Aerosp. Electron. Syst. 2019. [Google Scholar] [CrossRef]
- Shan, T.; Liu, S.; Zhang, Y.D.; Amin, M.G.; Tao, R.; Feng, Y. Efficient architecture and hardware implementation of coherent integration processor for digital video broadcast-based passive bistatic radar. IET Radar Sonar Nav. 2016, 10, 97–106. [Google Scholar] [CrossRef]
- Cristallini, D.; Pisciottano, I.; Kuschel, H. Multi-band passive radar imaging using satellite illumination. In Proceedings of the 2018 International Conference on Radar (RADAR), Brisbane, QLD, Australia, 27–31 August 2018; pp. 1–6. [Google Scholar]
- Li, Z.; Santi, F.; Pastina, D.; Lombardo, P. Passive radar array with low-power satellite illuminators based on fractional Fourier transform. IEEE Sens. J. 2017, 17, 8378–8394. [Google Scholar] [CrossRef]
- Liu, S.; Ma, Y.; Huang, Y. Sea clutter cancellation for passive radar sensor exploiting multi-channel adaptive filters. IEEE Sens. J. 2019, 19, 982–995. [Google Scholar] [CrossRef]
- Wojaczek, P.; Colone, F.; Cristallini, D.; Lombardo, P. Reciprocal filter-based STAP for passive radar on moving platforms. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 967–988. [Google Scholar] [CrossRef]
- Olivadese, D.; Giusti, E.; Petri, D.; Martorella, M.; Capria, A.; Berizzi, F. Passive ISAR with DVB-T signals. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4508–4517. [Google Scholar] [CrossRef]
- Ulander, L.M.; Frölind, P.O.; Gustavsson, A.; Ragnarsson, R.; Stenström, G. Airborne passive SAR imaging based on DVB-T signals. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2408–2411. [Google Scholar]
- Feng, W.; Friedt, J.M.; Cherniak, G.; Hu, Z.; Sato, M. Direct path interference suppression for short-range passive bistatic synthetic aperture radar imaging based on atomic norm minimisation and Vandermonde decomposition. IET Radar Sonar Nav. 2019, 13, 1171–1179. [Google Scholar] [CrossRef]
- Capria, A.; Giusti, E.; Moscardini, C.; Conti, M.; Petri, D.; Martorella, M.; Berizzi, F. Multifunction imaging passive radar for harbour protection and navigation safety. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 30–38. [Google Scholar] [CrossRef]
- Bączyk, M.K.; Samczynski, P.; Krysik, P.; Kulpa, K. Traffic density monitoring using passive radars. IEEE Aerosp. Electron. Syst. Mag. 2017, 2, 14–21. [Google Scholar] [CrossRef]
- Chetty, K.; Smith, G.; Woodbridge, K. Through-the wall sensing of personnel using passive bistatic WiFi radar at standoff distances. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1218–1226. [Google Scholar] [CrossRef]
- Liu, F.; Antoniou, M.; Zeng, Z.; Cherniakov, M. Coherent change detection using passive GNSS-based BSAR: Experimental proof of concept. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4544–4555. [Google Scholar] [CrossRef]
- Feng, W.; Friedt, J.M.; Cherniak, G.; Sato, M. Passive radar Imaging by filling gaps between ISDB digital TV channels. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Pastina, D.; Sedehi, M.; Cristallini, D. Passive bistatic ISAR based on geostationary satellites for coastal surveillance. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 10–14 May 2010; pp. 865–870. [Google Scholar]
- Brisken, S.; Moscadelli, M.; Seidel, V.; Schwark, C. Passive radar imaging using DVB-S2. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017; pp. 552–556. [Google Scholar]
- Sun, Z.; Wang, T.; Jiang, T.; Chen, C.; Chen, W. Analysis of the properties of DVB-S signal for passive radar application. In Proceedings of the International Conference on Wireless Communications and Signal Processing, Hangzhou, China, 24–26 October 2013; pp. 1–5. [Google Scholar]
- Marques, P.; Ferreira, A.; Fortes, F.; Sampaio, P.; Rebelo, H.; Reis, L. A pedagogical passive radar using DVB-S signals. In Proceedings of the IEEE 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011; pp. 1–4. [Google Scholar]
- JSAT Corp. N-SAT-110 Coverage Area. Available online: https://www.jsat.net/en/contour/n-sat-110.html (accessed on 20 June 2019).
- Liu, J.; Li, H.; Himed, B. On the performance of the cross-correlation detector for passive radar applications. Signal Process. 2015, 113, 32–37. [Google Scholar] [CrossRef]
- Zuo, R. Bistatic Synthetic Aperture Radar Using GNSS as Transmitters of Opportunity. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2012. [Google Scholar]
- Wang, R.; Deng, Y. Bistatic SAR System and Signal Processing Technology; Springer: Singapore, 2018. [Google Scholar]
- Marques, P. Phase correction for passive radar using targets of opportunity. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 717–720. [Google Scholar]
- Glover, I.; Grant, P. Digital Communications; Englewood Cliffs: Bergen, NJ, USA, 1997. [Google Scholar]
- Greengard, L.; Lee, J.Y. Accelerating the nonuniform fast Fourier transform. SIAM Rev. 2004, 46, 443–454. [Google Scholar] [CrossRef]
- Qiu, W.; Giusti, E.; Bacci, A.; Martorella, M.; Berizzi, F.; Zhao, H.; Fu, Q. Compressed sensing-based algorithm for passive bistatic ISAR with DVB-T signals. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2166–2180. [Google Scholar] [CrossRef]
- Stankwitz, H.; Kosek, M. Sparse aperture fill for SAR using super-SVA. In Proceedings of the 1996 IEEE National Radar Conference, Ann Arbor, MI, USA, 13–16 May 1996; pp. 70–75. [Google Scholar]
- Stankwitz, H.; Dallaire, R.; Fienup, J. Nonlinear apodization for sidelobe control in SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 267–279. [Google Scholar] [CrossRef]
- Liu, S.; Shan, T.; Tao, R.; Zhang, Y.D.; Zhang, G.; Zhang, F.; Wang, Y. Sparse discrete fractional Fourier transform and its applications. IEEE Trans. Signal Process. 2014, 62, 6582–6595. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Nilsen, C.; Holm, S. Wiener beamforming and the coherence factor in ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1329–1346. [Google Scholar] [CrossRef]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 958–974. [Google Scholar] [CrossRef]
- Fortuny-Guasch, J. A fast and accurate far-field pseudopolar format radar imaging algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1187–1196. [Google Scholar] [CrossRef]
- Feng, W.; Nico, G.; Masci, O.; Sato, M. Airship based MIMO radar: Analysis of imaging and interferometric performances. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6492–6495. [Google Scholar]
- Cazzani, L.; Colesanti, C.; Leva, D.; Nesti, G.; Prati, C.; Rocca, F.; Tarchi, D. A ground-based parasitic SAR experiment. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2132–2141. [Google Scholar] [CrossRef]





| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| TV signal power | EIRP | 55 | dBW |
| Reference antenna gain | Gref | 34 | dB |
| Speed of light | c | 3 × 108 | m/s |
| Carrier frequency | fc | 12.51 | GHz |
| Wavelength | λ | 24 | mm |
| Direct path | R1,1 | 36,000 | km |
| Surveillance antenna gain | Gsurv | 15 | dB |
| Target RCS | σ | 10 | m2 |
| Satellite-target distance | R1,2 | 36,000.1 | km |
| Target–receiver distance | R2 | 100 | m |
| Noise temperature | T0 | 290 | K |
| Noise bandwidth | B0 | 34.5 | MHz |
| Boltzmann constant | k0 | 1.38 × 10−23 | J/K |
| Number of TV channels | N | 12 | 1 |
| Path loss of Ku band | Lr | 2 | dB |
| Synthetic aperture length | L | TBD | m |
| Antenna moving step | Δx | 5 | mm |
| Coherent integration time | Tint | TBD | μs |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Friedt, J.-M.; Nico, G.; Wang, S.; Martin, G.; Sato, M. Passive Bistatic Ground-Based Synthetic Aperture Radar: Concept, System, and Experiment Results. Remote Sens. 2019, 11, 1753. https://doi.org/10.3390/rs11151753
Feng W, Friedt J-M, Nico G, Wang S, Martin G, Sato M. Passive Bistatic Ground-Based Synthetic Aperture Radar: Concept, System, and Experiment Results. Remote Sensing. 2019; 11(15):1753. https://doi.org/10.3390/rs11151753
Chicago/Turabian StyleFeng, Weike, Jean-Michel Friedt, Giovanni Nico, Suyun Wang, Gilles Martin, and Motoyuki Sato. 2019. "Passive Bistatic Ground-Based Synthetic Aperture Radar: Concept, System, and Experiment Results" Remote Sensing 11, no. 15: 1753. https://doi.org/10.3390/rs11151753
APA StyleFeng, W., Friedt, J.-M., Nico, G., Wang, S., Martin, G., & Sato, M. (2019). Passive Bistatic Ground-Based Synthetic Aperture Radar: Concept, System, and Experiment Results. Remote Sensing, 11(15), 1753. https://doi.org/10.3390/rs11151753