A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water
Abstract
1. Introduction
1.1. The Need for Fiducial Reference Measurements for Satellite Validation
- An uncertainty budget for all FRM instruments and derived measurements is available and maintained, and is traceable where appropriate to the International System of Units/Système International d’unités (SI), ideally through a National Metrology Institute;
- FRM measurement protocols and community-wide management practices (measurement, processing, archive, documents, etc.) are defined and adhered to;
- FRM measurements have documented evidence of SI traceability that is validated by an intercomparison of instruments under operational-like conditions;
- FRM measurements are independent from the satellite retrieval process.
1.2. Scope and Definitions
1.3. Previous Protocol Reviews
- greater need for validation measurements in coastal and inland waters rather than the prior focus on oceanic waters
- preference for above-water measurement of rather than extrapolation from underwater profiles
- reduction in the cost of radiometers facilitating use of an irradiance sensor (instead of a radiance sensor and a reflectance plaque), and better availability of hyperspectral radiometers.
1.4. Overview of Methods
- Direct above-water measurement of with an upward-pointing irradiance sensor (“Irradiance sensor method”)
- Estimation of using a downward-pointing radiance sensor and a reflective plaque (“Reflectance plaque method”)
- Estimation of from direct sunphotometry and a clear sky atmospheric model (“Sunphotometry method”)
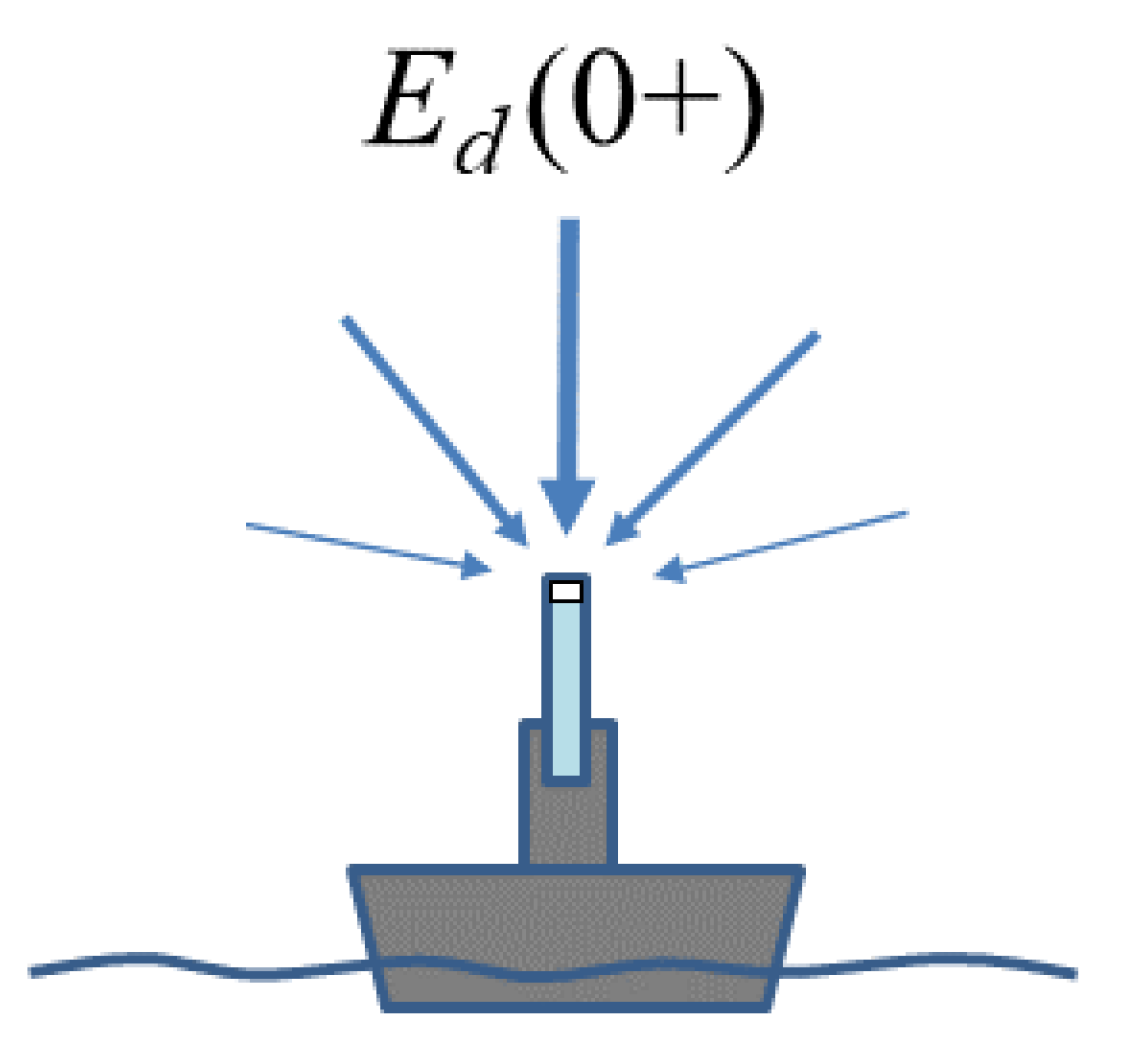
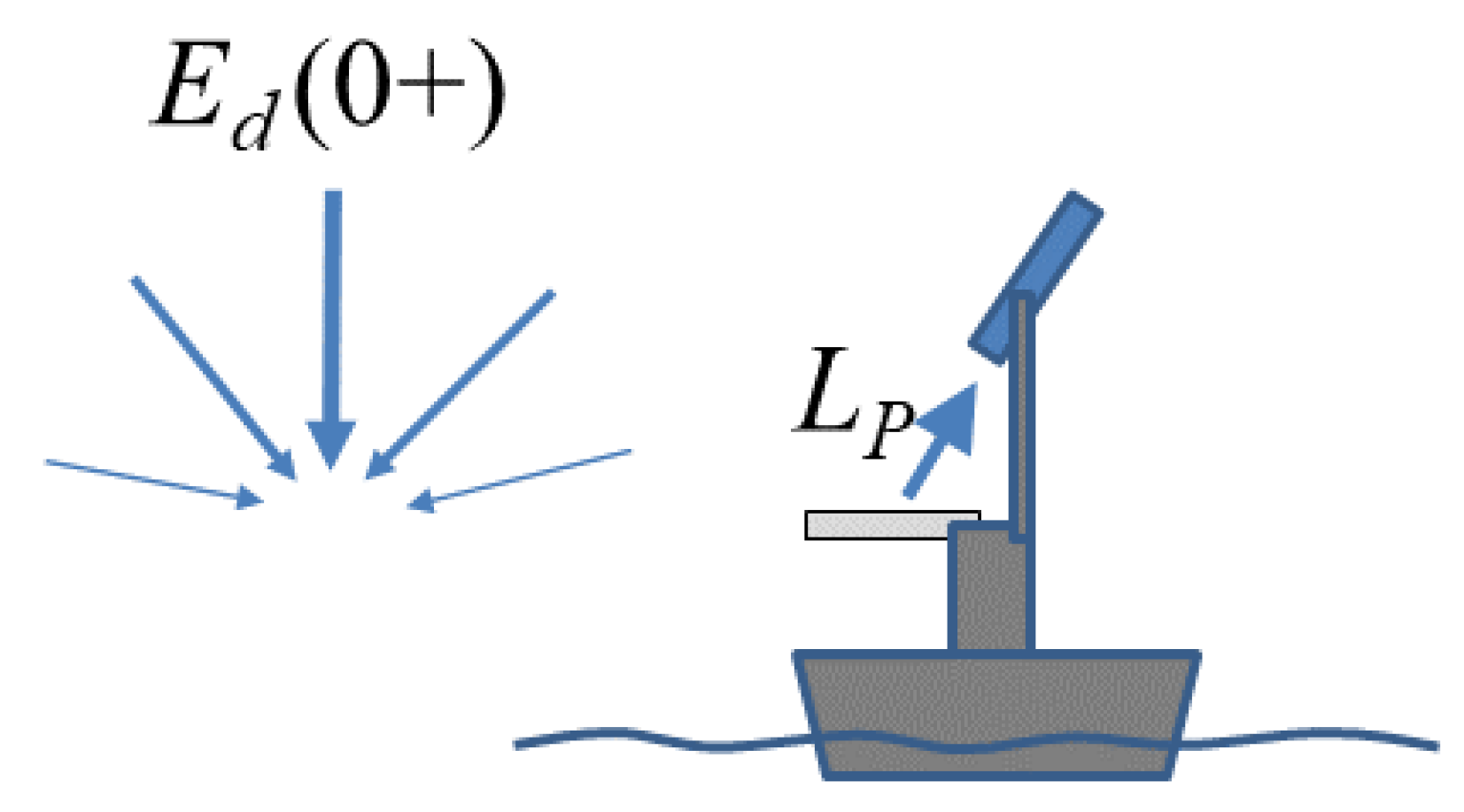
2. Direct above-Water Measurement of with an Upward-Pointing Irradiance Sensor
2.1. Measurement Equation
2.2. Protocol-Dependent Sources of Uncertainty
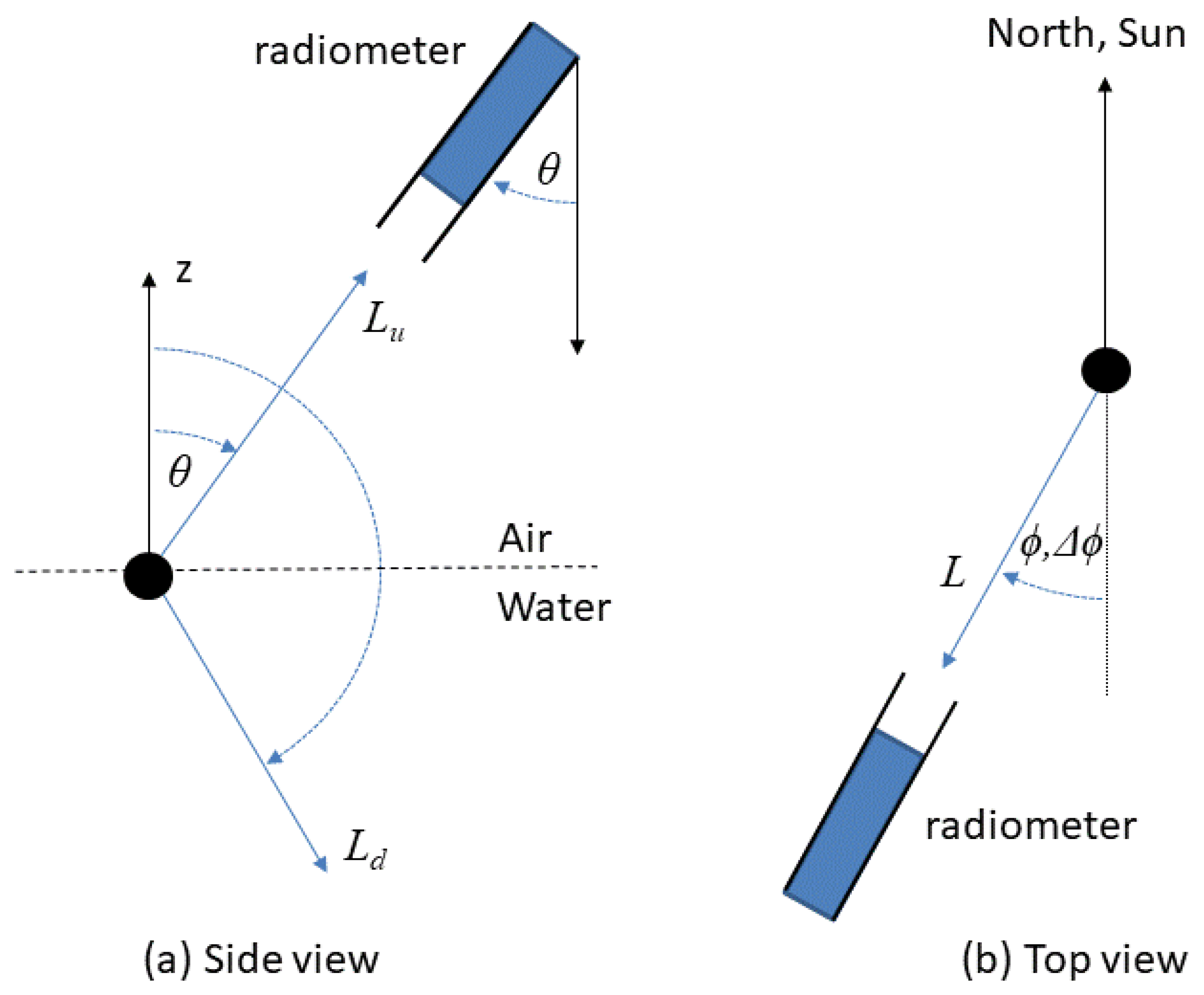
2.2.1. Tilt Effects
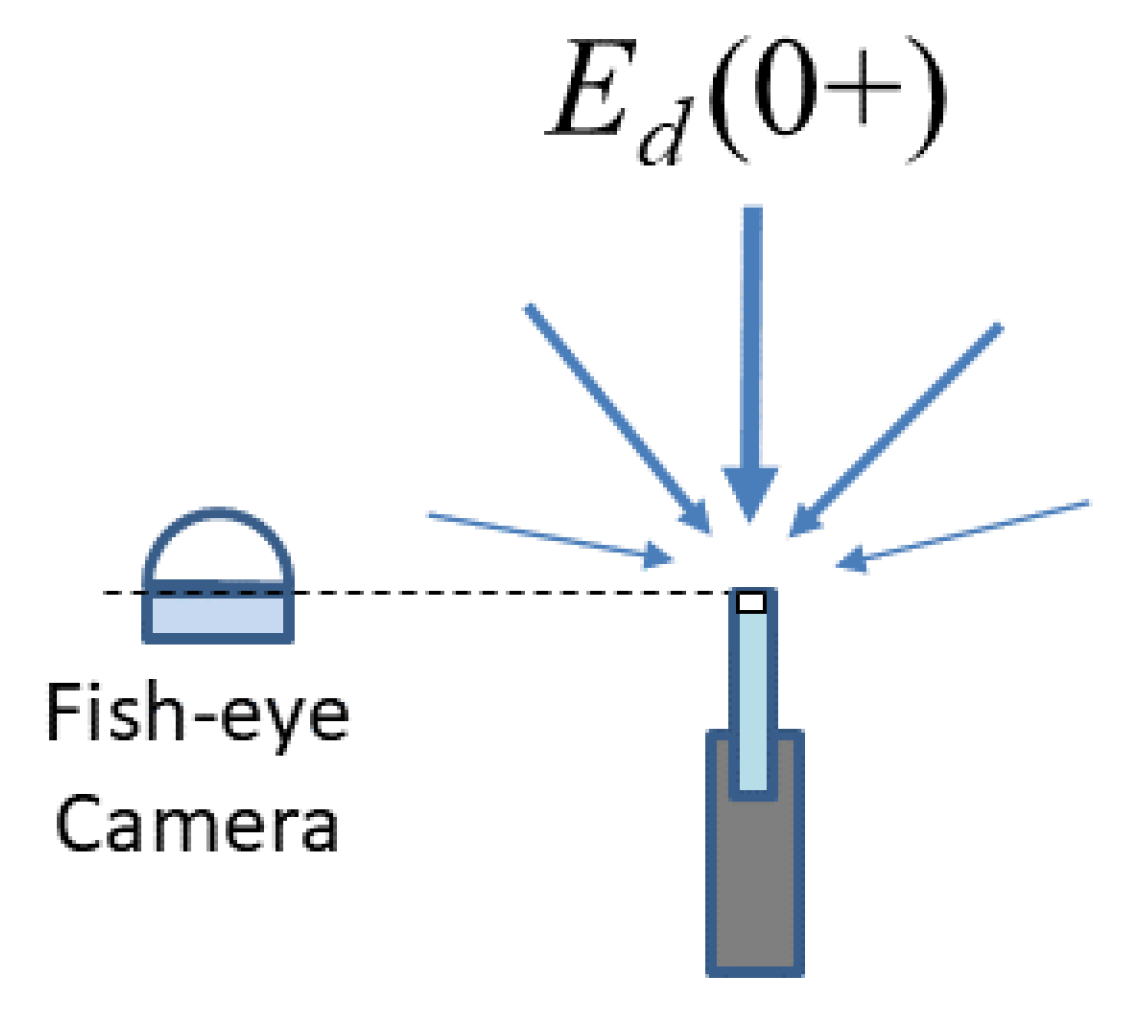
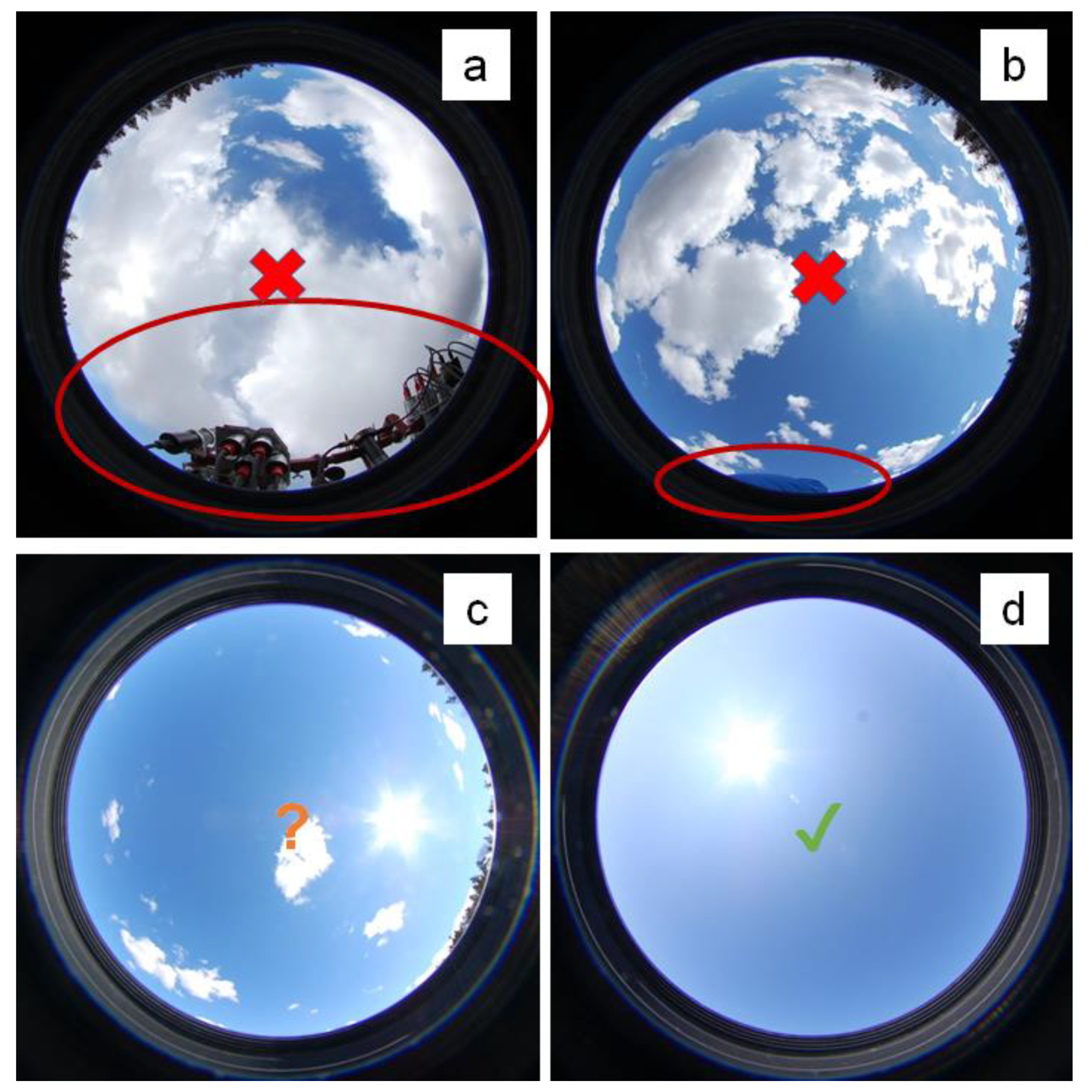
2.2.2. Shading from Superstructure
2.2.3. Fouling
2.2.4. Fast Natural Fluctuations
2.3. Variants on the Method of Direct above-Water Measurement of with an Upward-Pointing Irradiance Sensor
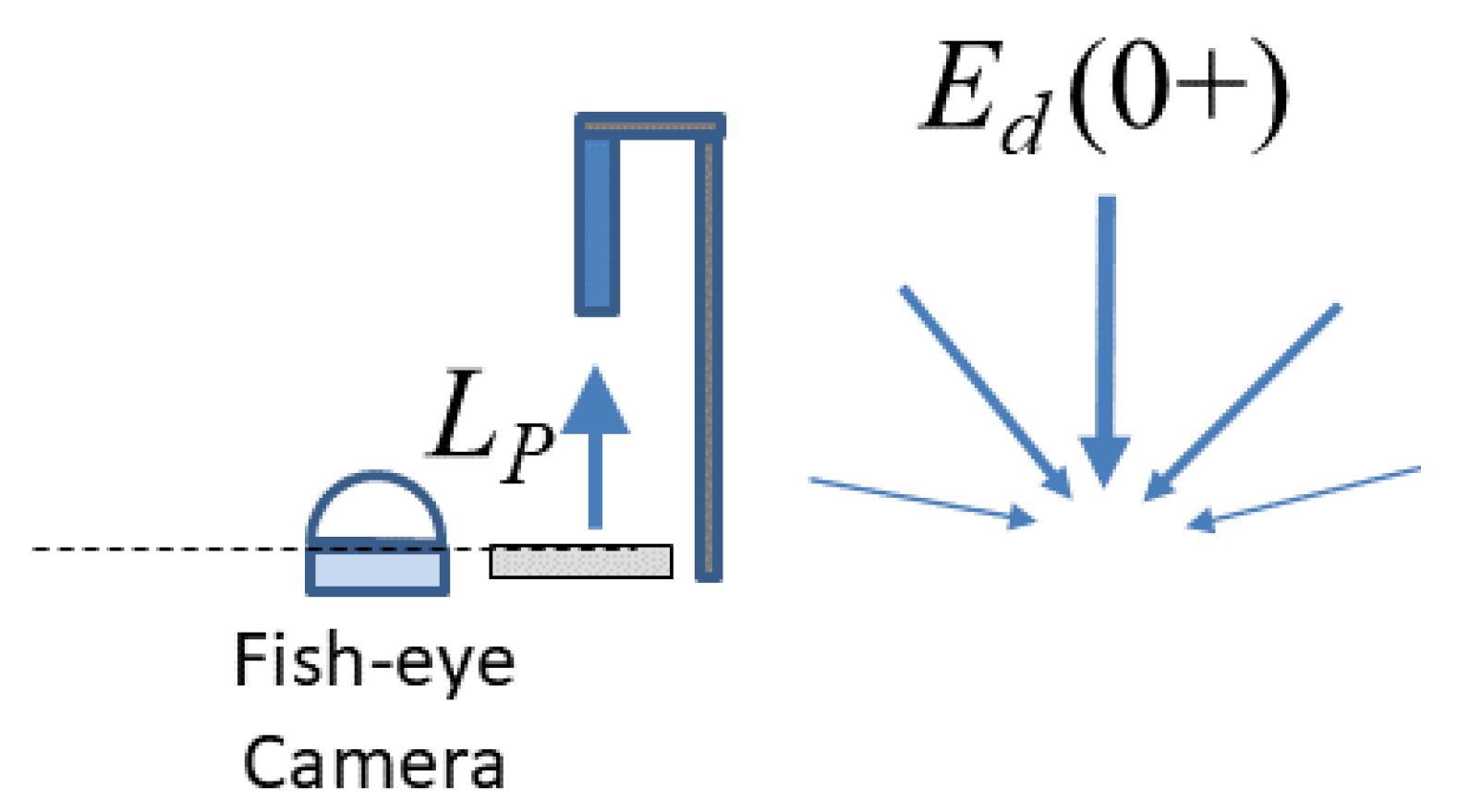
3. Estimation of Using a Downward-Pointing Radiance Sensor and a Reflective Plaque
3.1. Measurement Equation
3.1.1. Is It Necessary to Use a Calibrated Radiance Sensor?
- A calibrated radiance sensor will provide a calibrated , which can then be compared with clear sky models [39] for quality control purposes, and can be compared to satellite data to validate the computations of atmospheric transmittance (in addition to the more important products).
- The interpretation of in situ measurement intercomparison exercises [17], as required by the FRM process, necessitates a separation of uncertainties arising from and measurements, e.g., comparing measurements from a vertically-mounted irradiance sensor (impacted by cosine angle uncertainties, etc.) with measurements deduced from a radiance sensor viewing a reflectance plaque (impacted by BRDF uncertainties, etc.).
3.1.2. What Nadir Angle Should Be Used for Viewing a Reflectance Plaque?
3.2. Protocol-Dependent Sources of Uncertainty
3.2.1. Plaque Calibration
3.2.2. Plaque Homogeneity and Sensor Field of View
3.2.3. Tilt Effects
3.2.4. Shading from Superstructure and Radiometers and Mounting Equipment
- Firstly, there will always be some shading of sky radiance onto the plaque from the radiometer itself. The radiometer must be held above the plaque at a height that is sufficiently small so that the plaque fills the whole field of view of the radiometer. The exact height depends on the radiometer and the size of the plaque. Shading from the radiometer (and any associated fixations) will be related to the zenith cosine-weighted solid angle of sky filled by the radiometer, as seen from any point on the reflectance plaque, and will be worse for radiometers held close to the plaque or that have a large diameter.
- Secondly, while it is typical to mount irradiance sensors high on poles/masts (Section 2.2.2) and certainly above head height, measurements with a reflectance plaque are nearly always made much lower on a ship/platform for practical reasons: it is generally necessary to manipulate the radiometer (e.g., to then point to water and sky) and the plaque (e.g., to protect it when not measuring). Optical contamination from ship/platform sides, upper decks, masts, and even humans (often including those making the measurement) can be significant and difficult to quantify.
3.2.5. Fouling
3.2.6. Fast Natural Fluctuations
3.2.7. Bidirectional Reflectance of Plaques
3.3. Variants on the Method for Measurement of Using a Downward-Pointing Radiance Sensor and a Reflectance Plaque
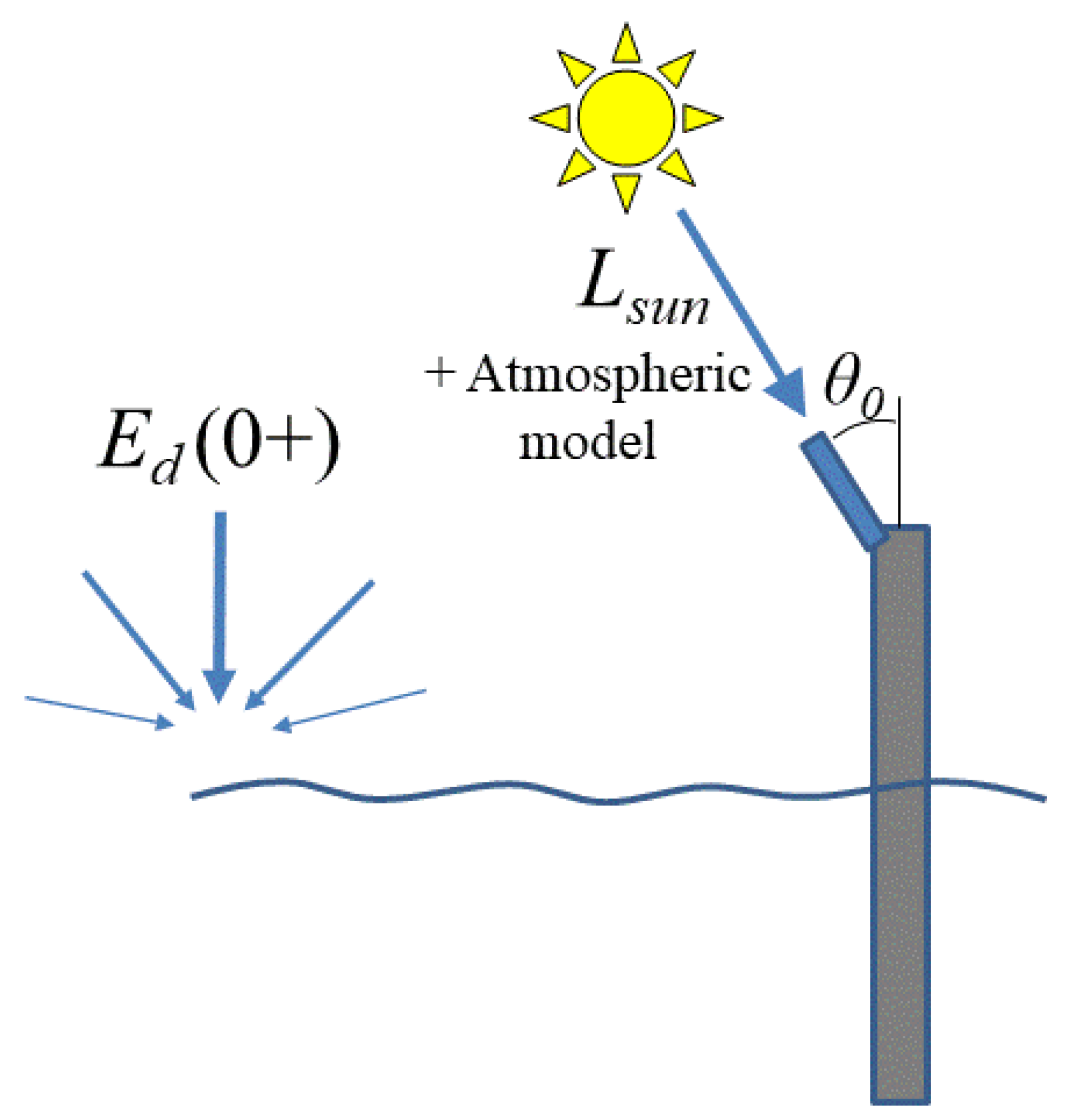
4. Estimation of from Direct Sunphotometry and a Clear Sky Atmospheric Model
4.1. Measurement Equation
4.2. Protocol-Dependent Sources of Uncertainty
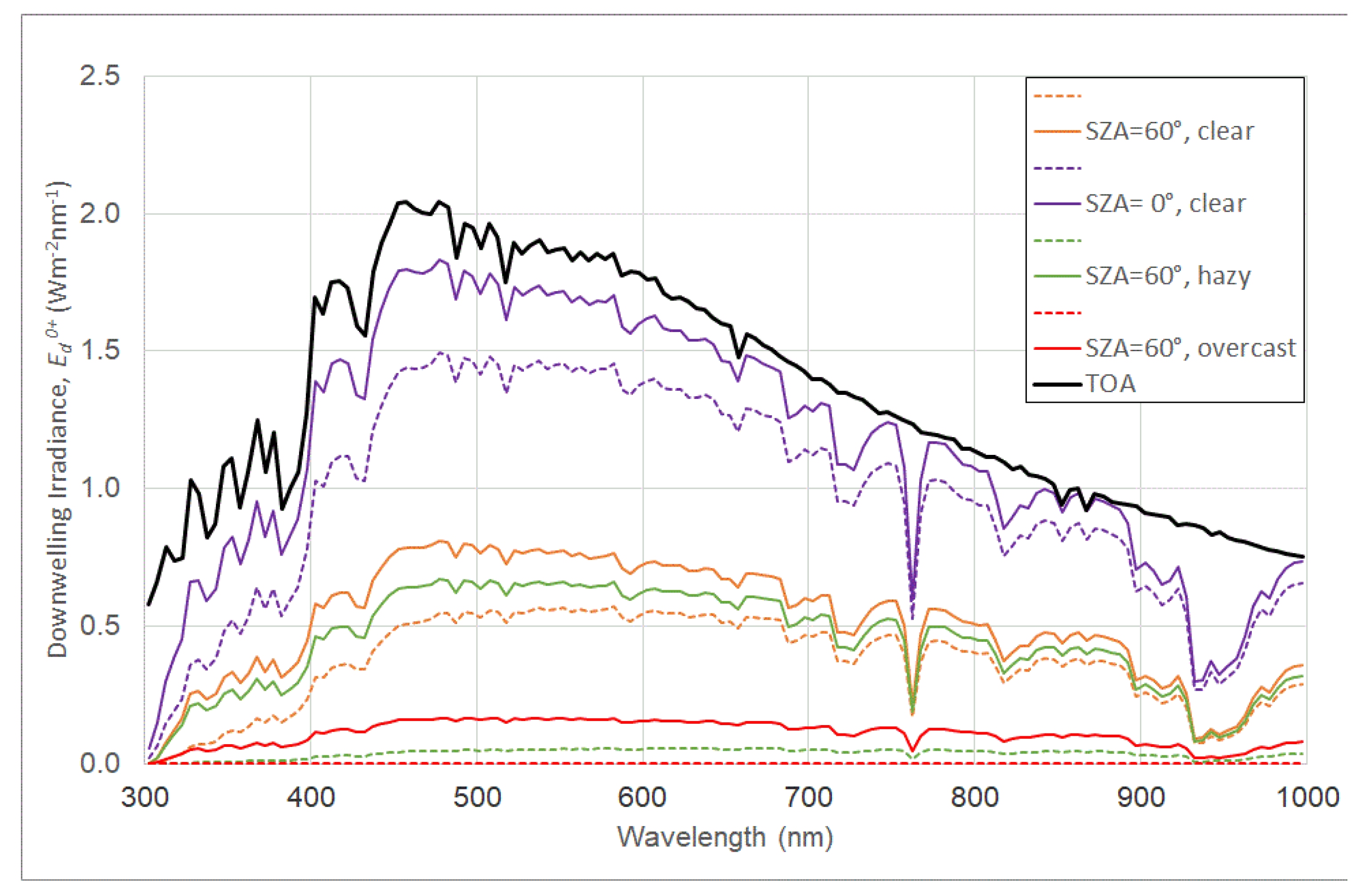
4.2.1. Atmospheric Radiative Transfer Model
4.2.2. Sky Conditions
4.2.3. Pointing Effects
4.2.4. Shading
4.2.5. Fouling
4.2.6. Fast Natural Fluctuations
4.3. Variants on the Method of Measurement of from Direct Sunphotometry and a Clear Sky Atmospheric Model
5. Estimation of from Underwater Measurements
6. Conclusions
6.1. Summary of the State of the Art
- Direct above-water measurement of with an upward pointing irradiance sensor
- Estimation of using a downward pointing radiance sensor and a reflective plaque
- Estimation of from direct sunphotometry and a clear sky atmospheric model
6.2. Irradiance Sensor or Reflectance Plaque?
- There be no humans above the level of the reflectance plaque/irradiance sensor (and thereby affecting the sky radiance contributing to in a way that is highly variable and essentially not quantifiable in an uncertainty estimate),
- The reflectance plaque/irradiance sensor be mounted as high as possible on the ship/platform, typically higher than any superstructure elements with significant solid angle as viewed from the plaque/sensor,
- The reflectance plaque/irradiance sensor be mounted on a fixed structure, not hand-held, and associated with an inclinometer allowing the estimation of uncertainties associated with non-horizontal/vertical measurements,
- The measurements made using the reflective plaque/irradiance sensor be supported by experiments and/or simulations to estimate the measurement uncertainties associated with any superstructure shading of the plaque/irradiance sensor.
6.3. Future Perspectives
- Improvements in the design and usage of calibration monitoring devices, which can be used in the field, are likely to improve the identification of fore-optics fouling and radiometer sensitivity changes.
- Model simulations of the 3D light field and experiments for deployments with structures above the irradiance sensor/reflectance plaque are likely to improve estimations of related uncertainties.
- Improvements in the stability and reduction in the cost of telescopic masts may reduce superstructure shading effects.
- Reduction in the cost of pointing systems, thanks to the video camera surveillance industry, should improve the protection (“parking”) of irradiance sensors when not in use, and thus reduce fouling for long-term deployments.
- Improvements in automatic gimballing systems might reduce the tilt effects for the irradiance sensor method.
- Greater use of full sky imaging cameras, whether calibrated (expensive) or not (inexpensive), will allow the better identification of suboptimal measurement conditions.
- The tendency to move to highly automated systems with long-term, e.g., one year, essentially maintenance-free deployments is likely to significantly improve the quantity of data available for validation.
- The advent of operational satellite missions such as NPP/VIIRS, Sentinel-3/OLCI, Sentinel-2/MSI, and Landsat-8/OLI with the need for a guaranteed long-term validated data stream will increase the need for FRM.
- The huge increase in optical satellite missions used for aquatic remote sensing will also increase the need for highly automated measurement systems.
- As regards the needs of the validation community, it is recommended to:
- Update this review, e.g., on a 10-year time frame, to take account of developments in the protocols, particularly in the estimation of uncertainties. Such an update is best preceded by community discussion at an international workshop.
- Organize regular, e.g., on a two-year time frame, intercomparison exercises to ensure that measurement protocols and scientists remain state of the art (as required by the FRM context).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclaimer
References
- International Ocean Colour Coordinating Group (IOCCG). Why Ocean Colour? The Societal Benefits of Ocean-Colour Technology; IOCCG Report 7; IOCCG: Dartmouth, NS, Canada, 2008; p. 141. [Google Scholar]
- Donlon, C.J.; Wimmer, W.; Robinson, I.; Fisher, G.; Ferlet, M.; Nightingale, T.; Bras, B. A second-generation blackbody system for the calibration and verification of seagoing infrared radiometers. J. Atmospheric Ocean. Technol. 2014, 31, 1104–1127. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: London, UK, 1994. [Google Scholar]
- Mueller, J.L.; Morel, A. Fundamental definitions, relationships and conventions. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume I: Introduction, Background and Conventions; NASA/TM; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; Chapter 2; pp. 11–30. [Google Scholar]
- Ruddick, K.; Voss, K.; Boss, E.; Castagna, A.; Frouin, R.J.; Gilerson, A.; Hieronymi, M.; Johnson, B.C.; Kuusk, J.; Lee, Z.; et al. A review of protocols for Fiducial Reference Measurements of water-leaving radiance for validation of satellite remote sensing data over water. Remote Sens. (submitted to this volume).
- Vermote, E.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcette, J.J.; Kotchenova, S.Y. Second Simulation of the Satellite Signal in the Solar Spectrum-Vector (6SV). 6S User Guide Version 3. 2006, p. 134. Available online: http://6s.ltdri.org/pages/manual.html (accessed on 23 July 2019).
- Mobley, C. Light from the Sun. Available online: http://www.oceanopticsbook.info/view/light_and_radiometry/level_2/light_from_the_sun (accessed on 17 May 2019).
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Fröhlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Müller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Am. Meteorol. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Wild, M. Global dimming and brightening: A review. J. Geophys. Res. Atmos. 2009, 114, 1984–2012. [Google Scholar] [CrossRef]
- Smith, R.C.; Prezelin, B.B.; Baker, K.S.; Bidigare, R.R.; Boucher, N.P.; Coley, T.; Karentz, D.; MacIntyre, S.; Matlick, H.A.; Menzies, D.; et al. Ozone depletion: ultraviolet radiation and phytoplankton biology in antarctic waters. Science 1992, 255, 952–959. [Google Scholar] [CrossRef]
- Eerme, K.; Veismann, U.; Lätt, S. Proxy-based reconstruction of erythemal UV doses over Estonia for 1955–2004. Ann. Geophys. 2006, 24, 1767–1782. [Google Scholar] [CrossRef]
- Balzarolo, M.; Anderson, K.; Nichol, C.; Rossini, M.; Vescovo, L.; Arriga, N.; Wohlfahrt, G.; Calvet, J.-C.; Carrara, A.; Cerasoli, S.; et al. Ground-based optical measurements at European flux sites: a review of methods, instruments and current controversies. Sensors 2011, 11, 7954–7981. [Google Scholar] [CrossRef]
- Frouin, R.; Ramon, D.; Boss, E.; Jolivet, D.; Compiègne, M.; Tan, J.; Bouman, H.; Jackson, T.; Franz, B.; Platt, T.; et al. Satellite radiation products for ocean biology and biogeochemistry: Needs, state-of-the-art, gaps, development priorities, and opportunities. Front. Mar. Sci. 2018, 5, 3. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- International Standards Organisation (ISO). Space Environment (Natural And Artificial)—Process for Determining Solar Irradiances; ISO Report 21348:2007; International Standards Organisation (ISO): Geneva, Switzerland, 2007. [Google Scholar]
- Hooker, S.B.; Zibordi, G.; Maritorena, S. The Second SeaWiFs Ocean Optics DARR (DARR-00). In Results of the Second SeaWiFS Data Analysis Round Robin, March 2000 (DARR-00); SeaWiFS Postlaunch Technical Report Series; NASA Goddard Space Flight Space Center: Greenbelt, MD, USA, 2001; Volume 15, pp. 4–45. [Google Scholar]
- Zibordi, G.; Ruddick, K.; Ansko, I.; Moore, G.; Kratzer, S.; Icely, J.; Reinart, A. In situ determination of the remote sensing reflectance: an inter-comparison. Ocean Sci. 2012, 8, 567–586. [Google Scholar] [CrossRef]
- Ondrusek, M.; Lance, V.P.; Arnone, R.; Ladner, S.; Goode, W.; Vandermeulen, R.; Freeman, S.; Chaves, J.E.; Mannino, A.; Gilerson, A.; et al. Report for Dedicated JPSS VIIRS Ocean Color December 2015 Calibration/Validation Cruise; NOAA Technical Report 148; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service: Washington, DC, USA, 2016; p. 66.
- International Standards Organisation (ISO) Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; JCGM 101: 2008; International Standards Organisation (ISO): Geneva, Switerland, 2008.
- Mueller, J.L.; Fargion, G.S.; McClain, C.R. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Technical Memorandum TM-2003-21621/Revision 5; NASA Goddard Space Flight Space Center: Greenbelt, MD, USA, 2004. [Google Scholar]
- Zibordi, G.; Voss, K.J. In situ optical radiometry in the visible and near infrared. In Optical Radiometry for Ocean Climate Measurements; Zibordi, G., Donlon, C., Parr, A.C., Eds.; 2014; pp. 248–305. [Google Scholar]
- Zibordi, G.; Voss, K. Protocols for Satellite Ocean Color Data Validation: In situ Optical Radiometry; IOCCG Protocols Document; IOCCG: Dartmouth, Canada, 2019. [Google Scholar]
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Laboratory intercomparison of radiometers used for satellite validation in the 400–900 nm range. Remote Sens. 2019, 11, 1101. [Google Scholar] [CrossRef]
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Field intercomparison of radiometers used for satellite validation in the 400–900 nm range. Remote Sens. 2019, 11, 1129. [Google Scholar] [CrossRef]
- Ruddick, K.; De Cauwer, V.; Park, Y.; Moore, G. Seaborne measurements of near infrared water-leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef]
- Zibordi, G.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Mélin, F.; Berthon, J.-F.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A network for the validation of ocean color primary product. J. Atmospheric Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Claustre, H.; Bernard, S.; Berthon, J.-F.; Bishop, J.; Boss, E.; Coaranoan, C.; D’Ortenzio, F.; Johnson, K.; Lotliker, A.; Ulloa, O. Bio-Optical Sensors on Argo Floats; IOCCG Report; IOCCG: Dartmouth, NS, Canada, 2011. [Google Scholar]
- Mekaoui, S.; Zibordi, G. Cosine error for a class of hyperspectral irradiance sensors. Metrologia 2013, 50, 187–199. [Google Scholar] [CrossRef]
- Hlaing, S.; Harmel, T.; Ibrahim, A.; Ioannou, I.; Tonizzo, A.; Gilerson, A.; Ahmed, S. Validation of ocean color satellite sensors using coastal observational platform in Long Island Sound. In Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2010; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; pp. 782504-1–782504-8. [Google Scholar]
- Brando, V.E.; Lovell, J.L.; King, E.A.; Boadle, D.; Scott, R.; Schroeder, T. The potential of autonomous ship-borne hyperspectral radiometers for the validation of ocean color radiometry data. Remote Sens. 2016, 8, 150. [Google Scholar] [CrossRef]
- Slivkoff, M.M. Ocean Colour Remote Sensing of the Great Barrier Reef waters. PhD Thesis, Curtin University, Bentley, Australia, 2014. [Google Scholar]
- Antoine, D.; Guevel, P.; Desté, J.-F.; Bécu, G.; Louis, F.; Scott, A.J.; Bardey, P. The “BOUSSOLE” buoy-a new transparent-to-swell taut mooring dedicated to marine optics: Design, tests, and performance at sea. J. Atmospheric Ocean. Technol. 2008, 25, 968–989. [Google Scholar] [CrossRef]
- Voss, K.J.; Chapin, A.L. Upwelling radiance distribution camera system, NURADS. Opt. Express 2005, 13, 4250. [Google Scholar] [CrossRef]
- Vansteenwegen, D.; Ruddick, K.; Cattrijsse, A.; Vanhellemont, Q.; Beck, M. The pan-and-tilt hyperspectral radiometer system (PANTHYR) for autonomous satellite validation measurements – prototype design and testing. Remote Sens. 2019, 11, 1360. [Google Scholar] [CrossRef]
- Hooker, S.B. The telescopic mount for advanced solar technologies (T-MAST). In Advances in Measuring the Apparent Optical Properties (AOPs) of Optically Complex Waters; NASA/TM; NASA Goddard Space Flight Space Center: Greenbelt, MD, USA, 2010; Volume 215856. [Google Scholar]
- Vaskuri, A.; Greenwell, C.; Hessey, I.; Tompkins, J.; Woolliams, E. Contamination and UV ageing of diffuser targets used in satellite inflight and ground reference test site calibrations. J. Phys. Conf. Ser. 2018, 972, 012001. [Google Scholar] [CrossRef]
- Hooker, S.B.; Maritorena, S. An evaluation of oceanographic radiometers and deployment methodologies. J. Atmospheric Ocean. Technol. 2000, 17, 811–830. [Google Scholar] [CrossRef]
- Kuusk, J.; Kuusk, A. Hyperspectral radiometer for automated measurement of global and diffuse sky irradiance. J. Quant. Spectrosc. Radiat. Transf. 2018, 204, 272–280. [Google Scholar] [CrossRef]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Kalisch, J.; Macke, A. Estimation of the total cloud cover with high temporal resolution and parametrization of short-term fluctuations of sea surface insolation. Meteorol. Z. 2008, 17, 603–611. [Google Scholar] [CrossRef]
- Batlles, F.J.; Olmo, F.J.; Alados-Arboledas, L. On shadowband correction methods for diffuse irradiance measurements. Sol. Energy 1995, 54, 105–114. [Google Scholar] [CrossRef]
- Castagna, A.; Johnson, B.C.; Voss, K.; Dierssen, H.M.; Patrick, H.; Germer, T.; Sabbe, K.; Vyverman, W. Uncertainty in global downwelling plane irradiance estimates from sintered polytetrafluoroethylene plaque radiance measurements. Appl. Opt. 2019, 58, 4497–4511. [Google Scholar] [CrossRef] [PubMed]
- Early, E.A.; Barnes, P.Y.; Johnson, B.C.; Butler, J.J.; Bruegge, C.J.; Biggar, S.F.; Spyak, P.R.; Pavlov, M.M. Bidirectional Reflectance Round-Robin in Support of the Earth Observing System Program. J. Atmos. Ocean. Technol. 2000, 17, 1077–1091. [Google Scholar] [CrossRef]
- Niemi, K.; Metsämäki, S.; Pulliainen, J.; Suokanerva, H.; Böttcher, K.; Leppäranta, M.; Pellikka, P. The behaviour of mast-borne spectra in a snow-covered boreal forest. Remote Sens. Environ. 2012, 124, 551–563. [Google Scholar] [CrossRef]
- Leeuw, T.; Boss, E. The hydrocolor app: above water measurements of remote sensing reflectance and turbidity using a smartphone camera. Sensors 2018, 18, 256. [Google Scholar] [CrossRef]
- Mueller, J.L.; Davis, C.; Arnone, R.; Frouin, R.; Carder, K.; Lee, Z.P.; Steward, R.G.; Hooker, S.; Mobley, C.D.; McLean, S. Above-water radiance and remote sensing reflectance measurements and analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation Revision 4; National Aeronautical and Space Administration: Greenbelt, MD, USA, 2003; Volume III, Chapter 3; pp. 21–31. [Google Scholar]
- Salim, S.G.R.; Fox, N.P.; Theocharous, E.; Sun, T.; Grattan, K.T.V. Temperature and nonlinearity corrections for a photodiode array spectrometer used in the field. Appl. Opt. 2011, 50, 866–875. [Google Scholar] [CrossRef]
- Yoon, H.W.; Butler, J.J.; Larason, T.C.; Eppeldauer, G.P. Linearity of InGaAs photodiodes. Metrologia 2003, 40, S154–S158. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Doxaran, D.; Cherukuru, N.C.; Lavender, S.J.; Moore, G.F. Use of a Spectralon panel to measure the downwelling irradiance signal: case studies and recommendations. Appl. Opt. 2004, 43, 5981. [Google Scholar] [CrossRef]
- Behnert, I.D.; Deadman, A.J.; Fox, N.P.; Harris, P.M.; Gürol, S.; Özen, H.; Bachmann, M.; Boucher, Y.; Lachérade, S. Measurement Report CEOS WGCV Pilot Comparison of Techniques and Instruments Used for the Vicarious Calibration of Land Surface Imaging through a Ground Reference Standard Test Site 2009; NPL Report OP5; National Physical Laboratory: Teddington, UK, 2010. [Google Scholar]
- Stiegman, A.E.; Bruegge, C.J.; Springsteen, A.W. Ultraviolet stability and contamination analysis of Spectralon diffuse reflectance material. Opt. Eng. 1993, 32, 799–804. [Google Scholar] [CrossRef]
- Georgiev, G.T.; Butler, J.J. Long-term calibration monitoring of Spectralon diffusers BRDF in the air-ultraviolet. Appl. Opt. 2007, 46, 7892–7899. [Google Scholar] [CrossRef] [PubMed]
- Georgi, G.T.; James, J. Butler BRDF Study of Gray-Scale Spectralon; SPIE Proceedings 7081; SPIE: Bellingham, WA, USA, 2008; p. 9. [Google Scholar]
- Georgiev, G.T.; Butler, J.J. The Effect of Incident Light Polarization on Spectralon BRDF Measurements; SPIE Proceedings 5570; SPIE: Bellingham, WA, USA, 2004; p. 492. [Google Scholar]
- Germer, T.A. Full four-dimensional and reciprocal Mueller matrix bidirectional reflectance distribution function of sintered polytetrafluoroethylene. Appl. Opt. 2017, 56, 9333–9340. [Google Scholar] [CrossRef]
- Deschamps, P.-Y.; Fougnie, B.; Frouin, R.; Lecomte, P.; Verwaerde, C. SIMBAD: A field radiometer for satellite ocean color validation. Appl. Opt. 2004, 43, 4055–4069. [Google Scholar] [CrossRef]
- Holben, B.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Segal-Rosenheimer, M.; Russell, P.B.; Schmid, B.; Redemann, J.; Livingston, J.M.; Flynn, C.J.; Johnson, R.R.; Dunagan, S.E.; Shinozuka, Y.; Herman, J.; et al. Tracking elevated pollution layers with a newly developed hyperspectral Sun/Sky spectrometer (4STAR): Results from the TCAP 2012 and 2013 campaigns. J. Geophys. Res. Atmos. 2014, 119, 2013JD020884. [Google Scholar] [CrossRef]
- Thuillier, G.; Herse, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Deuzé, J.L.; Herman, M.; Santer, R. Fourier series expansion of the transfer equation in the atmosphere-ocean system. J. Quant. Spectrosc. Radiat. Transf. 1989, 41, 483–494. [Google Scholar] [CrossRef]
- Tanré, D.; Herman, M.; Deschamps, P.-Y.; de Leffe, A. Atmospheric modeling for space measurements of ground reflectances, including bidirectional properties. Appl. Opt. 1979, 18, 3587–3594. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Du, T.; Zhang, T. Remote sensing of ocean color and aerosol properties: resolving the issue of aerosol absorption. Appl. Opt. 1997, 36, 8670–8684. [Google Scholar] [CrossRef] [PubMed]
- Emde, C.; Barlakas, V.; Cornet, C.; Evans, F.; Korkin, S.; Ota, Y.; Labonnote, L.C.; Lyapustin, A.; Macke, A.; Mayer, B.; et al. IPRT polarized radiative transfer model intercomparison project—Phase A. J. Quant. Spectrosc. Radiat. Transf. 2015, 164, 8–36. [Google Scholar] [CrossRef]
- Hooker, S.B.; Bernhard, G.; Morrow, J.H.; Booth, C.R.; Comer, T.; Lind, R.N.; Quang, V. Optical Sensors for Planetary Radiant Energy (OSPREy): Calibration and Validation of Current and Next-Generation NASA Missions; NASA Goddard Space Flight Space Center: Greenbelt, MD, USA, 2012. [Google Scholar]
- Mueller, J.L. In-water radiometric profile measurements and data analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume III: Radiometric Measurements and Data Analysis Protocols; NASA/TM; NASA Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; Chapter 2; pp. 7–20. [Google Scholar]
- Frouin, R.; Pinker, R.T. Estimating Photosynthetically Active Radiation (PAR) at the earth’s surface from satellite observations. Remote Sens. Land Surf. Stud. Glob. Chang. 1995, 51, 98–107. [Google Scholar] [CrossRef]
| Upward-Pointing Irradiance Sensor | Radiance Sensor and Reflective Plaque | Direct Sunphotometry | |
|---|---|---|---|
| Equipment | Irradiance sensor (cosine response) Inclinometer | Radiance sensor Reflective plaque Inclinometer | Sunphotometer (radiance) sensor Pointing mechanism Atmosphere radiative transfer model |
| Variants | Surfacing of underwater drifting floats. Shadowband for diffuse/direct. | White/grey plaques | Hand-held or robotic pointing |
| Other notes | Uncalibrated radiometers? (see Section 3.1.1) Plaque viewing nadir angle? (see Section 3.1.2) |
| Method | Upward-Pointing Irradiance Sensor | Radiance Sensor and Reflective Plaque | Direct Sunphotometry |
|---|---|---|---|
| Plaque cal and characterization | N/A | I: BRDF-calibrated, homogeneous plaque fills FOV R: Tests to check FOV U: Plaque certificate including BRDF, experiments for homogeneity and height above plaque/FOV | N/A |
| Tilt/pointing | I: Deploy vertical R: Monitor with inclinometer U: Modeling/experiments | I: Deploy horizontal R: Monitor with inclinometer U: Modeling/experiments | I: Sensor FOV contains and centered on Sun R: Small FOV, accurate pointing, check AOT U: Via estimation of AOT |
| Superstructure shading | I: Deploy above all structures R: Use mast and fish-eye photos U: Experiments (different heights/locations) and modeling | I: Deploy above all structures (except radiometer) R: Use mast and fish-eye photos U: Experiments (different heights/locations) and modeling | I: Clear radiometer–direct Sun path R: Check with video surveillance and data QC U: N/A (if not rejected) |
| Fouling | I: Keep fore-optics clean R: Inspect/clean/protect, monitor with portable cal devices U: Pre-/post-cleaning cal of radiometer | I: Keep radiometer fore-optics and plaque clean R: Inspect/clean/protect, monitor radiometer with portable cal devices U: Pre-/post-cleaning cals for radiometer and plaque | I: Keep fore-optics clean R: Inspect/clean/protect U: Pre-/post-cleaning cals |
| Fast natural fluctuations | I: Reject if unstable illumination R: Compare replicates/time series U: S.D. of accepted measurements | I: Reject if unstable illumination R: Compare replicates/time series U: S.D. of accepted measurements | I: Reject if unstable illumination R: Compare replicates/time series U: S.D. of accepted measurements |
| Sky conditions and atmospheric r/t model | N/A | N/A | I: Perfectly cloud-free sky, horizontally homogeneous atmosphere and surface. Perfect r/t model and inputs R: Reject if clouds detected. Intercompare r/t models, check inputs U: Modeling. See Section 4.2.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sens. 2019, 11, 1742. https://doi.org/10.3390/rs11151742
Ruddick KG, Voss K, Banks AC, Boss E, Castagna A, Frouin R, Hieronymi M, Jamet C, Johnson BC, Kuusk J, et al. A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sensing. 2019; 11(15):1742. https://doi.org/10.3390/rs11151742
Chicago/Turabian StyleRuddick, Kevin G., Kenneth Voss, Andrew C. Banks, Emmanuel Boss, Alexandre Castagna, Robert Frouin, Martin Hieronymi, Cedric Jamet, B. Carol Johnson, Joel Kuusk, and et al. 2019. "A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water" Remote Sensing 11, no. 15: 1742. https://doi.org/10.3390/rs11151742
APA StyleRuddick, K. G., Voss, K., Banks, A. C., Boss, E., Castagna, A., Frouin, R., Hieronymi, M., Jamet, C., Johnson, B. C., Kuusk, J., Lee, Z., Ondrusek, M., Vabson, V., & Vendt, R. (2019). A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sensing, 11(15), 1742. https://doi.org/10.3390/rs11151742









