Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China
Abstract
1. Introduction
2. Materials and Methods
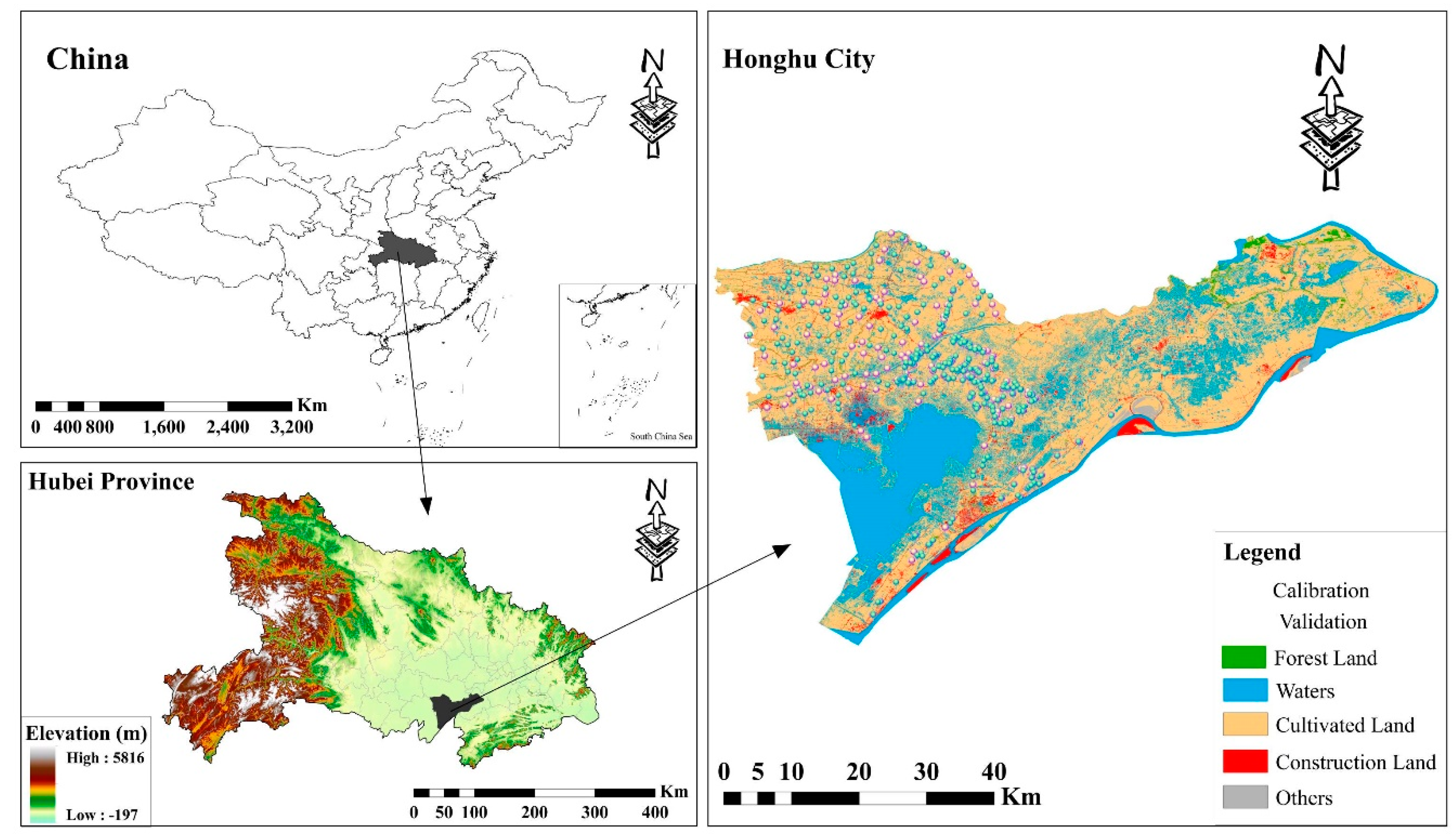
2.1. Study Area and Sampling
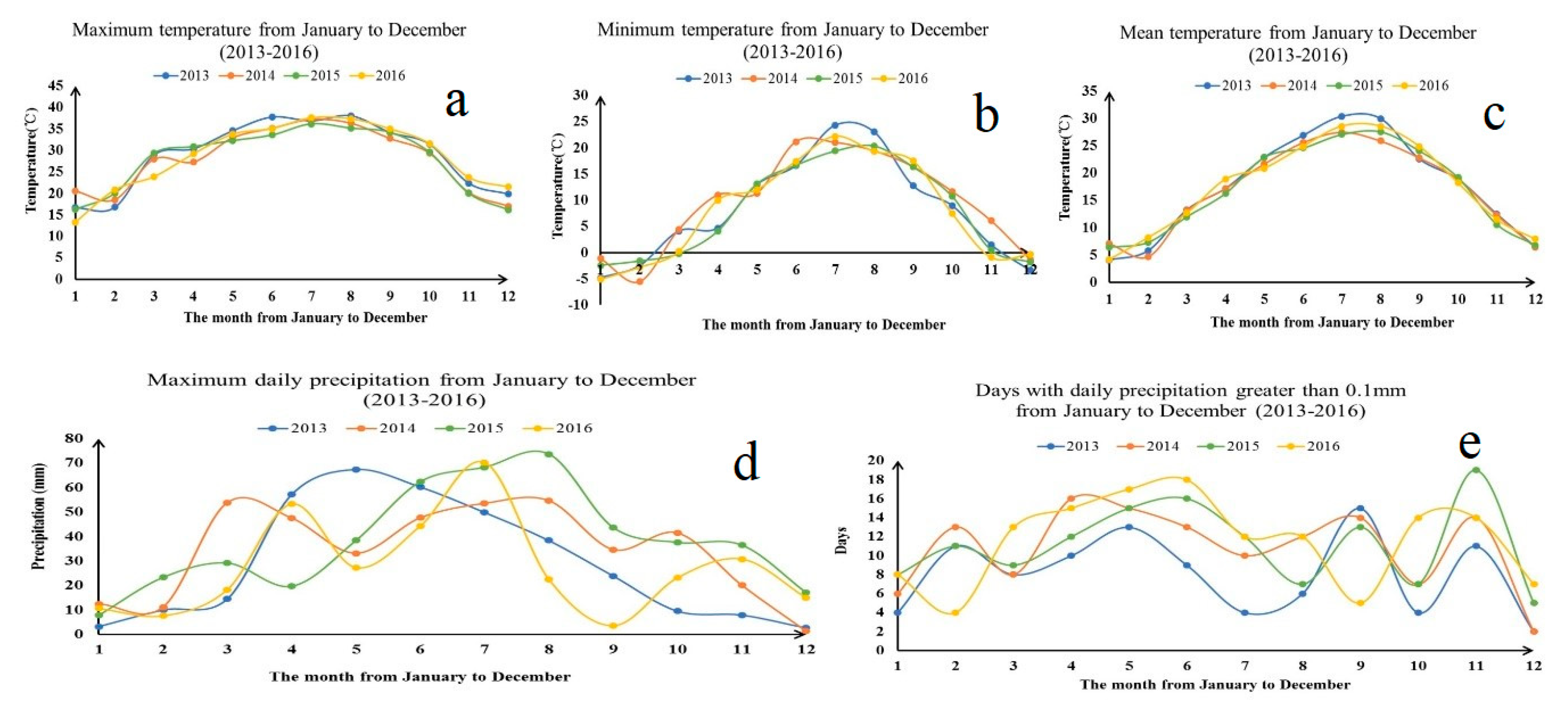
2.2. Data Source and Processing
2.3. Prediction Models
2.3.1. Stepwise Linear Regression (SLR) Model
2.3.2. Ordinary Kriging (OK) Model
2.3.3. Partial Least Squares Regression (PLSR) Model
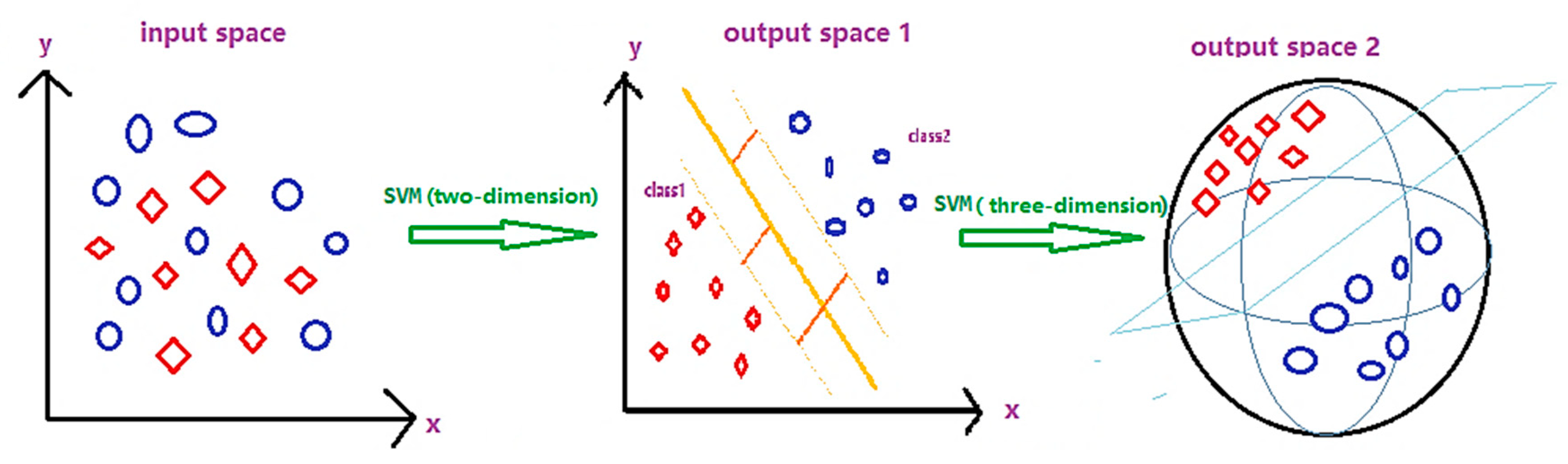
2.3.4. Support Vector Machine (SVM) Model
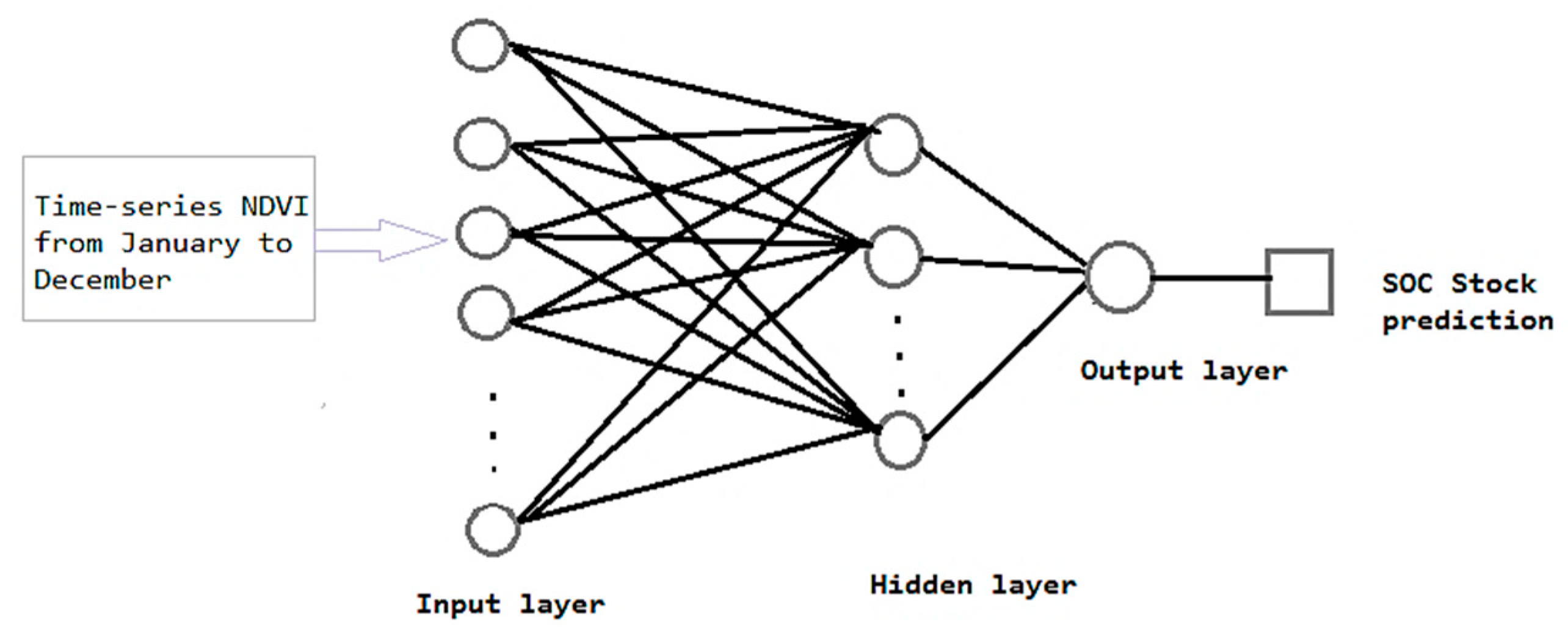
2.3.5. Artificial Neural Network (ANN) Model
2.4. Model Validation and Evaluation
3. Results
3.1. Basic Statistics of SOC and NDVIs
3.2. Relationship Between SOC and NDVI Time Series Data
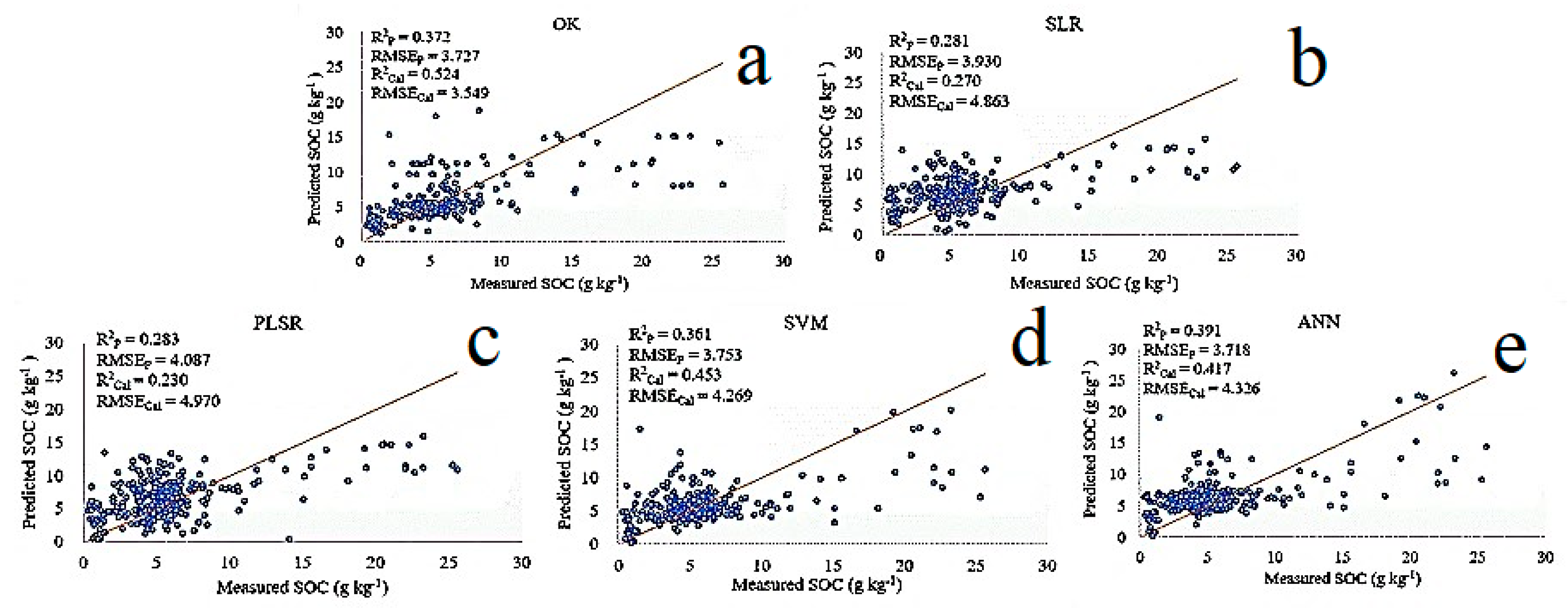
3.3. Prediction of SOC Using Different Predictive Models
3.4. Validation and Evaluation
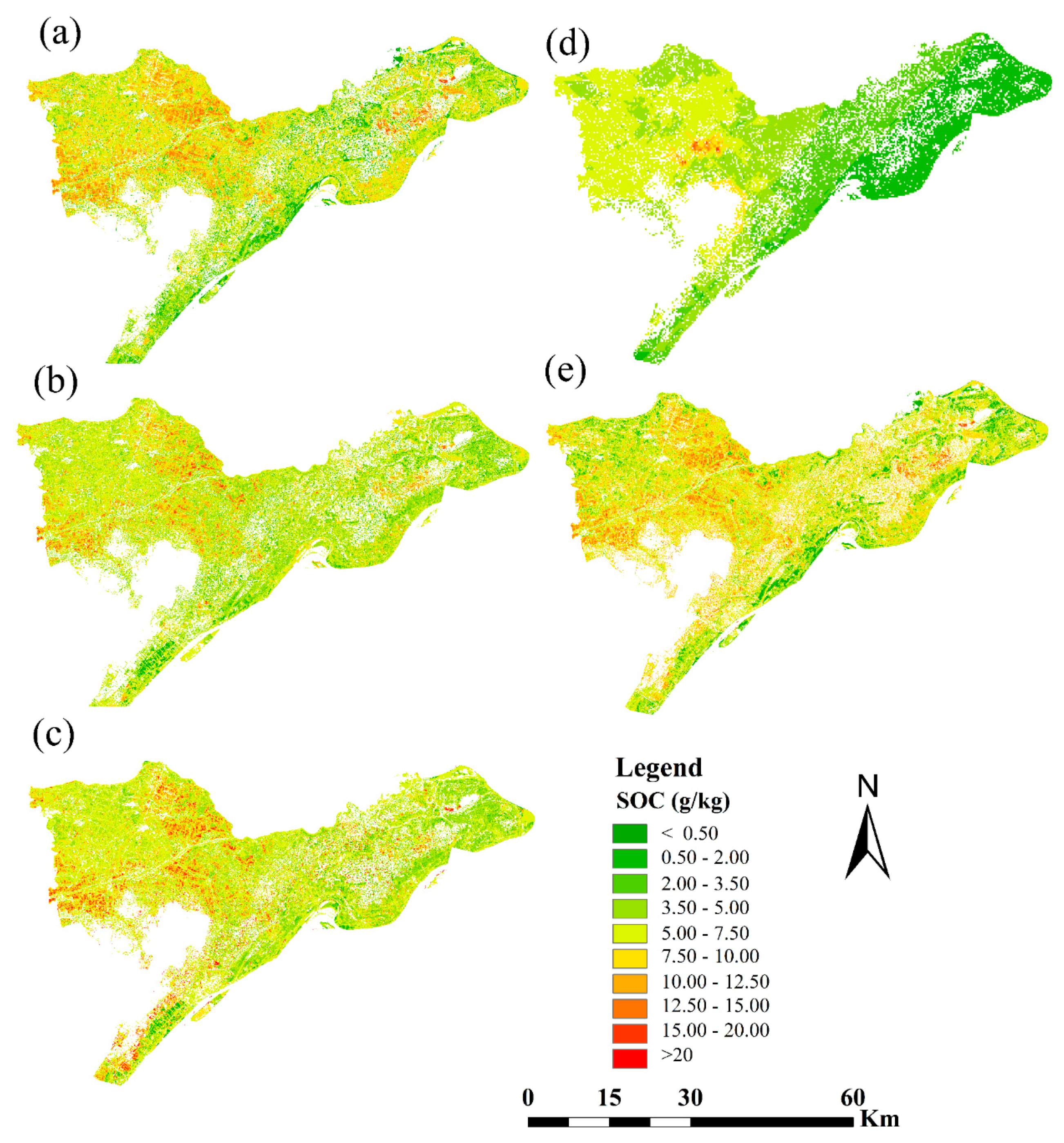
3.5. Digital Mapping of SOC
4. Discussion
4.1. Comparisons of Model Performance in SOC Prediction
4.2. Superiority of Time Series NDVI Approach
4.2.1. Exploring the Deep Mechanism of the Relationship Between SOC and NDVI Time Series
4.2.2. Effect of Terrain Factors on SOC Prediction
4.3. Limitations of Research
5. Conclusions
- (1)
- The results demonstrated that NDVI time series was correlated with SOC stock. A significant positive correlation was observed between the SOC content and NDVI in July and August. By contrast, a significant negative correlation was observed between the SOC content and NDVI in January, February, March, April, November, and December. This finding was attributed to the cultivation of farming work and the phenophase of the crops that influenced the land surface vegetation landscapes.
- (2)
- The comparison result of different methods showed that ANN was the overall best method with the lowest RMSEP of 3.718 and highest R2P of 0.391, followed by SVM (RMSEP = 3.753, R2P = 0.361), OK (RMSEP = 3.727, R2P of 0.372), PLSR (RMSEP = 4.087, R2P = 0.283), and SLR (RMSEP = 3.930, R2P = 0.281). Thus, ANN was the optimal model to predict SOC using the NDVI time series.
- (3)
- The SOC maps estimated by the five models were similar. The SOC content from east to west of the study area showed distribution ranging from low to high (0.3–40 g kg−1). However, the local details clearly indicated that OK interpolation smoothed the result, and the maps generated by the SLR and PLSR models highlighted high values in the center of the maps. Moreover, the map acquired by SVM tended more toward the middle and low values compared with that of the ANN model, which mostly presented middle and high values with lesser low values. These results confirmed that the spatial distribution of the SOC content can be digitally mapped through NDVI time series.
- (4)
- The prediction of SOC using single-data NDVI showed unsatisfactory accuracy, indicating the unpredictability of single-data NDVI compared with multi-time NDVI. The prediction results of two short NDVI time series, which were correlated to summer and winter crop production, respectively, manifested that short NDVI time series can be used for SOC prediction to some extent, but its prediction accuracy was lower than that of long time series. In addition, the correlation between topographic parameters and SOC was low. The terrain variables used as predictors in the model failed to produce good results. Hence, the effect of topography for SOC was negligible in this small-scale plain area.
Author Contributions
Funding
Conflicts of Interest
References
- Batjes, N.H. Total carbon and nitrogen in the soils of the world. Eur. J. Soil Sci. 1996, 47, 151–163. [Google Scholar] [CrossRef]
- Meersmans, J.; De Ridder, F.; Canters, F.; De Baets, S.; Van Molle, M. A multiple regression approach to assess the spatial distribution of soil organic carbon (soc) at the regional scale (flanders, belgium). Geoderma 2008, 143, 1–13. [Google Scholar] [CrossRef]
- Batjes, N.H.; Sombroek, W.G. Possibilities for carbon sequestration in tropical and subtropical soils. Glob. Chang. Biol. 1997, 3, 161–173. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, Q.L.; Wang, Q.B.; Jin, X.X.; Han, C.L. Mapping stocks of soil organic carbon and soil total nitrogen in liaoning province of china. Geoderma 2017, 305, 250–263. [Google Scholar] [CrossRef]
- Sreenivas, K.; Dadhwal, V.K.; Kumar, S.; Harsha, G.S.; Mitran, T.; Sujatha, G.; Suresh, G.J.R.; Fyzee, M.A.; Ravisankar, T. Digital mapping of soil organic and inorganic carbon status in india. Geoderma 2016, 269, 160–173. [Google Scholar] [CrossRef]
- McGrath, D.; Zhang, C.S. Spatial distribution of soil organic carbon concentrations in grassland of ireland. Appl. Geochem. 2003, 18, 1629–1639. [Google Scholar] [CrossRef]
- Grimm, R.; Behrens, T.; Marker, M.; Elsenbeer, H. Soil organic carbon concentrations and stocks on barro colorado island—Digital soil mapping using random forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Zhao, M.S.; Rossiter, D.G.; Li, D.C.; Zhao, Y.G.; Liu, F.; Zhang, G.L. Mapping soil organic matter in low-relief areas based on land surface diurnal temperature difference and a vegetation index. Ecol. Indic. 2014, 39, 120–133. [Google Scholar] [CrossRef]
- Malone, B.P.; Styc, Q.; Minasny, B.; McBratney, A.B. Digital soil mapping of soil carbon at the farm scale: A spatial downscaling approach in consideration of measured and uncertain data. Geoderma 2017, 290, 91–99. [Google Scholar] [CrossRef]
- Tao, Z.; Peijun, S.H.I.; Jinying, L.U.O.; Zhenyan, S. Estimation of soil organic carbon based on remote sensing and process model. J. Remote Sens. 2007, 11, 127–136. [Google Scholar]
- Chen, Z.; Chen, G.; Zhong, X.; Yang, Y. Review on estimations of soil organic carbon content based on hyperspectral measurements. J. Subtrop. Resour. Environ. 2009, 4, 78–87. [Google Scholar]
- Rabenhorst, M.C.; Stolt, M.H. Field estimations of soil organic carbon. Soil Sci. Soc. Am. J. 2012, 76, 1478–1481. [Google Scholar] [CrossRef]
- Wu, H.Y.; Zeng, F.P.; Song, T.Q.; Peng, W.X.; Li, X.H.; OuYang, Z.W. Spatial variations of soil organic carbon and nitrogen in peak-cluster depression areas of karst region. Plant Nutr. Fertitizer Sci. 2009, 15, 1029–1036. [Google Scholar]
- Zhang, L.; Gao, P.; Wang, C.; Liu, S.; Li, X. Spatial distribution of soil organic carbon in the forestland of the yaoxiang small watershed in central and southern shandong province. Sci. Soil Water Conserv. 2015, 13, 83–89. [Google Scholar]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189, 627–634. [Google Scholar] [CrossRef]
- Chabala, L.M.; Mulolwa, A.; Lungu, O. Application of ordinary kriging in mapping soil organic carbon in zambia. Pedosphere 2017, 27, 338–343. [Google Scholar] [CrossRef]
- Lu, F.; Zhao, Y.; Huang, B.; Wang, J. Comparison of predicting methods for mapping the spatial distribution of topsoil organic matter content in cropland of hailun. J. Soil Sci. 2012, 43, 662–667. [Google Scholar]
- Xu, E.; Zhang, H. Multi-scale analysis of kriging interpolation and conditional simulation for soil organic matters in newly reclaimed area in yili. Soils 2013, 45, 91–98. [Google Scholar]
- Zhao, D.; Zhao, H.; Rao, J.; Gao, X. Analysis of the spatial distribution pattern of cultivated land quality and the influential factors based on trend-surface. Res. Soil Water Conserv. 2015, 22, 219–223. [Google Scholar]
- Guo, L.; Linderman, M.; Shi, T.Z.; Chen, Y.Y.; Duan, L.J.; Zhang, H.T. Exploring the sensitivity of sampling density in digital mapping of soil organic carbon and its application in soil sampling. Remote Sens. 2018, 10, 27. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, A.; Qin, C.; Li, B.; Pei, T. A soil sampling method based on representativeness grade of sampling points. Acta Pedol. Sin. 2011, 48, 938–946. [Google Scholar]
- Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. Comparing geospatial techniques to predict soc stocks. Soil Tillage Res. 2015, 148, 46–58. [Google Scholar] [CrossRef]
- Malone, B.P.; Jha, S.K.; Minasny, B.; McBratney, A.B. Comparing regression-based digital soil mapping and multiple-point geostatistics for the spatial extrapolation of soil data. Geoderma 2016, 262, 243–253. [Google Scholar] [CrossRef]
- Song, X.-D.; Brus, D.J.; Liu, F.; Li, D.-C.; Zhao, Y.-G.; Yang, J.-L.; Zhang, G.-L. Mapping soil organic carbon content by geographically weighted regression: A case study in the heihe river basin, china. Geoderma 2016, 261, 11–22. [Google Scholar] [CrossRef]
- Wang, S.; Fan, J.; Zhong, H.; Li, Y.; Zhu, H.; Qiao, Y.; Zhang, H. A multi-factor weighted regression approach for estimating the spatial distribution of soil organic carbon in grasslands. Catena 2019, 174, 248–258. [Google Scholar] [CrossRef]
- Khormali, F.; Ajami, M.; Ayoubi, S.; Srinivasarao, C.; Wani, S.P. Role of deforestation and hillslope position on soil quality attributes of loess-derived soils in golestan province, Iran. Agric. Ecosyst. Environ. 2009, 134, 178–189. [Google Scholar] [CrossRef]
- Ma, Y.; Li, X.; Li, D.; Han, Z.; Zhang, G.; Zhang, W.; Hu, C.; Shao, Y. Spatial variation of soil organic carbon contentin farmland and its influencing factors in mengcheng county, northern Anhui plain. Acta Pedol. Sin. 2014, 51, 1153–1159. [Google Scholar]
- Ajami, M.; Heidari, A.; Khormali, F.; Gorji, M.; Ayoubi, S. Environmental factors controlling soil organic carbon storage in loess soils of a subhumid region, northern Iran. Geoderma 2016, 281, 1–10. [Google Scholar] [CrossRef]
- Zhu, A.; Liu, F.; Li, B.; Pei, T.; Qin, C.; Liu, G.; Wang, Y.; Chen, Y.; Ma, X.; Qi, F.; et al. Differentiation of soil conditions over low relief areas using feedback dynamic patterns. Soil Sci. Soc. Am. J. 2010, 74, 861–869. [Google Scholar] [CrossRef]
- Liu, F.; Geng, X.; Zhu, A.-X.; Fraser, W.; Waddell, A.J.G. Soil texture mapping over low relief areas using land surface feedback dynamic patterns extracted from MODIS. Geoderma 2012, 171, 44–52. [Google Scholar] [CrossRef]
- Zeng, C.; Zhu, A.X.; Liu, F.; Yang, L.; Rossiter, D.G.; Liu, J.; Wang, D. The impact of rainfall magnitude on the performance of digital soil mapping over low-relief areas using a land surface dynamic feedback method. Ecol. Indic. 2017, 72, 297–309. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.T.; Shi, T.Z.; Chen, Y.Y.; Jiang, Q.H.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Johnson, J.M.-F.; Franzluebbers, A.J.; Weyers, S.L.; Reicosky, D.C. Agricultural opportunities to mitigate greenhouse gas emissions. Environ. Pollut. 2007, 150, 107–124. [Google Scholar] [CrossRef] [PubMed]
- Snyder, C.; Bruulsema, T.; Jensen, T.; Fixen, P. Review of greenhouse gas emissions from crop production systems and fertilizer management effects. Agric. Ecosyst. 2009, 133, 247–266. [Google Scholar] [CrossRef]
- D’Hose, T.; Cougnon, M.; De Vliegher, A.; Vandecasteele, B.; Viaene, N.; Cornelis, W.; Van Bockstaele, E.; Reheul, D. The positive relationship between soil quality and crop production: A case study on the effect of farm compost application. Appl. Soil Ecol. 2014, 75, 189–198. [Google Scholar] [CrossRef]
- Jin, X.-L.; Diao, W.-Y.; Xiao, C.-H.; Wang, F.-Y.; Chen, B.; Wang, K.-R.; Li, S.-K. Estimation of wheat agronomic parameters using new spectral indices. PLoS ONE 2013, 8, e72736. [Google Scholar] [CrossRef] [PubMed]
- Lawal, B.A.; Oni, F.G.O.; Egedegbe, G.O.; Omogoye, A.M. Effects of calcium on agronomic parameters and nutritional quality of soybean Glycine max (L.) merrill grown in ogbomoso, nigeria. Crop Res. (Hisar) 2019, 54, 28–32. [Google Scholar]
- Sanghamitra, P.; Sah, R.P.; Bagchi, T.B.; Sharma, S.G.; Kumar, A.; Munda, S.; Sahu, R.K. Evaluation of variability and environmental stability of grain quality and agronomic parameters of pigmented rice (O-sativa L.). J. Food Sci. Technol. Mysore 2018, 55, 879–890. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the modis vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Dinh, N.Q.; Reichstein, M.; Vesala, T.; Keronen, P. Similarities in ground- and satellite-based ndvi time series and their relationship to physiological activity of a scots pine forest in finland. Remote Sens. Environ. 2004, 93, 225–237. [Google Scholar] [CrossRef]
- Kheir, R.B.; Greve, M.H.; Bocher, P.K.; Greve, M.B.; Larsen, R.; McCloy, K. Predictive mapping of soil organic carbon in wet cultivated lands using classification-tree based models: The case study of denmark. J. Environ. Manag. 2010, 91, 1150–1160. [Google Scholar] [CrossRef] [PubMed]
- Burnham, J.H.; Sletten, R.S. Spatial distribution of soil organic carbon in northwest greenland and underestimates of high arctic carbon stores. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Kerry, R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in baneh region, Iran. Geoderma 2016, 266, 98–110. [Google Scholar] [CrossRef]
- Shen, J.; Chang, Q.; Li, F.; Wang, L. Extraction of winter wheat information based on time-series ndvi in guanzhong area. Trans. Chin. Soc. Agric. Mach. 2017, 48, 215–220. [Google Scholar]
- Li, H.; Lei, J.; Wu, J. Analysis of land damage and recovery process in rare earth mining area based on multi-source sequential NDVI. Trans. Chin. Soc. Agric. Eng. 2018, 34, 232–240. [Google Scholar]
- Wardlow, B.D.; Egbert, S.L. Large-area crop mapping using time-series modis 250m ndvi data: An assessment for the U.S. Central great plains. Remote Sens. Environ. 2008, 112, 1096–1116. [Google Scholar] [CrossRef]
- Testa, S.; Soudani, K.; Boschetti, L.; Mondino, E.B. Modis-derived evi, ndvi and wdrvi time series to estimate phenological metrics in French deciduous forests. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Nagy, A.; Fehér, J.; Tamás, J. Wheat and maize yield forecasting for the tisza river catchment using modis ndvi time series and reported crop statistics. Comput. Electron. Agric. 2018, 151, 41–49. [Google Scholar] [CrossRef]
- Ichii, K.; Kondo, M.; Okabe, Y.; Ueyama, M.; Kobayashi, H.; Lee, S.-J.; Saigusa, N.; Zhu, Z.; Myneni, R.B. Recent changes in terrestrial gross primary productivity in Asia from 1982 to 2011. Remote Sens. 2013, 5, 6043–6062. [Google Scholar] [CrossRef]
- FAO. World Reference Base for Soil Resources; Food & Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. A rapid and accurate procedure for estimation of organic carbon in soils. Proceedings 1975, 84, 456–462. [Google Scholar]
- Guo, L.; Chen, Y.Y.; Shi, T.Z.; Zhao, C.; Liu, Y.L.; Wang, S.Q.; Zhang, H.T. Exploring the role of the spatial characteristics of visible and near-infrared reflectance in predicting soil organic carbon density. ISPRS Int. Geo-Inf. 2017, 6, 17. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Boote, K.J.; Kimball, B.A.; Ziska, L.H.; Izaurralde, R.C.; Ort, D.; Thomson, A.M.; Wolfe, D. Climate impacts on agriculture: Implications for crop production. Agron. J. 2011, 103, 351–370. [Google Scholar] [CrossRef]
- Paula Llano, M.; Vargas, W.; Naumann, G. Climate variability in areas of the world with high production of soya beans and corn: Its relationship to crop yields. Meteorol. Appl. 2012, 19, 385–396. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. Why are agricultural impacts of climate change so uncertain? The importance of temperature relative to precipitation. Environ. Res. Lett. 2008, 3, 034007. [Google Scholar] [CrossRef]
- Ross, S.M. Peirce’s criterion for the elimination of suspect experimental data. J. Eng. Technol. 2003, 20, 38–41. [Google Scholar]
- Wold, S.; Martens, H.; Wold, H. The multivariate calibration-problem in chemistry solved by the PLS method. Lect. Notes Math. 1983, 973, 286–293. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression—A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Tahmasbian, I.; Xu, Z.H.; Boyd, S.; Zhou, J.; Esmaeilani, R.; Che, R.X.; Bai, S.H. Laboratory-based hyperspectral image analysis for predicting soil carbon, nitrogen and their isotopic compositions. Geoderma 2018, 330, 254–263. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J. The collinearity problem in linear-regression—The partial least-squares (PLS) approach to generalized inverses. Siam J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Wang, C.; Pan, X.; Zhou, R.; Liu, Y.; Li, Y.; Xie, X. Prediction of soil properties using plsr-based soil-environment models. Acta Pedol. Sin. 2012, 49, 237–245. [Google Scholar]
- Cherkassky, V. The nature of statistical learning theory. IEEE Trans. Neural Netw. 1997, 8, 1564. [Google Scholar] [CrossRef] [PubMed]
- Were, K.; Bui, D.T.; Dick, O.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Shukla, S. Support vector machine based modeling of evapotranspiration using hydro-climatic variables in a sub-tropical environment. Agric. For. Meteorol. 2015, 200, 172–184. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Shamshirband, S.; Haghi, D.Z.; Azani, A.; Bonakdari, H.; Ebtehaj, I. Application of firefly algorithm-based support vector machines for prediction of field capacity and permanent wilting point. Soil Tillage Res. 2017, 172, 32–38. [Google Scholar] [CrossRef]
- Fan, J.L.; Wu, L.F.; Zhang, F.C.; Cai, H.J.; Wang, X.K.; Lu, X.H.; Xiang, Y.Z. Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renew. Sustain. Energy Rev. 2018, 94, 732–747. [Google Scholar] [CrossRef]
- Wise, B. PLS Toolbox Version 1.4 For Use With MATLABe, The Math Works: Natick, MA, USA, 1994.
- Aitkenhead, M.J.; Coull, M.C. Mapping soil carbon stocks across Scotland using a neural network model. Geoderma 2016, 262, 187–198. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Dai, F.Q.; Zhou, Q.G.; Lv, Z.Q.; Wang, X.M.; Liu, G.C. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan plateau. Ecol. Indic. 2014, 45, 184–194. [Google Scholar] [CrossRef]
- Wilding, L.P. Spatial variability: Its documentation, accommodation and implication to soil surveys. Soil Spat. Var. 1985, 166–194. [Google Scholar]
- Moore, F.; Sheykhi, V.; Salari, M.; Bagheri, A. Soil quality assessment using gis-based chemometric approach and pollution indices: Nakhlak mining district, central Iran. Environ. Monit. Assess. 2016, 188, 214. [Google Scholar] [CrossRef] [PubMed]
- Chien, Y.J.; Lee, D.Y.; Guo, H.Y.; Houng, K.H. Geostatistical analysis of soil properties of mid-west Taiwan soils. Soil Sci. 1997, 162, 291–298. [Google Scholar] [CrossRef]
- Zhen, J.; Pei, T.; Xie, S. Kriging methods with auxiliary nighttime lights data to detect potentially toxic metals concentrations in soil. Sci. Total Environ. 2018, 659, 363–371. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Besalatpour, A.A.; Ayoubi, S.; Hajabbasi, M.A.; Mosaddeghi, M.R.; Schulin, R. Estimating wet soil aggregate stability from easily available properties in a highly mountainous watershed. Catena 2013, 111, 72–79. [Google Scholar] [CrossRef]
- Kuang, B.Y.; Tekin, Y.; Mouazen, A.M. Comparison between artificial neural network and partial least squares for on-line visible and near infrared spectroscopy measurement of soil organic carbon, ph and clay content. Soil Tillage Res. 2015, 146, 243–252. [Google Scholar] [CrossRef]
- Tekin, Y.; Tumsavas, Z.; Mouazen, A.M. Effect of moisture content on prediction of organic carbon and ph using visible and near-infrared spectroscopy. Soil Sci. Soc. Am. J. 2012, 76, 188–198. [Google Scholar] [CrossRef]
- Stenberg, B. Effects of soil sample pretreatments and standardised rewetting as interacted with sand classes on vis-nir predictions of clay and soil organic carbon. Geoderma 2010, 158, 15–22. [Google Scholar] [CrossRef]
- Chen, F.; Qin, F.; Li, X.; Peng, G. Inversion for spatial distribution of soil organic matter content based on multivariate geostatistics. Trans. Chin. Soc. Agric. Eng. 2012, 28, 188–194. [Google Scholar]
- Zhao, Y.; Shi, X.; Yu, D.; Zhao, Y.; Sun, W.; Wang, H. Different methods for prediction of spatial patterns of soil organic carbon density in Hebei province, china. Acta Pedol. Sin. 2005, 42, 379–385. [Google Scholar]
- Gu, C. Application of kriging method in spatial prediction of regional soil organic carbon. Soil Fertil. Sci. China 2014, 3, 93–97. [Google Scholar]
- Tiessen, H.; Cuevas, E.; Chacon, P. The role of soil organic matter in sustaining soil fertility. Nature 1994, 371, 783–785. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, S.; Chen, J.; Zhou, G.; Zhang, L.; Li, Y.; Meng, Z.; Chen, D. Study of multiple vegetation indices reveals photosynthetic phenology in a subtropical evergreen forest. Acta Ecol. Sin. 2018, 38, 5771–5781. [Google Scholar]
- Monteith, J.L. Solar-radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. Ser. B-Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Dong, T.; Meng, J.; Wu, B. Overview on methods of deriving fraction of absorbed photosynthetically active radiation(fpar) using remote sensing. Acta Ecol. Sin. 2012, 32, 7190–7201. [Google Scholar] [CrossRef]
- Almond, S.; Boyd, D.S.; Dash, J.; Curran, P.J.; Hill, R.A.; Foody, G.M. Estimating terrestrial gross primary productivity with the envisat medium resolution imaging spectrometer (meris) terrestrial chlorophyll index (mtci). In Proceedings of the Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Harris, A.; Dash, J. The potential of the meris terrestrial chlorophyll index for carbon flux estimation. Remote Sens. Environ. 2010, 114, 1856–1862. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Huemmrich, K.F. Relationship between fraction of radiation absorbed by photosynthesizing maize and soybean canopies and ndvi from remotely sensed data taken at close range and from modis 250 m resolution data. Remote Sens. Environ. 2014, 147, 108–120. [Google Scholar] [CrossRef]
- Shao, P.; Chai, R.; Lin, Z.; Fang, S. Remote estimation of leaf gross primary productivity based on hyperspectral data. J. China Agric. Univ. 2018, 23, 109–117. [Google Scholar]
- Heinemeyer, A.; Wilkinson, M.; Vargas, R.; Subke, J.A.; Casella, E.; Morison, J.I.L.; Ineson, P. Exploring the “overflow tap” theory: Linking forest soil co2 fluxes and individual mycorrhizosphere components to photosynthesis. Biogeosciences 2012, 9, 79–95. [Google Scholar] [CrossRef]
- Kimball, J.S.; Jones, L.A.; Zhang, K.; Heinsch, F.A.; McDonald, K.C.; Oechel, W.C. A satellite approach to estimate land-atmosphere co2 exchange for boreal and arctic biomes using modis and amsr-e. IEEE Trans. Geosci. Remote Sens. 2009, 47, 569–587. [Google Scholar] [CrossRef]
- Chang, Y.; Yu, Y.; Cui, L.; Hou, J.; Zeng, D. Vegetation absorbed photosynthetically active radiation estimates based on hj-1a satellite hsi data. For. Eng. 2017, 33, 22–32. [Google Scholar]
- Kalambukattu, J.G.; Kumar, S.; Raj, R.A. Digital soil mapping in a himalayan watershed using remote sensing and terrain parameters employing artificial neural network model. Environ. Earth Sci. 2018, 77, 14. [Google Scholar] [CrossRef]
- Guo, P.-T.; Wu, W.; Sheng, Q.-K.; Li, M.-F.; Liu, H.-B.; Wang, Z.-Y. Prediction of soil organic matter using artificial neural network and topographic indicators in hilly areas. Nutr. Cycl. Agroecosyst. 2013, 95, 333–344. [Google Scholar] [CrossRef]
- Song, X.; Liu, F.; Zhang, G.; Li, D.; Zhao, Y.; Yang, J. Mapping soil organic carbon using local terrain attributes: A comparison of different polynomial models. Pedosphere 2017, 27, 681–693. [Google Scholar] [CrossRef]
- Johnson, K.D.; Scatena, F.N.; Johnson, A.H.; Pan, Y. Controls on soil organic matter content within a northern hardwood forest. Geoderma 2008, 148, 346–356. [Google Scholar] [CrossRef]
- Stoorvogel, J.J.; Kempen, B.; Heuvelink, G.B.M.; de Bruin, S. Implementation and evaluation of existing knowledge for digital soil mapping in senegal. Geoderma 2009, 149, 161–170. [Google Scholar] [CrossRef]
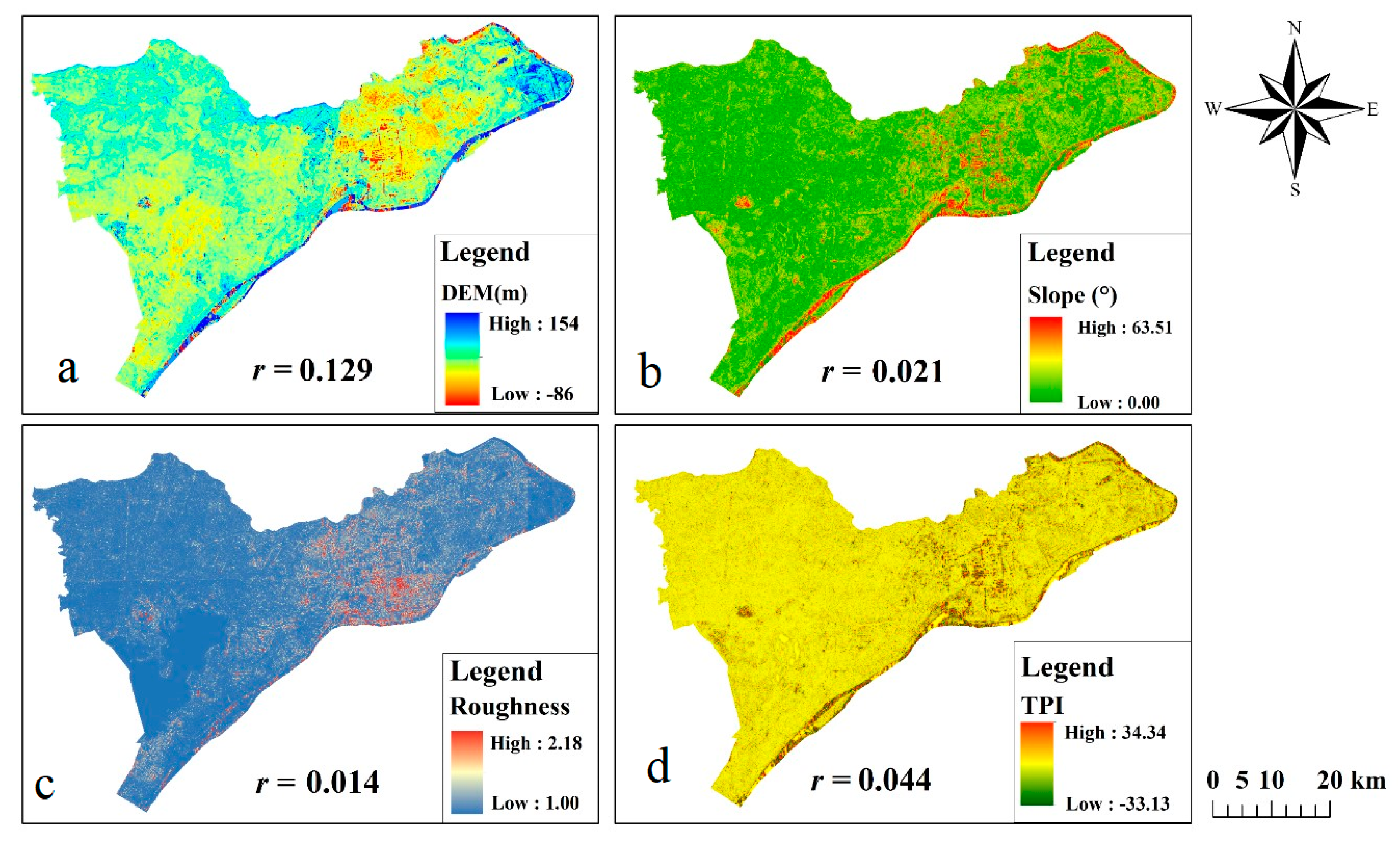
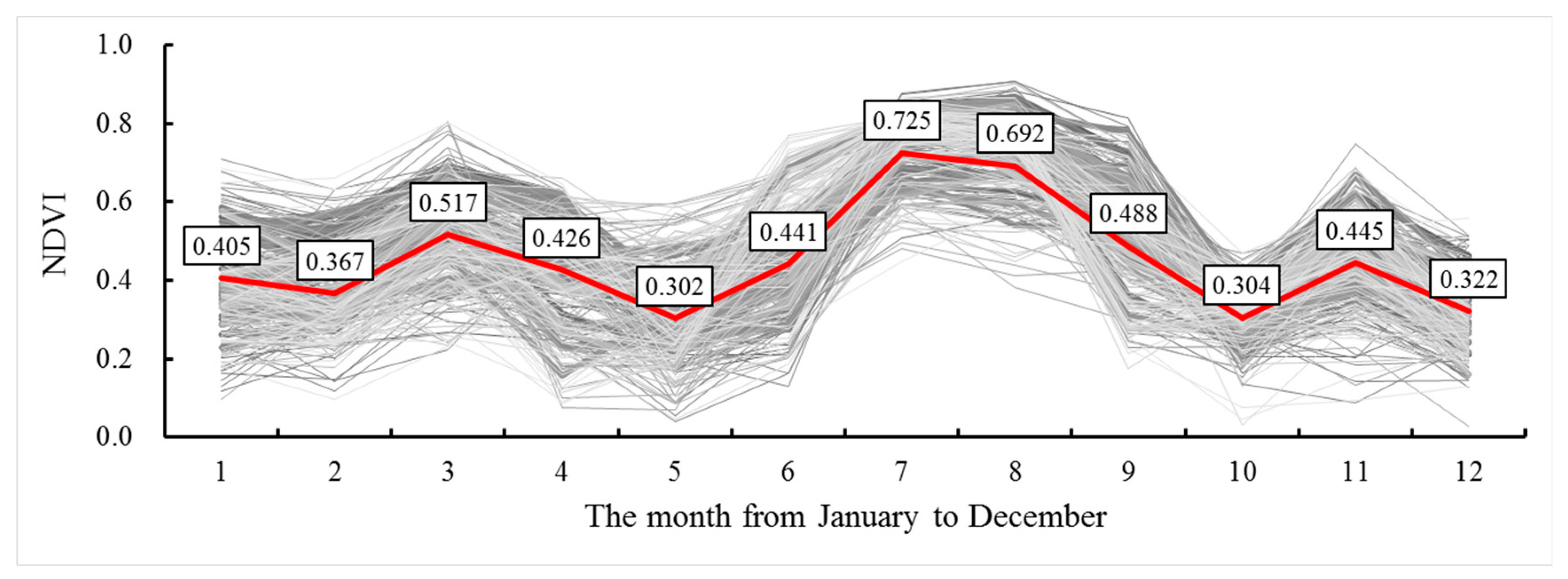
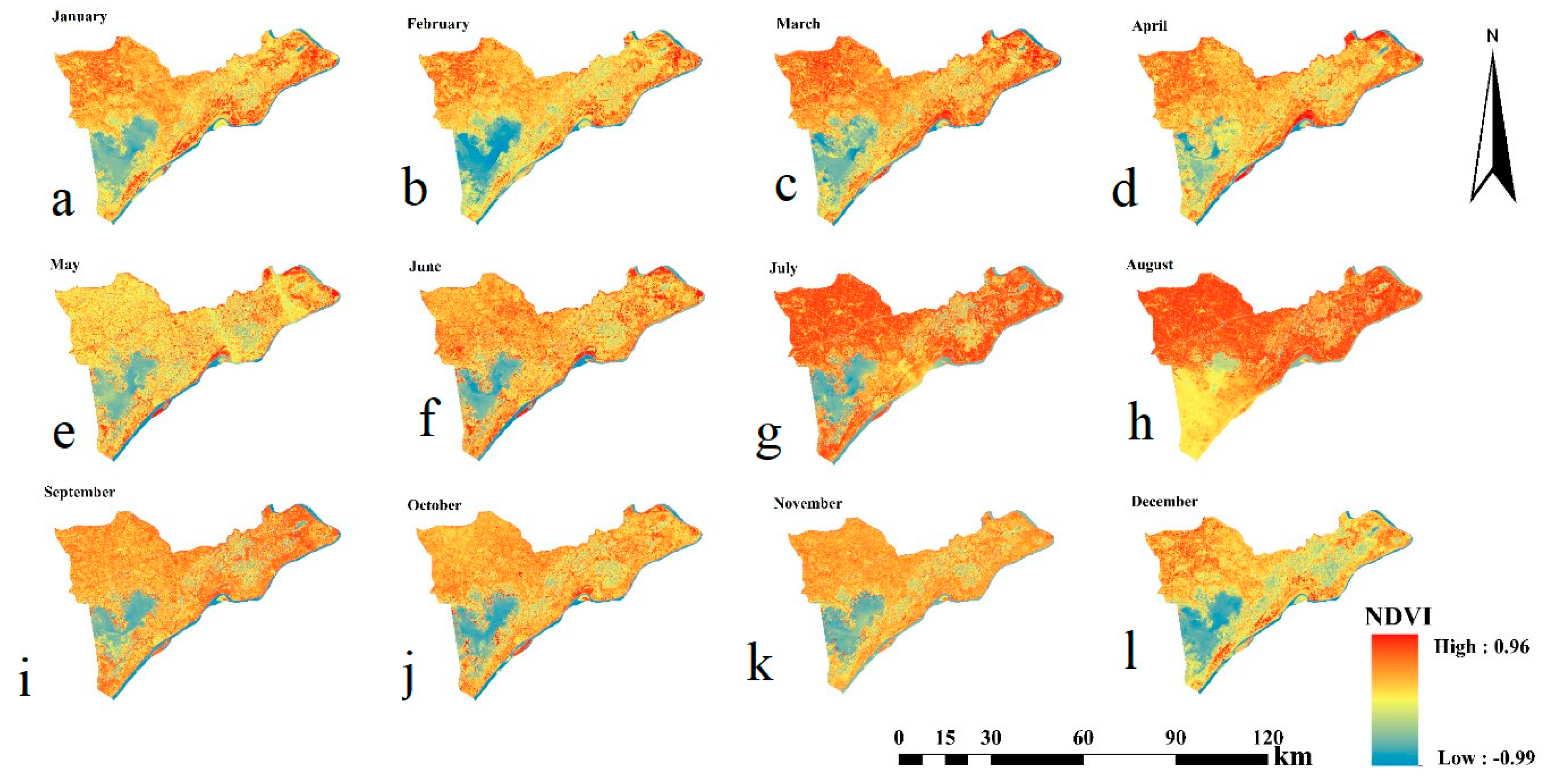
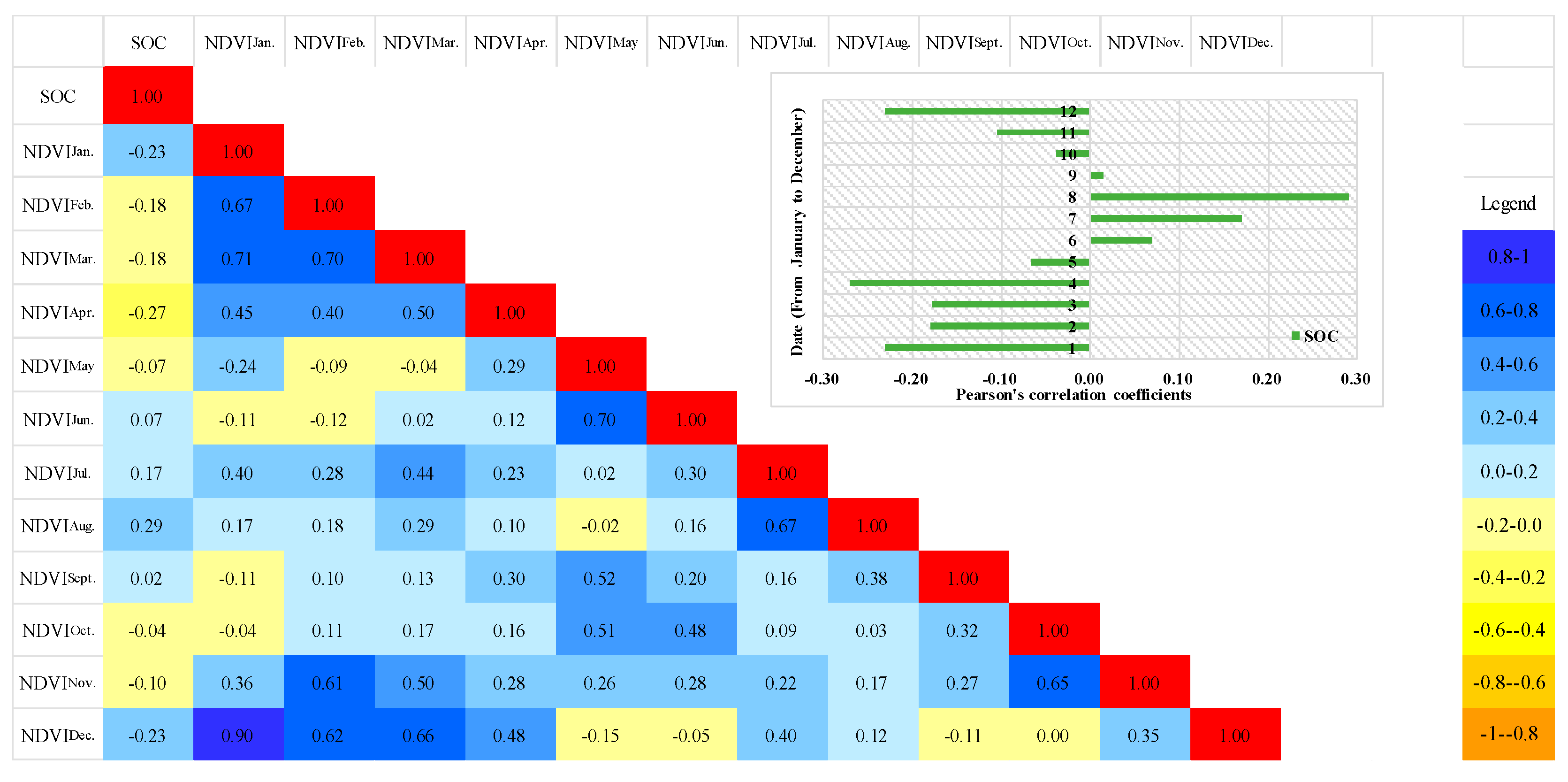
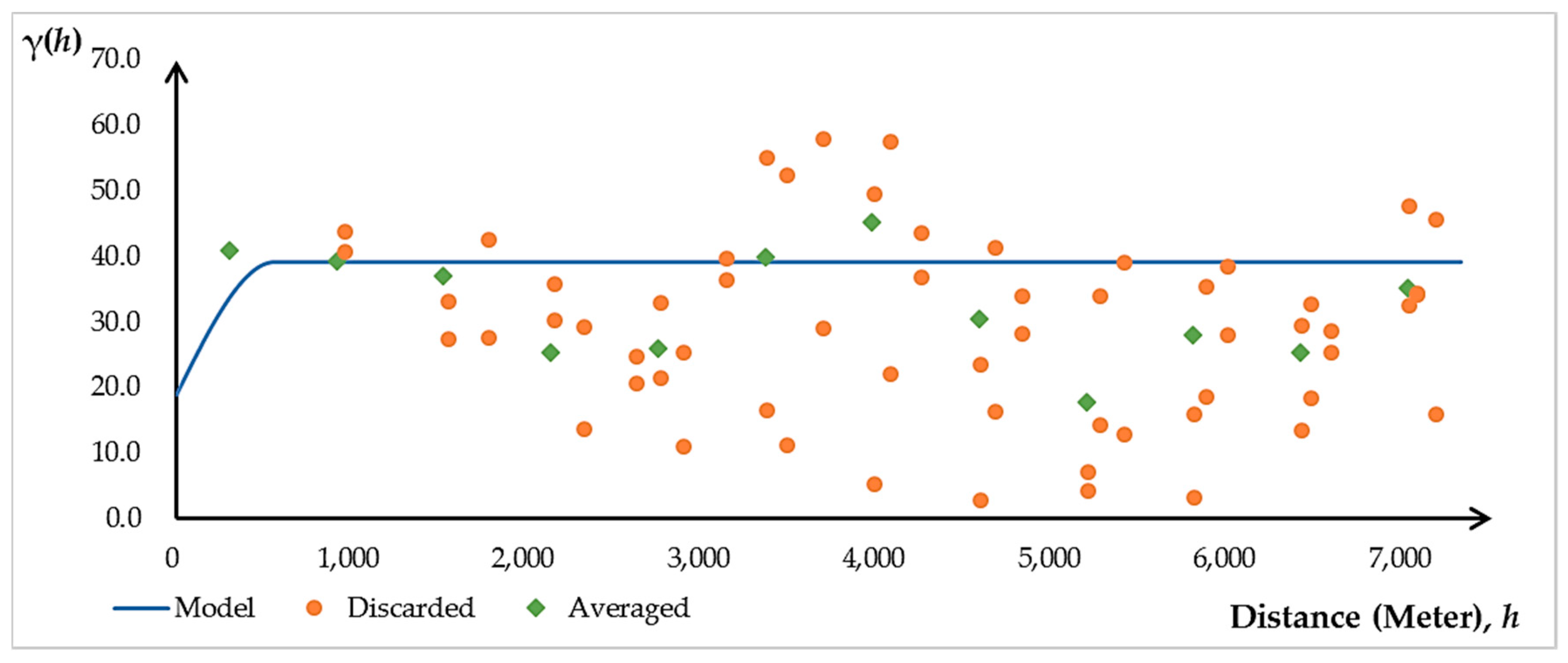
| Num. | Date | Path/Row | Cloud Cover (%) | ID |
|---|---|---|---|---|
| 1 | 2014-01-23 | 123/39 | 19.72 | LC81230392014023LGN00 |
| 2 | 2016-03-01 | 123/39 | 3.87 | LC81230392016061LGN00 |
| 3 | 2015-03-31 | 123/39 | 8.99 | LC81230392015090LGN00 |
| 4 | 2013-04-26 | 123/39 | 2.25 | LC81230392013116LGN01 |
| 5 | 2013-05-28 | 123/39 | 1.49 | LC81230392013148LGN01 |
| 6 | 2013-06-13 | 123/39 | 0.28 | LC81230392013164LGN00 |
| 7 | 2013-07-31 | 123/39 | 1.22 | LC81230392013212LGN00 |
| 8 | 2013-08-16 | 123/39 | 13.88 | LC81230392013228LGN00 |
| 9 | 2013-09-17 | 123/39 | 0.12 | LC81230392013260LGN00 |
| 10 | 2015-10-25 | 123/39 | 20.03 | LC81230392015298LGN00 |
| 11 | 2015-11-26 | 123/39 | 6.70 | LC81230392015330LGN01 |
| 12 | 2013-12-06 | 123/39 | 49.93 | LC81230392013340LGN00 |
| Item | Num | Min | Max | Mean | Range | SD | CV (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|
| Totality | 787 | 0.32 | 33.95 | 6.24 | 33.63 | 5.02 | 80.44 | 2.25 | 5.42 |
| Points in croplands | 678 | 0.33 | 33.95 | 6.43 | 33.62 | 5.29 | 82.27 | 2.13 | 4.53 |
| Calibration dataset | 407 | 0.44 | 33.95 | 6.72 | 33.51 | 5.64 | 83.93 | 2.07 | 3.97 |
| Validation dataset | 271 | 0.33 | 25.59 | 6.00 | 25.26 | 4.70 | 78.33 | 2.14 | 5.17 |
| Unstandardized Coefficients | Normalized Coefficient | t | Significance | ||
|---|---|---|---|---|---|
| Beta | Standard Deviation | Beta | |||
| (constant) | 7.42 | 1.44 | -- | 5.15 | 0.00 |
| NDVIFeb. | −7.17 | 2.69 | −0.17 | −2.67 | 0.01 |
| NDVIJul. | 8.09 | 2.86 | 0.20 | 2.84 | 0.01 |
| NDVISept. | −11.22 | 1.85 | −0.33 | −6.07 | 0.00 |
| NDVIJan. | −5.12 | 2.50 | −0.14 | −2.05 | 0.04 |
| NDVIAug. | 5.20 | 1.88 | 0.19 | 2.77 | 0.01 |
| NDVIJun. | 5.30 | 1.81 | 0.15 | 2.93 | 0.00 |
| NDVIApr. | −4.78 | 2.28 | −0.12 | −2.10 | 0.04 |
| X-Block (NDVI) LVs | X-Block (NDVI) Cumulative | Y-Block (SOC) LVs | X-Block (NDVI) Cumulative | |
|---|---|---|---|---|
| 1 | 93.69 | 93.69 | 55.48 | 55.48 |
| 2 | 1.52 | 95.22 | 10.68 | 66.16 |
| 3 | 1.45 | 96.67 | 1.71 | 67.87 |
| Number Nodes | RMSEcal SOC | RMSEcv SOC |
|---|---|---|
| 1 | 4.67 | 4.89 |
| 2 | 4.39 | 4.84 |
| 3 | 4.22 | 4.81 |
| 4 | 4.33 | 4.79 |
| Modeling Accuracy | Prediction Accuracy | |||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| Stepwise Linear Regression (SLR) | 4.863 | 0.270 | 3.930 | 0.281 |
| Ordinary Kriging (OK) | 3.549 | 0.524 | 3.727 | 0.372 |
| Partial Least Squares Regression (PLSR) | 4.970 | 0.230 | 4.087 | 0.283 |
| Support Vector Machine (SVM) | 4.269 | 0.453 | 3.753 | 0.361 |
| Artificial Neural Network (ANN) | 4.326 | 0.417 | 3.718 | 0.391 |
| Dim | Eigenvalue | Condition Index | Variance Proportions | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Con | NDVIFeb. | NDVIJul. | NDVISept. | NDVIJan. | NDVIAug. | NDVIJun. | NDVIApr. | |||
| 1 | 7.52 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.20 | 6.09 | 0.00 | 0.07 | 0.00 | 0.03 | 0.09 | 0.00 | 0.10 | 0.00 |
| 3 | 0.08 | 9.44 | 0.00 | 0.01 | 0.00 | 0.33 | 0.04 | 0.02 | 0.38 | 0.00 |
| 4 | 0.08 | 9.61 | 0.00 | 0.01 | 0.02 | 0.05 | 0.01 | 0.18 | 0.04 | 0.24 |
| 5 | 0.05 | 12.92 | 0.02 | 0.56 | 0.00 | 0.02 | 0.06 | 0.05 | 0.08 | 0.43 |
| 6 | 0.03 | 15.69 | 0.38 | 0.01 | 0.02 | 0.27 | 0.41 | 0.00 | 0.25 | 0.12 |
| 7 | 0.03 | 16.35 | 0.30 | 0.34 | 0.00 | 0.18 | 0.36 | 0.17 | 0.06 | 0.20 |
| 8 | 0.01 | 27.10 | 0.30 | 0.00 | 0.95 | 0.12 | 0.03 | 0.58 | 0.09 | 0.01 |
| NDVIFeb. | NDVIJul. | NDVISept. | NDVIJan. | NDVIAug. | NDVIJun. | NDVIApr. | |
|---|---|---|---|---|---|---|---|
| Tolerance | 0.48 | 0.37 | 0.63 | 0.39 | 0.41 | 0.74 | 0.60 |
| VIF | 2.08 | 2.71 | 1.59 | 2.57 | 2.46 | 1.35 | 1.66 |
| Modeling Accuracy | Prediction Accuracy | |||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| NDVIJan. | 5.542 | 0.031 | 4.693 | 0.020 |
| NDVIFeb. | 5.407 | 0.077 | 4.710 | 0.032 |
| NDVIMar. | 5.498 | 0.046 | 4.688 | 0.023 |
| NDVIApr. | 5.441 | 0.065 | 4.793 | 0.058 |
| NDVIMAy | 5.608 | 0.007 | 4.747 | 0.004 |
| NDVIJun. | 5.529 | 0.035 | 4.574 | 0.064 |
| NDVIJul. | 5.536 | 0.032 | 4.625 | 0.060 |
| NDVIAug. | 5.568 | 0.021 | 4.600 | 0.071 |
| NDVISept. | 5.488 | 0.049 | 4.675 | 0.041 |
| NDVIOct. | 5.630 | 0.001 | 4.754 | 0.001 |
| NDVINov. | 5.565 | 0.022 | 4.799 | 0.001 |
| NDVIDec. | 5.583 | 0.016 | 4.692 | 0.021 |
| Predictors | Modeling Accuracy | Prediction Accuracy | ||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| Subset1(summer) for ANN: NDVIApr. NDVIMay NDVIJun. NDVIJul. NDVIAug. NDVISept. | 4.818 | 0.269 | 4.119 | 0.281 |
| Subset2 (winter) for ANN: NDVIJan. NDVIFeb. NDVIMar. NDVIOct. NDVINov. NDVIDec. | 4.855 | 0.141 | 4.980 | 0.137 |
| Subset1 (summer) for SVM: NDVIApr. NDVIMay NDVIJun. NDVIJul. NDVIAug. NDVISept. | 4.158 | 0.477 | 3.863 | 0.343 |
| Subset2 (winter) for SVM: NDVIJan. NDVIFeb. NDVIMar. NDVIOct. NDVINov. NDVIDec. | 4.575 | 0.237 | 4.908 | 0.162 |
| Modeling Accuracy | Prediction Accuracy | |||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| ANN | 5.580 | 0.019 | 4.829 | 0.027 |
| SVM | 5.199 | 0.021 | 5.305 | 0.012 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Guo, L.; Chen, Y.; Shi, T.; Luo, M.; Ju, Q.; Zhang, H.; Wang, S. Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sens. 2019, 11, 1683. https://doi.org/10.3390/rs11141683
Zhang Y, Guo L, Chen Y, Shi T, Luo M, Ju Q, Zhang H, Wang S. Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sensing. 2019; 11(14):1683. https://doi.org/10.3390/rs11141683
Chicago/Turabian StyleZhang, Yangchengsi, Long Guo, Yiyun Chen, Tiezhu Shi, Mei Luo, QingLan Ju, Haitao Zhang, and Shanqin Wang. 2019. "Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China" Remote Sensing 11, no. 14: 1683. https://doi.org/10.3390/rs11141683
APA StyleZhang, Y., Guo, L., Chen, Y., Shi, T., Luo, M., Ju, Q., Zhang, H., & Wang, S. (2019). Prediction of Soil Organic Carbon based on Landsat 8 Monthly NDVI Data for the Jianghan Plain in Hubei Province, China. Remote Sensing, 11(14), 1683. https://doi.org/10.3390/rs11141683







