Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Measurements
2.2. Calculations of APAR and LUE
2.3. Two-Leaf PRI Model
2.3.1. Estimations of Observed Fraction of Background
2.3.2. Estimations of PT and PS
2.3.3. Estimation of Two-Leaf PRI
2.4. Statistical Data Analysis
3. Results and Discussion
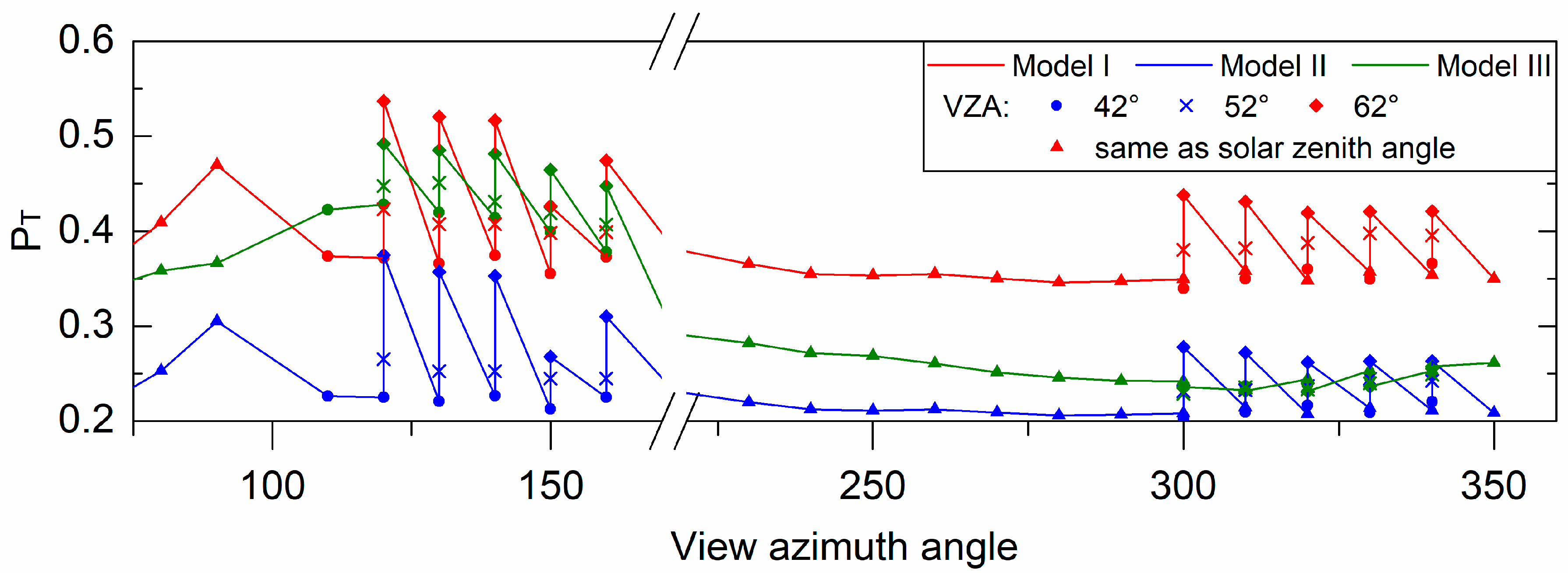
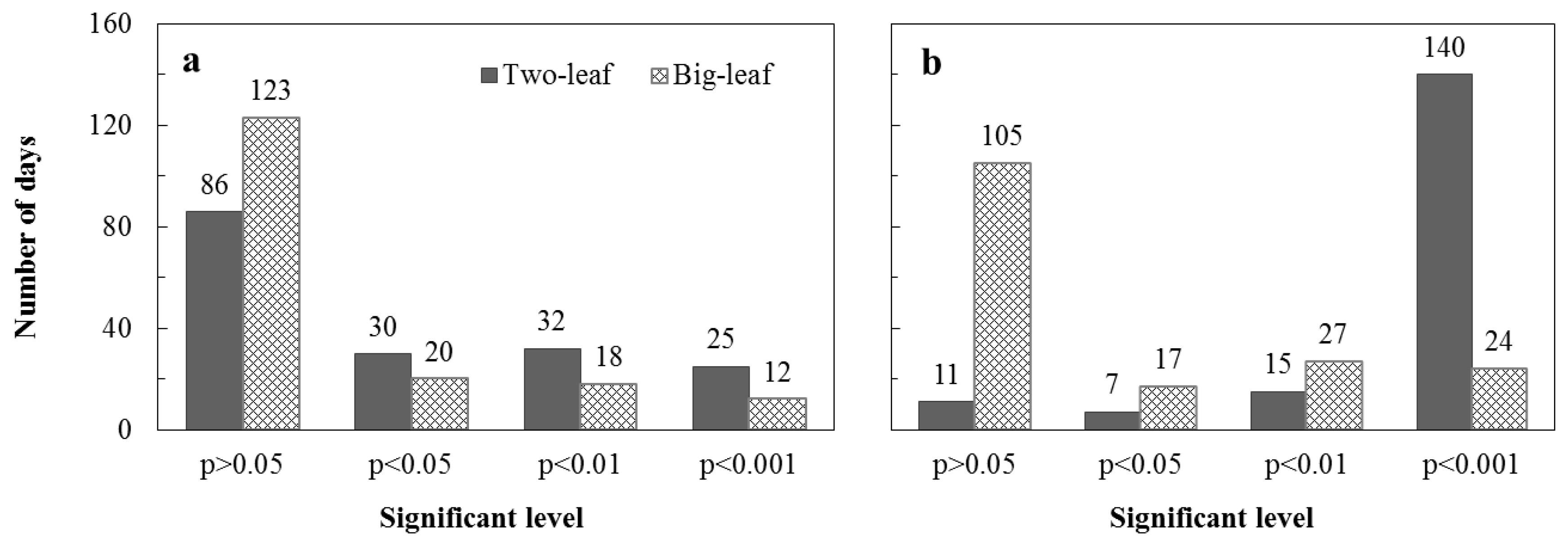
3.1. Test of Three Methods for Estimating the Fraction of Sunlit Leaves
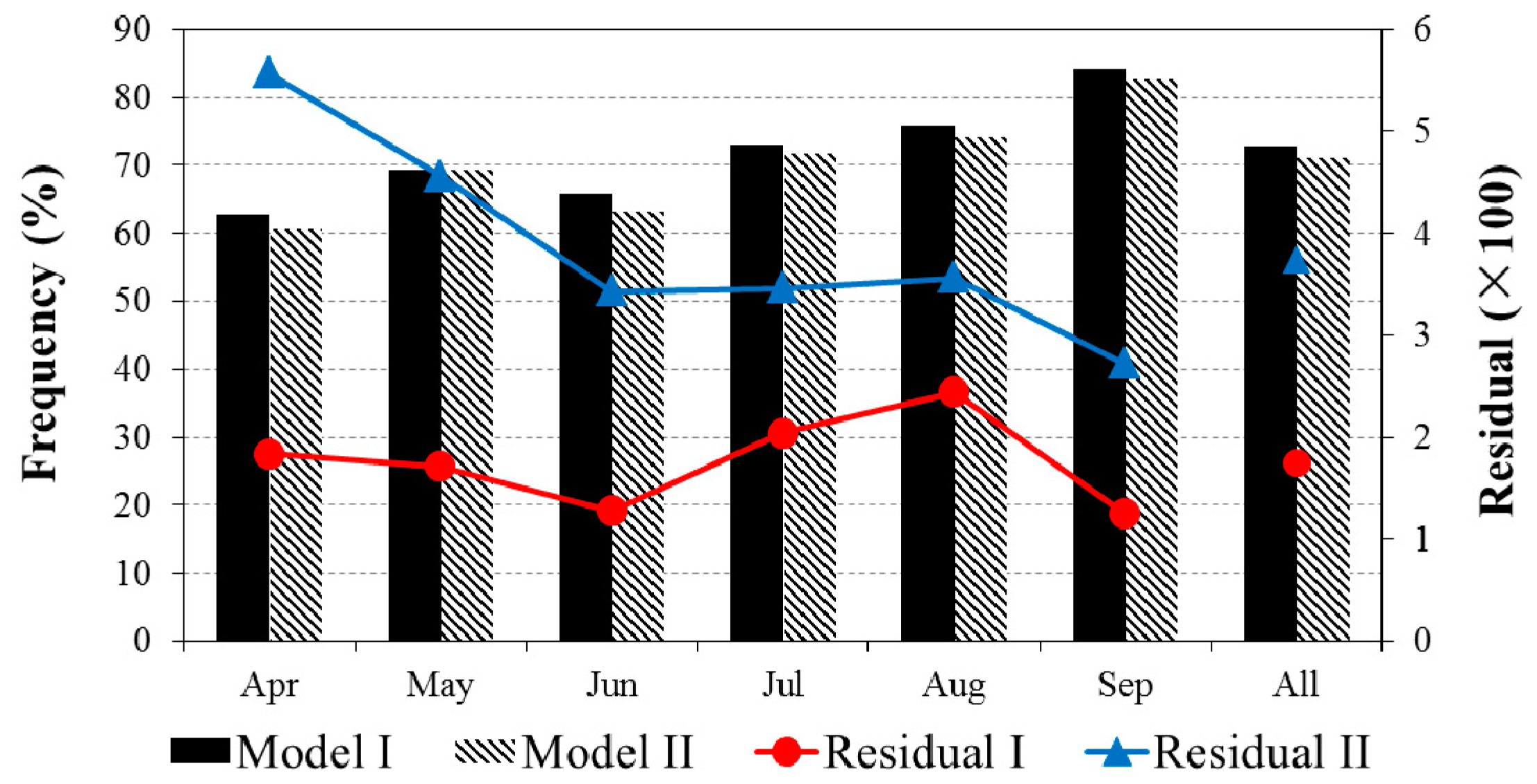
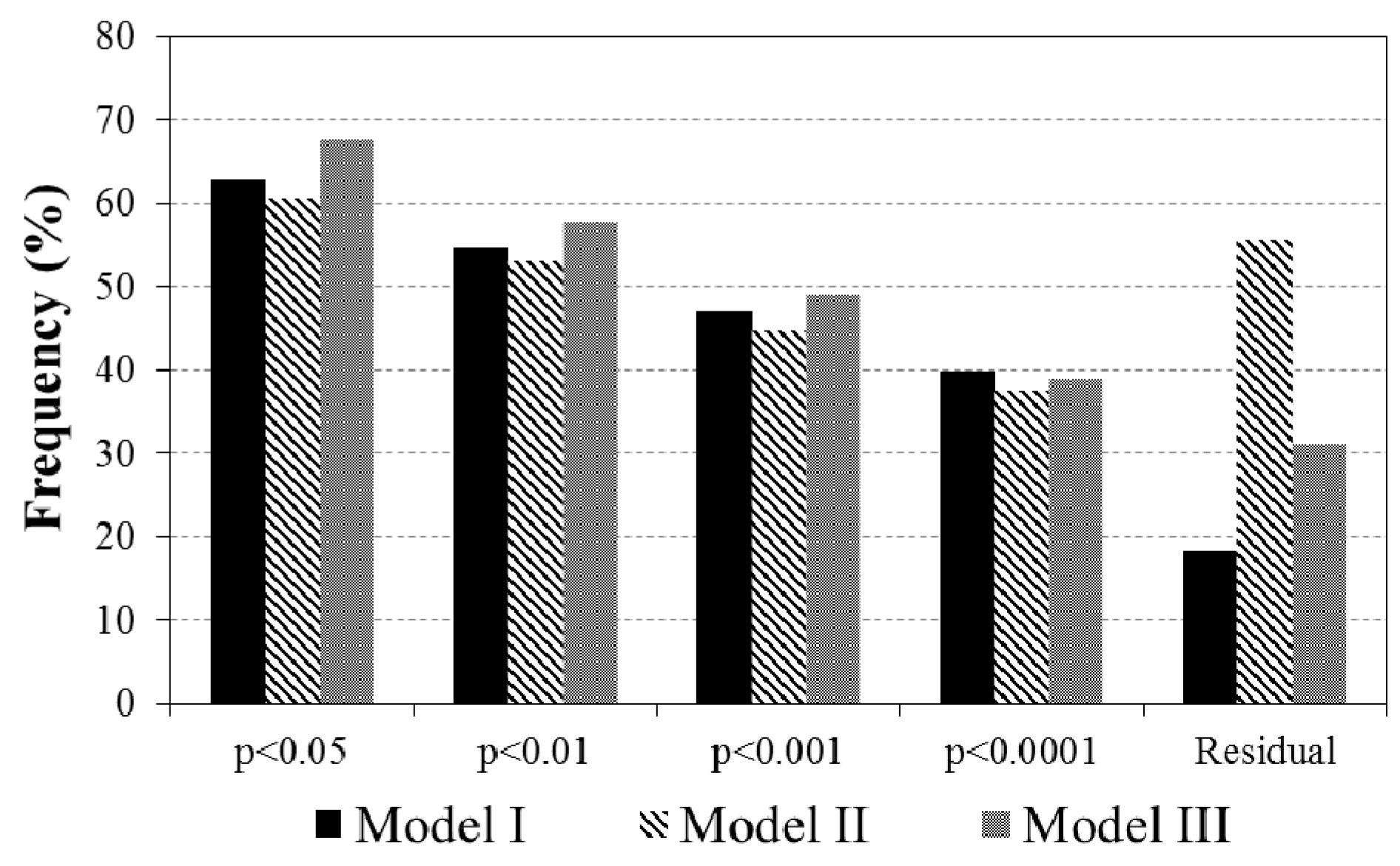
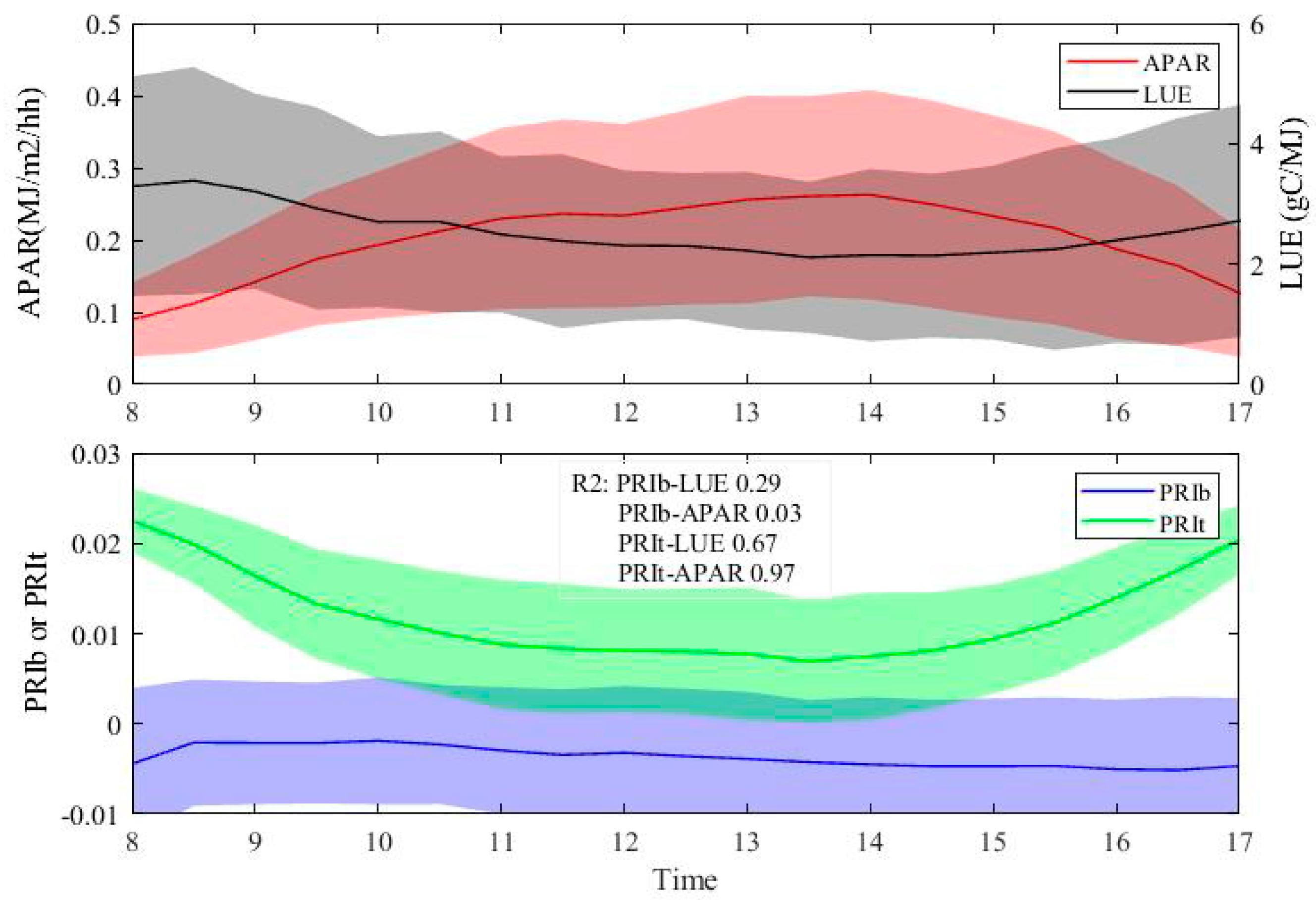
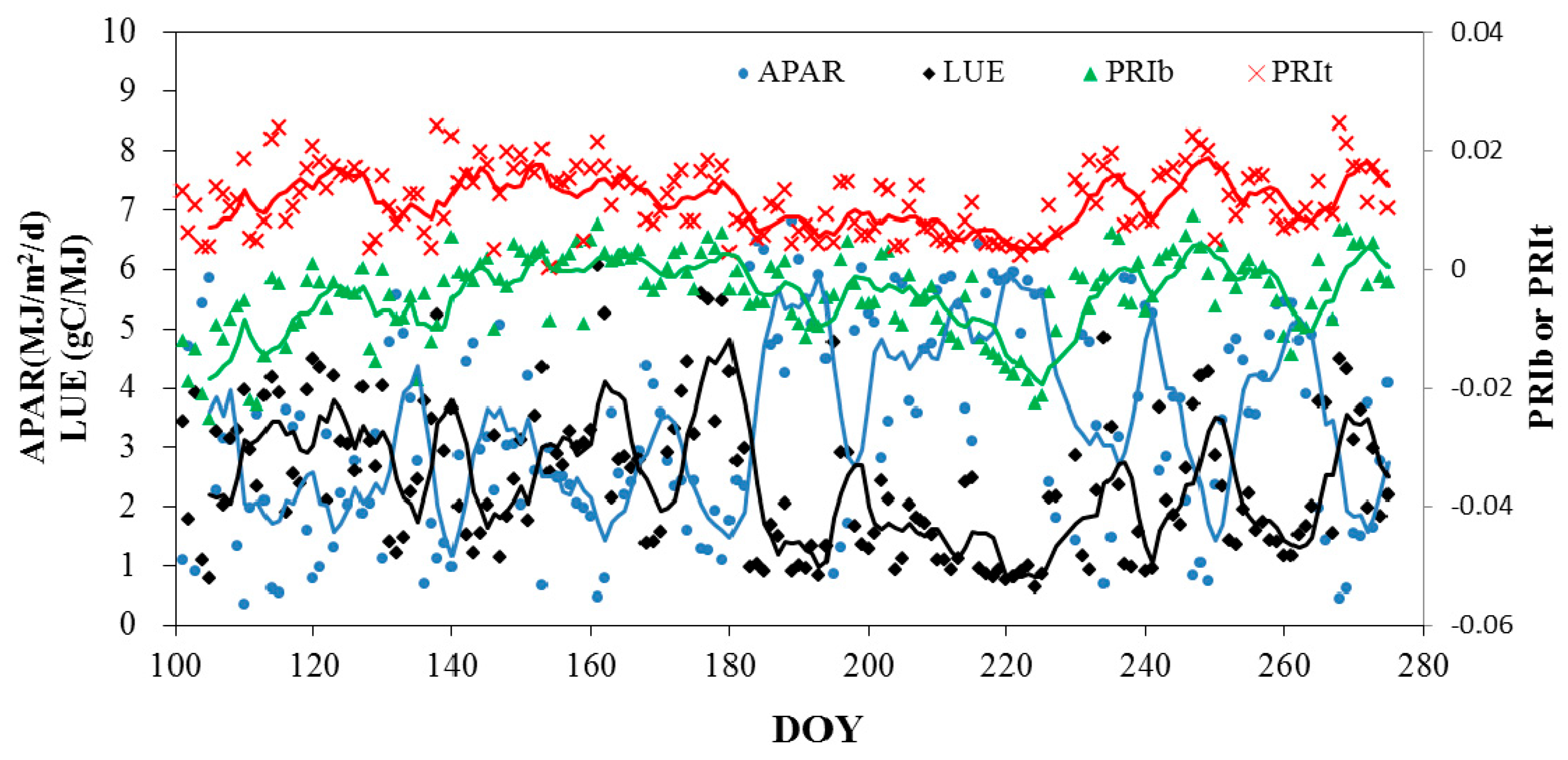
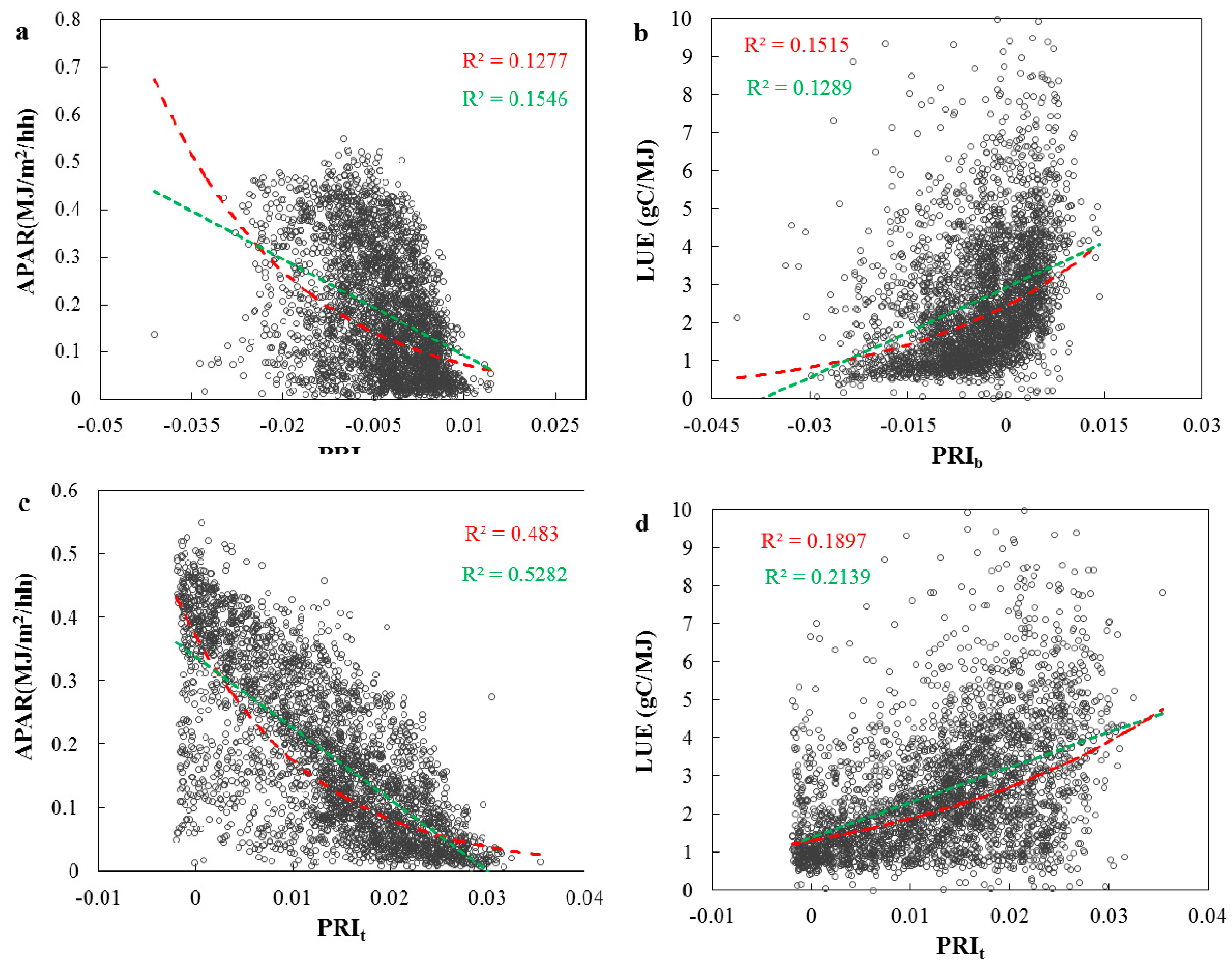
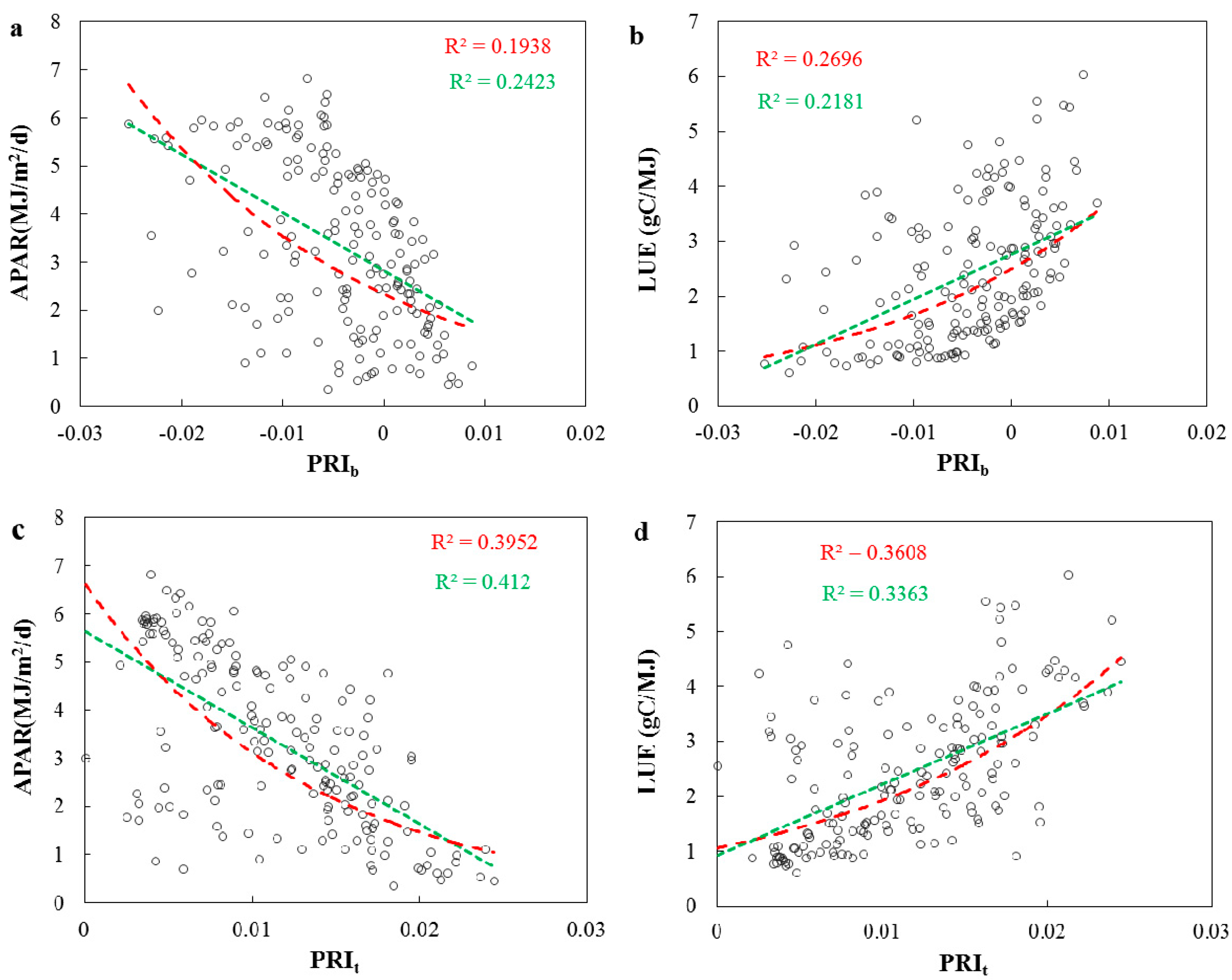
3.2. Evaluations of the Two-Leaf PRI (PRIt) to Indicate LUE and APAR
4. Conclusions
5. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| α | The half apex angle |
| αs | Shadow fractions (equal to PS) |
| ρ | Canopy reflectance from Unispec-DC |
| ρr | Radiance of the canopy sensor |
| ρi | Irradiance of the canopy sensor |
| ρiDC | Daytime DC for irradiance |
| ρrDC | Daytime DC for radiance |
| ξ | Angle between the sun and the viewer |
| θ | Solar zenith angle |
| θv | View zenith angle |
| Ω | The value of clumping index |
| γE | The needle-to-shoot area ratio |
| APAR | Absorbed photosynthetically active radiation |
| APARsun | Photosynthetically active radiation absorbed by sunlit leaves |
| APARsh | Photosynthetically active radiation absorbed by shaded leaves |
| BRDF | Bidirectional reflectance distribution function |
| CERN | Chinese Ecosystem Research Network |
| CHM | Canopy height model |
| Ci | The intercellular CO2 concentration |
| CI | Clearness index |
| CV | Coefficient of variation |
| DC | Dark current |
| DOY | Day of year |
| EC | Eddy covariance |
| FIP | The first intersection point |
| FPAR | The fraction of PAR |
| fAPARchl | The fraction of PAR absorbed by chlorophyll |
| G(θ) | The projection of unit leaf areas |
| GPP | Gross primary production |
| GOST | Geometric-optical model |
| Ha | The height of the lower part of the tree (trunk space) |
| Hb | The height of crown |
| LAI | Leaf area index |
| Lsun | Sunlit leaf area index |
| Lsh | Shaded leaf area index |
| LUE, ε | Light use efficiency |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NADPH | Reduced pyridine nucleotide |
| NDVI | Normalized difference vegetation index |
| NEE | Net ecosystem productivity |
| NPQ | Nonphotochemical quenching |
| PAR | Photosynthetically active radiation |
| PQ | Photochemical quenching |
| PRI | Photochemical reflectance index |
| PRIb | Big-leaf PRI |
| PRIinv | Inversely calculated PRI at each view angle |
| PRIobs | Observed PRI at each view angle |
| PRIsh | PRI of shaded leaves |
| PRIsun | PRI of sunlit leaves |
| PRIt | Two-leaf PRI |
| PS I, II | Photosystem I and II |
| PTU | Pan-tilt unit |
| PT | The observed fraction of sunlit leaves |
| PS | The observed fraction of shaded leaves |
| PVG | The observed fraction of background |
| PG | The observed fraction of sunlit background |
| PZ | The observed fraction of shade background |
| QYZ | Qianyanzhou Experimental Station |
| r | The diameter of the crown |
| R0 | The extraterrestrial radiation at the top of the atmosphere |
| Rcan | Canopy reflectance |
| RT | Reflectance of sunlit leaves |
| RG | Reflectance of sunlit background |
| RS | Reflectance of shaded leaves |
| RZ | Reflectance of shaded background |
| Rdif | The ratio of diffuse radiation to total radiation |
| Re | Daytime ecosystem respiration |
| Rg | The global solar radiation on the surface of the earth |
| Rleaf | Leaf reflectance |
| RSL | The ratio of canopy reflectance to leaf reflectance |
| Rh | Relative humidity |
| SPT | The ratio of the sunlit point in a tree |
| Ta | Air temperature |
| VPD | Vapor pressure deficit |
| WS | The mean width of elements shadows cast inside tree crowns |
Appendix A
References
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in pri using brdf models. Remote Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Tan, K.P.; Kanniah, K.D.; Cracknell, A.P. A review of remote sensing based productivity models and their suitability for studying oil palm productivity in tropical regions. Prog. Phys. Geogr. 2012, 36, 655–679. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahl, D.E.; Gower, S.T.; Mackay, D.S.; Burrows, S.N.; Norman, J.M.; Diak, G.R. Heterogeneity of light use efficiency in a northern wisconsin forest: Implications for modeling net primary production with remote sensing. Remote Sens. Environ. 2004, 93, 168–178. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. In Methods in Ecosystem Science; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophys. Res. Atmos. 1994, 99, 5263–5283. [Google Scholar] [CrossRef]
- Goetz, S.J.; Prince, S.D. Modelling terrestrial carbon exchange and storage: Evidence and implications of functional convergence in light-use efficiency. Adv. Ecol. Res. 1999, 28, 57–92. [Google Scholar]
- Lagergren, F.; Eklundh, L.; Grelle, A.; Lundblad, M.; Mölder, M.; Lankreijer, H.; Lindroth, A. Net primary production and light use efficiency in a mixed coniferous forest in sweden. Plant Cell Environ. 2005, 28, 412–423. [Google Scholar] [CrossRef]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Oliphant, A.J.; Goni, D.; Deng, B.; Grimmond, C.S.B.; Schmid, H.P.; Scott, S.L. The role of sky conditions on gross primary production in a mixed deciduous forest. Agric. For. Meteorol. 2011, 151, 781–791. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, G.R.; Zhuang, J.; Gentry, R.; Fu, Y.L.; Sun, X.M.; Zhang, L.M.; Wen, X.F.; Wang, Q.F.; Han, S.J. Effects of cloudiness change on net ecosystem exchange, light use efficiency, and water use efficiency in typical ecosystems of china. Agric. For. Meteorol. 2011, 151, 803–816. [Google Scholar] [CrossRef]
- Fleisher, D.H.; Timlin, D.J.; Reddy, V.R. Temperature influence on potato leaf and branch distribution and on canopy photosynthetic rate. Agron. J. 2006, 98, 1442–1452. [Google Scholar] [CrossRef]
- Nichol, C.J.; Huemmrich, K.F.; Black, T.A.; Jarvis, P.G.; Walthall, C.L.; Grace, J.; Hall, F.G. Remote sensing of photosynthetic-light-use efficiency of boreal forest. Agric. For. Meteorol. 2000, 101, 131–142. [Google Scholar] [CrossRef] [Green Version]
- Nichol, C.J.; Lloyd, J.; Shibistova, O.; Arneth, A.; Röser, C.; Knohl, A.; Matsubara, S.; Grace, J. Remote sensing of photosynthetic light use efficiency of a siberian boreal forest. Tellus B 2002, 54, 677–687. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on modis and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Hall, F.G.; Nichol, C.J.; Drolet, G.G. Estimation of light-use efficiency of terrestrial ecosystems from space: A status report. BioScience 2010, 60, 788–797. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, 626–640. [Google Scholar] [CrossRef]
- Li, D.; Ju, W.; Lu, D.; Zhou, Y.; Wang, H. Impact of estimated solar radiation on gross primary productivity simulation in subtropical plantation in southeast china. Sol. Energy 2015, 120, 175–186. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014–1017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roderick, M.L.; Farquhar, G.D.; Berry, S.L.; Noble, I.R. On the direct effect of clouds and atmospheric particles on the productivity and structure of vegetation. Oecologia 2001, 129, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Ju, W.; Zhou, Y.; He, M.; Law, B.E.; Black, T.A.; Margolis, H.A.; Cescatti, A.; Gu, L.; Montagnani, L. Performance of linear and nonlinear two-leaf light use efficiency models at different temporal scales. Remote Sens. 2015, 7, 2238–2278. [Google Scholar] [CrossRef]
- Gamon, J.A.; Penuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Adams, W.W., III; Winter, K.; Meyer, A.; Schreiber, U.; Pereira, J.S.; Krüger, A.; Czygan, F.-C.; Lange, O.L. Photochemical efficiency of photosystem ii, photon yield of o2 evolution, photosynthetic capacity, and carotenoid composition during the midday depression of net co2 uptake in arbutus unedo growing in portugal. Planta 1989, 177, 377–387. [Google Scholar] [CrossRef]
- Demmig-Adams, B. Survey of thermal energy dissipation and pigment composition in sun and shade leaves. Plant Cell Physiol. 1998, 39, 474–482. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Adams, W.W. Photoprotection and other responses of plants to high light stress. Annu. Rev. Plant Biol. 1992, 43, 599–626. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Adams, W.W. The role of xanthophyll cycle carotenoids in the protection of photosynthesis. Trends Plant Sci. 1996, 1, 21–26. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Adams, W.W. Photoprotection in an ecological context: The remarkable complexity of thermal energy dissipation. New Phytol. 2006, 172, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.; Serrano, L.; Surfus, J. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Barton, C.V.M.; North, P.R.J. Remote sensing of canopy light use efficiency using the photochemical reflectance index model and sensitivity analysis. Remote Sens. Environ. 2001, 78, 264–273. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Verhoef, W.; Schläpfer, D.; Garbari, S.; Schaepman, M. Impact of varying irradiance on vegetation indices and chlorophyll fluorescence derived from spectroscopy data. Remote Sens. Environ. 2015, 156, 202–215. [Google Scholar] [CrossRef]
- Drolet, G.G.; Huemmrich, K.F.; Hall, F.G.; Middleton, E.M.; Black, T.A.; Barr, A.G.; Margolis, H.A. A modis-derived photochemical reflectance index to detect inter-annual variations in the photosynthetic light-use efficiency of a boreal deciduous forest. Remote Sens. Environ. 2005, 98, 212–224. [Google Scholar] [CrossRef]
- Drolet, G.G.; Middleton, E.M.; Huemmrich, K.F.; Hall, F.G.; Amiro, B.D.; Barr, A.G.; Black, T.A.; McCaughey, J.H.; Margolis, H.A. Regional mapping of gross light-use efficiency using modis spectral indices. Remote Sens. Environ. 2008, 112, 3064–3078. [Google Scholar] [CrossRef]
- Gamon, J.A.; Bond, B. Effects of irradiance and photosynthetic downregulation on the photochemical reflectance index in douglas-fir and ponderosa pine. Remote Sens. Environ. 2013, 135, 141–149. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (pri) and the remote sensing of leaf, canopy and ecosystem radiation use efficienciesa review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; Navarro-Cerrillo, R.M.; Suárez, L.; Morales, F.; Zarco-Tejada, P.J. Assessing structural effects on pri for stress detection in conifer forests. Remote Sens. Environ. 2011, 115, 2360–2375. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Dufrêne, E.; Berveiller, D.; Delpierre, N.; Ourcival, J.-M.; Rambal, S.; Joffre, R. Relationships between photochemical reflectance index and light-use efficiency in deciduous and evergreen broadleaf forests. Remote Sens. Environ. 2014, 144, 73–84. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Middleton, E.M.; Zhang, Q.; Corp, L.A.; Dandois, J.; Kustas, W.P. The photochemical reflectance index from directional cornfield reflectances: Observations and simulations. Remote Sens. Environ. 2012, 124, 444–453. [Google Scholar] [CrossRef] [Green Version]
- Mõttus, M.; Takala, T.L.; Stenberg, P.; Knyazikhin, Y.; Yang, B.; Nilson, T. Diffuse sky radiation influences the relationship between canopy pri and shadow fraction. ISPRS J. Photogramm. Remote Sens. 2015, 105, 54–60. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Tracking seasonal changes of leaf and canopy light use efficiency in a phlomis fruticosa mediterranean ecosystem using field measurements and multi-angular satellite hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2014, 97, 138–151. [Google Scholar] [CrossRef]
- Zhou, Y.; Hilker, T.; Ju, W.; Coops, N.C.; Black, T.A.; Chen, J.M.; Wu, X. Modeling gross primary production for sunlit and shaded canopies across an evergreen and a deciduous site in canada. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1859–1873. [Google Scholar] [CrossRef]
- Peguero-Pina, J.J.; Morales, F.; Flexas, J.; Gil-Pelegrín, E.; Moya, I. Photochemistry, remotely sensed physiological reflectance index and de-epoxidation state of the xanthophyll cycle in quercus coccifera under intense drought. Oecologia 2008, 156, 1–11. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Garcia-Plazaola, J.I.; Nichol, C.J.; Kolari, P.; Olascoaga, B.; Kuusinen, N.; Fernández-Marín, B.; Pulkkinen, M.; Juurola, E.; Nikinmaa, E. Physiology of the seasonal relationship between the photochemical reflectance index and photosynthetic light use efficiency. Oecologia 2012, 170, 313–323. [Google Scholar] [CrossRef]
- Sims, D.A.; Luo, H.; Hastings, S.; Oechel, W.; Rahman, A.; Gamon, J. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a southern california chaparral ecosystem. Remote Sens. Environ. 2006, 103, 289–303. [Google Scholar] [CrossRef]
- Ogren, W.L. Photorespiration: Pathways, regulation, and modification. Annu. Rev. Plant Physiol. 1984, 35, 415–442. [Google Scholar] [CrossRef]
- Wingler, A.; Lea, P.J.; Quick, W.P.; Leegood, R.C. Photorespiration: Metabolic pathways and their role in stress protection. Philos. Trans. R. Soc. B Biol. Sci. 2000, 355, 1517–1529. [Google Scholar] [CrossRef]
- Asrar, G.; Myneni, R.B.; Choudhury, B.J. Spatial heterogeneity in vegetation canopies and remote sensing of absorbed photosynthetically active radiation: A modeling study. Remote Sens. Environ. 1992, 41, 85–103. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ramakrishna, R.; Nemani, R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 2002, 35, 1380–1393. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Y.B.; Lyapustin, A.I.; Wang, Y.; Gao, F.; Suyker, A.; Verma, S.; Middleton, E.M. Estimation of crop gross primary production (gpp): Fapar chl versus mod15a2 fpar. Remote Sens. Environ. 2014, 153, 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Y.B.; Lyapustin, A.I.; Wang, Y.; Xiao, X.; Suyker, A.; Verma, S.; Tan, B.; Middleton, E.M. Estimation of crop gross primary production (gpp): I. Impact of modis observation footprint and impact of vegetation brdf characteristics. Agric. For. Meteorol. 2014, 191, 51–63. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Y.B.; Lyapustin, A.I.; Wang, Y.; Zhang, X.; Suyker, A.; Verma, S.; Shuai, Y.; Middleton, E.M. Estimation of crop gross primary production (gpp): Ii. Do scaled modis vegetation indices improve performance? Agric. For. Meteorol. 2015, 200, 1–8. [Google Scholar] [CrossRef]
- Dong, T.; Wu, B.; Meng, J.; Xin, D.; Shang, J. Sensitivity analysis of retrieving fraction of absorbed photosynthetically active radiation (fpar) using remote sensing data. Acta Ecol. Sin. 2016, 36, 1–7. [Google Scholar] [CrossRef]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.C.; Running, S. Estimation of incident photosynthetically active radiation from moderate resolution imaging spectrometer data. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Liu, R.; Liang, S.; He, H.; Liu, J.; Zheng, T. Mapping incident photosynthetically active radiation from modis data over china. Remote Sens. Environ. 2008, 112, 998–1009. [Google Scholar]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef]
- Evain, S.; Flexas, J.; Moya, I. A new instrument for passive remote sensing: 2. Measurement of leaf and canopy reflectance changes at 531 nm and their relationship with photosynthesis and chlorophyll fluorescence. Remote Sens. Environ. 2004, 91, 175–185. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C. Photosynsat, photosynthesis from space: Theoretical foundations of a satellite concept and validation from tower and spaceborne data. Remote Sens. Environ. 2011, 115, 1918–1925. [Google Scholar] [CrossRef]
- Hall, F.G.; Hilker, T.; Coops, N.C.; Lyapustin, A.; Huemmrich, K.F.; Middleton, E.; Margolis, H.; Drolet, G.; Black, T.A. Multi-angle remote sensing of forest light use efficiency by observing pri variation with canopy shadow fraction. Remote Sens. Environ. 2008, 112, 3201–3211. [Google Scholar] [CrossRef]
- Hilker, T.; Leeuwen, M.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.L.B.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. Atmos. 2002, 107, ACL 2-1–ACL 2-23. [Google Scholar] [CrossRef]
- Ellsworth, D.S.; Reich, P.B. Canopy structure and vertical patterns of photosynthesis and related leaf traits in a deciduous forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef]
- Wilson, J.W. Stand structure and light penetration. Iii. Sunlit foliage area. J. Appl. Ecol. 1967, 4, 159. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Zhu, G. Gost: A geometric-optical model for sloping terrains. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5469–5482. [Google Scholar]
- Fan, W.; Li, J.; Liu, Q. Gost2: The improvement of the canopy reflectance model gost in separating the sunlit and shaded leaves. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1423–1431. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.M.; Ju, W.; Wang, H.; Qiu, F.; Yang, F.; Fan, W.; Huang, Q.; Wang, Y.P.; Feng, Y. Improving the ability of the photochemical reflectance index to track canopy light use efficiency through differentiating sunlit and shaded leaves. Remote Sens. Environ. 2017, 194, 1–15. [Google Scholar] [CrossRef]
- Stenberg, P. Penumbra in within-shoot and between-shoot shading in conifers and its significance for photosynthesis. Ecol. Model. 1995, 77, 215–231. [Google Scholar] [CrossRef]
- Wen, X.; Yu, G.-R.; Sun, X.-M.; Li, Q.-K.; Liu, Y.-F.; Zhang, L.-M.; Ren, C.-Y.; Fu, Y.-L.; Li, Z.-Q. Soil moisture effect on the temperature dependence of ecosystem respiration in a subtropical pinus plantation of southeastern china. Agric. For. Meteorol. 2006, 137, 166–175. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Han, D. Gap filling strategies for defensible annual sums of net ecosystem exchange ☆. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 315–323. [Google Scholar] [CrossRef]
- Zhang, Q.; Ju, W.; Chen, J.; Wang, H.; Yang, F.; Fan, W.; Huang, Q.; Zheng, T.; Feng, Y.; Zhou, Y.; et al. Ability of the photochemical reflectance index to track light use efficiency for a sub-tropical planted coniferous forest. Remote Sens. 2015, 7, 16938–16962. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Nesbitt, N. Hybrid geometric optical–radiative transfer model suitable for forests on slopes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5579–5586. [Google Scholar]
- Hilker, T.; Hall, F.G.; Coops, N.C.; Lyapustin, A.; Wang, Y.; Nesic, Z.; Grant, N.; Black, T.A.; Wulder, M.A.; Kljun, N. Remote sensing of photosynthetic light-use efficiency across two forested biomes: Spatial scaling. Remote Sens. Environ. 2010, 114, 2863–2874. [Google Scholar] [CrossRef]
- Middleton, E.M.; Cheng, Y.B.; Hilker, T.; Black, T.A.; Krishnan, P.; Coops, N.C.; Huemmrich, K.F. Linking foliage spectral responses to canopy-level ecosystem photosynthetic light-use efficiency at a douglas-fir forest in canada. Can. J. Remote Sens. 2009, 35, 166–188. [Google Scholar] [CrossRef]
- Hilker, T.; Gitelson, A.; Coops, N.C.; Hall, F.G.; Black, T.A. Tracking plant physiological properties from multi-angular tower-based remote sensing. Oecologia 2011, 165, 865–876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hilker, T.; Coops, N.C.; Schwalm, C.R. Effects of mutual shading of tree crowns on prediction of photosynthetic light-use efficiency in a coastal douglas fir forest. Tree Physiol. 2008, 28, 825–834. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.Y.; Gamon, J.A. Three causes of variation in the photochemical reflectance index (pri) in evergreen conifers. New Phytol. 2015, 206, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.A.; Field, C.; Bilger, W.; Björkman, O.; Fredeen, A.; Peñuelas, J. Remote sensing of the xanthophyll cycle and chlorophyll fluorescence in sunflower leaves and canopies. Oecologia 1990, 85, 1–7. [Google Scholar] [CrossRef]
- Butler, W.L. Energy distribution in the photochemical apparatus of photosynthesis. Annu. Rev. Plant Physiol. 1978, 29, 345–378. [Google Scholar] [CrossRef]
- Magney, T.S.; Eusden, S.A.; Eitel, J.U.H.; Logan, B.A.; Jiang, J.; Vierling, L.A. Assessing leaf photoprotective mechanisms using terrestrial lidar: Towards mapping canopy photosynthetic performance in three dimensions. New Phytol. 2014, 201, 344–356. [Google Scholar] [CrossRef]
- Magney, T.S.; Vierling, L.A.; Eitel, J.U.; Huggins, D.R.; Garrity, S.R. Response of high frequency photochemical reflectance index (pri) measurements to environmental conditions in wheat. Remote Sens. Environ. 2016, 173, 84–97. [Google Scholar] [CrossRef]
- Coops, N.C.; Hermosilla, T.; Hilker, T.; Andrew Black, T. Linking stand architecture with canopy reflectance to estimate vertical patterns of light-use efficiency. Remote Sens. Environ. 2017, 194, 322–330. [Google Scholar] [CrossRef]
| LAI | Ha | Hb | r | α | Ws | Ω | γE | G(θ) |
|---|---|---|---|---|---|---|---|---|
| 5.8 | 9 m | 4.5 m | 2.5 m | 25° | 0.17 m | 0.57 | 1 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Qiu, F.; Fan, W.; Liu, Y.; Zhang, Q. Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest. Remote Sens. 2019, 11, 1643. https://doi.org/10.3390/rs11141643
Huang Q, Qiu F, Fan W, Liu Y, Zhang Q. Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest. Remote Sensing. 2019; 11(14):1643. https://doi.org/10.3390/rs11141643
Chicago/Turabian StyleHuang, Qing, Feng Qiu, Weiliang Fan, Yibo Liu, and Qian Zhang. 2019. "Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest" Remote Sensing 11, no. 14: 1643. https://doi.org/10.3390/rs11141643
APA StyleHuang, Q., Qiu, F., Fan, W., Liu, Y., & Zhang, Q. (2019). Evaluation of Different Methods for Estimating the Fraction of Sunlit Leaves and Its Contribution for Photochemical Reflectance Index Utilization in a Coniferous Forest. Remote Sensing, 11(14), 1643. https://doi.org/10.3390/rs11141643





