Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations
Abstract
1. Introduction
2. Study Area and Data
3. Methods
3.1. Extreme Gradient Boosting (XGBoost)
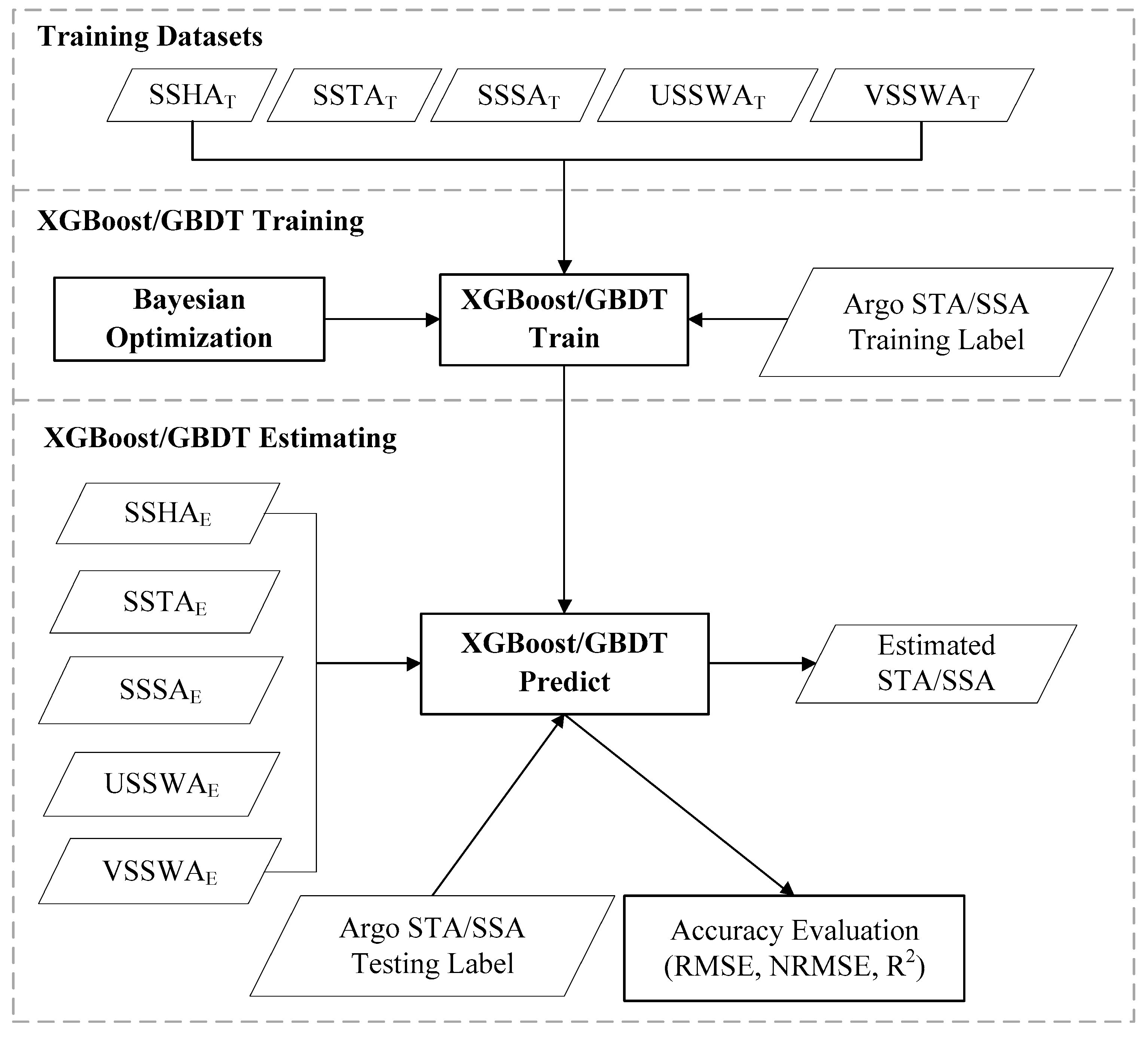
3.2. Experimental Setup
4. Results
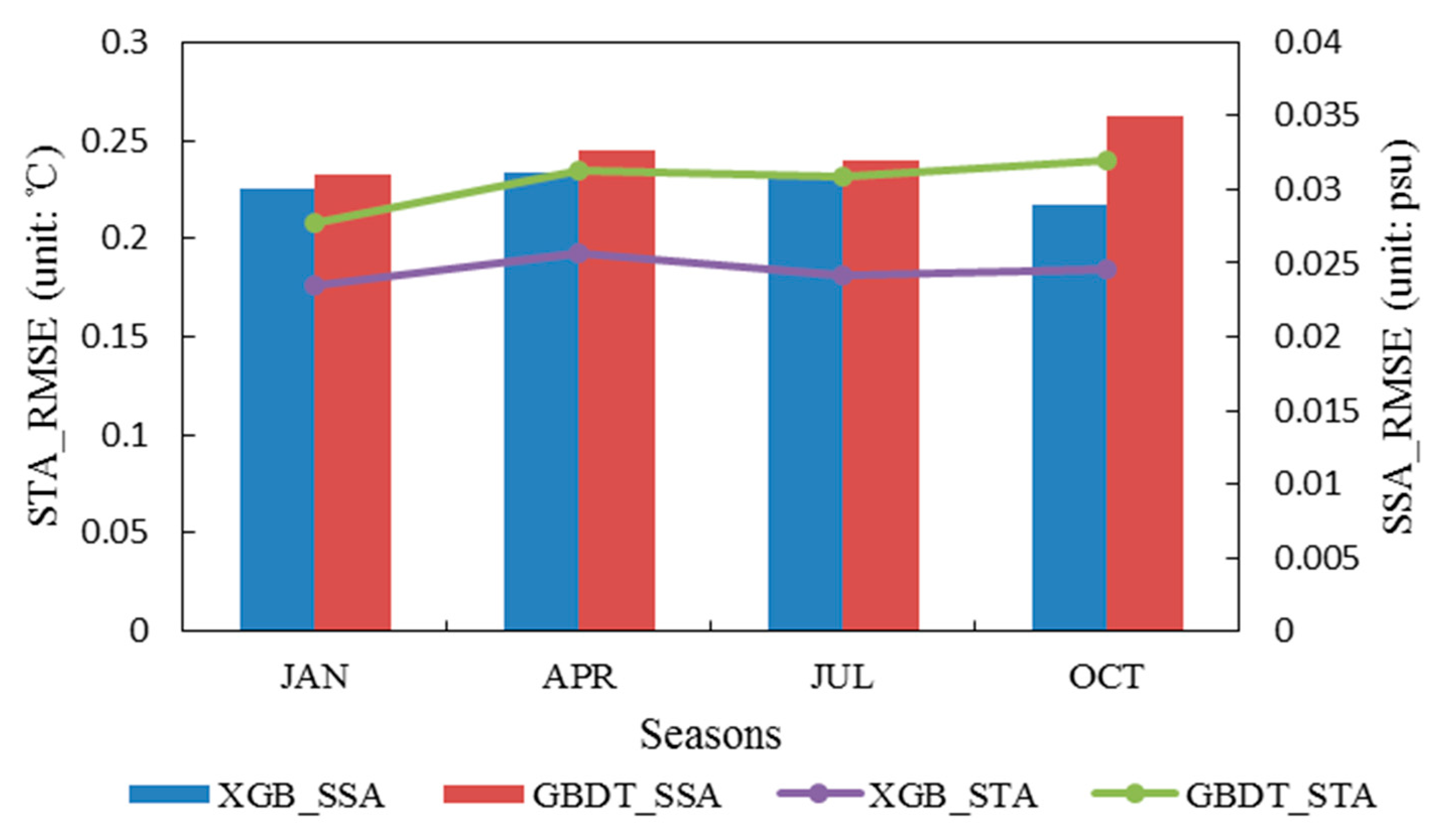
4.1. Accuracy Comparison between the XGBoost and GBDT Models
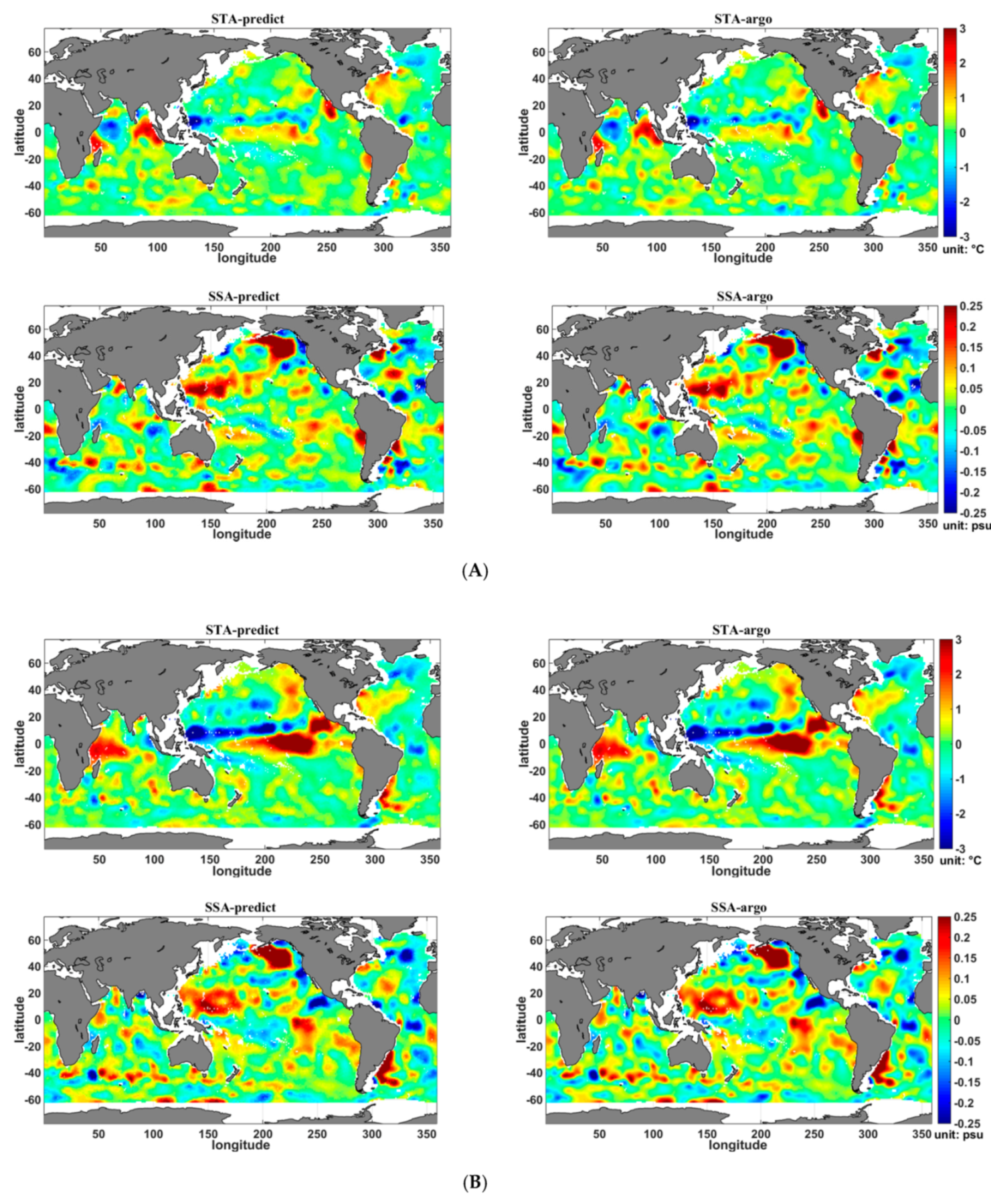
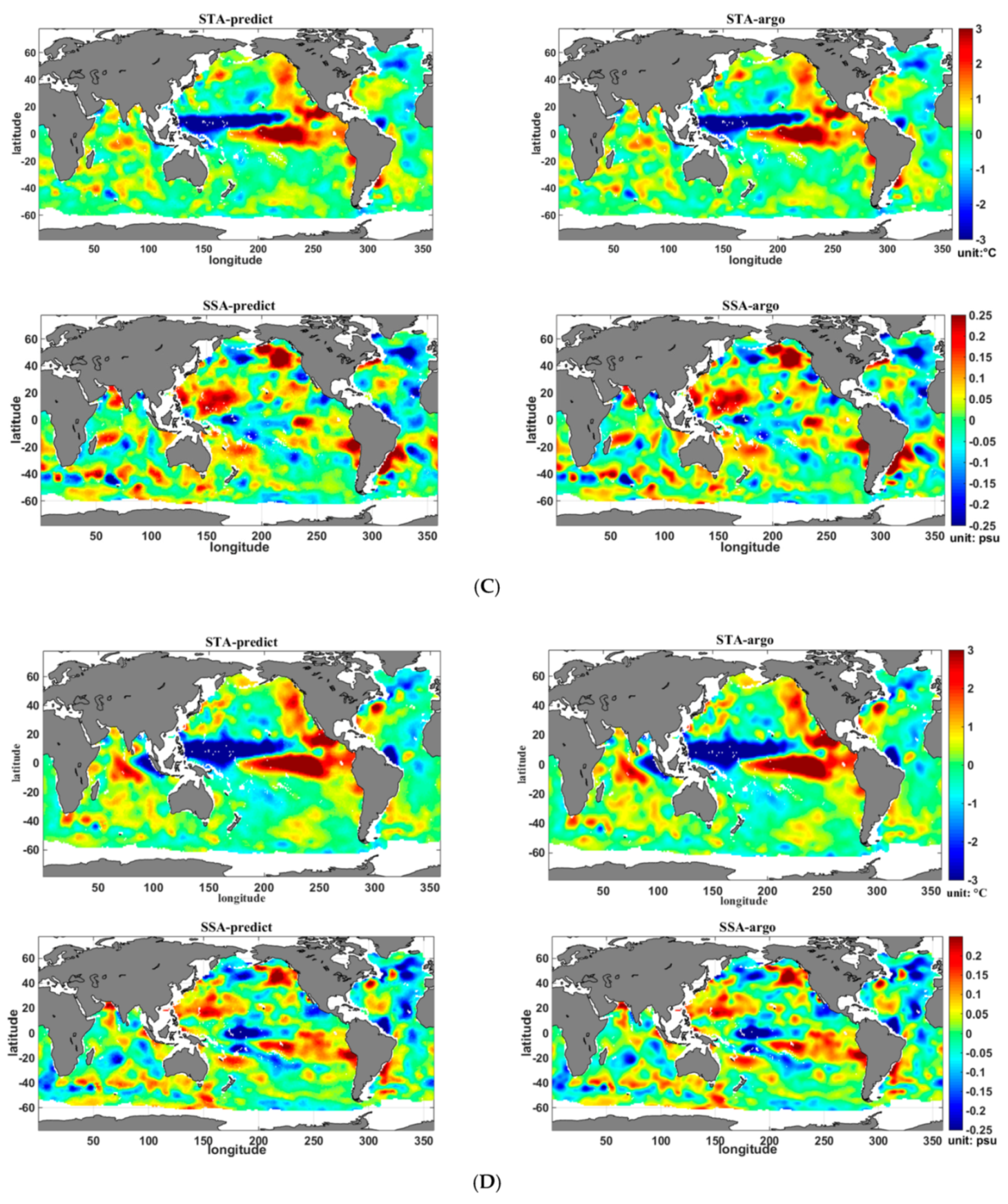
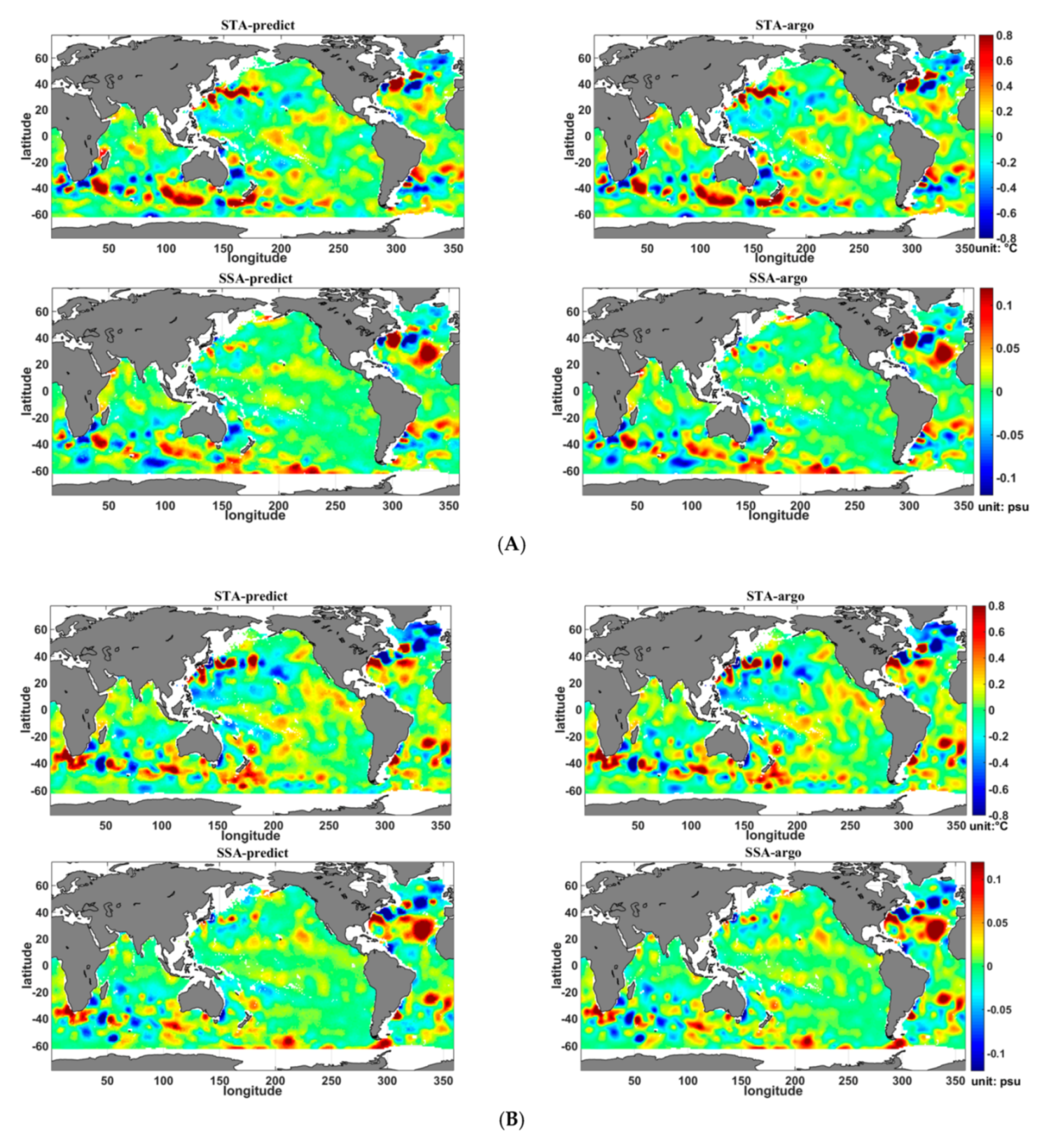
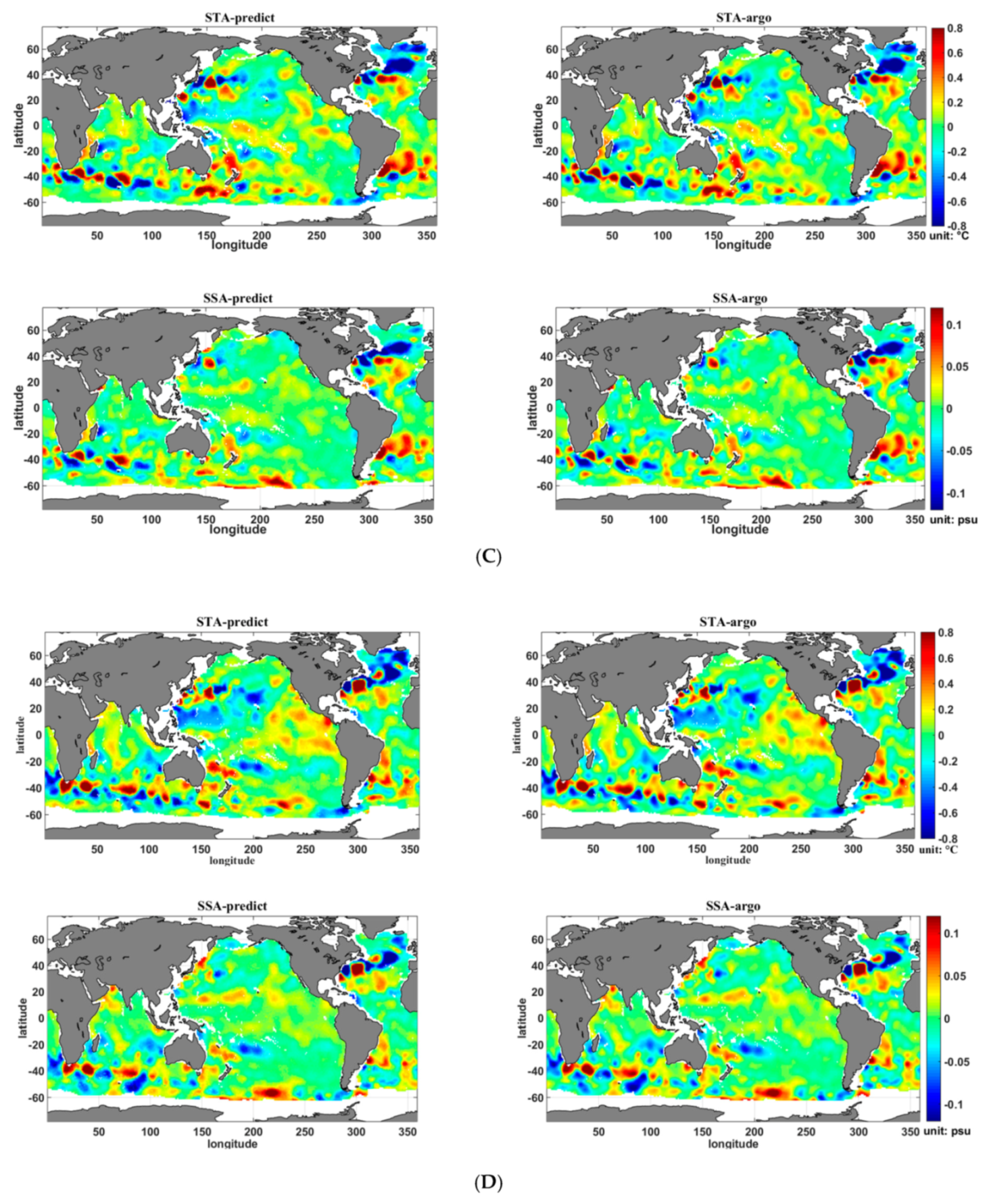
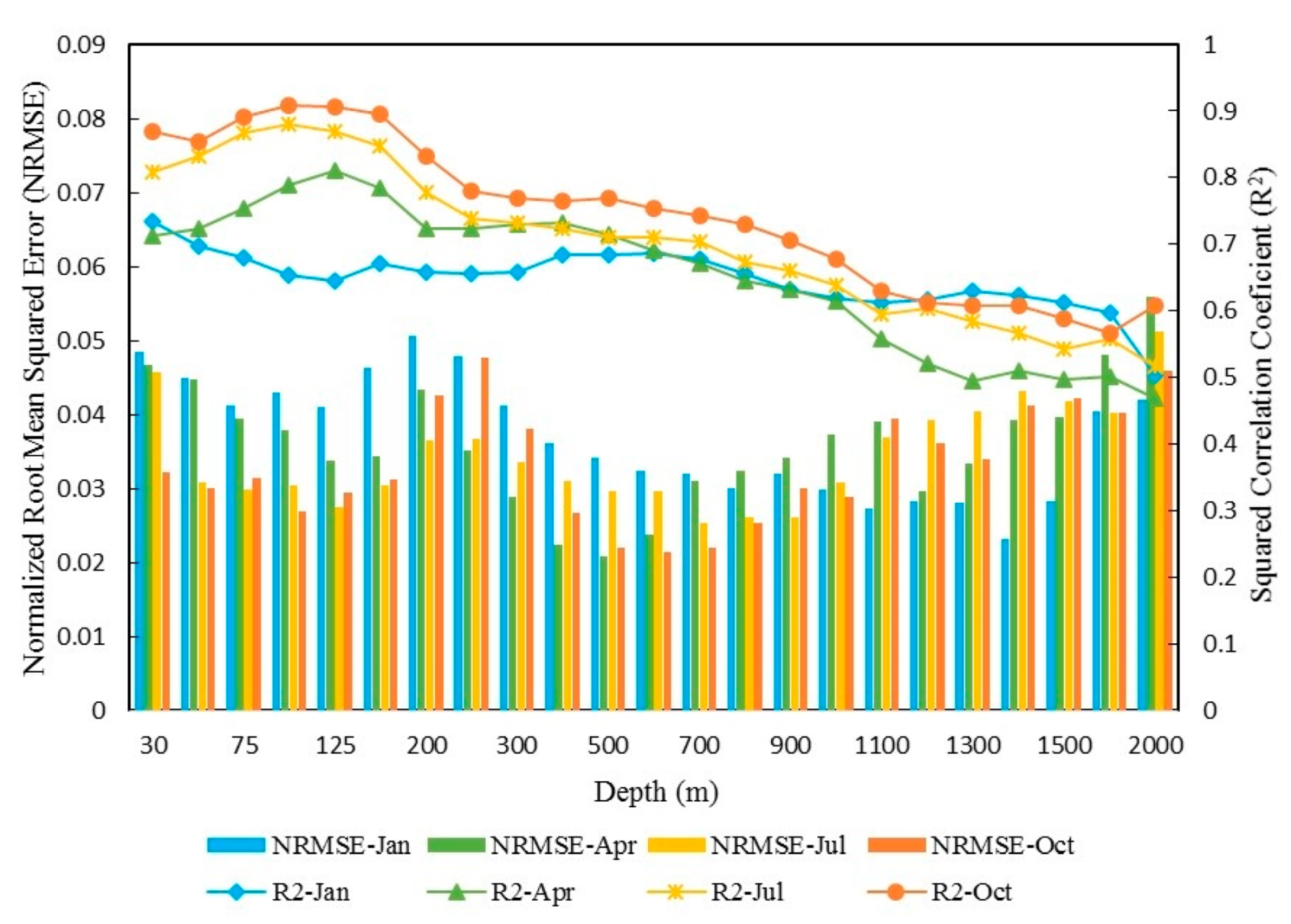
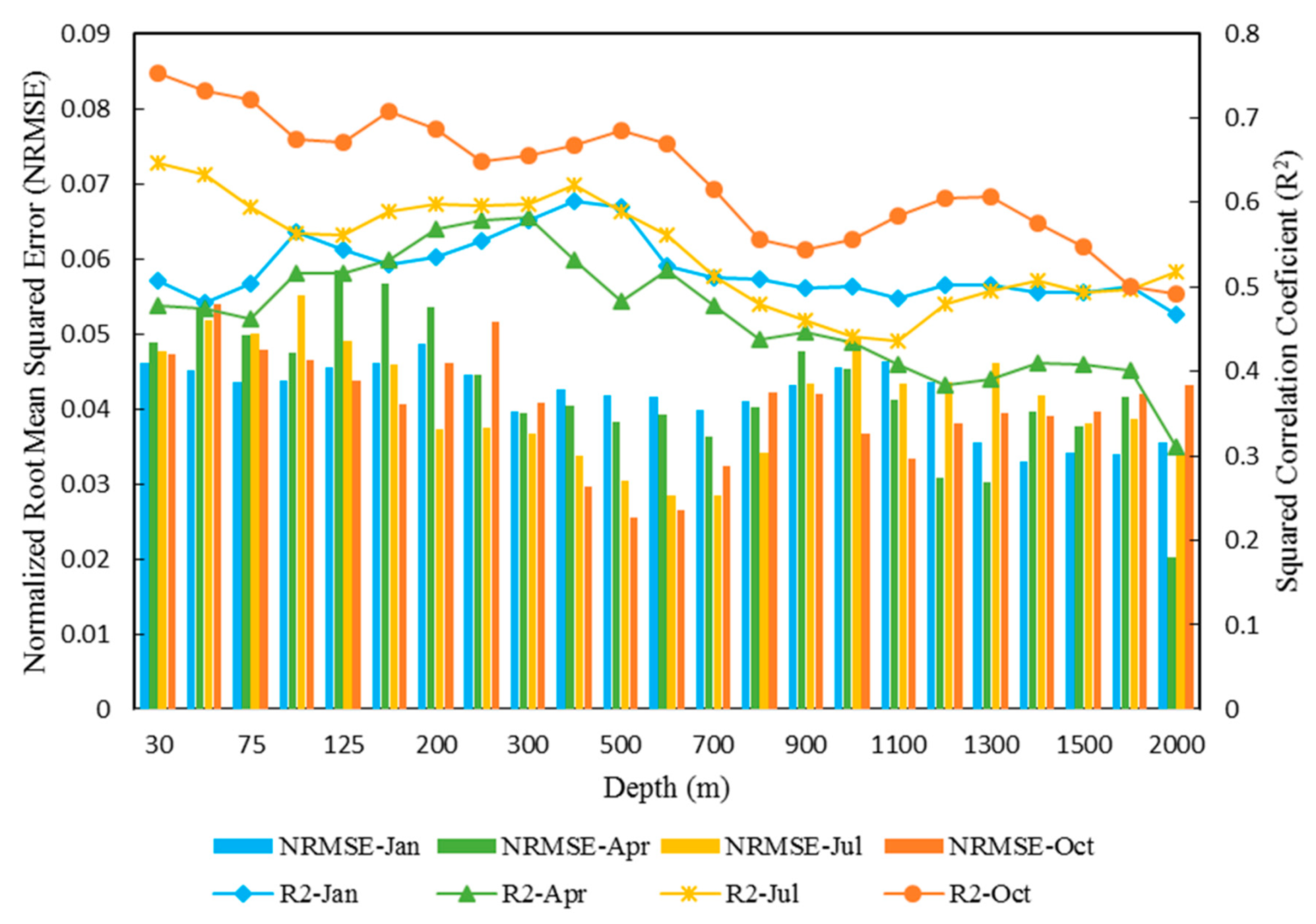
4.2. Analysis of the Seasonal Results
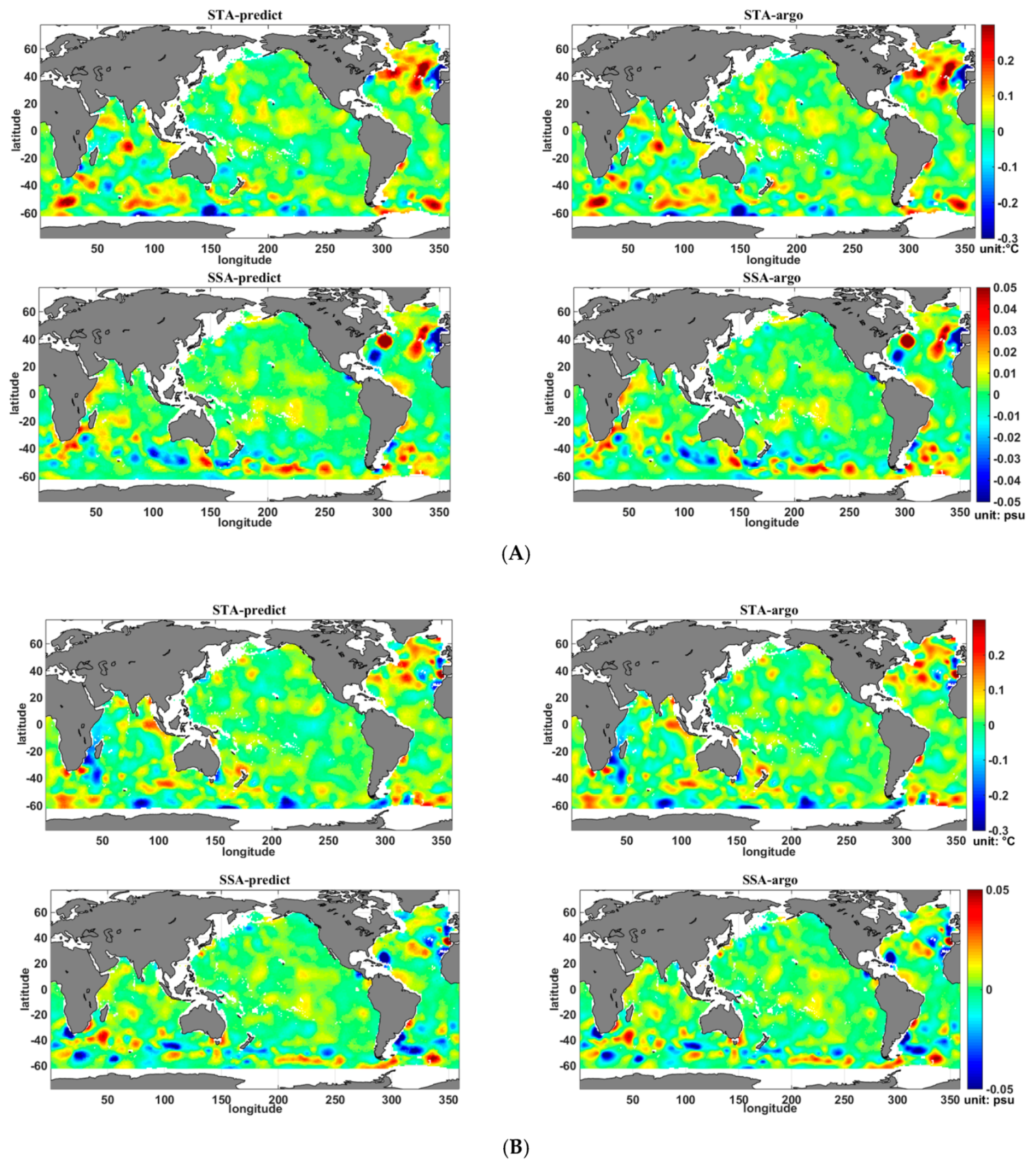
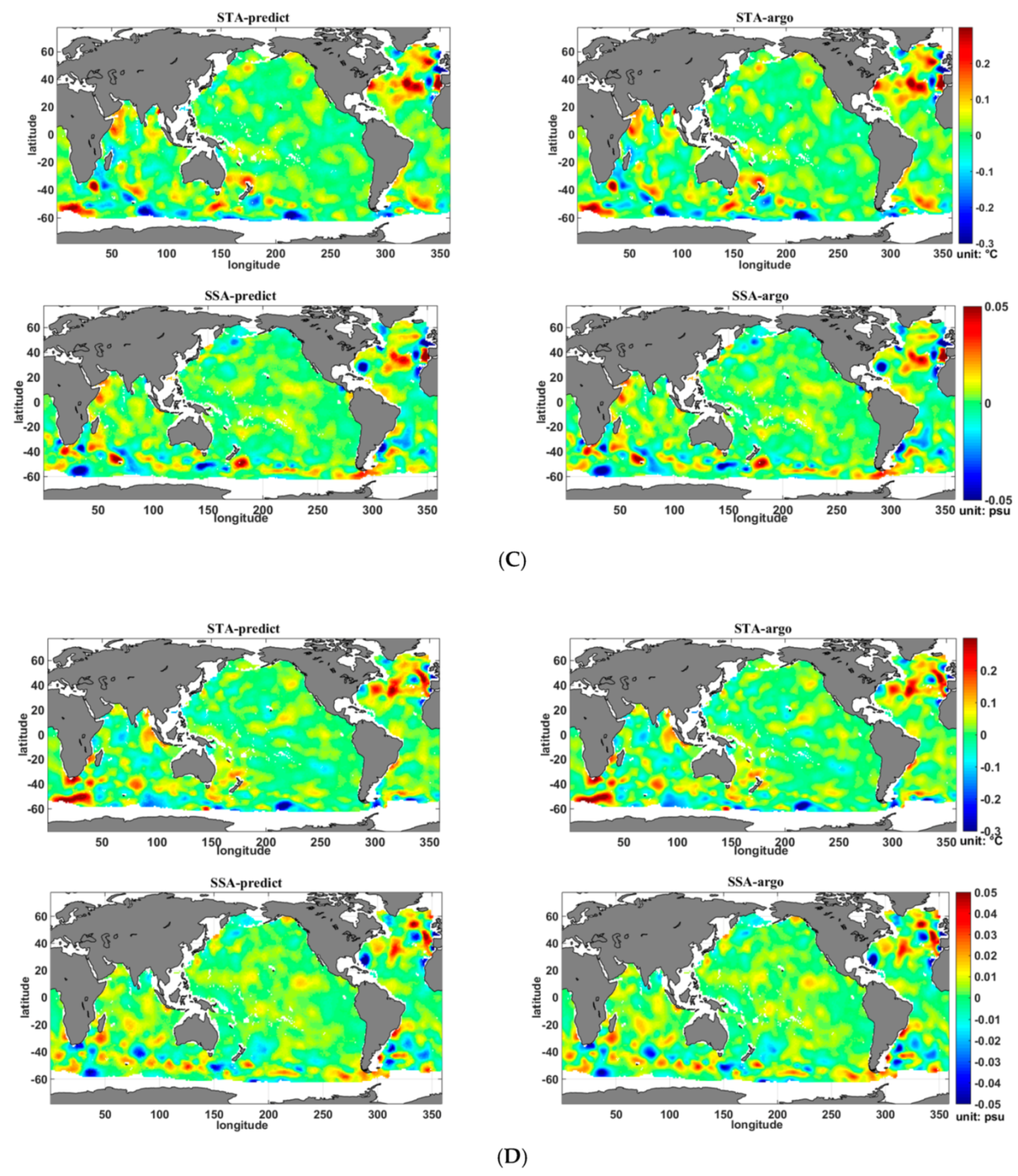
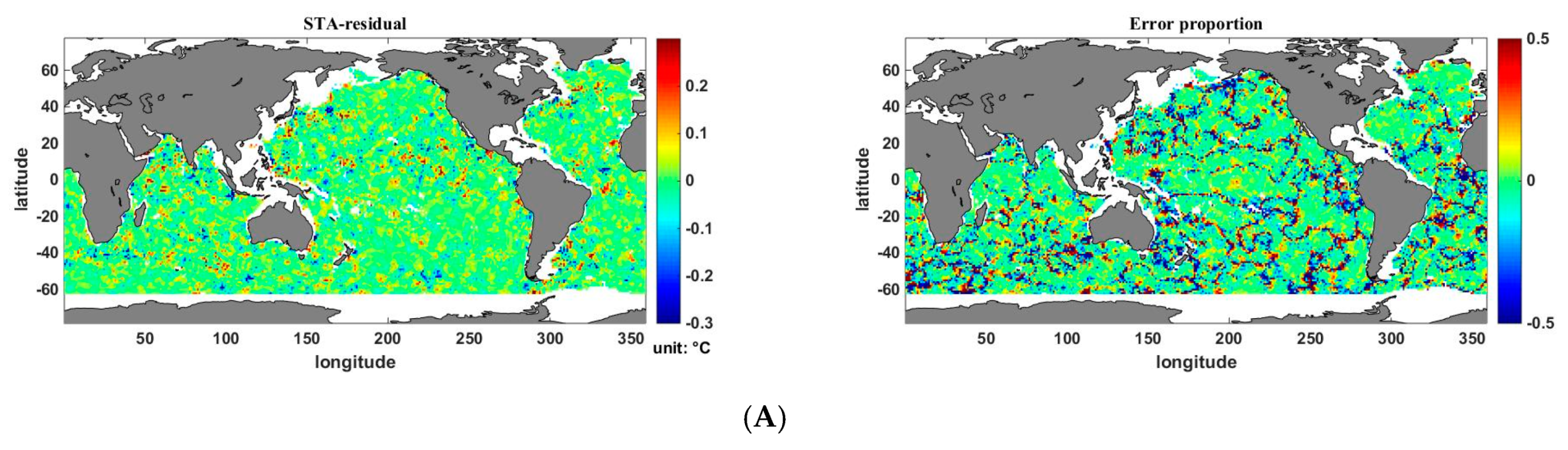
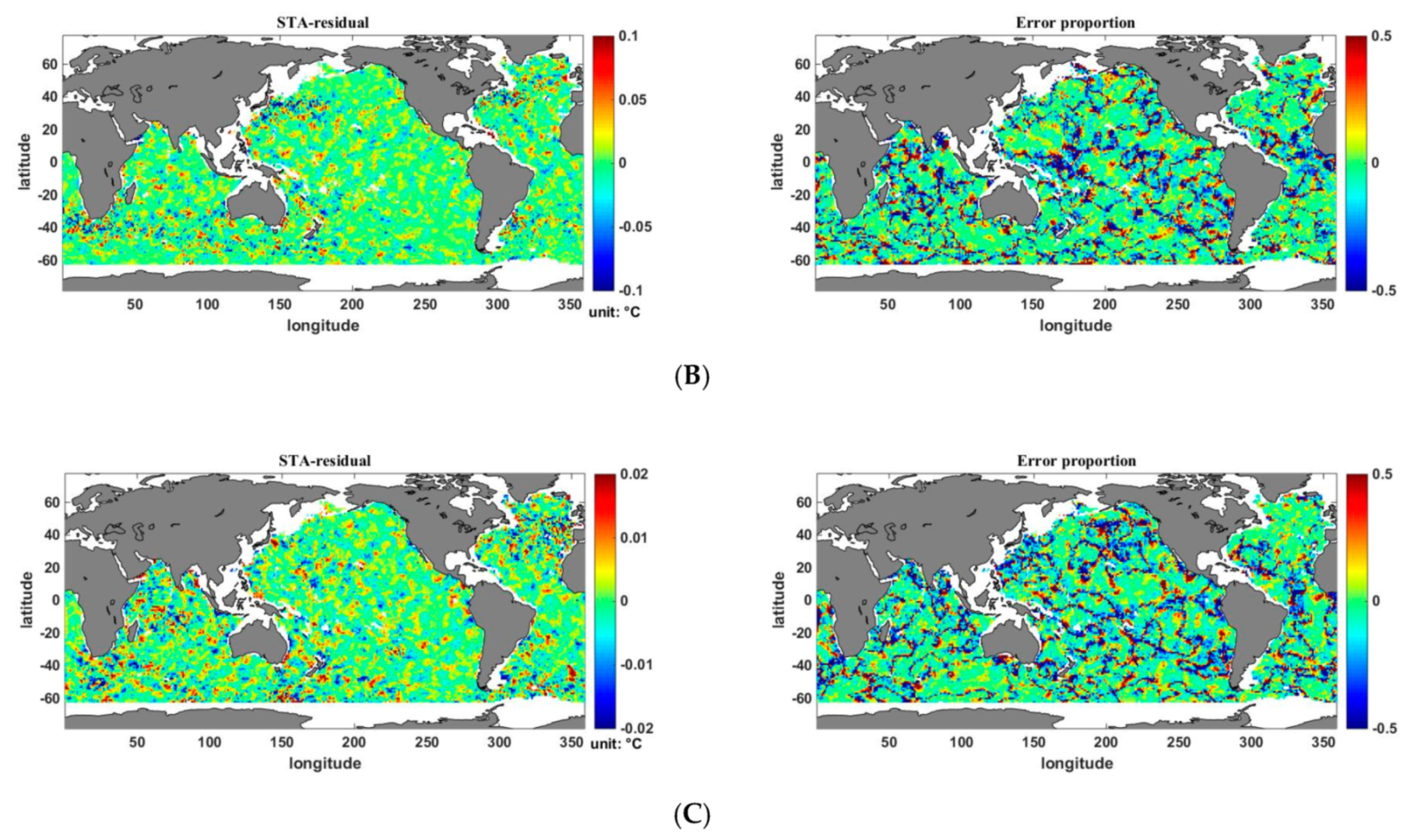
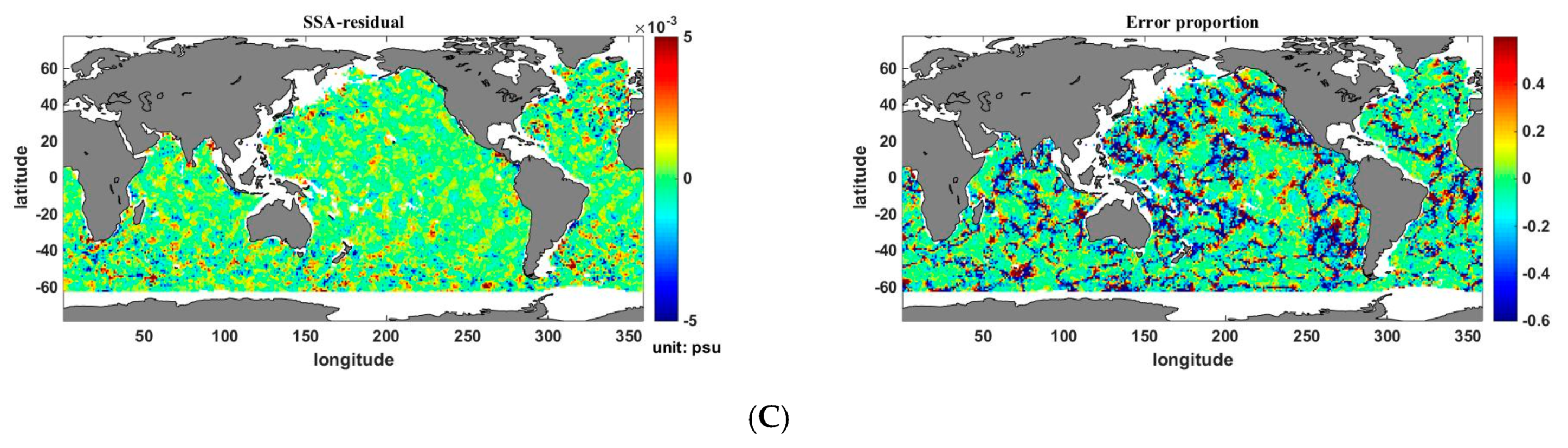
4.3. Estimation Error Analysis
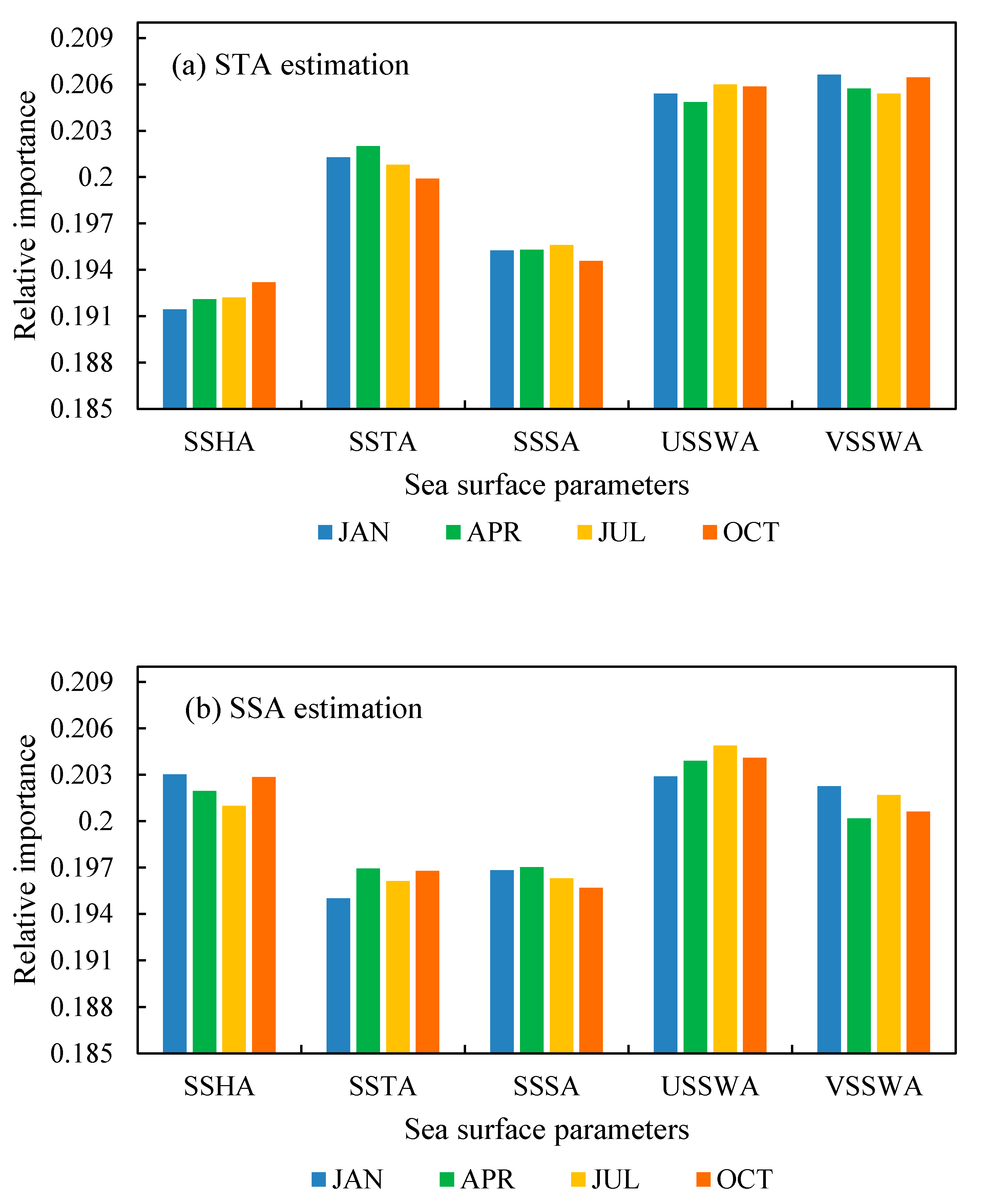
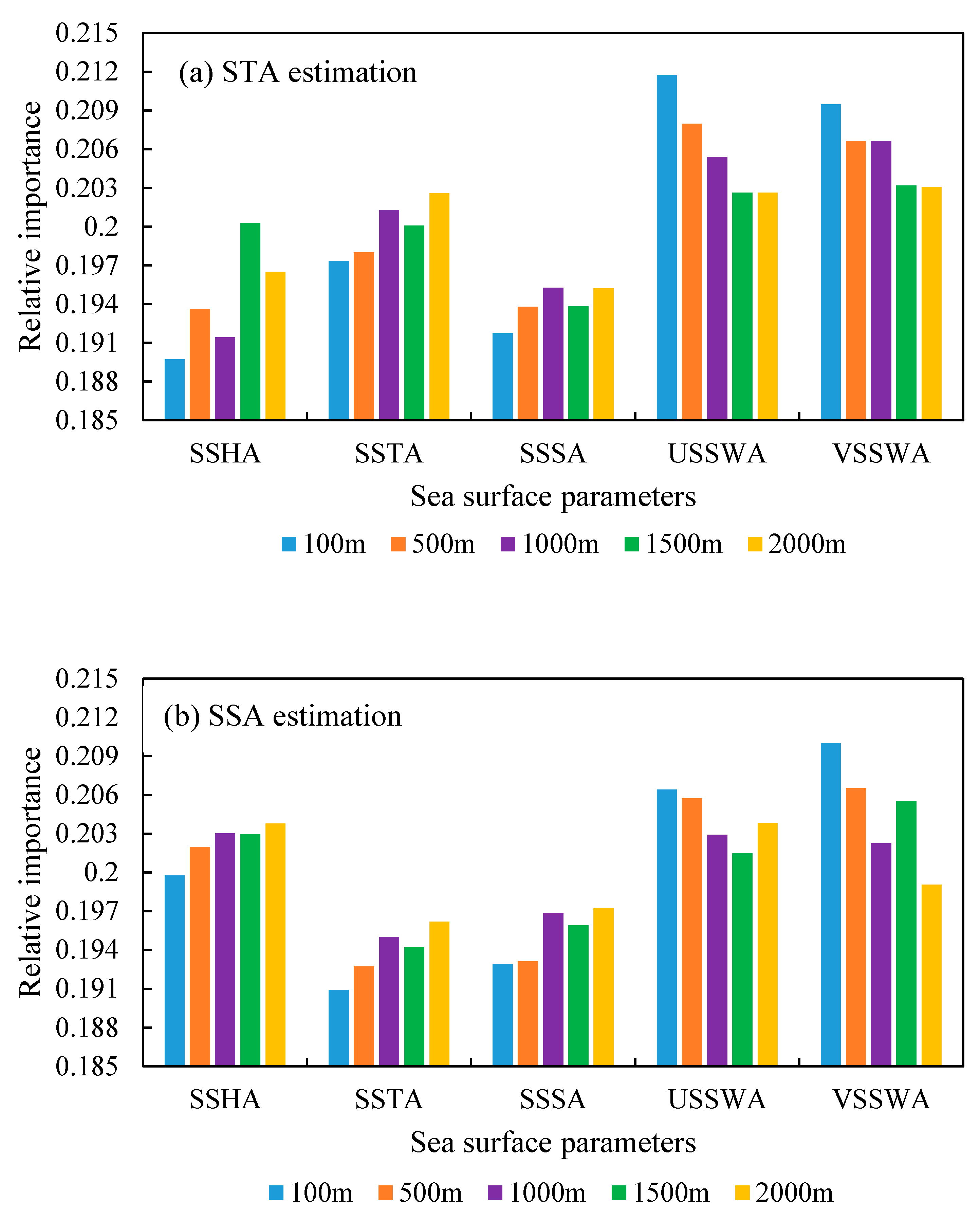
4.4. Relative Importance of the Sea Surface Parameters
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chang, L.; Xu, J.; Tie, X.; Wu, J. Impact of the 2015 El Nino event on winter air quality in china. Sci. Rep. 2016, 6, 34275. [Google Scholar] [CrossRef] [PubMed]
- Zhai, P.; Yu, R.; Guo, Y.; Li, Q.; Ren, X.; Wang, Y.; Xu, W. The strong El Niño of 2015/16 and its dominant impacts on global and china’s climate. J. Meteorol. Res. 2016, 30, 283–297. [Google Scholar] [CrossRef]
- Cheng, L.J.; Abraham, J.; Hausfather, Z.; Trenberth, K.E. How fast are the oceans warming? Science 2019, 363, 128–129. [Google Scholar] [CrossRef] [PubMed]
- Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
- Chen, X.; Tung, K.K. Varying planetary heat sink led to global-warming slowdown and acceleration. Science 2014, 345, 897–903. [Google Scholar] [CrossRef] [PubMed]
- Drijfhout, S.S.; Blaker, A.T.; Josey, S.A.; Nurser, A.J.G.; Sinha, B.; Balmaseda, M.A. Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophys. Res. Lett. 2014, 41, 7868–7874. [Google Scholar] [CrossRef]
- Yan, X.H.; Boyer, T.; Trenberth, K.; Karl, T.R.; Xie, S.P.; Nieves, V.; Tung, K.K.; Roemmich, D. The global warming hiatus: Slowdown or redistribution? Earth’s Future 2016, 4, 472–482. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Lu, W.; Zhang, W.; Yan, X.H. Inconsistent subsurface and deeper ocean warming signals during recent global warming and hiatus. J. Geophys. Res. Oceans 2017, 122, 8182–8195. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Q.; Yin, B. Seasonal variability in the thermohaline structure of the Western Pacific Warm Pool. Acta Oceanol. Sin. 2015, 34, 44–53. [Google Scholar] [CrossRef]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Wills, J.K. A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Klemas, V.; Yan, X.H. Subsurface and deeper ocean remote sensing from satellites: An overview and new results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
- Ali, M.M.; Swain, D.; Weller, R.A. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004, 31, L20308. [Google Scholar] [CrossRef]
- Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A review of ocean/sea subsurface water temperature studies from remote sensing and non-remote sensing methods. Water 2017, 9, 936. [Google Scholar] [CrossRef]
- Oke, P.R.; Schiller, A.; Griffin, D.A.; Brassington, G.B. Ensemble data assimilation for an eddy-resolving ocean model of the australian region. Q. J. R. Meteorol. Soc. 2005, 131, 3301–3311. [Google Scholar] [CrossRef]
- Wang, J.; Flierl, G.R.; Lacasce, J.H.; Mcclean, J.L.; Mahadevan, A. Reconstructing the ocean’s interior from surface data. J. Phys. Oceanogr. 2013, 43, 1611–1626. [Google Scholar] [CrossRef]
- Liu, L.; Peng, S.; Wang, J.; Huang, R.X. Retrieving density and velocity fields of the ocean’s interior from surface data. J. Geophys. Res. Oceans 2014, 119, 8512–8529. [Google Scholar] [CrossRef]
- Liu, L.; Peng, S.; Huang, R.X. Reconstruction of ocean’s interior from observed sea surface information. J. Geophys. Res. Oceans 2017, 122, 1042–1056. [Google Scholar] [CrossRef]
- Willis, J.K.; Roemmich, D.; Cornuelle, B. Combining altimetric height with broadscale profile data to estimate steric height, heat storage, subsurface temperature, and sea-surface temperature variability. J. Geophys. Res. 2003, 108, 3292. [Google Scholar] [CrossRef]
- Takano, A.; Yamazaki, H.; Nagai, T.; Honda, O. A method to estimate three-dimensional thermal structure from satellite altimetry data. J. Atmos. Ocean. Technol. 2010, 26, 2655–2664. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.-L.; Larnicol, G.; Le Traon, P.-Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Guinehut, S.; Le Traon, P.-Y.; Larnicol, G.; Philipps, S. Combining Argo and remote-sensing data to estimate the ocean three dimensional temperature fields—A first approach based on simulated observations. J. Mar. Syst. 2004, 46, 85–98. [Google Scholar] [CrossRef]
- Swart, S.; Speich, S.; Ansorge, I.J.; Lutjeharms, J.R.E. An altimetry-based gravest empirical mode south of Africa: 1. Development and validation. J. Geophys. Res. 2010, 115, C03002. [Google Scholar] [CrossRef]
- Meijers, A.J.S.; Bindoff, N.L.; Rintoul, S.R. Estimating the four-dimensional structure of the southern ocean using satellite altimetry. J. Atmos. Ocean. Technol. 2011, 28, 548–568. [Google Scholar] [CrossRef]
- Mulet, S.; Rio, M.H.; Mignot, A.; Guinehut, S.; Morrow, R. A new estimate of the global 3D geostrophic ocean circulation based on satellite data and in-situ measurements. Deep-Sea Res. 2012, 77–80, 70–81. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.H.; Jo, Y.H.; Liu, W.T. Estimation of subsurface temperature anomaly in the north Atlantic using a self-organizing map neural network. J. Atmos. Ocean. Technol. 2012, 29, 1675–1688. [Google Scholar] [CrossRef]
- Chapman, C.; Charantonis, A.A. Reconstruction of subsurface velocities from satellite observations using iterative self-organizing maps. IEEE Geosci. Remote Sens. Lett. 2017, 14, 617–620. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, R.; Yan, H.; Yu, Y.; Chen, J. Salinity Profile Estimation in the Pacific Ocean from Satellite Surface Salinity Observations. J. Atmos. Ocean. Technol. 2019, 36, 53–68. [Google Scholar] [CrossRef]
- Charantonis, A.A.; Badran, F.; Thiria, S. Retrieving the evolution of vertical profiles of Chlorophyll-a from satellite observations using Hidden Markov Models and Self-Organizing Topological Maps. Remote Sens. Environ. 2015, 163, 229–239. [Google Scholar] [CrossRef]
- Zhou, C.; Ding, X.; Zhang, J.; Yang, J.; Ma, Q. An objective algorithm for reconstructing the three-dimensional ocean temperature field based on Argo profiles and SST data. Ocean Dyn. 2017, 67, 1523–1533. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Yan, X.H.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Yan, X.H. Retrieving temperature anomaly in the global subsurface and deeper ocean from satellite observations. J. Geophys. Res. Oceans 2018, 123, 399–410. [Google Scholar] [CrossRef]
- Li, W.; Su, H.; Wang, X.; Yan, X.H. Estimation of global subsurface temperature anomaly based on multisource satellite observations. J. Remote Sens. 2017, 21, 881–891. [Google Scholar]
- Su, H.; Huang, L.; Li, W.; Yang, X.; Yan, X.H. Retrieving ocean subsurface temperature using a satellite-based geographically weighted regression model. J. Geophys. Res. Oceans 2018, 123, 5180–5193. [Google Scholar] [CrossRef]
- Chen, C.; Yang, K.; Ma, Y.; Wang, Y. Reconstructing the subsurface temperature field by using sea surface data through self-organizing map method. IEEE Geosci. Remote Sens. Lett. 2018, 1–10. [Google Scholar] [CrossRef]
- AVISO Altimetry. Available online: http://www.aviso.altimetry.fr (accessed on 25 November 2018).
- AMSR2 / AMSRE. Available online: http://www.remss.com/missions/amsr/ (accessed on 20 November 2018).
- CEC-Ifremer Dataset V02. Available online: https://www.catds.fr/Products/Available-products-from-CEC-OS/CEC-Ifremer-Dataset-V02 (accessed on 23 November 2018).
- CISL RDA: Cross-Calibrated Multi-Platform Ocean Surface Wind Vector Analysis Product V2, 1987 - ongoing. Available online: https://rda.ucar.edu/datasets/ds745.1/ (accessed on 23 November 2018).
- Argo Monthly Gridded Data on Standard Levels. Available online: http://apdrc.soest.hawaii.edu/projects/Argo/data/gridded/On_standard_levels/index-1.html (accessed on 20 November 2018).
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Annals Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- O’Gorman, P.A.; Dwyer, J.G. Using machine learning to parameterize moist convection: Potential for modeling of climate, climate change, and extreme events. J. Adv. Model. Earth Syst. 2018, 10, 2548–2563. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, C.; Li, Y.Y.; Liu, N. A boosted decision tree approach using bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Wolff, E. Very high resolution object-based land use-land cover urban classification using extreme gradient boosting. IEEE Geosci. Remote Sens. Lett. 2017, 15, 607–611. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Si, Y. A data-driven design for fault detection of wind turbines using random forests and xgboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Lu, W.; Su, H.; Yang, X.; Yan, X.H. Subsurface temperature estimation from remote sensing data using a clustering-neural network method. Remote Sens. Environ. 2019, 229, 213–222. [Google Scholar] [CrossRef]

| Some Hyper-Parameters | Meaning (Default Values) | Optimal Values |
|---|---|---|
| learning_rate | Makes the model more robust by shrinking the weights on each step (0.3) | 0.1 |
| min_child_weight | The minimum sum of weights of all observations required in a child (1) | 2 |
| max_depth | The maximum depth of a tree (6) | 16 |
| colsample_bytree | The fraction of columns to be randomly sampled for each tree (1) | 0.8 |
| subsample | The fraction of observations to be randomly sampled for each tree (1) | 0.8 |
| gamma | The minimum loss reduction required to make a split (0) | 0 |
| reg_alpha | L1 regularization term on weights (0) | 0.1 |
| reg_lambda | L2 regularization term on weights (1) | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Yang, X.; Lu, W.; Yan, X.-H. Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations. Remote Sens. 2019, 11, 1598. https://doi.org/10.3390/rs11131598
Su H, Yang X, Lu W, Yan X-H. Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations. Remote Sensing. 2019; 11(13):1598. https://doi.org/10.3390/rs11131598
Chicago/Turabian StyleSu, Hua, Xin Yang, Wenfang Lu, and Xiao-Hai Yan. 2019. "Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations" Remote Sensing 11, no. 13: 1598. https://doi.org/10.3390/rs11131598
APA StyleSu, H., Yang, X., Lu, W., & Yan, X.-H. (2019). Estimating Subsurface Thermohaline Structure of the Global Ocean Using Surface Remote Sensing Observations. Remote Sensing, 11(13), 1598. https://doi.org/10.3390/rs11131598








