Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction
Abstract
:1. Introduction
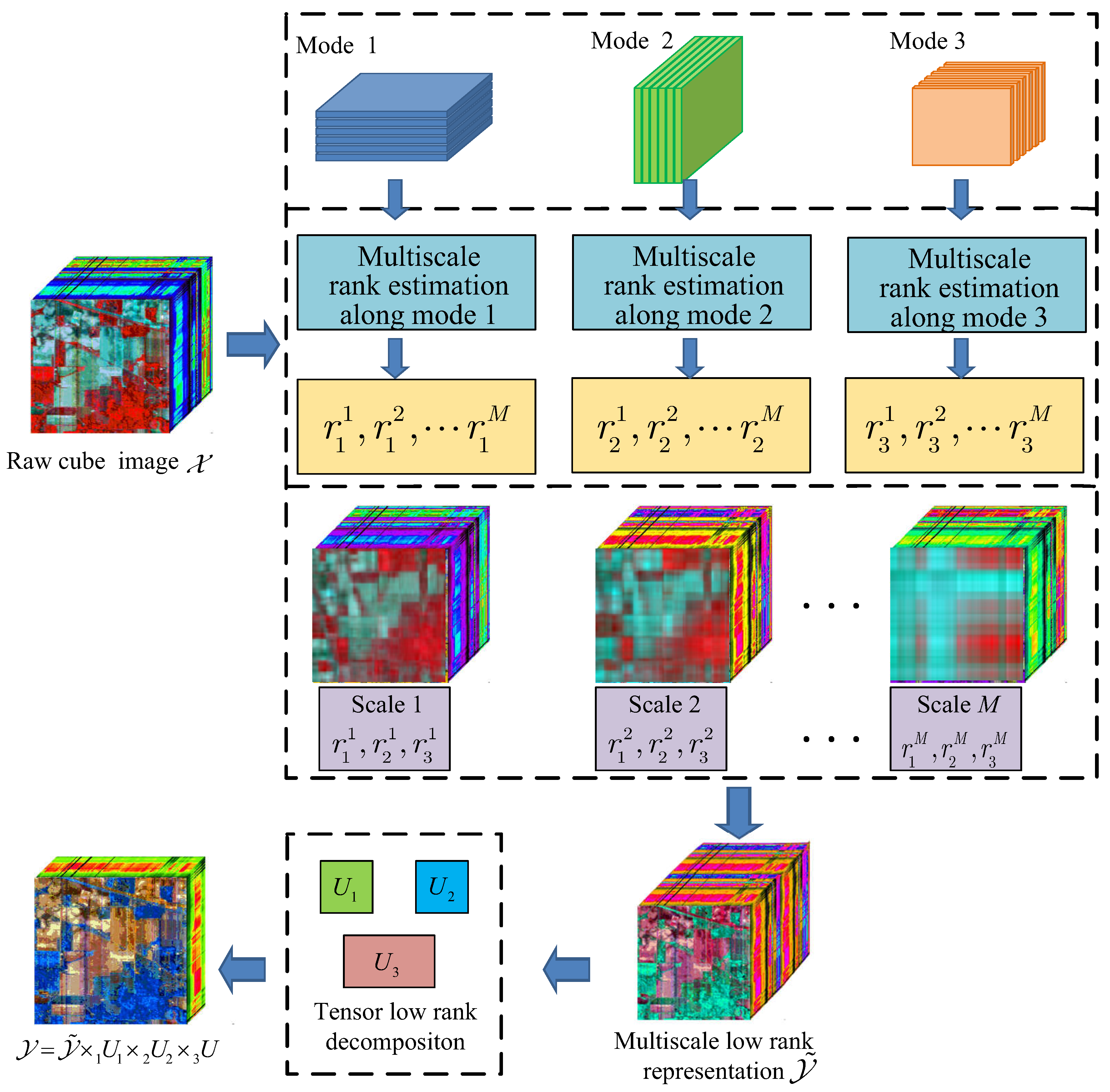
2. Tensor Based Multiscale Low Rank Decomposition
2.1. Definition and Notations
2.2. Tensor Low Rank Decomposition
3. Hyperspectral Image Multiscale Low Rank Representation and Fusion
3.1. Adaptive Hypepspectral Image Low Rank Estimating
3.2. Hyperspectral Image Multiscale Representation and Low Rank Fusion
| Algorithm 1: Proposed T-MLRD algorithm |
|
|
4. Experimental Results and Analysis
4.1. Experimental Setup
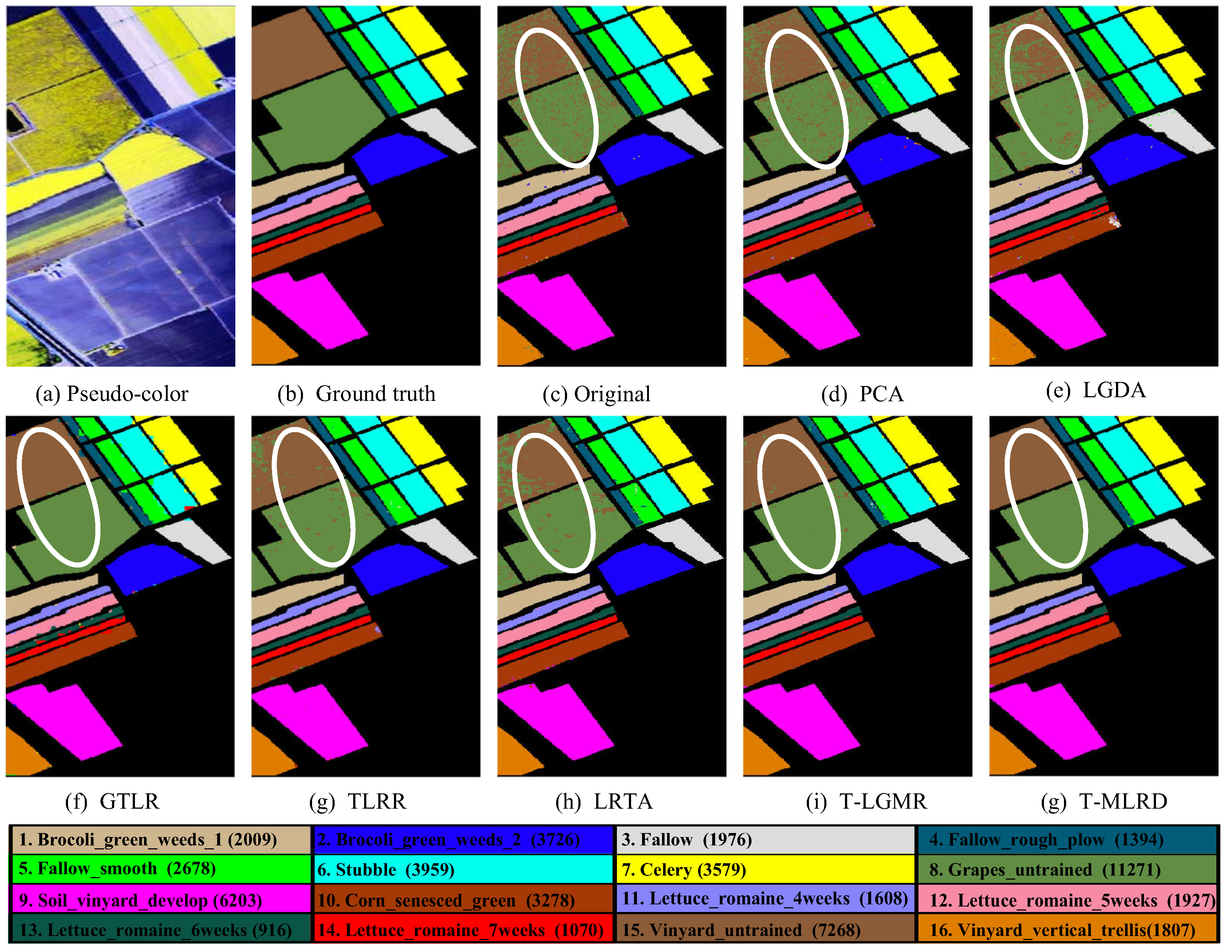
4.2. Classification Results
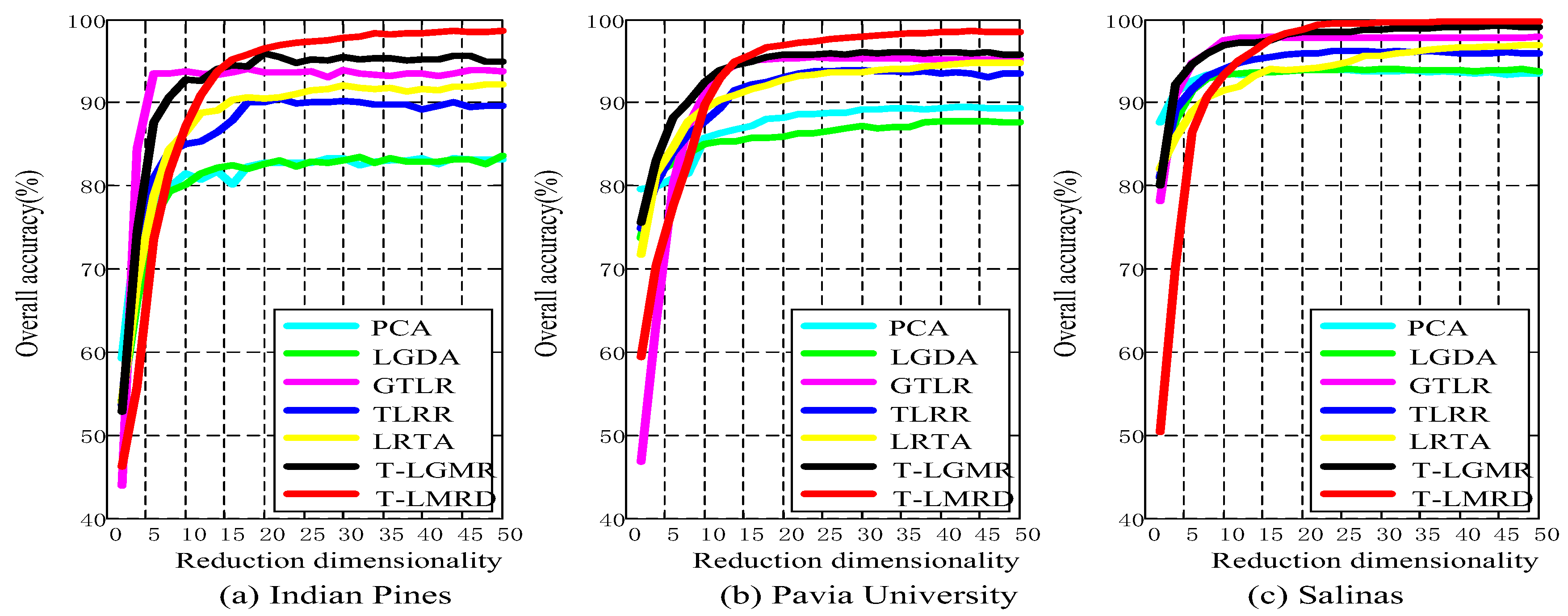
4.3. Analysis of Different Reduced Dimensionality
4.4. Analysis of Computational Costs
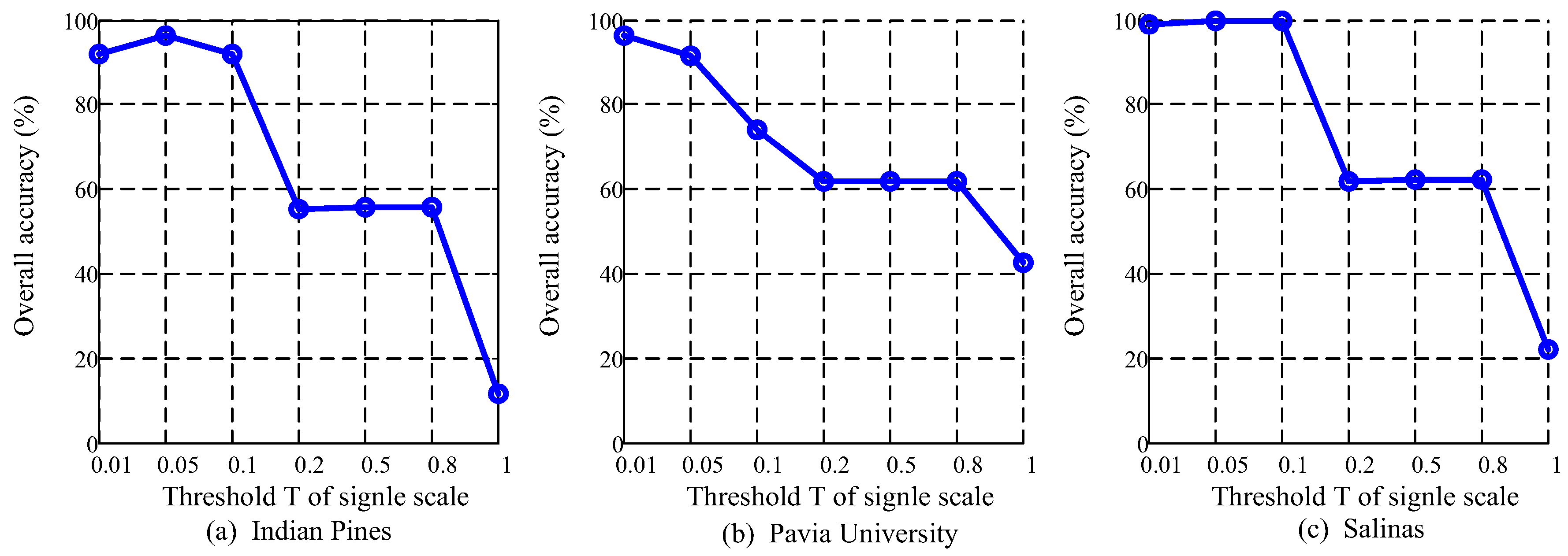
4.5. Analysis of Different Scales
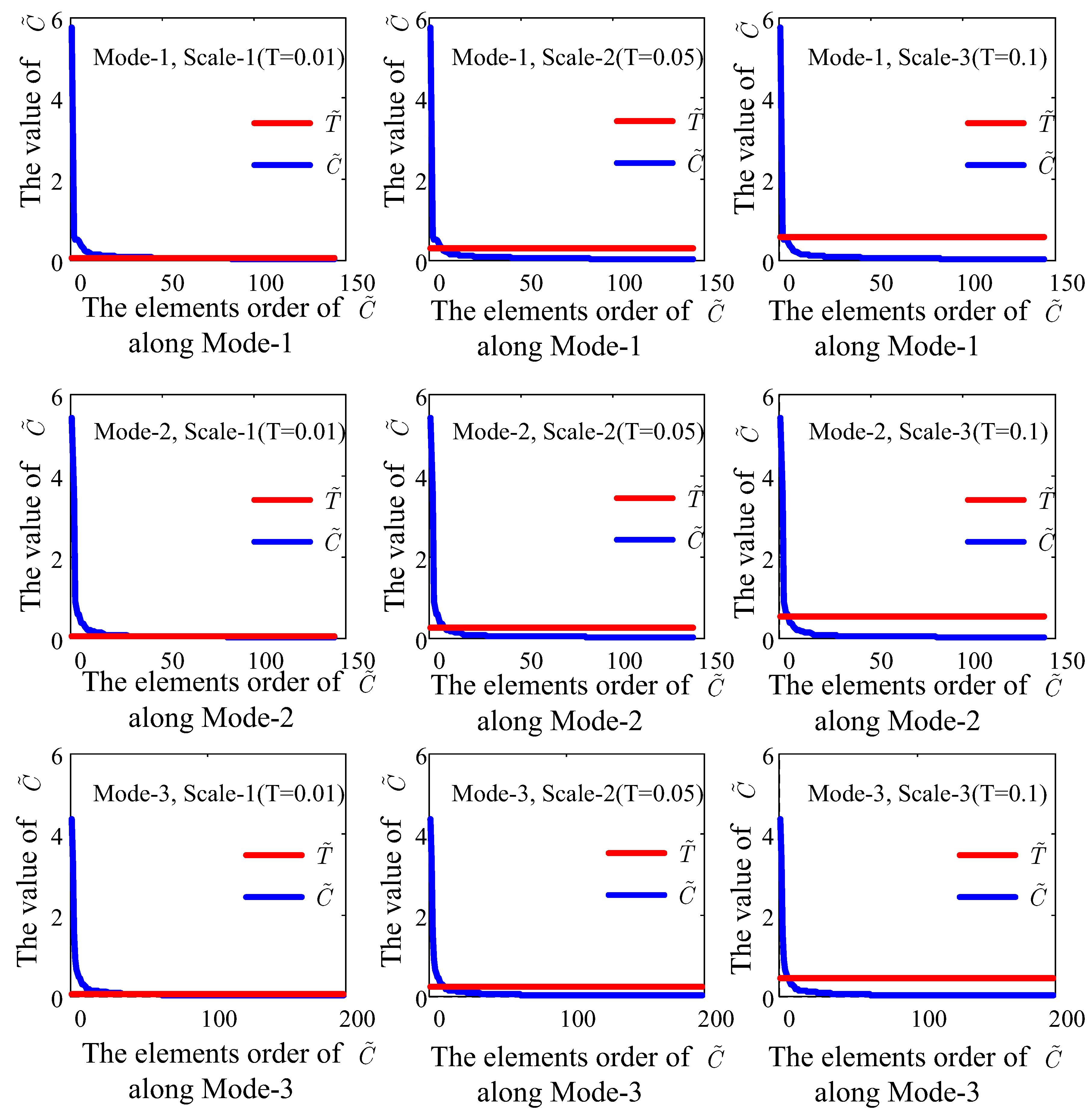
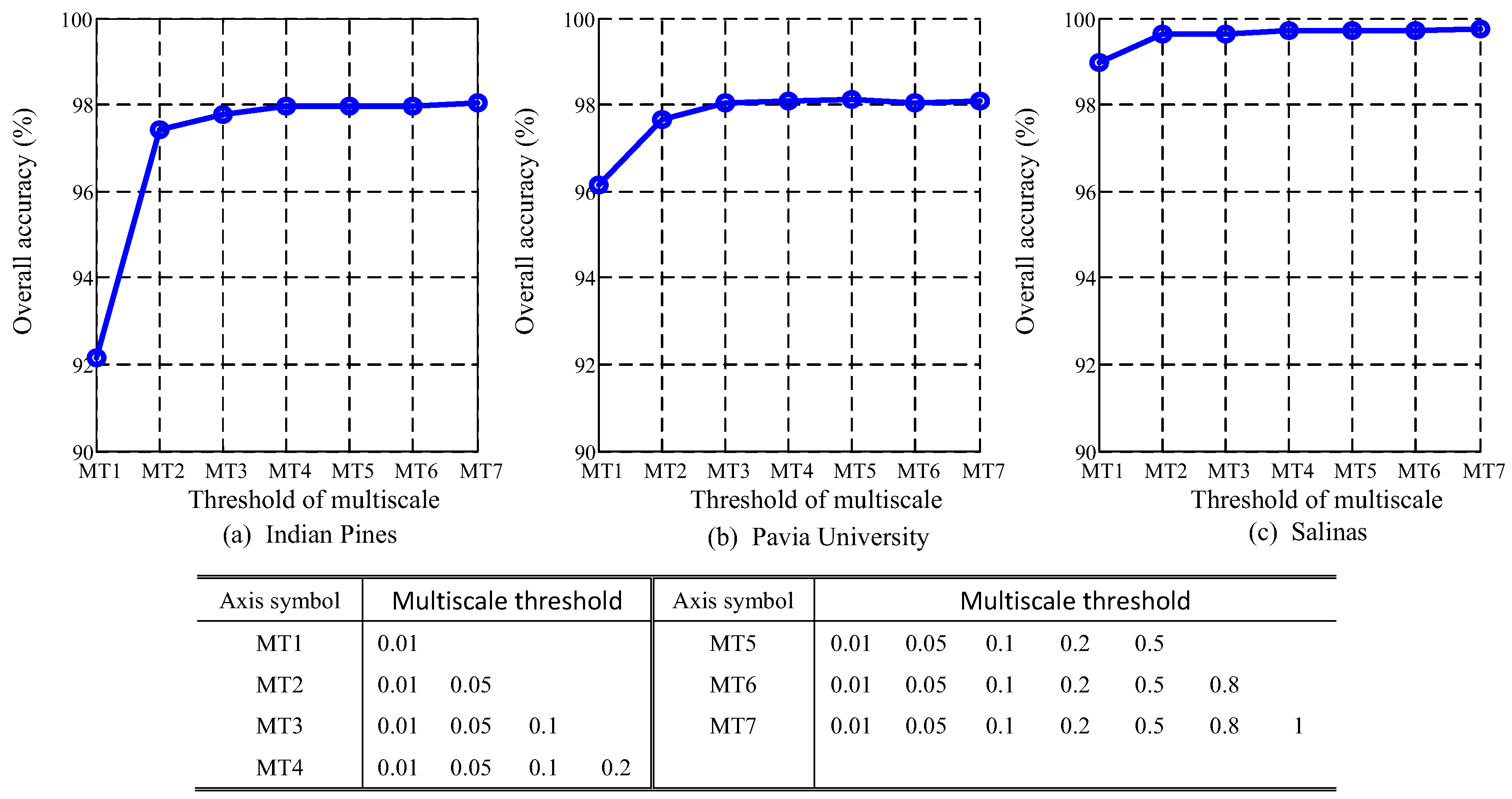
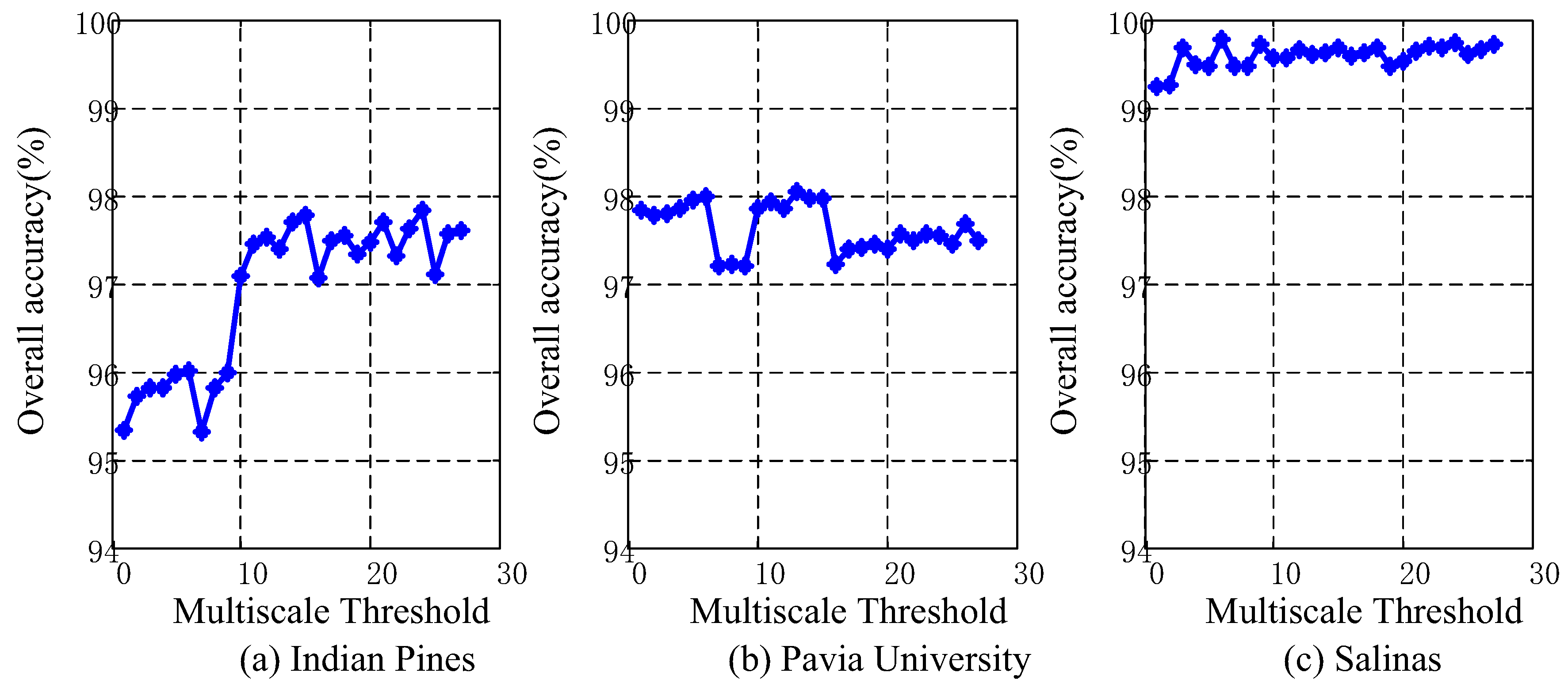
4.6. Analysis of Multiscale Threshold Values
5. Discussion
5.1. Classification Results of Different Reduced Dimensionality
5.2. Multiscale Threshold Values
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, X.; Gao, Z.; Jiao, L.; Zhou, H. Multifeature Hyperspectral Image Classification With Local and Nonlocal Spatial Information via Markov Random Field in Semantic Space. IEEE Trans. Geosci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Li, C.; Ning, H.; Jiao, L.; Zhou, H. Recursive Autoencoders-Based Unsupervised Feature Learning for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1928–1932. [Google Scholar] [CrossRef] [Green Version]
- Kwon, H.; Nasrabadi, N.M. Kernel Matched Subspace Detectors for Hyperspectral Target Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 28, 178–194. [Google Scholar] [CrossRef]
- Manolakis, D.; Siracusa, C.; Shaw, G. Hyperspectral subpixel target detection using the linear mixing model. Geosci. Remote Sens. IEEE Trans. 2001, 39, 1392–1409. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial Spectral-Graph-Regularized Low-Rank Tensor Decomposition for Multispectral and Hyperspectral Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
- Zhang, X.; Li, C.; Zhang, J.; Chen, Q.; Feng, J.; Jiao, L.; Zhou, H. Hyperspectral Unmixing via Low-Rank Representation with Space Consistency Constraint and Spectral Library Pruning. Remote Sens. 2018, 10, 339. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, X.; Cheng, Y.; Wang, Z.J. Dimensionality Reduction for Hyperspectral Data Based on Class-Aware Tensor Neighborhood Graph and Patch Alignment. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1582–1593. [Google Scholar] [PubMed]
- Feng, F.; Li, W.; Du, Q.; Zhang, B. Dimensionality Reduction of Hyperspectral Image with Graph-Based Discriminant Analysis Considering Spectral Similarity. Remote Sens. 2017, 9, 323. [Google Scholar] [CrossRef]
- Liu, S.; Du, Q.; Tong, X.; Samat, A.; Pan, H.; Ma, X. Band Selection-Based Dimensionality Reduction for Change Detection in Multi-Temporal Hyperspectral Images. Remote Sens. 2017, 9, 1008. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.U.; Yong, Y.U.; Yi, M.A. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Y.; Jiao, L.; Shang, R.; Hou, B.; Zhang, X. Local Collaborative Representation With Adaptive Dictionary Selection for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1482–1486. [Google Scholar] [CrossRef]
- Wei, L.; Liu, J.; Qian, D. Sparse and Low-Rank Graph for Discriminant Analysis of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4094–4105. [Google Scholar]
- Rasti, B.; Ghamisi, P.; Plaza, J.; Plaza, A. Fusion of Hyperspectral and LiDAR Data Using Sparse and Low-Rank Component Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6354–6365. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.Q.; Yang, J. Hyperspectral Image Denoising via Sparse Representation and Low-Rank Constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 296–308. [Google Scholar] [CrossRef]
- Gao, L.; Yao, D.; Li, Q.; Zhuang, L.; Zhang, B.; Bioucas-Dias, J. A New Low-Rank Representation Based Hyperspectral Image Denoising Method for Mineral Mapping. Remote Sens. 2017, 9, 1145. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Laplacian Regularized Collaborative Graph for Discriminant Analysis of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7066–7076. [Google Scholar] [CrossRef]
- Renard, N.; Bourennane, S.; Blanc-Talon, J. Denoising and Dimensionality Reduction Using Multilinear Tools for Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 138–142. [Google Scholar] [CrossRef]
- Zhong, Z.; Fan, B.; Duan, J.; Wang, L.; Ding, K.; Xiang, S.; Pan, C. Discriminant Tensor Spectral Spatial Feature Extraction for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 12, 1028–1032. [Google Scholar] [CrossRef]
- Xian, G.; Xin, H.; Zhang, L.; Zhang, L.; Plaza, A.; Benediktsson, J.A. Support Tensor Machines for Classification of Hyperspectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3248–3264. [Google Scholar]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-Based Classification Models for Hyperspectral Data Analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6884–6898. [Google Scholar] [CrossRef]
- An, J.; Zhang, X.; Zhou, H.; Jiao, L. Tensor-Based Low-Rank Graph With Multimanifold Regularization for Dimensionality Reduction of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4731–4746. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Han, Z.; He, S. Hyperspectral Image Super-Resolution via Nonlocal Low-Rank Tensor Approximation and Total Variation Regularization. Remote Sens. 2017, 9, 1286. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y.; Huang, J.; Mei, X.; Ma, J. Hyperspectral image denoising using the robust low-rank tensor recovery. J. Opt. Soc. Am. Opt. Image Sci. Vis. 2015, 32, 1604–1612. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Zhang, M.; Zhang, L.; Hu, R.; Tao, D. PLTD: Patch-Based Low-Rank Tensor Decomposition for Hyperspectral Images. IEEE Trans. Multimed. 2017, 19, 67–79. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Fang, L. Learning a Low Tensor-Train Rank Representation for Hyperspectral Image Super-Resolution. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef] [PubMed]
- An, J.; Zhang, X.; Jiao, L.C. Dimensionality Reduction Based on Group-Based Tensor Model for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1497–1501. [Google Scholar] [CrossRef]
- Pan, L.; Li, H.C.; Deng, Y.J.; Zhang, F.; Chen, X.D.; Du, Q. Hyperspectral Dimensionality Reduction by Tensor Sparse and Low-Rank Graph-Based Discriminant Analysis. Remote Sens. 2017, 9, 452. [Google Scholar] [CrossRef]
- Fan, H.; Chen, Y.; Guo, Y.; Zhang, H.; Kuang, G. Hyperspectral Image Restoration Using Low-Rank Tensor Recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4589–4604. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, J.; Tien, D.; Lin, Z.; Hong, X. Tensor LRR and Sparse Coding-Based Subspace Clustering. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 2120–2133. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Qian, J. Hyperspectral Image Classification via Multiscale Joint Collaborative Representation With Locally Adaptive Dictionary. IEEE Geosci. Remote Sens. Lett. 2018, 15, 112–116. [Google Scholar] [CrossRef]
- Yu, H.; Gao, L.; Liao, W.; Zhang, B.; Pizurica, A.; Philips, W.; Yu, H.; Gao, L.; Liao, W.; Zhang, B. Multiscale Superpixel-Level Subspace-Based Support Vector Machines for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, Y.; Feng, C. Spectral Spatial Classification of Hyperspectral Images Using Probabilistic Weighted Strategy for Multifeature Fusion. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1562–1566. [Google Scholar]
- Tong, F.; Tong, H.; Jiang, J.; Zhang, Y. Multiscale Union Regions Adaptive Sparse Representation for Hyperspectral Image Classification. Remote Sens. 2017, 9, 872. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Haut, J.M.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature Extraction With Multiscale Covariance Maps for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1–15. [Google Scholar] [CrossRef]
- Liang, M.; Jiao, L.; Yang, S.; Fang, L.; Hou, B.; Chen, H. Deep Multiscale Spectral-Spatial Feature Fusion for Hyperspectral Images Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1–14. [Google Scholar] [CrossRef]
- Li, H.; Song, Y.; Chen, C.L.P. Hyperspectral Image Classification Based on Multiscale Spatial Information Fusion. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5302–5312. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral Spatial Hyperspectral Image Classification via Multiscale Adaptive Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7738–7749. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Fu, W.; Fang, L. Multiscale Superpixel-Based Sparse Representation for Hyperspectral Image Classification. Remote Sens. 2017, 9, 139. [Google Scholar] [CrossRef]
- Lathauwer, L.D.; Moor, B.D.; Vandewalle, J. On the best rank-1 and rank-(R1, R2,...,RN ) approximation of higher-order tensor. Siam J. Matrix Anal. Appl. 2000, 21, 1324–1342. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: Berlin, Germany, 2010; pp. 41–64. [Google Scholar]



| Class | Original | PCA | LGDA | SGDA | SLGDA | TLRR | TSR | PT-SLG | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | |
| 1 | 73.75 ±10.68 | 67.92 ±12.89 | 63.13 ±10.29 | 59.79 ±10.91 | 65.73 ±12.71 | 65.10 ±7.68 | 84.38 ±10.72 | 83.75 ±9.10 | 79.17 ±8.07 | 77.50 ±5.78 | 83.13 ±10.18 | 80.83 ±7.53 | 93.33 ±4.52 | 95.42 ±4.97 | 96.04 ±4.41 | 94.58 ±4.68 |
| 2 | 83.77 ±1.17 | 63.33 ±1.42 | 76.60 ±2.16 | 62.40 ±3.19 | 76.64 ±2.70 | 67.35 ±3.10 | 91.12 ±1.73 | 91.42 ±1.41 | 90.47 ±1.40 | 86.57 ±1.49 | 90.53 ±1.59 | 90.41 ±1.44 | 94.57 ±1.27 | 94.09 ±1.24 | 96.83 ±1.59 | 98.47 ±0.75 |
| 3 | 78.93 ±2.39 | 62.37 ±1.72 | 66.15 ±3.12 | 57.55 ±2.14 | 64.91 ±2.93 | 62.38 ±2.95 | 88.21 ±5.08 | 89.01 ±3.26 | 83.28 ±1.51 | 74.77 ±2.29 | 84.88 ±2.69 | 86.39 ±1.61 | 91.57 ±3.06 | 92.59 ±3.10 | 97.15 ±1.07 | 97.39 ±1.29 |
| 4 | 70.10 ±7.43 | 46.10 ±7.81 | 50.19 ±5.46 | 44.52 ±3.73 | 74.02 ±8.36 | 44.17 ±5.30 | 87.29 ±3.95 | 87.48 ±4.28 | 77.33 ±5.44 | 76.95 ±4.28 | 86.71 ±6.32 | 86.95 ±3.27 | 90.95 ±2.63 | 87.62 ±5.76 | 98.19 ±1.49 | 97.81 ±2.27 |
| 5 | 94.05 ±1.63 | 91.59 ±2.01 | 88.28 ±2.73 | 87.74 ±2.70 | 91.15 ±2.55 | 88.81 ±2.36 | 96.69 ±2.01 | 96.51 ±2.18 | 93.69 ±2.28 | 93.87 ±3.07 | 96.40 ±2.26 | 95.10 ±2.24 | 94.59 ±3.35 | 95.48 ±3.64 | 96.2 ±1.97 | 95.44 ±1.91 |
| 6 | 96.67 ±1.11 | 94.67 ±1.29 | 94.49 ±1.43 | 93.91 ±1.78 | 95.05 ±2.38 | 94.07 ±1.44 | 95.98 ±3.90 | 96.59 ±3.13 | 96.88 ±2.37 | 93.63 ±2.47 | 99.54 ±0.57 | 99.79 ±0.19 | 98.07 ±1.27 | 97.32 ±1.27 | 99.64 ±0.29 | 99.75 ±0.22 |
| 7 | 78.26 ±10.2 | 83.48 ±7.78 | 77.39 ±10.07 | 82.61 ±7.53 | 78.70 ±14.08 | 75.87 ±14.45 | 99.50 ±1.58 | 99.10 ±2.02 | 83.48 ±3.64 | 76.52 ±10.01 | 87.39 ±8.31 | 85.65 ±10.6 | 88.70 ±16.1 | 77.39 ±16.6 | 90.87 ±7.39 | 93.91 ±7.33 |
| 8 | 98.18 ±0.89 | 98.05 ±0.83 | 97.34 ±1.15 | 96.95 ±1.14 | 98.20 ±0.79 | 98.15 ±0.73 | 97.36 ±3.98 | 97.36 ±3.98 | 99.50 ±0.10 | 99.68 ±0.20 | 99.38 ±1.34 | 99.40 ±1.05 | 99.64 ±0.20 | 99.64 ±0.20 | 99.86 ±0.29 | 99.75 ±0.31 |
| 9 | 72.22 ±17.10 | 57.78 ±9.30 | 20.56 ±9.64 | 23.33 ±13.33 | 50.83 ±21.17 | 41.39 ±18.3 | 36.36 ±24.27 | 39.43 ±31.7 | 61.11 ±25.76 | 66.67 ±23.9 | 83.33 ±23.72 | 91.67 ±9.53 | 78.89 ±14.3 | 82.22 ±17.3 | 90.56 ±23.1 | 80.00 ±14.74 |
| 10 | 78.99 ±2.35 | 74.28 ±2.39 | 76.00 ±1.93 | 70.49 ±2.41 | 67.07 ±5.45 | 75.96 ±3.91 | 92.79 ±3.75 | 92.61 ±3.38 | 82.46 ±3.27 | 73.87 ±3.08 | 86.96 ±2.04 | 92.22 ±1.09 | 92.74 ±1.45 | 94.76 ±0.99 | 95.88 ±2.05 | 96.6 ±1.09 |
| 11 | 84.07 ±1.43 | 77.03 ±2.13 | 83.37 ±1.04 | 75.27 ±0.86 | 84.77 ±2.04 | 78.07 ±1.76 | 98.54 ±1.34 | 98.22 ±1.46 | 88.54 ±1.70 | 88.71 ±0.73 | 89.58 ±1.68 | 94.17 ±0.92 | 95.61 ±1.27 | 96.88 ±1.39 | 98.57 ±0.48 | 99.17 ±0.37 |
| 12 | 84.42 ±2.62 | 58.80 ±4.19 | 66.34 ±3.54 | 53.26 ±2.78 | 75.7 ±5.41 | 58.89 ±3.31 | 80.24 ±5.42 | 81.39 ±3.23 | 88.01 ±4.10 | 76.09 ±3.27 | 91.05 ±2.90 | 90.16 ±2.08 | 94.64 ±2.15 | 94.24 ±1.83 | 95.94 ±1.40 | 95.91 ±2.01 |
| 13 | 99.05 ±0.69 | 98.00 ±1.36 | 96.11 ±2.32 | 96.68 ±1.94 | 98.29 ±2.02 | 97.74 ±1.88 | 94.89 ±8.06 | 94.89 ±8.06 | 99.26 ±0.29 | 98.42 ±0.64 | 99.30 ±1.16 | 98.70 ±1.89 | 97.37 ±2.93 | 96.00 ±4.20 | 100 ±0 | 99.95 ±0.16 |
| 14 | 94.64 ±1.43 | 93.06 ±1.39 | 95.15 ±0.84 | 93.17 ±0.92 | 96.84 ±0.74 | 92.64 ±1.63 | 96.73 ±3.12 | 96.13 ±3.14 | 95.45 ±1.72 | 97.25 ±0.47 | 96.35 ±1.33 | 98.11 ±0.75 | 98.30 ±1.21 | 99.02 ±0.51 | 99.35 ±0.54 | 99.09 ±0.75 |
| 15 | 61.05 ±6.07 | 42.40 ±3.74 | 51.17 ±4.12 | 38.48 ±1.87 | 51.84 ±4.71 | 39.80 ±5.67 | 93.33 ±4.53 | 93.33 ±4.53 | 79.53 ±3.27 | 79.47 ±5.33 | 85.94 ±5.13 | 86.64 ±3.73 | 96.14 ±1.67 | 95.85 ±1.84 | 97.13 ±2.48 | 98.83 ±1.37 |
| 16 | 90.82 ±3.37 | 93.18 ±3.16 | 55.06 ±9.39 | 89.18 ±4.46 | 87.65 ±4.84 | 86.35 ±5.17 | 61.41 ±12.8 | 64.82 ±12.04 | 88.47 ±4.19 | 85.65 ±1.93 | 95.65 ±4.44 | 94.12 ±5.08 | 90.35 ±4.19 | 91.76 ±2.20 | 90.94 ±4.79 | 92.47 ±5.89 |
| OA | 85.67 ±0.37 | 76.12 ±0.69 | 80.35 ±0.43 | 73.87 ±0.21 | 81.72 ±1.01 | 76.59 ±1.23 | 93.43 ±0.66 | 93.54 ±0.74 | 89.53 ±0.39 | 86.78 ±0.59 | 91.57 ±0.47 | 93.39 ±0.45 | 95.31 ±0.65 | 95.76 ±0.54 | 97.78 ±0.44 | 98.22 ±0.25 |
| AA | 83.71 ±0.49 | 75.13 ±1.14 | 72.33 ±1.61 | 70.33 ±1.29 | 78.59 ±2.06 | 72.92 ±2.27 | 86.22 ±2.50 | 87.62 ±2.74 | 86.66 ±1.87 | 84.10 ±1.67 | 91.09 ±1.56 | 91.99 ±1.22 | 93.47 ±2.40 | 93.14 ±2.44 | 96.45 ±1.97 | 96.19 ±1.59 |
| Kappa | 0.85 ±0 | 0.75 ±0.01 | 0.8 ±0 | 0.73 ±0 | 0.81 ±0.01 | 0.76 ±0.01 | 0.93 ±0.01 | 0.93 ±0.01 | 0.89 ±0 | 0.86 ±0.01 | 0.91 ±0 | 0.93 ±0 | 0.95 ±0.01 | 0.96 ±0.01 | 0.98 ±0 | 0.98 ±0 |
| Class | Original | PCA | LGDA | SGDA | SLGDA | TLRR | TSR | PT-SLG | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | |
| 1 | 89.65 ±0.69 | 75.92 ±0.99 | 89.65 ±0.6 | 77.97 ±0.79 | 92.62 ±0.76 | 84.00 ±1.30 | 94.21 ±1.32 | 94.61 ±1.03 | 94.08 ±0.83 | 70.67 ±2.85 | 93.67 ±0.55 | 96.77 ±0.43 | 96.41 ±0.83 | 92.38 ±1.23 | 96.89 ±0.63 | 98.75 ±0.32 |
| 2 | 95.54 ±0.63 | 95.27 ±0.15 | 94.5 ±0.56 | 94.92 ±0.25 | 97.10 ±0.44 | 92.11 ±0.83 | 99.30 ±0.24 | 99.30 ±0.29 | 97.75 ±0.53 | 97.97 ±0.40 | 98.22 ±0.18 | 99.56 ±0.11 | 99.18 ±0.16 | 99.73 ±0.09 | 99.75 ±0.10 | 99.92 ±0.06 |
| 3 | 70.92 ±2.02 | 60.30 ±1.60 | 71.2 ±1.8 | 61.01 ±1.6 | 69.54 ±2.17 | 59.17 ±2.66 | 94.84 ±1.25 | 94.84 ±1.18 | 76.82 ±2.95 | 68.93 ±1.93 | 76.69 ±1.52 | 91.55 ±1.24 | 85.08 ±1.52 | 89.09 ±1.32 | 97.01 ±1.10 | 99.31 ±0.34 |
| 4 | 92.74 ±1.17 | 83.29 ±1.40 | 92.29 ±0.54 | 84.26 ±0.97 | 88.98 ±1.64 | 81.92 ±1.68 | 79.68 ±1.72 | 77.52 ±1.65 | 94.76 ±0.85 | 91.57 ±1.13 | 92.66 ±0.63 | 93.69 ±1.12 | 96.93 ±0.98 | 93.02 ±0.91 | 95.13 ±1.25 | 94.37 ±1.01 |
| 5 | 99.31 ±0.37 | 99.27 ±0.31 | 98.79 ±0.57 | 99.29 ±0.32 | 99.20 ±0.32 | 98.80 ±0.29 | 93.95 ±2.11 | 93.93 ±1.77 | 99.92 ±0.06 | 99.79 ±0.04 | 99.93 ±0.09 | 99.88 ±0.25 | 99.97 ±0.07 | 99.57 ±0.4 | 99.67 ±0.35 | 99.71 ±0.2 |
| 6 | 78.77 ±2.08 | 56.48 ±1.03 | 77.98 ±0.96 | 56.98 ±1.1 | 68.84 ±6.23 | 59.37 ±2.53 | 99.47 ±0.52 | 99.70 ±0.29 | 82.03 ±1.35 | 71.79 ±1.13 | 93.11 ±0.80 | 99.55 ±0.32 | 93.49 ±0.69 | 97.69 ±0.85 | 99.89 ±0.10 | 99.99 ±0.03 |
| 7 | 83.31 ±2.09 | 77.77 ±1.34 | 82.3 ±2.57 | 78.13 ±1.67 | 74.29 ±3.35 | 76.55 ±2.48 | 97.52 ±1.96 | 97.59 ±1.88 | 89.36 ±1.50 | 85.16 ±1.90 | 93.23 ±1.63 | 96.98 ±0.71 | 94.82 ±0.48 | 96.25 ±1.07 | 98.39 ±0.66 | 99.71 ±0.25 |
| 8 | 78.64 ±0.73 | 76.82 ±1.66 | 76.69 ±1.62 | 75.31 ±0.89 | 87.63 ±1.39 | 77.32 ±1.86 | 92.72 ±1.26 | 92.69 ±1.23 | 87.14 ±1.83 | 81.01 ±2.39 | 81.16 ±1.64 | 87.88 ±1.13 | 89.42 ±2.29 | 89.7 ±1.35 | 92.21 ±1.43 | 96.74 ±0.85 |
| 9 | 98.94 ±0.35 | 92.03 ±1.14 | 99.11 ±0.21 | 93.69 ±1.08 | 98.83 ±0.53 | 97.58 ±1.24 | 75.61 ±3.93 | 76.98 ±3.37 | 91.09 ±2.24 | 61.86 ±4.89 | 95.64 ±0.85 | 96.88 ±0.72 | 96.45 ±1.85 | 76.22 ±4.09 | 92.51 ±1.47 | 91.33 ±1.93 |
| OA | 89.54 ±0.25 | 82.93 ±0.37 | 88.78 ±0.34 | 83.19 ±0.2 | 89.67 ±0.80 | 83.14 ±0.84 | 94.41 ±0.21 | 95.36 ±0.23 | 92.78 ±0.95 | 86.03 ±1.21 | 93.73 ±0.11 | 97.10 ±0.13 | 96.17 ±0.22 | 95.74 ±0.43 | 97.94 ±0.21 | 98.79 ±0.14 |
| AA | 87.53 ±0.57 | 79.68 ±0.49 | 86.95 ±0.5 | 80.17 ±0.23 | 86.34 ±0.88 | 80.76 ±0.91 | 92.06 ±0.61 | 91.91 ±0.66 | 90.33 ±1.14 | 80.97 ±1.30 | 91.59 ±0.30 | 95.86 ±0.18 | 94.64 ±0.24 | 92.63 ±0.73 | 96.83 ±0.33 | 97.76 ±0.27 |
| Kappa | 0.88 ±0 | 0.80 ±0 | 0.87 ±0 | 0.8 ±0 | 0.88 ±0.01 | 0.80 ±0.01 | 0.95 ±0 | 0.95 ±0 | 0.91 ±0.01 | 0.83 ±0.03 | 0.93 ±0 | 0.97 ±0 | 0.95 ±0 | 0.95 ±0.01 | 0.98 ±0 | 0.99 ±0 |
| Class | Original | PCA | LGDA | SGDA | SLGDA | TLRR | TSR | PT-SLG | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | SVM | 1NN | |
| 1 | 99.57 ±0.30 | 99.36 ±0.38 | 99.24 ±0.7 | 99.18 ±0.51 | 99.28 ±0.33 | 98.34 ±0.44 | 99.12 ±0.86 | 99.04 ±0.84 | 99.93 ±0.15 | 99.88 ±0.21 | 99.88 ±0.18 | 99.82 ±0.19 | 99.98 ±0.05 | 99.93 ±0.09 | 100 ±0 | 100 ±0 |
| 2 | 99.67 ±0.26 | 99.18 ±0.15 | 99.7 ±0.21 | 99.33 ±0.23 | 99.85 ±0.16 | 99.66 ±0.18 | 99.37 ±0.62 | 99.36 ±0.62 | 100 ±0 | 99.99 ±0.02 | 99.90 ±0.22 | 99.89 ±0.31 | 100 ±0 | 100 ±0 | 100 ±0 | 100 ±0 |
| 3 | 99.71 ±0.26 | 98.14 ±0.41 | 99.43 ±0.48 | 97.76 ±0.74 | 99.31 ±0.29 | 97.36 ±0.82 | 98.93 ±0.70 | 99.13 ±0.76 | 99.99 ±0.03 | 99.89 ±0.11 | 99.94 ±0.09 | 99.87 ±0.15 | 99.99 ±0.03 | 100 ±0 | 99.98 ±0.05 | 99.98 ±0.04 |
| 4 | 99.25 ±0.60 | 99.49 ±0.27 | 99 ±0.68 | 99.38 ±0.27 | 99.37 ±0.24 | 99.09 ±0.47 | 93.62 ±2.07 | 94.12 ±1.76 | 98.87 ±0.37 | 98.68 ±0.43 | 97.20 ±1.13 | 98.41 ±0.50 | 98.28 ±1.19 | 98.92 ±0.42 | 98.51 ±0.72 | 98.87 ±0.57 |
| 5 | 99.18 ±0.45 | 97.16 ±0.75 | 99.21 ±0.23 | 97.15 ±0.59 | 98.95 ±0.34 | 97.95 ±0.43 | 95.31 ±1.04 | 96.28 ±0.74 | 99.37 ±0.42 | 99.25 ±0.18 | 98.49 ±0.34 | 99.17 ±0.30 | 98.76 ±0.64 | 98.84 ±0.44 | 99.51 ±0.28 | 99.29 ±0.3 |
| 6 | 99.87 ±0.16 | 99.84 ±0.19 | 99.74 ±0.21 | 99.67 ±0.16 | 99.91 ±0.08 | 99.86 ±0.10 | 97.14 ±0.76 | 97.21 ±0.79 | 99.99 ±0.01 | 99.99 ±0.02 | 99.98 ±0.01 | 99.95 ±0.03 | 99.65 ±0.12 | 99.58 ±0.19 | 99.97 ±0.04 | 99.95 ±0.07 |
| 7 | 99.80 ±0.13 | 99.59 ±0.06 | 99.62 ±0.17 | 99.42 ±0.15 | 99.72 ±0.19 | 99.57 ±0.14 | 97.78 ±0.51 | 97.44 ±0.69 | 99.94 ±0.09 | 99.95 ±0.06 | 100 ±0.01 | 100 ±0.01 | 99.94 ±0.06 | 99.98 ±0.03 | 99.98 ±0.03 | 99.95 ±0.07 |
| 8 | 84.26 ±0.90 | 78.34 ±0.95 | 86.9 ±0.96 | 77.92 ±0.79 | 89.90 ±0.76 | 71.82 ±0.94 | 99.23 ±0.25 | 99.24 ±0.33 | 95.27 ±0.76 | 94.58 ±1.39 | 92.65 ±0.95 | 93.89 ±0.40 | 98.39 ±0.66 | 99.14 ±0.30 | 99.63 ±0.19 | 99.9 ±0.04 |
| 9 | 99.84 ±0.22 | 99.24 ±0.27 | 99.55 ±0.3 | 99.19 ±0.15 | 99.82 ±0.23 | 99.20 ±0.38 | 99.64 ±0.20 | 99.59 ±0.26 | 99.92 ±0.09 | 99.98 ±0.02 | 99.72 ±0.22 | 99.93 ±0.03 | 99.99 ±0.02 | 99.99 ±0.02 | 99.91 ±0.16 | 99.98 ±0.04 |
| 10 | 96.89 ±0.77 | 94.43 ±0.69 | 96.99 ±0.72 | 94.94 ±0.66 | 94.72 ±0.75 | 91.15 ±0.87 | 97.45 ±1.39 | 97.54 ±0.81 | 98.49 ±0.47 | 98.70 ±0.22 | 99.31 ±0.32 | 99.09 ±0.26 | 99.44 ±0.22 | 99.52 ±0.13 | 99.34 ±0.33 | 99.71 ±0.21 |
| 11 | 99.23 ±0.26 | 98.88 ±0.40 | 98.87 ±0.92 | 98.69 ±0.75 | 97.48 ±1.48 | 94.56 ±1.43 | 95.56 ±3.82 | 94.64 ±2.83 | 99.83 ±0.17 | 99.83 ±0.12 | 99.75 ±0.11 | 99.35 ±0.30 | 99.19 ±0.55 | 99.38 ±0.88 | 99.46 ±0.42 | 99.49 ±0.27 |
| 12 | 99.87 ±0.22 | 99.75 ±0.21 | 99.9 ±0.14 | 99.91 ±0.08 | 99.79 ±0.14 | 98.98 ±0.36 | 94.98 ±1.19 | 95.32 ±1.52 | 99.94 ±0.06 | 99.82 ±0.13 | 99.88 ±0.09 | 99.61 ±0.22 | 99.61 ±0.16 | 99.54 ±0.14 | 99.46 ±0.38 | 99.6 ±0.34 |
| 13 | 99.22 ±0.82 | 98.03 ±0.50 | 99.09 ±0.9 | 98.24 ±0.76 | 98.95 ±0.51 | 97.75 ±0.64 | 85.80 ±4.88 | 87.40 ±4.59 | 99.83 ±0.25 | 99.68 ±0.32 | 99.31 ±0.38 | 98.93 ±0.29 | 97.67 ±1.79 | 97.48 ±1.65 | 99.3 ±0.44 | 99.47 ±0.49 |
| 14 | 98.07 ±0.66 | 94.77 ±0.68 | 98.22 ±0.62 | 95.38 ±1.13 | 96.01 ±0.94 | 93.57 ±0.92 | 87.32 ±4.20 | 84.69 ±5.51 | 98.40 ±0.55 | 98.57 ±0.57 | 99.14 ±0.44 | 98.61 ±0.72 | 97.78 ±0.63 | 98.15 ±1.15 | 97.91 ±0.76 | 98.9 ±0.55 |
| 15 | 75.59 ±1.19 | 68.38 ±0.78 | 78.81 ±0.95 | 67.73 ±0.51 | 58.84 ±2.84 | 58.25 ±1.49 | 99.08 ±0.33 | 98.87 ±0.34 | 88.64 ±0.26 | 91.31 ±1.90 | 81.07 ±0.94 | 92.37 ±0.55 | 96.26 ±0.71 | 98.92 ±0.41 | 99.73 ±0.12 | 99.86 ±0.08 |
| 16 | 98.51 ±0.28 | 98.27 ±0.35 | 98.94 ±0.44 | 98.46 ±0.42 | 98.98 ±0.46 | 97.44 ±0.69 | 98.97 ±0.68 | 98.75 ±0.89 | 99.47 ±0.49 | 99.45 ±0.47 | 99.42 ±0.50 | 99.31 ±0.38 | 100 ±0 | 99.94 ±0.06 | 100 ±0 | 100 ±0 |
| OA | 92.98 ±0.23 | 90.25 ±0.24 | 93.9 ±0.24 | 90.09 ±0.24 | 91.69 ±0.51 | 87.16 ±0.33 | 97.86 ±0.16 | 97.84 ±0.21 | 97.27 ±0.20 | 97.48 ±0.54 | 95.64 ±0.11 | 97.45 ±0.08 | 98.88 ±0.14 | 99.42 ±0.08 | 99.69 ±0.04 | 99.81 ±0.03 |
| AA | 96.78 ±0.11 | 95.18 ±0.14 | 97.08 ±0.13 | 95.15 ±0.15 | 95.68 ±0.29 | 93.41 ±0.23 | 96.21 ±0.42 | 96.16 ±0.47 | 98.62 ±0.09 | 98.72 ±0.21 | 97.86 ±0.08 | 98.64 ±0.06 | 99.06 ±0.11 | 99.33 ±0.21 | 99.54 ±0.05 | 99.68 ±0.07 |
| Kappa | 0.93 ±0 | 0.90 ±0 | 0.94 ±0 | 0.9 ±0 | 0.92 ±0.01 | 0.87 ±0 | 0.98 ±0 | 0.98 ±0 | 0.97 ±0 | 0.97 ±0.01 | 0.96 ±0 | 0.97 ±0 | 0.99 ±0 | 0.99 ±0 | 1 ±0 | 1 ±0 |
| Original | PCA | LGDA | GTLR | TLRR | LRTA | T-LGMR | T-LMRD | |
|---|---|---|---|---|---|---|---|---|
| Indian Pines | 1.89 | 1.04 | 1.02 | 3.25 | 37.23 | 2.72 | 41.41 | 3.8 |
| Pavia University | 10.05 | 5.45 | 5.57 | 10.36 | 13.29 | 5.69 | 17.17 | 16.21 |
| Salinas | 18.02 | 7.05 | 7.12 | 13.71 | 34.74 | 9.14 | 39.24 | 18.01 |
| No. | Scale1 | Scale2 | Scale3 | No. | Scale1 | Scale2 | Scale3 | No. | Scale1 | Scale2 | Scale3 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.005 | 0.03 | 0.08 | 10 | 0.01 | 0.03 | 0.08 | 19 | 0.015 | 0.03 | 0.08 |
| 2 | 0.005 | 0.03 | 0.1 | 11 | 0.01 | 0.03 | 0.1 | 20 | 0.015 | 0.03 | 0.1 |
| 3 | 0.005 | 0.03 | 0.12 | 12 | 0.01 | 0.03 | 0.12 | 21 | 0.015 | 0.03 | 0.12 |
| 4 | 0.005 | 0.05 | 0.08 | 13 | 0.01 | 0.05 | 0.08 | 22 | 0.015 | 0.05 | 0.08 |
| 5 | 0.005 | 0.05 | 0.1 | 14 | 0.01 | 0.05 | 0.1 | 23 | 0.015 | 0.05 | 0.1 |
| 6 | 0.005 | 0.05 | 0.12 | 15 | 0.01 | 0.05 | 0.12 | 24 | 0.015 | 0.05 | 0.12 |
| 7 | 0.005 | 0.07 | 0.08 | 16 | 0.01 | 0.07 | 0.08 | 25 | 0.015 | 0.07 | 0.08 |
| 8 | 0.005 | 0.07 | 0.1 | 17 | 0.01 | 0.07 | 0.1 | 26 | 0.015 | 0.07 | 0.1 |
| 9 | 0.005 | 0.07 | 0.12 | 18 | 0.01 | 0.07 | 0.12 | 27 | 0.015 | 0.07 | 0.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, J.; Lei, J.; Song, Y.; Zhang, X.; Guo, J. Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction. Remote Sens. 2019, 11, 1485. https://doi.org/10.3390/rs11121485
An J, Lei J, Song Y, Zhang X, Guo J. Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction. Remote Sensing. 2019; 11(12):1485. https://doi.org/10.3390/rs11121485
Chicago/Turabian StyleAn, Jinliang, Jinhui Lei, Yuzhen Song, Xiangrong Zhang, and Jinmei Guo. 2019. "Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction" Remote Sensing 11, no. 12: 1485. https://doi.org/10.3390/rs11121485
APA StyleAn, J., Lei, J., Song, Y., Zhang, X., & Guo, J. (2019). Tensor Based Multiscale Low Rank Decomposition for Hyperspectral Images Dimensionality Reduction. Remote Sensing, 11(12), 1485. https://doi.org/10.3390/rs11121485





