Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds
Abstract
1. Introduction
2. Materials and Methods
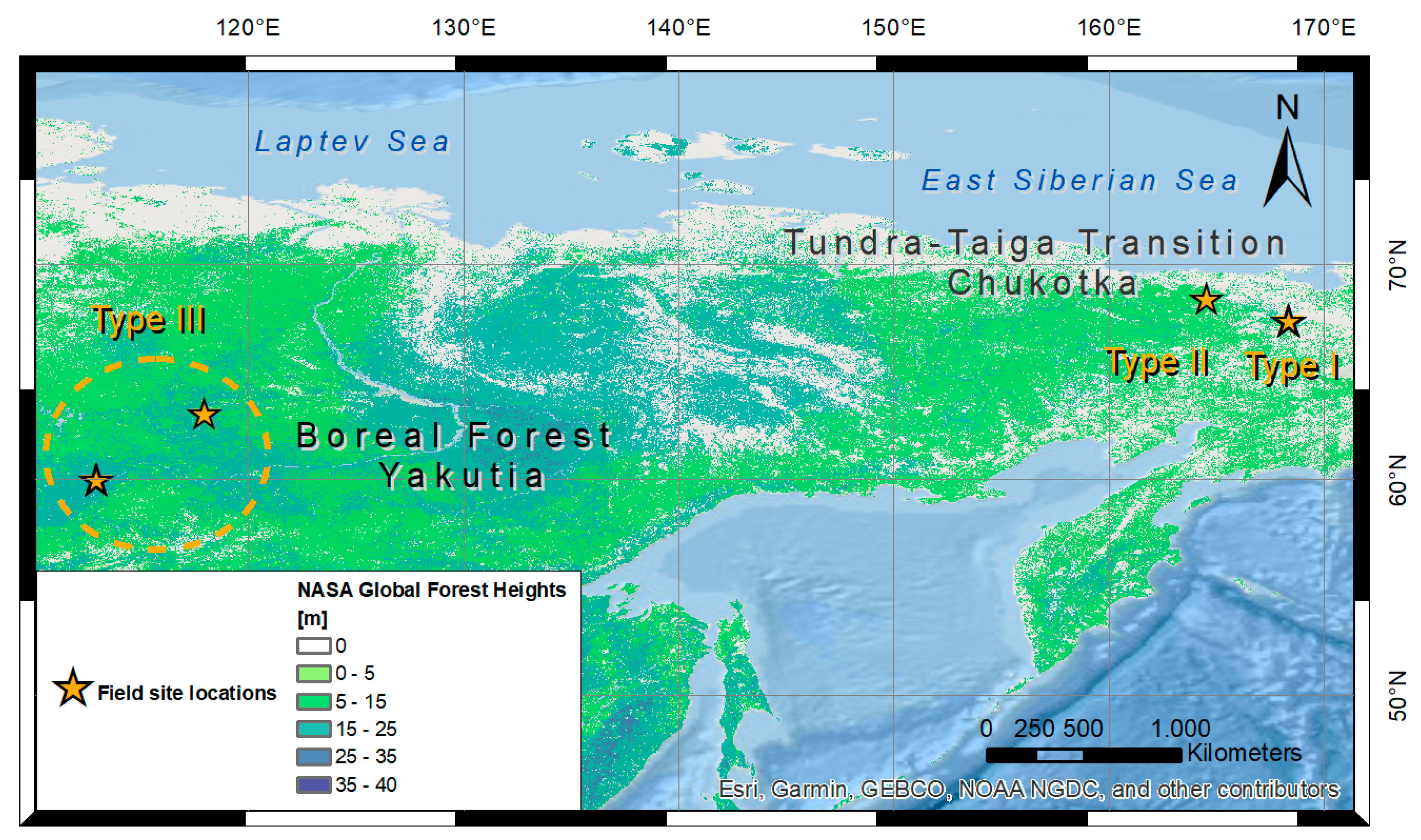
2.1. Study Sites
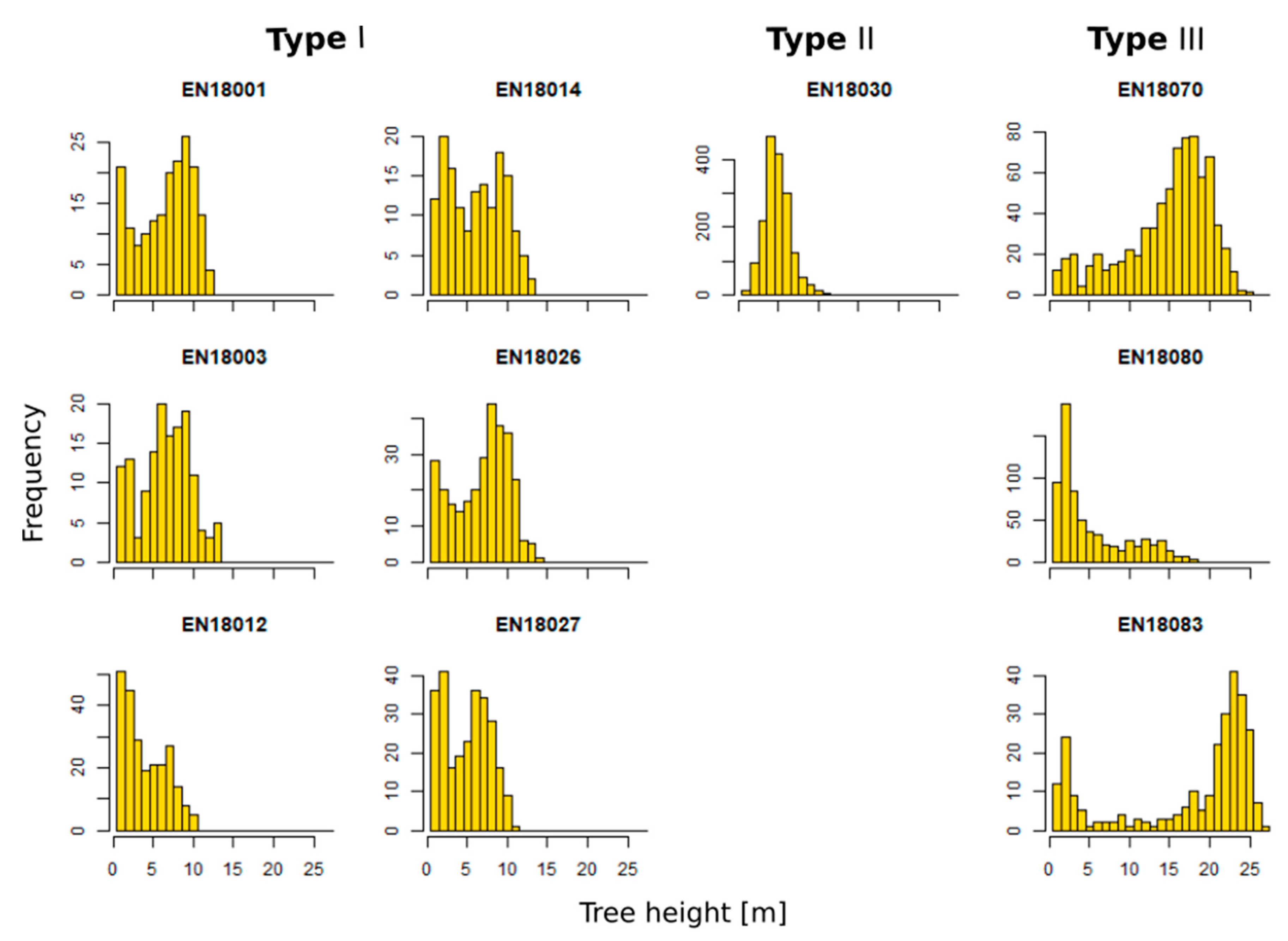
2.1.1. Type I: Open, Larch Dominated Stands
2.1.2. Type II: Dense, Larch Dominated Stands
2.1.3. Type III: Dense, Mixed Tree Species Stands
2.2. Data Acquisition
2.3. Ground Classification and the Derivation of Digital Elevation Models
2.4. Individual Tree Detection and Crown Segmentation
2.5. Forest Stand Metric Derivation
2.6. Validation
3. Results
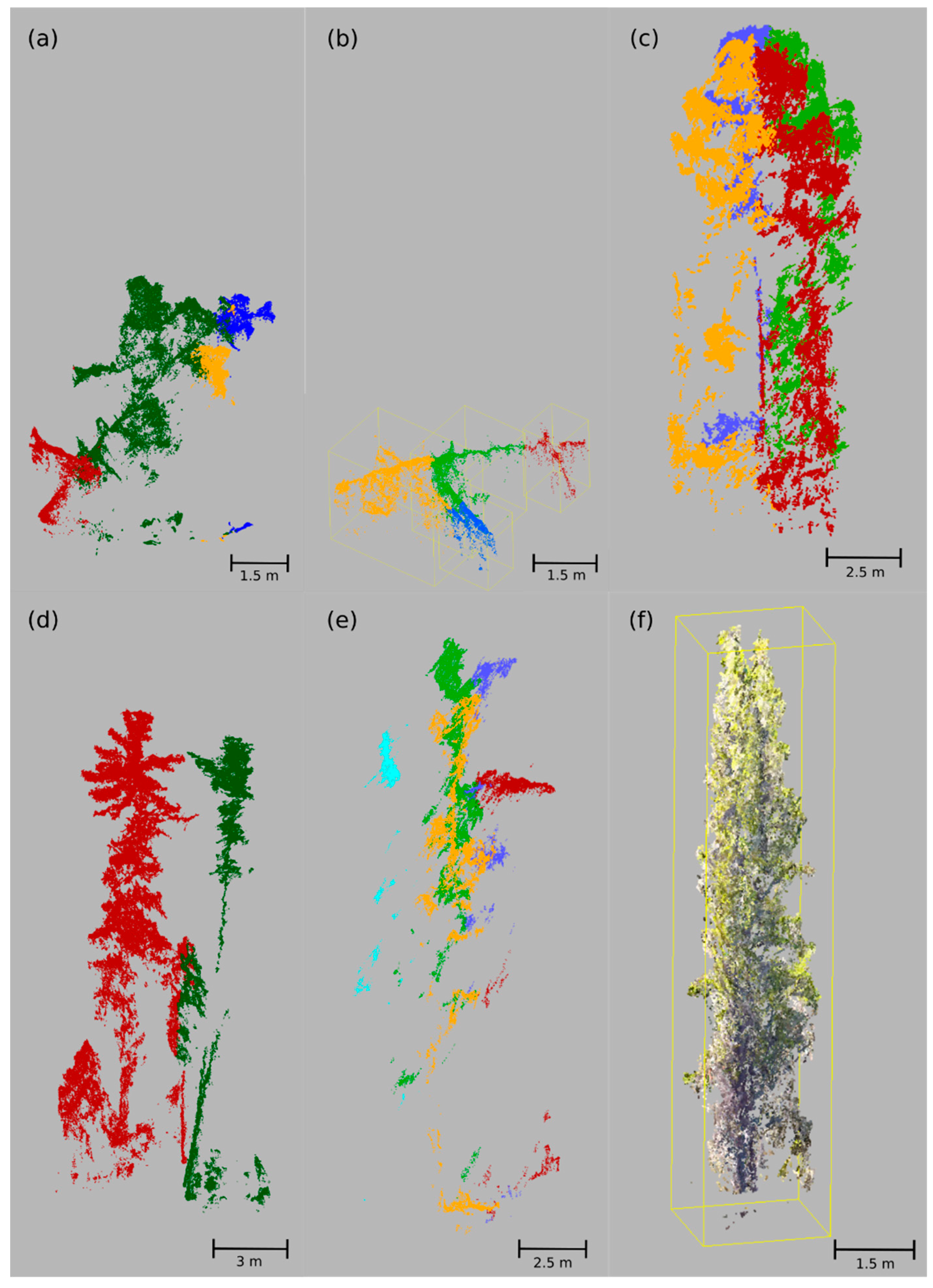
3.1. Point Cloud Reconstruction and Individual Tree Detection
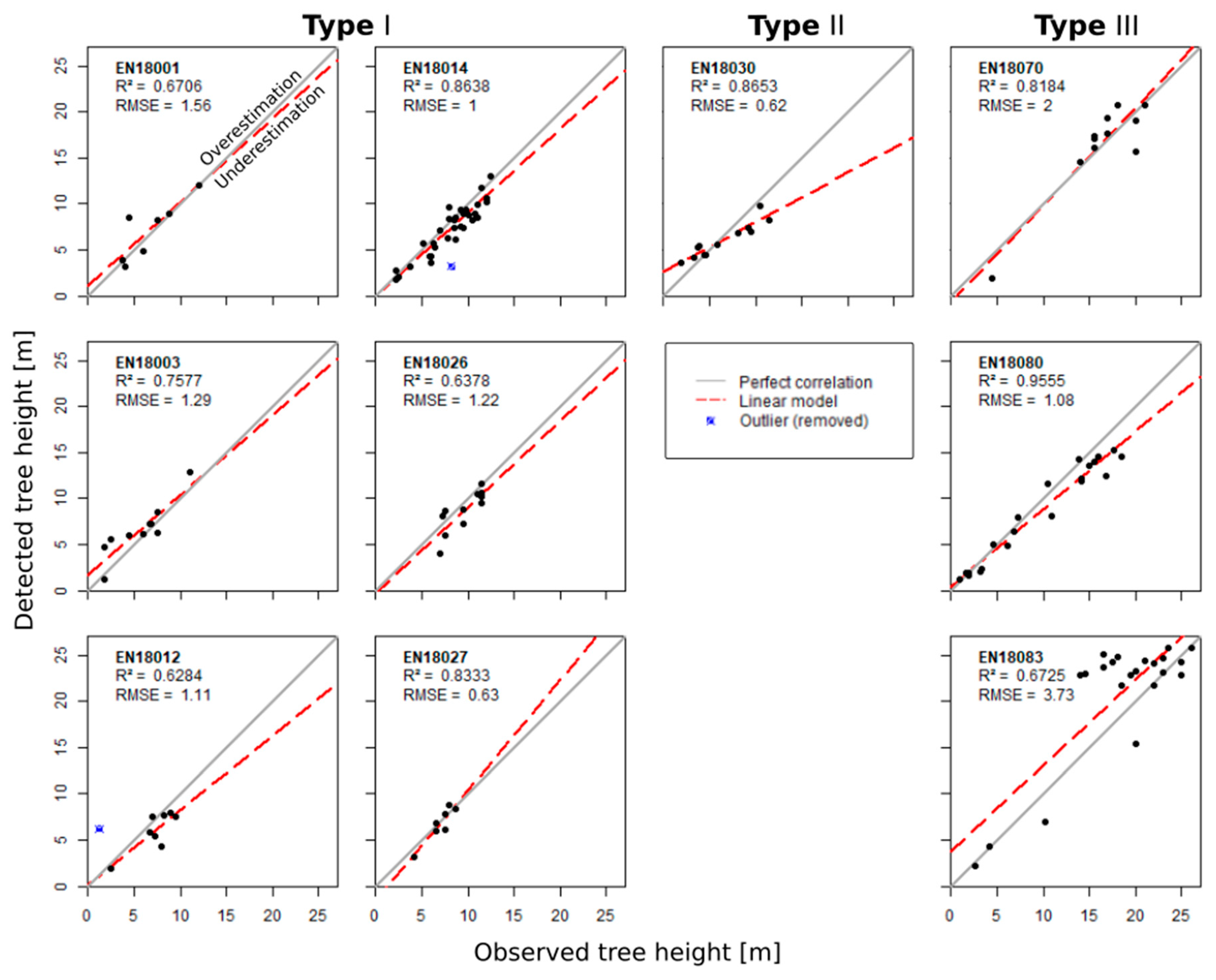
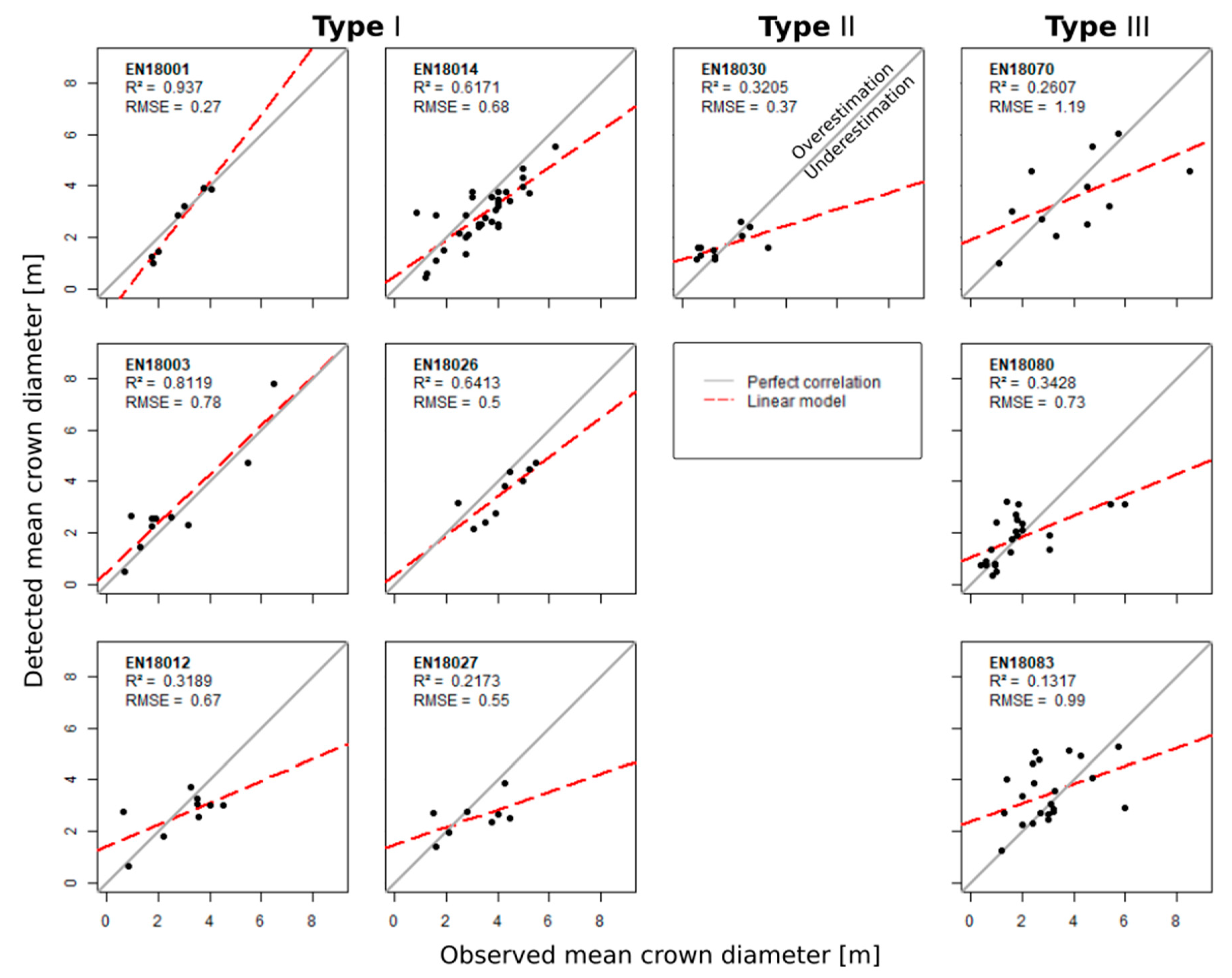
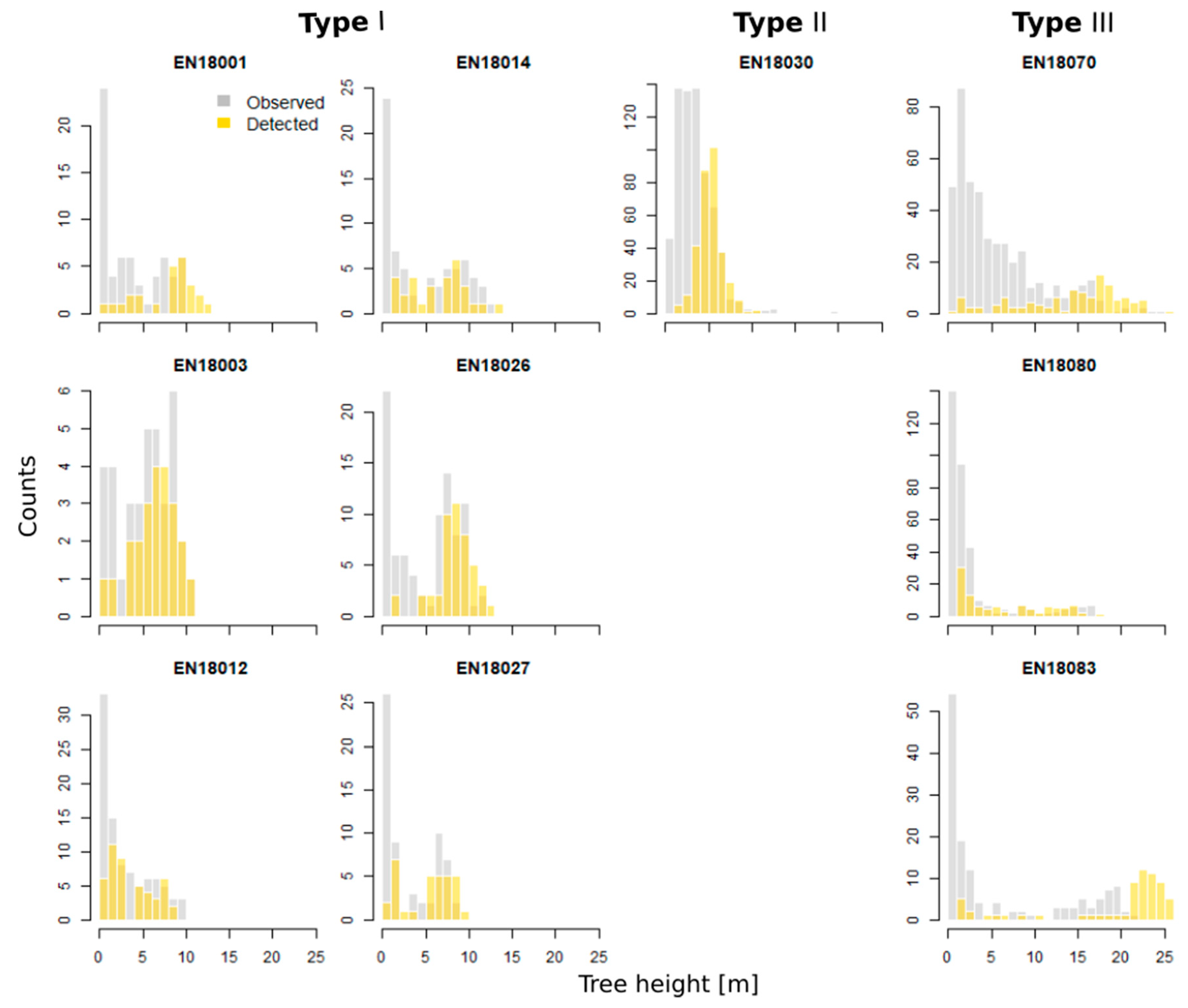
3.2. Validation of Individual Tree Characteristics
3.3. Validation of the Stand Structure
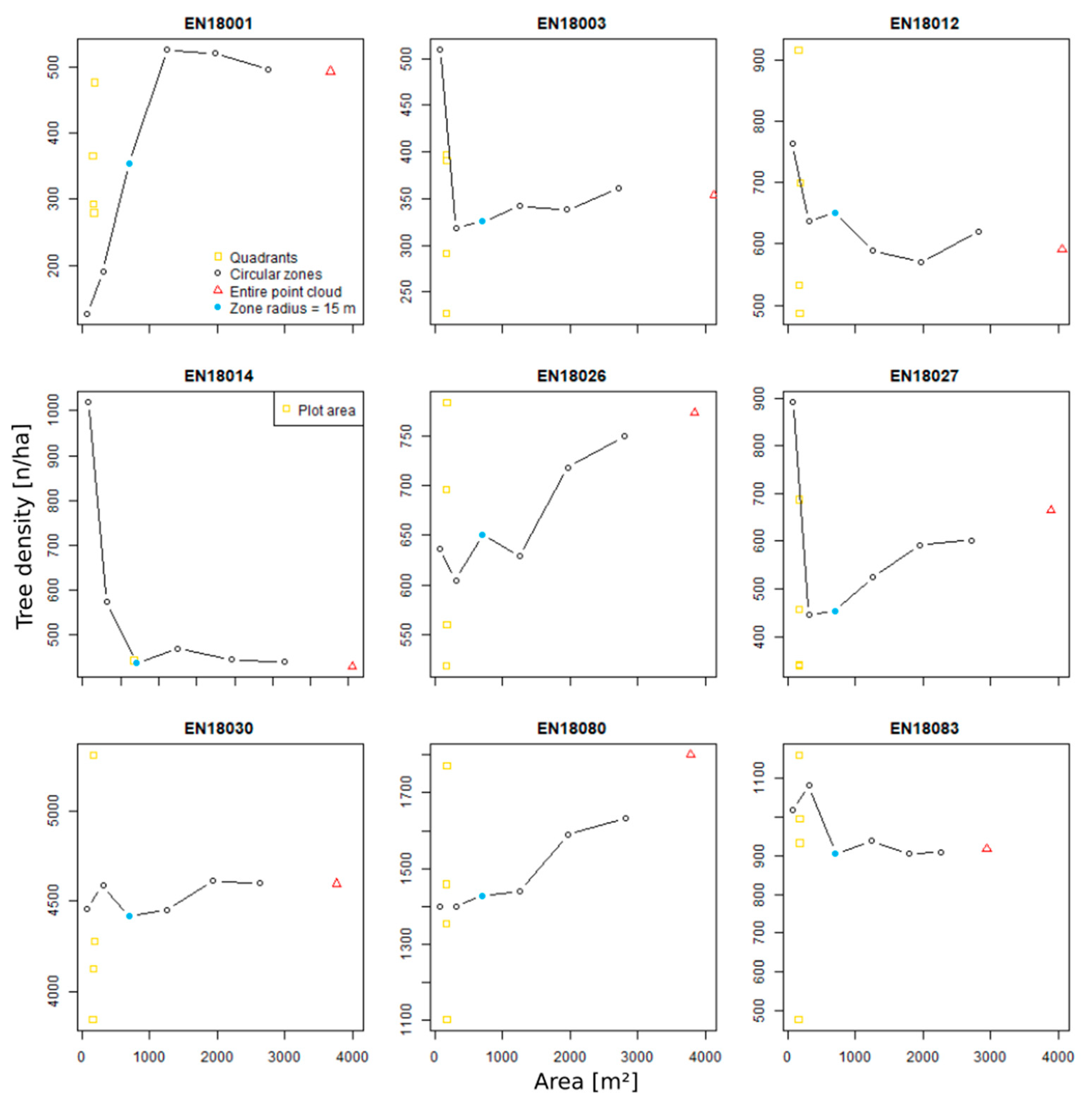
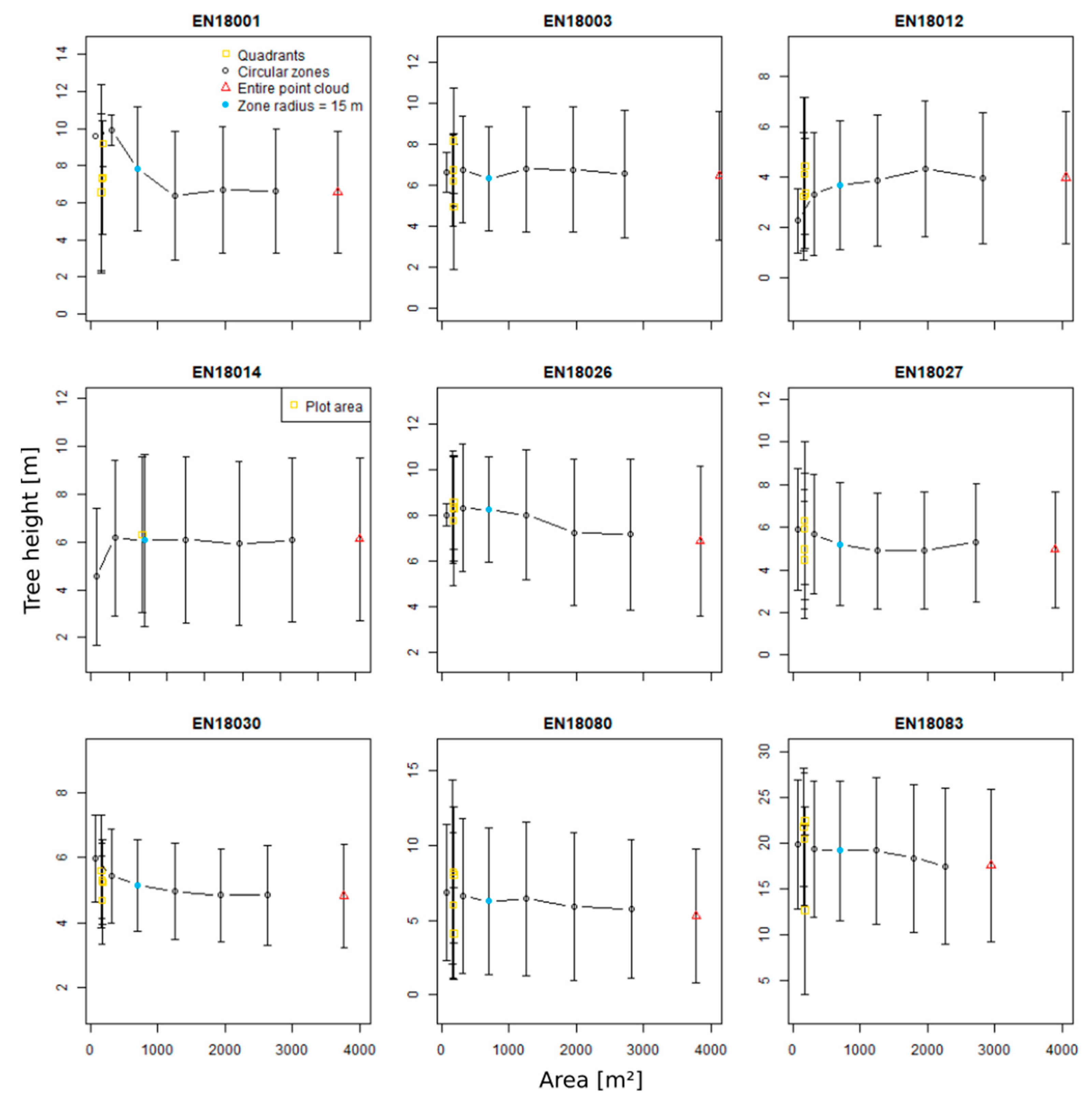
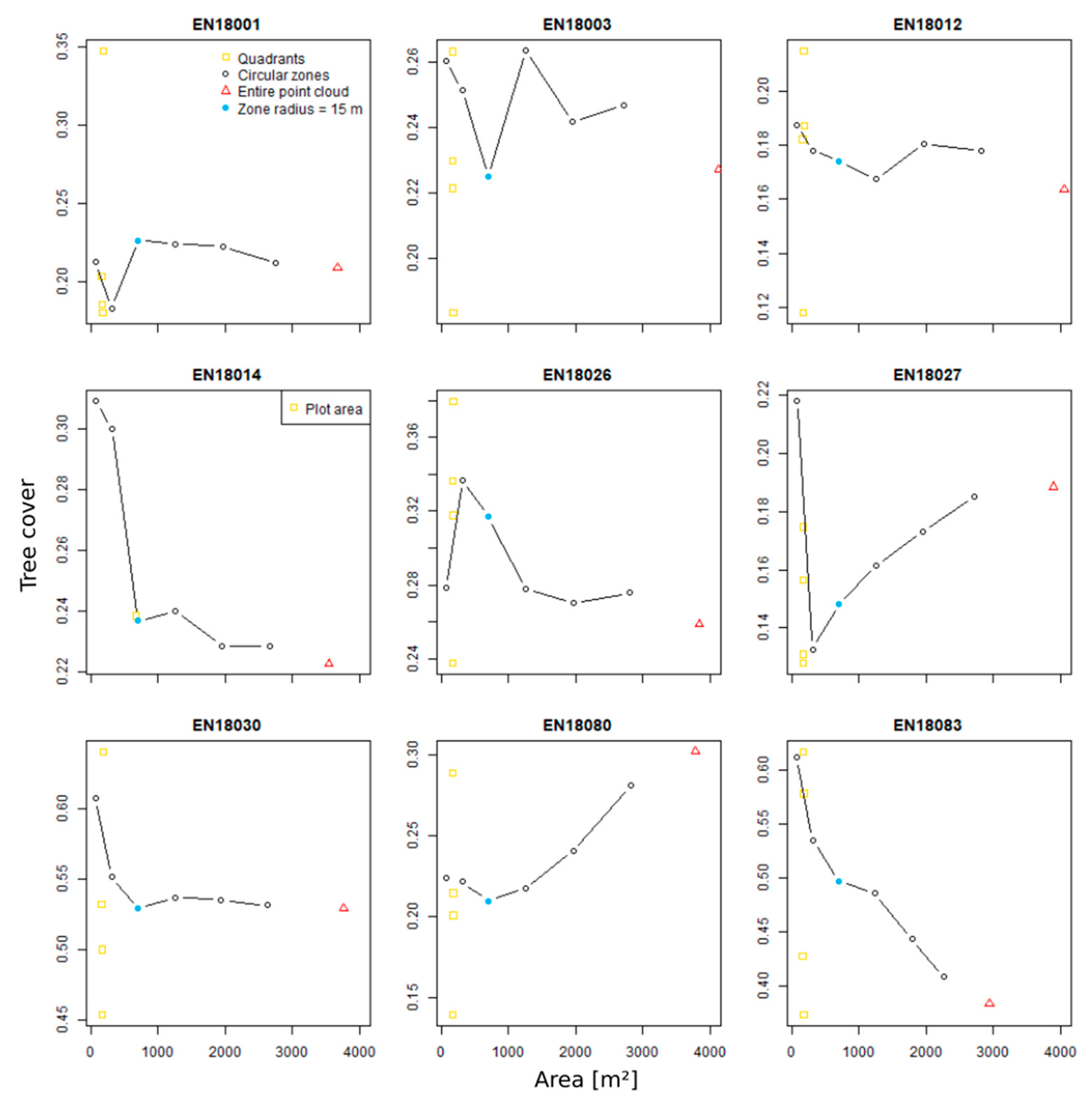
3.4. Zonal Homogeneity Analysis
4. Discussion
4.1. Methodology Applicability for Various Forest Structures
4.2. Challenges in the Tree Segmentation Based on Canopy Height Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Site | No | W (cm) | H (cm) | Wdiff (cm) | Hdiff (cm) |
|---|---|---|---|---|---|
| EN18001 | 1 | 23.9 | 29.3 | −0.4 | 2.9 |
| EN18001 | 2 | 21.2 | 31.2 | 1.5 | 0.2 |
| EN18001 | 3 | 21.9 | 28.8 | −0.9 | 0.9 |
| EN18003 | 1 | 22.4 | 30.4 | 0.7 | 1.4 |
| EN18003 | 2 | 20.9 | 30.1 | 0.4 | −0.1 |
| EN18003 | 3 | 23 | 30.4 | 0.7 | 2 |
| EN18012 | 1 | 20.3 | 30.4 | 0.7 | −0.7 |
| EN18012 | 2 | 21.5 | 30.4 | 0.7 | 0.5 |
| EN18012 | 3 | 20.9 | 29.2 | −0.5 | −0.1 |
| EN18014 | 1 | 22.5 | 30.3 | 0.6 | 1.5 |
| EN18014 | 2 | 21.8 | 30.7 | 1 | 0.8 |
| EN18014 | 3 | 22 | 30.9 | 1.2 | 1 |
| EN18026 | 1 | 21.4 | 27.7 | −2 | 0.4 |
| EN18026 | 2 | 21.1 | 30.3 | 0.6 | 0.1 |
| EN18026 | 3 | 21.4 | 28.7 | −1 | 0.4 |
| EN18027 | 1 | 21 | 29 | −0.7 | 0 |
| EN18027 | 2 | 23.3 | 29.5 | −0.2 | 2.3 |
| EN18027 | 3 | 21.2 | 31.2 | 1.5 | 0.2 |
| EN18030 | 1 | 20.2 | 29.6 | −0.1 | −0.8 |
| EN18030 | 2 | 20.2 | 29.7 | 0 | −0.8 |
| EN18030 | 3 | 20.7 | 30.6 | 0.9 | −0.3 |
| EN18070 | 1 | 22.6 | 30.7 | 1 | 1.6 |
| EN18070 | 2 | 23.2 | 32.1 | 2.4 | 2.2 |
| EN18070 | 3 | 21.2 | 29.7 | 0 | 0.2 |
| EN18080 | 1 | 21.3 | 28.6 | −1.1 | 0.3 |
| EN18080 | 2 | 22.6 | 30.4 | 0.7 | 1.6 |
| EN18080 | 3 | 20.4 | 30.8 | 1.1 | −0.6 |
| EN18083 | 1 | 22.2 | 31.2 | 1.5 | 1.2 |
| EN18083 | 2 | 23 | 26 | −3.7 | 2 |
| EN18083 | 3 | 22.4 | 32.5 | 2.8 | 1.4 |
| MeanDiff | SD | ||||
| 0.51833333 | 1.15057836 |
References
- Holland, M.M.; Bitz, C.M. Polar amplification of climate change in coupled models. Clim. Dyn. 2003, 21, 221–232. [Google Scholar] [CrossRef]
- Bekryaev, R.V.; Polyakov, I.V.; Alexeev, V.A. Role of polar amplification in long-term surface air temperature variations and modern arctic warming. J. Clim. 2010, 23, 3888–3906. [Google Scholar] [CrossRef]
- Snyder, P.K.; Delire, C.; Foley, J.A. Evaluating the influence of different vegetation biomes on the global climate. Clim. Dyn. 2004, 23, 279–302. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Ranson, K.J.; Montesano, P.M.; Nelson, R. Object-based mapping of the circumpolar taiga-tundra ecotone with MODIS tree cover. Remote Sens. Environ. 2011, 115, 3670–3680. [Google Scholar] [CrossRef]
- Kravtsova, V.I.; Tutubalina, O.V.; Hofgaard, A. Aerospace Mapping of the Status and Position of Northern Forest Limit. Geogr. Environ. Sustain. 2012, 5, 28–47. [Google Scholar] [CrossRef]
- Frost, G.V.; Epstein, H.E. Tall shrub and tree expansion in Siberian tundra ecotones since the 1960s. Glob. Chang. Biol. 2014, 20, 1264–1277. [Google Scholar] [CrossRef]
- Wieczorek, M.; Kruse, S.; Epp, L.S.; Kolmogorov, A.; Nikolaev, A.N.; Heinrich, I.; Jeltsch, F.; Pestryakova, L.A.; Zibulski, R.; Herzschuh, U. Dissimilar responses of larch stands in northern Siberia to increasing temperatures—A field and simulation based study. Ecology 2017, 98, 2343–2355. [Google Scholar] [CrossRef]
- Kruse, S.; Wieczorek, M.; Jeltsch, F.; Herzschuh, U. Treeline dynamics in Siberia under changing climates as inferred from an individual-based model for Larix. Ecol. Modell. 2016, 338, 101–121. [Google Scholar] [CrossRef]
- Kruse, S.; Gerdes, A.; Kath, N.J.; Epp, L.S.; Stoof-Leichsenring, K.R.; Pestryakova, L.A.; Herzschuh, U. Dispersal distances and migration rates at the arctic treeline in Siberia; a genetic and simulation based study. Biogeosciences 2019, 16, 1211–1224. [Google Scholar] [CrossRef]
- Grace, J.; Berninger, F.; Nagy, L. Impacts of climate change on the tree line. Ann. Bot. 2002, 90, 537–544. [Google Scholar] [CrossRef] [PubMed]
- Ranson, K.J.; Sun, G.; Kharuk, V.I.; Kovacs, K. Assessing tundra-taiga boundary with multi-sensor satellite data. Remote Sens. Environ. 2004, 93, 283–295. [Google Scholar] [CrossRef]
- Mathisen, I.E.; Mikheeva, A.; Tutubalina, O.V.; Aune, S.; Hofgaard, A. Fifty years of tree line change in the Khibiny Mountains, Russia: Advantages of combined remote sensing and dendroecological approaches. Appl. Veg. Sci. 2014, 17, 6–16. [Google Scholar] [CrossRef]
- Montesano, P.M.; Neigh, C.S.R.; Sexton, J.; Feng, M.; Channan, S.; Ranson, K.J.; Townshend, J.R. Calibration and Validation of Landsat Tree Cover in the Taiga-Tundra Ecotone. Remote Sens. 2016, 8, 551. [Google Scholar] [CrossRef]
- Mikheeva, A.I.; Tutubalina, O.V.; Zimin, M.V.; Golubeva, E.I. A Subpixel Classification of Multispectral Satellite Imagery for Interpetation of Tundra-Taiga Ecotone Vegetation (Case Study on Tuliok River Valley, Khibiny, Russia). Izv. Atmos. Ocean. Phys. 2017, 53, 1164–1173. [Google Scholar] [CrossRef]
- Nilsson, M. Estimation of tree heights and stand volume using an airborne lidar system. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Rees, W.G. Characterisation of Arctic treelines by LiDAR and multispectral imagery. Polar Rec. (Gr. Br.) 2007, 43, 345–352. [Google Scholar] [CrossRef]
- Edson, C.; Wing, M.G. Airborne light detection and ranging (LiDAR) for individual tree stem location, height, and biomass measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Plowright, A. Extracting Trees in An Urban Environment Using Airborne LiDAR. Doctoral Dissertation, University of British Columbia Library, Vancouver, BC, Canada, 2015. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; McFadden, J.P.; Sun, A.; Roberts, D.A. Mapping urban forest leaf area index with airborne lidar using penetration metrics and allometry. Remote Sens. Environ. 2015, 162, 141–153. [Google Scholar] [CrossRef]
- Baguskas, S.A.; Peterson, S.H.; Bookhagen, B.; Still, C.J. Evaluating spatial patterns of drought-induced tree mortality in a coastal California pine forest. For. Ecol. Manag. 2014, 315, 43–53. [Google Scholar] [CrossRef]
- Mathews, A.J.; Jensen, J.L.R. Visualizing and quantifying vineyard canopy LAI using an unmanned aerial vehicle (UAV) collected high density structure from motion point cloud. Remote Sens. 2013, 5, 2164–2183. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Fraser, R.H.; Olthof, I.; Lantz, T.C.; Schmitt, C. UAV photogrammetry for mapping vegetation in the low-Arctic. Arct. Sci. 2016, 2, 79–102. [Google Scholar] [CrossRef]
- Jensen, J.L.R.; Mathews, A.J. Assessment of image-based point cloud products to generate a bare earth surface and estimate canopy heights in a woodland ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Frey, J.; Kovach, K.; Stemmler, S.; Koch, B. UAV Photogrammetry of Forests as a Vulnerable Process. A Sensitivity Analysis for a Structure from Motion RGB-Image Pipeline. Remote Sens. 2018, 10, 912. [Google Scholar] [CrossRef]
- Bohlin, J.; Wallerman, J.; Fransson, J.E.S. Forest variable estimation using photogrammetric matching of digital aerial images in combination with a high-resolution DEM. Scand. J. For. Res. 2012, 27, 692–699. [Google Scholar] [CrossRef]
- Fritz, A.; Kattenborn, T.; Koch, B. UAV-based photogrammetric point clouds—Tree stem Mapping in open stands in Comparison to Terrestrial Laser Scanner Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2013, XL-1/W2, 141–146. [Google Scholar] [CrossRef]
- St-Onge, B.; Audet, F.A.; Bégin, J. Characterizing the height structure and composition of a boreal forest using an individual tree crown approach applied to photogrammetric point clouds. Forests 2015, 6, 3899–3922. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground biomass estimation using structure from motion approach with aerial photographs in a seasonal tropical forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer Stacking: A Novel Algorithm for Individual Forest Tree Segmentation from LiDAR Point Clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Pirotti, F.; Kobal, M.; Roussel, J.R. A Comparison of Tree Segmentation Methods Using Very High Density Airborne Laser Scanner Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 285–290. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Vertical stratification of forest canopy for segmentation of understory trees within small-footprint airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 385–392. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. A local projection-based approach to individual tree detection and 3-d crown delineation in multistoried coniferous forests using high-density airborne LiDAR data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1168–1182. [Google Scholar] [CrossRef]
- Pix4D SA Pix4Dcapture, App Version 4.3.0. 2018. Available online: https://www.pix4d.com/product/pix4dcapture (accessed on 15 May 2019).
- Agisoft LLC. Agisoft PhotoScan Professional, Version 1.4.3; Agisoft LLC: St. Petersburg, Russia, 2018.
- Kobler, A.; Pfeifer, N.; Ogrinc, P.; Todorovski, L.; Oštir, K.; Džeroski, S. Repetitive interpolation: A robust algorithm for DTM generation from Aerial Laser Scanner Data in forested terrain. Remote Sens. Environ. 2007, 108, 9–23. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering Airborne Laser Scanning Data with Morphological Methods. Photogramm. Eng. Remote Sens. 2013, 73, 175–185. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An improved simple morphological filter for the terrain classification of airborne LIDAR data. ISPRS J. Photogramm. Remote Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Qi, J. RCSF: Airborne LiDAR Filtering Method Based on Cloth Simulation. R Package Version 1.0.1. 2018. Available online: https://CRAN.R-project.org/package=RCSF (accessed on 17 May 2019).
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8, 340. [Google Scholar] [CrossRef]
- Gombin, J.; Vaidyanathan, R.; Agafonkin, V. Concaveman: A Very Fast 2D Concave Hull Algorithm. R Package Version 1.0.0. 2017. Available online: https://CRAN.R-project.org/package=concaveman (accessed on 17 May 2019).
- Plowright, A. ForestTools: Analyzing Remotely Sensed Forest Data. R Package Version 0.2.0. 2018. Available online: https://github.com/AndyPL22/ForestTools (accessed on 17 May 2019).
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: Using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Meyer, F.; Beucher, S. Morphological Segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A.; Klauberg, C.; Cardil, A. rLiDAR: LiDAR Data Processing and Visualization. R Package Version 0.1.1. 2017. Available online: https://CRAN.R-project.org/package=rLiDAR (accessed on 17 May 2019).
- ESRI. ArcGIS Desktop, version 10.5.1; ESRI: Redlands, CA, USA, 2019.
- Hijmans, R.J. raster: Geographic Data Analysis and Modeling. R Package Version 2.8-19. 2019. Available online: https://CRAN.R-project.org/package=raster (accessed on 17 May 2019).
- Horn, B.K.P. Hill Shading and the Reflectance Map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Pebesma, E.J.; Bivand, R.S. Classes and Methods for Spatial Data in R. R News 5 (2). 2005. Available online: https://cran.r-project.org/doc/Rnews (accessed on 17 May 2019).
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation-evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of Individual Longleaf Pine (Pinus palustris Mill.) Tree Attributes from Field and LiDAR Data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovskỳ, Z.; Turner, D.; Vopěnka, P. Assessment of forest structure using two UAV techniques: A comparison of airborne laser scanning and structure from motion (SfM) point clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Osawa, A.; Zyryanova, O.A.; Matsuura, Y.; Kajimoto, T.; Wein, R.W. Permafrost Ecosystems: Siberian Larch Forests; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 9781402096921. [Google Scholar]


| Sites | Rigidness | Cloth Resolution (m) | Classification Threshold (m) |
|---|---|---|---|
| EN18001/03/12 | 1 | 0.1 | 0.1 |
| EN18014/26/27 | 1 | 0.2 | 0.1 |
| EN18030/80 | 1 | 0.2 | 0.2 |
| EN18070 | 2 | 0.2 | 0.3 |
| EN18083 | 2 | 0.1 | 0.2 |
| Sites | r (h) | Comments |
|---|---|---|
| EN18001/03/12/14/27 | 0.045 h + 0.8 | Small and widely spaced trees |
| EN18070/26/80 | 0.020 h + 0.6 | Narrow and tall trees |
| EN18083 | 0.020 h + 0.4 | Tall trees |
| EN18030 | 0.035 h + 0.05 | Narrow, closely spaced, and small trees |
| Sites | Type I | Type II | Type III | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EN18001 | EN18003 | EN18012 | EN18014 | EN18026 | EN18027 | EN18030 | EN18070 | EN18080 | EN18083 | |
| Latitude | 67.3927 | 67.3969 | 67.4021 | 67.3953 | 67.3961 | 67.3934 | 68.4055 | 63.0829 | 59.9771 | 59.9747 |
| Longitude | 168.3468 | 168.3471 | 168.3781 | 168.3491 | 168.3543 | 168.3590 | 164.5327 | 117.9850 | 112.9613 | 113.0029 |
| Plot area (m2) | 3673.84 | 4130.72 | 3895.52 | 4058.5 | 3549.85 | 3841.82 | 3769.85 | 9474.81 | 3782.64 | 2943.26 |
| Mean slope (°) | 12.5 | 23.01 | 12.07 | 12 | 14.93 | 15.66 | 15.13 | 13.89 | 16.02 | 16.98 |
| Mean aspect (°) | 163.22 | 164.96 | 184.41 | 128.24 | 154.25 | 170.48 | 167.97 | 179.63 | 182.8 | 212.09 |
| Total detected | 181 | 146 | 259 | 240 | 153 | 297 | 1733 | 759 | 681 | 270 |
| Tree density (n/h) | 492.67 | 353.45 | 664.87 | 591.35 | 431 | 773.07 | 4597 | 801.07 | 1800.33 | 917.35 |
| Cover | 0.21 | 0.23 | 0.19 | 0.16 | 0.22 | 0.26 | 0.53 | 0.4 | 0.3 | 0.38 |
| Mean height (m) | 6.58 | 6.48 | 4.95 | 3.99 | 6.13 | 6.86 | 4.82 | 14.76 | 5.26 | 17.56 |
| SD height | 3.27 | 3.11 | 2.71 | 2.63 | 3.41 | 3.28 | 1.59 | 5.4 | 4.46 | 8.39 |
| Mean crown area (m2) | 4.24 | 6.42 | 2.83 | 2.77 | 5.17 | 3.35 | 1.15 | 4.98 | 1.68 | 4.18 |
| SD crown area | 3.84 | 5.83 | 2.43 | 2.85 | 4.18 | 2.75 | 0.74 | 4.26 | 2.09 | 3.98 |
| Mean crown diameter (m) | 2.31 | 2.95 | 1.91 | 1.81 | 2.67 | 2.16 | 1.31 | 2.74 | 1.44 | 2.47 |
| SD mean crown diameter | 1.33 | 1.44 | 0.94 | 1.1 | 1.2 | 0.99 | 0.45 | 1.23 | 0.92 | 1.29 |
| Site | Type I | Type II | Type III | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EN18001 | EN18003 | EN18012 | EN18014 | EN18026 | EN18027 | EN18030 | EN18070 | EN18080 | EN18083 | |
| ND/NO | 7/10 | 10/11 | 9/11 | 33/68 | 11/15 | 8/10 | 12/12 | 11/20 | 23/30 | 23/32 |
| Percentage ND/NO | 70 | 91 | 82 | 49 | 73 | 80 | 100 | 55 | 77 | 72 |
| Mean H | 5.1 | 5.25 | 6.07 | 4.51 | 7.37 | 5.76 | 6.39 | 11.1 | 7.53 | 14.12 |
| SD H | 3.52 | 3.04 | 3.21 | 4.15 | 4.14 | 2.7 | 3.21 | 7.31 | 6.45 | 8.73 |
| Smallest detected | 3.75 | 1.8 | 1.65 | 2.2 | 7 | 4.1 | 1.95 | 4.5 | 0.96 | 2.6 |
| Tallest un-detected | 2.05 | 1.75 | 1.23 | 8 | 2.9 | 1.7 | - | 9 | 2.5 | 12 |
| H R2 | 0.67 | 0.76 | 0.63 | 0.86 | 0.64 | 0.83 | 0.87 | 0.82 | 0.96 | 0.67 |
| H RMSE | 1.56 | 1.29 | 1.11 | 1 | 1.22 | 0.63 | 0.62 | 2 | 1.08 | 3.73 |
| H RMSE% | 28.32 | 21.77 | 18.58 | 3.52 | 22.52 | 16.06 | 9.55 | 26.17 | 7.3 | 28.41 |
| Mean CD | 2.1 | 2.42 | 2.42 | 1.99 | 3.1 | 2.56 | 1.51 | 2.95 | 1.54 | 2.42 |
| SD CD | 1.28 | 1.93 | 1.43 | 1.77 | 1.89 | 1.51 | 0.95 | 2.09 | 1.35 | 1.43 |
| CD R2 | 0.94 | 0.81 | 0.13 | 0.62 | 0.64 | 0.22 | 0.32 | 0.26 | 0.34 | 0.13 |
| CD RMSE | 0.27 | 0.78 | 0.99 | 0.68 | 0.5 | 0.55 | 0.37 | 1.19 | 0.73 | 0.99 |
| CD RMSE% | 10.63 | 26.65 | 28.73 | 23.54 | 15.81 | 21.89 | 22.63 | 33.34 | 40.82 | 28.73 |
| Over-Segmentation (Commission Errors) | Under-Segmentation (Omission Errors) | Height Underestimation | |
|---|---|---|---|
| Narrow search | - Occasional wide or very flat crowns - Occasional fragmented crowns - Occasional complete crowns - Leaning trees | - | - |
| Wide search | - | - Occasional narrow crowns - Partially overlapping trees | - |
| Low min. height | - Misclassified ground vegetation - Elevated horizontal dead wood | - | - |
| High min. height | - | - Small trees will not be detected | - |
| Strong smoothing | - | - Very closely spaced tree tops - Partially overlapping trees - Small, narrow trees will not be detected | - |
| Weak smoothing | - Side branches create multiple local maxima - Occasional fragmented crowns - Leaning trees with multiple local maxima | - | - |
| Always | - | - Overlapping crowns (subordinated trees) | - Trees with thin, leafless tops - Leaning trees - Small, shrub like trees |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brieger, F.; Herzschuh, U.; Pestryakova, L.A.; Bookhagen, B.; Zakharov, E.S.; Kruse, S. Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds. Remote Sens. 2019, 11, 1447. https://doi.org/10.3390/rs11121447
Brieger F, Herzschuh U, Pestryakova LA, Bookhagen B, Zakharov ES, Kruse S. Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds. Remote Sensing. 2019; 11(12):1447. https://doi.org/10.3390/rs11121447
Chicago/Turabian StyleBrieger, Frederic, Ulrike Herzschuh, Luidmila A. Pestryakova, Bodo Bookhagen, Evgenii S. Zakharov, and Stefan Kruse. 2019. "Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds" Remote Sensing 11, no. 12: 1447. https://doi.org/10.3390/rs11121447
APA StyleBrieger, F., Herzschuh, U., Pestryakova, L. A., Bookhagen, B., Zakharov, E. S., & Kruse, S. (2019). Advances in the Derivation of Northeast Siberian Forest Metrics Using High-Resolution UAV-Based Photogrammetric Point Clouds. Remote Sensing, 11(12), 1447. https://doi.org/10.3390/rs11121447





