Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification
Abstract
1. Introduction
2. Materials and Methods
2.1. Discrete Cosine Transform (DCT)
2.2. 2D-Discrete Cosine Transform (2D-DCT)
2.3. Spatial Adaptive Wiener Filter (2D-AWF)
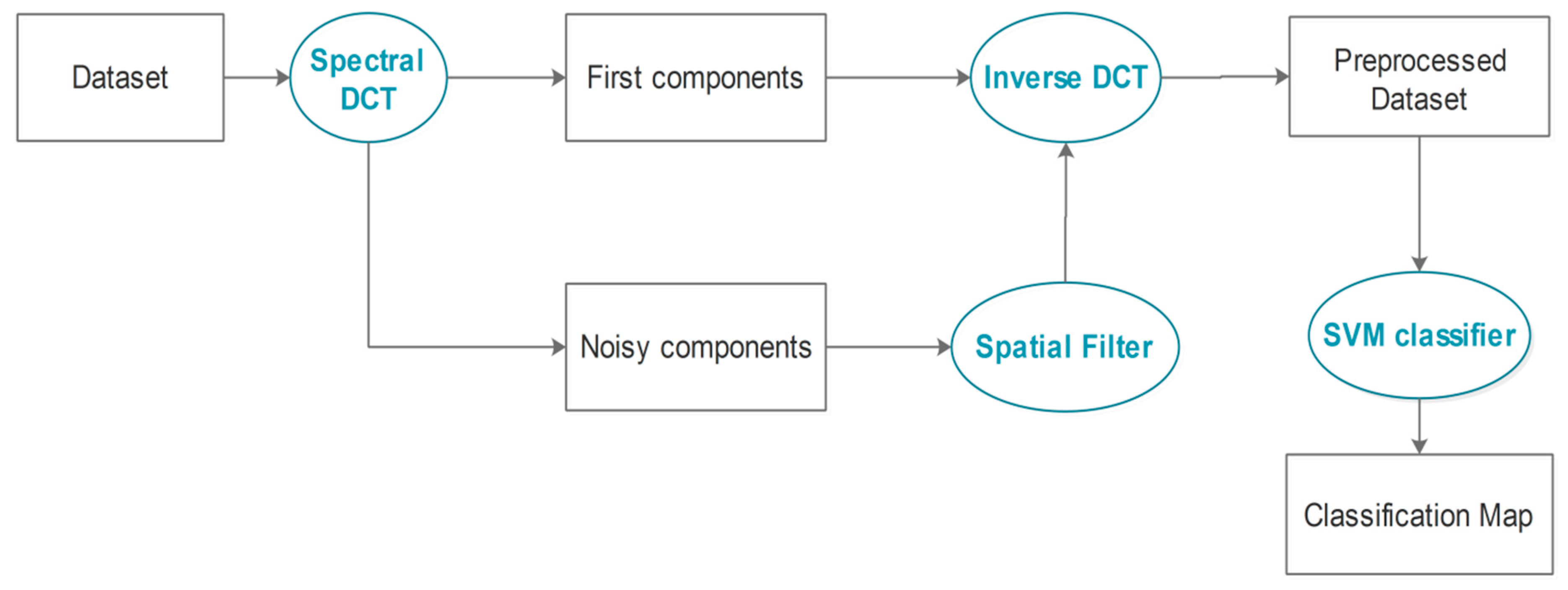
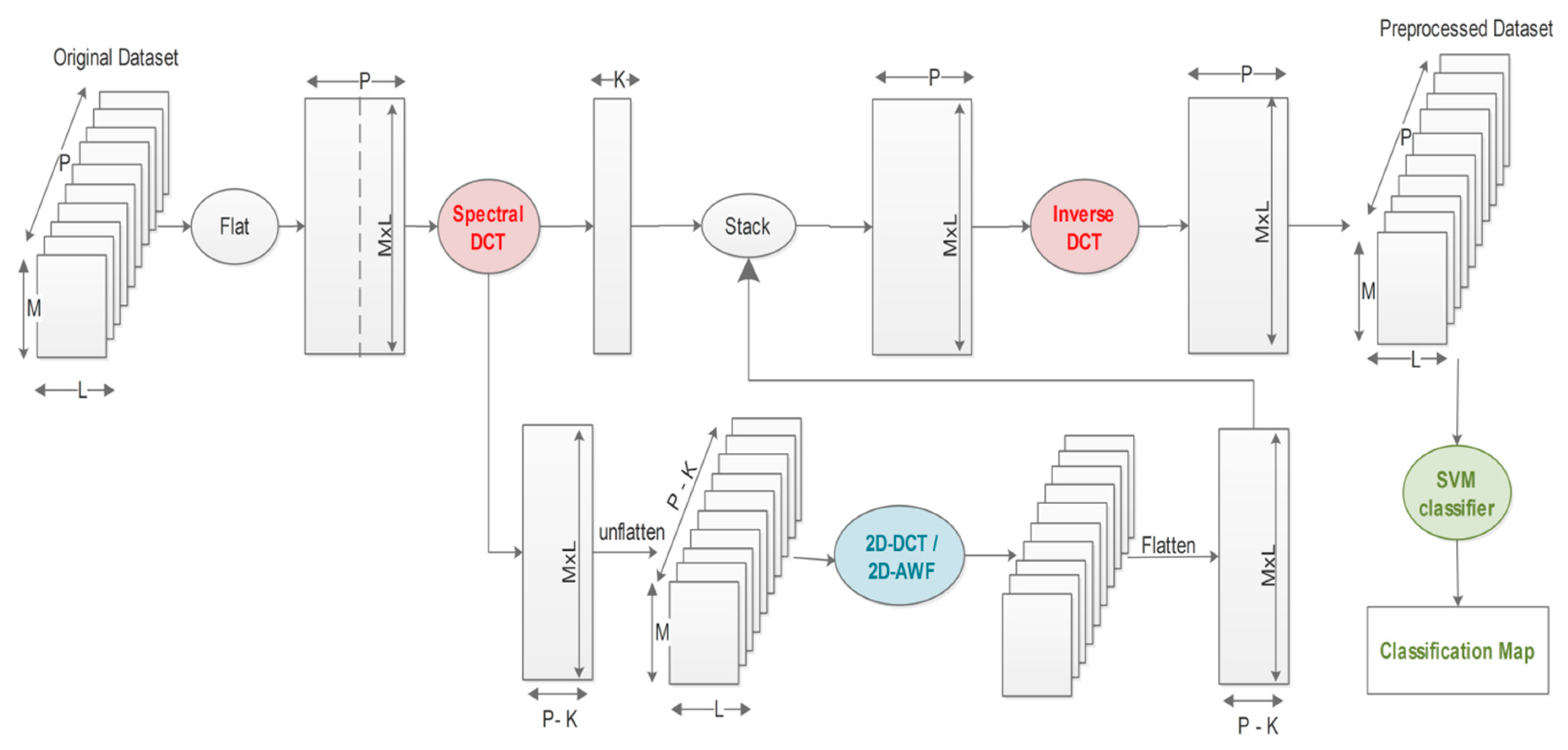
3. The Proposed Approach
- -
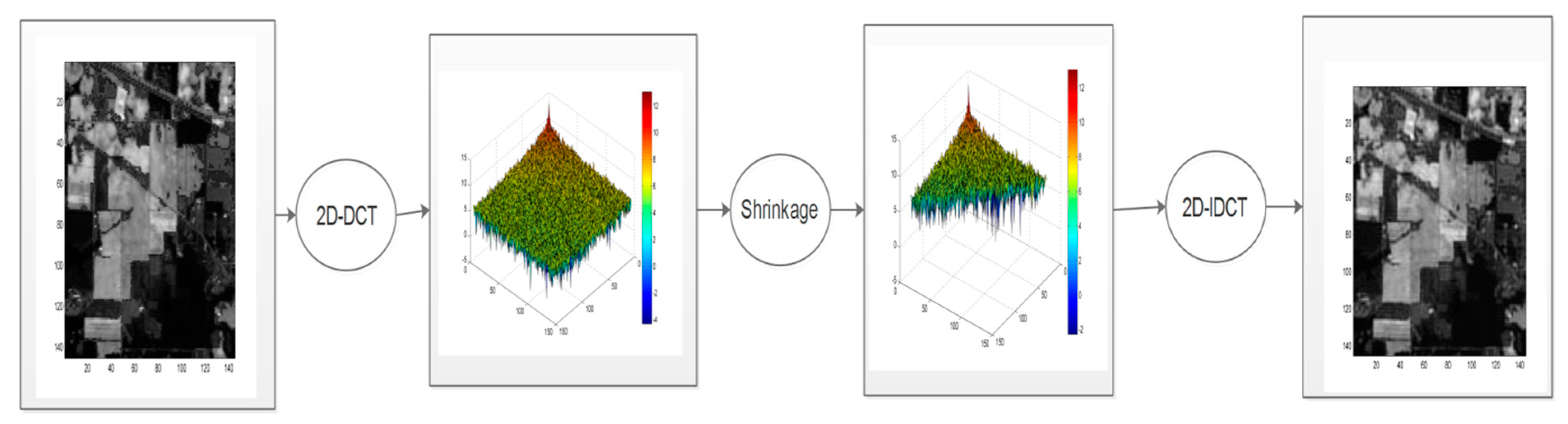
- The 2D-DCT filtering step consists of performing a global 2D-DCT filter on each matrix Rm(M,L) where the high-frequency components are discarded using an empirical estimated hard threshold. Then, an inverse DCT is applied to the matrix Rm(M, L). Figure 3 illustrates this spatial filtering step.
- -
- 2D-AWF approach filtering step consists on dividing the matrix Rm(M, L) into blocks or patches of a specified size and processing them using a local 2D-AWF.
4. Data and Evaluation Process
4.1. Data
4.2. Evaluation Process
5. Experimental Results and Analysis
5.1. Parameter Settings
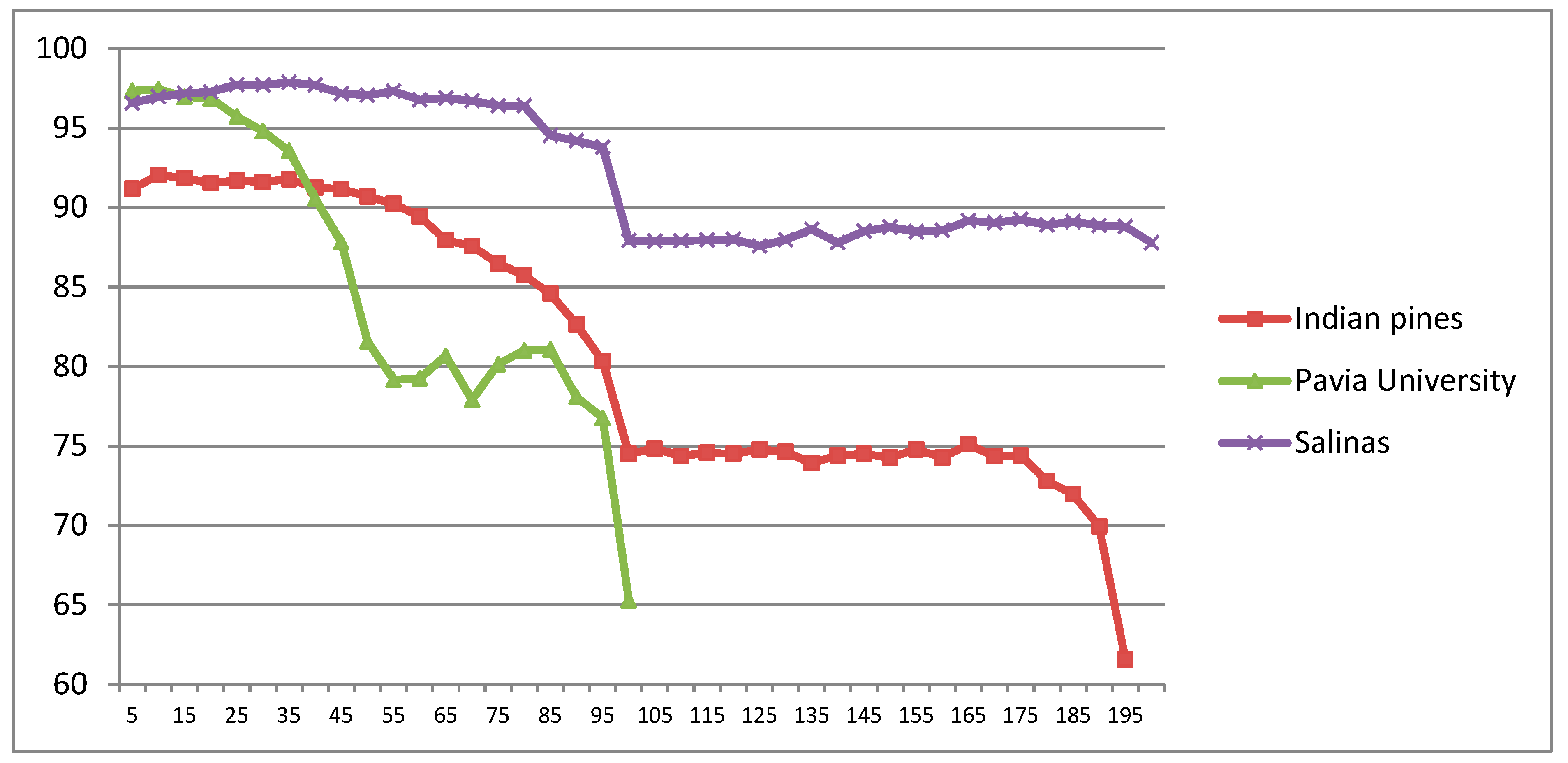
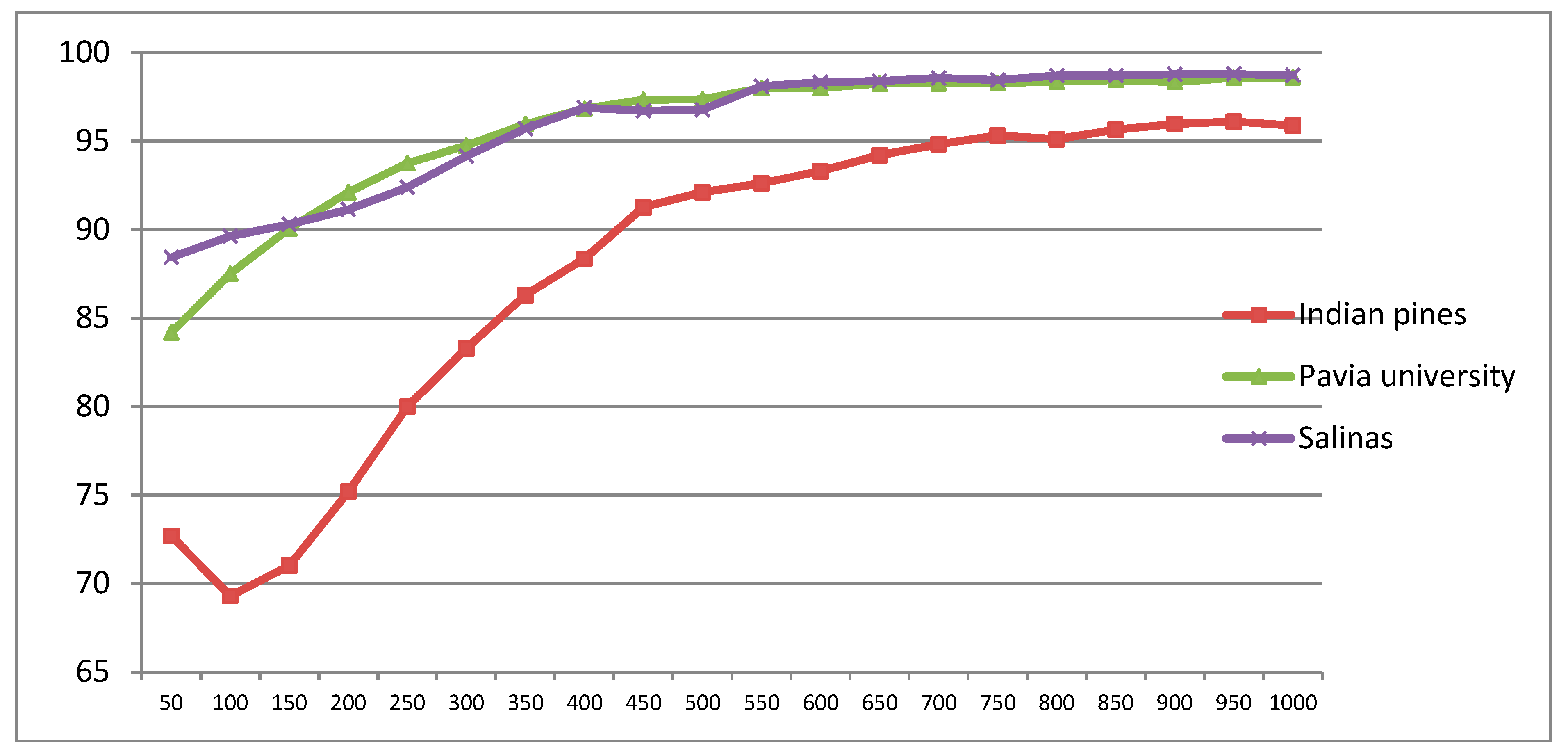
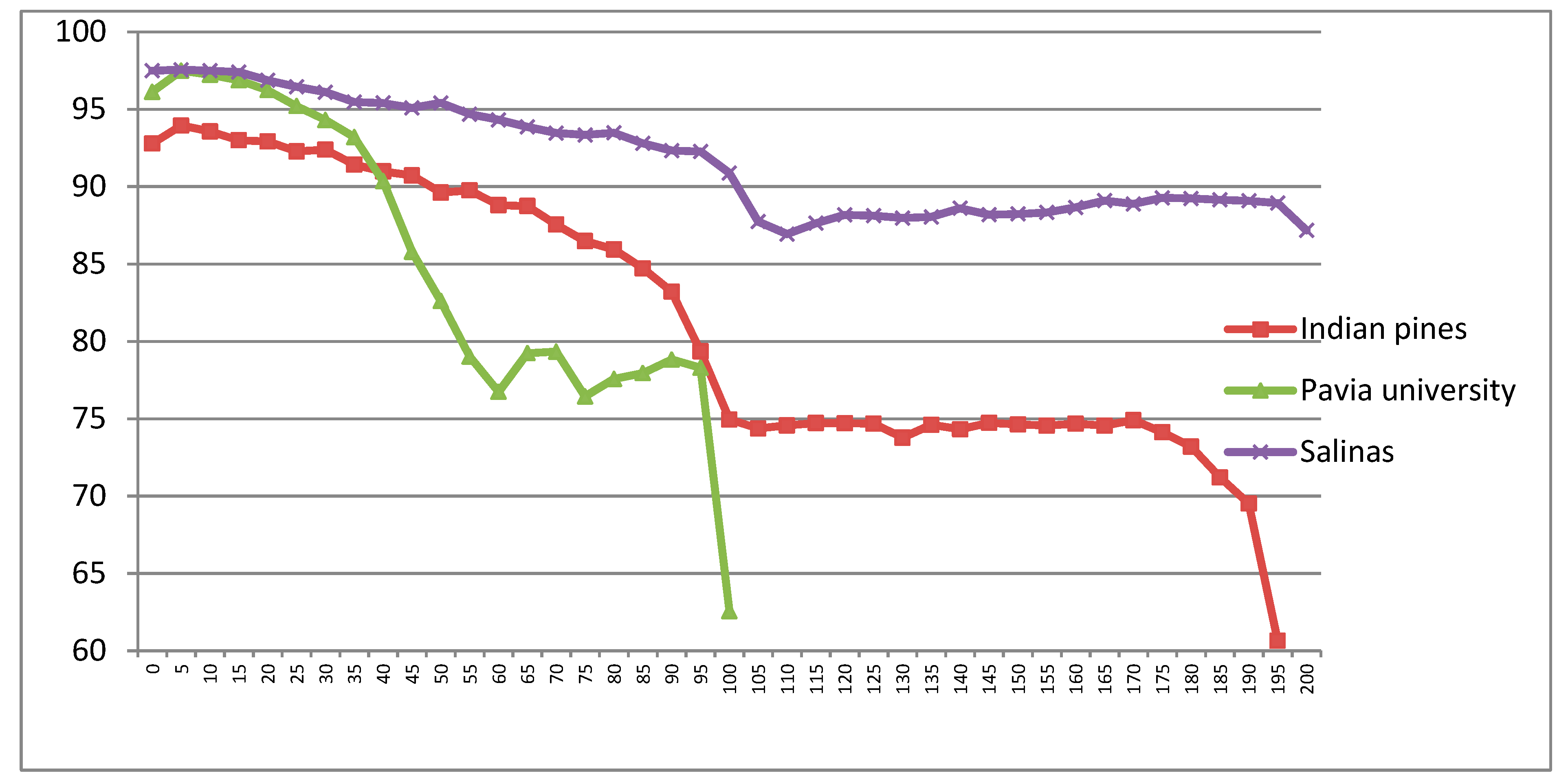
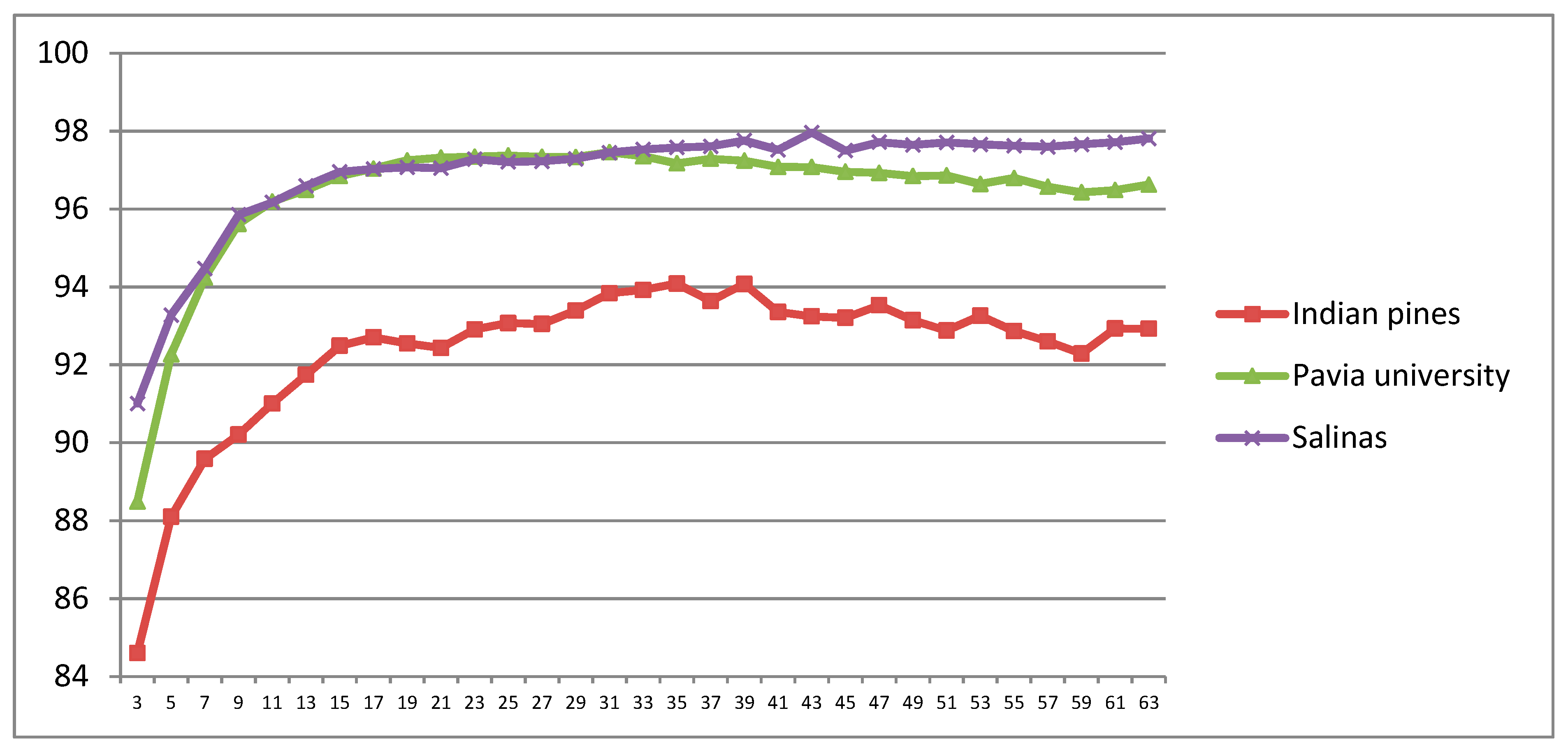
5.1.1. CDCT-2DCT_SVM Framework Parameter Estimation
5.1.2. CDCT-WF_SVM Framework Parameter Estimation
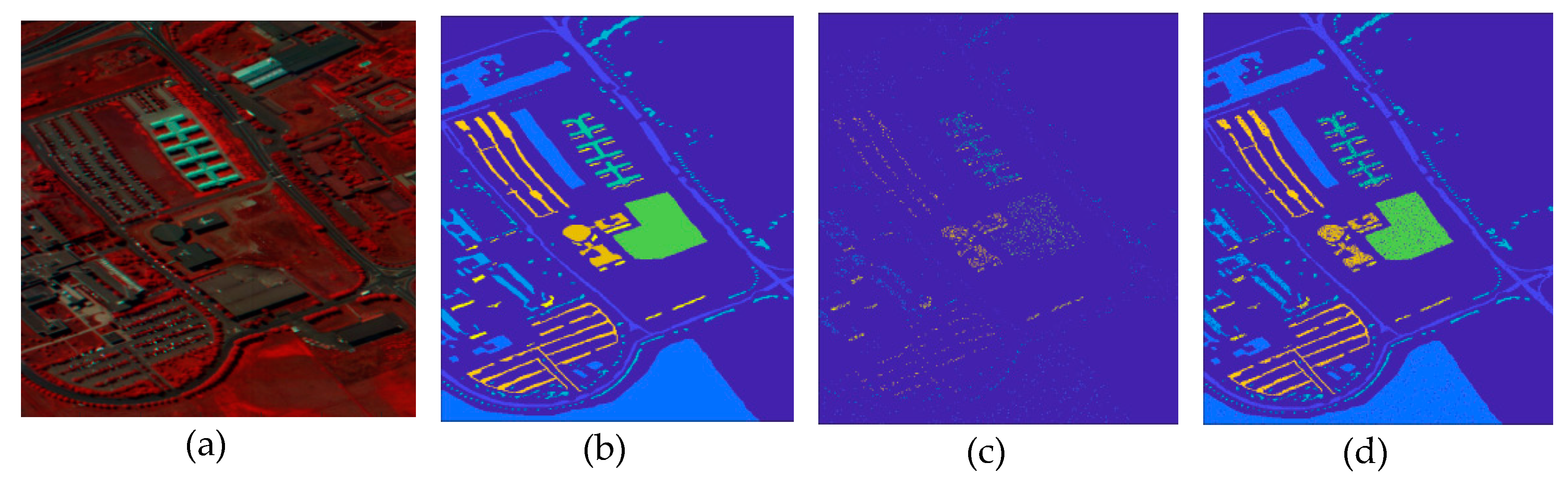
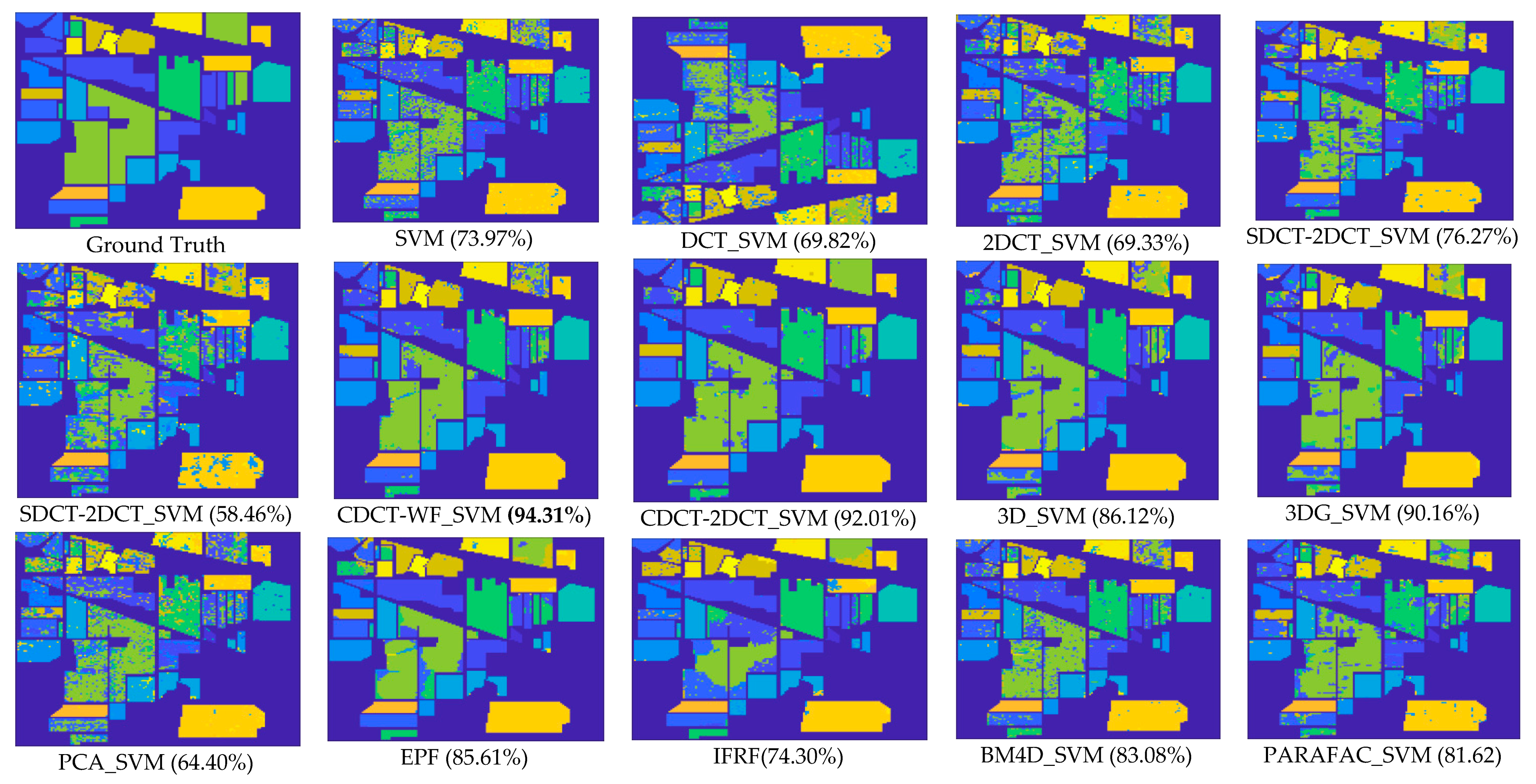
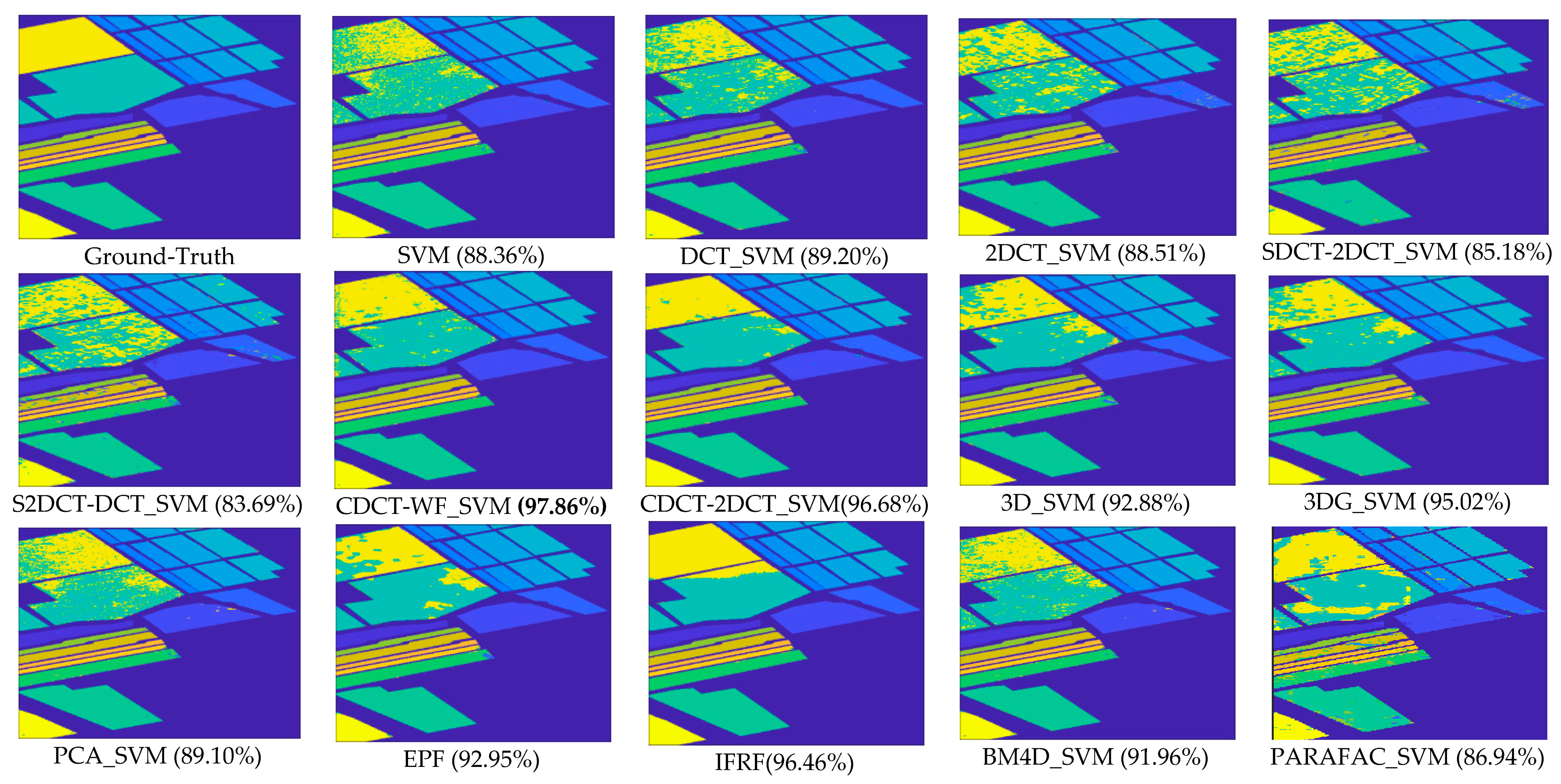
5.2. Classification of Indian Pines Dataset
- -
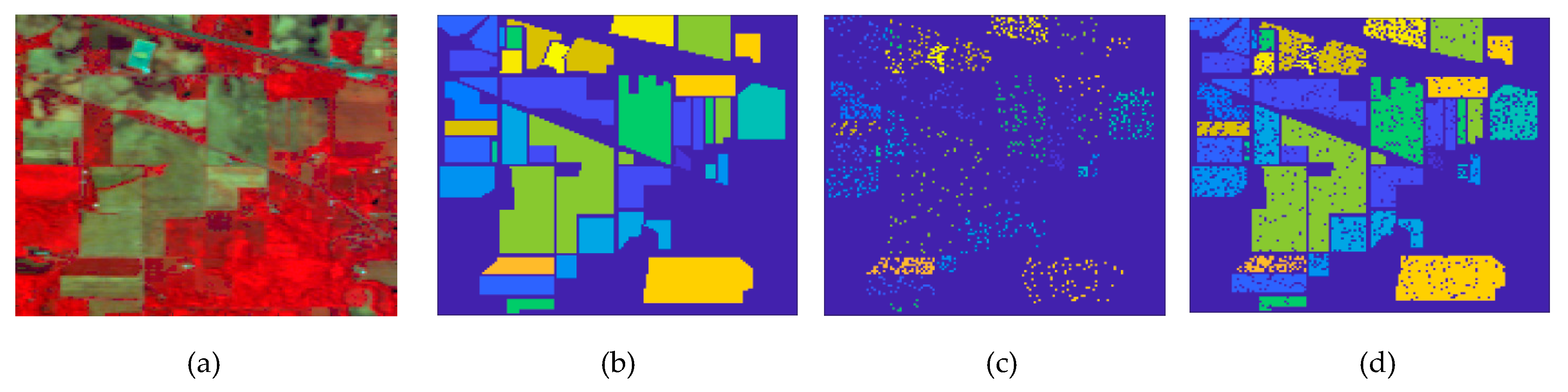
- The approaches exploring only the spectral information, including SVM, PCA_SVM, and SDCT_SVM, attain poorer results when compared with the other techniques, which can be confirmed in Figure 11, where it is clear that the classification maps resulted from these techniques are degraded by salt-and-pepper noise. Nevertheless, the classification accuracy of SDCT_SVM (73.07% OA) is higher than PCA_SVM (64.40% OA) owing to the effectiveness ofDCT energy compaction that concentrates the energy of the spectral signature in a few low-frequency components where noisy data is embedded in the high-frequency components; instead of selecting the first PCs in PCA which cannot guarantee that image quality decreases for PCs with lower variances. The 2D-DCT_SVM approach only filters spatial information and therefore yielded less accurate results.
- -
- The methods considering both the spectral and spatial information, including 3DG_SVM, 3D_SVM, EPF, IFRF, BM4D_SVM, and PARAFAC_SVM, are most accurate. The 3DG_SVM, and_3DSV methods delivered the third and fourth highest accuracies (90.32% OA and 86.12% OA, respectively) given the efficiency of wavelet features in structural filtering. Nevertheless, by considering hyperspectral image data as a 3D cube where the spatial and spectral features must be treated as a whole in 3D-DWT approaches, we implicitly assume that the noise variance is the same in the three dimensions and ignores dissimilarity between the spatial and the spectral dimensions where the degree of irregularity is higher in the spectral dimension than in the spatial dimensions. The proposed CDCT-WF_SVM and CDCT-2DCT_SVM approaches overcome this issue by filtering the spectral dimension and the spatial dimensions separately to achieve higher performance than wavelet-based filtering approaches. Moreover, the highest accuracy (94.31% OA) was achieved by CDCT-WF_SVM, which combines two different filters and take advantage of both of them. Additionally, it can be seen in Figure 11 that 3D_SVM, 3DG_SVM, EPF, and IFRF achieved smoother classification maps than the two well-known denoising-based approaches, BM4D_SVM and PARAFAC_SVM.
- -
- Serial filtering-based approaches including SDCT-2DCT_SVM and S2DCT-DCT_SVM obtained by performing spectral and spatial filters on the same information cannot be effective in improving the classification accuracy, since performing a second filter on the already filtered information will alter the useful information rather than discarding more noise. In contrast, the proposed CDCT-WF_SVM and CDCT-2DCT_SVM perform a spatial filter on the noisy part from the spectral filter.
- -
- Regarding the computational cost, Table 6 shows that the shortest classification time was 1.48 s and was achieved with the IFRF method, which had low classification accuracy (74.30% OA). The other spectral-spatial-based methods including EPF (85.61%OA), 3D_SVM (86.12%OA), 3DG_VM ((90.32%OA) achieved higher classification accuracies, but they are time-consuming using 85.61s, 86.12s, and 210.16s, respectively. Similarly, denoising-based techniques are also time-consuming with 83.08s for BM4D_SVM and 81.62 for PARAFAC_SVM. However, the proposed CDCT-WF_SVM and CDCT-2DCT_SVM achieved the two first highest classification accuracies within a short execution time. For example, CDCT-WF_SVM achieved an OA of 94.31% in 13.30s where CDCT-2DCT_SVM achieves an OA of 92.01% in 13.91s. Moreover, in the proposed approaches, the SDCT is performed on each pixel, and the spatial filter is performed on each band. Hence, our approaches are easily parallelized, which could further reduce the computational time.
5.3. Classification of SALINAS Dataset
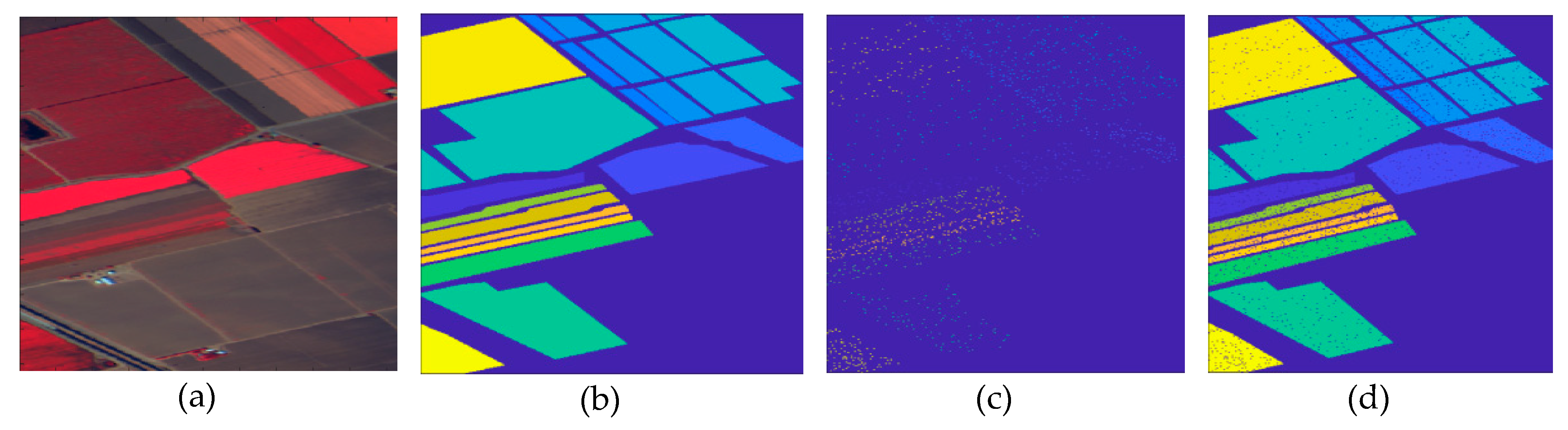
5.4. Classification of Pavia University Dataset
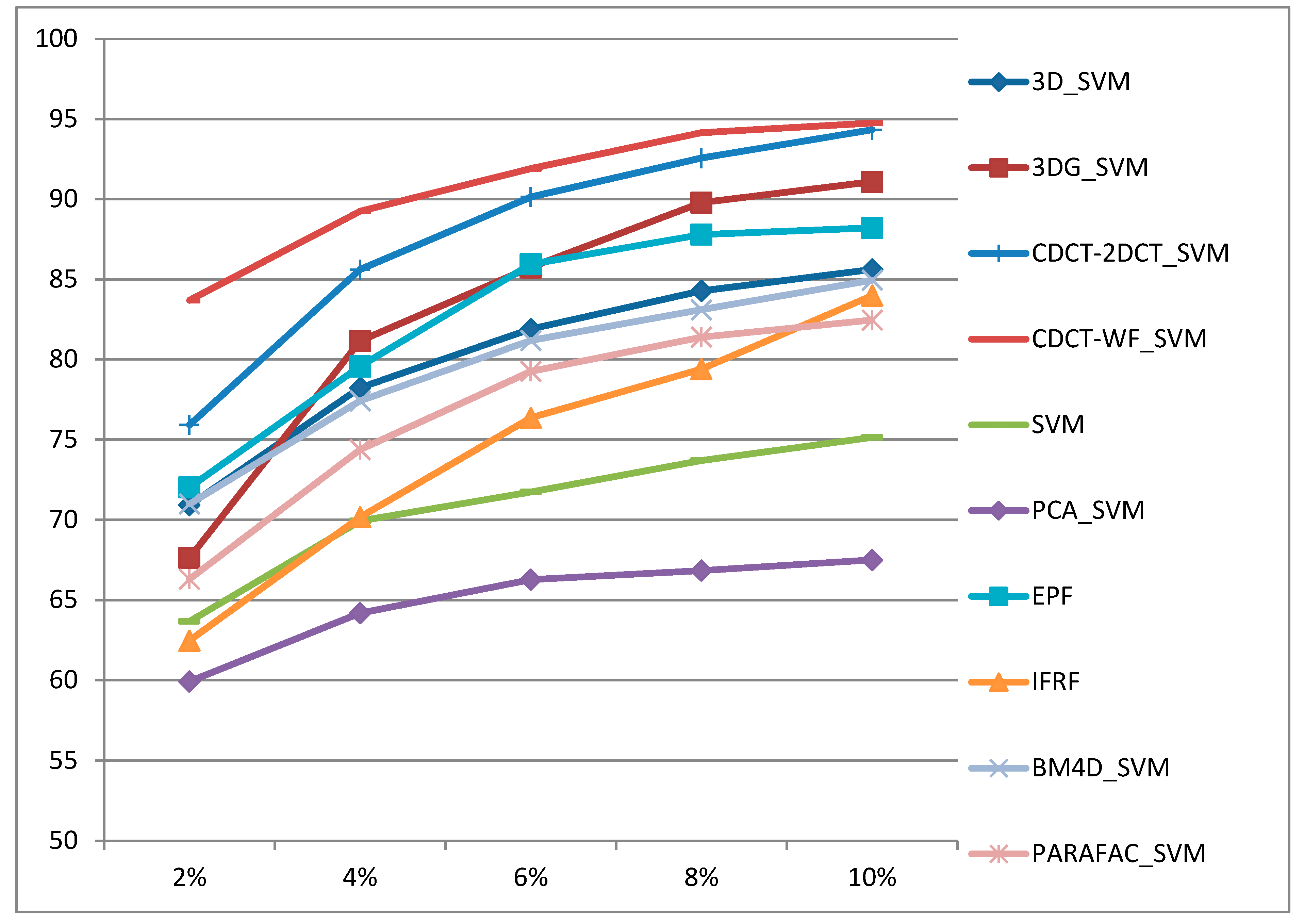
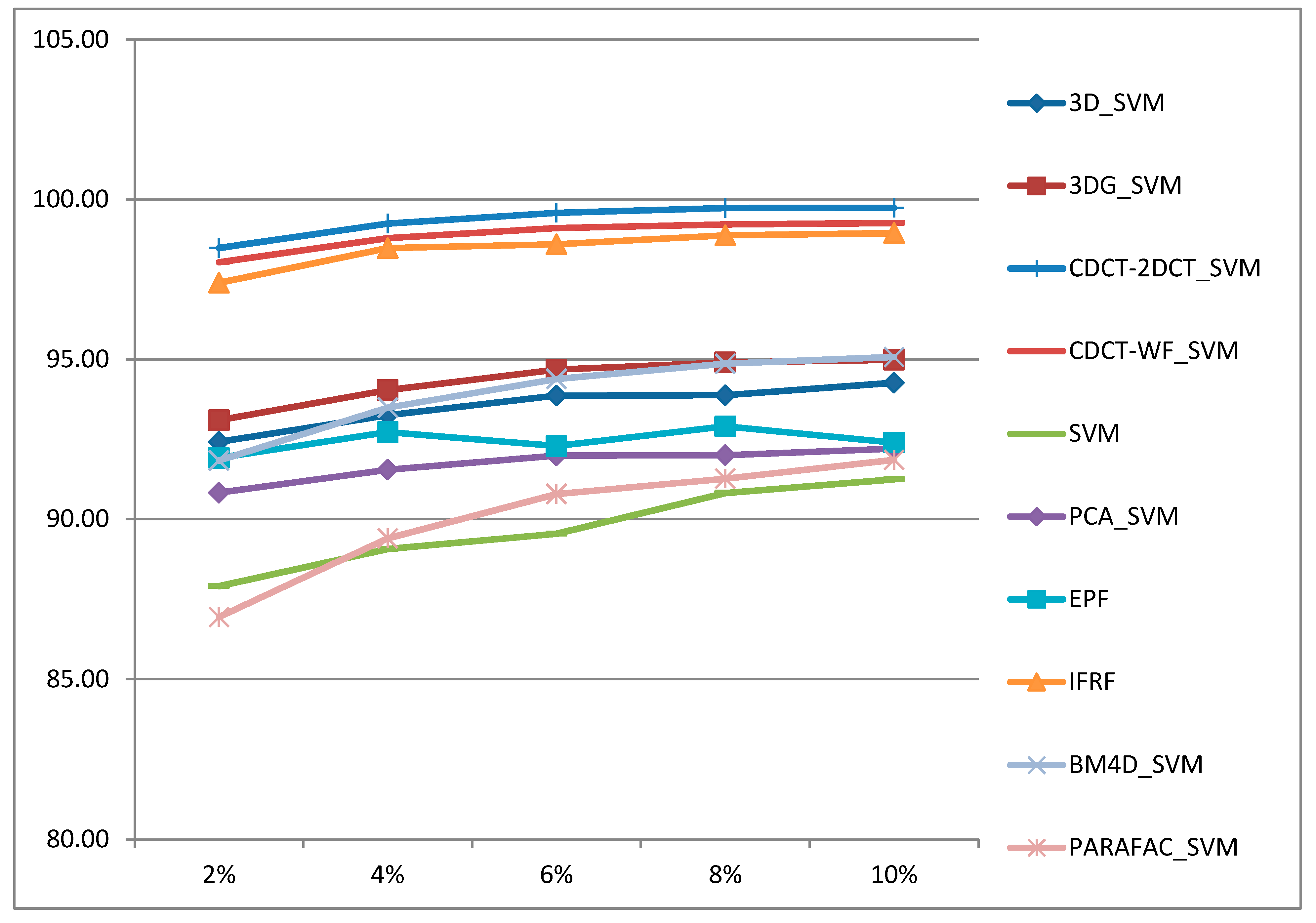
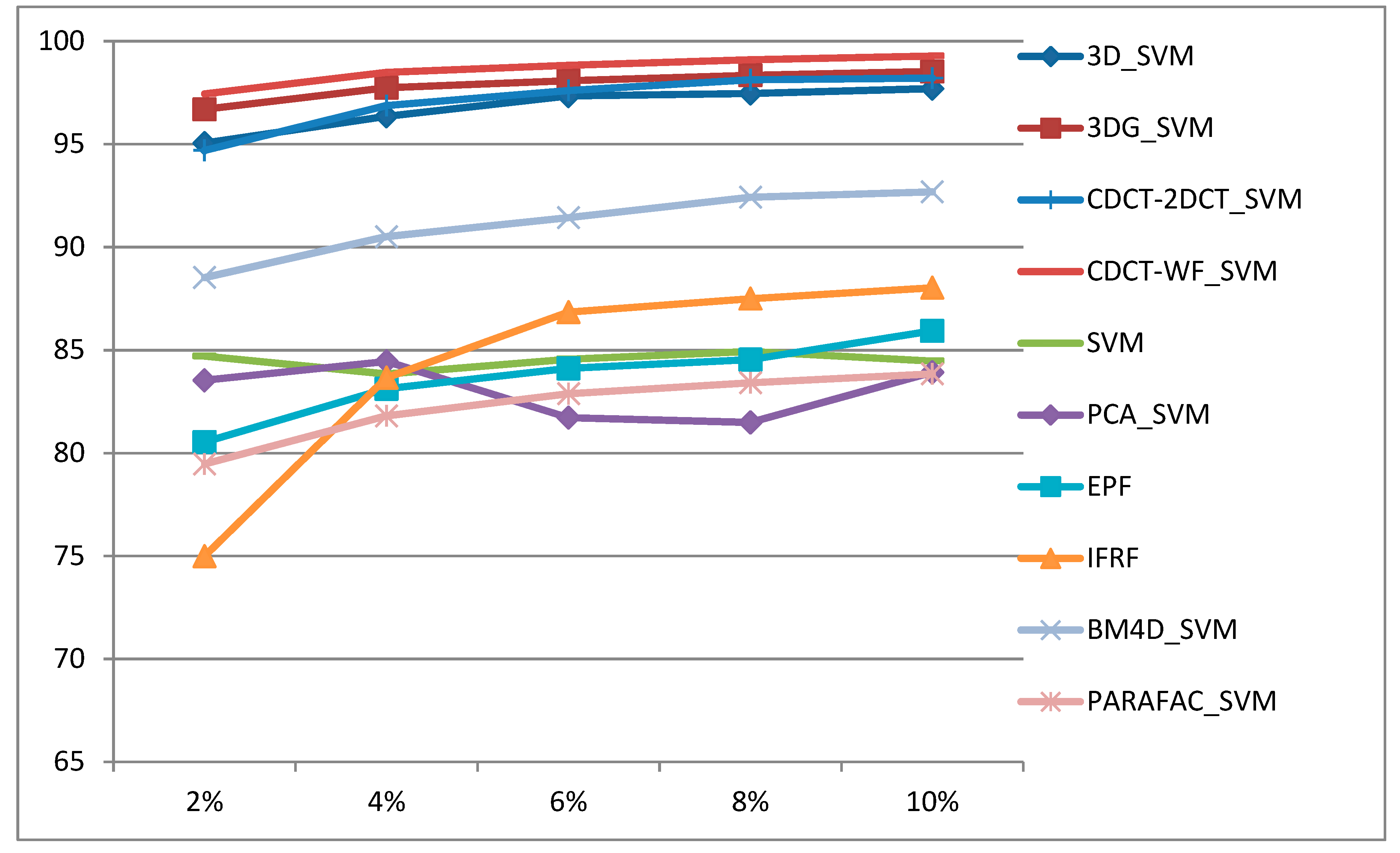
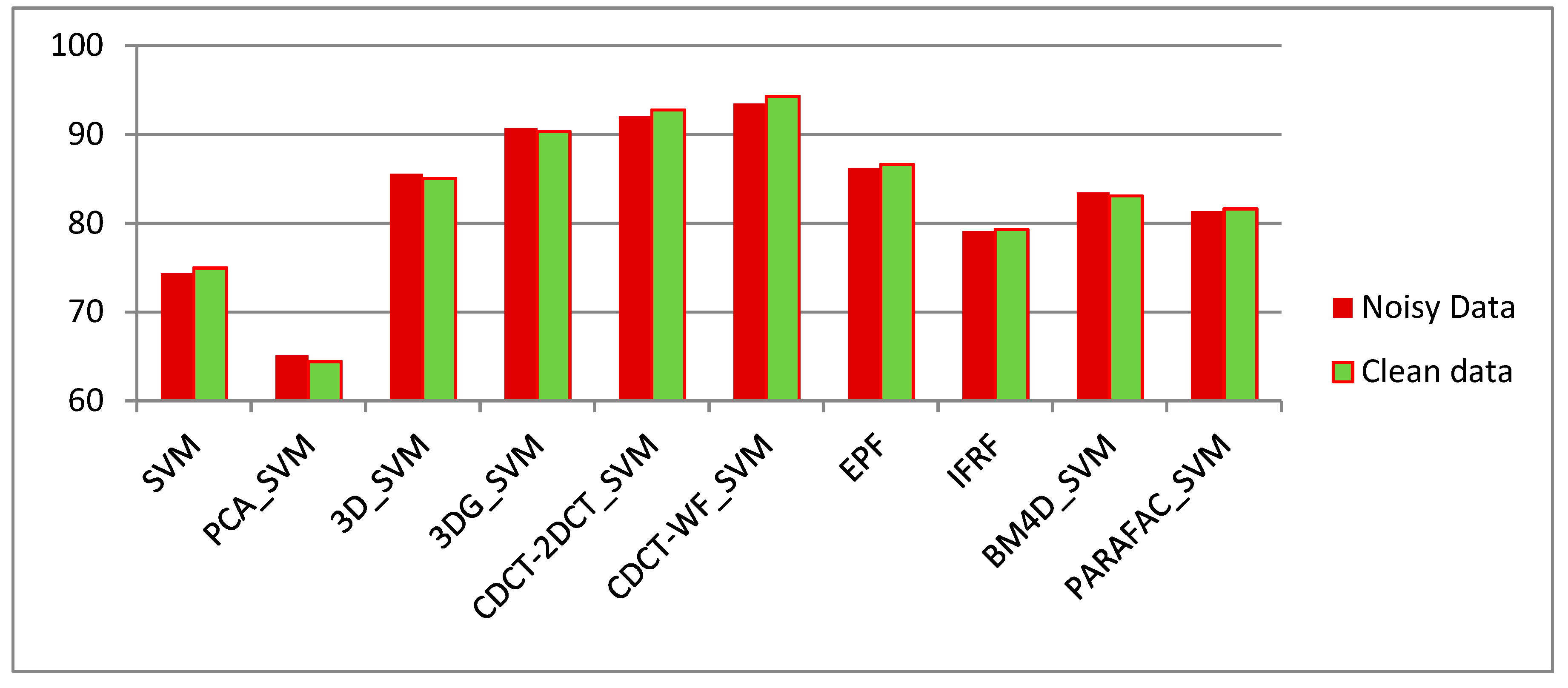
5.5. Classification in Noisy Scenario
6. Summary and Conclusions
- -
- The proposed approaches outperform the other considered methods; in particular, our proposed CDCT-WF_SVM method, which delivers higher accuracy on the three datasets with a smoother classification map than the other tested techniques.
- -
- The proposed approaches deliver higher classification accuracies regardless of the size of training samples, and they are robust to noise.
- -
- A major advantage of the proposed frameworks is that they are computationally efficient along with a reasonable tradeoff between accuracy and computational time. Thus, they will be quite useful for applications such as flood monitoring and risk management, which require a fast response. Moreover, as the DCT is performed on each pixel, and both WF with 2D-DCT are performed on each band, our approaches are easily parallelized, which could further reduce the computational time.
- -
- The results obtained illustrate that the proposed approaches can deal with different spatial resolutions (20 m, 3.7 m, and 1.7 m). In particular, for Indian pines dataset with 20m spatial resolution, our proposed CDCT-WF_SVM and CDCT-2DCT_SVM approaches achieve first and the second highest accuracy. Thus, our proposed approaches can effectively deal with low spatial resolution images.
- -
- For the three datasets, structural-based filtering methods have stable performance, including our proposed frameworks and wavelet-based methods. However, the IFRF method cannot provide stable performance by providing the third-highest accuracy on Salinas dataset and low accuracy on the two other datasets.
- -
- The proposed approaches require the selection of only two parameters to achieve high classification accuracy in low computational time, which allows their potential use in practical applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tong, Q.; Xue, Y.; Zhang, L. Progress in Hyperspectral Remote Sensing Science and Technology in China Over the Past Three Decades. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 70–91. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Yokoya, N.; Chan, J.C.-W.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef]
- He, J.; He, Y.; Zhang, A.C. Determination and Visualization of Peimine and Peiminine Content in Fritillaria thunbergii Bulbi Treated by Sulfur Fumigation Using Hyperspectral Imaging with Chemometrics. Molecules 2017, 22, 1402. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492. [Google Scholar] [CrossRef]
- Ratle, F.; Camps-Valls, G.; Weston, J. Semisupervised neural networks for efficient hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2271–2282. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, L. An adaptive artificial immune network for supervised classification of multi-/hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 894–909. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification via Kernel Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef]
- Castrodad, A.; Xing, Z.; Greer, J.B.; Bosch, E.; Carin, L.; Sapiro, G. Learning Discriminative Sparse Representations for Modeling, Source Separation, and Mapping of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4263–4281. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral-spatial classification of hyperspectral data using loopy belief propagation and active learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Di, W.; Crawford, M.M. View generation for multiview maximum disagreement based active learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1942–1954. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, H. Classification of Hyperspectral Images by SVM Using a Composite Kernel by Employing Spectral, Spatial and Hierarchical Structure Information. Remote Sens. 2018, 10, 441. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Tuia, D.; Bruzzone, L.; Benediktsson, J.A. Advances in hyperspectral image classification: Earth monitoring with statistical learning methods. IEEE Signal Process. Mag. 2014, 31, 45–54. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent advances on spectral-spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Plaza, A.; Martinez, P.; Plaza, J.; Perez, R. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 466. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of Hyperspectral Data from Urban Areas Based on Extended Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480. [Google Scholar] [CrossRef]
- Xia, J.; Chanussot, J.; Du, P.; He, X. Spectral-spatial classification for hyperspectral data using rotation forests with local feature extraction and Markov random fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2532–2546. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Ghassemian, H.; Bioucas-Dias, J.M.; Li, X. Spectral–Spatial Classification of Hyperspectral Data Using Local and Global Probabilities for Mixed Pixel Characterization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6298. [Google Scholar] [CrossRef]
- Peng, J.; Zhou, Y.; Chen, C.L.P. Region-kernel-based support vector machines for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4810–4824. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973. [Google Scholar] [CrossRef]
- Lu, Z.; He, J. Spectral-spatial hyperspectral image classification with adaptive mean filter and jump regression detection. Electron. Lett. 2015, 51, 1658–1660. [Google Scholar] [CrossRef]
- Golipour, M.; Ghassemian, H.; Mirzapour, F. Integrating Hierarchical Segmentation Maps with MRF Prior for Classification of Hyperspectral Images in a Bayesian Framework. IEEE Trans. Geosci. Remote Sens. 2016, 54, 805. [Google Scholar] [CrossRef]
- Oktem, R.; Ponomarenko, N.N. Image filtering based on discrete cosine transform. Telecommun. Radio Eng. 2007, 66. [Google Scholar] [CrossRef]
- Guo, X.; Huang, X.; Zhang, L. Three-Dimensional Wavelet Texture Feature Extraction and Classification for Multi/Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2183. [Google Scholar]
- Sun, S.; Zhong, P.; Xiao, H.; Wang, R. An MRF model-based active learning framework for the spectral-spatial classification of hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2015, 9, 1074–1088. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Hyperspectral image classification using Gaussian mixture models and Markov random fields. IEEE Geosci. Remote Sens. Lett. 2014, 11, 153–157. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Cavallaro, G.; Plaza, A. Automatic Framework for Spectral–Spatial Classification Based on Supervised Feature Extraction and Morphological Attribute Profiles. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2147. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Jia, X.; Benediktsson, J.A.; Chanussot, J. Nonlinear multiple kernel learning with multiple-structure-element extended morphological profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3235–3247. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: a new deep-learning-based hyperspectral image classification method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. MugNet: deep learning for hyperspectral image classification using limited samples. ISPRS J. Photogramm. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. Hierarchical guidance filtering-based ensemble classification for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4177–4189. [Google Scholar] [CrossRef]
- Ni, D.; Ma, H. Hyperspectral image classification via sparse code histogram. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1843–1847. [Google Scholar]
- Du, P.; Xue, Z.; Li, J.; Plaza, A. Learning discriminative sparse representations for hyperspectral image classification. IEEE J. Sel. Top. Signal Process. 2015, 9, 1089–1104. [Google Scholar] [CrossRef]
- Song, H.; Wang, Y. A spectral-spatial classification of hyperspectral images based on the algebraic multigrid method and hierarchical segmentation algorithm. Remote Sens. 2016, 8, 296. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H.; Zhang, Y. Spectral-spatial classification of hyperspectral images using joint bilateral filter and graph cut based model. Remote Sens. 2016, 8, 748. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral-spatial classification of hyperspectral images with a superpixel-based discriminative sparse model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Cao, X.; Ji, B.; Ji, Y.; Wang, L.; Jiao, L. Hyperspectral image classification based on filtering: A comparative study. J. Appl. Remote Sens. 2017, 11, 35007. [Google Scholar] [CrossRef]
- Liu, K.-H.; Lin, Y.-Y.; Chen, C.-S. Linear spectral mixture analysis via multiple-kernel learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2254–2269. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Extreme learning machine with composite kernels for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2351–2360. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Lu, Y.; Yuan, H. Hyperspectral image classification based on three-dimensional scattering wavelet transform. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2467–2480. [Google Scholar] [CrossRef]
- Rajadell, O.; Garcia-Sevilla, P.; Pla, F. Spectral–Spatial Pixel Characterization Using Gabor Filters for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 860. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Plaza, A.; Li, Y. Discriminative low-rank Gabor filtering for spectral-spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1381–1395. [Google Scholar] [CrossRef]
- Phillips, R.D.; Blinn, C.E.; Watson, L.T.; Wynne, R.H. An Adaptive Noise-Filtering Algorithm for AVIRIS Data With Implications for Classification Accuracy. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3168–3179. [Google Scholar] [CrossRef]
- Bourennane, S.; Fossati, C.; Cailly, A. Improvement of classification for hyperspectral images based on tensor modeling. IEEE Geosci. Remote Sens. Lett. 2010, 7, 801–805. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Jeon, G.; Jeong, J. An efficient spatial deblocking of images with DCT compression. Digit. Signal Process. A Rev. J. 2015, 42, 80–88. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.-E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Boukhechba, K.; Wu, H.; Bazine, R. DCT-Based Preprocessing Approach for ICA in Hyperspectral Data Analysis. Sensors 2018, 18, 1138. [Google Scholar] [CrossRef]
- Jing, L.; Yi, L. Hyperspectral remote sensing images terrain classification in DCT SRDA subspace. J. China Univ. Posts Telecommun. 2015, 22, 65–71. [Google Scholar] [CrossRef]
- Pennebaker, W.B.; Mitchell, J.L. JPEG: Still Image Data Compression Standard; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete Cosine Transform. Comput. IEEE Trans. 1974, C-23, 90–93. [Google Scholar] [CrossRef]
- Fevralev, D.V.; Ponomarenko, N.N.; Lukin, V.V.; Abramov, S.K.; Egiazarian, K.O.; Astola, J.T. Efficiency analysis of DCT-based filters for color image database. In Image Processing: Algorithms and Systems IX; IS & T—The Society for Imaging Science and Technology: San Francisco, CA, USA, 2011; Volume 7870, p. 78700R. [Google Scholar] [CrossRef]
- Roy, A.B.; Dey, D.; Banerjee, D.; Mohanty, B. Comparison of FFT, DCT, DWT, WHT Compression Techniques on Electrocardiogram and Photoplethysmography Signals. IJCA Spec. Issue Int. Conf. Comput. Commun. Sens. Netw. 2013, CCSN2012, 6–11. [Google Scholar]
- Clarke, R.J. Transform Coding of Images. Astrophysics; Academic Press, Inc.: Orlando, FL, USA, 1985. [Google Scholar]
- Gao, L.R.; Zhang, B.; Zhang, X.; Zhang, W.J.; Tong, Q.X. A New Operational Method for Estimating Noise in Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2008, 5, 83–87. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.-E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Acito, N.; Diani, M.; Corsini, G. Signal-Dependent Noise Modeling and Model Parameter Estimation in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2957–2971. [Google Scholar] [CrossRef]
- Wiener, N. The Interpolation, Extrapolation and Smoothing of Stationary Time Series; MIT Press: New York, NY, USA, 1949. [Google Scholar]
- Lim, J.S. Two-dimensional Signal and Image Processing; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1990; ISBN 0-13-935322-4. [Google Scholar]
- Lee, J.-S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 165–168. [Google Scholar] [CrossRef]
- Cao, X.; Xu, L.; Meng, D.; Zhao, Q.; Xu, Z. Integration of 3-dimensional discrete wavelet transform and Markov random field for hyperspectral image classification. Neurocomputing 2016. [Google Scholar] [CrossRef]
- Prasad, S.; Bruce, L.M. Limitations of principal components analysis for hyperspectral target recognition. IEEE Geosci. Remote Sens. Lett. 2008, 5, 625–629. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral-Spatial Hyperspectral Image Classification With Edge-Preserving Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature extraction of hyperspectral images with image fusion and recursive filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3742–3752. [Google Scholar] [CrossRef]
- Maggioni, M.; Foi, A. Nonlocal transform-domain denoising of volumetric data with groupwise adaptive variance estimation. Comput. Imaging X 2012, 8296, 82960O. [Google Scholar]
- Liu, X.; Bourennane, S.; Fossati, C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3717–3724. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. {LIBSVM}: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Estimation of signal subspace on hyperspectral data. Proc. SPIE 2005, 5982, 59820L. [Google Scholar]
- Story, M.; Congalton, R.G. Accuracy assessment: A user’s perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar]
- Kaewpijit, S.; Le Moigne, J.; El-Ghazawi, T. Automatic Reduction of Hyperspectral Imagery using Wavelet Spectral Analysis. IEEE Trans. Geosci. Remote Sens. 2003, 41, 863–871. [Google Scholar] [CrossRef]
| Class | Type | Samples | Training | Testing |
|---|---|---|---|---|
| 1 | Alfalfa | 46 | 23 | 23 |
| 2 | Corn-notill | 1428 | 100 | 1328 |
| 3 | Corn-mintill | 830 | 100 | 730 |
| 4 | Corn | 237 | 100 | 137 |
| 5 | Grass-pasture | 483 | 100 | 383 |
| 6 | Grass-trees | 730 | 100 | 630 |
| 7 | Grass-pasture-mowed | 28 | 14 | 14 |
| 8 | Hay-windrowed | 478 | 100 | 378 |
| 9 | Oats | 20 | 10 | 10 |
| 10 | Soybean-notill | 972 | 100 | 872 |
| 11 | Soybean-mintill | 2455 | 100 | 2355 |
| 12 | Soybean-clean | 593 | 100 | 493 |
| 13 | Wheat | 205 | 100 | 105 |
| 14 | Woods | 1265 | 100 | 1165 |
| 15 | Buildings-Grass-Trees-Drives | 386 | 100 | 286 |
| 16 | Stone-Steel-Towers | 93 | 47 | 46 |
| Total | 10,249 | 1294 | 8955 |
| Class | Type | Samples | Training | Testing |
|---|---|---|---|---|
| 1 | Brocoli greenweeds1 | 2009 | 100 | 1909 |
| 2 | Brocoligreenweeds2 | 3726 | 100 | 3626 |
| 3 | Fallow | 1976 | 100 | 1876 |
| 4 | Fallowroughplow | 1394 | 100 | 1294 |
| 5 | Fallowsmooth | 2678 | 100 | 2578 |
| 6 | Stubble | 3959 | 100 | 3859 |
| 7 | Celery | 3579 | 100 | 3479 |
| 8 | Grapesuntrained | 11,271 | 100 | 11,171 |
| 9 | Soilvinyarddevelop | 6203 | 100 | 6103 |
| 10 | Cornsenescedgreenweeds | 3278 | 100 | 3178 |
| 11 | Lettuceromaine4wk | 1068 | 100 | 968 |
| 12 | Lettuceromaine5wk | 1927 | 100 | 1827 |
| 13 | Lettuceromaine6wk | 916 | 100 | 816 |
| 14 | Lettuceromaine7wk | 1070 | 100 | 970 |
| 15 | Vinyarduntrained | 7268 | 100 | 7168 |
| 16 | Vinyardverticaltrellis | 1807 | 100 | 1707 |
| Total | 54,129 | 1600 | 52,529 |
| Class | Type | Samples | Training | Testing |
|---|---|---|---|---|
| 1 | Asphalt | 6631 | 300 | 6331 |
| 2 | Meadows | 18,649 | 300 | 18,349 |
| 3 | Gravel | 2099 | 300 | 1799 |
| 4 | Trees | 3064 | 300 | 2764 |
| 5 | Painted metal sheets | 1345 | 300 | 1045 |
| 6 | Bare Soil | 5029 | 300 | 4729 |
| 7 | Bitumen | 1330 | 300 | 1030 |
| 8 | Self-Blocking Bricks | 3682 | 300 | 3382 |
| 9 | Shadows | 947 | 300 | 647 |
| Total | 42,776 | 2700 | 40,076 |
| Abbreviations | Methods |
|---|---|
| SVM | Support Vector Machine |
| PCA_SVM | Principal Component Analysis followed by SVM |
| DCT_SVM | Spectral one-dimensional Discrete Cosine Transform followed by SVM |
| 2DCT_SVM | Two- dimensional DCT followed by SVM |
| CDCT-2DCT_SVM | Cascade spectral DCT spatial 2D-DCT followed by SVM |
| CDCT-WF_SVM | Cascade spectral DCT spatial Wiener filter followed by SVM |
| SDCT-2DCT_SVM | Serial spectral DCT spatial 2D-DCT followed by SVM |
| S2DCT-DCT_SVM | Serial spatial 2D-DCT spectral DCT followed by SVM |
| 3D_SVM | Three-dimensional Wavelet followed by SVM |
| 3DG_ SVM | Three-dimensional Wavelet with Graph Cut followed by SVM |
| EPF | Edge-Preserving Filtering |
| IFRF | Image Fusion and Recursive Filtering |
| BM4D_SVM | Block-Matching 4-D Filtering followed by SVM |
| PARAFAC_SVM | Parallel Factor Analysis followed by SVM |
| Methods | Parameters | Indian Pines | Salinas | Pavia University |
|---|---|---|---|---|
| CDCT-2DCT_SVM | - The count of the retained Spectral DCT coefficients | 10 | 10 | 10 |
| - 2D-DCT threshold | 500 | 500 | 500 | |
| CDCT-WF_SVM | - The count of the retained Spectral DCT coefficients | 5 | 5 | 5 |
| - Wiener filter patch size | 39 × 39 | 43 × 43 | 31 × 31 | |
| PCA_SVM | The count of PCs | 18 | 20 | 45 |
| All methods | The training samples size per class | 100 | 100 | 300 |
| Class | SVM | PCA_SVM | DCT_SVM | 2DCT_SVM | SDCT-2DCT_SVM | S2DCT-DCT_SVM | 3D_SVM | 3DG_SVM | EPF | IFRF | BM4D_SVM | PARAFAC_SVM | CDCT-WF_SVM | CDCT-2DCT_SVM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 88.70 | 78.26 | 86.96 | 90.00 | 94.35 | 84.78 | 98.68 | 98.70 | 100.00 | 71.70 | 91.74 | 93.48 | 98.70 | 96.96 |
| 2 | 72.71 | 56.44 | 71.50 | 63.83 | 77.51 | 57.58 | 76.42 | 81.31 | 85.71 | 74.25 | 83.25 | 77.64 | 92.12 | 90.16 |
| 3 | 70.11 | 59.40 | 66.55 | 68.16 | 81.90 | 54.77 | 81.59 | 90.92 | 90.79 | 49.74 | 80.78 | 73.90 | 94.44 | 95.00 |
| 4 | 80.95 | 75.26 | 86.57 | 90.80 | 97.15 | 80.00 | 98.32 | 99.64 | 65.07 | 63.15 | 91.68 | 96.50 | 97.88 | 98.83 |
| 5 | 92.69 | 88.98 | 86.74 | 92.66 | 88.12 | 81.67 | 96.89 | 97.10 | 96.01 | 80.51 | 95.48 | 92.87 | 98.09 | 97.42 |
| 6 | 95.22 | 91.70 | 87.54 | 95.25 | 93.40 | 84.44 | 97.22 | 99.56 | 99.46 | 89.60 | 96.60 | 97.08 | 99.29 | 99.24 |
| 7 | 92.14 | 78.57 | 89.29 | 97.86 | 95.00 | 88.57 | 95.00 | 97.14 | 100.00 | 0.00 | 87.86 | 87.86 | 96.43 | 92.14 |
| 8 | 96.75 | 95.79 | 96.35 | 98.84 | 98.57 | 95.08 | 100.00 | 100.00 | 100.00 | 100.00 | 98.99 | 99.68 | 100.00 | 99.79 |
| 9 | 78.00 | 66.00 | 80.00 | 84.00 | 89.00 | 72.00 | 100.00 | 97.00 | 100.00 | 0.00 | 89.00 | 94.00 | 100.00 | 99.00 |
| 10 | 72.99 | 55.09 | 68.14 | 60.56 | 71.36 | 48.86 | 80.91 | 89.91 | 71.34 | 61.48 | 82.26 | 78.41 | 90.92 | 90.01 |
| 11 | 56.24 | 46.82 | 48.91 | 46.37 | 53.93 | 34.00 | 75.23 | 83.72 | 91.69 | 94.19 | 68.74 | 70.28 | 90.64 | 82.70 |
| 12 | 72.72 | 51.89 | 70.65 | 59.47 | 77.87 | 44.99 | 91.03 | 96.41 | 66.39 | 42.11 | 83.87 | 80.34 | 94.02 | 95.72 |
| 13 | 98.76 | 96.86 | 97.05 | 99.52 | 99.05 | 97.33 | 99.14 | 99.71 | 100.00 | 81.76 | 99.14 | 99.33 | 99.71 | 99.43 |
| 14 | 85.95 | 86.47 | 83.58 | 90.64 | 88.88 | 78.64 | 95.72 | 96.21 | 99.24 | 97.89 | 92.46 | 91.79 | 98.89 | 99.30 |
| 15 | 71.47 | 60.24 | 68.32 | 86.71 | 92.90 | 71.57 | 95.10 | 99.93 | 78.47 | 79.09 | 88.43 | 92.69 | 98.15 | 98.60 |
| 16 | 97.39 | 97.61 | 97.17 | 100.00 | 99.78 | 99.57 | 98.91 | 92.83 | 93.67 | 97.50 | 96.74 | 99.35 | 96.96 | 98.48 |
| κ | 70.40 (0.79) | 59.63 (1.24) | 65.83 (1.32) | 65.27 (0.74) | 73.07 (0.87) | 53.34 (1.62) | 83.84 (0.78) | 88.87 (1.18) | 84.68 (1.96) | 71.06 (1.66) | 80.66 (0.64) | 78.95 (1.03) | 93.44 (1.03) | 90.81 (1.05) |
| OA | 73.97 (0.71) | 64.40 (1.13) | 69.82 (1.19) | 69.33 (0.71) | 76.27 (0.80) | 58.46 (1.63) | 86.12 (0.70) | 90.32 (1.04) | 85.61 (1.72) | 74.30 (1.46) | 83.08 (0.56) | 81.62 (0.92) | 94.31 (1.05) | 92.01 (0.92) |
| AA | 82.67 (0.97) | 74.09 (1.41) | 80.33 (1.59) | 82.79 (0.89) | 87.42 (1.13) | 73.37 (1.36) | 92.51 (0.72) | 95.01 (0.70) | 89.87 (1.60) | 67.69 (1.80) | 89.19 (0.87) | 89.08 (1.00) | 96.64 (0.56) | 95.80 (0.43) |
| Time(s) | 3.10 | 42.72 | 43.37 | 4.12 | 15.95 | 53.24 | 53.41 | 210.16 | 6.80 | 1.48 | 351.37 | 297.39 | 13.30 | 13.91 |
| Class | SVM | PCA_SVM | DCT_SVM | 2DCT_SVM | SDCT-2DCT_SVM | S2DCT-DCT_SVM | 3D_SVM | 3DG_SVM | EPF | IFRF | BM4D_SVM | PARAFAC_SVM | CDCT-WF_SVM | CDCT-2DCT_SVM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 99.13 | 99.36 | 97.53 | 99.64 | 97.02 | 96.89 | 99.19 | 99.70 | 100.00 | 98.99 | 99.25 | 97.33 | 99.52 | 99.50 |
| 2 | 99.51 | 99.52 | 98.83 | 99.13 | 96.64 | 97.43 | 99.35 | 99.68 | 99.97 | 100.00 | 99.63 | 96.05 | 99.78 | 99.59 |
| 3 | 99.58 | 99.09 | 99.47 | 94.88 | 91.92 | 90.36 | 97.48 | 98.95 | 96.07 | 99.84 | 99.77 | 96.08 | 98.97 | 99.39 |
| 4 | 99.34 | 99.35 | 99.18 | 98.98 | 98.56 | 97.98 | 99.36 | 99.43 | 98.43 | 90.05 | 99.30 | 96.02 | 99.23 | 99.51 |
| 5 | 98.74 | 97.78 | 98.03 | 96.57 | 94.84 | 94.17 | 98.98 | 99.46 | 99.80 | 99.98 | 98.55 | 86.14 | 98.36 | 98.25 |
| 6 | 99.68 | 99.67 | 99.68 | 99.71 | 99.74 | 99.74 | 99.86 | 99.95 | 99.99 | 100.00 | 99.67 | 99.44 | 99.62 | 99.65 |
| 7 | 99.57 | 99.56 | 99.45 | 99.65 | 99.02 | 97.31 | 99.66 | 99.67 | 99.93 | 99.79 | 99.55 | 98.58 | 99.65 | 99.64 |
| 8 | 67.98 | 72.40 | 74.40 | 70.87 | 63.49 | 59.75 | 86.27 | 88.67 | 85.40 | 99.53 | 78.00 | 77.13 | 94.85 | 91.46 |
| 9 | 99.00 | 97.50 | 98.09 | 98.60 | 96.47 | 96.86 | 98.43 | 99.18 | 98.73 | 99.98 | 99.47 | 88.52 | 99.46 | 99.41 |
| 10 | 95.01 | 94.51 | 93.17 | 93.54 | 90.19 | 89.74 | 93.79 | 95.60 | 93.60 | 99.72 | 96.36 | 73.28 | 97.76 | 95.15 |
| 11 | 98.90 | 98.75 | 97.23 | 97.22 | 94.29 | 94.63 | 99.68 | 99.93 | 97.58 | 99.02 | 98.97 | 85.23 | 98.80 | 99.52 |
| 12 | 99.82 | 99.70 | 99.57 | 97.62 | 95.64 | 89.59 | 99.97 | 99.87 | 99.67 | 98.82 | 99.84 | 82.19 | 99.93 | 99.93 |
| 13 | 99.58 | 99.55 | 98.13 | 99.17 | 98.03 | 95.69 | 99.02 | 98.97 | 99.83 | 97.70 | 99.72 | 89.34 | 99.46 | 99.90 |
| 14 | 97.76 | 97.92 | 95.59 | 97.70 | 98.43 | 96.55 | 98.01 | 98.19 | 97.89 | 97.58 | 98.43 | 93.89 | 98.12 | 99.04 |
| 15 | 70.04 | 70.51 | 69.71 | 70.55 | 65.84 | 64.22 | 75.92 | 85.52 | 77.68 | 83.06 | 79.72 | 81.56 | 96.19 | 93.62 |
| 16 | 98.86 | 98.88 | 98.51 | 98.71 | 97.87 | 96.07 | 98.83 | 98.70 | 99.71 | 100.00 | 98.48 | 95.72 | 98.87 | 99.21 |
| κ | 87.04 (0.62) | 87.86 (1.07) | 87.96 (0.86) | 87.20 (0.73) | 83.52 (0.53) | 81.86 (0.95) | 92.05 (0.41) | 94.44 (0.89) | 92.13 (0.90) | 96.28 (0.27) | 91.04 (0.69) | 85.49 (0.47) | 97.62 (0.33) | 96.30 (0.80) |
| OA | 88.36 (0.57) | 89.10 (0.97) | 89.20 (0.78) | 88.51 (0.65) | 85.18 (0.48) | 83.69 (0.86) | 92.88 (0.37) | 95.02 (0.79) | 92.95 (0.81) | 96.46 (0.25) | 91.96 (0.62) | 86.94 (0.73) | 97.86 (0.30) | 96.68 (0.72) |
| AA | 95.16 (0.20) | 95.25 (0.41) | 94.78 (0.34) | 94.53 (0.36) | 92.37 (0.23) | 91.06 (0.45) | 96.49 (0.15) | 97.59 (0.36) | 96.52 (0.31) | 97.65 (0.29) | 96.54 (0.21) | 89.78 (0.39) | 98.66 (0.16) | 98.30 (0.32) |
| Time(s) | 7.24 | 13.18 | 64.46 | 12.81 | 90.42 | 102.00 | 183.59 | 1142.52 | 19.29 | 4.77 | 1854.07 | 1634.3 | 61.22 | 70.56 |
| Class | SVM | PCA_SVM | DCT_SVM | 2DCT_SVM | SDCT-2DCT_SVM | S2DCT-DCT_SVM | 3D_SVM | 3DG_SVM | EPF | IFRF | BM4D_SVM | PARAFAC_SVM | CDCT-WF_SVM | CDCT-2DCT_SVM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 71.71 | 72.13 | 74.59 | 58.67 | 54.54 | 65.52 | 96.89 | 98.88 | 98.68 | 76.18 | 80.07 | 77.90 | 97.96 | 96.21 |
| 2 | 82.91 | 82.79 | 79.16 | 65.90 | 60.75 | 67.14 | 97.64 | 98.91 | 97.20 | 97.90 | 89.49 | 85.37 | 99.66 | 98.02 |
| 3 | 78.89 | 78.23 | 81.89 | 61.86 | 54.57 | 62.01 | 88.15 | 90.08 | 92.51 | 52.39 | 82.61 | 70.81 | 98.87 | 97.23 |
| 4 | 91.89 | 91.00 | 86.28 | 87.64 | 83.49 | 80.34 | 99.01 | 99.42 | 67.81 | 84.99 | 94.15 | 93.85 | 95.92 | 97.38 |
| 5 | 99.70 | 99.70 | 99.75 | 99.89 | 99.92 | 99.88 | 100.00 | 100.00 | 99.89 | 98.85 | 99.66 | 99.78 | 99.78 | 99.77 |
| 6 | 84.39 | 77.94 | 68.45 | 63.63 | 56.13 | 55.24 | 96.68 | 99.16 | 64.31 | 92.74 | 89.76 | 84.83 | 99.39 | 98.16 |
| 7 | 76.96 | 77.57 | 84.98 | 60.96 | 57.36 | 71.27 | 98.91 | 99.53 | 77.25 | 64.22 | 85.59 | 77.89 | 99.49 | 98.63 |
| 8 | 69.44 | 71.07 | 75.54 | 53.59 | 47.35 | 59.56 | 94.64 | 96.08 | 84.40 | 53.24 | 75.88 | 74.30 | 97.62 | 93.75 |
| 9 | 99.91 | 99.86 | 99.94 | 99.72 | 99.77 | 99.86 | 99.63 | 99.72 | 96.17 | 43.63 | 99.88 | 99.92 | 99.88 | 99.91 |
| κ | 75.24 (1.43) | 74.25 (2.16) | 71.74 (1.15) | 56.52 (1.95) | 50.32 (1.39) | 57.58 (1.36) | 95.88 (0.30) | 97.82 (0.12) | 82.79 (1.03) | 77.63 (0.25) | 83.00 (1.40) | 80.91 (0.47) | 97.87 (0.26) | 96.48 (0.42) |
| OA | 81.18 (1.15) | 80.49 (1.75) | 78.51 (1.14) | 66.07 (1.56) | 60.95 (2.00) | 67.01 (1.82) | 96.95 (0.22) | 98.39 (0.09) | 86.81 (1.68) | 83.14 (0.19) | 87.23 (1.10) | 83.99 (0.40) | 98.71 (0.19) | 97.40 (0.32) |
| AA | 83.98 (0.69) | 83.37 (1.68) | 83.40 (1.73) | 72.43 (1.47) | 68.21 (1.64) | 73.42 (1.52) | 96.84 (0.14) | 97.98 (0.12) | 86.47 (1.01) | 73.79 (0.17) | 88.57 (0.79) | 84.96 (0.40) | 98.73 (0.19) | 97.67 (0.18) |
| Time(s) | 80.05 | 78.68 | 186.10 | 116.79 | 252.69 | 216.92 | 485.92 | 2142.40 | 52.84 | 18.14 | 1535.13 | 1275.06 | 124.93 | 142.74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazine, R.; Wu, H.; Boukhechba, K. Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification. Remote Sens. 2019, 11, 1405. https://doi.org/10.3390/rs11121405
Bazine R, Wu H, Boukhechba K. Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification. Remote Sensing. 2019; 11(12):1405. https://doi.org/10.3390/rs11121405
Chicago/Turabian StyleBazine, Razika, Huayi Wu, and Kamel Boukhechba. 2019. "Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification" Remote Sensing 11, no. 12: 1405. https://doi.org/10.3390/rs11121405
APA StyleBazine, R., Wu, H., & Boukhechba, K. (2019). Spatial Filtering in DCT Domain-Based Frameworks for Hyperspectral Imagery Classification. Remote Sensing, 11(12), 1405. https://doi.org/10.3390/rs11121405






