Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy
Abstract
1. Introduction
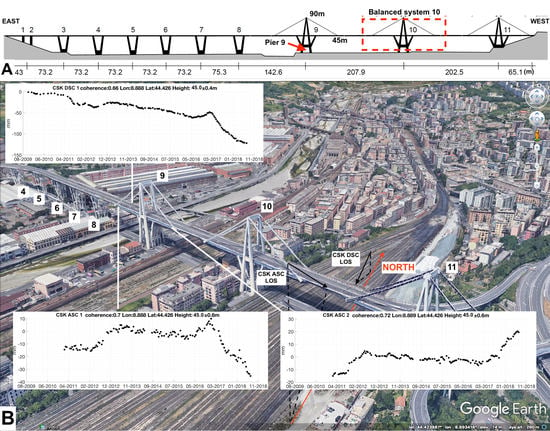
1.1. The Morandi Bridge
2. Materials and Methods
2.1. Multi-Temporal InSAR
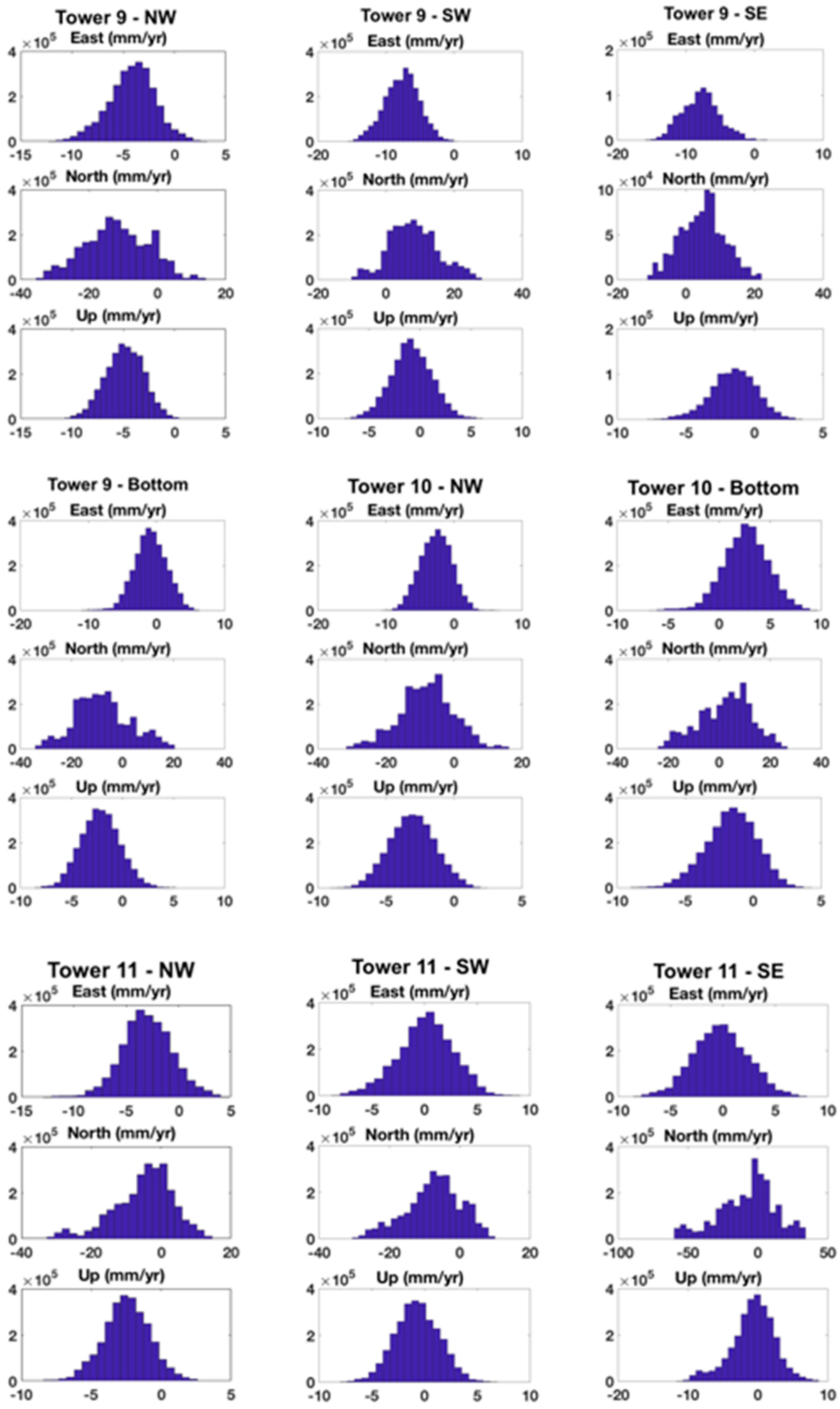
2.2. Markov Chain Monte Carlo
| Algorithm 1. Markov Chain Monte Carlo Algorithm steps |
| 1. Initialize E, N, U initial value Calculate CSK, ASC/DSC and SNT LOS projections |
| 2. Calculate error |
| 3. Random increment in (E,N,U) |
| 4. Recalculate and |
| If uniformly distributed random number in the interval (0,1) < 5. Then keep solution and iterate from points 1. to 5. until reaching 3 MLN of kept solutions |
| Else reiterate from points 3 to 5. |
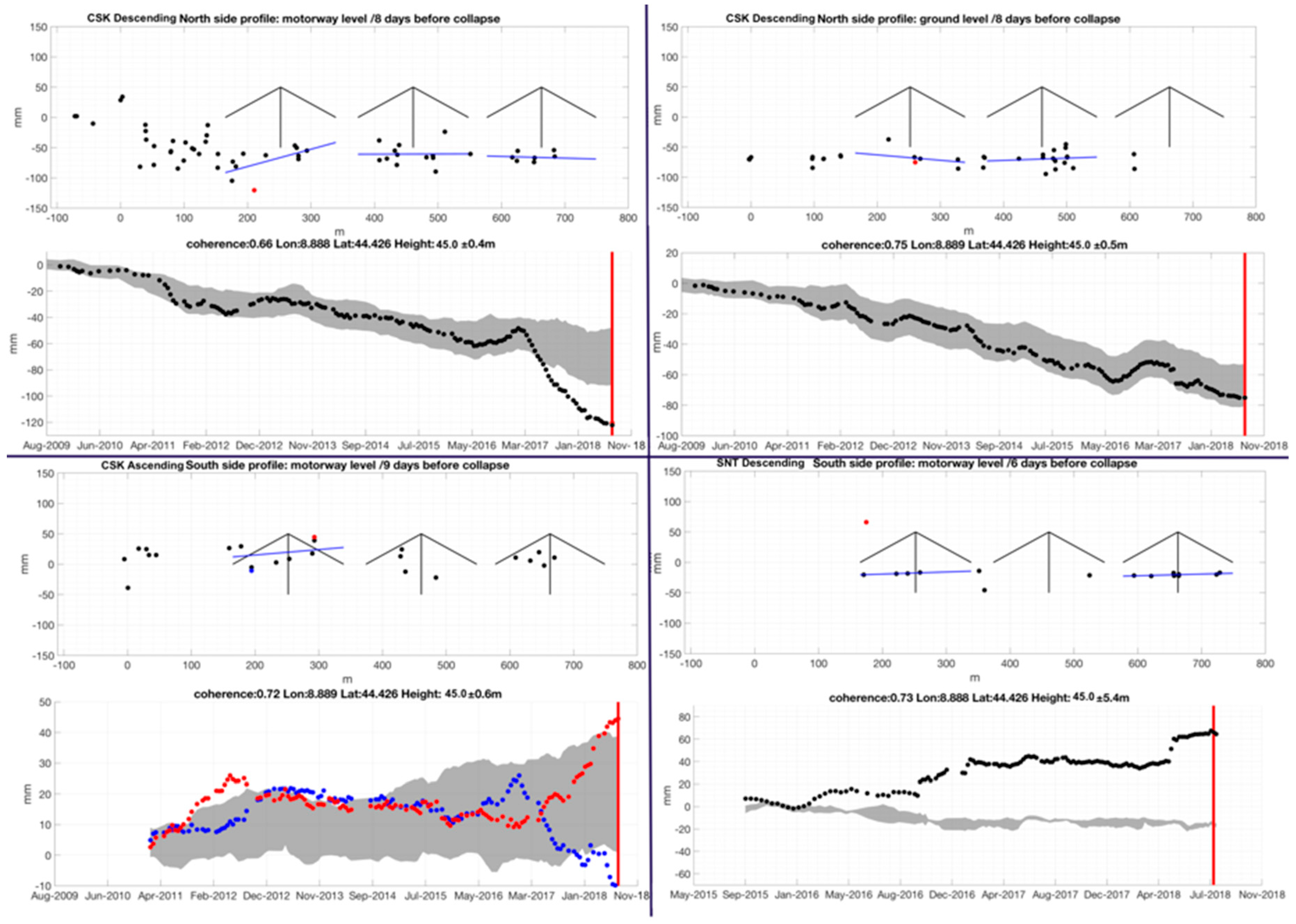
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Milillo, P.; Bürgmann, R.; Lundgren, P.; Salzer, J.; Perissin, D.; Fielding, E.; Biondi, F.; Milillo, G. Space geodetic monitoring of engineered structures: The ongoing destabilisation of the Mosul dam, Iraq. Sci. Rep. 2016, 6, 37408. [Google Scholar] [CrossRef]
- Cigna, F.; Lasaponara, R.; Masini, N.; Milillo, P.; Tapete, D. Persistent Scatterer Interferometry Processing of COSMO-SkyMed StripMap HIMAGE Time Series to Depict Deformation of the Historic Centre of Rome, Italy. Remote Sens. 2014, 6, 12593–12618. [Google Scholar] [CrossRef]
- Boni, R.; Bosino, A.; Meisina, C.; Novellino, A.; Bateson, L.; McCormack, H. A Methodology to Detect and Characterize Uplift Phenomena in Urban Areas Using Sentinel-1 Data. Remote Sens. 2018, 10, 607. [Google Scholar] [CrossRef]
- Chatterjee, R.; Fruneau, B.; Rudant, J.; Roy, P.; Frison, P.-L.; Lakhera, R.; Dadhwal, V.; Saha, R.; Dadhwal, V. Subsidence of Kolkata (Calcutta) City, India during the 1990s as observed from space by Differential Synthetic Aperture Radar Interferometry (D-InSAR) technique. Remote Sens. Environ. 2006, 102, 176–185. [Google Scholar] [CrossRef]
- Floris, M.; Fontana, A.; Tessari, G.; Mulè, M. Subsidence Zonation Through Satellite Interferometry in Coastal Plain Environments of NE Italy: A Possible Tool for Geological and Geomorphological Mapping in Urban Areas. Remote Sens. 2019, 11, 165. [Google Scholar] [CrossRef]
- Stramondo, S.; Bozzano, F.; Marra, F.; Wegmuller, U.; Cinti, F.; Moro, M.; Saroli, M. Subsidence induced by urbanisation in the city of Rome detected by advanced InSAR technique and geotechnical investigations. Remote Sens. Environ. 2008, 112, 3160–3172. [Google Scholar] [CrossRef]
- Bozzano, F.; Esposito, C.; Mazzanti, P.; Patti, M.; Scancella, S. Imaging Multi-Age Construction Settlement Behaviour by Advanced SAR Interferometry. Remote Sens. 2018, 10, 1137. [Google Scholar] [CrossRef]
- Ma, P.; Lin, H.; Lan, H.; Chen, F. Multi-dimensional SAR tomography for monitoring the deformation of newly built concrete buildings. ISPRS J. Photogramm. Remote Sens. 2015, 106, 118–128. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; DeJong, M.J.; Perissin, D.; Milillo, G. Multi-Temporal InSAR Structural Damage Assessment: The London Crossrail Case Study. Remote Sens. 2018, 10, 287. [Google Scholar] [CrossRef]
- Giardina, G.; Milillo, P.; DeJong, M.; Perissin, D.; Milillo, G. Evaluation of InSAR monitoring data for post-tunnelling settlement damage assessment. Struct. Control Health Monit. 2019, 26, e2285. [Google Scholar] [CrossRef]
- Roccheggiani, M.; Piacentini, D.; Tirincanti, E.; Perissin, D.; Menichetti, M. Detection and Monitoring of Tunneling Induced Ground Movements Using Sentinel-1 SAR Interferometry. Remote Sens. 2019, 11, 639. [Google Scholar] [CrossRef]
- Rousset, B.; Jolivet, R.; Simons, M.; Lasserre, C.; Riel, B.; Milillo, P.; Çakir, Z.; Renard, F. An aseismic slip transient on the North Anatolian Fault. Geophys. Res. Lett. 2016, 43, 3254–3262. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M. A Weighted Overlay Method for Liquefaction-Related Urban Damage Detection: A Case Study of the 6 September 2018 Hokkaido Eastern Iburi Earthquake, Japan. Geosci. 2018, 8, 487. [Google Scholar] [CrossRef]
- Di Naccio, D.; Kastelic, V.; Carafa, M.M.C.; Esposito, C.; Milillo, P.; Di Lorenzo, C. Gravity Versus Tectonics: The Case of 2016 Amatrice and Norcia (Central Italy) Earthquakes Surface Coseismic Fractures. J. Geophys. Res. Earth Surf. 2019, 124, 994–1017. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.; Baker, B. Remote sensing of ground deformation for monitoring groundwater management practices: Application to the Santa Clara Valley during the 2012–2015 California drough. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Confuorto, P.; Di Martire, D.; Infante, D.; Novellino, A.; Papa, R.; Calcaterra, D.; Ramondini, M. Monitoring of remedial works performance on landslide-affected areas through ground- and satellite-based techniques. Catena 2019, 178, 77–89. [Google Scholar] [CrossRef]
- Sousa, J.J.; Bastos, L. Multi-temporal SAR interferometry reveals acceleration of bridge sinking before collapse. Nat. Hazards Earth Syst. Sci. 2013, 13, 659–667. [Google Scholar] [CrossRef]
- Selvakumaran, S.; Plank, S.; Geiß, C.; Rossi, C.; Middleton, C. Remote monitoring to predict bridge scour failure using Interferometric Synthetic Aperture Radar (InSAR) stacking techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Milillo, P.; Riel, B.; Minchew, B.; Yun, S.-H.; Simons, M.; Lundgren, P. On the Synergistic Use of SAR Constellations Data Exploitation for Earth Science and Natural Hazard Response. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1095–1100. [Google Scholar] [CrossRef]
- Morandi, R. Concrete Cable-stayed Structures; L’Industria Italiana del Cemento: Rome, Italy, 1980; Volume 10, pp. 887–910. (In Italian) [Google Scholar]
- Morandi, R. Il viadotto sul Polcevera per l’autostrada Genova-Savona; L’Industria Italiana del Cemento: Rome, Italy, 1967; Volume 12, pp. 849–873. (In Italian) [Google Scholar]
- Gentile, C.; Cabrera, F.M.Y. Dynamic investigation of a repaired cable-stayed bridge. Earthq. Eng. Struct. Dyn. 1997, 26, 41–59. [Google Scholar] [CrossRef]
- Bazzucchi, F.; Restuccia, L.; Ferro, G. Considerations over the Italian road bridge infrastructure safety after the Polcevera viaduct collapse: Past errors and future perspectives. Frattura ed Integrità Strutturale 2018, 12, 400–421. [Google Scholar] [CrossRef]
- Malerba, P.G. Inspecting and repairing old bridges: Experiences and lessons. Struct. Infrastruct. Eng. 2014, 10, 443–470. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation isong permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Costantini, M.; Ferretti, A.; Minati, F.; Falco, S.; Trillo, F.; Colombo, D.; Novali, F.; Malvarosa, F.; Mammone, C.; Vecchioli, F.; et al. Analysis of surface deformations over the whole Italian territory by interferometric processing of ERS, Envisat and COSMO-SkyMed radar data. Remote Sens. Environ. 2017, 202, 250–275. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Mortellaro, A.; Ievolella, G.; Lombardo, F.; Nuti, C.; Nanzi, I. Relazione della Commissione Ispettiva Ministeriale crollo Viadotto Polcevera; Ministero delle Infrastrutture e dei Trasporti: Roma, Italy, 2018. Available online: http://www.mit.gov.it/comunicazione/news/ponte-crollo-ponte-morandi-commissione-ispettiva-genova/ponte-morandi-online-la (accessed on 19 May 2019).
- Calvi, G.M.; Moratti, M.; O’Reilly, G.J.; Scattarreggia, N.; Monteiro, R.; Malomo, D.; Calvi, P.M.; Pinho, R. Once upon a Time in Italy: The Tale of the Morandi Bridge. Struct. Eng. Int. 2018, 29, 198–217. [Google Scholar] [CrossRef]
- Wolff, M.; Starossek, U. Cable loss and progressive collapse in cable-stayed bridges. Bridg. Struct. 2009, 5, 17–28. [Google Scholar] [CrossRef]
- Costantini, M.; Malvarosa, F.; Minati, F.; Trillo, F.; Vecchioli, F. Complementarity of high-resolution COSMO-SkyMed and medium-resolution Sentinel-1 SAR interferometry: Quantitative analysis of real target displacement and 3D positioning measurement precision, and potential operational scenarios. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 2017, Fort Worth, TX, USA, 23–28 July 2017; pp. 4602–4605. [Google Scholar]
- Bovenga, F.; Belmonte, A.; Refice, A.; Pasquariello, G.; Nutricato, R.; Nitti, D.O.; Chiaradia, M.T. Performance Analysis of Satellite Missions for Multi-Temporal SAR Interferometry. Sensors 2018, 18, 1359. [Google Scholar] [CrossRef]

| Dataset | Incidence Angle (Degree) | Heading Angle (Degree) | Average Acq. Sampling (Days) | Resolution RNG (m) × AZ (m) |
|---|---|---|---|---|
| CSK Ascending | 33.98 | –10.6 | 16 | 3 × 3 |
| CSK Descending | 26.63 | –168.5 | 16 | 3 × 3 |
| SNT Descending | 33.90 | –169.2 | 6 | 5 × 20 |
| 2018–2015 | Sentinel DSC (mm/yr) | CSK DSC (mm/yr) | CSK ASC (mm/yr) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| WEST | AVG. | EAST | WEST | AVG. | EAST | WEST | AVG. | EAST | |
| System 9 North | –4.8 | –2.9 | 0 | –5.3 | –3.7 | 0 | –0.5 | –0.6 | 0 |
| System 10 North | 5 | 2.2 | 0 | 3.6 | 1.2 | 0 | –3.6 | –4 | 0 |
| System 11 North | –4.8 | –1.3 | 0 | –1.3 | 0.3 | 0 | –0.4 | 1.6 | 0 |
| System 9 South | –0.5 | 0.6 | –0.5 | / | / | / | 5.6 | 1.4 | 6.8 |
| System 10 South | / | / | / | / | / | / | –3 | –3.4 | –2.7 |
| System 11 South | 0.4 | –0.7 | 0 | / | / | / | 0.1 | –0.2 | 0.4 |
| System 9 Ground | / | –3 | / | / | 0.1 | / | / | –0.6 | / |
| System 10 Ground | / | –0.6 | / | / | –0.1 | / | / | –3.3 | / |
| System 11 Ground | / | –1.5 | / | / | 2 | / | / | / | / |
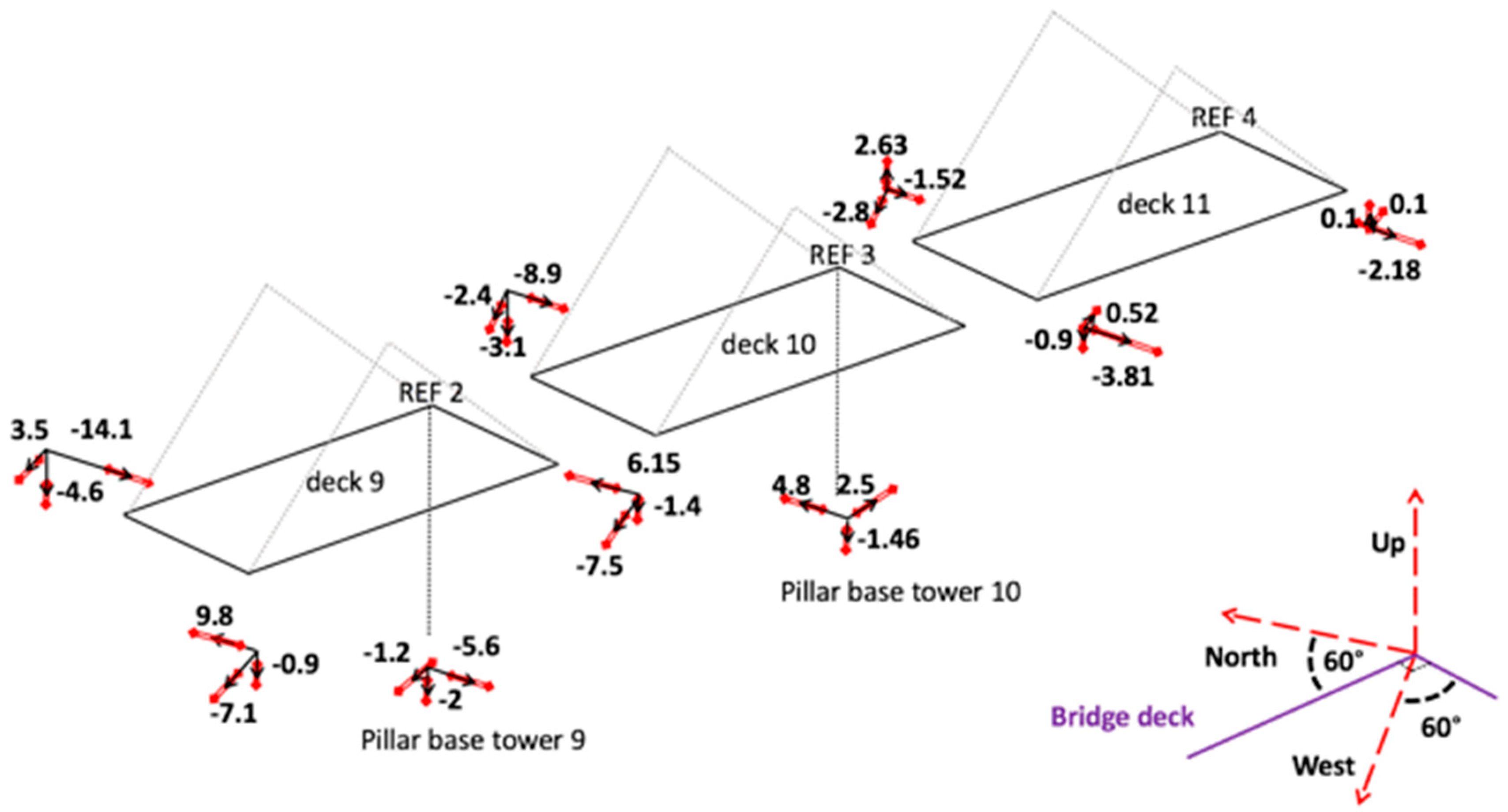
| Trends (mm/yr) | Accuracy(mm/yr) | |||||
|---|---|---|---|---|---|---|
| E | N | U | EE | EN | EU | |
| Deck 9 NW | –3.5 | –14.1 | –4.6 | 2.1 | 7.5 | 1.1 |
| Deck 9 SW | –7.1 | 9.8 | –0.9 | 2 | 6.1 | 1 |
| Deck 9 SE | –7.5 | 6.15 | –1.4 | 3.5 | 6 | 1.1 |
| Deck 9 B | –1.2 | –5.6 | –2 | 2 | 5.3 | 1.5 |
| Deck 10 NW | –2.4 | –8.9 | –3.1 | 2.1 | 4.5 | 1.1 |
| Deck 10 B | 2.5 | 4.8 | –1.46 | 2.1 | 6.5 | 1.1 |
| Deck 11 NW | –2.8 | –1.52 | 2.63 | 2.2 | 4 | 1.1 |
| Deck 11 SW | 0.52 | –3.81 | –0.9 | 0.7 | 5.1 | 1.3 |
| Deck 11 SE | 0.1 | –2.18 | 0.1 | 1.3 | 6 | 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sens. 2019, 11, 1403. https://doi.org/10.3390/rs11121403
Milillo P, Giardina G, Perissin D, Milillo G, Coletta A, Terranova C. Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sensing. 2019; 11(12):1403. https://doi.org/10.3390/rs11121403
Chicago/Turabian StyleMilillo, Pietro, Giorgia Giardina, Daniele Perissin, Giovanni Milillo, Alessandro Coletta, and Carlo Terranova. 2019. "Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy" Remote Sensing 11, no. 12: 1403. https://doi.org/10.3390/rs11121403
APA StyleMilillo, P., Giardina, G., Perissin, D., Milillo, G., Coletta, A., & Terranova, C. (2019). Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sensing, 11(12), 1403. https://doi.org/10.3390/rs11121403