Predicting Taxi Demand Based on 3D Convolutional Neural Network and Multi-task Learning
Abstract
:1. Introduction
- First of all, traffic data are affected by complex spatial–temporal correlation, and there is an apparent periodicity in traffic data. Traffic states between different regions will affect each other, and there may be interactions between regions that are far away. Although the models combining CNN, RNN and their variants have achieved good results, this kind of method separates the interaction between temporal correlation and spatial correlation.
- Secondly, there is little work in predicting taxi drop-off demand. If there is a high taxi demand for drop-off in a particular region at a certain time, the vacancy rate of taxis in this region will be high, and it will be required for reasonable evacuation. At the same time, the high traffic volume will be a test for the infrastructure and road conditions of the corresponding region. Therefore, predicting taxi demand for drop-off can provide advice to taxi drivers and city managers. Besides, taxi demand for pick-up and drop-off may affect each other, since empty cars may stimulate people’s desire to take a taxi and increase the number of taxi pick-ups in surrounding areas.
- We propose to consider the prediction of taxi demand for pick-up and drop-off as related tasks, and we constructed a feature extraction component based on multi-task learning and 3D CNN to extract spatiotemporal features concurrently.
- We propose to deem the demand situation of the urban taxi as a video and use 3D CNN to capture the spatiotemporal correlation and the complex correlation between taxi demand for pick-up and drop-off.
- We combined external factors, such as weather, day of the week and public transport conditions, to simultaneously predict taxi demand for pick-up and drop-off.
- We conducted extensive theoretical analysis and experiments on a real-world dataset in Chengdu and achieved better performance and efficiency than other baselines.
2. Related Work
2.1. Traditional Approach
2.2. Deep Learning Approach
3. Preliminary
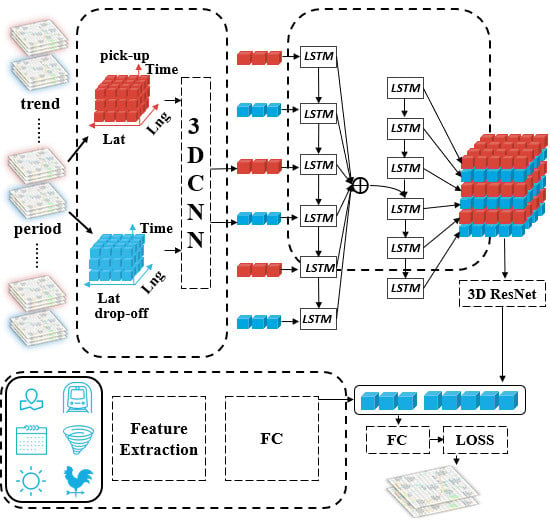
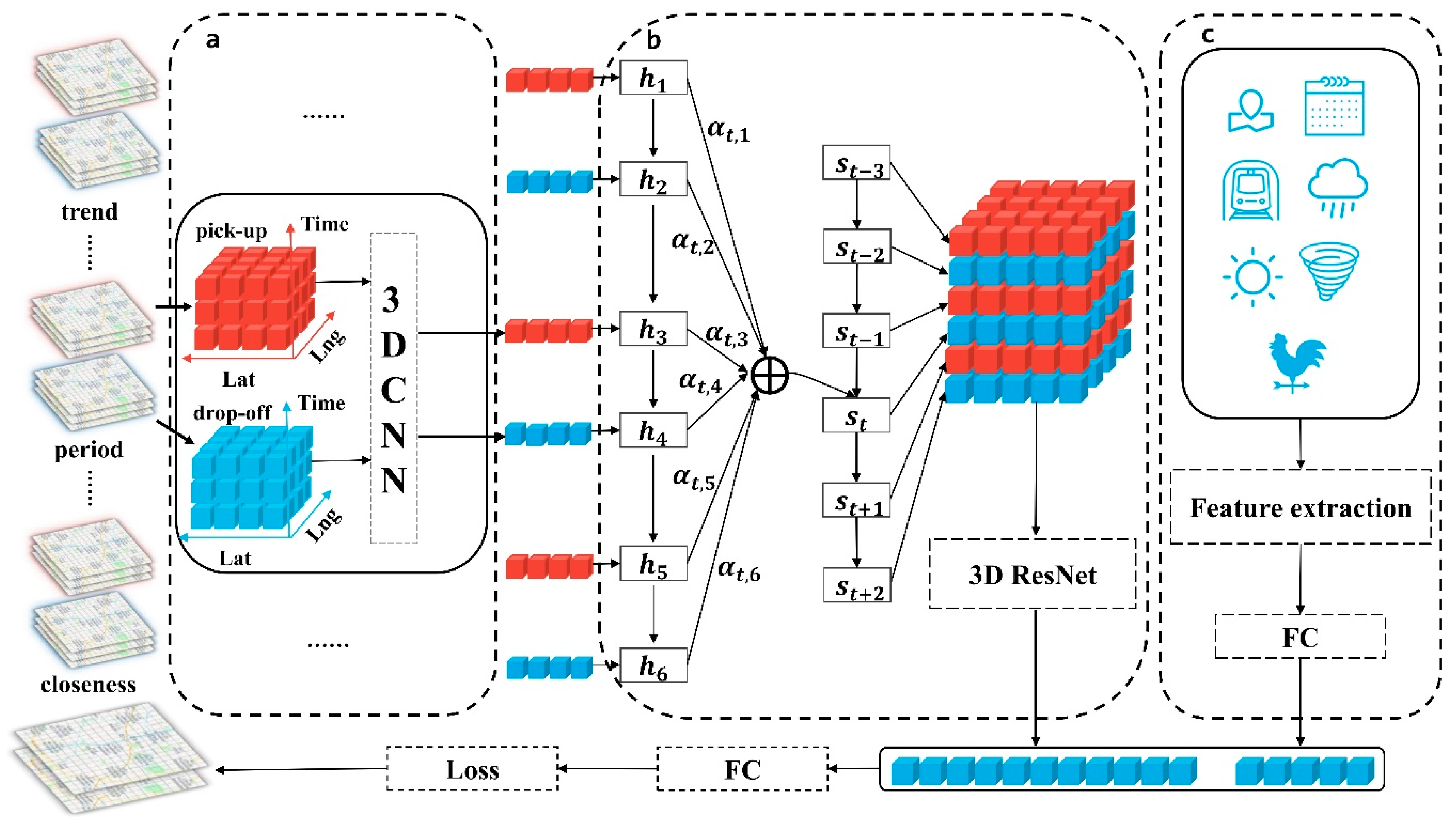
4. Method
- is the category of data, that is, for taxi pick-up data and taxi drop-off data.
- is the depth of data.
- is the number of grid columns.
- is the number of grid rows.
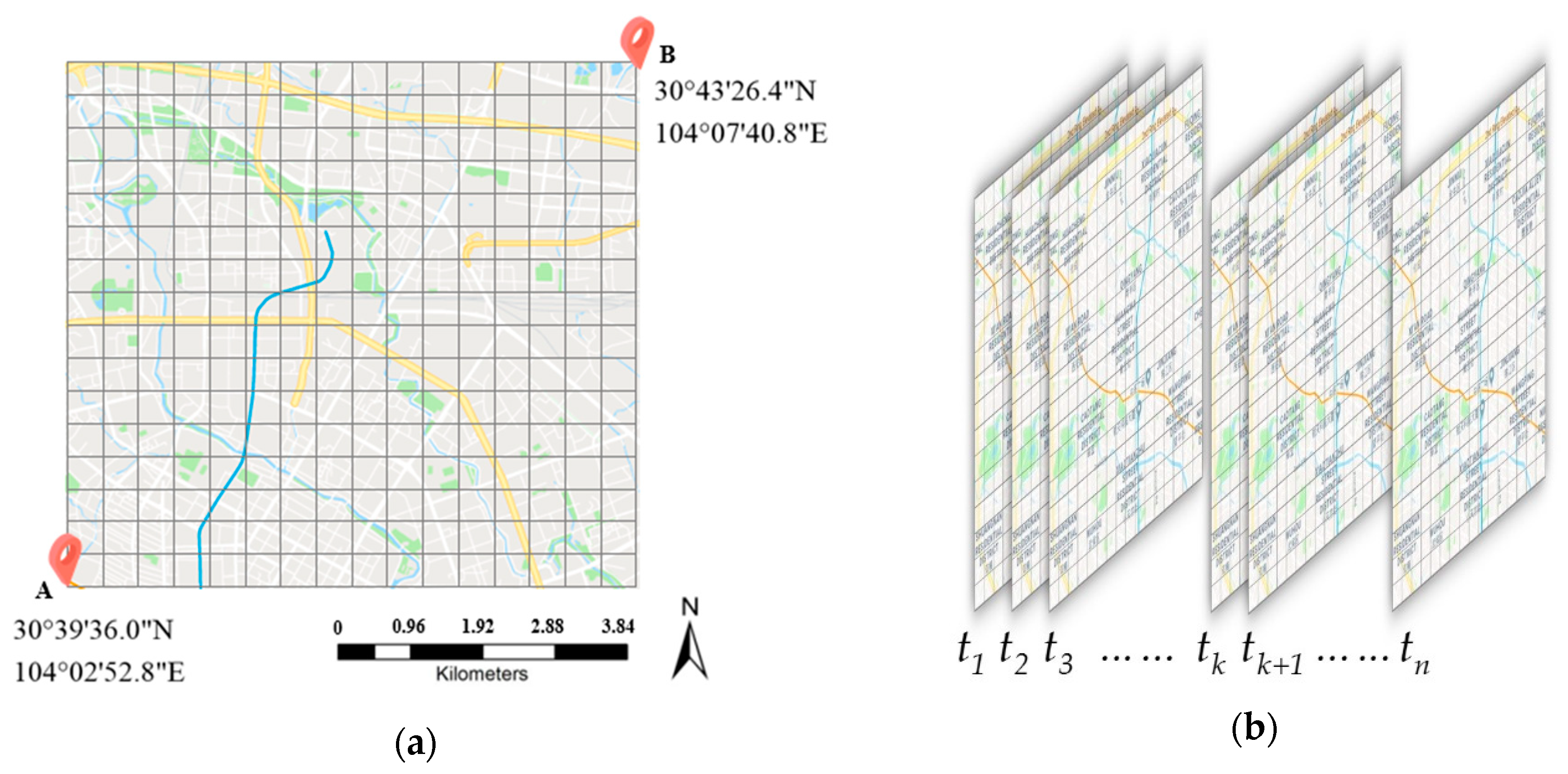
4.1. Partition of Historical Data
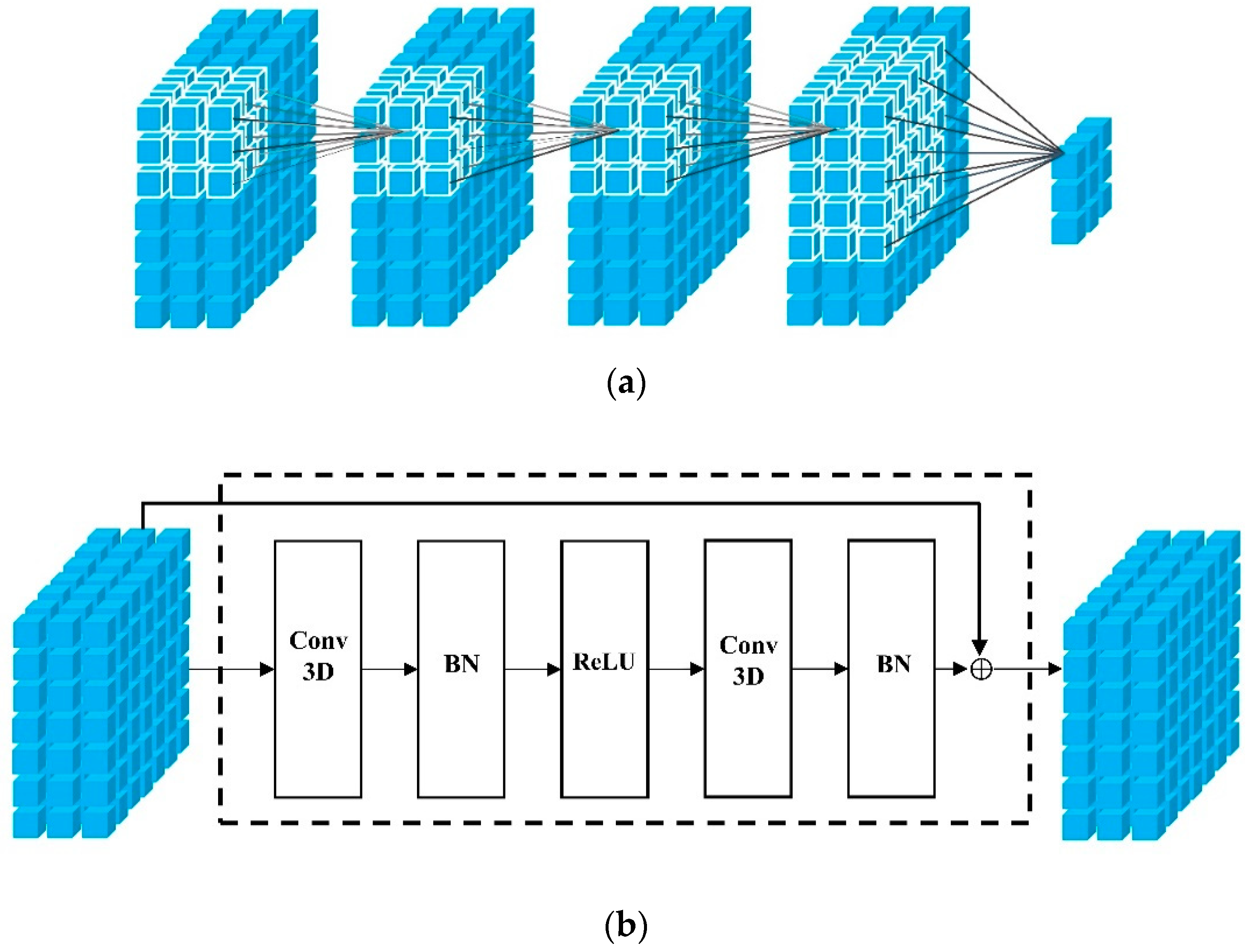
4.2. Multi-Task Spatiotemporal Feature Extraction Component
4.3. Feature Embedding Component
4.4. External Factors Component
4.5. Prediction Component
5. Experiment and Discussion
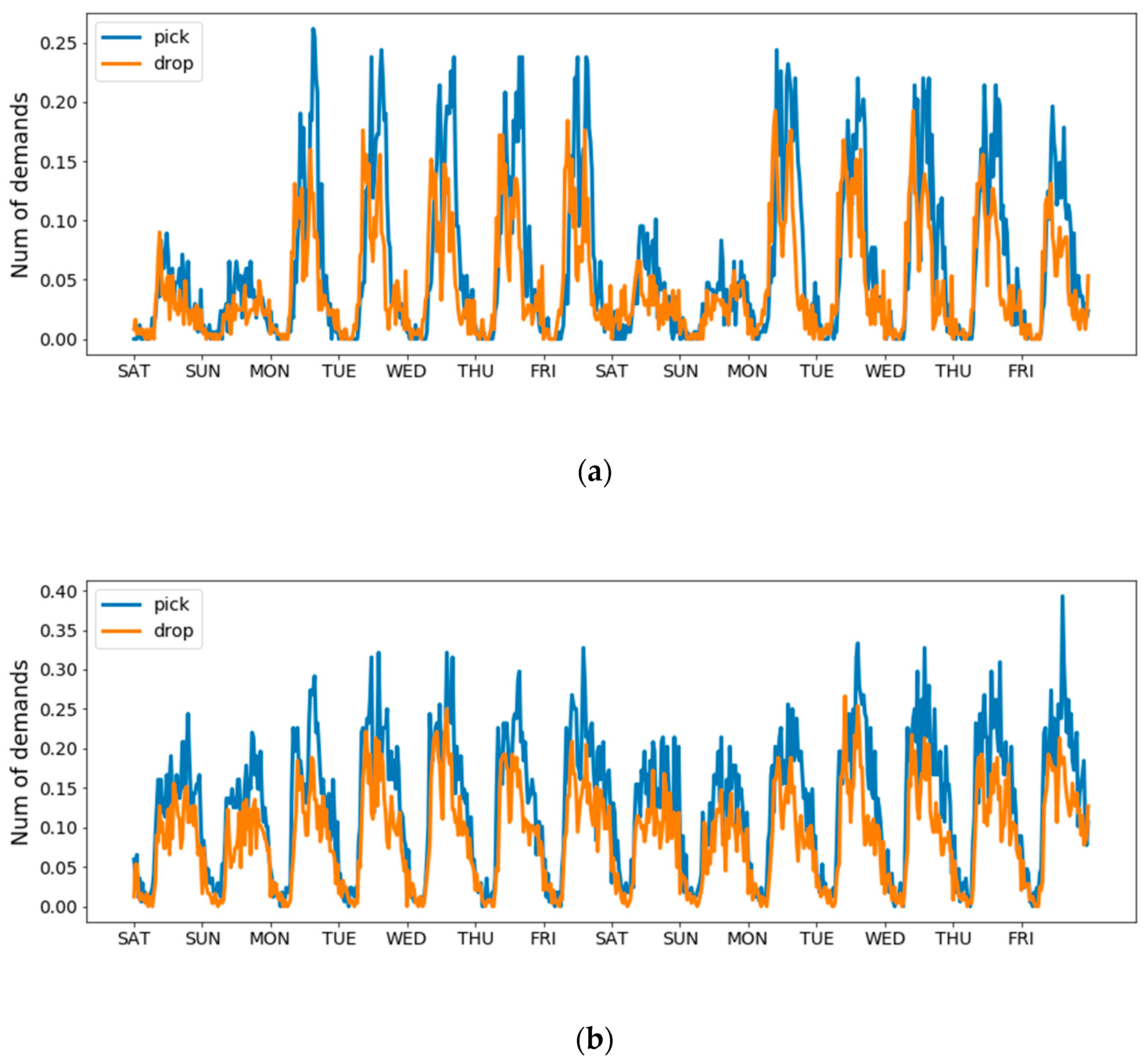
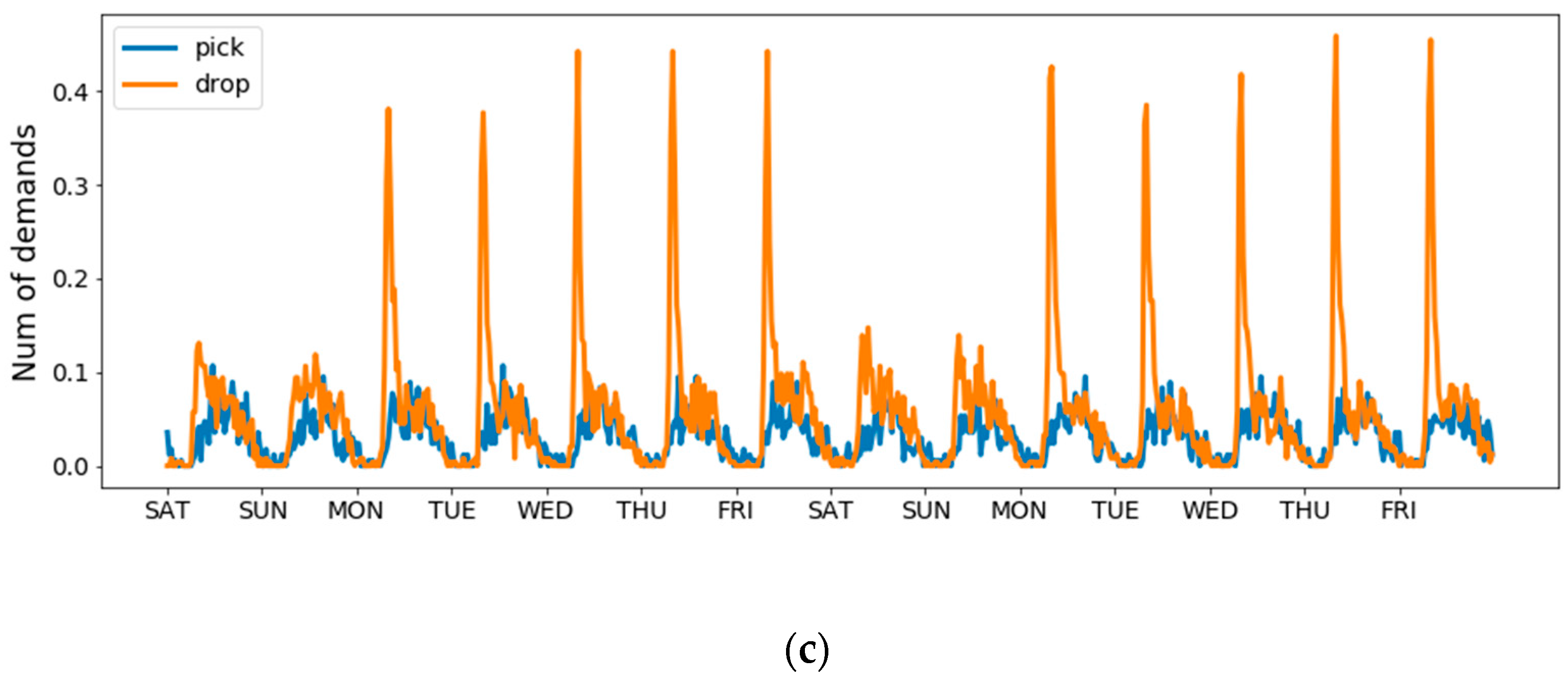
5.1. Dataset
5.2. Experimental Settings
5.3. Baselines
- Historical average (HA): By simply averaging the values of previous taxi pick-up and taxi drop-off demands at the same location and the same time interval, we can get the predicted value.
- Autoregressive integrated moving average (ARIMA): ARIMA is a well-known model for predicting times series.
- XGBoost: XGBoost is a well-known powerful model and is widely used by data scientists to achieve state-of-the-art results on many machine learning challenges [56].
- Multiple layer perceptron (MLP): We compared our model with an MLP which consisted of 4 hidden layers. Each layer had 128, 128, 128, and 64 hidden units, respectively.
- Long Short-Term Memory: LSTM is a special kind of RNN, capable of learning long-term dependencies, and it is widely used in time series processing.
- ST-ResNet [8]: ST-ResNet is an end-to-end traffic prediction approach based on deep learning, which uses the residual network to capture the spatial and temporal characteristics of crowd traffic, and also combines with external factors.
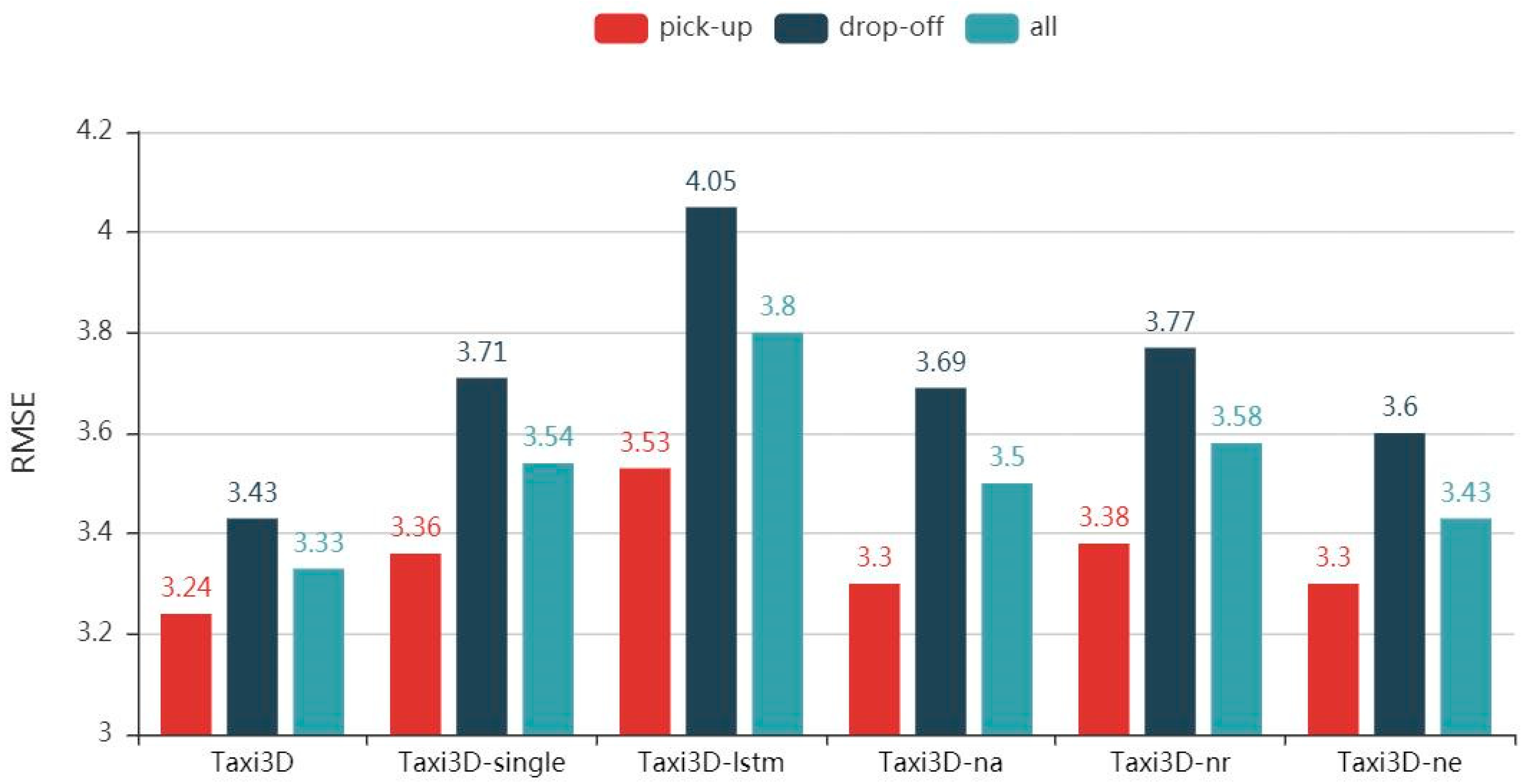
- Taxi3D-single: To verify the effectiveness of MTL, in this variant, we designed two independent networks which extracted spatiotemporal features from taxi pick-up data and drop-off data respectively. We then stacked the outputs and fed them into the feature embedding component as Taxi3D does.
- Taxi3D-lstm: In this variant, we fed the output of the multi-task spatiotemporal feature extraction component into the LSTM for predicting.
- Taxi3D-na: Taxi3D without attention-based LSTM; we simply reshaped the output of Figure 2a and stacked them into tensor, which was taken as the input of 3D ResNet.
- Taxi3D-nr: We used a 4-layers 3D CNN instead of 3D ResNet in feature embedding component.
- Taxi3D-ne: This variant removes the external factors component.
5.4. Evaluation Metric
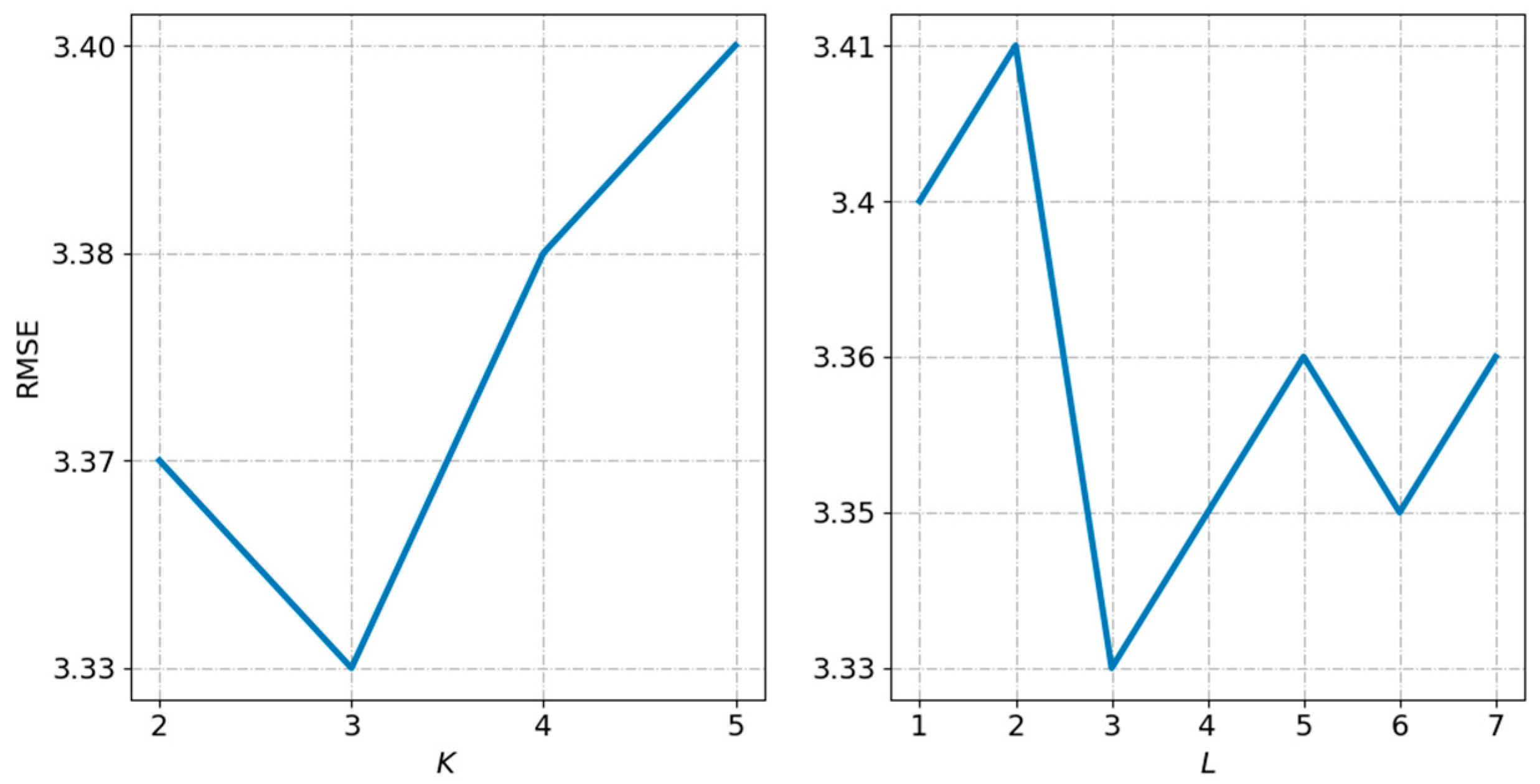
5.5. Tuning Hyperparameters
5.6. Model Comparsion
5.7. Variants Comparsion
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williams, B.M.; Hoel, L.A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Shekhar, S.; Williams, B. Adaptive seasonal time series models for forecasting short-term traffic flow. Transp. Res. Rec. J. Transp. Res. Board 2008, 2024, 116–125. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Gama, J.; Ferreira, M.; Mendes-Moreira, J.; Damas, L. Predicting taxi–passenger demand using streaming data. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1393–1402. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Ma, X.; Yu, H.; Wang, Y.; Wang, Y. Large-scale transportation network congestion evolution prediction using deep learning theory. PLoS ONE 2015, 10, e0119044. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X. DNN-based prediction model for spatio-temporal data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Burlingame, CA, USA, 31 October–3 Novembe 2016; p. 92. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In Proceedings of the AAAI, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Xu, J.; Rahmatizadeh, R.; Bölöni, L.; Turgut, D. Real-time prediction of taxi demand using recurrent neural networks. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2572–2581. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H. Short-Term Traffic Flow Forecasting with Spatial–Temporal Correlation in a Hybrid Deep Learning Framework. Available online: https://arxiv.org/pdf/1612.01022.pdf (accessed on 28 May 2019).
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef]
- Yao, H.; Wu, F.; Ke, J.; Tang, X.; Jia, Y.; Lu, S.; Gong, P.; Ye, J.; Li, Z. Deep multi-view spatial-temporal network for taxi demand prediction. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Yin, Y.; Chen, L.; Wan, J. Location-aware service recommendation with enhanced probabilistic matrix factorization. IEEE Access 2018, 6, 62815–62825. [Google Scholar] [CrossRef]
- Yin, Y.; Aihua, S.; Min, G.; Yueshen, X.; Shuoping, W. QoS prediction for web service recommendation with network location-aware neighbor selection. Inter. J. Softw. Eng. Knowl. Eng. 2016, 26, 611–632. [Google Scholar] [CrossRef]
- Yin, Y.; Xu, Y.; Xu, W.; Gao, M.; Yu, L.; Pei, Y. Collaborative service selection via ensemble learning in mixed mobile network environments. Entropy 2017, 19, 358. [Google Scholar] [CrossRef]
- Gao, H.; Miao, H.; Liu, L.; Kai, J.; Zhao, K. Automated quantitative verification for service-based system design: A visualization transform tool perspective. Inter. J. Softw. Eng. Knowl. Eng. 2018, 28, 1369–1397. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, K.; Yang, J.; Wu, F.; Liu, H. Applying improved particle swarm optimization for dynamic service composition focusing on quality of service evaluations under hybrid networks. Inter. J. Distrib. Sensor Netw. 2018, 14, 1550147718761583. [Google Scholar] [CrossRef]
- Gao, H.; Mao, S.; Huang, W.; Yang, X. Applying Probabilistic Model Checking to Financial Production Risk Evaluation and Control: A Case Study of Alibaba’s Yu’e Bao. IEEE Trans. Comput. Soc. Syst. 2018, 5, 785–795. [Google Scholar] [CrossRef]
- Gao, H.; Chu, D.; Duan, Y.; Yin, Y. Probabilistic model checking-based service selection method for business process modeling. Inter. J. Softw. Eng. Knowl. Eng. 2017, 27, 897–923. [Google Scholar] [CrossRef]
- Gao, H.; Huang, W.; Yang, X.; Duan, Y.; Yin, Y. Toward service selection for workflow reconfiguration: An interface-based computing solution. Future Gener. Comput. Syst. 2018, 87, 298–311. [Google Scholar] [CrossRef]
- De, G.; Gao, W. Forecasting China’s Natural Gas Consumption Based on AdaBoost-Particle Swarm Optimization-Extreme Learning Machine Integrated Learning Method. Energies 2018, 11, 2938. [Google Scholar] [CrossRef]
- Li, C.; Zheng, X.; Yang, Z.; Kuang, L. Predicting Short-Term Electricity Demand by Combining the Advantages of Arma and Xgboost in Fog Computing Environment. Available online: https://www.hindawi.com/journals/wcmc/2018/5018053/ (accessed on 28 May 2019).
- Kuang, L.; Yu, L.; Huang, L.; Wang, Y.; Ma, P.; Li, C.; Zhu, Y. A personalized qos prediction approach for cps service recommendation based on reputation and location-aware collaborative filtering. Sensors 2018, 18, 1556. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Xu, W.; Xu, Y.; Li, H.; Yu, L. Collaborative QoS Prediction for Mobile Service with Data Filtering and SlopeOne Model. Available online: https://www.hindawi.com/journals/misy/2017/7356213/ (accessed on 28 May 2019).
- Deng, S.; Xiang, Z.; Yin, J.; Taheri, J.; Zomaya, A.Y. Composition-driven IoT service provisioning in distributed edges. IEEE Access 2018, 6, 54258–54269. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, S.; Ma, H.; Yin, J. Deploying Data-Intensive Applications with Multiple Services Components on Edge. Available online: https://doi.org/10.1007/s11036-019-01245-3 (accessed on 28 May 2019).
- Deng, S.; Huang, L.; Xu, G.; Wu, X.; Wu, Z. On deep learning for trust-aware recommendations in social networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1164–1177. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, L.; Xu, Y.; Wan, J.; Zhang, H.; Mai, Z. QoS Prediction for Service Recommendation with Deep Feature Learning in Edge Computing Environment. Available online: https://doi.org/10.1007/s11036-019-01241-7 (accessed on 28 May 2019).
- Gao, H.; Duan, Y.; Miao, H.; Yin, Y. An approach to data consistency checking for the dynamic replacement of service process. IEEE Access 2017, 5, 11700–11711. [Google Scholar] [CrossRef]
- Padmanabhan, J.; Johnson Premkumar, M.J. Machine learning in automatic speech recognition: A survey. IETE Tech. Rev. 2015, 32, 240–251. [Google Scholar] [CrossRef]
- Fei, H.; Tan, F. Bidirectional Grid Long Short-Term Memory (BiGridLSTM): A Method to Address Context-Sensitivity and Vanishing Gradient. Algorithms 2018, 11, 172. [Google Scholar] [CrossRef]
- Siniscalchi, S.M.; Salerno, V.M. Adaptation to new microphones using artificial neural networks with trainable activation functions. IEEE Trans. Neural Net. Learn. Syst. 2016, 28, 1959–1965. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. An overview of multi-task learning. Natl. Sci. Rev. 2017, 5, 30–43. [Google Scholar] [CrossRef] [Green Version]
- Hamed, M.M.; Al-Masaeid, H.R.; Said, Z.M.B. Short-term prediction of traffic volume in urban arterials. J.Transp. Eng. 1995, 121, 249–254. [Google Scholar] [CrossRef]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining Kohonen maps with ARIMA time series models to forecast traffic flow. Transp. Res. Part. C Emerg. Tech. 1996, 4, 307–318. [Google Scholar] [CrossRef]
- Williams, B. Multivariate vehicular traffic flow prediction: Evaluation of ARIMAX modeling. Transp. Res. Rec. J. Transp. Res. Board 2001, 1776, 194–200. [Google Scholar] [CrossRef]
- Wu, C.-H.; Ho, J.-M.; Lee, D.-T. Travel-time prediction with support vector regression. IEEE Trans. Intell. Transp. Syst. 2004, 5, 276–281. [Google Scholar] [CrossRef]
- Zheng, W.; Lee, D.-H.; Shi, Q. Short-term freeway traffic flow prediction: Bayesian combined neural network approach. J. Transp. Eng. 2006, 132, 114–121. [Google Scholar] [CrossRef]
- Kuang, L.; Yan, H.; Zhu, Y.; Tu, S.; Fan, X. Predicting duration of traffic accidents based on cost-sensitive Bayesian network and weighted K-nearest neighbor. J. Intell. Transp. Syst. 2019, 23, 161–174. [Google Scholar] [CrossRef]
- Chang, H.; Lee, Y.; Yoon, B.; Baek, S. Dynamic near-term traffic flow prediction: Systemoriented approach based on past experiences. IET Intell. Transp. Syst. 2012, 6, 292–305. [Google Scholar] [CrossRef]
- Xia, D.; Wang, B.; Li, H.; Li, Y.; Zhang, Z. A distributed spatial–temporal weighted model on MapReduce for short-term traffic flow forecasting. Neurocomputing 2016, 179, 246–263. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Zhou, X.; Shen, Y.; Zhu, Y.; Huang, L. Predicting multi-step citywide passenger demands using attention-based neural networks. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, USA, 5–9 February 2018; pp. 736–744. [Google Scholar]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Boston, MA, USA, 7–12 June 2015; pp. 4489–4497. [Google Scholar]
- Yosinski, J.; Clune, J.; Nguyen, A.; Fuchs, T.; Lipson, H. Understanding Neural Networks through Deep Visualization. Available online: https://arxiv.org/abs/1506.06579 (accessed on 28 May 2019).
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6 –11 July 2015; pp. 448–456. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 13–16 December 2015; pp. 1440–1448. [Google Scholar]
- Didi Chuxing. Available online: https://gaia.didichuxing.com (accessed on 16 December 2018).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the Future of Gradient-Based Machine Learning Software and Techniques (Autodiff) in Thetwenty-Ninth Annual Conference on Neural Information Processingsystems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]

| Method | RMSE | ||
|---|---|---|---|
| Pick-up | Drop-off | All | |
| MLP | 4.81 | 5.48 | 5.31 |
| HA | 3.88 | 4.32 | 4.11 |
| ARIMA | 4.09 | 4.15 | 4.13 |
| XGBoost | 3.58 | 3.85 | 3.84 |
| LSTM | 3.76 | 4.19 | 4.00 |
| ST-ResNet | 3.54 | 3.72 | 3.54 |
| Taxi3D | 3.24 | 3.43 | 3.33 |
| Taxi3D-single | 3.36 | 3.71 | 3.54 |
| Taxi3D-lstm | 3.53 | 4.05 | 3.80 |
| Taxi3D-na | 3.30 | 3.69 | 3.50 |
| Taxi3D-nr | 3.38 | 3.77 | 3.58 |
| Taxi3D-ne | 3.30 | 3.60 | 3.45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, L.; Yan, X.; Tan, X.; Li, S.; Yang, X. Predicting Taxi Demand Based on 3D Convolutional Neural Network and Multi-task Learning. Remote Sens. 2019, 11, 1265. https://doi.org/10.3390/rs11111265
Kuang L, Yan X, Tan X, Li S, Yang X. Predicting Taxi Demand Based on 3D Convolutional Neural Network and Multi-task Learning. Remote Sensing. 2019; 11(11):1265. https://doi.org/10.3390/rs11111265
Chicago/Turabian StyleKuang, Li, Xuejin Yan, Xianhan Tan, Shuqi Li, and Xiaoxian Yang. 2019. "Predicting Taxi Demand Based on 3D Convolutional Neural Network and Multi-task Learning" Remote Sensing 11, no. 11: 1265. https://doi.org/10.3390/rs11111265