Sea State Bias Variability in Satellite Altimetry Data
Abstract
1. Introduction
2. Data and Methods
3. Global mean SSB Evolution Analysis
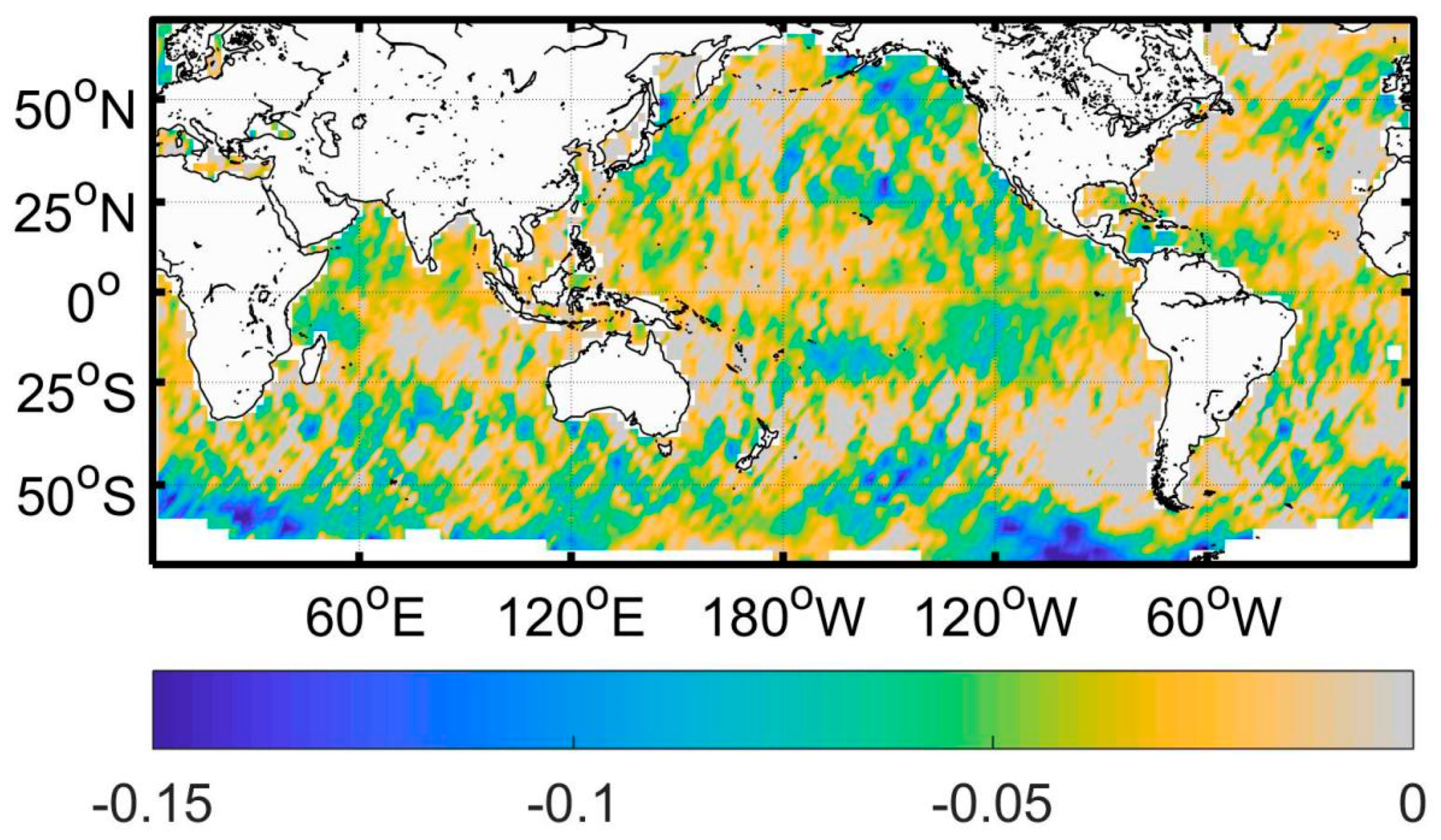
4. Spatial Pattern of SSB Trend
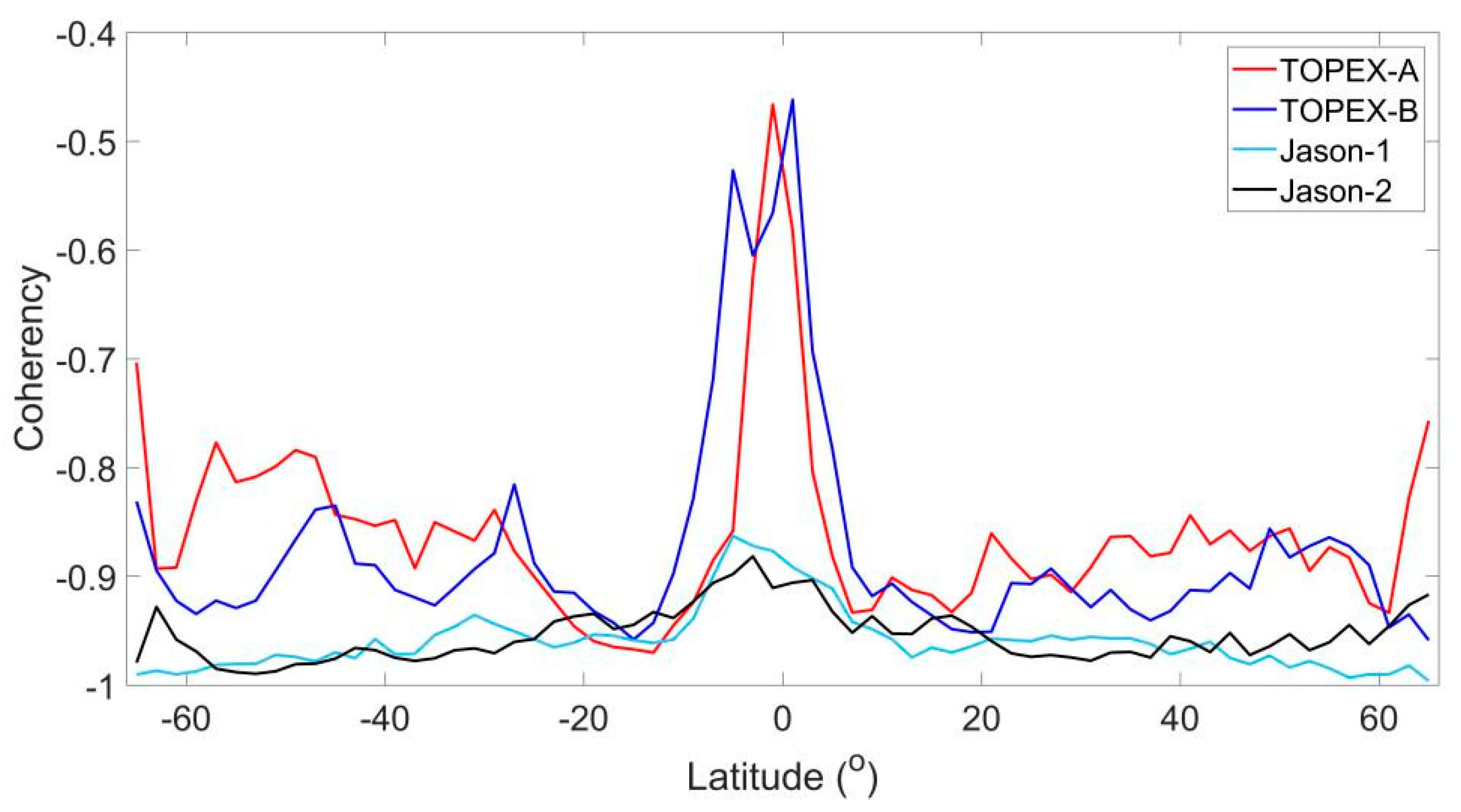
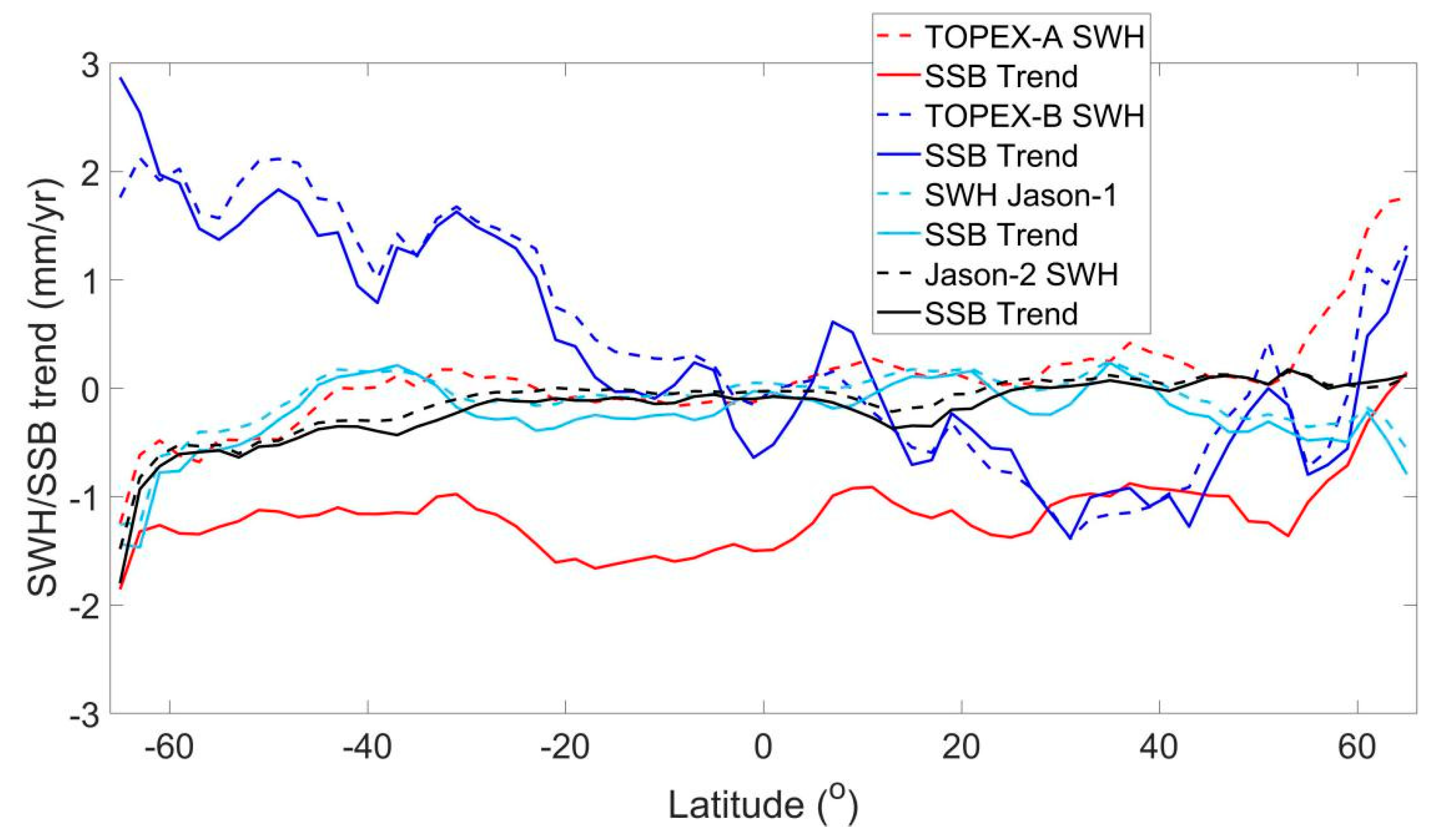
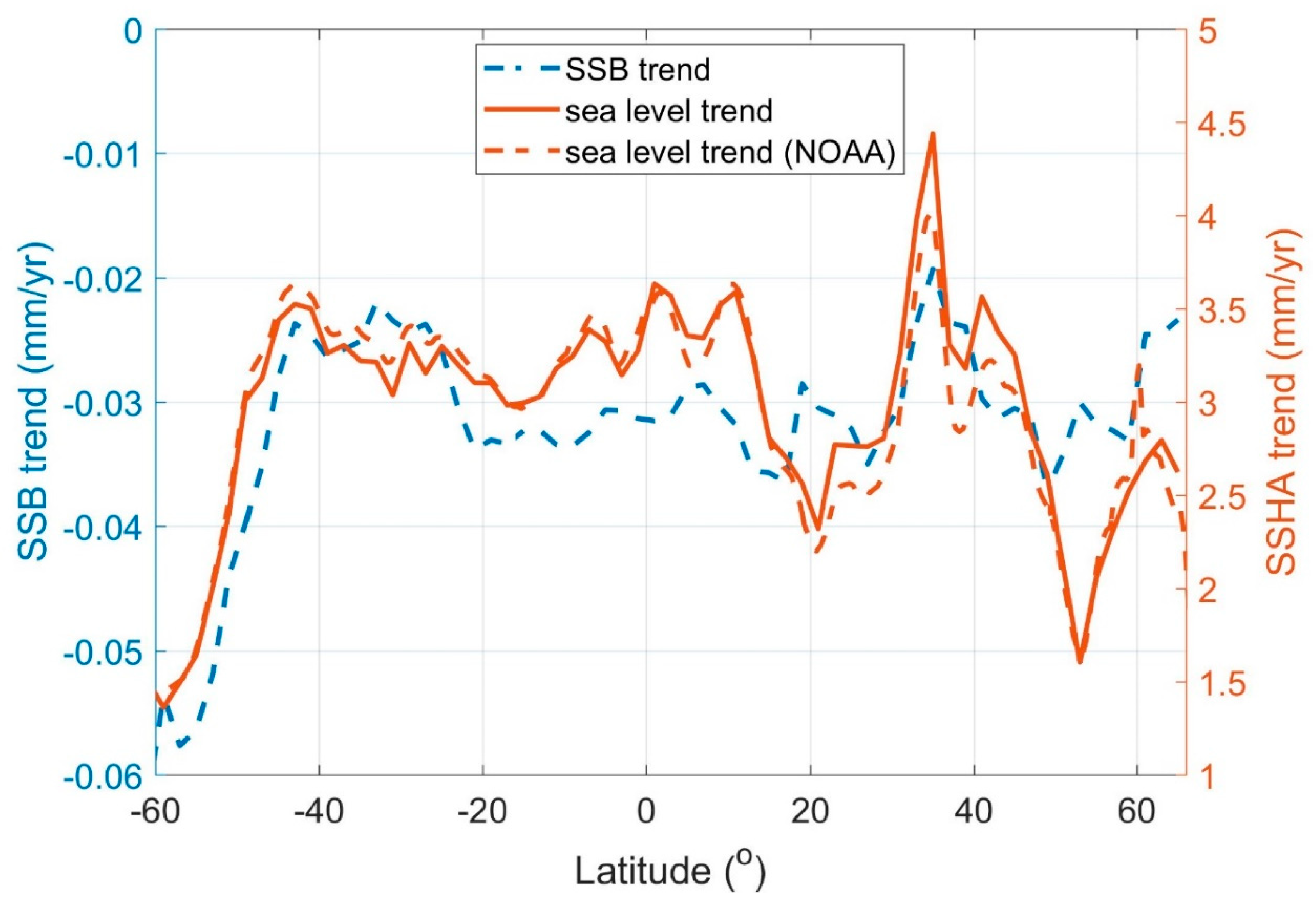
5. Zonal SWH and SSB Trends
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ablain, M.; Cazenave, A.; Larnicol, G.; Balmaseda, M.; Cipollini, P.; Faugère, Y.; Fernandes, M.; Henry, O.; Johannessen, J.; Knudsen, P. Improved sea level record over the satellite altimetry era (1993–2010) from the climate change initiative project. Ocean Sci. 2015, 11, 67–82. [Google Scholar] [CrossRef]
- Ablain, M.; Legeais, J.F.; Prandi, P.; Marcos, M.; Fenoglio-Marc, L.; Dieng, H.B.; Benveniste, J.; Cazenave, A. Satellite altimetry-based sea level at global and regional scales. Surv. Geophys. 2017, 38, 7–31. [Google Scholar] [CrossRef]
- Nerem, R.; Chambers, D.; Choe, C.; Mitchum, G. Estimating mean sea level change from the topex and jason altimeter missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Masters, D.; Nerem, R.; Choe, C.; Leuliette, E.; Beckley, B.; White, N.; Ablain, M. Comparison of global mean sea level time series from topex/poseidon, jason-1, and jason-2. Mar. Geod. 2012, 35, 20–41. [Google Scholar] [CrossRef]
- Gaspar, P.; Ogor, F.; Le Traon, P.Y.; Zanife, O.Z. Estimating the sea state bias of the topex and poseidon altimeters from crossover differences. J. Geophys. Res. Ocean. 1994, 99, 24981–24994. [Google Scholar] [CrossRef]
- Chambers, D.P.; Hayes, S.A.; Ries, J.C.; Urban, T.J. New topex sea state bias models and their effect on global mean sea level. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Ablain, M.; Cazenave, A.; Valladeau, G.; Guinehut, S. A new assessment of the error budget of global mean sea level rate estimated by satellite altimetry over 1993–2008. Ocean Sci. 2009, 5, 193–201. [Google Scholar] [CrossRef]
- Labroue, S.; Gaspar, P.; Dorandeu, J.; Zanife, O.; Mertz, F.; Vincent, P.; Choquet, D. Nonparametric estimates of the sea state bias for the jason-1 radar altimeter. Mar. Geod. 2004, 27, 453–481. [Google Scholar] [CrossRef]
- Tran, N.; Labroue, S.; Philipps, S.; Bronner, E.; Picot, N. Overview and update of the sea state bias corrections for the jason-2, jason-1 and topex missions. Mar. Geod. 2010, 33, 348–362. [Google Scholar] [CrossRef]
- Chelton, D.B. The sea state bias in altimeter estimates of sea level from collinear analysis of topex data. J. Geophys. Res. Ocean. 1994, 99, 24995–25008. [Google Scholar] [CrossRef]
- Vandemark, D.; Tran, N.; Beckley, B.; Chapron, B.; Gaspar, P. Direct estimation of sea state impacts on radar altimeter sea level measurements. Geophys. Res. Lett. 2002, 29, 1-1–1-4. [Google Scholar] [CrossRef]
- Chapron, B.; Vandemark, D.; Elfouhaily, T.; Thompson, D.; Gaspar, P.; Labroue, S. Altimeter sea state bias: A new look at global range error estimates. Geophys. Res. Lett. 2001, 28, 3947–3950. [Google Scholar] [CrossRef]
- Gaspar, P.; Florens, J.P. Estimation of the sea state bias in radar altimeter measurements of sea level: Results from a new nonparametric method. J. Geophys. Res. Ocean. 1998, 103, 15803–15814. [Google Scholar] [CrossRef]
- Feng, H.; Yao, S.; Li, L.; Tran, N.; Vandemark, D.; Labroue, S. Spline-based nonparametric estimation of the altimeter sea-state bias correction. IEEE Geosci. Remote Sens. Lett. 2010, 7, 577–581. [Google Scholar] [CrossRef]
- Gaspar, P.; Labroue, S.; Ogor, F.; Lafitte, G.; Marchal, L.; Rafanel, M. Improving nonparametric estimates of the sea state bias in radar altimeter measurements of sea level. J. Atmos. Ocean. Technol. 2002, 19, 1690–1707. [Google Scholar] [CrossRef]
- Fu, L.L.; Glazman, R. The effect of the degree of wave development on the sea state bias in radar altimetry measurement. J. Geophys. Res. Ocean. 1991, 96, 829–834. [Google Scholar] [CrossRef]
- Glazman, R.; Fabrikant, A.; Srokosz, M. Numerical analysis of the sea state bias for satellite altimetry. J. Geophys. Res. Ocean. 1996, 101, 3789–3799. [Google Scholar] [CrossRef]
- Andersen, O.B.; Cheng, Y. Long term changes of altimeter range and geophysical corrections at altimetry calibration sites. Adv. Space Res. 2013, 51, 1468–1477. [Google Scholar] [CrossRef]
- Cheng, Y.; Andersen, O.B. Impacts of altimeter corrections on local linear sea level trends around taiwan. Int. J. Remote Sens. 2013, 34, 6738–6748. [Google Scholar] [CrossRef]
- Cheng, Y.; Xu, Q.; Andersen, O.B. Sea-level trend in the south china sea observed from 20 years of along-track satellite altimetric data. Int. J. Remote Sens. 2014, 35, 4329–4339. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Labroue, S.; Feng, H.; Chapron, B.; Tolman, H.; Lambin, J.; Picot, N. Sea state bias in altimeter sea level estimates determined by combining wave model and satellite data. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Pires, N.; Fernandes, M.; Gommenginger, C.; Scharroo, R. A conceptually simple modeling approach for jason-1 sea state bias correction based on 3 parameters exclusively derived from altimetric information. Remote Sens. 2016, 8, 576. [Google Scholar] [CrossRef]
- Jiang, M.F.; Xu, K.; Liu, Y.L.; Wang, L. Estimating the sea state bias of jason-2 altimeter from crossover differences by using a three-dimensional nonparametric model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5023–5043. [Google Scholar] [CrossRef]
- Passaro, M.; Nadzir, Z.A.; Quartly, G.D. Improving the precision of sea level data from satellite altimetry with high-frequency and regional sea state bias corrections. Remote Sens. Environ. 2018, 218, 245–254. [Google Scholar] [CrossRef]
- Wang, X.; Ichikawa, K. Effect of High-Frequency Sea Waves on Wave Period Retrieval from Radar Altimeter and Buoy Data. Remote Sens. 2016, 8, 764. [Google Scholar] [CrossRef]
- Watson, C.S.; White, N.J.; Church, J.A.; King, M.A.; Burgette, R.J.; Legresy, B. Unabated global mean sea-level rise over the satellite altimeter era. Nat. Clim. Chang. 2015, 5, 565. [Google Scholar] [CrossRef]
- Dieng, H.B.; Cazenave, A.; Meyssignac, B.; Ablain, M. New estimate of the current rate of sea level rise from a sea level budget approach. Geophys. Res. Lett. 2017, 44, 3744–3751. [Google Scholar] [CrossRef]
- Beckley, B.D.; Callahan, P.S.; Hancock, D.W.; Mitchum, G.T.; Ray, R.D. On the “cal-mode” correction to topex satellite altimetry and its effect on the global mean sea level time series. J. Geophys. Res. Ocean. 2017, 122, 8371–8384. [Google Scholar] [CrossRef]
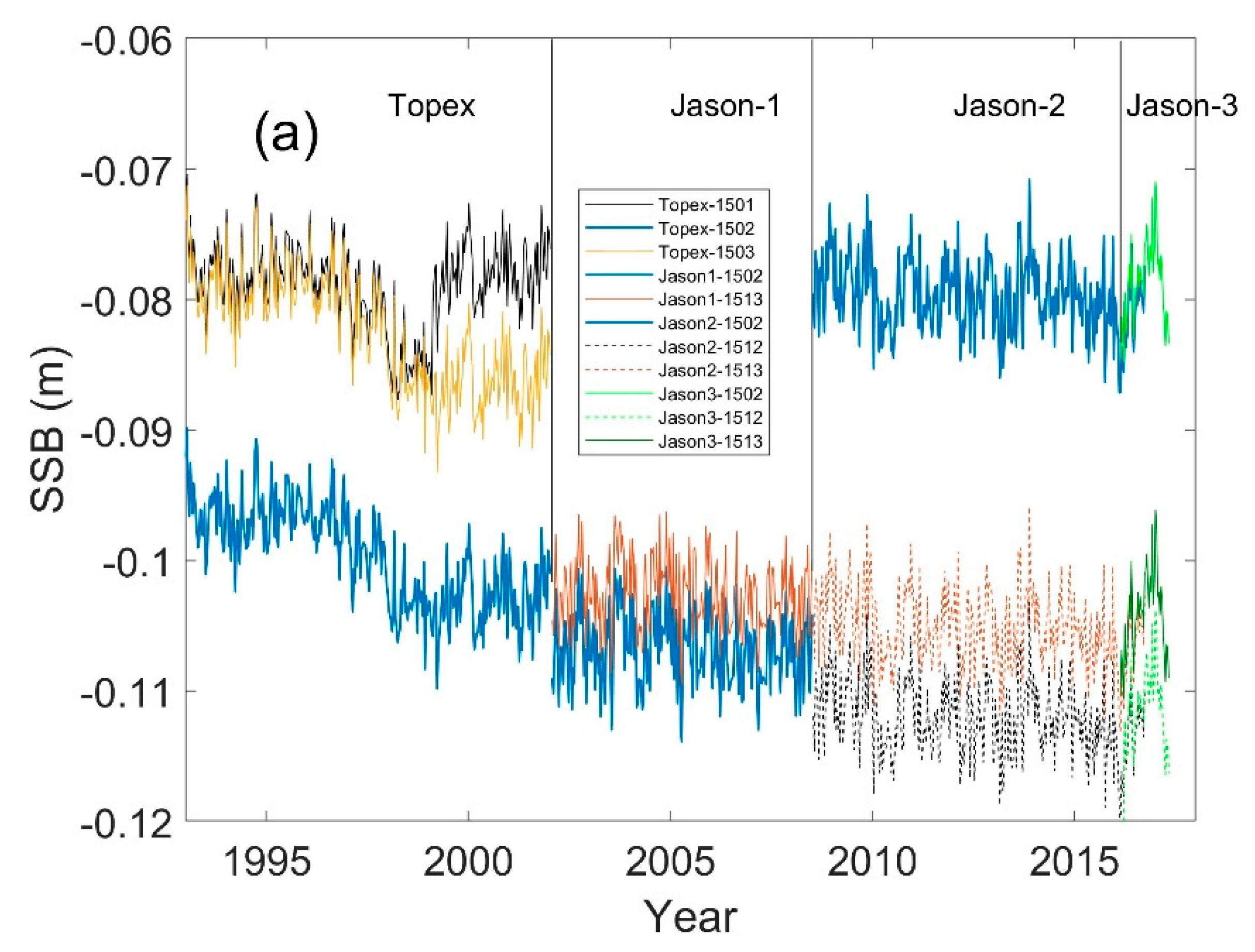
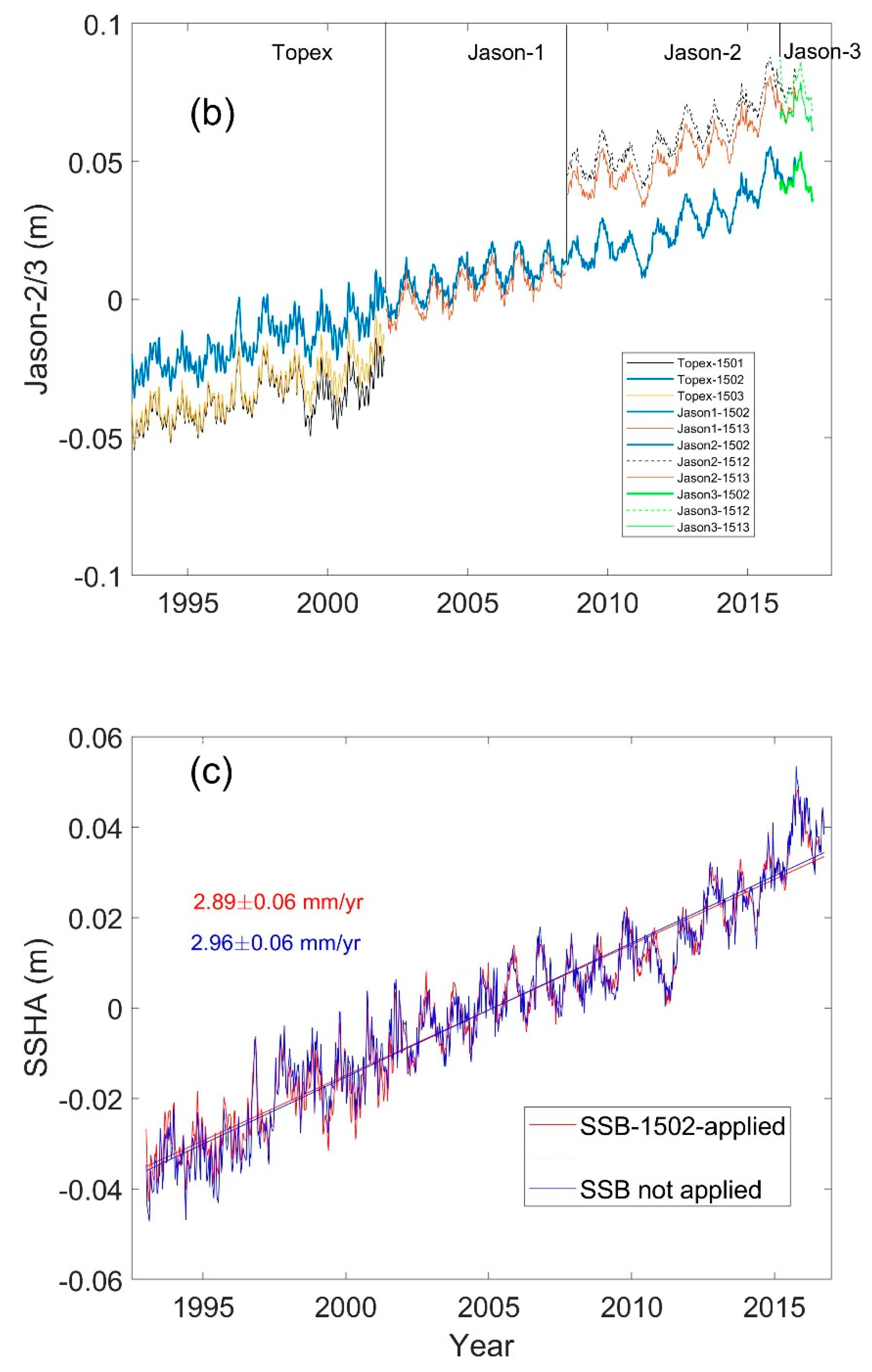
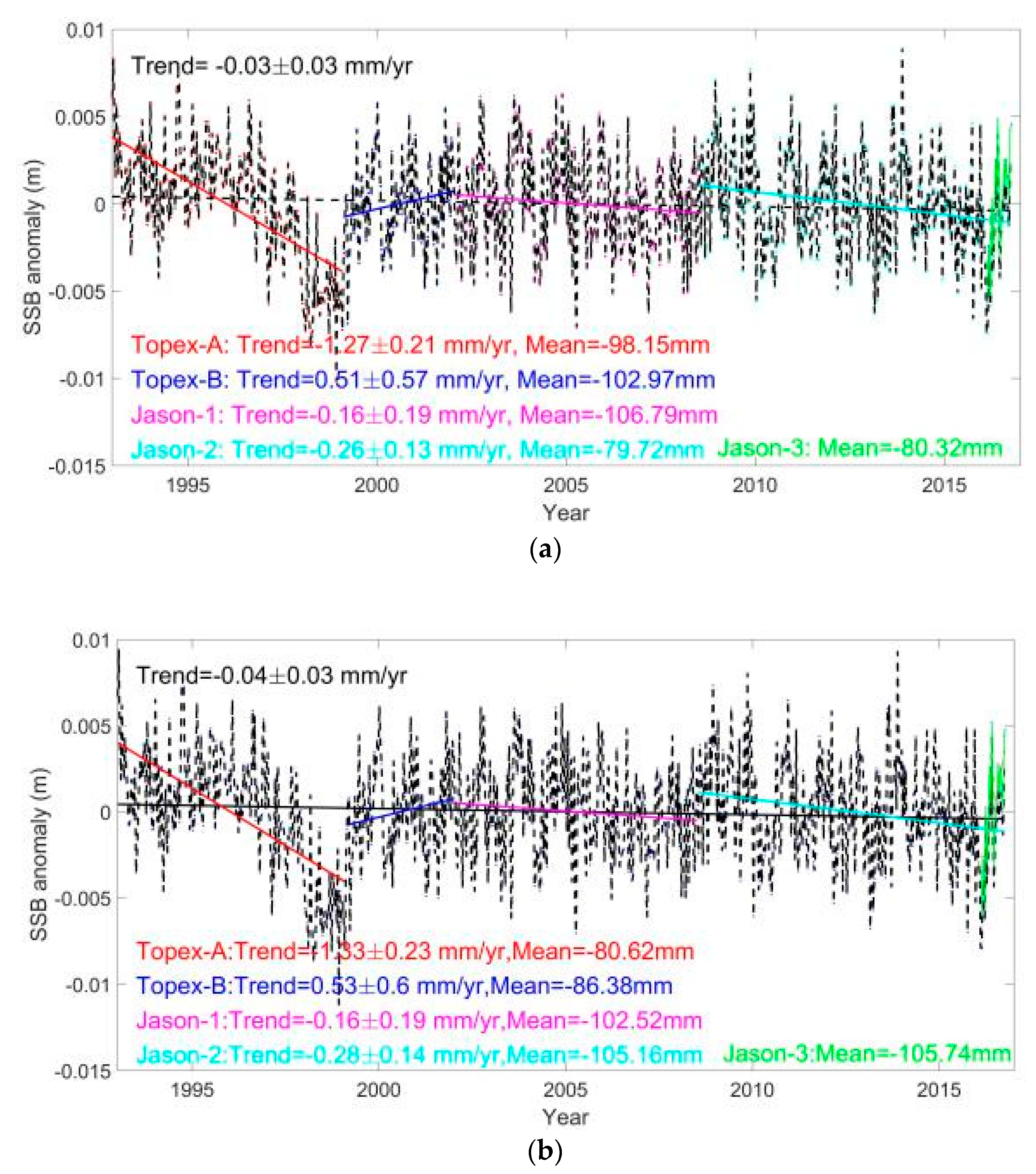
| SSB (Code in RADS) | TOPEX (C011–C343) | Jason-1 (C001-C239) | Jason-2 (C001-C303) | Jason-3 (C001-045) |
|---|---|---|---|---|
| Parametric (1501 [5]) | Y | |||
| CLS 2D non-parametric * (1502 [8,15]) | Y | Y | Y | Y |
| CSR BM4 (1503 [6]) | Y | |||
| CLS non-parametric (MLE3 1512) | Y | Y | ||
| 3D non-parametric (1513 [21]) | Y | Y | Y |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Xu, Q.; Gao, L.; Li, X.; Zou, B.; Liu, T. Sea State Bias Variability in Satellite Altimetry Data. Remote Sens. 2019, 11, 1176. https://doi.org/10.3390/rs11101176
Cheng Y, Xu Q, Gao L, Li X, Zou B, Liu T. Sea State Bias Variability in Satellite Altimetry Data. Remote Sensing. 2019; 11(10):1176. https://doi.org/10.3390/rs11101176
Chicago/Turabian StyleCheng, Yongcun, Qing Xu, Le Gao, Xiaofeng Li, Bin Zou, and Ting Liu. 2019. "Sea State Bias Variability in Satellite Altimetry Data" Remote Sensing 11, no. 10: 1176. https://doi.org/10.3390/rs11101176
APA StyleCheng, Y., Xu, Q., Gao, L., Li, X., Zou, B., & Liu, T. (2019). Sea State Bias Variability in Satellite Altimetry Data. Remote Sensing, 11(10), 1176. https://doi.org/10.3390/rs11101176







