Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal
Abstract
1. Introduction
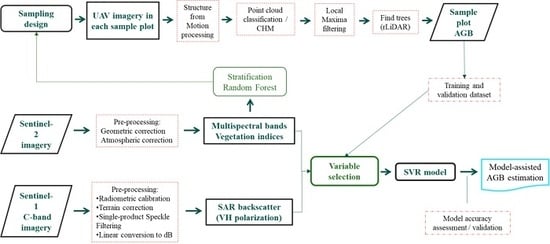
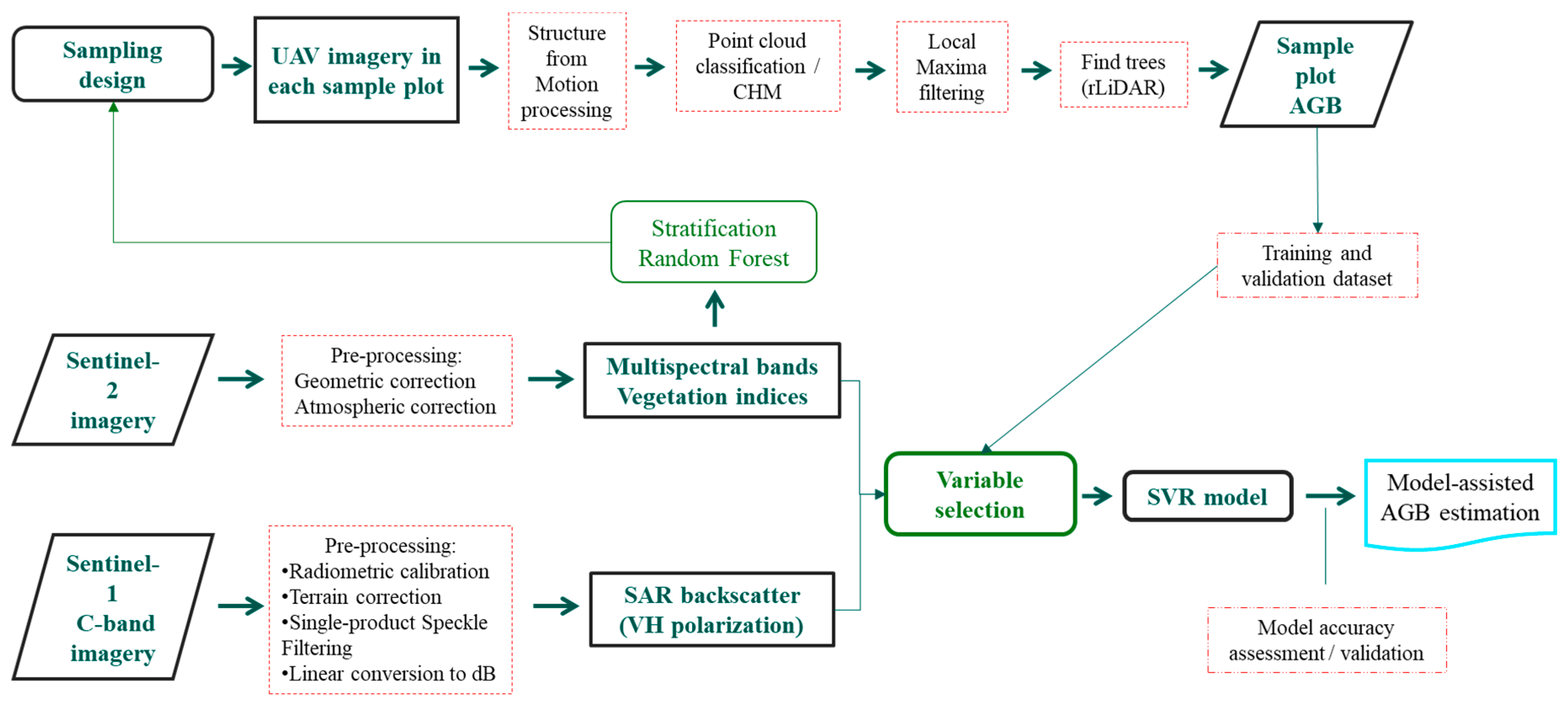
2. Materials and Methods
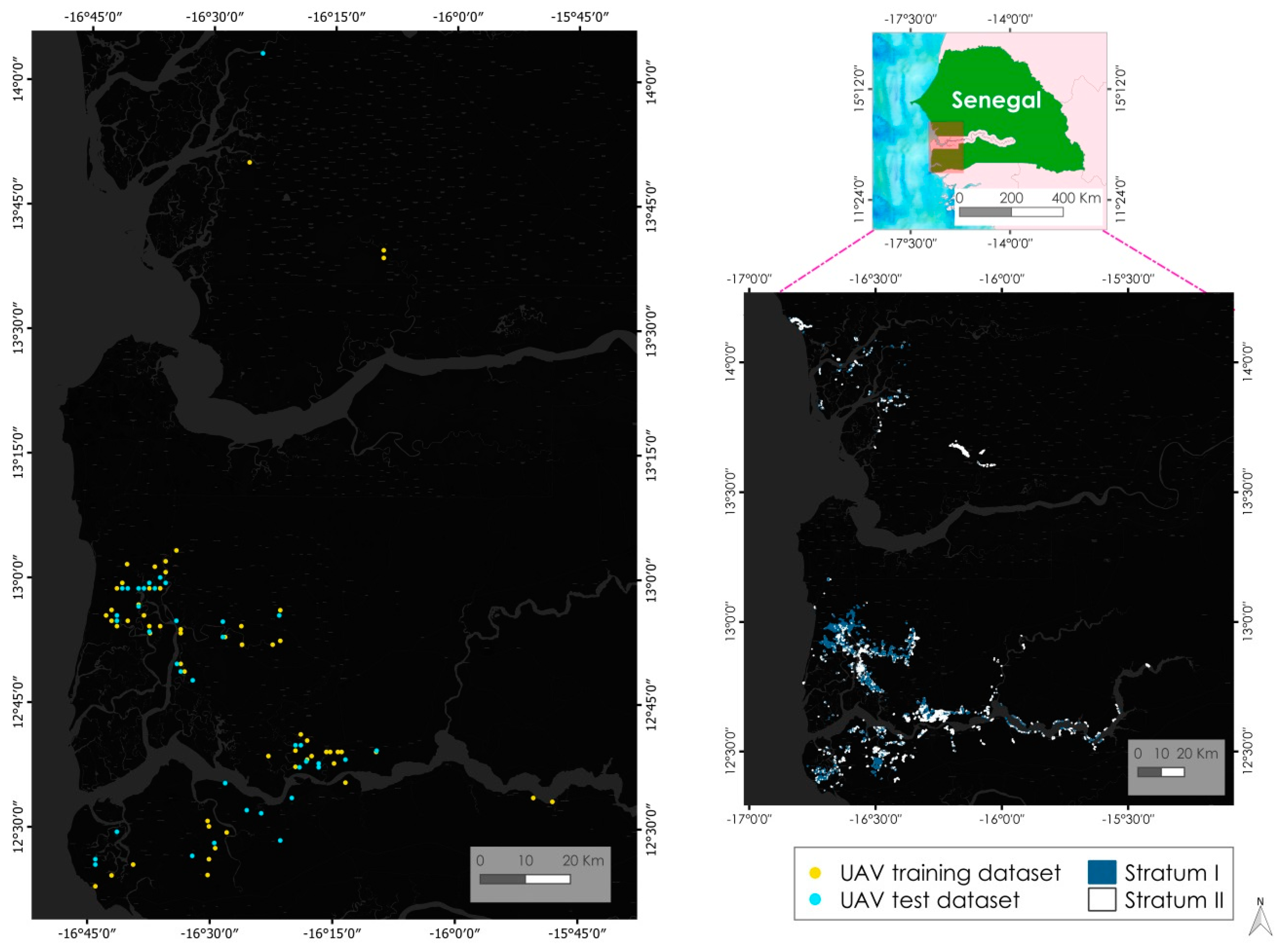
2.1. Study Area
2.2. Satellite Data. Acquisition, and Preprocessing
2.3. Stratification and Sampling Design
2.4. Sampling Data Collection and Processing
2.5. Allometric Equation
2.6. Aboveground Biomass Modelling and Performance Assessment
2.7. Aboveground Biomass Estimation Methods
3. Results
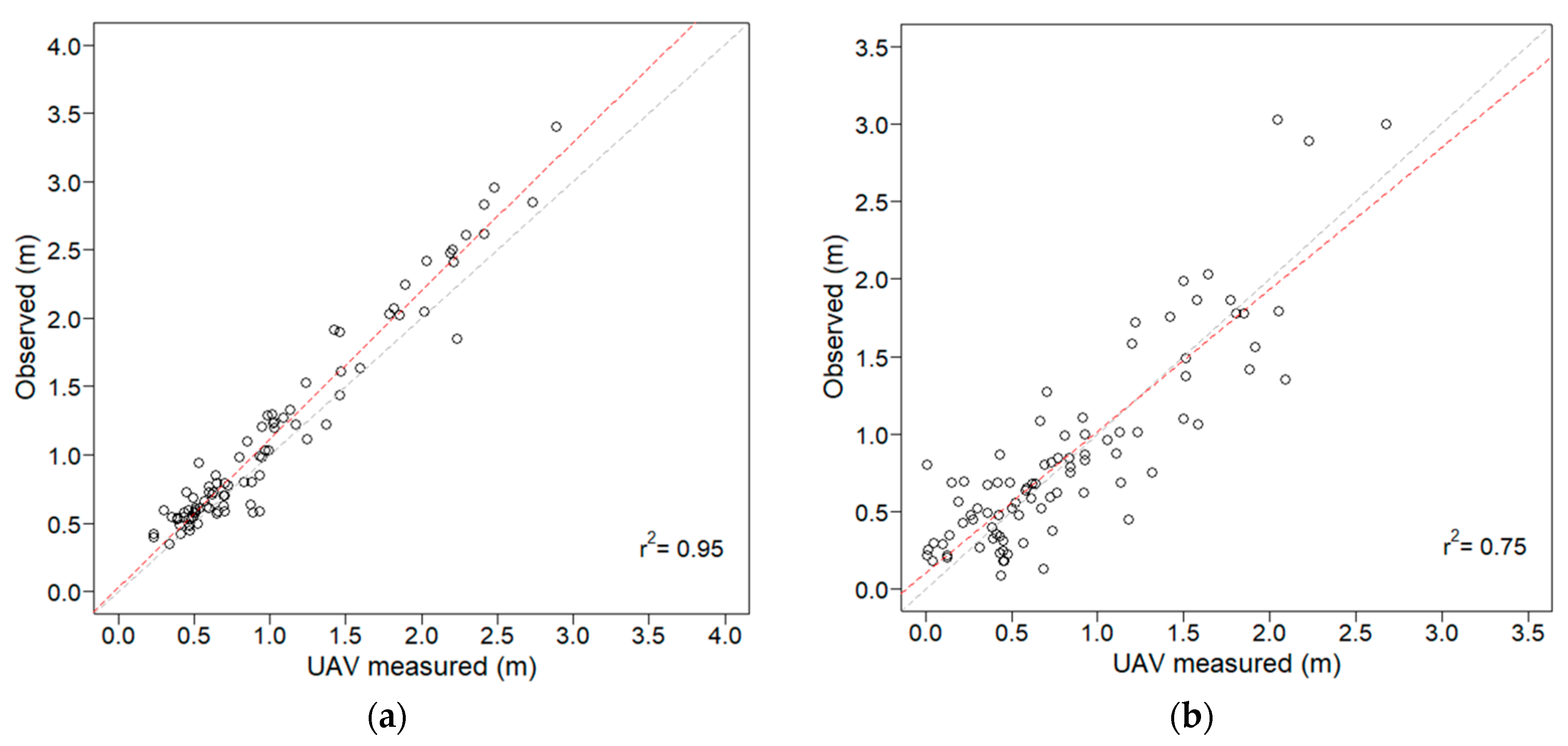
3.1. Tree Measurements
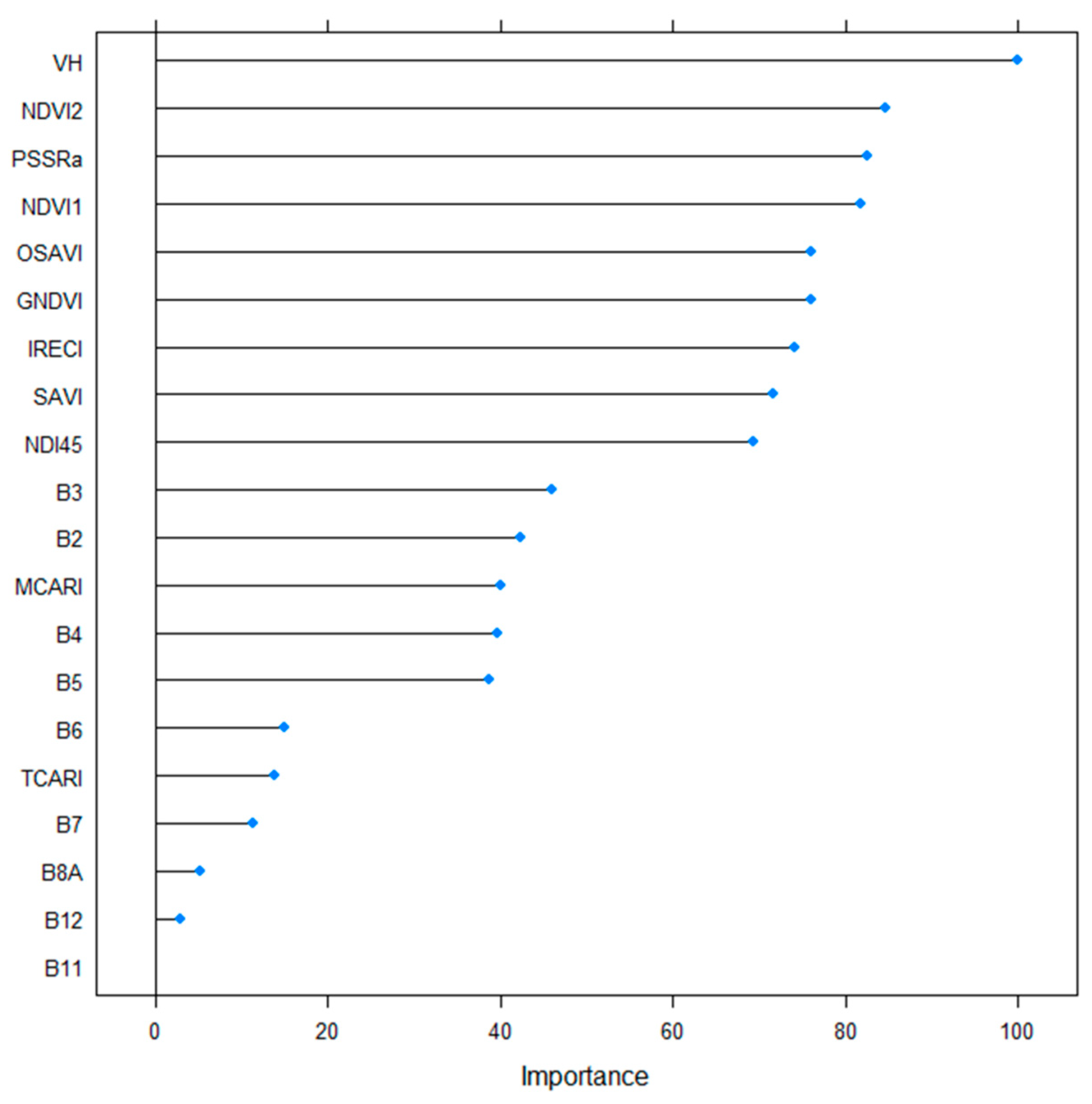
3.2. Model Fitting
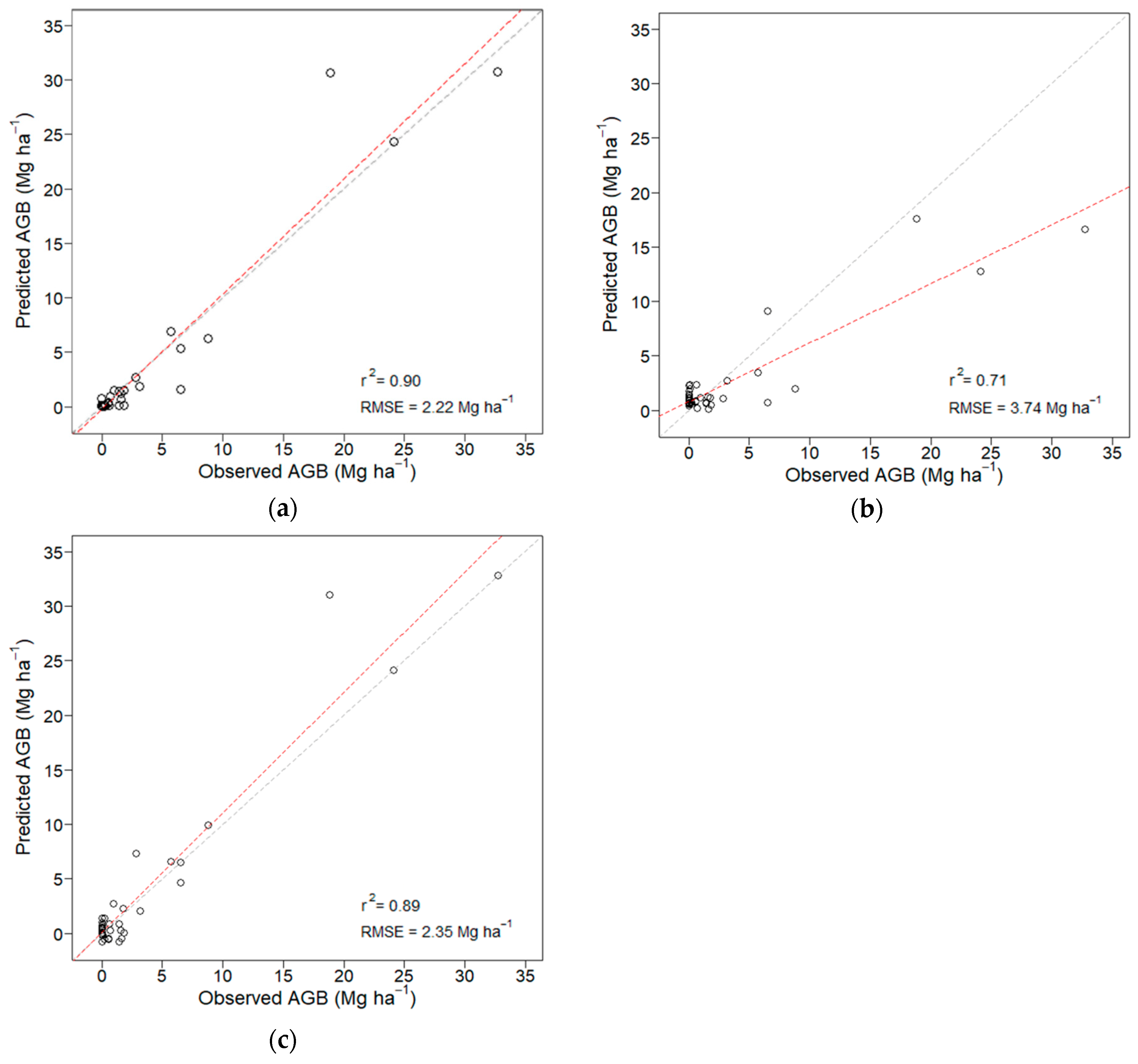
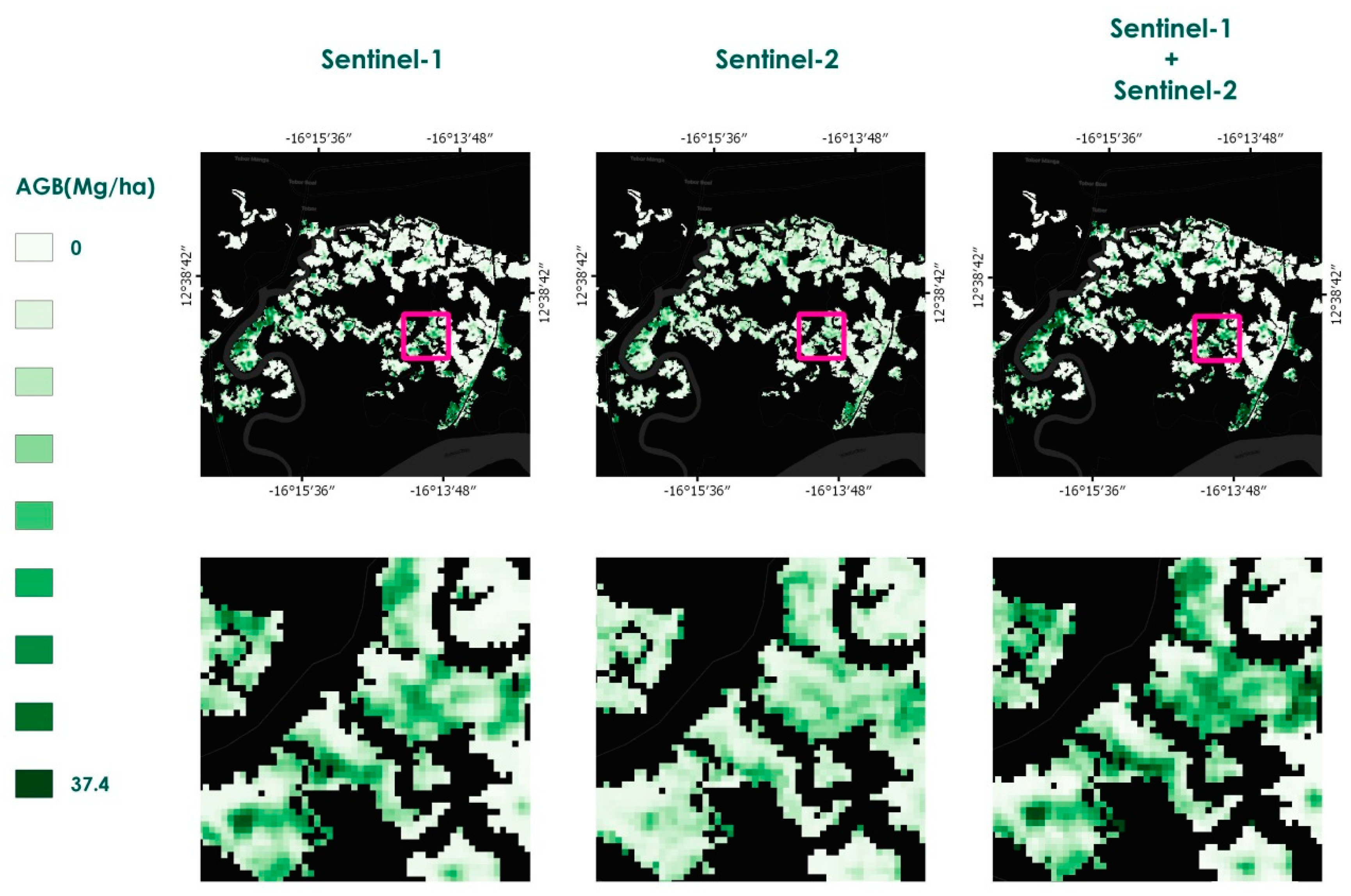
3.3. Estimations of Aboveground Biomass
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Murdiyarso, D.; Donato, D.; Kauffman, J.B.; Kurnianto, S.; Stidham, M.; Kanninen, M. Carbon Storage in Mangrove and Peatland Ecosystems. A Preliminary Account from Plots in Indonesia; Center for International Forestry Research: Bogor, Indonesia, 2009. [Google Scholar]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon sequestration in mangrove forests. Carbon Manag. 2012, 3, 313–322. [Google Scholar] [CrossRef]
- Barbier, E.B.; Hacker, S.D.; Kennedy, C.; Koch, E.W.; Stier, A.C.; Silliman, B.R. The value of estuarine and coastal ecosystem services. Ecol. Monogr. 2011. [Google Scholar] [CrossRef]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Environ.Conserv. 2002. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.K.; Feliciano, E.; Trettin, C.; Simard, M. A comparison of mangrove Canopy height using multiple independent measurements from land, air, and space. Remote Sens. 2016, 8. [Google Scholar] [CrossRef] [PubMed]
- Köhl, M.; Magnussen, S.; Marchetti, M. Sampling Methods, Remote Sensing and GIS Multiresource Forest Inventory; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3, ISBN 9783540490289. [Google Scholar]
- Gardner, T.A.; Barlow, J.; Araujo, I.S.; Ávila-Pires, T.C.; Bonaldo, A.B.; Costa, J.E.; Esposito, M.C.; Ferreira, L.V.; Hawes, J.; Hernandez, M.I.M.; et al. The cost-effectiveness of biodiversity surveys in tropical forests. Ecol. Lett. 2008, 11, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D.; Lee, S.K.; Fatoyinbo, T.E. Estimating mangrove canopy height and above-ground biomass in the Everglades National Park with airborne LiDAR and TanDEM-X data. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Surový, P.; Almeida Ribeiro, N.; Panagiotidis, D. Estimation of positions and heights from UAV-sensed imagery in tree plantations in agrosilvopastoral systems. Int. J. Remote Sens. 2018, 1–15. [Google Scholar] [CrossRef]
- Adame, M.F.; Fry, B. Source and stability of soil carbon in mangrove and freshwater wetlands of the Mexican Pacific coast. Wetl. Ecol. Manag. 2016, 24, 129–137. [Google Scholar] [CrossRef]
- Shapiro, A.; Trettin, C.; Küchly, H.; Alavinapanah, S.; Bandeira, S. The Mangroves of the Zambezi Delta: Increase in Extent Observed via Satellite from 1994 to 2013. Remote Sens. 2015, 7, 16504–16518. [Google Scholar] [CrossRef]
- Dutta, D.; Das, P.K.; Paul, S.; Sharma, J.R.; Dadhwal, V.K. Assessment of ecological disturbance in the mangrove forest of Sundarbans caused by cyclones using MODIS time-series data (2001–2011). Nat. Hazards 2015, 79, 775–790. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Characterizing the Spatial Structure of Mangrove Features for Optimizing Image-Based Mangrove Mapping. Remote Sens. 2014, 6, 984–1006. [Google Scholar] [CrossRef]
- Simard, M.; Zhang, K.; Rivera-monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-moya, E.; Twilley, R.R.; Rodriguez, E. Mapping Height and Biomass of Mangrove Forests in Everglades National Park with SRTM Elevation Data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Simard, M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of Mozambique’s mangrove, forests with Landsat ETM+ and Shuttle Radar Topography Mission elevation data. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Lee, S.K.; Fatoyinbo, T.E. TanDEM-X Pol-InSAR Inversion for Mangrove Canopy Height Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3608–3618. [Google Scholar] [CrossRef]
- Lee, S.K.; Fatoyinbo, T.; Lagomasino, D.; Osmanoglu, B.; Simard, M.; Trettin, C.; Rahman, M.; Ahmed, I. Large-scale mangrove canopy height map generation from TanDEM-X data by means of Pol-InSAR techniques. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2895–2898. [Google Scholar]
- Lola Fatoyinbo, T.; Feliciano, E.; Lagomasino, D.; Kuk Lee, S.; Trettin, C. Estimating mangrove aboveground biomass from airborne LiDAR data: A case study from the Zambezi River delta. Environ. Res. Lett. 2017. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Remote Sens. 2018, 12. [Google Scholar] [CrossRef]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating Forest Biomass to SAR Data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Lucas, R.; Lule, A.V.; Rodríguez, M.T.; Kamal, M.; Thomas, N.; Asbridge, E.; Kuenzer, C. Spatial Ecology of Mangrove Forests: A Remote Sensing Perspective. Mangr. Ecosyst. Glob. Biogeogr. Perspect. 2017, 87–112. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Proisy, C.; Mougin, E.; Fromard, F.; Trichon, V.; Karam, M.A. On the influence of canopy structure on the radar backscattering of mangrove forests. Int. J. Remote Sens. 2002. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Bui, D.T. Improving accuracy estimation of Forest Aboveground Biomass based on incorporation of ALOS-2 PALSAR-2 and Sentinel-2A imagery and machine learning: A case study of the Hyrcanian forest area (Iran). Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.N.; Bui, D.T. Estimating aboveground biomass of a mangrove plantation on the Northern coast of Vietnam using machine learning techniques with an integration of ALOS-2 PALSAR-2 and Sentinel-2A data. Int. J. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Solberg, S.; McRoberts, R.E. The effects of field plot size on model-assisted estimation of aboveground biomass change using multitemporal interferometric SAR and airborne laser scanning data. Remote Sens. Environ. 2015, 168, 252–264. [Google Scholar] [CrossRef]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Solberg, S.; Gregoire, T.G.; Nelson, R.; Ståhl, G.; Weydahl, D. Model-assisted regional forest biomass estimation using LiDAR and InSAR as auxiliary data: A case study from a boreal forest area. Remote Sens. Environ. 2011, 115, 3599–3614. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Ståhl, G.; Næsset, E.; Gobakken, T.; Nelson, R.; Holm, S. Model-assisted estimation of biomass in a LiDAR sample survey in Hedmark County, NorwayThis article is one of a selection of papers from Extending Forest Inventory and Monitoring over Space and Time. Can. J. For. Res. 2011, 41, 83–95. [Google Scholar] [CrossRef]
- Sannier, C.; McRoberts, R.E.; Fichet, L.V.; Makaga, E.M.K. Using the regression estimator with landsat data to estimate proportion forest cover and net proportion deforestation in gabon. Remote Sens. Environ. 2014, 151, 138–148. [Google Scholar] [CrossRef]
- Güneralp, I.; Filippi, A.M.; Randall, J. Estimation of floodplain aboveground biomass using multispectralremote sensing and nonparametric modeling. Int. J. Appl. Earth Obs. Geoinf. 2014. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L. Estimating forest aboveground biomass by combining optical and SAR data: A case study in genhe, inner Mongolia, China. Sensors (Switzerland) 2016, 16. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Bui, D.T. Biomass estimation of Sonneratia caseolaris (l.) Engler at a coastal area of Hai Phong city (Vietnam) using ALOS-2 PALSAR imagery and GIS-based multi-layer perceptron neural networks. GISci. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Baffetta, F.; Corona, P.; Fattorini, L. Design-based diagnostics for k-NN estimators of forest resources. Can. J. For. Res. 2011. [Google Scholar] [CrossRef]
- Magnussen, S.; Tomppo, E. Model-calibrated k-nearest neighbor estimators. Scand. J. For. Res. 2016. [Google Scholar] [CrossRef]
- Gehrke, S.; Morin, K.; Downey, M.; Boehrer, N.; Fuchs, T. Semi-global matching: An alternative to lidar for dsm generation? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVIII-B1, 1–6. [Google Scholar]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the Art in High Density Image Matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Pitt, D.G.; Woods, M.; Penner, M. A comparison of point clouds derived from stereo imagery and airborne laser scanning for the area-based estimation of forest inventory attributes in Boreal Ontario. Can. J. Remote Sens. 2014, 40. [Google Scholar] [CrossRef]
- Penner, M.; Woods, M.; Pitt, D.G. A Comparison of Airborne Laser Scanning and Image Point Cloud Derived Tree Size Class Distribution Models in Boreal Ontario. Forests 2015, 6, 4034–4054. [Google Scholar] [CrossRef]
- Vastaranta, M.; Wulder, M.A.; White, J.C.; Pekkarinen, A.; Tuominen, S.; Ginzler, C.; Kankare, V.; Holopainen, M.; Hyyppä, J.; Hyyppä, H. Airborne laser scanning and digital stereo imagery measures of forest structure: Comparative results and implications to forest mapping and inventory update. Can. J. Remote Sens. 2013, 39, 382–395. [Google Scholar] [CrossRef]
- Mohan, M.; Silva, C.A.; Klauberg, C.; Jat, P.; Catts, G.; Cardil, A.; Hudak, A.T.; Dia, M. Individual tree detection from unmanned aerial vehicle (UAV) derived canopy height model in an open canopy mixed conifer forest. Forests 2017, 8. [Google Scholar] [CrossRef]
- Tao, W.; Lei, Y.; Mooney, P. Dense point cloud extraction from UAV captured images in forest area. In Proceedings of the 2011 IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services, Fuzhou, China, 29 June–1 July 2011; pp. 389–392. [Google Scholar]
- Gini, R.; Passoni, D.; Pinto, L.; Sona, G. Aerial images from a UAV system: 3D modelling and tree species classification in a park area. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B1, 361–366. [Google Scholar] [CrossRef]
- Lisein, J. Creation of a Canopy Height Model from mini-UAV Imagery. In Proceedings of the ForestSAT 2012, Corvallis, OR, USA, 12–14 September 2012; Available online: https://orbi.uliege.be/handle/2268/129781 (accessed on 15 November 2018).
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Puliti, S.; Saarela, S.; Gobakken, T.; Ståhl, G.; Næsset, E. Combining UAV and Sentinel-2 auxiliary data for forest growing stock volume estimation through hierarchical model-based inference. Remote Sens. Environ. 2018, 204, 485–497. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; Crawford, P. Assessing the status of forest regeneration using digital aerial photogrammetry and unmanned aerial systems. Int. J. Remote Sens. 2017, 00, 1–19. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Iizuka, K.; Yonehara, T.; Itoh, M.; Kosugi, Y. Estimating Tree Height and Diameter at Breast Height (DBH) from Digital Surface Models and Orthophotos Obtained with an Unmanned Aerial System for a Japanese Cypress (Chamaecyparis obtusa) Forest. Remote Sens. 2017, 10, 13. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Mweresa, I.A.; Odera, P.A.; Kuria, D.N.; Kenduiywo, B.K. Estimation of tree distribution and canopy heights in Ifakara, Tanzania, using unmanned aerial system ({UAS}) stereo imagery. Am. J. Geogr. Inf. Syst. 2017, 6, 187–200. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Li, X.; Gong, H.; Shi, C.; Zhong, R.; Liu, X. Comparison of UAV and WorldView-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Otero, V.; Van De Kerchove, R.; Satyanarayana, B.; Martínez-Espinosa, C.; Fisol, M.A.B.; Ibrahim, M.R.B.; Sulong, I.; Mohd-Lokman, H.; Lucas, R.; Dahdouh-Guebas, F. Managing mangrove forests from the sky: Forest inventory using field data and Unmanned Aerial Vehicle (UAV) imagery in the Matang Mangrove Forest Reserve, peninsular Malaysia. For. Ecol. Manag. 2018, 411, 35–45. [Google Scholar] [CrossRef]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-Based mangrove species classification using unmanned aerial vehicle hyperspectral images and digital surface models. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Puliti, S.; Olerka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Mlambo, R.; Woodhouse, I.H.; Gerard, F.; Anderson, K. Structure from motion (SfM) photogrammetry with drone data: A low cost method for monitoring greenhouse gas emissions from forests in developing countries. Forests 2017, 8. [Google Scholar] [CrossRef]
- Mayr, M.J.; Malß, S.; Ofner, E.; Samimi, C. Disturbance feedbacks on the height of woody vegetation in a savannah: A multi-plot assessment using an unmanned aerial vehicle (UAV). Int. J. Remote Sens. 2017, 1–25. [Google Scholar] [CrossRef]
- Agresta, S. Coop. In Project Description: Livelihoods’ Mangrove Restoration Grouped Project in Senegal; VCS Project Database: Madrid, Spain, 2014; Available online: http://www.vcsprojectdatabase.org/services/publicViewServices/downloadDocumentById/29057 (accessed on 15 November 2018).
- Andrieu, J. Landscape Dynamics in Northern Regions of Rivières-du-Sud; Univeristè Paris Diderot Paris: Paris, France, 2008. [Google Scholar]
- Deugué-Namboma, R.M. Contribution des reboisements de mangrove de la RBDS à la séquestration du carbone atmosphérique: Cas des villages de Djirnda et de Sanghako du Delta du Saloum (Sénégal); UCAD—DEA Sciences de l’Environnement, 2007. Available online: https://www.memoireonline.com/12/09/3025/Contribution-des-reboisements-de-mangrove-du-delta-du-saloum-senegal-a-la-se.html (accessed on 15 November 2018).
- Guèye, A.K.; Janicot, S.; Niang, A.; Sawadogo, S.; Sultan, B.; Diongue-Niang, A.; Thiria, S. Weather regimes over Senegal during the summer monsoon season using self-organizing maps and hierarchical ascendant classification. Part II: Interannual time scale. Clim. Dyn. 2012. [Google Scholar] [CrossRef]
- Zuhlke, M.; Fomferra, N.; Brockmann, C.; Peters, M.; Veci, L.; Malik, J.; Regner, P. SNAP (Sentinel Application Platform) and the ESA Sentinel 3 Toolbox. In Proceedings of the Sentinel-3 for Science Workshop, Venice, Italy, 2–5 June 2015; Volume 12, pp. 21–8, ISBN 978-92-9221-298-8. [Google Scholar]
- Huang, X.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of Forest above Ground Biomass Estimation Using Multi-Temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 Data. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Müller-Wilm, U. Sentinel-2 MSI—Level-2A Prototype Processor Installation and User Manual. Spec. Publ. ESA SP 2016, 49, 1–51. [Google Scholar]
- Hijmans, R.J.; van Etten, J. Raster: Geographic Data Analysis and Modeling with Raster Data, R Packag. version 2.5-8; 2016. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 15 November 2018).
- R Core Team R Core Team. R: A Language and Environment for Statistical Computing; R Core Team R Core Team: Vienna, Austria, 2015; pp. 275–286. ISBN 3-900051-07-0. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. VSURF: An R Package for Variable Selection Using Random Forests. R J. 2015, 7, 19–33. [Google Scholar]
- Pix4D SA. Pix4D Support. Available online: https://support.pix4d.com (accessed on 23 February 2018).
- Cunliffe, A.M.; Brazier, R.E.; Anderson, K. Ultra-fine grain landscape-scale quantification of dryland vegetation structure with drone-acquired structure-from-motion photogrammetry. Remote Sens. Environ. 2016, 183, 129–143. [Google Scholar] [CrossRef]
- Pix4D SA. Pix4Dmapper. Available online: https://www.pix4d.com/product/pix4dmapper-photogrammetry-software (accessed on 15 November 2018).
- Isenburg, M. LAStools—Efficient LiDAR Processing Software (version 141017, unlicensed). 2014. Available online: http://rapidlasso.com/LAStools (accessed on 15 November 2018).
- Mcgaughey, R.J.; Carson, W.W. Fusing LIDAR Data, Photographs, and Other Data Using 2D and 3D Visualization Techniques. Proc. Terrain Data Appl. Vis.—Mak. Connect. 2003, 28–30. Available online: https://www.fs.fed.us/pnw/olympia/silv/publications/opt/488_McGaugheyCarson2003.pdf (accessed on 15 November 2018).
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the Trees in the Forest: Using Lidar and Multispectral Data Fusion with Local Filtering and Variable Window Size for Estimating Tree Height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Kini, A.U.; Popescu, S.C. TreeVaW: A versatile tool for analyzing forest canopy LIDAR data: A preview with an eye towards future. In Proceedings of the ASPRS 2004 Fall Conference, Kansas City, Missouri, 12–16 September 2004. [Google Scholar]
- Silva, C.A.; Crookston, N.L.; Hudak, A.T.; Vierling, L.A. Package ‘rLiDAR’: LiDAR Data Processing and Visualization. Available online: https://cran.r-project.org/web/packages/rLiDAR/rLiDAR.pdf (accessed on 15 November 2018).
- Agresta, S. Coop. Monitoring Report: Livelihoods’ Mangrove Restoration Grouped Project in Senegal. Madrid, Spain, 2017. Available online: http://www.vcsprojectdatabase.org/services/publicViewServices/downloadDocumentById/29202 (accessed on 15 November 2018).
- Englhart, S.; Keuck, V.; Siegert, F. Modeling aboveground biomass in tropical forests using multi-frequency SAR data-A comparison of methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 298–306. [Google Scholar] [CrossRef]
- Jachowski, N.R.A.; Quak, M.S.Y.; Friess, D.A.; Duangnamon, D.; Webb, E.L.; Ziegler, A.D. Mangrove biomass estimation in Southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A Comparison of Machine Learning Techniques Applied to Landsat-5 TM Spectral Data for Biomass Estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; Volume 8, ISBN 0387987800. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training. R Package 6.0-73. Available online: https://cran.r-project.org/package=caret (accessed on 15 November 2018).
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Frate, F. Del; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Särndal, C.-E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer Series in Statistics; Springer Publishing: New York, NY, USA, 1992; ISBN 0-387-97528-4. [Google Scholar]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating tree heights with images from an unmanned aerial vehicle. Geomatics Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef]
- Jensen, J.L.R.; Mathews, A.J. Assessment of image-based point cloud products to generate a bare earth surface and estimate canopy heights in a woodland ecosystem. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; González-Ferreiro, E.; Sarmento, A.; Silva, J.; Nunes, A.; Correia, A.C.; Fontes, L.; Tomé, M.; Díaz-Varela, R. Using high resolution UAV imagery to estimate tree variables in Pinus pinea plantation in Portugal. For. Syst. 2016. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Torres-Sánchez, J.; López-Granados, F.; Serrano, N.; Arquero, O.; Peña, J.M. High-throughput 3-D monitoring of agricultural-tree plantations with Unmanned Aerial Vehicle (UAV) technology. PLoS ONE 2015, 10. [Google Scholar] [CrossRef]
- Gong, P.; Sheng, Y.; Blging, G.S. 3D Model-Based Tree Measurement from High-Resolution Aerial Imagery. Photogrammtric Eng. Remote Sens. 2002. [Google Scholar]
- McRoberts, R.E.; Westfall, J.A. Effects of uncertainty in model predictions of individual tree volume on large area volume estimates. For. Sci. 2014. [Google Scholar] [CrossRef]
- Aslan, A.; Rahman, A.F.; Warren, M.W.; Robeson, S.M. Mapping spatial distribution and biomass of coastal wetland vegetation in Indonesian Papua by combining active and passive remotely sensed data. Remote Sens. Environ. 2016. [Google Scholar] [CrossRef]
- Alan, J.; Castillo, A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. ISPRS Journal of Photogrammetry and Remote Sensing Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using Sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Hamdan, O.; Khali Aziz, H.; Mohd Hasmadi, I. L-band ALOS PALSAR for biomass estimation of Matang Mangroves, Malaysia. Remote Sens. Environ. 2014. [Google Scholar] [CrossRef]
- Lucas, R.; Bunting, P.; Clewley, D.; Armston, J.; Fairfax, R.; Fensham, R.; Accad, A.; Kelley, J.; Laidlaw, M.; Eyre, T.; et al. An Evaluation of the ALOS PALSAR L-Band Backscatter—Above Ground Biomass Relationship Queensland, Australia: Impacts of Surface Moisture Condition and Vegetation Structure. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Examining the potential of Sentinel-2 MSI spectral resolution in quantifying above ground biomass across different fertilizer treatments. ISPRS J. Photogramm. Remote Sens. 2015. [Google Scholar] [CrossRef]

| Sensor | Application | Acquisition Period | Processing Levels | Bands |
|---|---|---|---|---|
| S2 | Stratification | February 2017 March 2017 (7 scenes) | Level-1C | B2, B3, B4, B5, B6, B7, B8A, B9, B11, B12 |
| AGB prediction | July 2017 August 2017 (6 scenes) | |||
| S1 | AGB prediction | July 2017 September 2017 (6 scenes) | Level-1 GRD | C-band (VH polarization) |
| Predictor Variable | Band/Index | Definition |
|---|---|---|
| Multispectral bands | B2 | Blue, 490 nm |
| B3 | Green, 560 nm | |
| B4 | Red, 665 nm | |
| B5 | Red edge, 705 nm | |
| B6 | Red edge, 749 nm | |
| B7 | Red edge, 783 nm | |
| B8 | Near Infrared (NIR), 842 nm | |
| B8A | Near Infrared (NIR), 865 nm | |
| B9 | Water vapor, 945 nm | |
| B11 | Short-wavelength infrared (SWIR-1), 1610 nm | |
| B12 | Short-wavelength infrared (SWIR-2), 2190 nm | |
| Vegetation indices | NDVI1 | (B8 – B4)/(B8 + B4) |
| NDVI2 | (B8A – B4)/(B8A + B4) | |
| NDI45 | (B5 − B4)/(B5 + B4), | |
| SAVI | (B8 − B4)/(B8 + B4 + L) * (1.0 + L) L = 0.5 | |
| TCARI | 3 * [(B5 − B4) − 0.2 * (B5 − B3) * (B5/B4)] | |
| OSAVI | (1.16) * (B8 – B4)/(B8 + B4 + 0.16) | |
| MCARI | [(B5 – B4) − 0.2 (B5 – B3)] * (B5/B4) | |
| GNDVI | (B8 – B3)/(B8 + B3) | |
| PSSRa | B8/B4 | |
| IRECI | (B8 –B4)/(B5/B6) |
| Images Date | RF Predictor Variables | VSURF Selected Variables |
|---|---|---|
| 9 March 2017 | B2, B3, B4, B5, B6, B7, B8, B8A, B9, B12, NDVI1, NDVI2, NDI45, SAVI, TCARI, OSAVI, MCARI, GNDVI, PSSRa, IRECI | B3, B12, OSAVI, NDVI2, NDI45, B9, B8 |
| 24 February 2017 | B2, B3, B4, B5, B6, B7, B8, B8A, B9, B12, NDVI1, NDVI2, NDI45, SAVI, TCARI, OSAVI, MCARI, GNDVI, PSSRa, IRECI | NDVI2, B3, B9, B12 |
| Equation | r2 | Number of Individuals | CD Range (cm) | h Range (cm) |
|---|---|---|---|---|
| 0.93 | 71 | 10.5–210.0 | 37–285 |
| Stratum | Number of Plots | Minimum | Mean | Maximum | Standard. Deviation |
|---|---|---|---|---|---|
| I | 55 | 0.00 | 0.33 | 1.60 | 0.49 |
| II | 42 | 0.00 | 8.05 | 36.93 | 9.72 |
| Field Tree Height | UAV Tree Height | Field Tree Crown Diameter | UAV Tree Crown Diameter | |
|---|---|---|---|---|
| Minimum | 0.35 | 0.23 | 0.08 | 0.01 |
| Mean | 1.12 | 1.00 | 0.85 | 0.81 |
| Maximum | 3.40 | 2.89 | 3.03 | 2.67 |
| Inputs | Selected Variables | r2 | RMSE (Mg ha−1) | MAE (Mg ha−1) | AIC |
|---|---|---|---|---|---|
| Sentinel-1 | VH | 0.90 | 2.22 | 0.89 | 89.27 |
| Sentinel-2 | PSSRa, NDVI2, GNDVI, IRECI, OSAVI | 0.71 | 3.74 | 1.91 | 218.23 |
| Sentinel-1 + Sentinel-2 | VH, IRECI, SAVI, OSAVI | 0.89 | 2.35 | 1.20 | 67.33 |
| Stratum | UAV-Based | Model-Assisted | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sentinel-1 | Sentinel-2 | Sentinel-1 + Sentinel-2 | |||||||||
| SE | SE | RE | SE | RE | SE | RE | |||||
| I | 0.33 | 0.35 | 0.99 | 0.31 | 1.27 | 0.75 | 0.30 | 1.32 | 0.95 | 0.35 | 0.98 |
| II | 8.05 | 1.50 | 8.50 | 0.97 | 2.37 | 6.04 | 1.16 | 1.68 | 9.12 | 0.88 | 2.87 |
| All | 2.90 | 0.55 | 3.49 | 0.38 | 2.06 | 2.51 | 0.43 | 1.61 | 3.66 | 0.38 | 2.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. https://doi.org/10.3390/rs11010077
Navarro JA, Algeet N, Fernández-Landa A, Esteban J, Rodríguez-Noriega P, Guillén-Climent ML. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sensing. 2019; 11(1):77. https://doi.org/10.3390/rs11010077
Chicago/Turabian StyleNavarro, José Antonio, Nur Algeet, Alfredo Fernández-Landa, Jessica Esteban, Pablo Rodríguez-Noriega, and María Luz Guillén-Climent. 2019. "Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal" Remote Sensing 11, no. 1: 77. https://doi.org/10.3390/rs11010077
APA StyleNavarro, J. A., Algeet, N., Fernández-Landa, A., Esteban, J., Rodríguez-Noriega, P., & Guillén-Climent, M. L. (2019). Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sensing, 11(1), 77. https://doi.org/10.3390/rs11010077