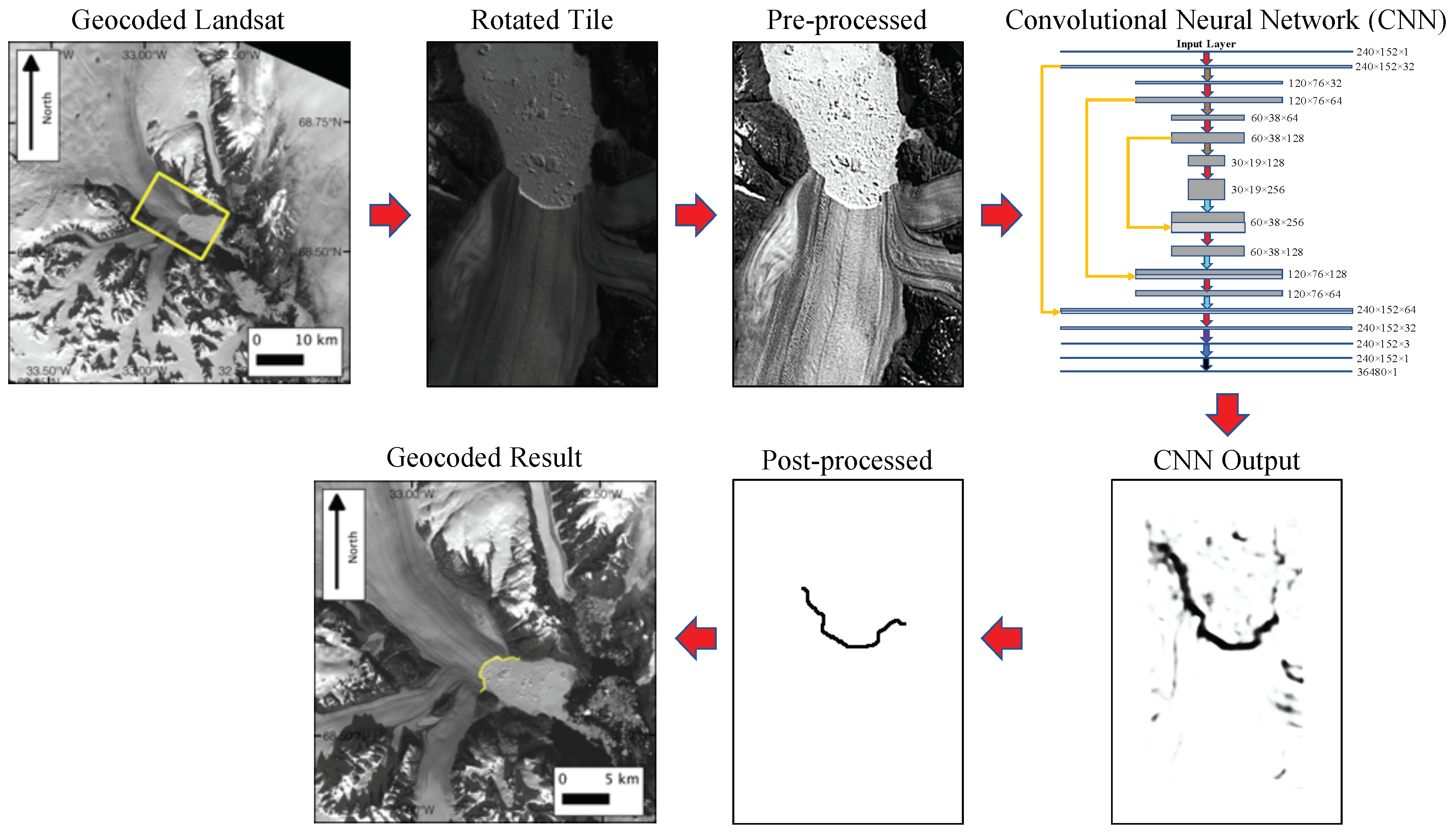
1. Introduction
In recent decades, tidewater glaciers discharging ice from the Greenland Ice Sheet have been thinning, speeding up and retreating inland [
1,
2,
3,
4,
5,
6]. The position of glacier ice fronts reflects a delicate balance of advection and ablation processes [
7] and hence is an important proxy for the impacts of regional changes in climate and ocean state on the mass balance in the Greenland Ice Sheet. To assess records of ice front retreat over time, ice front positions are typically manually digitized from aerial imagery [
4] or satellite imagery [
2,
5] using Geographic Information System (GIS) software. Since the launch of Landsat 5 in 1984, the Landsat fleet has captured images of the Greenland Ice Sheet with a repeat cycle of 16 days. However, because the manual ice front digitization process requires a considerable time investment, most current records of calving front retreat are limited to only a few ice front positions per glacier per year, if any. This shortage of data poses a challenge to seasonal analyses of calving glaciers (e.g., [
8,
9,
10,
11]), yet seasonal factors may be critical to understanding the pattern of long term retreat of Greenland’s glaciers [
12] or to understand for instance the level above which a glacier may be pushed out of balance compared to its state of seasonal, natural variability [
6]. In effect, an automated system to rapidly delineate calving front positions would provide a foundation for understanding regional changes on the periphery of the ice sheet over the past several decades, especially with the emergence of a new generation of satellites with high data volume, a high number of acquisitions and higher resolution (e.g., [
13,
14,
15,
16]).
Detecting glacier calving fronts in images falls under a more general category of problems that deal with image segmentation. Generally, image segmentation techniques focus on either dividing an image into different regions (e.g., clustering, classification, region extraction) or finding the boundaries between regions (i.e., detection of discontinuities, edge detection). A detailed overview of these categories and techniques is given by [
17]. Various techniques have been developed in the past for this class of problems. One of the most prominent of these analytical techniques is the Sobel filter, which uses gradients with a given threshold to detect edges [
18]. Other approaches include the “Scale-Space” technique, which, first developed by Witkin et al. [
19], detects the desired feature at a coarser scale and tracks it continuously at a higher resolution. This approach was further improved by Perona and Malik [
20] by using an anisotropic diffusion process to keep the spatial accuracy of the features and detect edges. Applying these techniques to geophysical images such as ice-covered fjords and geologic formations is challenging due to the noisy nature of the data, variable atmospheric conditions (particularly clouds) and temporal changes on the ground. Seale et al. [
3] analyzed the evolution of calving fronts for 32 glaciers in Greenland using a Sobel filter as well as a brightness profiling technique applied to MODIS data. While achieving reasonable results below the resolution of MODIS (0.25 km), this approach relies on the proper selection of subregions around the calving front and heavy use of quality assurance and post-removal of anomalies. Furthermore, analytical techniques relying on brightness gradients in images are dependent on the particular nature of the data. For example, the same gradient thresholds may not be applicable to other instruments and spectral bands. They would also not be applicable to other data types such as radar interferometry (see Massonnet and Feigl [
21]). Finally, while this process provides an approximation of overall glacier retreat, it does not yield a digitized-front product which can be used by the glaciological community.
An alternative approach for overcoming these problems is the use of neural networks (see LeCun et al. [
22]) that can be trained on any data type to detect glacier fronts. Image segmentation techniques have improved rapidly in recent years due to the progress in deep learning and semantic image segmentation with Convolutional Neural Networks (CNNs) (e.g., see Krizhevsky et al. [
23]). Large neural networks with thousands or millions of parameters have allowed much more accurate classification and segmentation of images. In fact, deep neural networks with rectified activation units have already surpassed human performance in some visual recognition tasks (see He et al. [
24]).
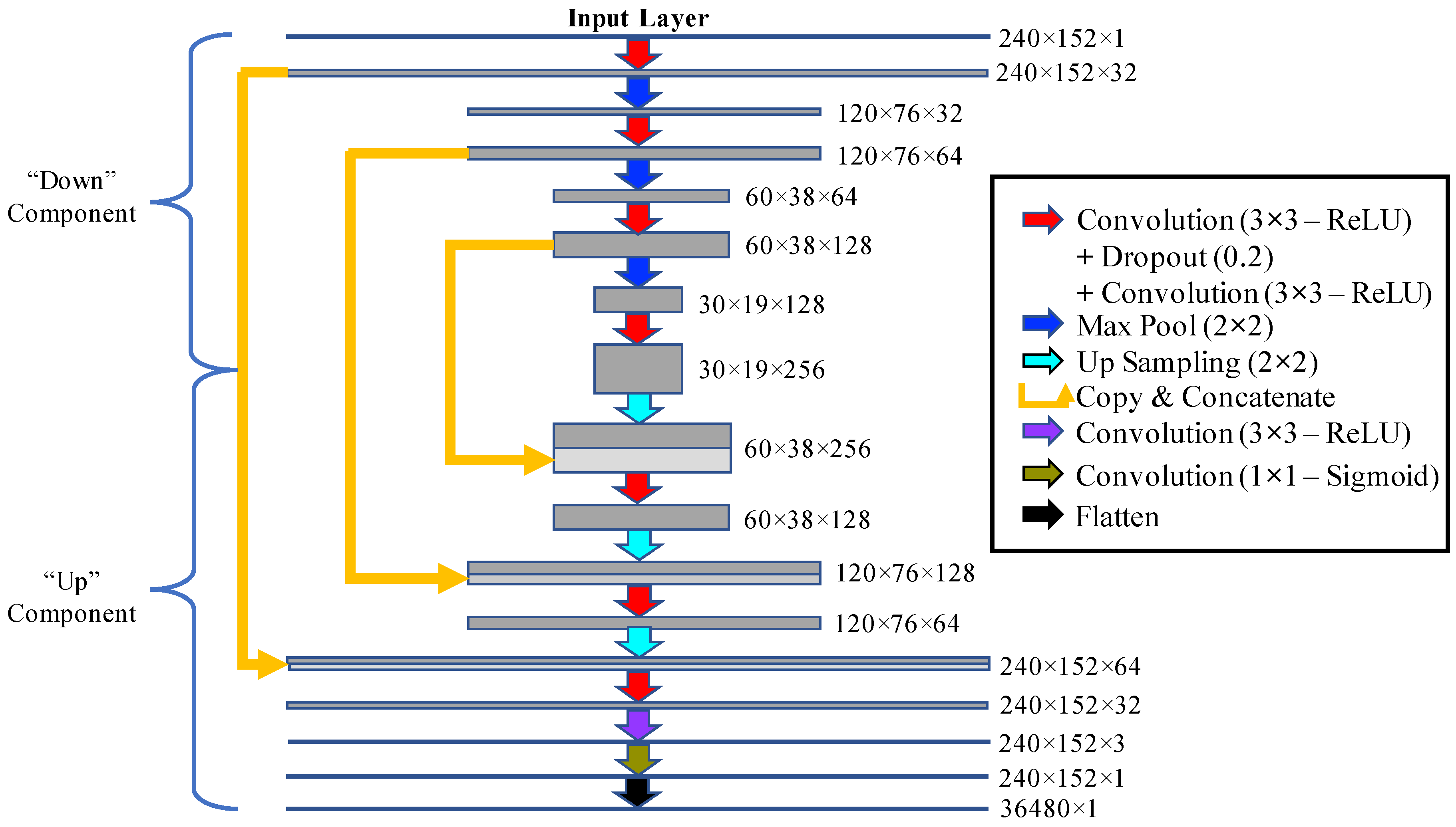
The issue with such deep neural networks for image segmentation is the need for very large training datasets where the desired features (in this case calving fronts) have already been determined for thousands of images. For many fields of research the shortage of vast training data limits the use of such tools. However, a recent deep neural network architecture developed for biomedical image segmentation, U-Net [
25], has been shown to provide highly accurate image segmentation with minimal training data through the use of data augmentation in a deep convolutional neural network. Here we develop a modified version of the U-Net architecture that can identify and extract glacier calving fronts from optical satellite imagery. We discuss our results for a set of glaciers on the Greenland ice sheet. We compare our trained network with the Sobel filter. We conclude on the application of CNN technology to the detection of ice sheet calving margins.
3. Results
We train the neural network on a set of 123 preprocessed
input images from Jakobshavn, Sverdrup, and Kangerlussuaq glaciers. Note that while this may seem like a limited number of training instances, one of the advantages of the utilized network architecture used in this study is its ability to perform well with an extremely limited set of training data. In fact, the U-Net architecture used by Ronneberger et al. [
25] used a training set that consisted of 30
pixel images. Training success with few training images is in part enabled by data augmentation, which plays an important role in reducing our output errors, as discussed below. We leave aside 10% of the images chosen randomly during training for cross-validation. The validation dataset is used to prevent overfitting. The training is halted when the validation loss starts to increase as a result of overfitting. In addition, in order to test the ability of the neural network to predict calving fronts beyond the training set for different glacier geometries, we test the trained network on images of Helheim glacier, whose geometry is unknown to the NN during training. Note that this test dataset is in addition to the cross-validation data used during training. We minimize the custom-weighted binary cross-entropy loss function discussed in
Section 2 using the Adam optimizer [
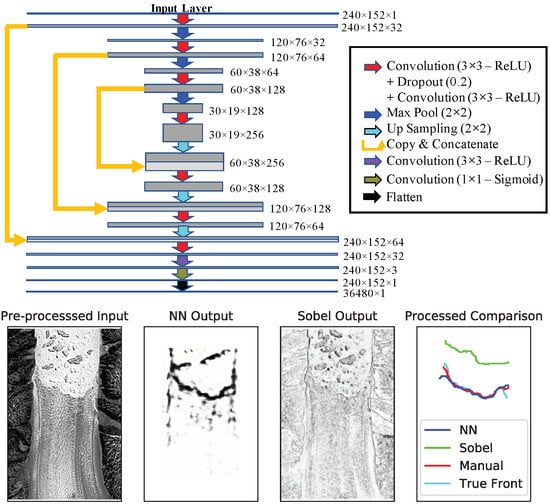
32] with batches of 10 images at a time. Furthermore, we use a variable learning rate, which is reduced by half after every 5 epochs without any improvements to the accuracy. We test the performance of a variety of NN configurations (discussed in the next section) and find that training the NN described in
Figure 2 with horizontal mirroring augmentation with batches sizes of 10 leads to excellent agreement between the “generated” and “true” fronts. Training the network for 54 epochs leads to an accuracy of 92.4% in the training set and 93.6% in the validation set, after which the validation loss starts to increase as a result of over-fitting.
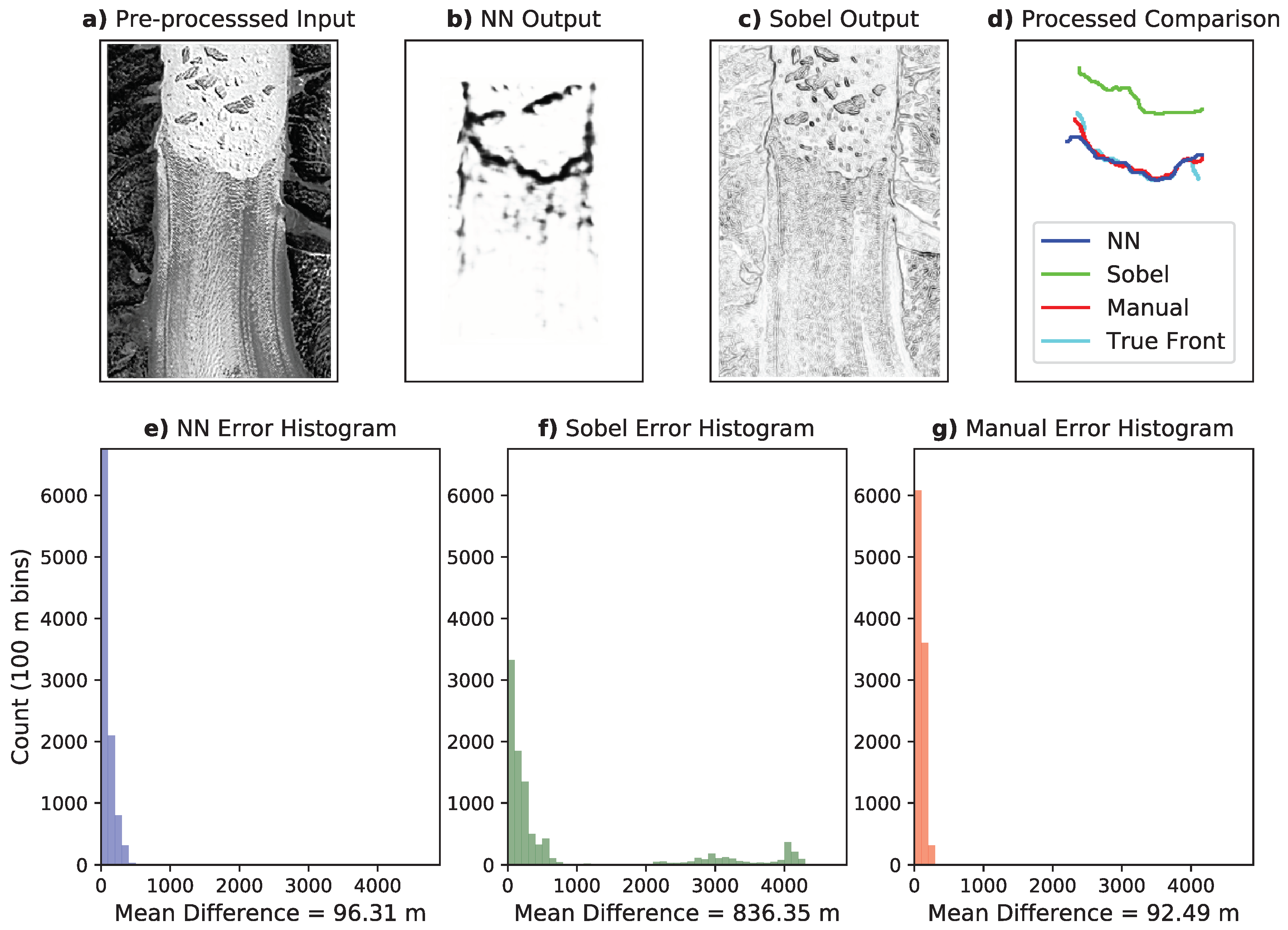
Figure 3 shows the result of the NN network on a particularly noisy test image.
Panel (a) shows the pre-processed input image. Note that we pick this example as an instance of an image that can mislead analytical edge detection filters, but the reported results and errors are drawn from the complete test dataset. The raw output of the NN is shown in Panel (b). It is evident that the neural network is able to extract the calving front from the input image.
Figure 3 also compares the output of the NN to the Sobel filter, a common analytic edge detection algorithm that has been used in previous studies (e.g., see Seale et al. [
3]). It is clear from Panel (c) that the Sobel filter is very sensitive to noise and identifies many gradients in the texture of the glacier, the icebergs, and the surrounding topography as calving boundaries, which could lead to a false identification of the position of the calving front. Panel (d) shows the extracted fronts in post-processing (as discussed in
Section 2.3). Note that we have also included a manually-determined front in addition to the “true” front. While the true front has also been determined manually on the original high resolution (i.e., uninterpolated) geocoded data, the “manual” comparison in
Figure 3 refers to hand-drawn fronts on the pre-processed lower resolution rasterized images that are also used for the NN and Sobel processing for an equal comparison of the performances. The neural network performs remarkably well compared with the true boundary. However it is evident that the Sobel filter is not able to extract the calving front as accurately as the NN. Furthermore, the performance of the neural network appears to be comparable to manually-determined front. Results for other test images are provided in the
Supplementary Material (Figure S2.1–10).
While Panels (a)–(d) of
Figure 3 showcase the output of one image, Panels (e) and (f) show the error analysis obtained from the complete set of test images for the NN, Sobel filter, and manual results. We quantify the errors by breaking the extracted calving fronts of Helheim glacier (which was not used during training) into 1000 smaller line segments and calculating the mean difference between the corresponding segments of the generated and true fronts.
Figure 3 shows the distribution of the differences for the NN (e) the Sobel filter (f), and manual results (g). We calculate the total error in the glacier fronts as the mean deviation between all 10,000 line segments in the outputted and true glacier front boundaries. The NN has a mean difference of 96.3 m, equivalent to 1.97 pixels, which is more than 8 times smaller than that of the Sobel filter. The manual output has a mean error of 92.5 m (1.89 pixels), only slightly below the error of the NN. Considering line segments only from the 8 scenes were the Sobel filter is able to successfully delineate the calving front, the errors are 85.3 m (1.74 pixels), 193.0 m (3.94 pixels), and 89.1 m (1.82 pixels) for the NN, Sobel, and manual approaches, respectively. Most of the error in the NN output is attributed to the edges of the calving front, as can be seen in the
Supplementary Material. Furthermore, it appears that the Sobel errors have a multimodal distribution. In other words, when the Sobel filter identifies the correct gradient as the calving front, it is in good agreement with the NN results. However, the filter can be easily mislead by other gradients in the image, resulting in a complete mis-identification and large errors for some images, leading to additional peaks in the histogram and larger overall errors. However, even when only the successful Sobel cases are compared, the NN mean error is less than half of that of the Sobel. The manual error histogram shows a more narrow distribution of errors, similar to the NN. The results from the NN, Sobel filter, and the manual technique for individual test images, along with the corresponding errors, can be viewed in the
Supplementary Material.
Note that the errors are dependent on the resolution of the input images. As noted before, the resolution of our inputs are less than that of the native Landsat images in order to account for the possible span of ice fronts while minimizing image sizes and training time. However, the errors could be improved further by increasing the resolution and the areal extent of the input images, requiring more computational resources and increased training time. Thus, our benchmark analysis shown above is conducted on the same glacier to limit the influence of resolution and image size on the performance comparison of NN configurations and analytical filter and manual results. We performed the training with the interpolated images on an Intel 2.9 GHz CPU node with 5 Gigabytes of allotted memory. The training took 2 min and 17 s per epoch, resulting in just over two hours of training in total. More computational resources, in particular the use of Graphical Processing Units (GPUs), could result in significant improvements to the training time.
4. Discussion
Images of glacier calving fronts are inherently noisy, with a variety of surfaces and boundaries. Therefore, the application of analytical edge detection schemes such as the Sobel filter [
18] results in many false-positive predictions, where any sharp gradients on the surface of the glacier, icebergs, valley walls, and surrounding topography are likely to be labeled as glacier calving fronts. In contrast, a convolutional neural network is able to learn the desired features in the images in order to correctly identify the calving front and mostly ignore other boundaries and sharp gradients. As discussed in
Figure 3, the glacier fronts extracted from the output of the NN are in very close agreement to the true front and have similar errors as manually-determined fronts on the same resolution. The analytical filter, however, appears to be very sensitive to noise. It returns noisy images of sharp gradients from which the calving front cannot be correctly extracted in some cases. While customized analytical edge-detection schemes may be able to achieve reasonable results (see Seale et al. [
3]), they often rely on dataset-specific parameterizations and thresholds that are not readily applicable to various imagery solutions. The application of neural networks, on the other hand, does not require analytical customization for different datasets. The NN can be trained on any imagery product with the proper training labels. The applicability of NNs for the detection of calving fronts goes beyond optical imagery, and can be potentially applied to other forms of data such as radar, which will be explored in future studies.
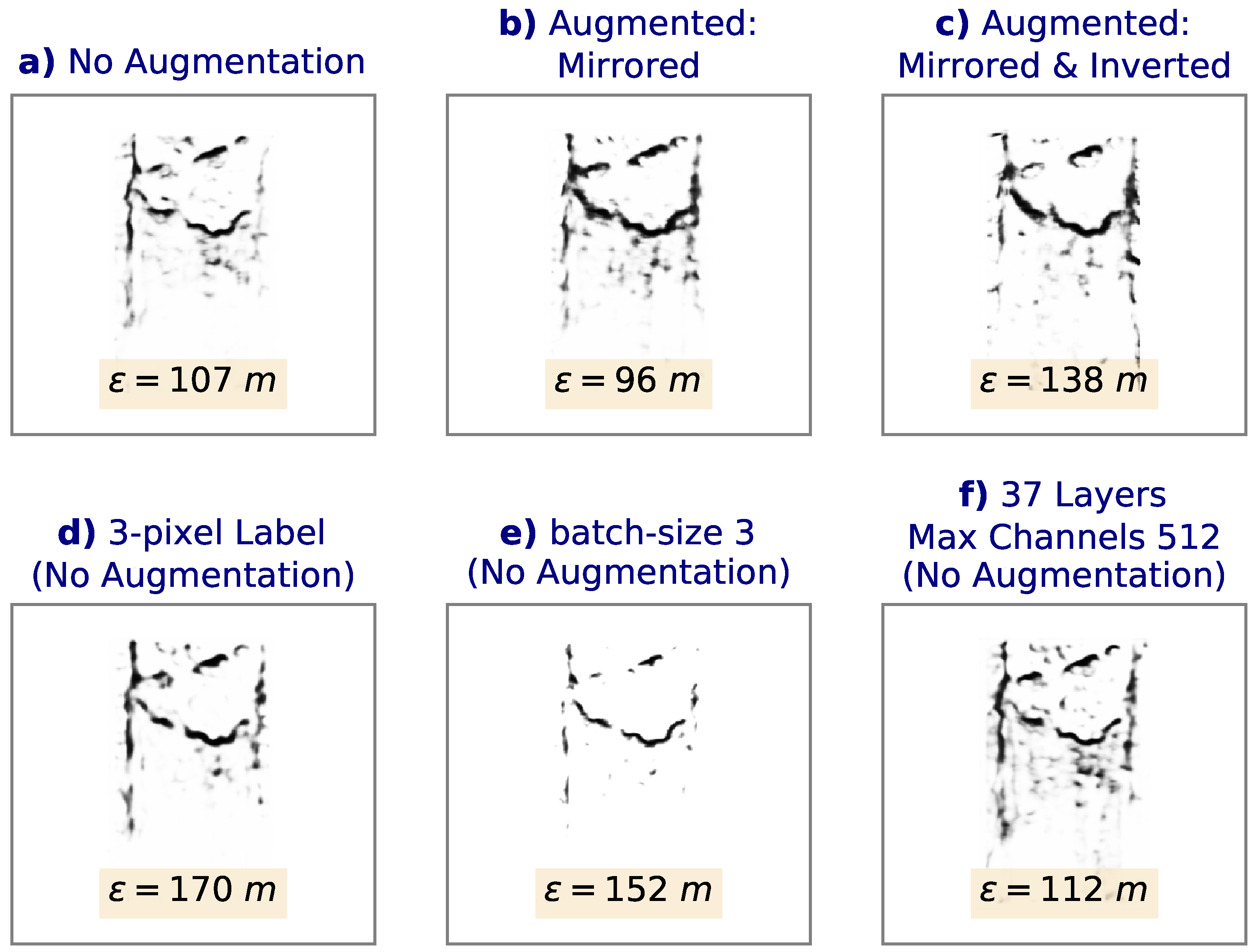
The proper configuration and training of the NN can have a significant effect on the accuracy of the generated calving fronts.
Figure 4 showcases various alterations to the NN on the same image used in
Figure 3. Panels (a)–(c) use the architecture of the NN shown in
Figure 2 without any data augmentation (a), horizontally mirroring the images (b), and horizontally mirroring and inverting the colors of the images (c) during training. We find that data augmentation results in more continuous calving fronts while generally reducing the “noise” (number of false-positives). However, color inversion does not seem to contribute further to the performance of the network. In fact, while horizontal mirroring produces a mean deviation error of 96 m, the addition of inversion increases the error to 138 m. Furthermore, note that data augmentation increases the training time by several fold, depending on the number of alterations. Adding color inversion augmentation increases the training time per epoch from 137 to 217 seconds. As a result, it is desirable to use minimal augmentation while maintaining a low error. Therefore, we restrict the augmentation to horizontal mirroring. Furthermore, Panel (d) shows the effect of increasing the width of the glacier front lines in the training labels from 1 pixel to 3 pixels. While the mean error increases due to the loss of spatial precision, it is interesting to note that the noise, or number of false-positives, also decreases noticeably. This may be a result of the smaller class imbalance and weight ratio in the loss function (which decreases from 241.15 to 82.22), reducing the relative cost for a false classification of the calving fronts compared to background pixels. Therefore, if more pronounced calving front lines with minimal noise are required in post-processing, thicker labels may be desired.
We also find that the number of batches used during training has a significant effect on the results. We use batch sizes of 10 in the chosen NN. On the one hand, using larger batch sizes increases the noise in the output of the neural network, significantly decreasing the accuracy metric in the validation dataset. On the other hand, while using smaller batch sizes reduces the background noise, it also decreases the accuracy, with the mean error changing from 107 m (10 batches) to 152 m (3 batches), as shown in Panel (e). However, smaller batch sizes might be desirable if fewer false-negatives (at the cost of less continuous calving fronts) are required. Note that while smaller batch sizes increase training time per epoch, fewer iterations are required before overfitting in validation loss becomes evident.
Lastly, we also examine the effect of the depth and size of the neural network on the test results. While increasing the depth leads to smaller errors compared to increasing the width or the number of units in each layer (not shown), there are no improvements with respect to the 29-layer NN, as shown in Panel (f). This may be due to the limited availability of training data for a deeper NN. The 37-layer NN (with one more downsample/upsamppling step compared to
Figure 2) shows a more noisy output with a mean error of 112 m, slightly larger than the mean error of the corresponding 29-layer output in Panel (a). Note that the same relationship is true with the addition of augmentation. However, in the case of a larger and more varied training dataset, a deeper NN could potentially lead to further improvements.
5. Conclusions
We have used a Convolutional Neural Network (CNN) with a U-Net architecture [
25] to automatically detect glacier calving fronts in images obtained from Landsat 5 (“green” band) and Landsat 7 and 8 (“panchromatic” band). After exploring different network architectures and training and augmentation configurations, we find remarkable agreements between the true hand-drawn calving fronts and those obtained by a 29-layer deep neural network with
ReLU convolutional layers [
29], regularization with 0.2 Dropout layers [
30],
downsamplinig (MaxPooling [
28]) and upsampling layers, a sample-weighted loss function based on the ratio of calving-front vs. non-calving-front pixels, and the utilization of data augmentation. We test the performance of the network not only on new images in the validation dataset, but also on an entirely new glacier with higher spatial resolution to test the effect of different fjord geometries and spatial resolutions on the trained network. After training the NN on Jakobshavn, Sverdrup, and Kangerlussuaq glaciers, we test it on Helheim glacier and obtain a mean deviation error of 96.3 m, equivalent to 1.97 pixels on average, which is comparable to the mean error of 92.5 m obtained from hand-drawn results on the same resolution. As a comparison, the Sobel filter [
18], a commonly used analytical edge-detection method (e.g., see Seale et al. [
3]) results in a mean error of 836.3 m on the same dataset. Comparing only the successful cases of the Sobel filter, the errors are 85.3 m (1.74 pixels), 193.0 m (3.94 pixels), and 89.1 m (1.82 pixels) for the NN, Sobel, and manual techniques, respectively.
The success of the neural network (NN) in automatically detecting calving fronts, along with the need for a relatively small training set and short training times, makes this approach highly desirable for the continuous monitoring of numerous glaciers around the globe with the ever-growing wealth of remote-sensing data. The use of more spectral bands from various satellites can potentially improve the performance of the NN in the future. Furthermore, unlike analytical edge-detection techniques, the use of neural networks is not limited to optical imagery and can potentially be extended to many data forms such as radar. Therefore, the use of convolutional neural networks in the detection of calving fronts can be a widely applicable and powerful approach for future studies in order to monitor the retreat of numerous glaciers in real time.