Deformable Faster R-CNN with Aggregating Multi-Layer Features for Partially Occluded Object Detection in Optical Remote Sensing Images
Abstract
1. Introduction
- ➢
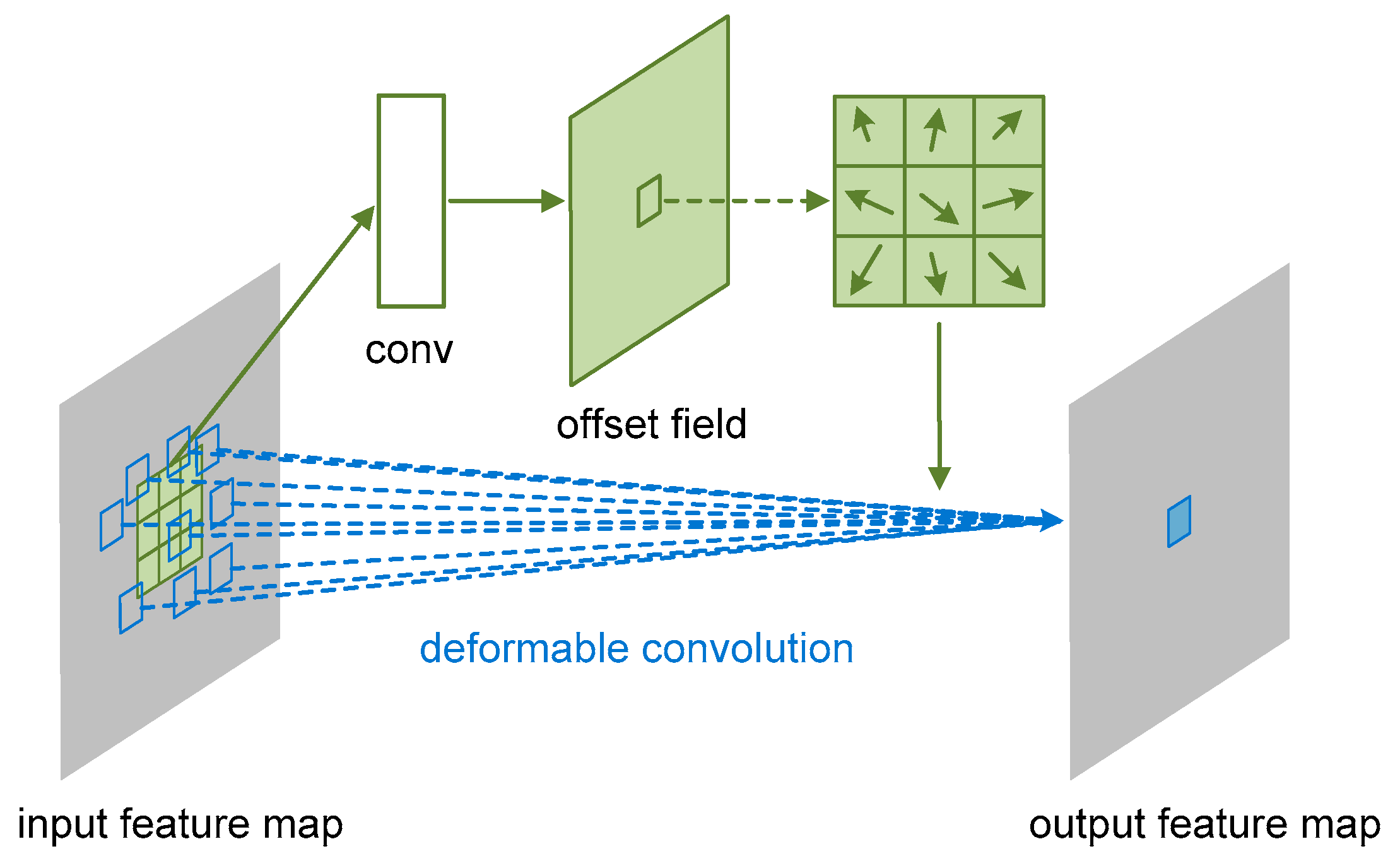
- A unified deformable Faster R-CNN is introduced for object detection in optical remote sensing images. Geometric variation modeling is completed within the deformable convolution layers. Feature maps extracted by deformable ConvNet contain more information about various geometric transformations.
- ➢
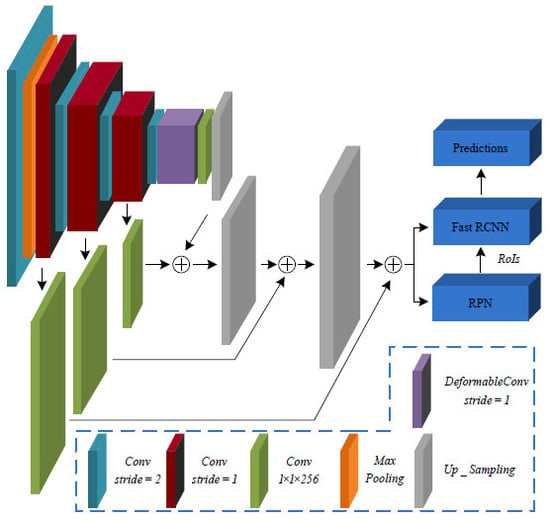
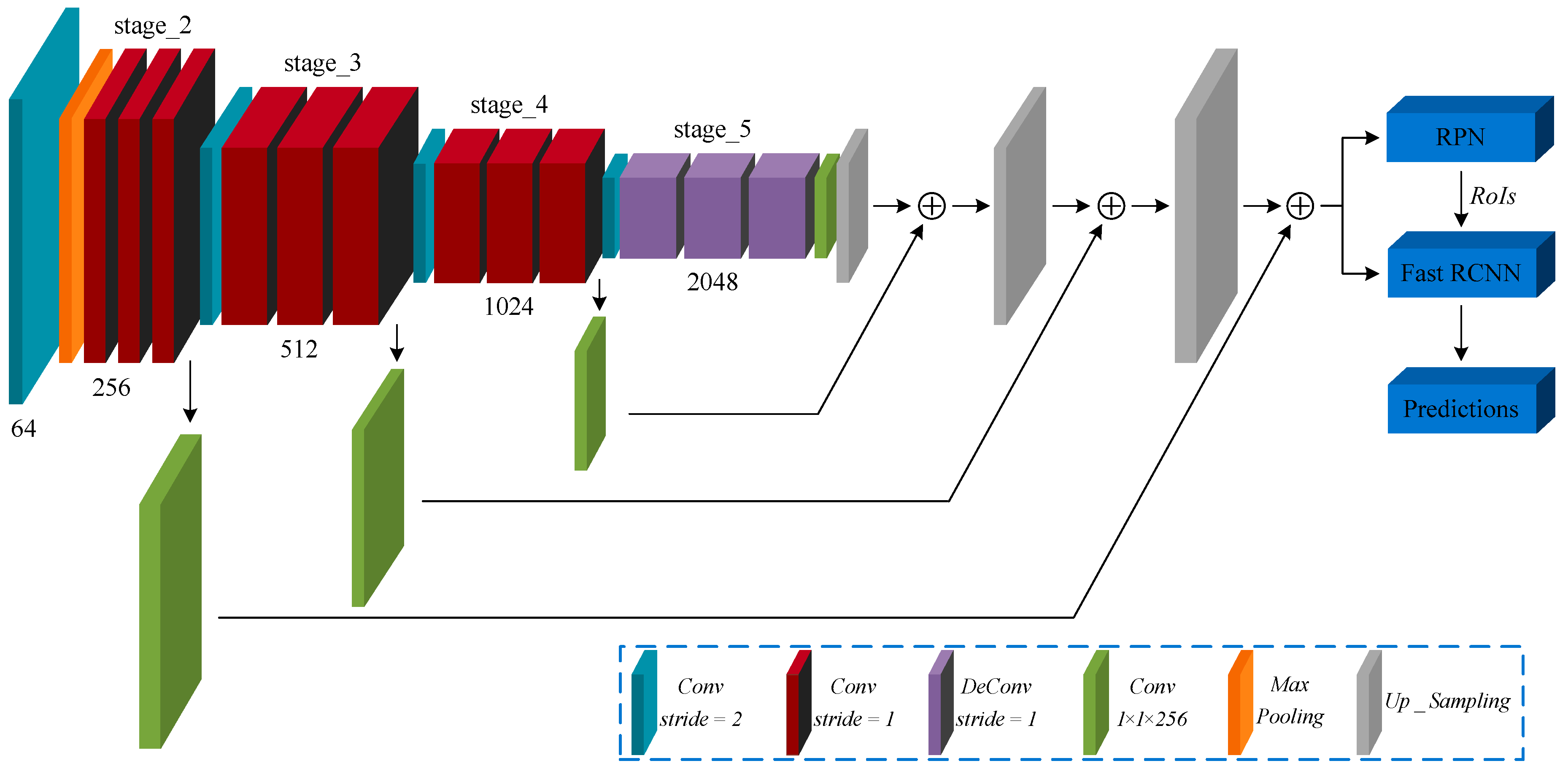
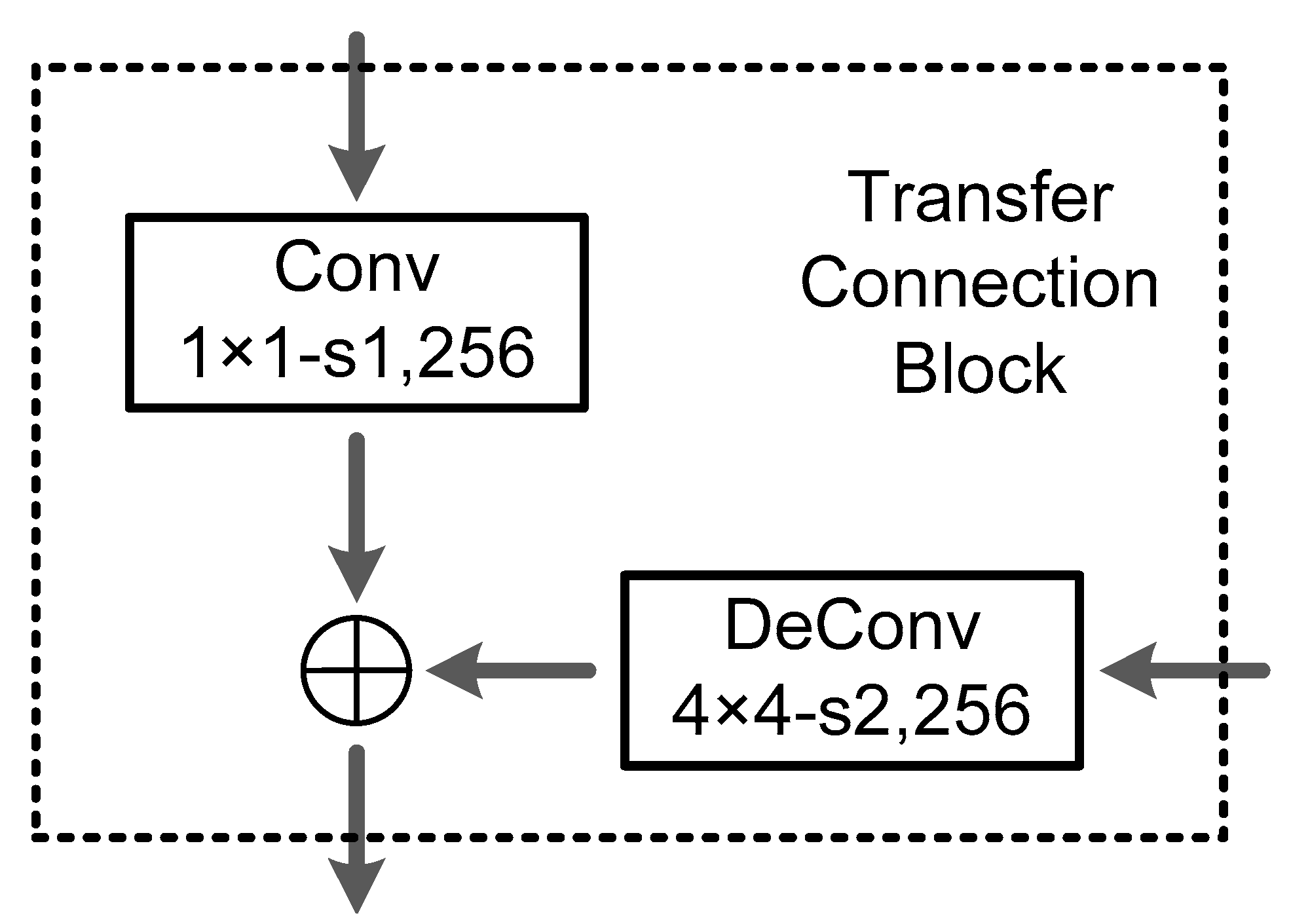
- A modified backbone network is specially designed for small object to generate more abundant feature maps with high semantic information at low layer. Therefore, a Transfer Connection Block (TCB) adopting top-down and skip connections is presented to produce a single high-level feature map of a fine resolution.
- ➢
- A simple, yet effective, data augmentation technique named Random Covering is proposed for training CNN. In training phase, it randomly selects a rectangle region in a region of interest and covers its pixels with random values. Hence, we can obtain augmented training samples with random levels of occlusion, which are fed into the model to enhance the generalization ability of the CNN model.
2. Methodology
2.1. Deformable Convolution
2.2. Transfer Connection Block
2.3. Random Covering
| Algorithm 1: Random Covering Procedure |
| Input: Input image ; Area of image ; Covering probability ; Area ratio range and ; Aspect ratio range and ; Weight coefficient range and ; Output: Covering image . Initialization: . if then ; return . else ; ; ; , ; , ; ; ; ; ; ; return . end |
3. Dataset and Experimental Settings
3.1. Evaluation Metrics
3.2. Dataset and Implementation Details
4. Experimental Results and Discussion
4.1. Quantitative Evaluation of NWPU VHR-10 Dataset
4.2. Quantitative Evaluation of SORSI Dataset
4.3. Quantitative Evaluation of HRRS Dataset
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lecun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014. [Google Scholar]
- Stankov, K.; He, D.C. Detection of buildings in multispectral very high spatial resolution images using the percentage occupancy hit-or-miss transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4069–4080. [Google Scholar] [CrossRef]
- Ok, A.O.; Başeski, E. Circular oil tank detection from panchromatic satellite images: A new automated approach. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1347–1351. [Google Scholar] [CrossRef]
- Wen, X.; Shao, L.; Fang, W.; Xue, Y. Efficient Feature Selection and Classification for Vehicle Detection. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 508–517. [Google Scholar]
- An, Z.; Shi, Z.; Teng, X.; Yu, X.; Tang, W. An automated airplane detection system for large panchromatic image with high spatial resolution. Optik-Int. J. Light Electron Opt. 2014, 125, 2768–2775. [Google Scholar] [CrossRef]
- Jain, A.K.; Ratha, N.K.; Lakshmanan, S. Object detection using Gabor filters. Pattern Recognit. 1997, 30, 295–309. [Google Scholar] [CrossRef]
- Leninisha, S.; Vani, K. Water flow based geometric active deformable model for road network. ISPRS J. Photogramm. Remote Sens. 2015, 102, 140–147. [Google Scholar] [CrossRef]
- Ok, A.O. Automated detection of buildings from single VHR multispectral images using shadow information and graph cuts. ISPRS J. Photogramm. Remote Sens. 2013, 86, 21–40. [Google Scholar] [CrossRef]
- Ok, A.O.; Senaras, C.; Yuksel, B. Automated detection of arbitrarily shaped buildings in complex environments from monocular VHR optical satellite imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1701–1717. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F.; et al. Geographic object-based image analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single shot multibox detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Cheng, G.; Zhou, P.; Han, J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable Convolutional Networks. 2017. Available online: http://openaccess.thecvf.com/content_ICCV_2017/papers/Dai_Deformable_Convolutional_Networks_ICCV_2017_paper.pdf (accessed on 22 August 2018).
- Lin, T.Y.; Dollár, P.; Girshick, R.B.; He, K.; Hariharan, B.; Belongie, S.J. Feature Pyramid Networks for Object Detection. 2017. Available online: http://openaccess.thecvf.com/content_cvpr_2017/papers/Lin_Feature_Pyramid_Networks_CVPR_2017_paper.pdf (accessed on 22 August 2018).
- Ren, Y.; Zhu, C.; Xiao, S. Object Detection Based on Fast/Faster RCNN Employing Fully Convolutional Architectures. Math. Probl. Eng. 2018, 2018, 3598316. [Google Scholar] [CrossRef]
- Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; Yang, Y. Random erasing data augmentation. arXiv, 2017; arXiv:1708.04896. [Google Scholar]
- Cheng, G.; Han, J.A. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, C.; Xiao, S. Small Object Detection in Optical Remote Sensing Images via Modified Faster R-CNN. Appl. Sci. 2018, 8, 813. [Google Scholar] [CrossRef]
- Qiu, S.; Wen, G.; Fan, Y. Occluded object detection in high-resolution remote sensing images using partial configuration object model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1909–1925. [Google Scholar] [CrossRef]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014. [Google Scholar]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training region-based object detectors with online hard example mining. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Han, X.; Zhong, Y.; Zhang, L. An efficient and robust integrated geospatial object detection framework for high spatial resolution remote sensing imagery. Remote Sens. 2017, 9, 666. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, X.; Wang, L.; Yang, R.; Pu, F. Deformable ConvNet with Aspect Ratio Constrained NMS for Object Detection in Remote Sensing Imagery. Remote Sens. 2017, 9, 1312. [Google Scholar] [CrossRef]

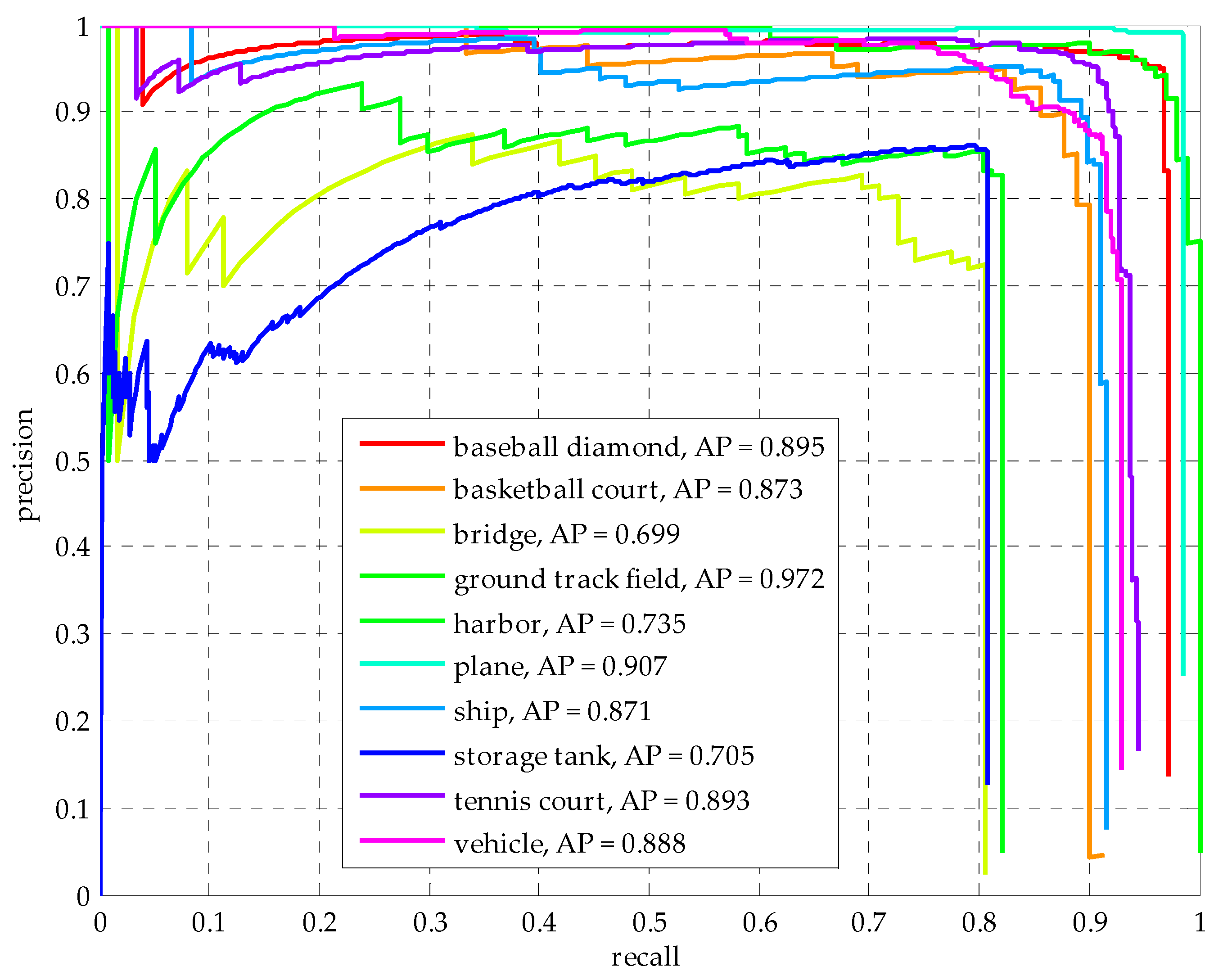
| Method | RICNN | SSD | R-P-Faster R-CNN | Deformable R-FCN (ResNet-101) with arcNMS | Deformable Faster RCNN (ResNet-50) with TCB |
|---|---|---|---|---|---|
| Airplane | 0.884 | 0.957 | 0.904 | 0.873 | 0.907 |
| Ship | 0.773 | 0.829 | 0.75 | 0.814 | 0.871 |
| Storage tank | 0.853 | 0.856 | 0.444 | 0.636 | 0.705 |
| Baseball diamond | 0.881 | 0.966 | 0.899 | 0.904 | 0.895 |
| Tennis court | 0.408 | 0.821 | 0.79 | 0.816 | 0.893 |
| Basketball court | 0.585 | 0.856 | 0.776 | 0.741 | 0.873 |
| Ground track field | 0.867 | 0.582 | 0.877 | 0.903 | 0.972 |
| Harbor | 0.686 | 0.548 | 0.791 | 0.753 | 0.735 |
| Bridge | 0.615 | 0.419 | 0.682 | 0.714 | 0.699 |
| Vehicle | 0.711 | 0.756 | 0.732 | 0.755 | 0.888 |
| mean AP | 0.726 | 0.759 | 0.765 | 0.791 | 0.844 |
| Method | Baseline | Faster RCNN with TCB | Deformable Faster RCNN with TCB | Deformable Faster RCNN with TCB (+OHEM) |
|---|---|---|---|---|
| plane | 0.729 | 0.778 | 0.792 | 0.862 |
| Ship | 0.850 | 0.826 | 0.831 | 0.903 |
| mean AP | 0.789 | 0.802 | 0.812 | 0.883 |
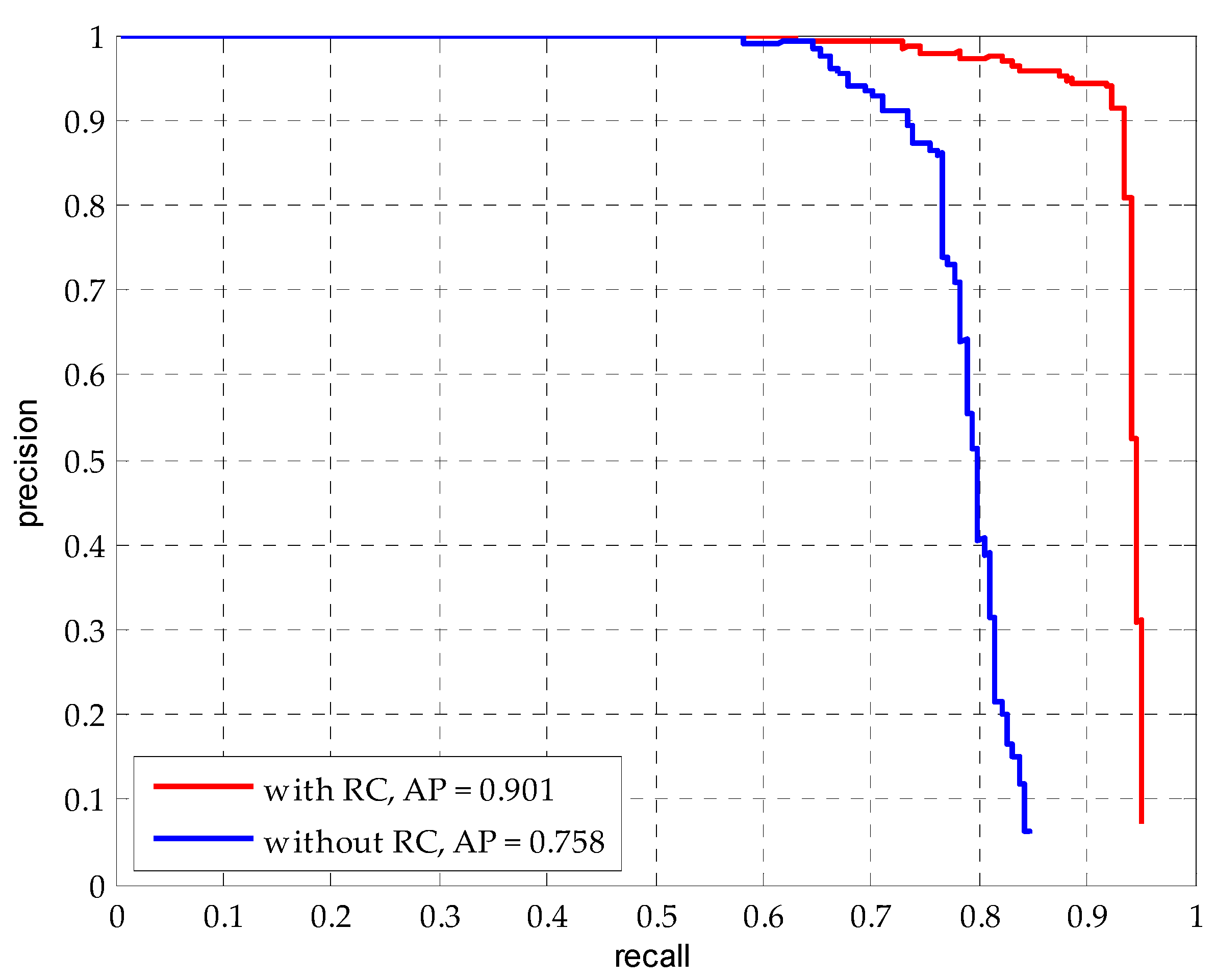
| Method | with RC | without RC |
|---|---|---|
| AP/#TP | 0.901/96 | 0.758/77 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Zhu, C.; Xiao, S. Deformable Faster R-CNN with Aggregating Multi-Layer Features for Partially Occluded Object Detection in Optical Remote Sensing Images. Remote Sens. 2018, 10, 1470. https://doi.org/10.3390/rs10091470
Ren Y, Zhu C, Xiao S. Deformable Faster R-CNN with Aggregating Multi-Layer Features for Partially Occluded Object Detection in Optical Remote Sensing Images. Remote Sensing. 2018; 10(9):1470. https://doi.org/10.3390/rs10091470
Chicago/Turabian StyleRen, Yun, Changren Zhu, and Shunping Xiao. 2018. "Deformable Faster R-CNN with Aggregating Multi-Layer Features for Partially Occluded Object Detection in Optical Remote Sensing Images" Remote Sensing 10, no. 9: 1470. https://doi.org/10.3390/rs10091470
APA StyleRen, Y., Zhu, C., & Xiao, S. (2018). Deformable Faster R-CNN with Aggregating Multi-Layer Features for Partially Occluded Object Detection in Optical Remote Sensing Images. Remote Sensing, 10(9), 1470. https://doi.org/10.3390/rs10091470