Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar
Abstract
:1. Introduction
2. Materials and Methods
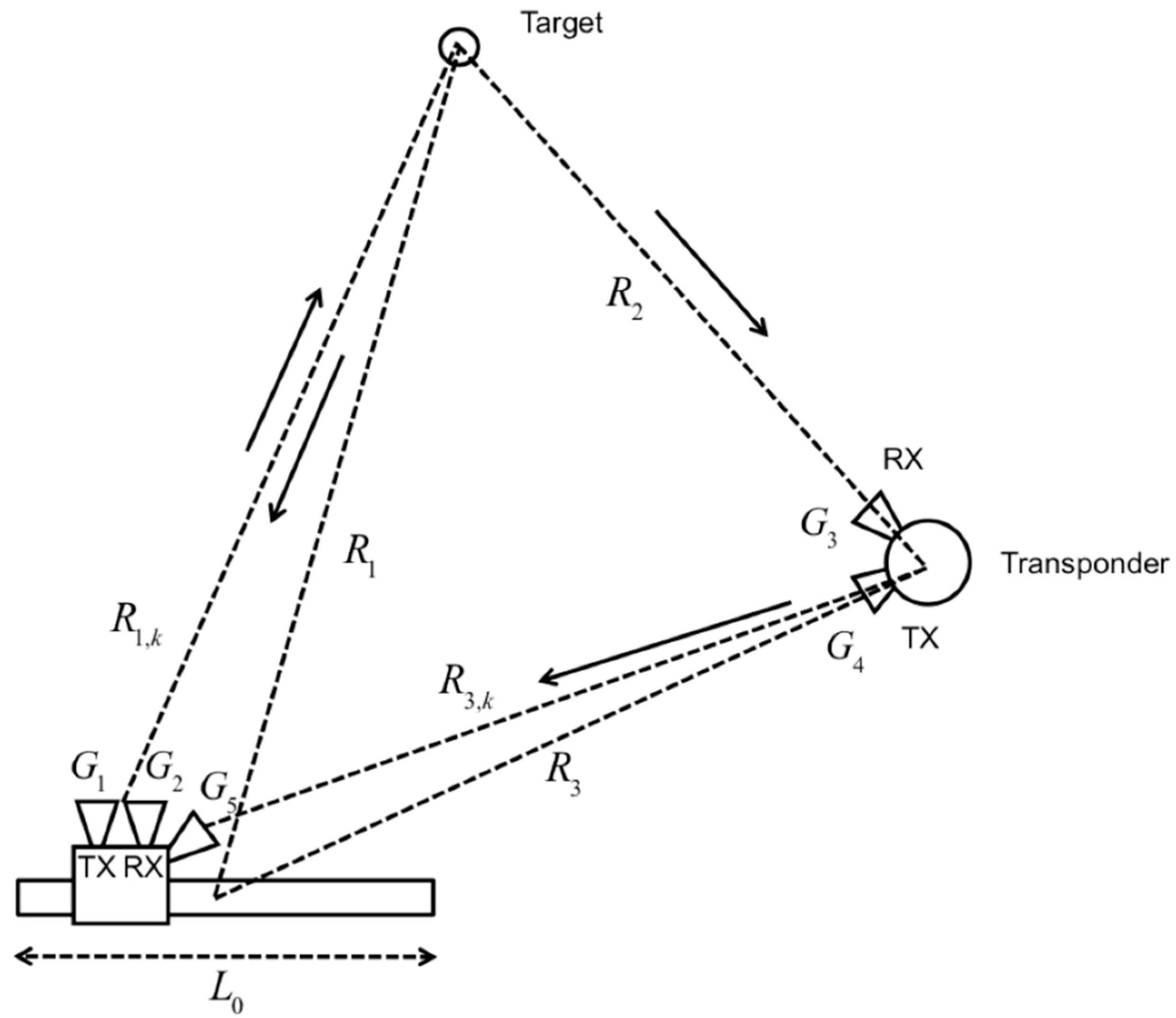
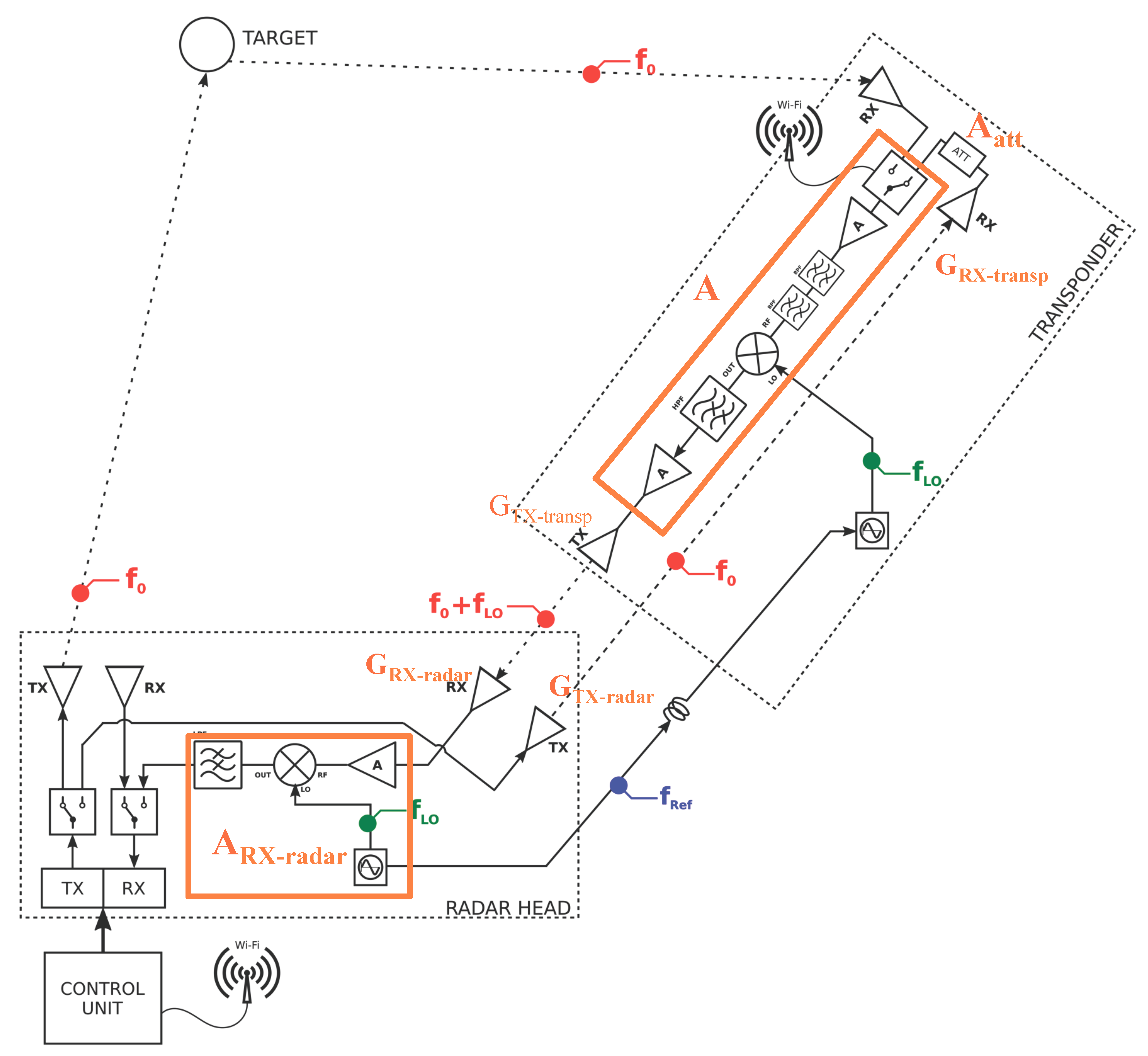
2.1. Working Principle of Monostatic/Bistatic GBSAR
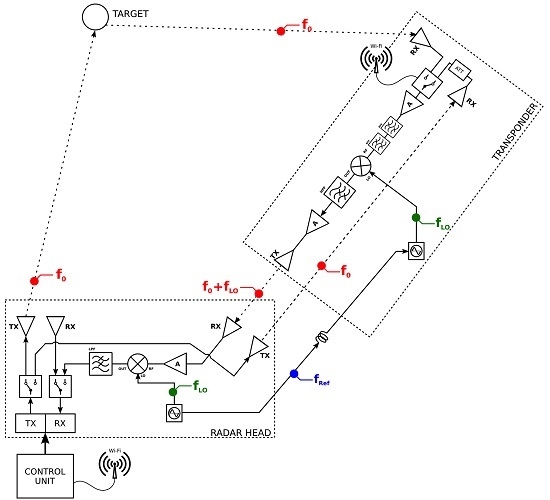
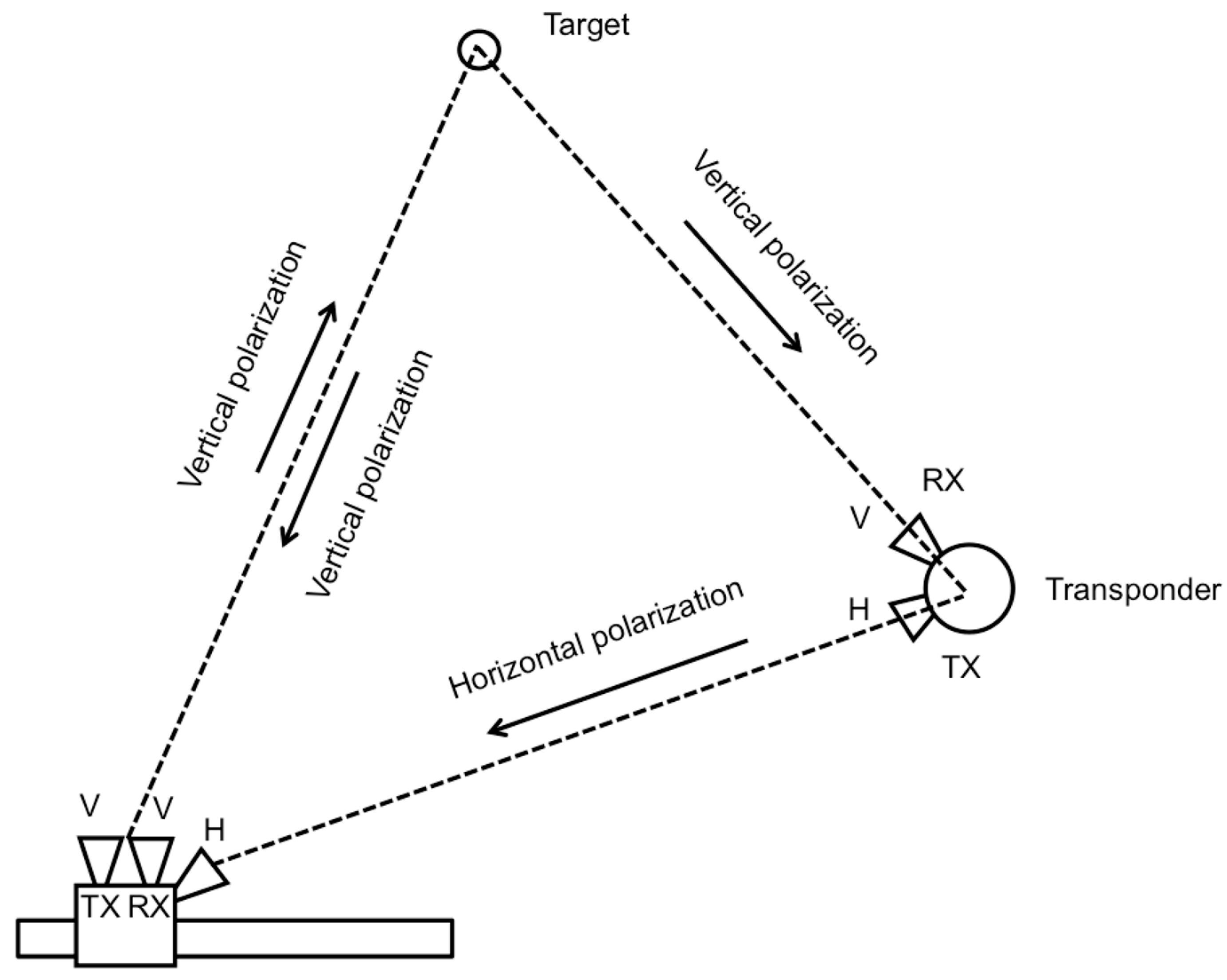
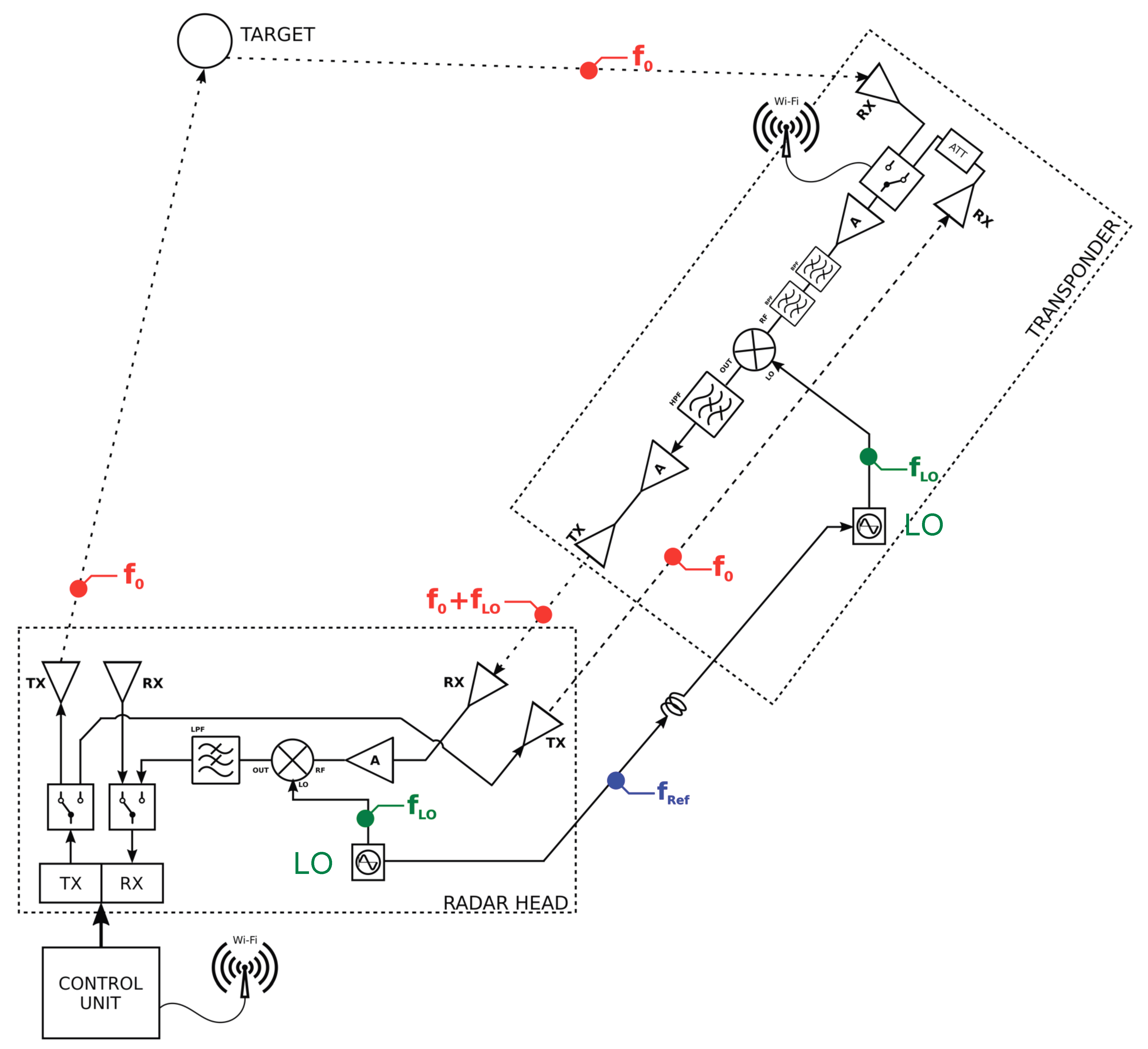
2.2. The Cross-Pol Transponder with Frequency Shifter
3. Results
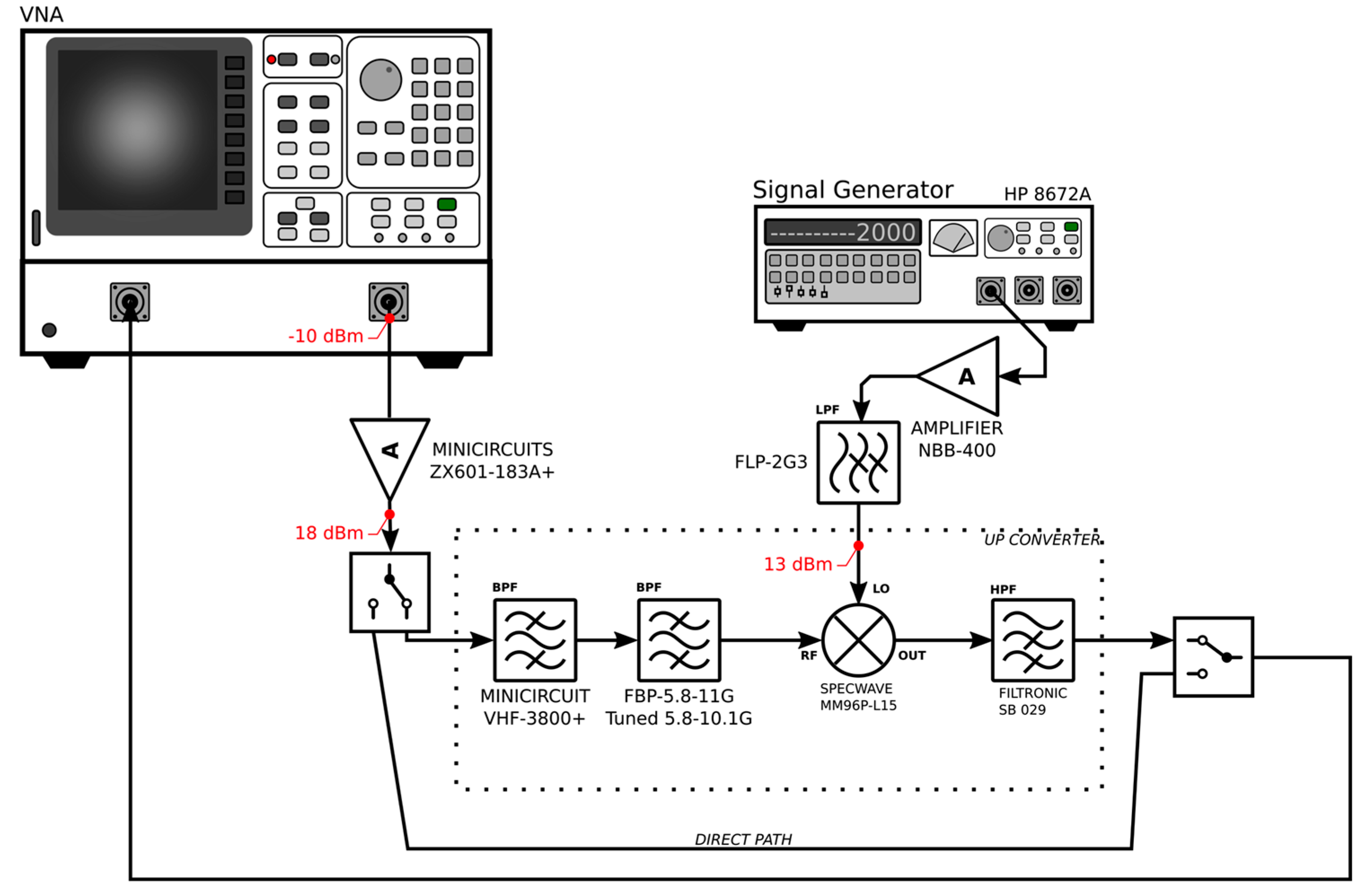
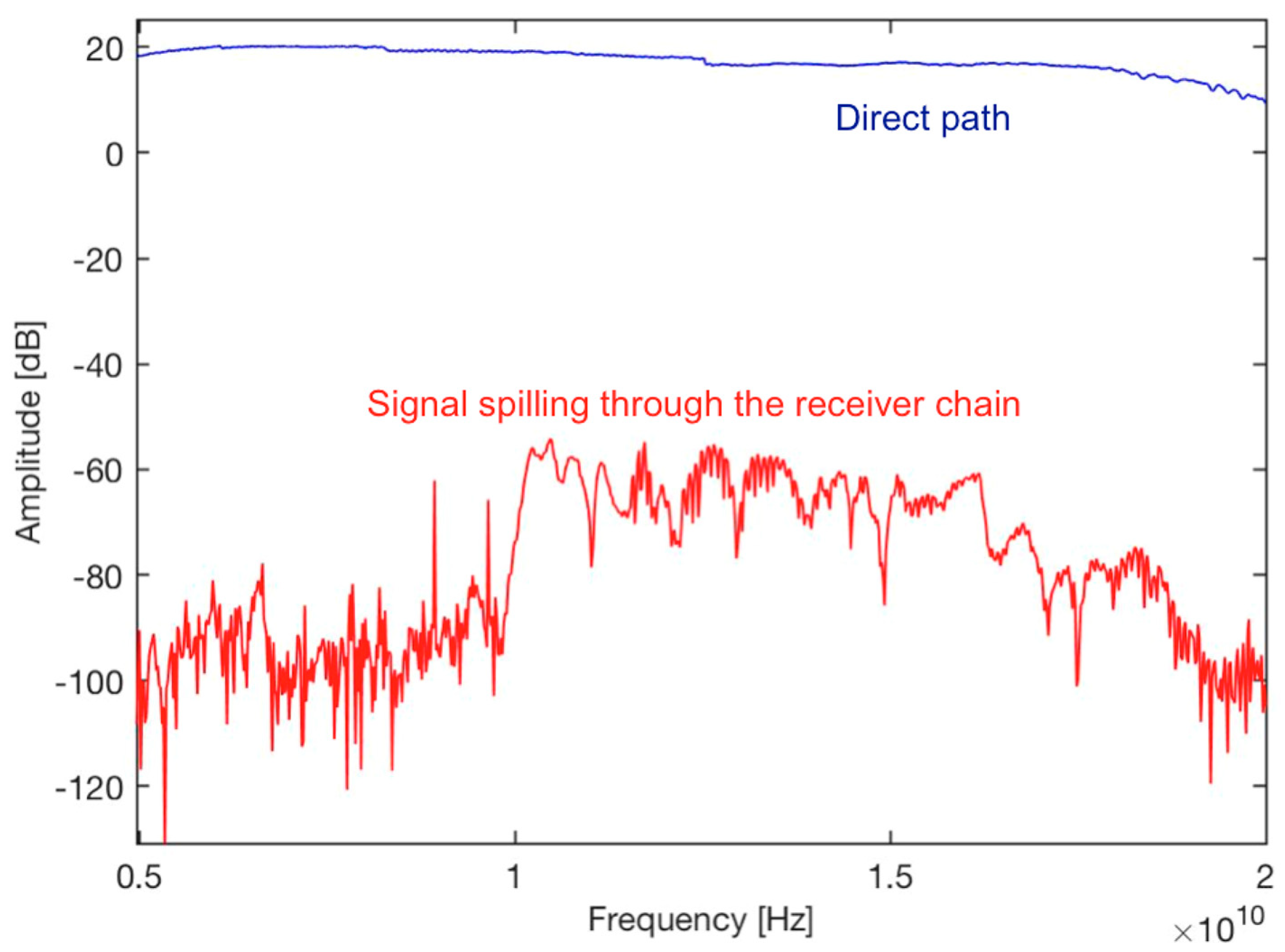
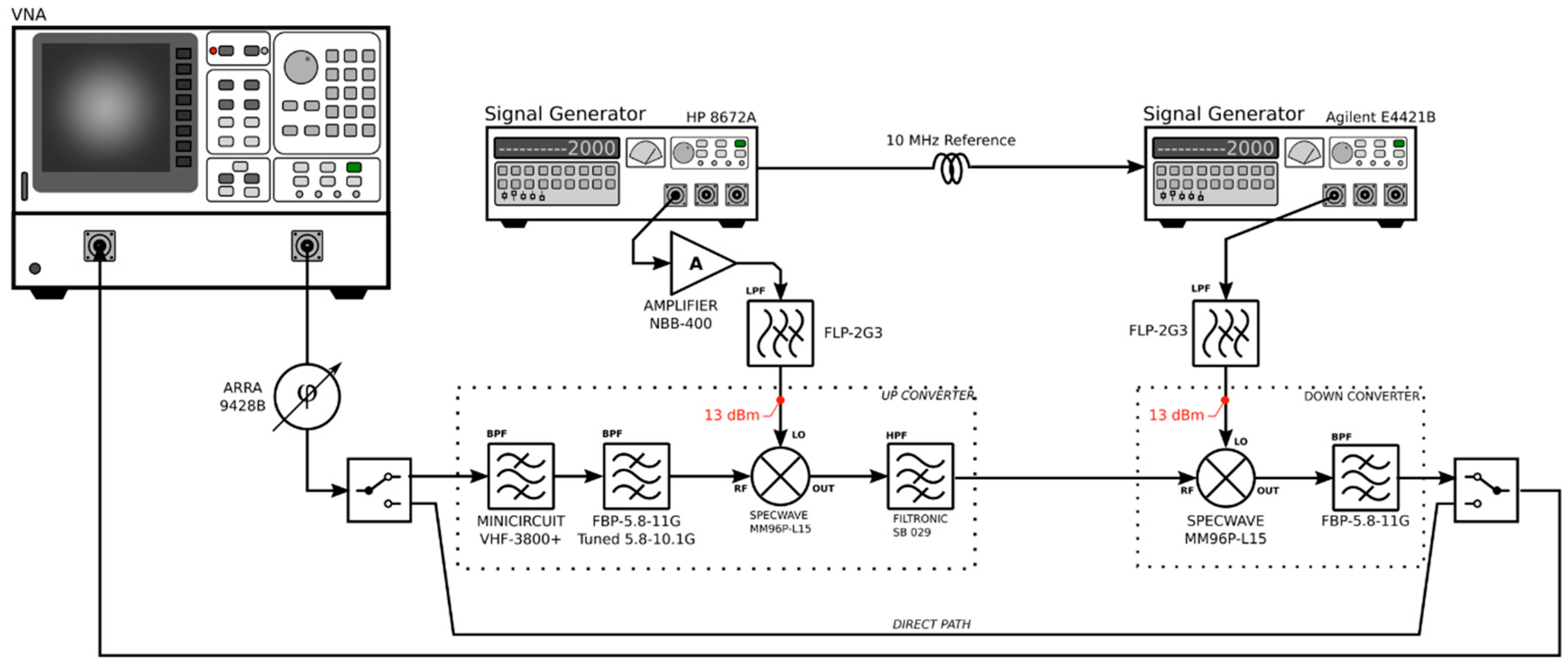
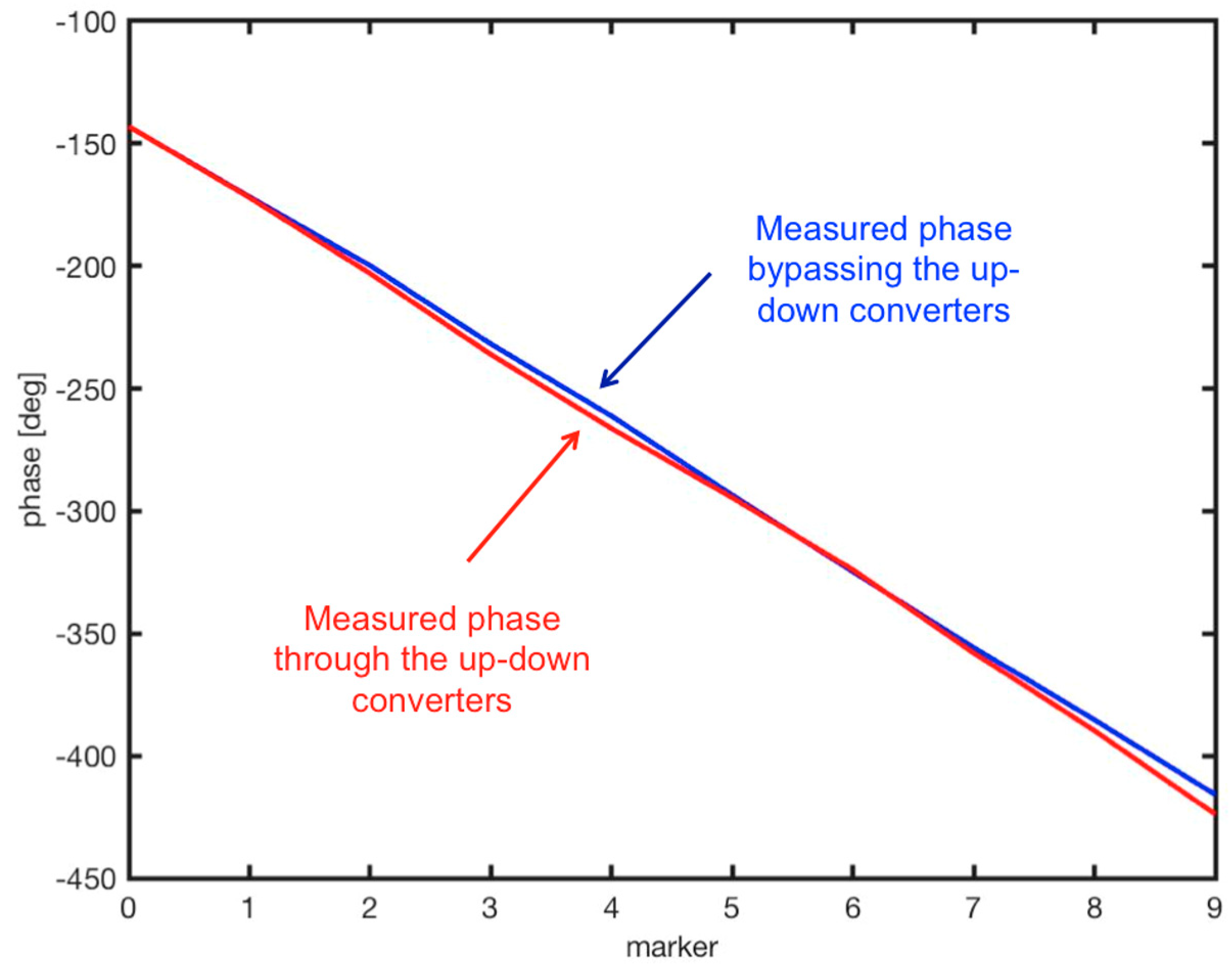
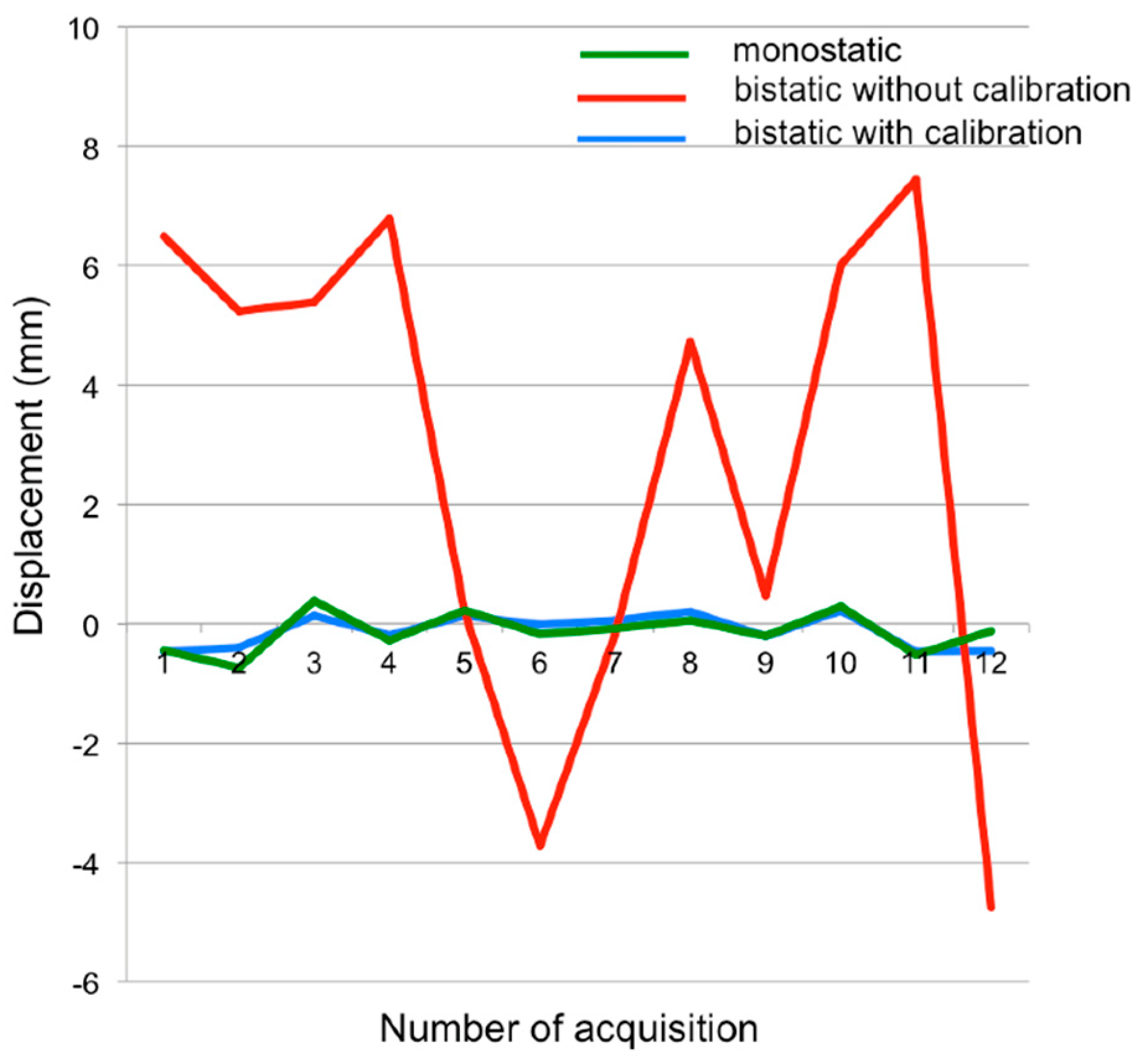
3.1. Test Bench of the System
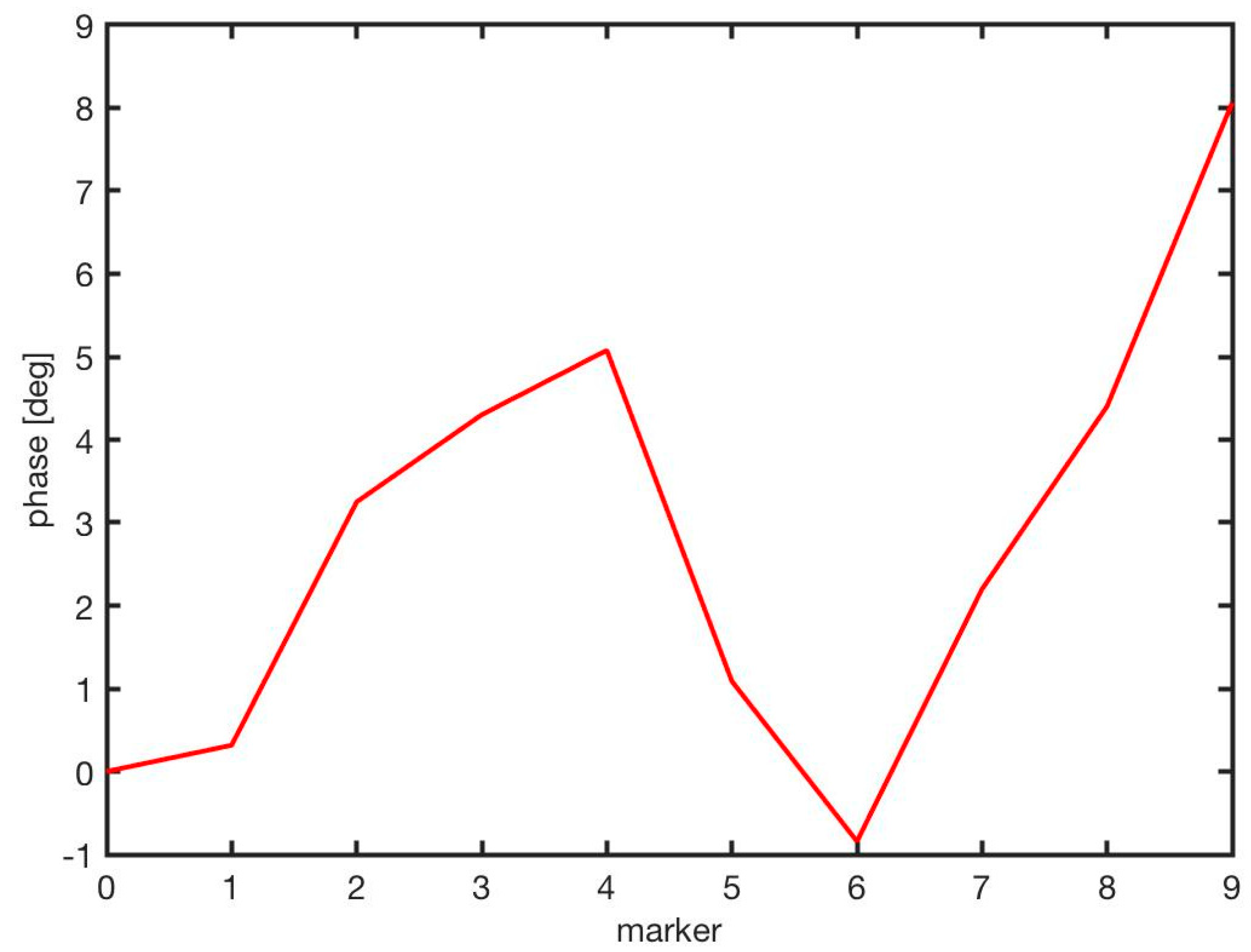
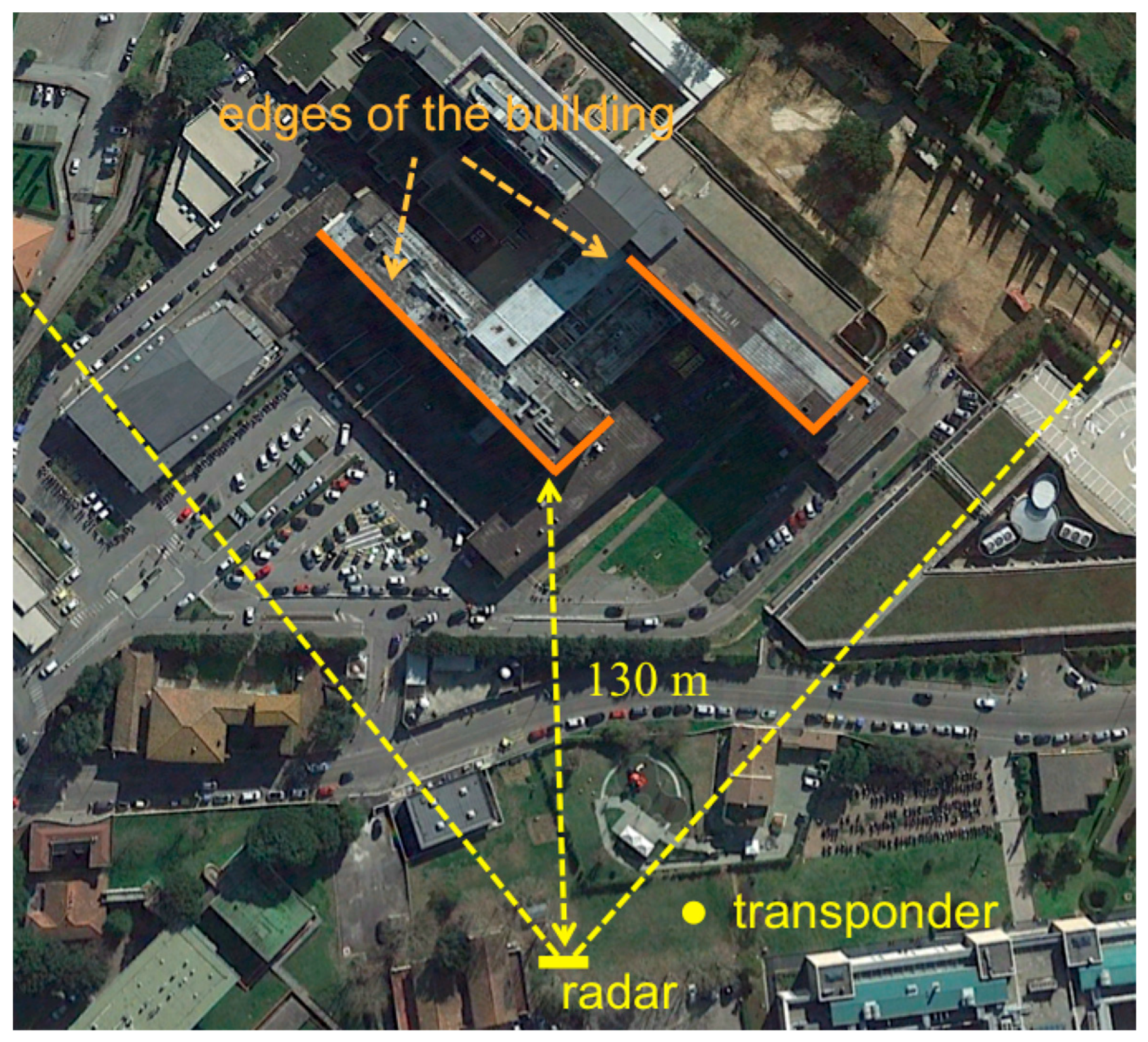
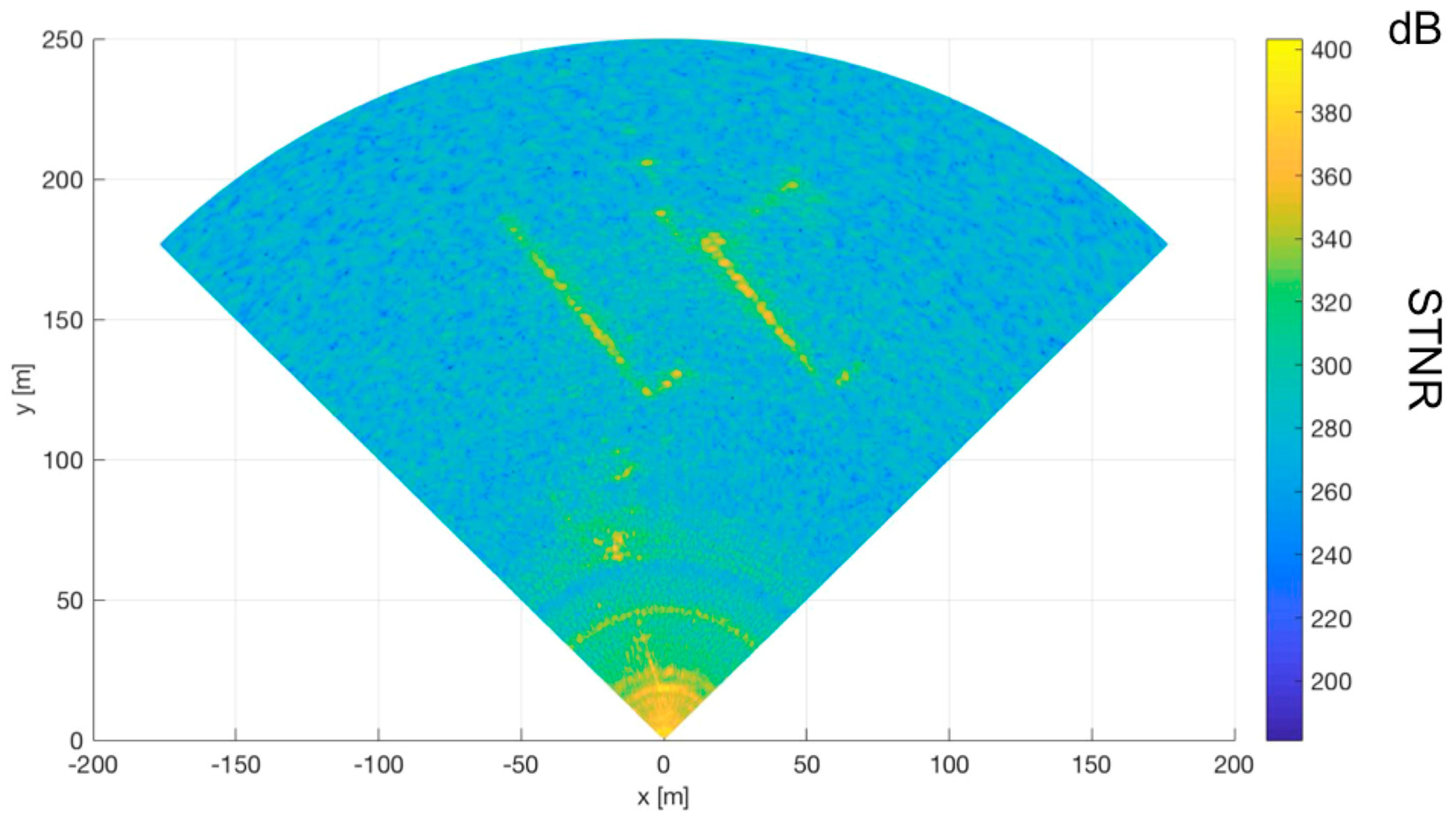
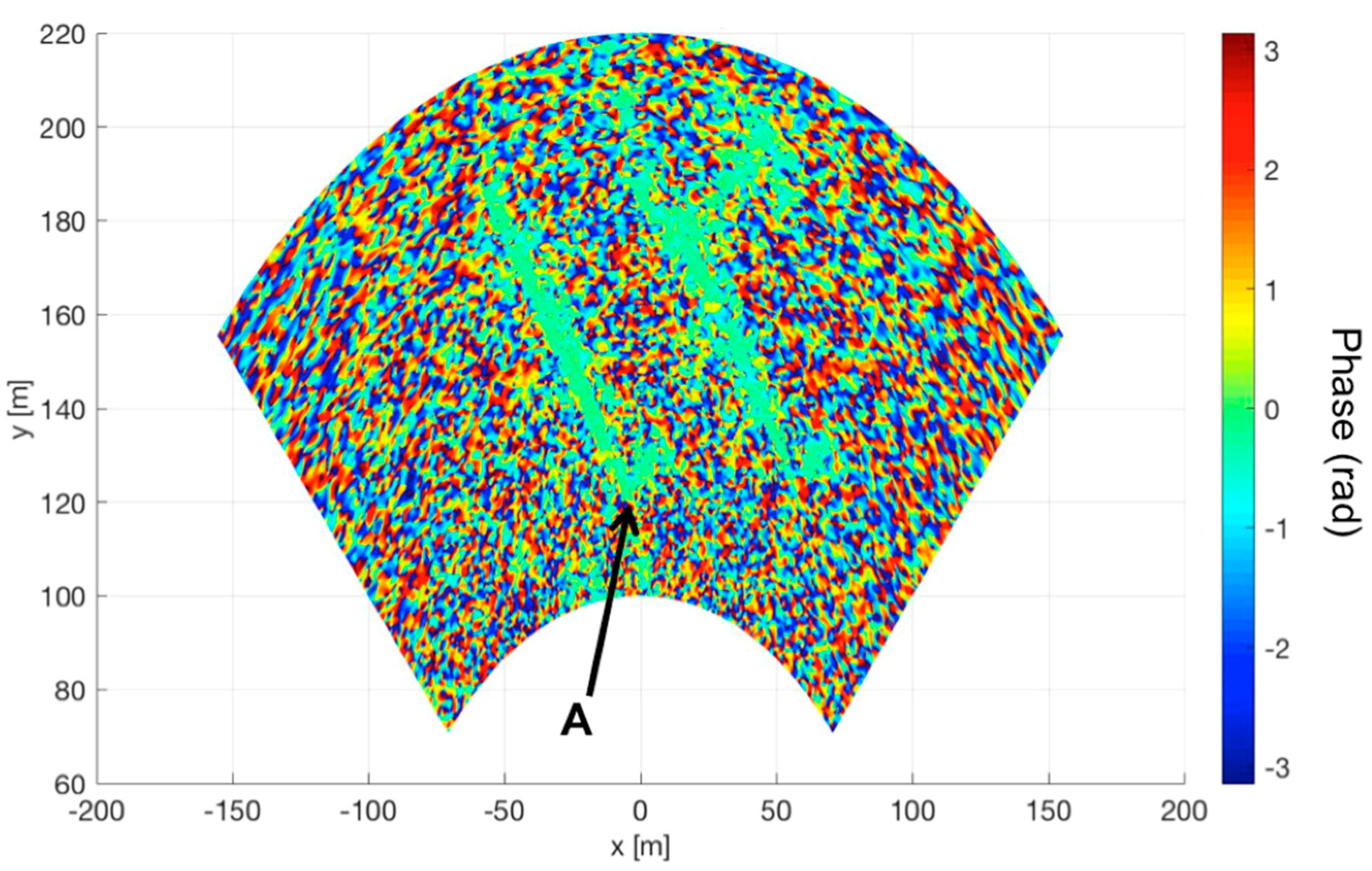
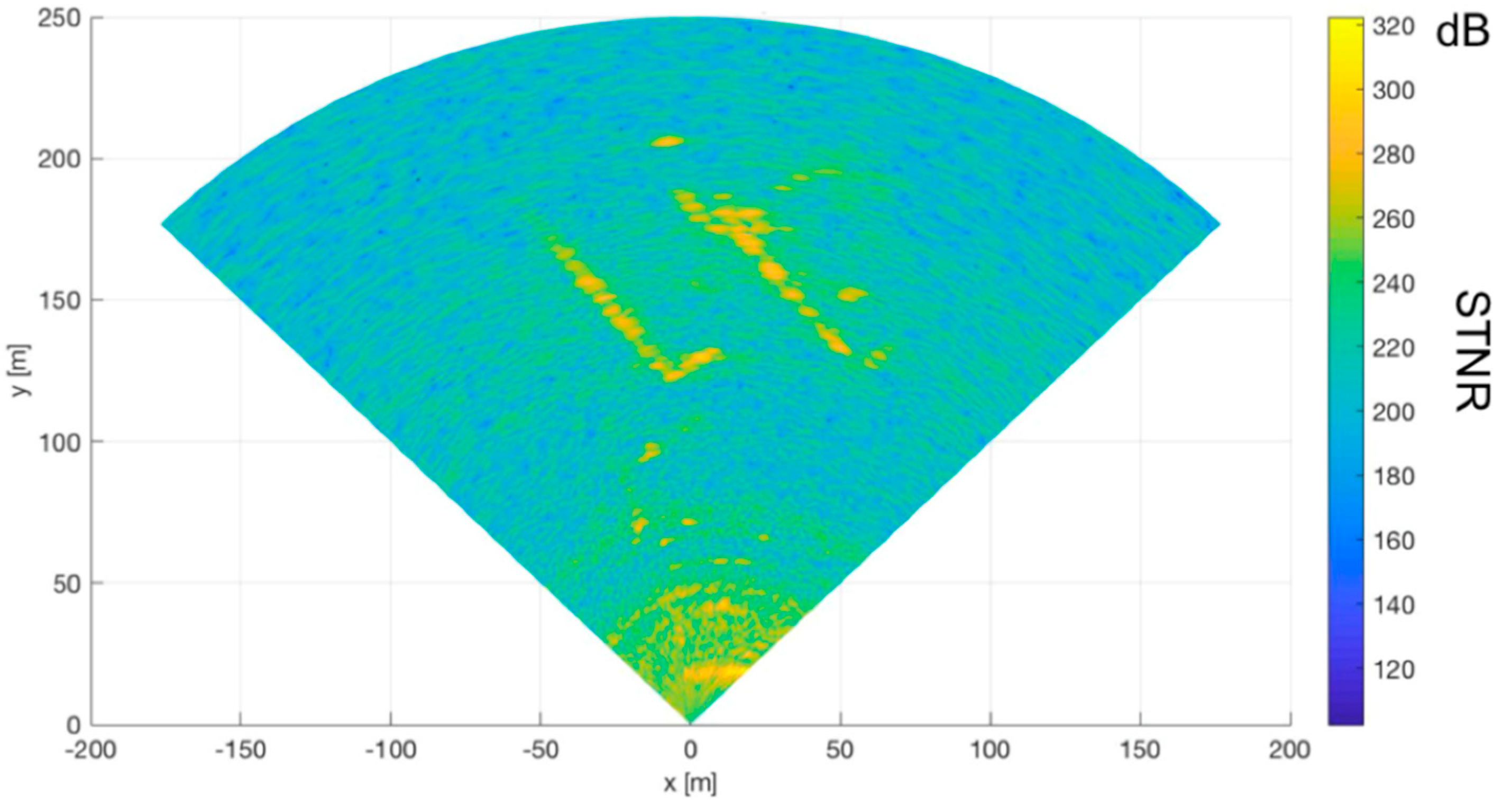
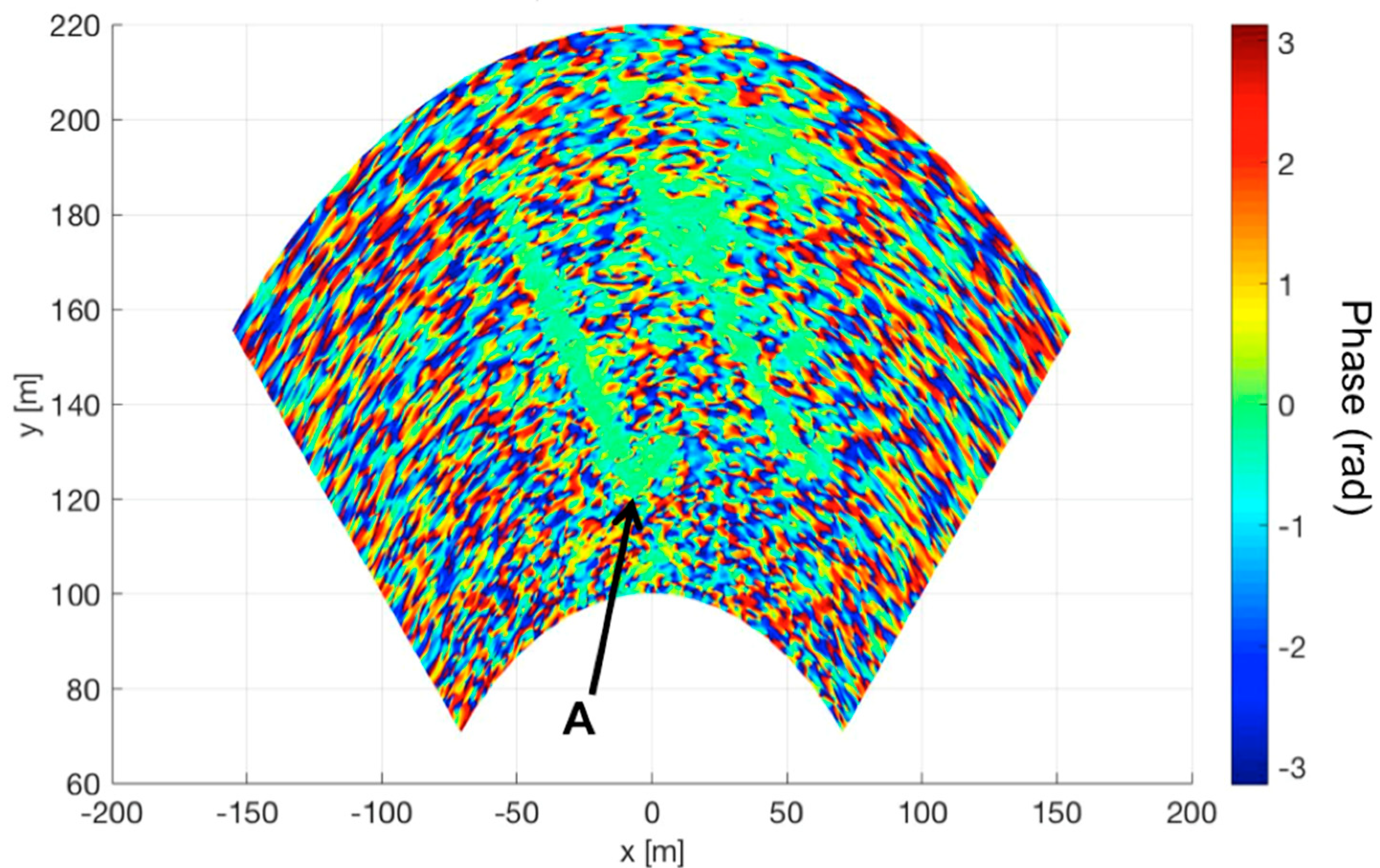
3.2. Field Test
4. Conclusions
5. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Noferini, L.; Takayama, T.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Analysis of ground-based SAR data with diverse temporal baselines. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1614–1623. [Google Scholar] [CrossRef]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Macaluso, G.; Tamburini, A.; Atzeni, C. Monitoring of an alpine glacier by means of ground-based SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2007, 4, 495–499. [Google Scholar] [CrossRef]
- Severin, J.; Eberhardt, E.; Leoni, L.; Fortin, S. Development and application of a pseudo-3D pit slope displacement map derived from ground-based radar. Eng. Geol. 2014, 181, 202–211. [Google Scholar] [CrossRef]
- Pieraccini, M.; Tarchi, D.; Rudolf, H.; Leva, D.; Luzi, G.; Bartoli, G.; Atzeni, C. Structural static testing by interferometric synthetic radar. NDT E Int. 2000, 33, 565–570. [Google Scholar] [CrossRef]
- Jenkins, W.; Rosenblad, B.; Gomez, F.; Le-garsky, J.; Loehr, E. Deformation measurements of earth dams using a ground based inter-ferometric radar. In Proceedings of the 2012 ASDSO Annual Conference on Dam Safety, Denver, CO, USA, 16–21 September 2012. [Google Scholar]
- Pieraccini, M.; Miccinesi, L.; Rojhani, N. A GBSAR Operating in Monostatic and Bistatic Modalities for Retrieving the Displacement Vector. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1494–1498. [Google Scholar] [CrossRef]
- Skolnik, M. Introduction to Radar Systems; McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Zhou, S.G.; Tan, P.K.; Chio, T.H. Low-profile, wideband dual-polarized antenna with high isolation and low cross polarization. Antennas Wirel. Propag. Lett. 2012, 11, 1032–1035. [Google Scholar] [CrossRef]
- Pieraccini, M. Noise Performance Comparison Between Continuous Wave and Stroboscopic Pulse Ground Penetrating Radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 222–226. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. ArcSAR: Theory, simulations, and experimental verification. IEEE Trans. Microw. Theory Tech. 2017, 65, 293–301. [Google Scholar] [CrossRef]
- Dei, D.; Pieraccini, M.; Fratini, M.; Atzeni, C.; Bartoli, G. Detection of vertical bending and torsional movements of a bridge using a coherent radar. NDT E Int. 2009, 42, 741–747. [Google Scholar] [CrossRef]
- Pieraccini, M.; Tarchi, D.; Rudolf, H.; Leva, D.; Luzi, G.; Atzeni, C. Interferometric radar for remote monitoring of building deformations. Electron. Lett. 2000, 36, 569–570. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pieraccini, M.; Miccinesi, L. Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar. Remote Sens. 2018, 10, 1364. https://doi.org/10.3390/rs10091364
Pieraccini M, Miccinesi L. Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar. Remote Sensing. 2018; 10(9):1364. https://doi.org/10.3390/rs10091364
Chicago/Turabian StylePieraccini, Massimiliano, and Lapo Miccinesi. 2018. "Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar" Remote Sensing 10, no. 9: 1364. https://doi.org/10.3390/rs10091364
APA StylePieraccini, M., & Miccinesi, L. (2018). Cross-Pol Transponder with Frequency Shifter for Bistatic Ground-Based Synthetic Aperture Radar. Remote Sensing, 10(9), 1364. https://doi.org/10.3390/rs10091364