Simulation of Bidirectional Reflectance in Broken Clouds: From Individual Realization to Averaging over an Ensemble of Cloud Fields
Abstract
1. Introduction
2. Model of the Atmosphere and Calculation Algorithms
2.1. Atmospheric Model
2.1.1. Poisson Cloud Model
2.1.2. Optical Model of the Atmosphere
2.2. Calculation Algorithms
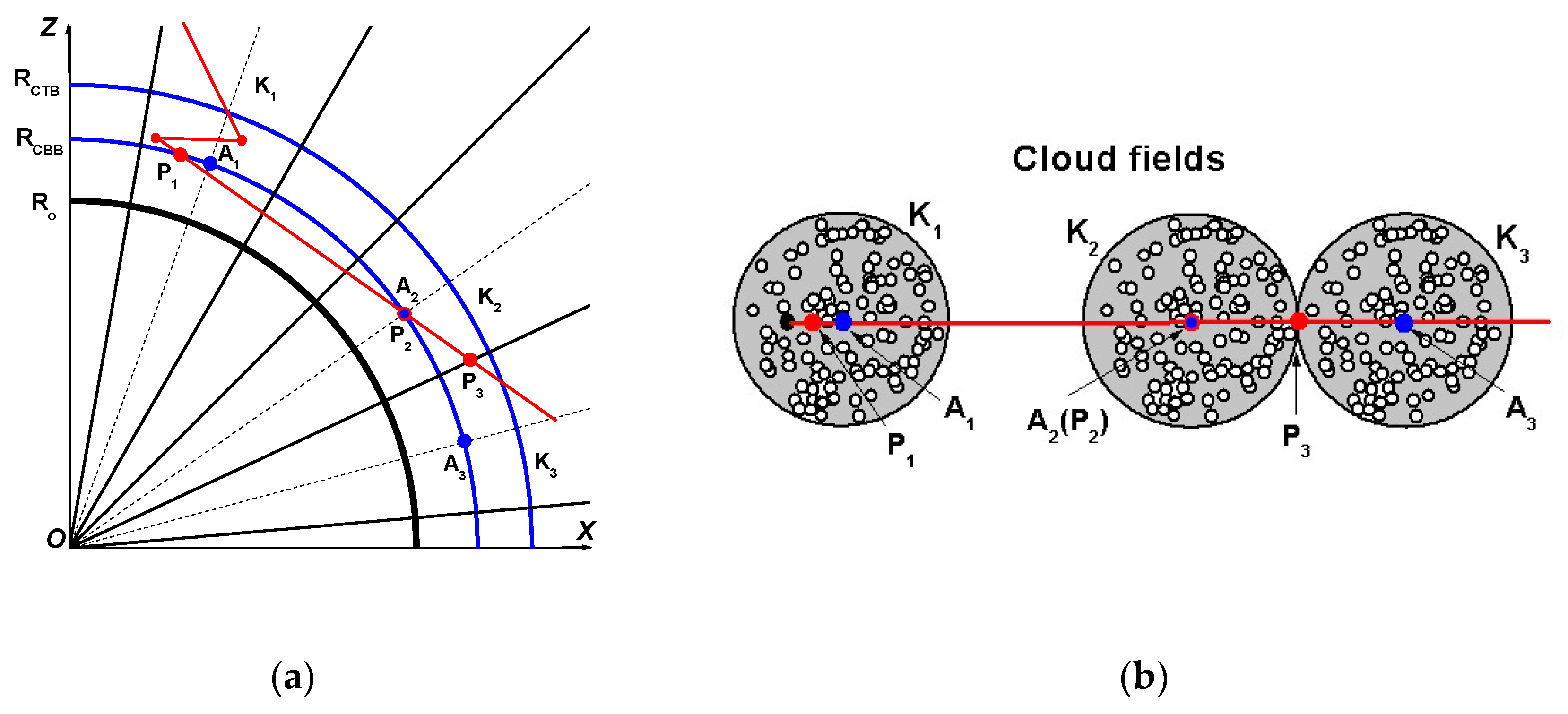
2.2.1. 3D Cloud Fields
2.2.2. Averaging over Ensemble of Realizations
3. Results of Numerical Simulation
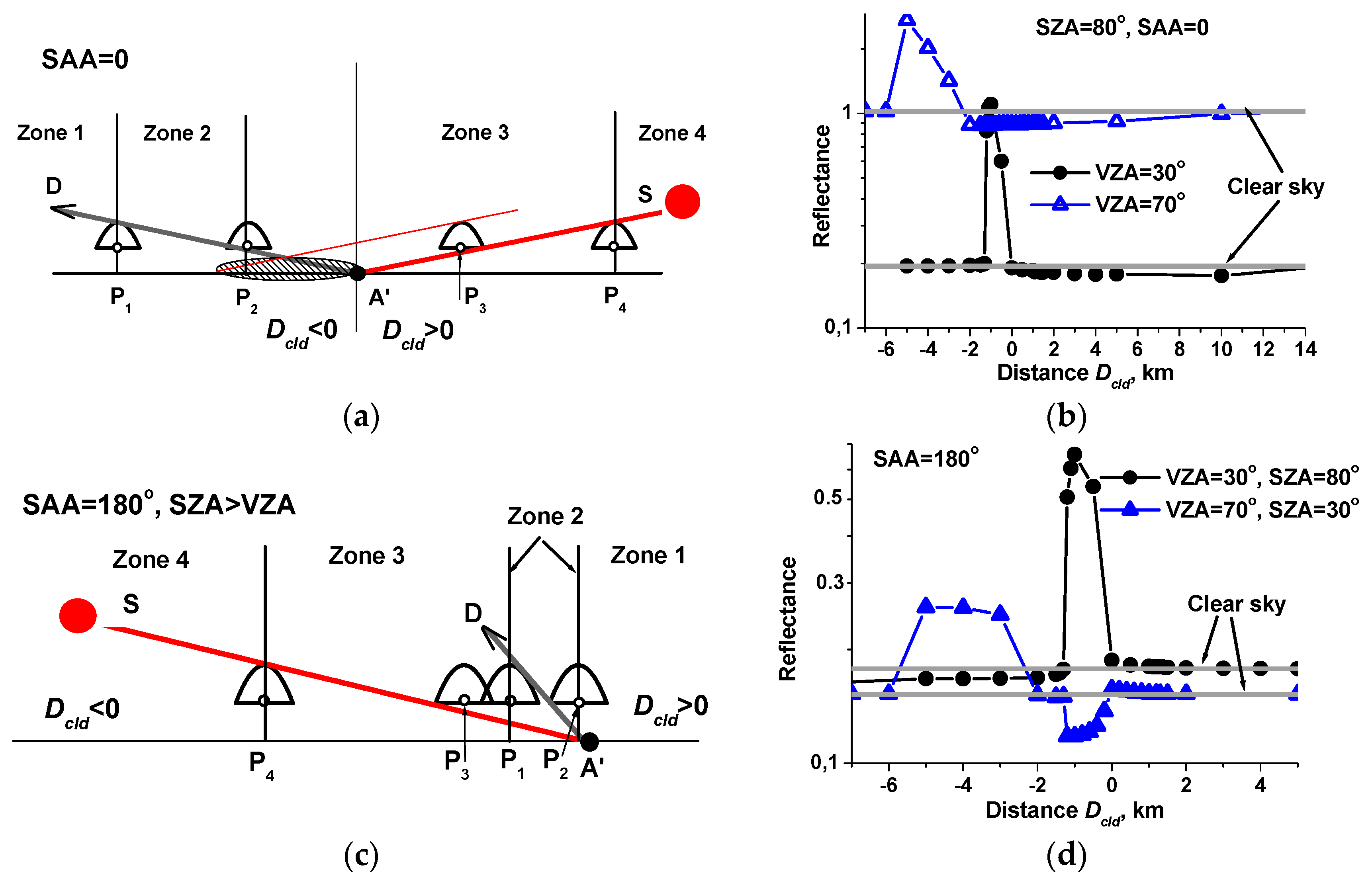
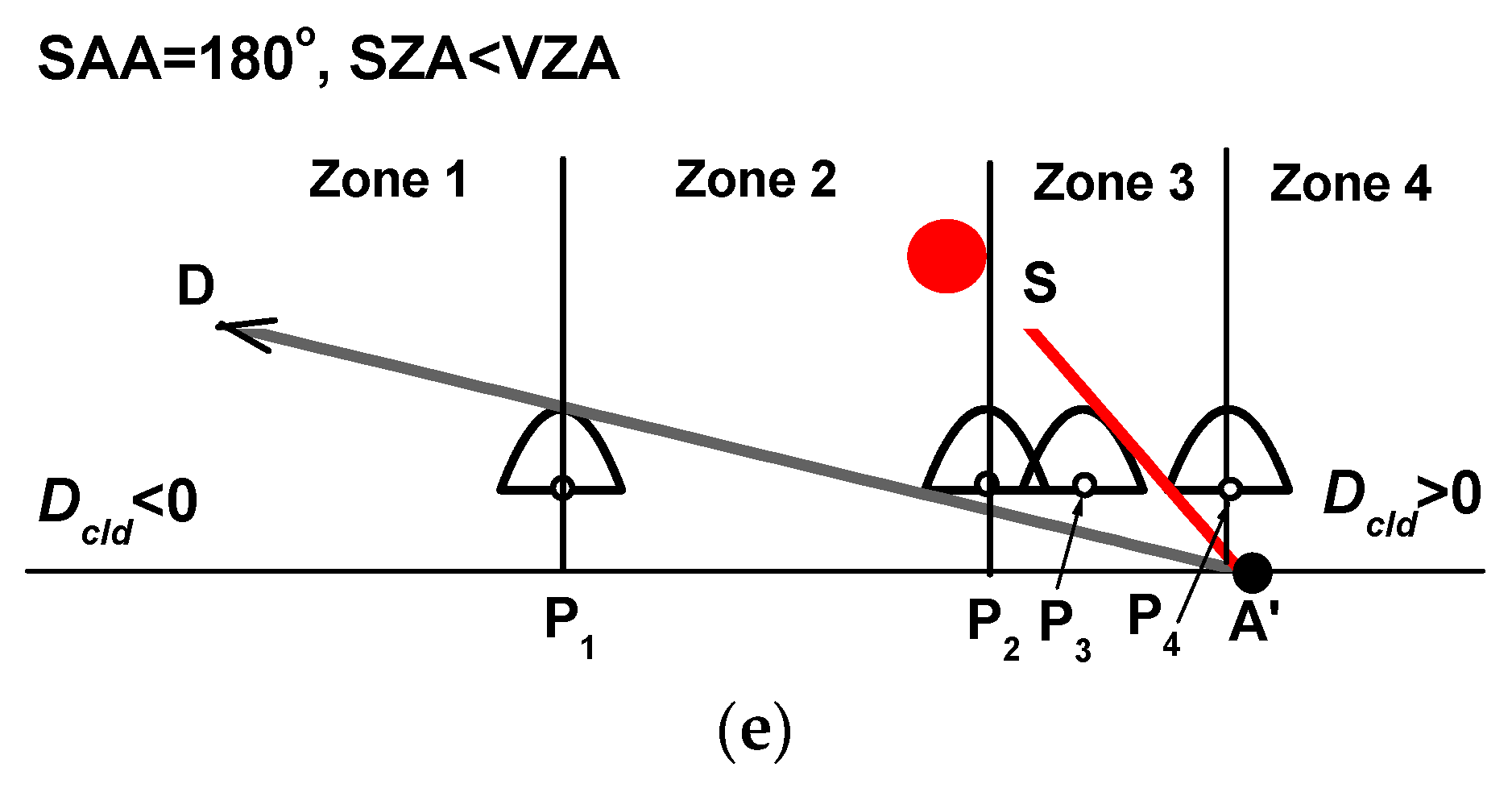
3.1. Isolated Cloud
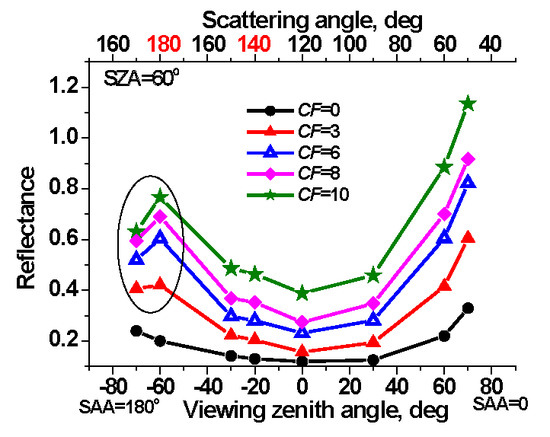
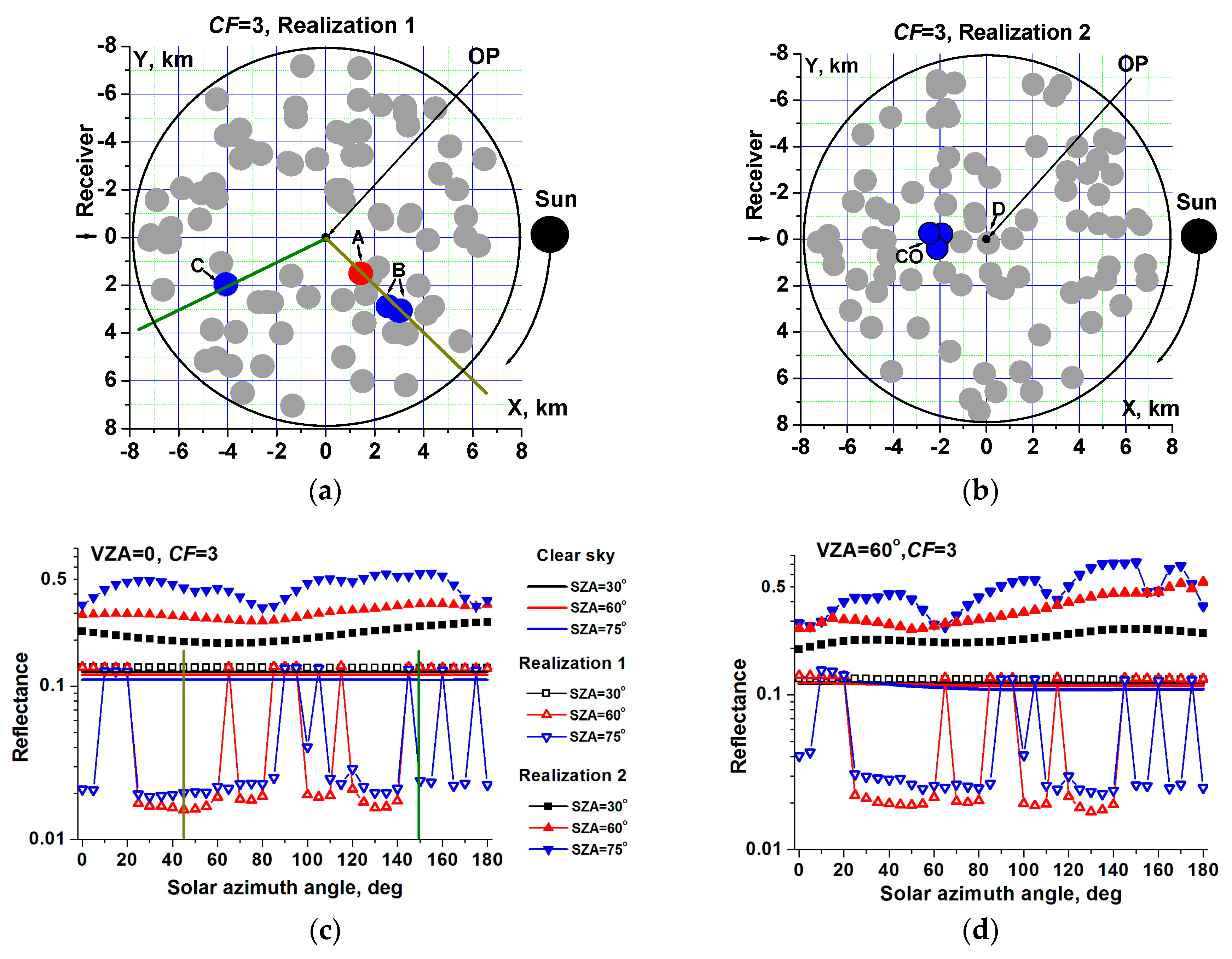
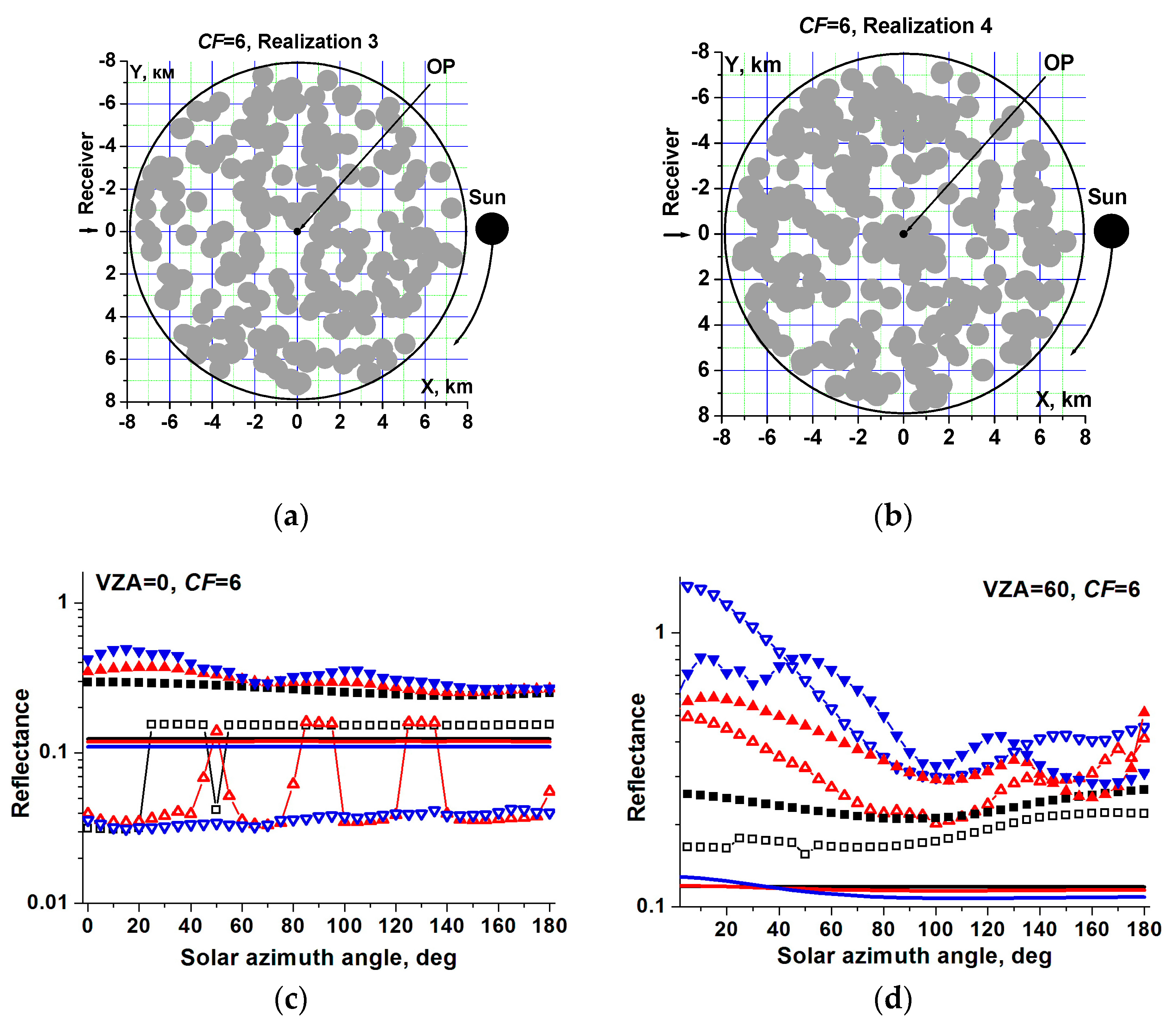
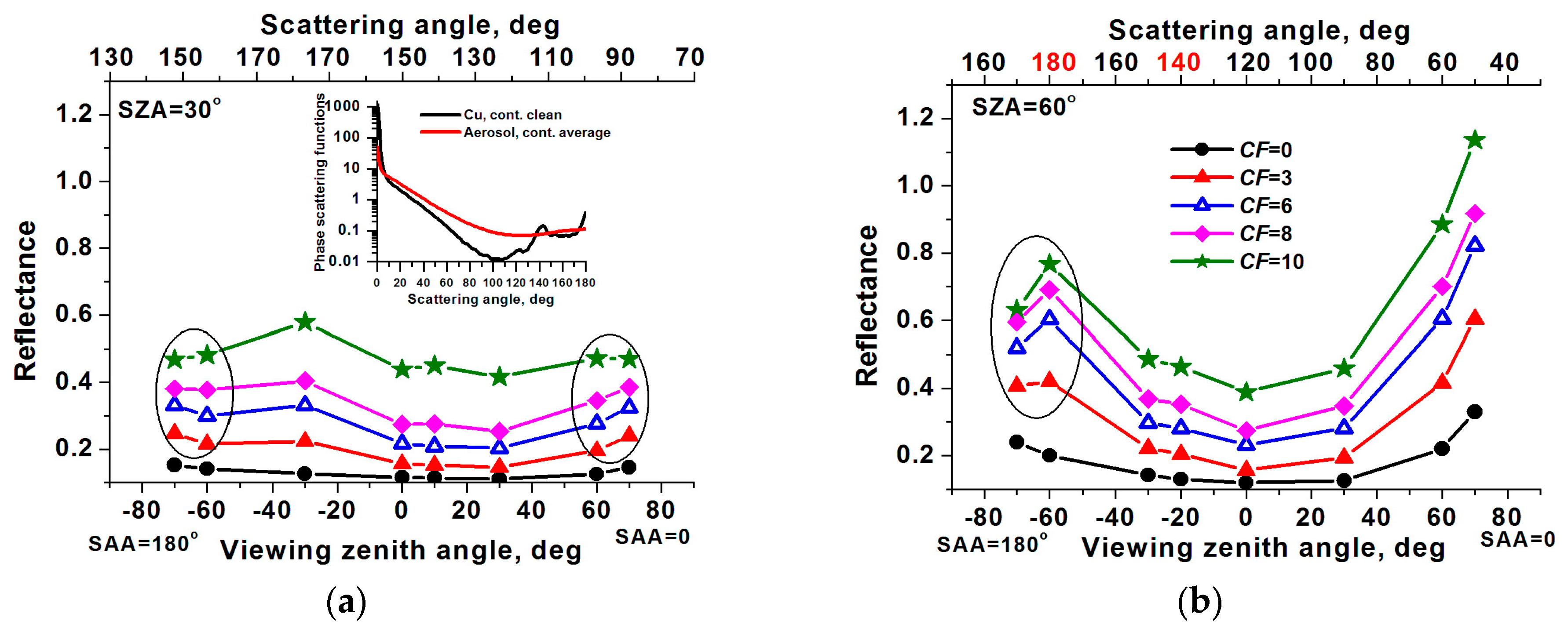
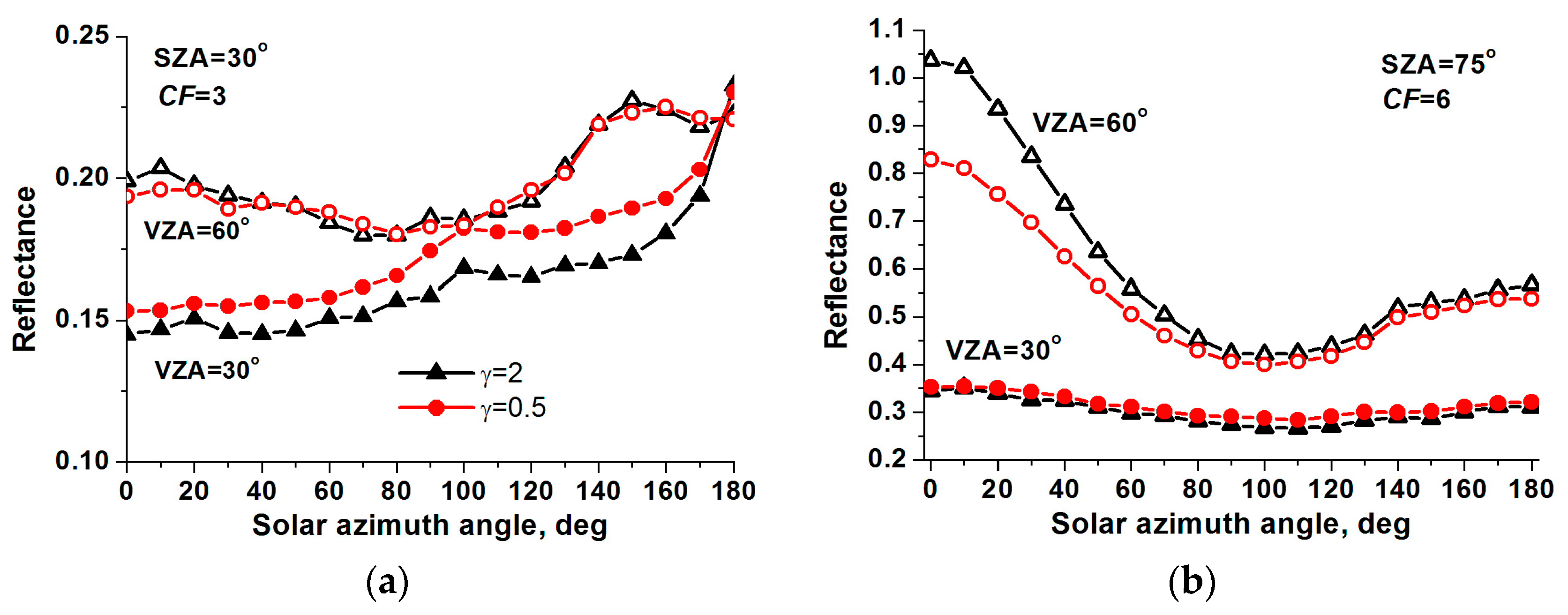
3.2. Broken Cloud Field
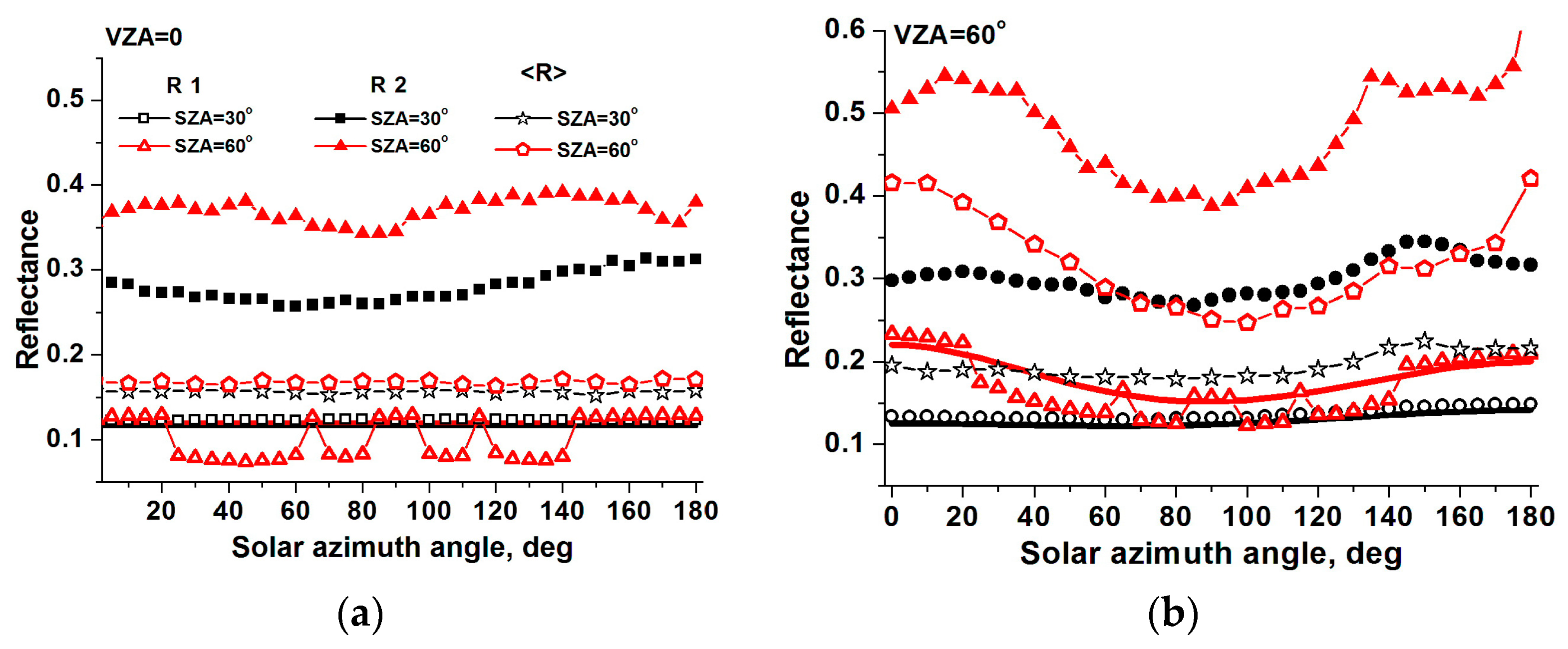
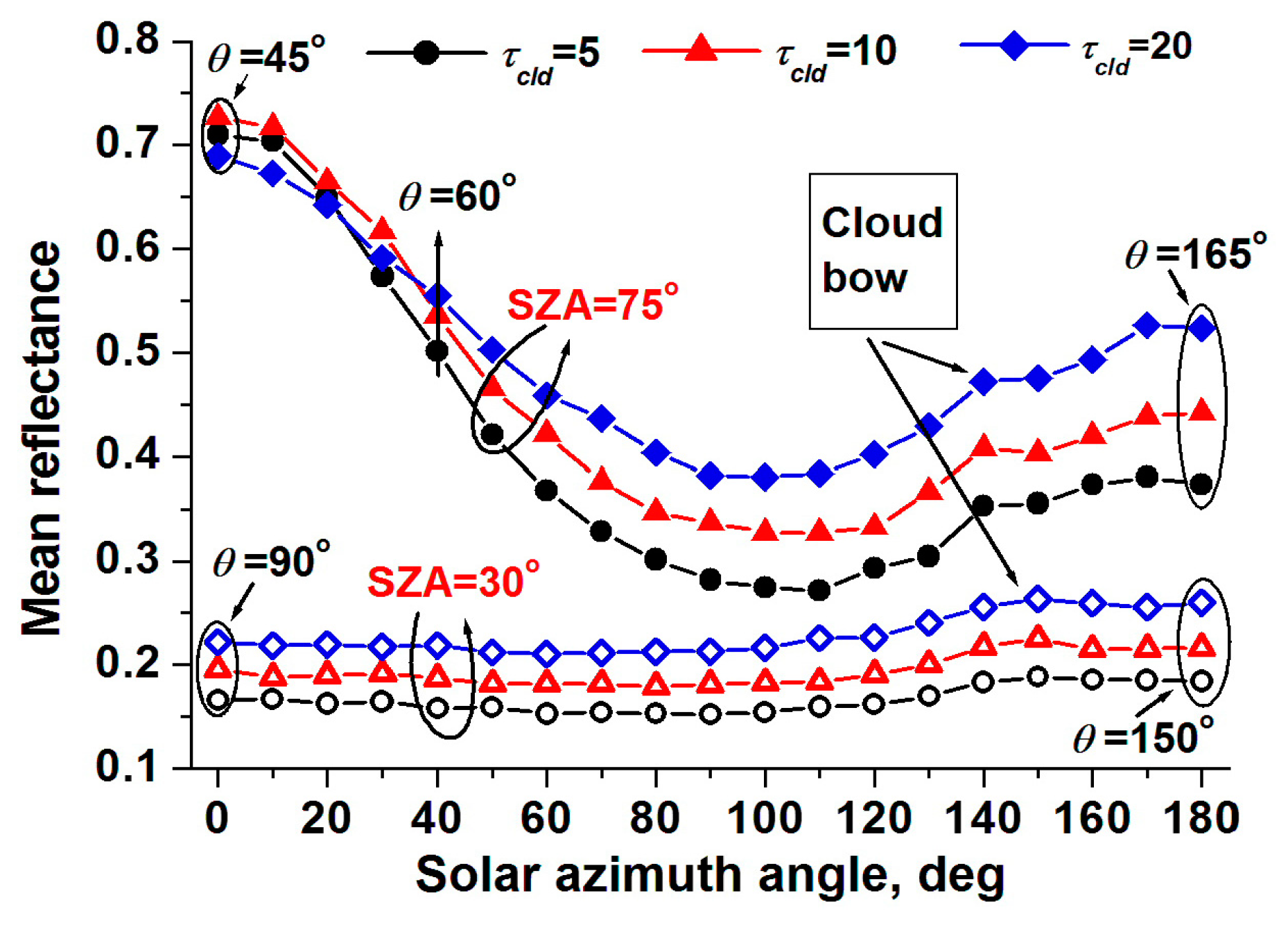
3.3. Averaging over Realizations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LOC | local coordinate system |
| LS | line of sight |
| MATHART | Monte CArlo Codes for THree-DimensionAl Radiative Transfer |
| OP | observation point |
| RTE | radiative transfer equation; |
| SAA | solar azimuth angle |
| SZA | solar zenith angle |
| TOA | top of the atmosphere |
| VZA | viewing zenith angle |
| surface albedo | |
| CF | cloud fraction |
| distance between the observation point and projection of paraboloid center onto Earth in local coordinate system | |
| cloud geometrical thickness | |
| I | intensity of solar radiation |
| intensity of solar radiation, averaged over an ensemble of cloud realizations | |
| number of cloud field realizations | |
| number of photon trajectories | |
| semiaxes of cloud base | |
| R | reflectance in an individual cloud realization |
| reflectance, averaged over an ensemble of cloud realizations | |
| clear-sky reflectance | |
| the Earth’s radius | |
| effective radius of cloud particles | |
| S | cloud field area |
| height of cloud bottom boundary | |
| γ | cloud aspect ratio |
| azimuth angle, characterizing the position of projection of paraboloid center onto the Earth in local coordinate system | |
| cloud extinction coefficient | |
| cloud optical depth | |
| λ | wavelength |
Appendix A
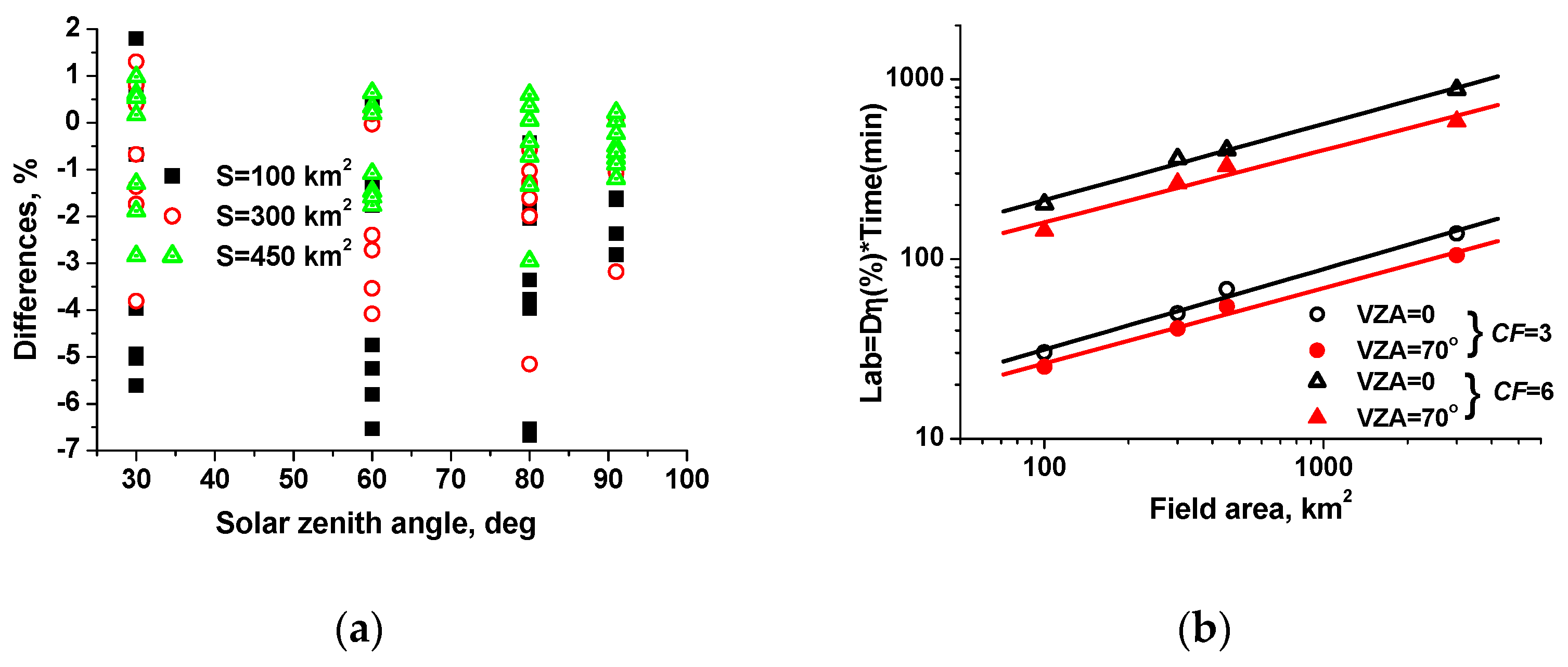
Appendix A.1. Laboriousness of Mean Intensity Computations
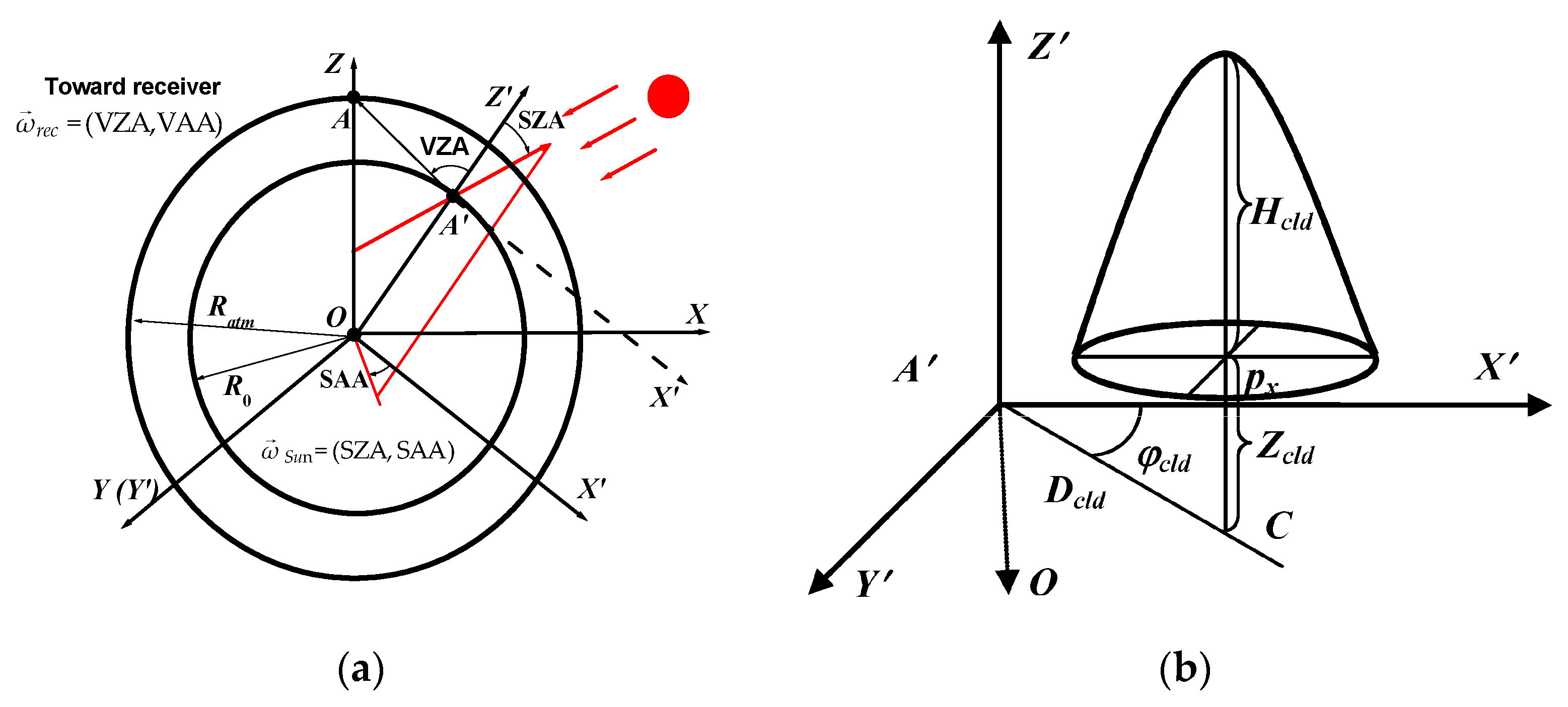
Appendix A.2. Size of Cloud Field and Its Position in Space
References
- Varnai, T.; Marshak, A. Observations of three-dimensional radiative effects that influence MODIS cloud optical thickness retrievals. J. Atmos. Sci. 2002, 59, 1607–1618. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Marshak, A.; Cairns, B.; Lacis, A.A.; Carlson, B.E. Automated cloud screening algorithm for MFRSR data. Geophys. Res. Lett. 2004, 31, L04118. [Google Scholar] [CrossRef]
- Horvath, A.; Davies, R. Anisotropy of water cloud reflectance: A comparison of measurements and 1D theory. Geophys. Res. Lett. 2004, 31, L01102. [Google Scholar] [CrossRef]
- Marshak, A.; Platnick, S.; Varnai, T.; Wen, G.; Cahalan, R.F. Impact of three-dimensional radiative effects on satellite retrievals of cloud droplet sizes. J. Geophys. Res. 2006, 111, D09207. [Google Scholar] [CrossRef]
- Koren, I.; Remer, L.A.; Kaufman, Y.J.; Rudich, Y.; Martins, J.V. On the twilight zone between clouds and aerosols. Geophys. Res. Lett. 2007, 34, L08805. [Google Scholar] [CrossRef]
- Wen, G.; Marshak, A.; Cahalan, R.F.; Remer, L.A.; Kleidman, R.G. 3-D aerosol-cloud radiative interaction observed in collocated MODIS and ASTER images of cumulus cloud fields. J. Geophys. Res. 2007, 112, D13204. [Google Scholar] [CrossRef]
- Chiu, J.C.; Marshak, A.; Knyazikhin, Y.; Pilewskie, P.; Wiscombe, W. Physical interpretation of the spectral radiative signature in the transition zone between cloud-free and cloudy regions. Atmos. Chem. Phys. 2009, 9, 1419–1430. [Google Scholar] [CrossRef]
- Varnai, T.; Marshak, A. MODIS observations of enhanced clear sky reflectance near clouds. Geophys. Res. Lett. 2009, 36, L06807. [Google Scholar] [CrossRef]
- Kassianov, E.I.; Ovchinnikov, M.; Berg, L.K.; McFarlane, S.A.; Flynn, C.J.; Ferrare, R.; Hostetler, C.; Alexandrov, M. Retrieval of aerosol optical depth in vicinity of broken clouds from reflectance ratios: Case study. Atmos. Meas. Technol. 2010, 3, 1333–1349. [Google Scholar] [CrossRef]
- Wen, G.; Marshak, A.; Levy, R.; Remer, L.; Loeb, N.; Varnai, T.; Cahalan, R. Implementation of the correction algorithm of the MODIS aerosol retrievals near clouds. J. Geophys. Res. 2013, 118, 9168–9181. [Google Scholar] [CrossRef]
- Marshak, A.; Evans, K.V.; Varnai, T.; Wen, G. Extending 3D near-cloud corrections from shorter to longer wavelengths. J. Quant. Spectrosc. Radiat. Transf. 2014, 147, 79–85. [Google Scholar] [CrossRef]
- Eck, T.F.; Holben, B.N.; Reid, J.S.; Arola, A.; Ferrare, R.A.; Hostetler, C.A.; Crumeyrolle, S.N.; Berkoff, T.A.; Welton, E.J.; Lolli, S.; et al. Observations of rapid aerosol optical depth enhancements in the vicinity of polluted cumulus clouds. Atmos. Chem. Phys. 2014, 14, 11633–11656. [Google Scholar] [CrossRef]
- Smirnov, A.; Holben, B.N.; Eck, T.F.; Dubovik, O.; Slutsker, I. Cloud screening and quality control algorithms for the AERONET database. Remote Sens. Environ. 2000, 73, 337–349. [Google Scholar] [CrossRef]
- Stevens, B.; Moeng, C.-H.; Ackerman, A.S.; Bretherton, C.S.; Chlond, A.; de Roode, S.; Edwards, J.; Golaz, J.-C.; Jiang, H.; Khairoutdinov, M.; et al. Evaluation of large-eddy simulations via observations of nocturnal marine stratocumulus. Mon. Weather Rev. 2005, 133, 1443–1462. [Google Scholar] [CrossRef]
- Mullamaa, Y.-A.R.; Sulev, M.A.; Pyldmaa, V.K.; Okhvril, K.A.; Niilisk, K.Y.; Allenov, M.I.; Chubakov, L.G.; Kuusk, A.E. Stochastic Structure of Cloud and Radiation Fields; Academy of Sciences of Estonian SSR, Institute of Physics and Astronomy: Tartu, Estonia, 1972. [Google Scholar]
- Kargin, B.A.; Prigarin, S.M. Imitational simulation of cumulus clouds for studying solar radiative transfer in the atmosphere by the Monte Carlo method. Atmos. Ocean. Opt. 1994, 7, 690–696. [Google Scholar]
- Geogdzhaev, I.V.; Kondranin, T.V.; Rublev, A.N.; Chubarova, N.E. Simulation of UV radiative transfer through broken clouds and comparison with experiment. Izv. Akad. Nauk SSSR Ser. Fiz. Atm. Okeana 1997, 33, 680–686. (In Russian) [Google Scholar]
- Cahalan, R.F. Bounded cascade clouds: Albedo and effective thickness. Nonlinear Proc. Geophys. 1994, 1, 156–167. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A.; Cahalan, R.F.; Wiscombe, W.J. Bounded cascade models as nonstationary multifractals. Phys. Rev. E 1994, 49, 55–69. [Google Scholar] [CrossRef]
- Titov, G. Statistical description of radiative transfer in clouds. J. Atmos. Sci. 1990, 47, 24–38. [Google Scholar] [CrossRef]
- Zuev, V.E.; Titov, G.A. Atmospheric Optics and Climate; Spektr: IAO SB RAS: Tomsk, Russia, 1996. (In Russian) [Google Scholar]
- Evans, K.F.; Wiscombe, W.J. An algorithm for generating stochastic cloud fields from radar profile statistics. Atmos. Res. 2004, 72, 263–289. [Google Scholar] [CrossRef]
- Hogan, R.J.; Kew, S.F. A 3D stochastic cloud model for investigating the radiative properties of inhomogeneous cirrus clouds. Q. J. R. Meteorol. Soc. 2005, 131, 2585–2608. [Google Scholar] [CrossRef]
- Venema, V.; Bachner, S.; Rust, H.W.; Simmer, C. Statistical characteristics of surrogate data based on geophysical measurements. Nonlinear Proc. Geophys. 2006, 13, 449–466. [Google Scholar] [CrossRef]
- Schmidt, K.S.; Venema, V.; Giuseppe, F.D.; Scheirer, R.; Wendisch, M.; Pilewskie, P. Reproducing cloud microphysics and irradiance measurements using three 3D cloud generators. Q. J. R. Meteorol. Soc. 2007, 133, 765–780. [Google Scholar] [CrossRef]
- Prigarin, S.M.; Marshak, A. A simple stochastic model for generating broken cloud optical depth and cloud-top height fields. J. Atmos. Sci. 2009, 66, 92–104. [Google Scholar] [CrossRef]
- Mikhailov, G.A. Optimization of Weighted Monte Carlo Methods; Nauka: Moscow, Russia, 1987. (In Russian) [Google Scholar]
- Avaste, O.A.; Vainikko, G.M. Solar radiative transfer in broken clouds. Izv. Acad. Sci. USSR Atmos. Ocean. Phys. 1974, 10, 1054–1061. [Google Scholar]
- Malvagi, F.; Byrne, R.N.; Pomraning, G.; Somerville, R.C.J. Stochastic radiative transfer in a partially cloudy atmosphere. J. Atmos. Sci. 1993, 50, 2146–2158. [Google Scholar] [CrossRef]
- Lane-Veron, D.E.; Somerville, R.C.J. Stochastic theory of radiative transfer through generalized cloud field. J. Geophys. Res. 2004, 109, D18113. [Google Scholar] [CrossRef]
- Doicu, A.; Efremenko, D.S.; Loyola, D.; Trautmann, T. Approximate models for broken clouds in stochastic radiative transfer theory. J. Quant. Spectrosc. Radiat. Transf. 2014, 145, 74–87. [Google Scholar] [CrossRef]
- Huang, D.; Liu, Y. A novel approach for introducing cloud spatial structure into cloud radiative transfer parameterizations. Environ. Res. Lett. 2014, 9, 124022. [Google Scholar] [CrossRef]
- Shabanov, N.V.; Knyazikhin, Y.; Baret, F.; Myneni, R.B. Stochastic modeling of radiation regime in discontinuous vegetation canopies. Remote Sens. Environ. 2000, 74, 125–144. [Google Scholar] [CrossRef]
- Huang, D.; Knyazikhin, Y.; Wang, W.; Deering, D.W.; Stenberg, P.; Shabanov, N.; Tan, B.; Myneni, R.B. Stochastic transport theory for investigating the three-dimensional canopy structure from space measurements. Remote Sens. Environ. 2008, 112, 35–50. [Google Scholar] [CrossRef]
- Stuhlmann, R.; Minnis, P.; Smith, G.L. Cloud bidirectional reflectance functions: A comparison of experimental and theoretical results. Appl. Opt. 1985, 24, 396–401. [Google Scholar] [CrossRef] [PubMed]
- Loeb, N.G.; Coakley, J.A., Jr. Inference of marine stratus cloud optical depths from satellite measurements: Does 1D theory apply? J. Clim. 1998, 11, 215–233. [Google Scholar] [CrossRef]
- Descloitres, J.; Buriez, J.C.; Parol, F.; Fouquart, Y. POLDER observations of cloud bidirectional reflectances compared to a plane-parallel model using the International Satellite Cloud Climatology Project cloud phase functions. J. Geophys. Res. 1998, 103, 11411–11418. [Google Scholar] [CrossRef]
- Loeb, N.G.; Davies, R. Angular dependence of observed reflectances: A comparison with plane parallel theory. J. Geophys. Res. 1997, 102, 6865–6881. [Google Scholar] [CrossRef]
- Cornet, C.; Davies, R. Use of MISR measurements to study the radiative transfer of an isolated convective cloud: Implications for cloud optical thickness retrieval. J. Geophys. Res. 2008, 113, D04202. [Google Scholar] [CrossRef]
- Loeb, N.G.; Varnai, T.; Davies, R. Effect of cloud inhomogeneities on the solar zenith angle dependence of nadir reflectance. J. Geophys. Res. 1997, 102, 9387–9395. [Google Scholar] [CrossRef]
- Loeb, N.G.; Varnai, T.; Winker, D.M. Influence of subpixel-scale cloud-top structure on reflectances from overcast stratiform cloud layers. J. Atmos. Sci. 1998, 55, 2960–2973. [Google Scholar] [CrossRef]
- Varnai, T.; Marshak, A. View angle dependence of cloud optical thicknesses retrieved by Moderate Resolution Imaging Spectroradiometer (MODIS). J. Geophys. Res. 2007, 112, D06203. [Google Scholar] [CrossRef]
- Kato, S.; Marshak, A. Solar zenith and viewing geometry-dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. 2009, 114, D01202. [Google Scholar] [CrossRef]
- Zhang, Z.; Ackerman, A.S.; Feingold, G.; Platnick, S.; Pincus, R.; Xue, H. Effects of cloud horizontal inhomogeneity and drizzle on remote sensing of cloud droplet effective radius: Case studies based on large-eddy simulations. J. Geophys. Res. 2012, 117, D19208. [Google Scholar] [CrossRef]
- Liang, L.; Di Girolamo, L. A global analysis on the view-angle dependence of plane-parallel oceanic liquid water cloud optical thickness using data synergy from MISR and MODIS. J. Geophys. Res. Atmos. 2013, 118, 2389–2403. [Google Scholar] [CrossRef]
- Horvath, A.; Seethala, C.; Deneke, H. View angle dependence of MODIS liquid water path retrievals in warm oceanic clouds. J. Geophys. Res. Atmos. 2014, 119, 8304–8328. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lu, D.; Huo, J. Impact of cloud inhomogeneity on bi-directional reflectance. Chin. Sci. Bull. 2008, 53, 124–130. [Google Scholar] [CrossRef]
- Cahalan, R.; Oreopoulos, R.; Marshak, A.; Evans, K.F.; Davis, A.; Pincus, R.; Yetzer, K.; Mayer, B.; Davies, R.; Ackerman, T.; et al. The I3RC: Bringing together the most advanced radiative transfer tools for cloudy atmospheres. Bull. Am. Meteorol. Soc. 2005, 86, 1275–1293. [Google Scholar] [CrossRef]
- Kassianov, E.I. Stochastic radiative transfer in multilayer broken clouds. Part I: Markovian approach. J. Quant. Spectrosc. Radiat. Transf. 2003, 77, 373–393. [Google Scholar] [CrossRef]
- Zhuravleva, T.B.; Nasrtdinov, I.M.; Russkova, T.V.; Chesnokova, T.Y. Mathematical simulation of brightness fields in broken clouds for observations from Earth’s surface and from space in plane and spherical atmospheric models. In Proceedings of the 22nd International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Tomsk, Russia, 30 June–3 July 2016; Volume 10035, p. 1003502. [Google Scholar] [CrossRef]
- Zhuravleva, T.B.; Nasrtdinov, I.M.; Russkova, T.V. Influence of 3D cloud effects on spatial-angular characteristics of the reflected solar radiation field. Atmos. Ocean. Opt. 2017, 30, 103–110. [Google Scholar] [CrossRef]
- Zhuravleva, T.B.; Nasrtdinov, I.M. Simulation of the mean intensity of reflected solar radiation in broken clouds: Spherical model of atmosphere. In Proceedings of the 23rd International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Irkutsk, Russia, 3–7 July 2017; Volume 10466, p. 1046608. [Google Scholar] [CrossRef]
- Kopytov, N.P.; Mityushov, E.A. Universal algorithm for uniform distribution of points over random analytical surfaces in 3D space. Fundam. Issled. 2013, 4, 618–622. (In Russian) [Google Scholar]
- World Climate Research Programme, International Association for Meteorology and Atmospheric Physics; Radiation Commission. A Preliminary Cloudless Standard Atmosphere for Radiation Computation; World Climate Research Programme; WCP: Boulder, CO, USA, 1986; p. 112. [Google Scholar]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Kneizys, F.X.; Robertson, D.S.; Abreu, L.W.; Acharya, P.; Anderson, G.P.; Rothman, L.S.; Chetwynd, J.H.; Selby, J.E.A.; Shetle, E.P.; Gallery, W.O.; et al. The MODTRAN 2/3 Report and LOWTRAN 7 Model; Abreu, L.W., Anderson, G.P., Eds.; Ontar Corporation: North Andover, MA, USA, 1996. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Goody, R.; West, R.; Chen, L.; Crisp, D. The correlated-k method for radiation calculations in nonhomogeneous atmospheres. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 539–550. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A.B. 3D Radiative Transfer in Cloudy Atmospheres; Marshak, A., Davis, A.B., Eds.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Marchuk, G.I.; Mikhailov, G.; Nazaraliev, M.; Darbinjan, R.; Kargin, B.; Elepov, B. The Monte Carlo Methods in Atmospheric Optics; Springer: Heidelberg, Germany, 1980. [Google Scholar]
- Zhuravleva, T.B. Simulation of solar radiative transfer under different atmospheric conditions. Part I. The deterministic atmosphere. Atmos. Ocean. Opt. 2008, 21, 81–95. [Google Scholar]
- Feigelson, E.M.; Krasnokutskaya, L.D. Solar Radiation Fluxes in Clouds; Gidrometeoizdat: Leningrad, Russia, 1978. (In Russian) [Google Scholar]
- Gatebe, C.K.; King, M.D. Airborne spectral BRDF of various surface types (ocean, vegetation, snow, desert, wetlands, cloud decks, smoke layers) for remote sensing applications. Remote Sens. Environ. 2016, 179, 131–148. [Google Scholar] [CrossRef]
- Marshak, A.; Herman, J.; Szabo, A.; Blank, K.; Carn, S.; Cede, A.; Geogdzhayev, I.; Huang, D.; Huang, L.; Knyazikhin, Y.; et al. Earth observations from DSCOVR/EPIC Instrument. Bull. Am. Meteorol. Soc. 2018, in press. [Google Scholar] [CrossRef]
- Yang, W.; Marshak, A.; Várnai, T.; Knyazikhin, Y. EPIC Spectral Observations of Variability in Earth’s Global Reflectance. Remote Sens. 2018, 10, 254. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Mõttus, M.; Rautiainen, M.; Stenberg, P.; Yan, L.; Chen, C.; Yan, K.; Choi, S.; Park, T.; et al. Estimation of leaf area index and its sunlit portion from DSCOVR 1019 EPIC data: Theoretical basis. Remote Sens. Environ. 2017, 198, 69–84. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuravleva, T.; Nasrtdinov, I. Simulation of Bidirectional Reflectance in Broken Clouds: From Individual Realization to Averaging over an Ensemble of Cloud Fields. Remote Sens. 2018, 10, 1342. https://doi.org/10.3390/rs10091342
Zhuravleva T, Nasrtdinov I. Simulation of Bidirectional Reflectance in Broken Clouds: From Individual Realization to Averaging over an Ensemble of Cloud Fields. Remote Sensing. 2018; 10(9):1342. https://doi.org/10.3390/rs10091342
Chicago/Turabian StyleZhuravleva, Tatiana, and Ilmir Nasrtdinov. 2018. "Simulation of Bidirectional Reflectance in Broken Clouds: From Individual Realization to Averaging over an Ensemble of Cloud Fields" Remote Sensing 10, no. 9: 1342. https://doi.org/10.3390/rs10091342
APA StyleZhuravleva, T., & Nasrtdinov, I. (2018). Simulation of Bidirectional Reflectance in Broken Clouds: From Individual Realization to Averaging over an Ensemble of Cloud Fields. Remote Sensing, 10(9), 1342. https://doi.org/10.3390/rs10091342