ERN: Edge Loss Reinforced Semantic Segmentation Network for Remote Sensing Images
Abstract
1. Introduction
2. Background
3. Proposed Edge Loss Reinforced Semantic Segmentation Network
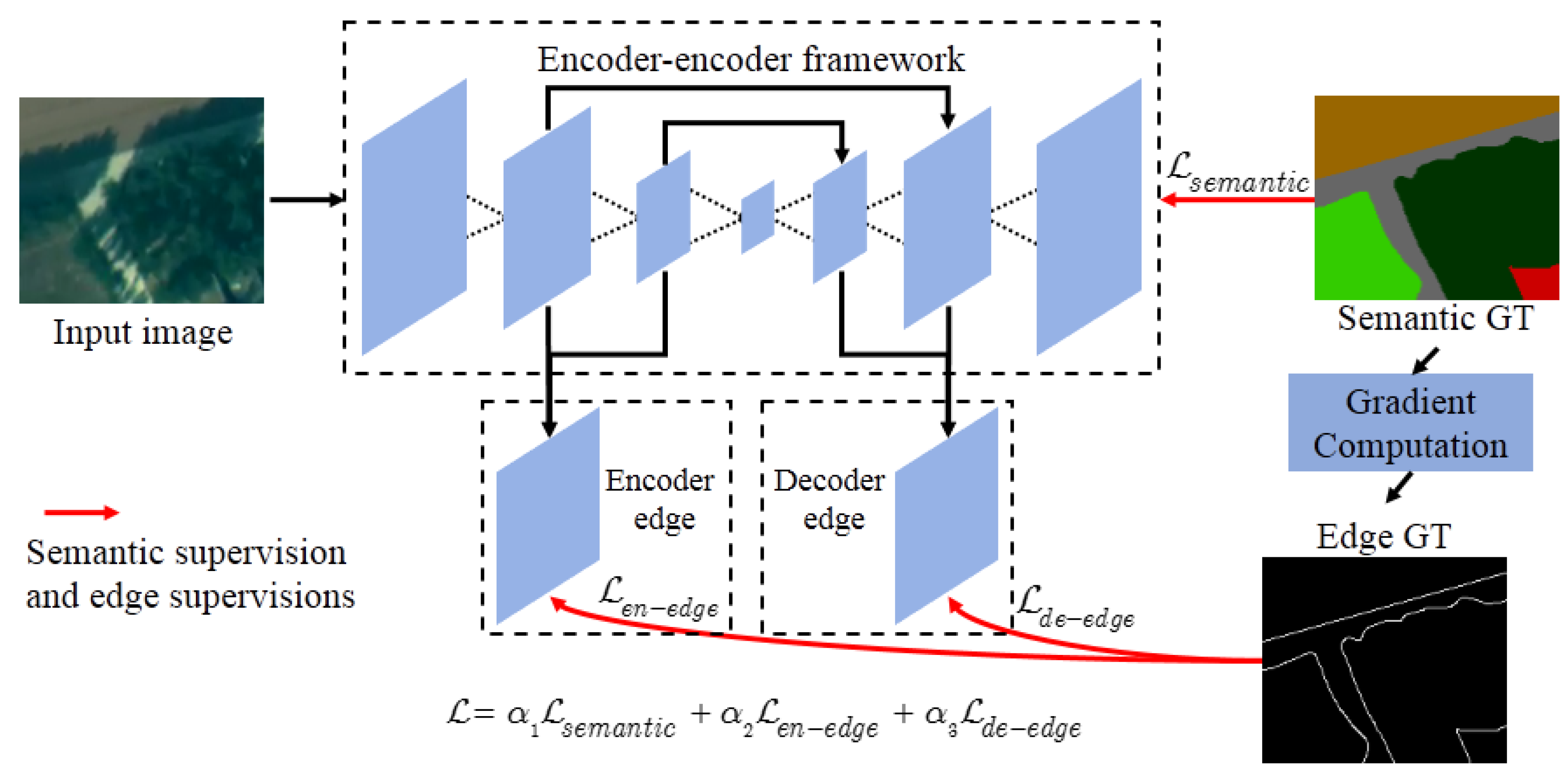
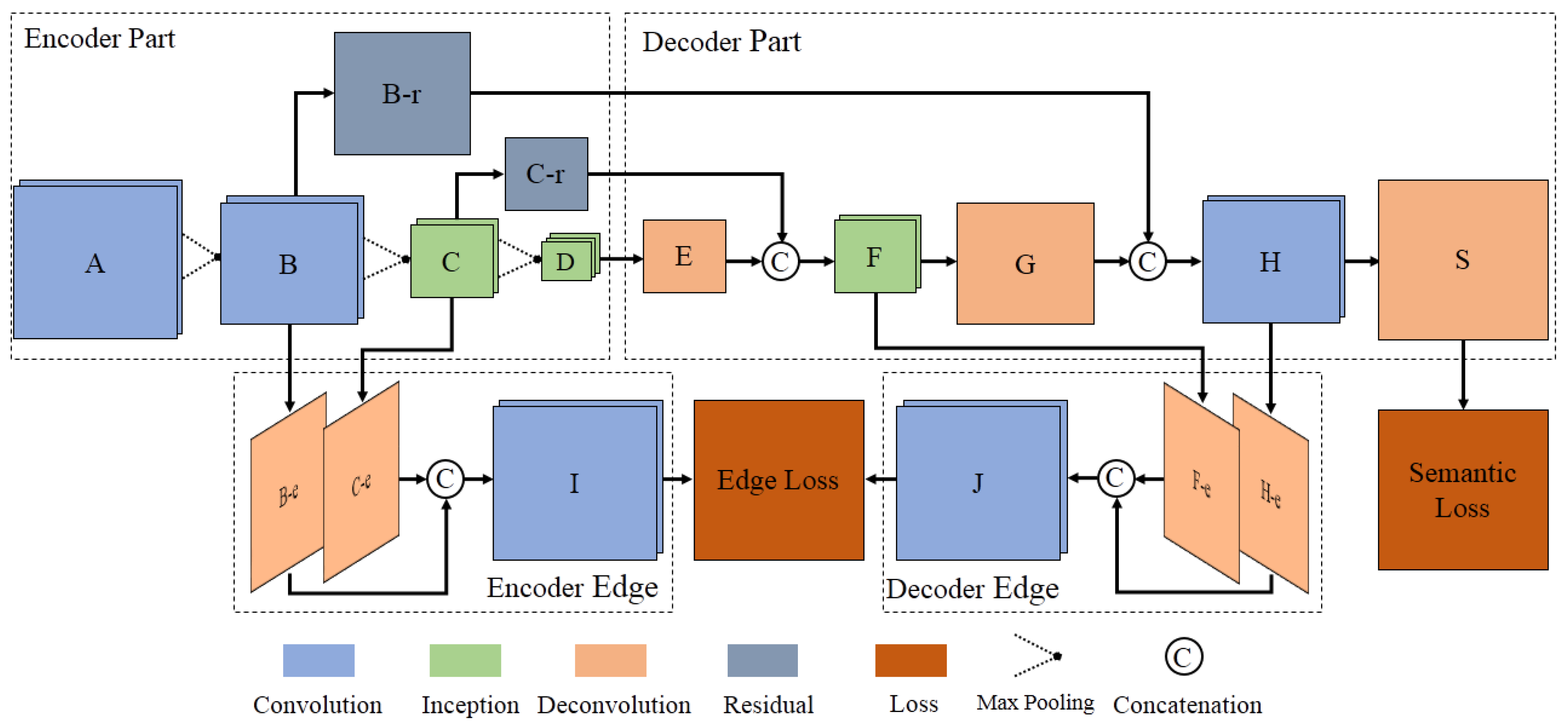
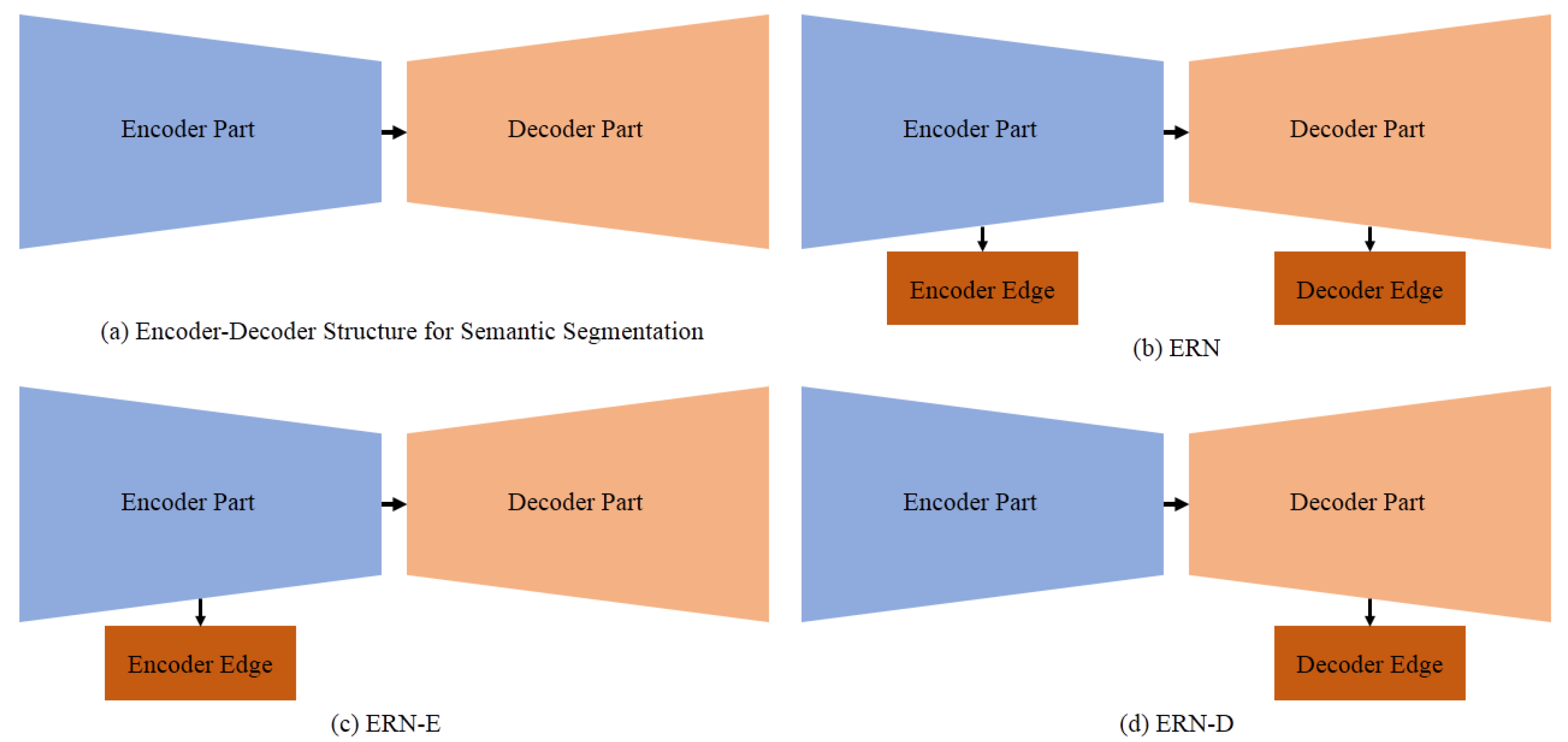
3.1. Model Overview
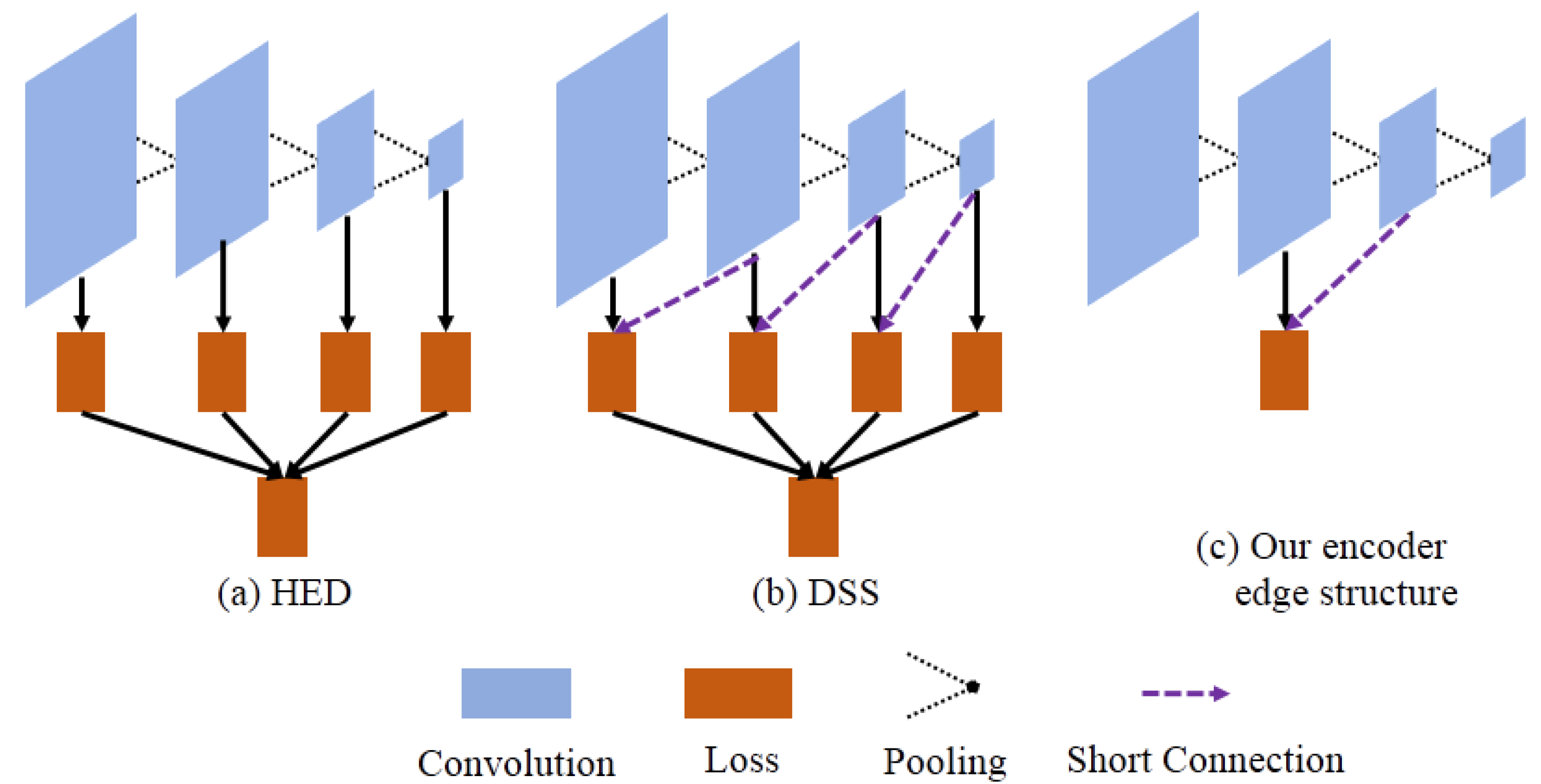
3.2. The Edge Loss Reinforced Structure Based on Short Connection
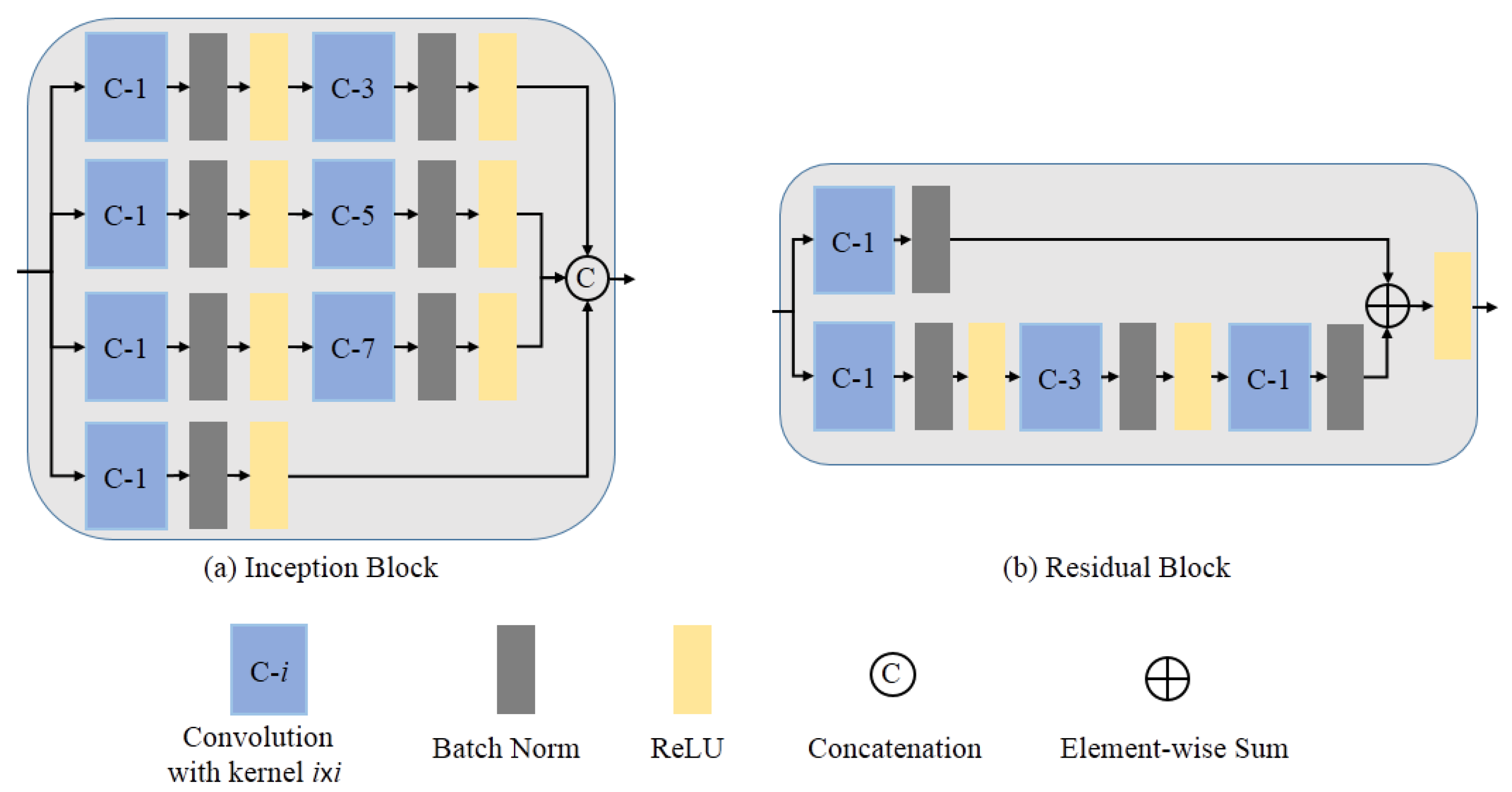
3.3. Inception and Residual Learning
3.4. Joint Semantic Loss and Edge Loss
4. Experimental Design and Results
4.1. Datasets
4.2. Training and Testing
4.3. Evaluation Metrics
4.4. Results
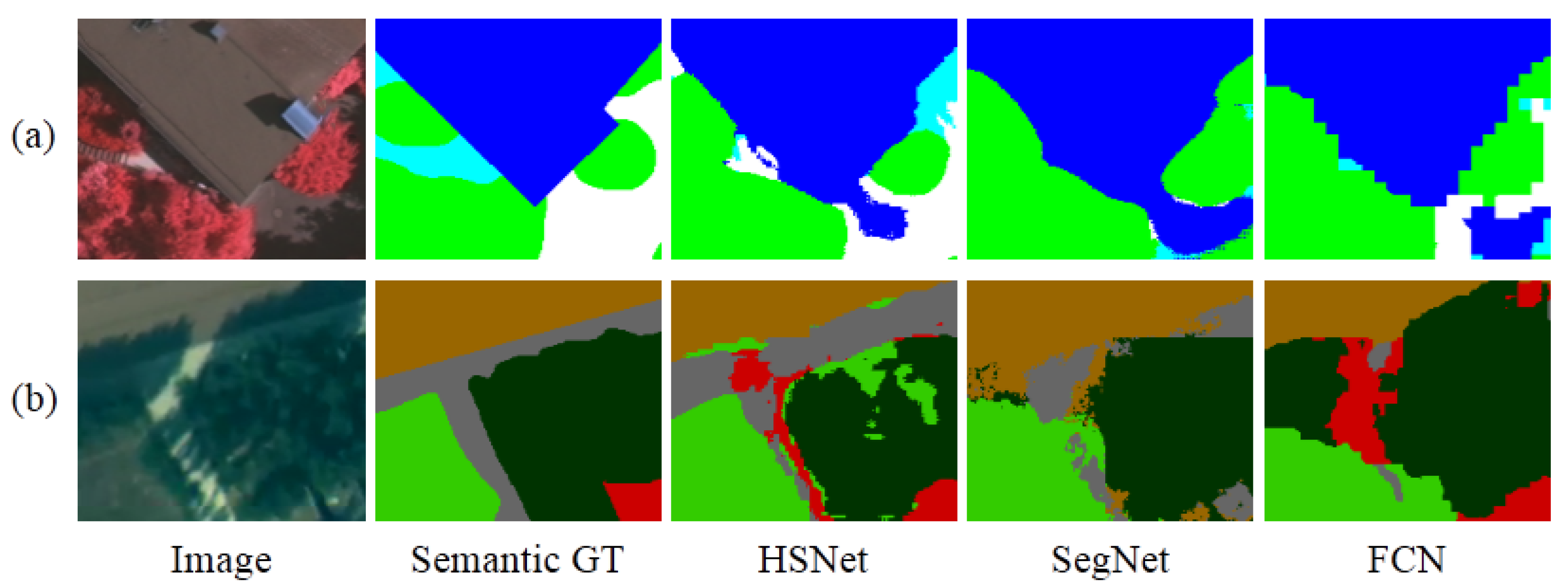
4.4.1. Results of UAV Image Dataset
4.4.2. Results of ISPRS Vaihingen Dataset
4.5. Performance in Shadow-Affected Regions
5. Discussion
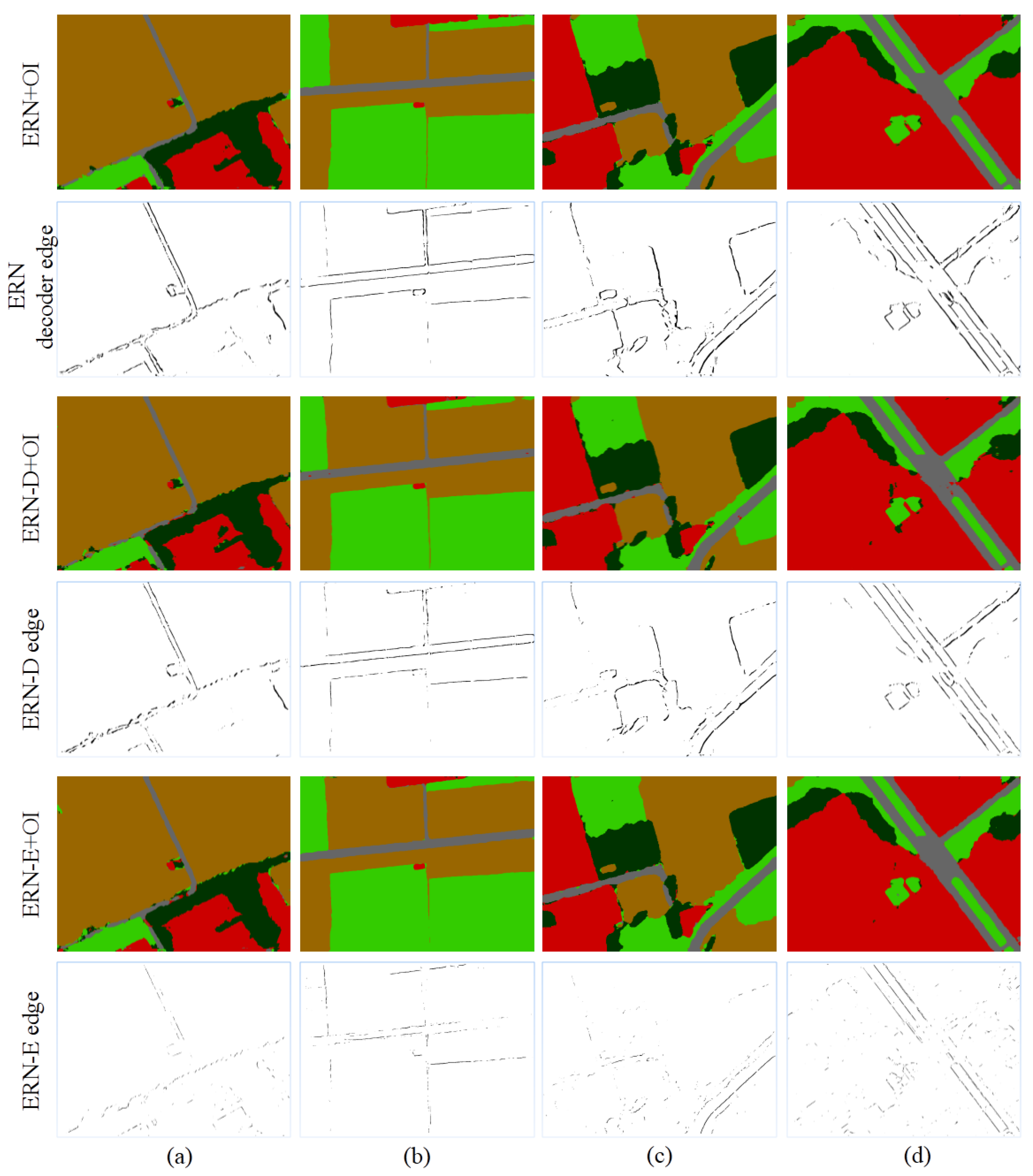
5.1. Edge Loss Analysis
5.2. General Analysis
5.3. Efficiency Limitation
5.4. Future Work
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Confusion Matrices
| Buildings | Road | Grass | Tree | Land | ||
|---|---|---|---|---|---|---|
| FCN [17] | Buildings | 89.90 | 1.47 | 1.91 | 6.10 | 0.62 |
| Road | 7.5 | 83.16 | 3.5 | 1.9 | 3.94 | |
| Grass | 2.44 | 0.63 | 74.10 | 19.53 | 3.3 | |
| Tree | 8.28 | 0.26 | 1.52 | 87.90 | 2.04 | |
| Land | 1.09 | 0.38 | 2.66 | 2.81 | 93.06 | |
| SegNet [19] | Buildings | 86.49 | 4.64 | 2.34 | 2.86 | 3.67 |
| Road | 2.04 | 78.67 | 2.20 | 0.66 | 16.42 | |
| LowVeg | 0.82 | 0.87 | 81.04 | 13.41 | 3.87 | |
| Tree | 7.52 | 0.45 | 2.65 | 79.88 | 9.5 | |
| Land | 0.15 | 0.18 | 2.16 | 0.49 | 97.03 | |
| HSNet [24] | Buildings | 91.28 | 1.97 | 3.33 | 3.16 | 0.26 |
| Road | 8.03 | 84.21 | 5.32 | 0.25 | 2.18 | |
| Grass | 2.12 | 0.77 | 92.46 | 3.29 | 1.37 | |
| Tree | 10.90 | 1.02 | 6.79 | 78.44 | 2.58 | |
| Land | 0.39 | 0.68 | 5.46 | 0.29 | 93.18 | |
| ERN | Buildings | 92.94 | 1.12 | 1.11 | 4.49 | 0.33 |
| Road | 9.57 | 84.25 | 2.60 | 1.35 | 2.23 | |
| Grass | 0.94 | 0.72 | 90.28 | 6.44 | 1.62 | |
| Tree | 6.77 | 0.59 | 7.09 | 82.34 | 3.21 | |
| Land | 0.22 | 0.37 | 3.26 | 0.92 | 95.22 |
| Imp.Surf | Buildings | LowVeg | Tree | Car | ||
|---|---|---|---|---|---|---|
| FCN [17] | Imp.Surf | 88.99 | 3.14 | 5.39 | 1.09 | 1.38 |
| Buildings | 3.89 | 93.21 | 2.22 | 0.57 | 0.11 | |
| LowVeg | 5.88 | 2.47 | 74.11 | 17.32 | 0.22 | |
| Tree | 0.92 | 0.37 | 9.36 | 89.35 | 0.01 | |
| Car | 15.60 | 1.71 | 1.00 | 0.57 | 81.11 | |
| SegNet [19] | Imp.Surf | 91.68 | 2.46 | 3.87 | 1.18 | 0.81 |
| Buildings | 4.16 | 93.22 | 2.02 | 0.55 | 0.05 | |
| LowVeg | 6.62 | 2.44 | 73.63 | 17.22 | 0.09 | |
| Tree | 0.93 | 0.46 | 14.28 | 84.32 | 0.01 | |
| Car | 17.31 | 0.80 | 0.90 | 0.72 | 80.27 | |
| HSNet [24] | Imp.Surf | 92.64 | 2.54 | 3.71 | 0.65 | 0.46 |
| Buildings | 3.50 | 94.11 | 2.18 | 0.18 | 0.03 | |
| LowVeg | 6.73 | 2.44 | 78.09 | 12.67 | 0.08 | |
| Tree | 1.24 | 0.35 | 10.96 | 87.44 | 0.01 | |
| Car | 15.91 | 1.96 | 1.22 | 0.32 | 80.59 | |
| ERN | Imp.Surf | 91.18 | 2.63 | 4.62 | 1.13 | 0.33 |
| Buildings | 2.67 | 94.80 | 2.15 | 0.35 | 0.02 | |
| LowVeg | 5.07 | 1.88 | 77.96 | 15.06 | 0.03 | |
| Tree | 0.80 | 0.20 | 8.82 | 90.17 | 0.01 | |
| Car | 6.39 | 3.07 | 0.46 | 0.71 | 89.23 |
References
- Plaza, A.; Plaza, J.; Paz, A.; Sanchez, S. Parallel Hyperspectral Image and Signal Processing [Applications Corner]. IEEE Signal Process. Mag. 2011, 28, 119–126. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Zhang, B.; Gu, J.; Chen, C.; Han, J.; Su, X.; Cao, X.; Liu, J. One-two-one networks for compression artifacts reduction in remote sensing. ISPRS J. Photogramm. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning hierarchical features for scene labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed]
- Gaetano, R.; Scarpa, G.; Poggi, G. Hierarchical Texture-Based Segmentation of Multiresolution Remote-Sensing Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2129–2141. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; Van Westen, C.J.; Jetten, V.G.; Kumar, K.V. Segment Optimization and Data-Driven Thresholding for Knowledge-Based Landslide Detection by Object-Based Image Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Yao, X.; Han, J.; Cheng, G.; Qian, X.; Guo, L. Semantic Annotation of High-Resolution Satellite Images via Weakly Supervised Learning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3660–3671. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wang, L.; Bai, J.; Xiang, S.; Pan, C. Semantic labeling in very high resolution images via a self-cascaded convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Marcos, D.; Volpi, M.; Kellenberger, B.; Tuia, D. Land cover mapping at very high resolution with rotation equivariant CNNs: Towards small yet accurate models. ISPRS J. Photogramm. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C.; Tilton, J.C.; Tan, B.; Colstoun, E.C.B.D. HOTEX: An approach for global mapping of human built-up and settlement extent. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Liu, T.; Abd-Elrahman, A.; Zare, A.; Dewitt, B.A.; Flory, L.; Smith, S.E. A fully learnable context-driven object-based model for mapping land cover using multi-view data from unmanned aircraft systems. Remote Sens. Environ. 2018, 216, 328–344. [Google Scholar] [CrossRef]
- Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic object-based image analysis (GEOBIA): Emerging trends and future opportunities. GISci. Remote Sens. 2018, 55, 159–182. [Google Scholar] [CrossRef]
- Mostajabi, M.; Yadollahpour, P.; Shakhnarovich, G. Feedforward semantic segmentation with zoom-out features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3376–3385. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-scale Convolutional Architecture. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2016. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Scene Segmentation. IEEE Transact. Pattern Anal. Machine Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.; Milan, A.; Shen, C.; Reid, I.D. RefineNet: Multi-path Refinement Networks for High-Resolution Semantic Segmentation. IEEE Conf. Comput. Vis. Pattern Recognit. 2017, 1, 5168–5177. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention, Quebec, QC, Canada, 10–14 September 2015. [Google Scholar]
- Volpi, M.; Tuia, D. Dense Semantic Labeling of Subdecimeter Resolution Images With Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 881–893. [Google Scholar] [CrossRef]
- Liu, Y.; Minh Nguyen, D.; Deligiannis, N.; Ding, W.; Munteanu, A. Hourglass-ShapeNetwork Based Semantic Segmentation for High Resolution Aerial Imagery. Remote Sens. 2017, 9, 522. [Google Scholar] [CrossRef]
- Ghiasi, G.; Fowlkes, C.C. Laplacian Pyramid Reconstruction and Refinement for Semantic Segmentation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Kohli, P.; Torr, P.H.S. Robust higher order potentials for enforcing label consistency. Int. J. Comput. Vis. 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Russell, C. Associative hierarchical CRFs for object class image segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Angers, France, 17–21 May 2010. [Google Scholar]
- Arnab, A.; Jayasumana, S.; Zheng, S.; Torr, P.H.S. Higher Order Conditional Random Fields in Deep Neural Networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1395–1403. [Google Scholar]
- Bertasius, G.; Shi, J.; Torresani, L. High-for-Low and Low-for-High: Efficient Boundary Detection from Deep Object Features and Its Applications to High-Level Vision. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 504–512. [Google Scholar]
- Kokkinos, I. Pushing the Boundaries of Boundary Detection using Deep Learning. In Proceedings of the International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Chen, L.C.; Barron, J.T.; Papandreou, G.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Task-Specific Edge Detection Using CNNs and a Discriminatively Trained Domain Transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4545–4554. [Google Scholar]
- Cheng, D.; Meng, G.; Xiang, S.; Pan, C. FusionNet: Edge Aware Deep Convolutional Networks for Semantic Segmentation of Remote Sensing Harbor Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5769–5783. [Google Scholar] [CrossRef]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef]
- ISPRS 2D Semantic Labeling Contest. Available online: http://www2.isprs.org/commissions/comm3/ wg4/2d-sem-label-vaihingen.html (accessed on 7 July 2018).
- Garciagarcia, A.; Ortsescolano, S.; Oprea, S.; Villenamartinez, V.; Rodriguez, J.G. A Review on Deep Learning Techniques Applied to Semantic Segmentation. arXiv, 2017; arXiv:1704.06857. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Available online: http://arxiv.org/pdf/1409.1556v6.pdf (accessed on 18 December 2015).
- Zhang, B.; Yang, Y.; Chen, C.; Yang, L.; Han, J.; Shao, L. Action Recognition Using 3D Histograms of Texture and A Multi-class Boosting Classifier. IEEE Trans. Image Process. 2017, 26, 4648–4660. [Google Scholar] [CrossRef] [PubMed]
- Luan, S.; Chen, c.; Zhang, B.; han, j.; Liu, J. Gabor Convolutional Networks. IEEE Trans. Image Process. 2018, 27, 4357–4366. [Google Scholar] [CrossRef] [PubMed]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient Graph-Based Image Segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Susstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Shotton, J.; Johnson, M.; Cipolla, R. Semantic texton forests for image categorization and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the International Conference on Learning Representations, San Juan, PR, 2–4 May 2016. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.P.; Yuille, A.L. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.P.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Persello, C.; Stein, A. Deep Fully Convolutional Networks for the Detection of Informal Settlements in VHR Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2325–2329. [Google Scholar] [CrossRef]
- Zheng, S.; Jayasumana, S.; Romera-Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P.H.S. Conditional Random Fields as Recurrent Neural Networks. In Proceedings of the IEEE Conference on International Conference on Computer Vision, Los Alamitos, CA, USA, 7–13 December 2015. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-Resolution Aerial Image Labeling with Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7092–7103. [Google Scholar] [CrossRef]
- Lee, C.; Xie, S.; Gallagher, P.W.; Zhang, Z.; Tu, Z. Deeply-Supervised Nets. In Proceedings of the International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 9–12 May 2015; pp. 562–570. [Google Scholar]
- Hou, Q.; Cheng, M.; Hu, X.; Borji, A.; Tu, Z.; Torr, P.H.S. Deeply Supervised Salient Object Detection with Short Connections. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honplulu, HI, USA, 21–26 July 2017; pp. 5300–5309. [Google Scholar]
- Ke, W.; Chen, J.; Jiao, J.; Zhao, G.; Ye, Q. SRN: Side-Output Residual Network for Object Symmetry Detection in the Wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honplulu, HI, USA, 21–26 July 2017; pp. 302–310. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic Segmentation of Small Objects and Modeling of Uncertainty in Urban Remote Sensing Images Using Deep Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Hwang, J.J.; Liu, T.L. Pixel-wise Deep Learning for Contour Detection. arXiv, 2015; arXiv:1504.01989. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2016. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. In Proceedings of the Acm International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar]
- Tsai, V.J.D. A comparative study on shadow compensation of color aerial images in invariant color models. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1661–1671. [Google Scholar] [CrossRef]
- Lu, C.; Xu, L.; Jia, J. Contrast preserving decolorization. In Proceedings of the IEEE International Conference on Computational Photography, Seattle, WA, USA, 28–29 April 2012; pp. 1–7. [Google Scholar]





| Layer ID | Type | Filter Size | Spatial Resolution | |
|---|---|---|---|---|
| Encoder | A | convolution × 2 | 3 × 3, 64 | 256 × 256 |
| B | convolution × 2 | 3 × 3, 128 | 128 × 128 | |
| B-r | residual block | -, 128 | 128 × 128 | |
| C | inception block× 2 | -, 256 | 64× 64 | |
| C-r | residual block | -, 256 | 64 ×64 | |
| D | inception block× 3 | -, 512 | 32 × 32 | |
| Decoder | E | deconvolution | -, 256 | 64 × 64 |
| F | inception block × 2 | -, 256 | 64 × 64 | |
| G | deconvolution | -, 128 | 128 × 128 | |
| H | convolution × 2 | 3 × 3, 128 | 128 × 128 | |
| SL | deconvolution | -, 6 | 256 × 256 | |
| Edge Loss | B-e | deconvolution | -,2 | 256 × 256 |
| C-e | deconvolution | -,2 | ||
| I | convolution × 2 | 3 × 3, 64 | ||
| EEL | convolution | 3 × 3, 2 | ||
| F-e | deconvolution | -, 2 | ||
| H-e | deconvolution | -, 2 | ||
| J | convolution × 2 | 3 × 3, 64 | ||
| DEL | convolution | 3 × 3, 2 |
| Layer ID | Convolution Configurations | Operation | Output Number | |
|---|---|---|---|---|
| C | 1 × 1, 128 | 3 × 3, 128 | concatenation | 256 |
| 1 × 1, 32 | 5 × 5, 32 | |||
| 1 × 1, 32 | 7 × 7, 32 | |||
| 1 × 1, 64 | ||||
| D | 1 × 1, 192 | 3 × 3, 256 | concatenation | 512 |
| 1 × 1, 64 | 5 × 5, 128 | |||
| 1 × 1, 32 | 7 × 7, 64 | |||
| 1 × 1, 64 | ||||
| F | 1 × 1, 256 | 3 × 3, 128 | concatenation | 256 |
| 1 × 1, 64 | 5 × 5, 32 | |||
| 1 × 1, 32 | 7 × 7, 32 | |||
| 1 × 1, 64 | ||||
| Layer ID | Convolution Configurations | Operation | Output Number | ||
|---|---|---|---|---|---|
| B-r | 1 × 1, 128 | element-wise sum | 128 | ||
| 1 × 1, 64 | 3 × 3, 128 | 1 × 1, 128 | |||
| C-r | 1 × 1, 256 | element-wise sum | 256 | ||
| 1 × 1, 64 | 3 × 3, 128 | 1 × 1, 256 | |||
| Methods | Buildings | Road | Grass | Tree | Land | Average F-Score | Overall Accuracy |
|---|---|---|---|---|---|---|---|
| FCN [17] | 91.88 | 84.06 | 81.12 | 60.96 | 94.59 | 82.52 | 87.09 |
| SegNet [19] | 91.45 | 73.85 | 85.52 | 67.85 | 93.48 | 82.43 | 87.98 |
| HSNet [24] | 92.78 | 81.92 | 85.35 | 63.45 | 95.45 | 83.79 | 89.42 |
| ERN | 94.43 | 85.27 | 90.17 | 72.43 | 96.38 | 87.74 | 91.90 |
| FCN [17] + OI | 92.27 | 84.96 | 81.58 | 61.39 | 94.87 | 83.01 | 87.50 |
| SegNet [19] + OI | 92.33 | 76.97 | 86.32 | 68.77 | 94.12 | 83.70 | 88.91 |
| HSNet [24] + OI | 93.47 | 84.04 | 86.21 | 65.26 | 95.88 | 84.97 | 90.25 |
| ERN + OI | 95.02 | 87.20 | 91.17 | 73.88 | 96.76 | 88.81 | 92.66 |
| Methods | Imp.Surf | Buildings | LowVeg | Tree | Car | Average F-Score | Overall Accuracy | |
|---|---|---|---|---|---|---|---|---|
| er-GT | FCN [17] | 89.41 | 93.80 | 76.46 | 86.63 | 71.32 | 83.52 | 86.75 |
| SegNet [19] | 90.15 | 94.11 | 77.35 | 87.40 | 77.31 | 85.27 | 87.59 | |
| HSNet [24] | 90.89 | 94.51 | 78.83 | 87.84 | 81.87 | 86.79 | 88.32 | |
| ERN | 91.48 | 95.11 | 79.42 | 88.18 | 89.00 | 88.64 | 88.88 | |
| GT | FCN [17] | 85.82 | 91.27 | 72.39 | 83.30 | 63.10 | 79.18 | 83.18 |
| SegNet [19] | 86.68 | 91.74 | 73.22 | 83.99 | 71.36 | 81.40 | 84.07 | |
| HSNet [24] | 87.57 | 92.20 | 75.03 | 84.44 | 75.16 | 82.88 | 84.92 | |
| ERN | 88.34 | 93.03 | 75.66 | 84.78 | 82.15 | 84.79 | 85.61 |
| Methods | Imp.Surf | Buildings | LowVeg | Tree | Car | Average F-Score | Overall Accuracy |
|---|---|---|---|---|---|---|---|
| FCN [17] | 75.70 | 66.10 | 67.20 | 70.22 | 29.30 | 61.70 | 69.70 |
| SegNet [19] | 76.49 | 69.26 | 68.50 | 69.30 | 26.40 | 61.99 | 70.77 |
| HSNet [24] | 79.50 | 69.18 | 69.51 | 72.22 | 51.30 | 68.34 | 73.17 |
| ERN | 80.39 | 71.02 | 70.33 | 74.21 | 62.74 | 71.74 | 74.37 |
| Methods | Edge Loss Weights | Buildings | Road | Grass | Tree | Land | Average F-Score | Overall Accuracy |
|---|---|---|---|---|---|---|---|---|
| ERN-E | 1 | 92.11 | 80.55 | 82.84 | 56.79 | 95.37 | 81.53 | 87.60 |
| 10 | 94.06 | 83.93 | 86.18 | 67.26 | 95.62 | 85.41 | 90.00 | |
| ERN-D | 1 | 92.48 | 81.41 | 82.26 | 60.26 | 95.23 | 82.33 | 88.07 |
| 10 | 93.34 | 84.64 | 89.32 | 67.95 | 96.27 | 86.30 | 90.78 | |
| ERN | 10, 10 | 94.38 | 84.69 | 88.82 | 71.81 | 96.19 | 87.18 | 91.45 |
| 20, 20 | 94.43 | 85.27 | 90.17 | 72.43 | 96.38 | 87.74 | 91.90 | |
| ERN-E+OI | 10 | 94.65 | 85.71 | 86.88 | 68.09 | 95.97 | 86.26 | 90.62 |
| ERN-E+OI | 10 | 93.88 | 86.46 | 90.33 | 69.26 | 96.62 | 87.31 | 91.51 |
| ERN+OI | 10, 10 | 94.94 | 86.67 | 89.94 | 73.31 | 96.54 | 88.28 | 92.24 |
| 20, 20 | 95.02 | 87.20 | 91.17 | 73.88 | 96.76 | 88.81 | 92.66 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Ding, W.; Liu, C.; Liu, Y.; Wang, Y.; Li, H. ERN: Edge Loss Reinforced Semantic Segmentation Network for Remote Sensing Images. Remote Sens. 2018, 10, 1339. https://doi.org/10.3390/rs10091339
Liu S, Ding W, Liu C, Liu Y, Wang Y, Li H. ERN: Edge Loss Reinforced Semantic Segmentation Network for Remote Sensing Images. Remote Sensing. 2018; 10(9):1339. https://doi.org/10.3390/rs10091339
Chicago/Turabian StyleLiu, Shuo, Wenrui Ding, Chunhui Liu, Yu Liu, Yufeng Wang, and Hongguang Li. 2018. "ERN: Edge Loss Reinforced Semantic Segmentation Network for Remote Sensing Images" Remote Sensing 10, no. 9: 1339. https://doi.org/10.3390/rs10091339
APA StyleLiu, S., Ding, W., Liu, C., Liu, Y., Wang, Y., & Li, H. (2018). ERN: Edge Loss Reinforced Semantic Segmentation Network for Remote Sensing Images. Remote Sensing, 10(9), 1339. https://doi.org/10.3390/rs10091339





