Multispectral Pansharpening with Radiative Transfer-Based Detail-Injection Modeling for Preserving Changes in Vegetation Cover
Abstract
1. Introduction
- (i)
- (ii)
- the multiplicative or contrast-based model, which is the basis of such techniques as high-pass modulation (HPM) [18], Brovey transform (BT) [19], the synthetic variable ratio (SVR) [20], UNBpansharp [21], smoothing filter-based intensity modulation (SFIM) [22] and the spectral distortion minimizing (SDM) injection model [23].
2. Spectral and Spatial Pansharpening Methods
2.1. Spectral or Component-Substitution Methods
2.2. Spatial or Multiresolution Analysis Methods
3. A Review of the Radiative Transfer Model
- : wave length of the electromagnetic radiation (m)
- : at-sensor spectral radiance (W·msrm)
- : surface reflectance (unitless)
- : upward transmittance of atmosphere (unitless)
- : mean TOA solar irradiance (W·mm)
- : solar zenith angle (degrees)
- : downward transmittance of atmosphere (unitless)
- : diffuse irradiance at the surface (W·mm)
- : Earth-Sun distance (astronomical units)
- : upward scattered radiance at TOA (W·msrm)
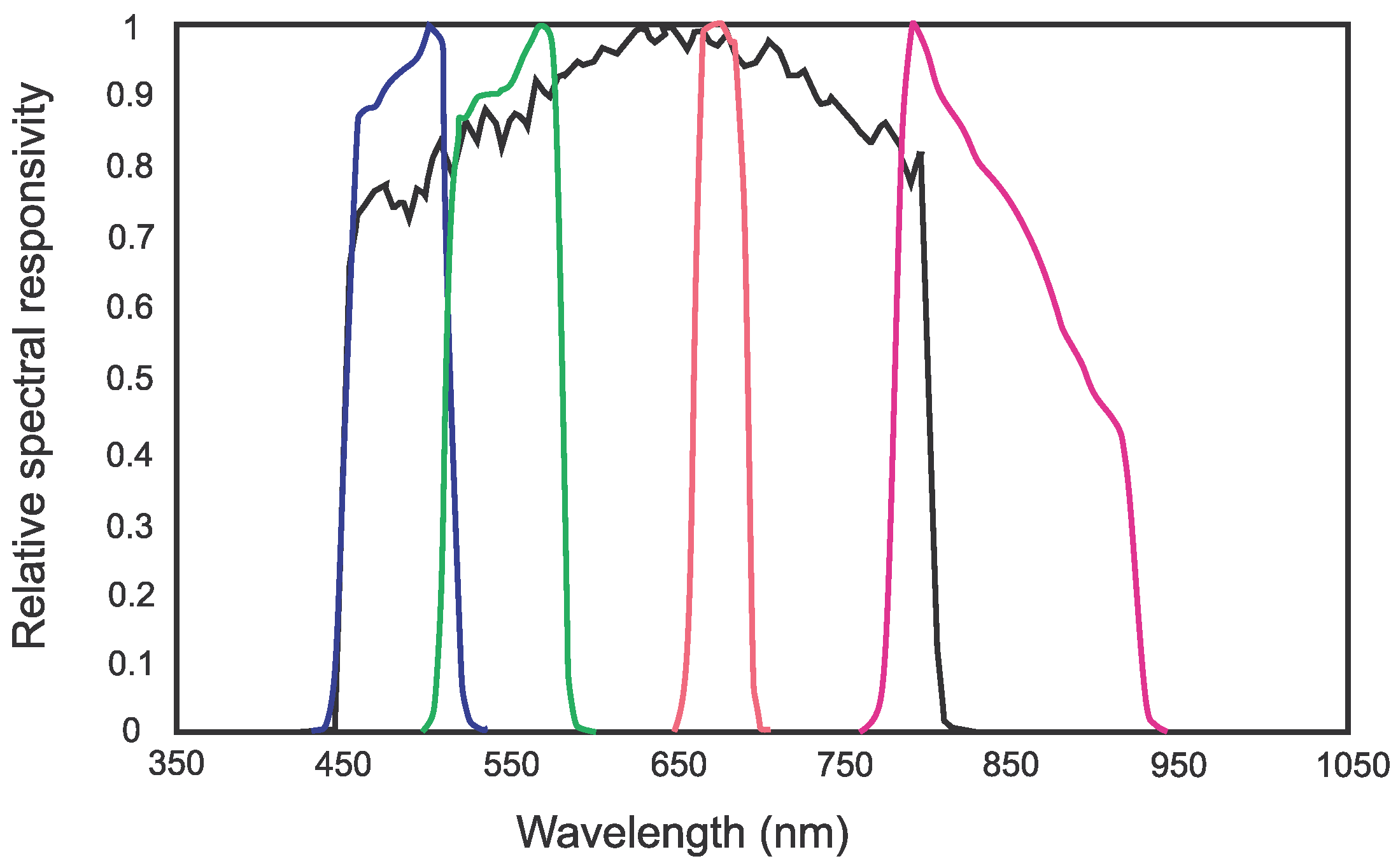
4. Data Formats and Products
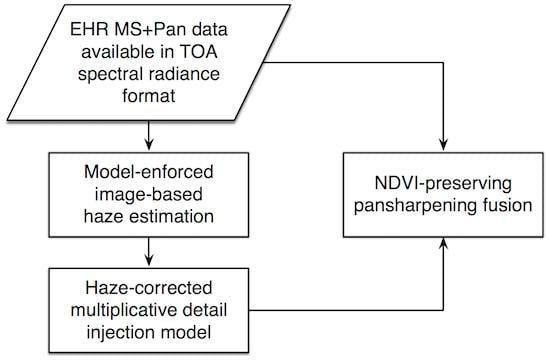
5. Contrast-Based Fusion with Haze Removal
6. Experimental Results
6.1. Methods
6.2. Dataset
6.3. Assessments
6.4. Estimation of Path Radiances
6.5. Fusion Simulations
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Zhang, H.K.; Huang, B. A new look at image fusion methods from a Bayesian perspective. Remote Sens. 2015, 7, 6828–6861. [Google Scholar] [CrossRef]
- Garzelli, A. A review of image fusion algorithms based on the super-resolution paradigm. Remote Sens. 2016, 8, 797. [Google Scholar] [CrossRef]
- Meng, X.; Shen, H.; Li, H.; Zhang, L.; Fu, R. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis. Inf. Fusion 2019, 46, 102–113. [Google Scholar] [CrossRef]
- Aly, H.A.; Sharma, G. A regularized model-based optimization framework for pan-sharpening. IEEE Trans. Image Process. 2014, 23, 2596–2608. [Google Scholar] [CrossRef] [PubMed]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison of pansharpening algorithms. In Proceedings of the IEEE IGARSS, Quebec City, QC, Canada, 13–18 July 2014; pp. 191–194. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Spatial methods for multispectral pansharpening: Multiresolution analysis demystified. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2563–2576. [Google Scholar] [CrossRef]
- Restaino, R.; Vivone, G.; Dalla Mura, M.; Chanussot, J. Fusion of multispectral and panchromatic images based on morphological operators. IEEE Trans. Image Process. 2016, 25, 2882–2895. [Google Scholar] [CrossRef] [PubMed]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor statistical matching for pansharpening: Theoretical issues and practical solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, H.K.; Huang, B. Revealing implicit assumptions of the component substitution pansharpening methods. Remote Sens. 2017, 9, 443. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A regression-based high-pass modulation pansharpening approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 984–996. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F. Fusion of panchromatic and multispectral images by genetic algorithms. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 3810–3813. [Google Scholar]
- Garzelli, A.; Nencini, F. Panchromatic sharpening of remote sensing images using a multiscale Kalman filter. Pattern Recognit. 2007, 40, 3568–3577. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Enhanced Gram-Schmidt spectral sharpening based on multivariate regression of MS and Pan data. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006; pp. 3806–3809. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, 2nd ed.; Academic Press: Orlando, FL, USA, 1997. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images-II. Channel ratio and “Chromaticity” Transform techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Munechika, C.K.; Warnick, J.S.; Salvaggio, C.; Schott, J.R. Resolution enhancement of multispectral image data to improve classification accuracy. Photogramm. Eng. Remote Sens. 1993, 59, 67–72. [Google Scholar]
- Zhang, Y. A new merging methods and its spectral and spatial effects. Int. J. Remote Sens. 1999, 20, 2003–2014. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing filter based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Sharpening of very high resolution images with spectral distortion minimization. In Proceedings of the 2003 IEEE International Symposium on Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 458–460. [Google Scholar]
- Aiazzi, B.; Baronti, S.; Lotti, F.; Selva, M. A comparison between global and context-adaptive pansharpening of multispectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 302–306. [Google Scholar] [CrossRef]
- Garzelli, A.; Benelli, G.; Barni, M.; Magini, C. Improving wavelet-based merging of panchromatic and multispectral images by contextual information. In Image and Signal Processing for Remote Sensing VI; Serpico, S.B., Ed.; SPIE: Bellingham, WA, USA, 2001; Volume 4170, pp. 82–91. [Google Scholar]
- Restaino, R.; Dalla Mura, M.; Vivone, G.; Chanussot, J. Context-adaptive pansharpening based on image segmentation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 753–766. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Dalla Mura, M.; Licciardi, G.; Chanussot, J. Contrast and error-based fusion schemes for multispectral image pansharpening. IEEE Geosci. Remote Sens. Lett. 2014, 11, 930–934. [Google Scholar] [CrossRef]
- Alparone, L.; Facheris, L.; Baronti, S.; Garzelli, A.; Nencini, F. Fusion of multispectral and SAR images by intensity modulation. In Proceedings of the Seventh International Conference on Information Fusion, Stockholm, Sweden, 28 June–1 July 2004; Volume 2, pp. 637–643. [Google Scholar]
- Pacifici, F.; Longbotham, N.; Emery, W.J. The importance of physical quantities for the analysis of multitemporal and multiangular optical very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6241–6256. [Google Scholar] [CrossRef]
- Jing, L.; Cheng, Q. Two improvement schemes of PAN modulation fusion methods for spectral distortion minimization. Int. J. Remote Sens. 2009, 30, 2119–2131. [Google Scholar] [CrossRef]
- Jing, L.; Cheng, Q. An image fusion method taking into account phenological analogies and haze. Int. J. Remote Sens. 2011, 32, 1675–1694. [Google Scholar] [CrossRef]
- Jing, L.; Cheng, Q. Spectral change directions of multispectral subpixels in image fusion. Int. J. Remote Sens. 2011, 32, 1695–1711. [Google Scholar] [CrossRef]
- Li, H.; Jing, L. Improvement of a pansharpening method taking into account haze. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5039–5055. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Image-based atmospheric corrections–Revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Fu, Q.; Liou, K.N. On the correlated k-distribution method for radiative transfer in nonhomogeneous atmospheres. J. Atmos. Sci. 1992, 49, 2139–2156. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze correction for contrast-based multispectral pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE Pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Garzelli, A. Pansharpening of multispectral images based on nonlocal parameter optimization. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2096–2107. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Argenti, F.; Baronti, S. Wavelet and pyramid techniques for multisensor data fusion: A performance comparison varying with scale ratios. In Image and Signal Processing for Remote Sensing V; Serpico, S.B., Ed.; SPIE: Bellingham, WA, USA, 1999; Volume 3871, pp. 251–262. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Barducci, A.; Baronti, S.; Pippi, I. Multispectral fusion of multisensor image data by the generalized Laplacian pyramid. In Proceedings of the 1999 IEEE International Symposium on Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; pp. 1183–1185. [Google Scholar]
- Garzelli, A.; Nencini, F.; Alparone, L.; Baronti, S. Multiresolution fusion of multispectral and panchromatic images through the curvelet transform. In Proceedings of the 2005 IEEE International Symposium on Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; pp. 2838–2841. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. Advantages of Laplacian pyramids over “à trous” wavelet transforms. In Image and Signal Processing for Remote Sensing XVIII; Bruzzone, L., Ed.; SPIE: Bellingham, WA, USA, 2012; Volume 8537, pp. 853704-1–853704-10. [Google Scholar]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Zhang, H.K.; Roy, D.P. Computationally inexpensive Landsat 8 Operational Land Imager (OLI) pansharpening. Remote Sens. 2016, 8, 180. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Capobianco, L.; Garzelli, A.; Marchesi, S.; Nencini, F. Analysis of the effects of pansharpening in change detection on VHR images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 53–57. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Sensitivity of pansharpening methods to temporal and instrumental changes between multispectral and panchromatic datasets. IEEE Trans. Geosci. Remote Sens. 2017, 55, 308–319. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.K.; Roy, D.P.; Yan, L.; Huang, H.; Li, J. Landsat 15-m panchromatic-assisted downscaling (LPAD) of the 30-m reflective wavelength bands to Sentinel-2 20-m resolution. Remote Sens. 2017, 9, 1–18. [Google Scholar]
- Johnson, B. Effects of pansharpening on vegetation indices. ISPRS Int. J. Geo-Inf. 2014, 3, 507–522. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Bi-cubic interpolation for shift-free pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2013, 86, 65–76. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R. Assessment of pyramid-based multisensor image data fusion. In Image and Signal Processing for Remote Sensing IV; Serpico, S.B., Ed.; SPIE: Bellingham, WA, USA, 1998; Volume 3500, pp. 237–248. [Google Scholar]
- Carlà, R.; Santurri, L.; Aiazzi, B.; Baronti, S. Full-scale assessment of pansharpening through polynomial fitting of multiscale measurements. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6344–6355. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening quality assessment using the modulation transfer functions of instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Full scale assessment of pansharpening methods and data products. In Image and Signal Processing for Remote Sensing XX; Bruzzone, L., Ed.; SPIE: Bellingham, WA, USA, 2014; Volume 9244, pp. 924402-1–924402-12. [Google Scholar]
- Alparone, L.; Selva, M.; Aiazzi, B.; Baronti, S.; Butera, F.; Chiarantini, L. Signal-dependent noise modelling and estimation of new-generation imaging spectrometers. In Proceedings of the 2009 First Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Grenoble, France, 26–28 August 2009; pp. 1–4. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Barducci, A.; Baronti, S.; Pippi, I. Estimating noise and information of multispectral imagery. Opt. Eng. 2002, 41, 656–668. [Google Scholar]
- Pani, S.; Wang, S.H.; Lin, N.H.; Tsay, S.C.; Lolli, S.; Chuang, M.T.; Lee, C.T.; Chantara, S.; Yu, J.Y. Assessment of aerosol optical property and radiative effect for the layer decoupling cases over the northern South China Sea during the 7-SEAS/Dongsha Experiment. J. Geophys. Res.-Atmos. 2016, 121, 4894–4906. [Google Scholar] [CrossRef]
- Tosca, M.; Campbell, J.; Garay, M.; Lolli, S.; Seidel, F.; Marquis, J.; Kalashnikova, O. Attributing accelerated summertime warming in thesoutheast United States to recent reductions in aerosol burden: Indications from vertically-resolved observations. Remote Sens. 2017, 9, 674. [Google Scholar] [CrossRef]
- Lolli, S.; Delaval, A.; Loth, C.; Garnier, A.; Flamant, P. 0.355-micrometer direct detection wind lidar under testing during a field campaign in consideration of ESA’s ADM-Aeolus mission. Atmos. Meas. Tech. 2013, 6, 3349–3358. [Google Scholar] [CrossRef]
- Campbell, J.; Ge, C.; Wang, J.; Welton, E.; Bucholtz, A.; Hyer, E.; Reid, E.; Chew, B.; Liew, S.C.; Salinas, S.; et al. Applying advanced ground-based remote sensing in the Southeast Asian maritime continent to characterize regional proficiencies in smoke transport modeling. J. Appl. Meteorol. Climatol. 2016, 55, 3–22. [Google Scholar] [CrossRef]
- Haeffelin, M.; Angelini, F.; Morille, Y.; Martucci, G.; Frey, S.; Gobbi, G.; Lolli, S.; O’Dowd, C.; Sauvage, L.; Xueref-Rémy, I.; et al. Evaluation of mixing-height retrievals from automatic profiling lidars and ceilometers in view of future integrated networks in Europe. Bound.-Lay. Meteorol. 2012, 143, 49–75. [Google Scholar] [CrossRef]
- Milroy, C.; Martucci, G.; Lolli, S.; Loaec, S.; Sauvage, L.; Xueref-Remy, I.; Lavrič, J.; Ciais, P.; Feist, D.; Biavati, G.; et al. An assessment of pseudo-operational ground-based light detection and ranging sensors to determine the boundary-layer structure in the coastal atmosphere. Adv. Meteorol. 2012, 2012, 929080. [Google Scholar] [CrossRef]
- Campbell, J.; Lolli, S.; Lewis, J.; Gu, Y.; Welton, E. Daytime cirrus cloud top-of-the-atmosphere radiative forcing properties at a midlatitude site and their global consequences. J. Appl. Meteorol. Climatol. 2016, 55, 1667–1679. [Google Scholar] [CrossRef]
- Lolli, S.; Madonna, F.; Rosoldi, M.; Campbell, J.R.; Welton, E.J.; Lewis, J.R.; Gu, Y.; Pappalardo, G. Impact of varying lidar measurement and data processing techniques in evaluating cirrus cloud and aerosol direct radiative effects. Atmos. Meas. Tech. 2018, 11, 1639–1651. [Google Scholar] [CrossRef]





| 27-May-2010 | QNR | QNR | HQNR | ||||
| EXP | 0.0000 | 0.0376 | 0.1160 | 0.0535 | 0.8840 | 0.9109 | 0.8507 |
| CSw/oPRC | 0.1033 | 0.0600 | 0.1471 | 0.0140 | 0.7648 | 0.9268 | 0.8017 |
| CSw/PRC | 0.0507 | 0.0467 | 0.0674 | 0.0209 | 0.8853 | 0.9334 | 0.8890 |
| MRAw/oPRC | 0.1043 | 0.0445 | 0.1514 | 0.0126 | 0.7601 | 0.9434 | 0.8109 |
| MRAw/PRC | 0.0523 | 0.0379 | 0.0666 | 0.0212 | 0.8846 | 0.9418 | 0.8981 |
| GS | 0.0621 | 0.1235 | 0.0592 | 0.0229 | 0.8823 | 0.8564 | 0.8246 |
| BDSD | 0.0326 | 0.0521 | 0.0538 | 0.0156 | 0.9154 | 0.9331 | 0.8970 |
| 13-July-2010 | QNR | QNR | HQNR | ||||
| EXP | 0.0000 | 0.0302 | 0.1673 | 0.0816 | 0.8327 | 0.8907 | 0.8076 |
| CSw/oPRC | 0.0962 | 0.0425 | 0.1044 | 0.0128 | 0.8095 | 0.9453 | 0.8576 |
| CSw/PRC | 0.0427 | 0.0348 | 0.0580 | 0.0242 | 0.9017 | 0.9419 | 0.9092 |
| MRAw/oPRC | 0.0923 | 0.0315 | 0.0939 | 0.0127 | 0.8224 | 0.9562 | 0.8776 |
| MRAw/PRC | 0.0417 | 0.0282 | 0.0554 | 0.0253 | 0.9052 | 0.9472 | 0.9180 |
| GS | 0.0452 | 0.0932 | 0.0739 | 0.0188 | 0.8843 | 0.8897 | 0.8399 |
| BDSD | 0.0192 | 0.0411 | 0.0275 | 0.0206 | 0.9538 | 0.9391 | 0.9325 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral Pansharpening with Radiative Transfer-Based Detail-Injection Modeling for Preserving Changes in Vegetation Cover. Remote Sens. 2018, 10, 1308. https://doi.org/10.3390/rs10081308
Garzelli A, Aiazzi B, Alparone L, Lolli S, Vivone G. Multispectral Pansharpening with Radiative Transfer-Based Detail-Injection Modeling for Preserving Changes in Vegetation Cover. Remote Sensing. 2018; 10(8):1308. https://doi.org/10.3390/rs10081308
Chicago/Turabian StyleGarzelli, Andrea, Bruno Aiazzi, Luciano Alparone, Simone Lolli, and Gemine Vivone. 2018. "Multispectral Pansharpening with Radiative Transfer-Based Detail-Injection Modeling for Preserving Changes in Vegetation Cover" Remote Sensing 10, no. 8: 1308. https://doi.org/10.3390/rs10081308
APA StyleGarzelli, A., Aiazzi, B., Alparone, L., Lolli, S., & Vivone, G. (2018). Multispectral Pansharpening with Radiative Transfer-Based Detail-Injection Modeling for Preserving Changes in Vegetation Cover. Remote Sensing, 10(8), 1308. https://doi.org/10.3390/rs10081308