Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle
Abstract
1. Introduction
2. Modeling and Analysis
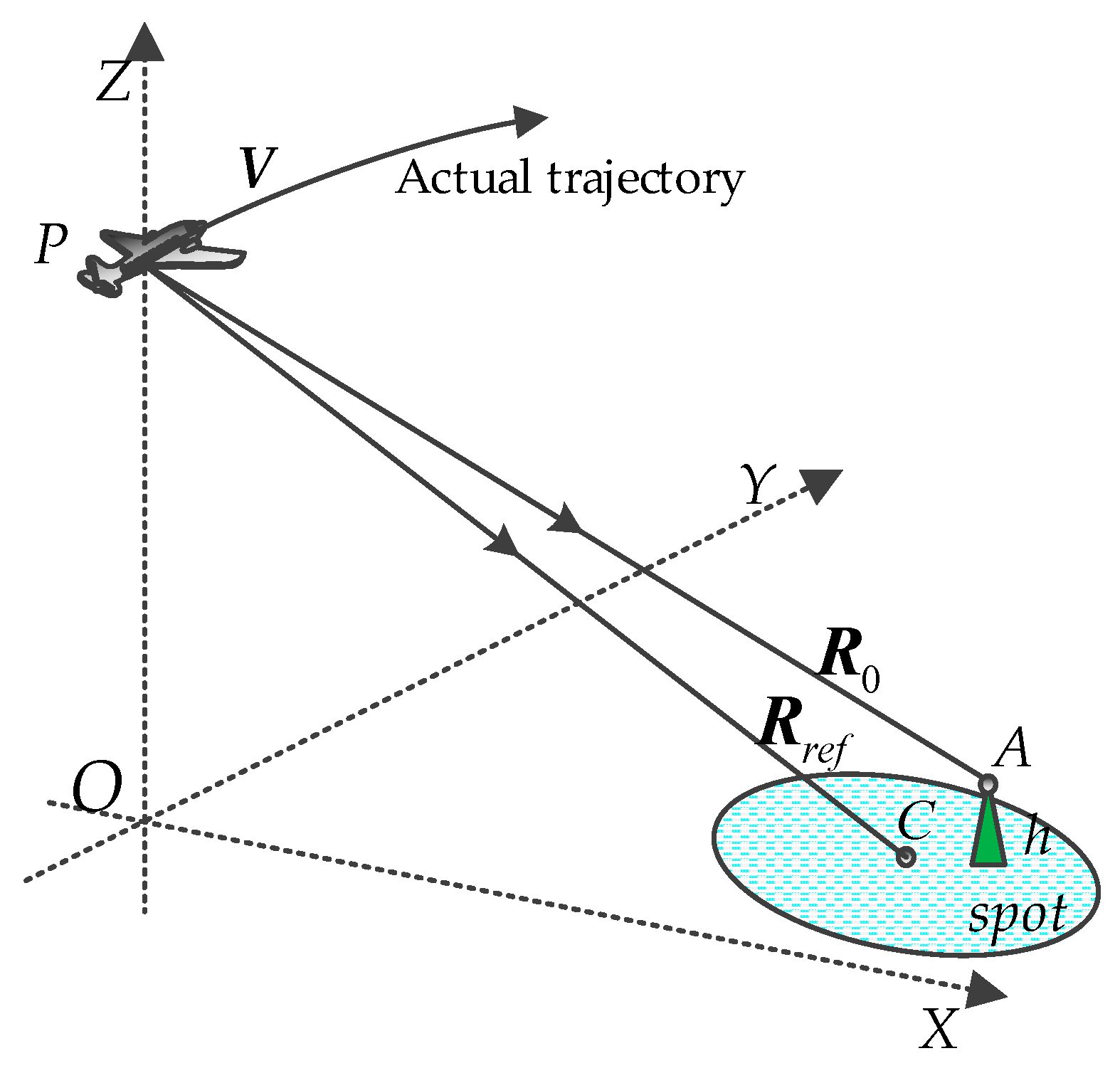
2.1. Modeling of Airborne SAR
2.2. Problem
- (1)
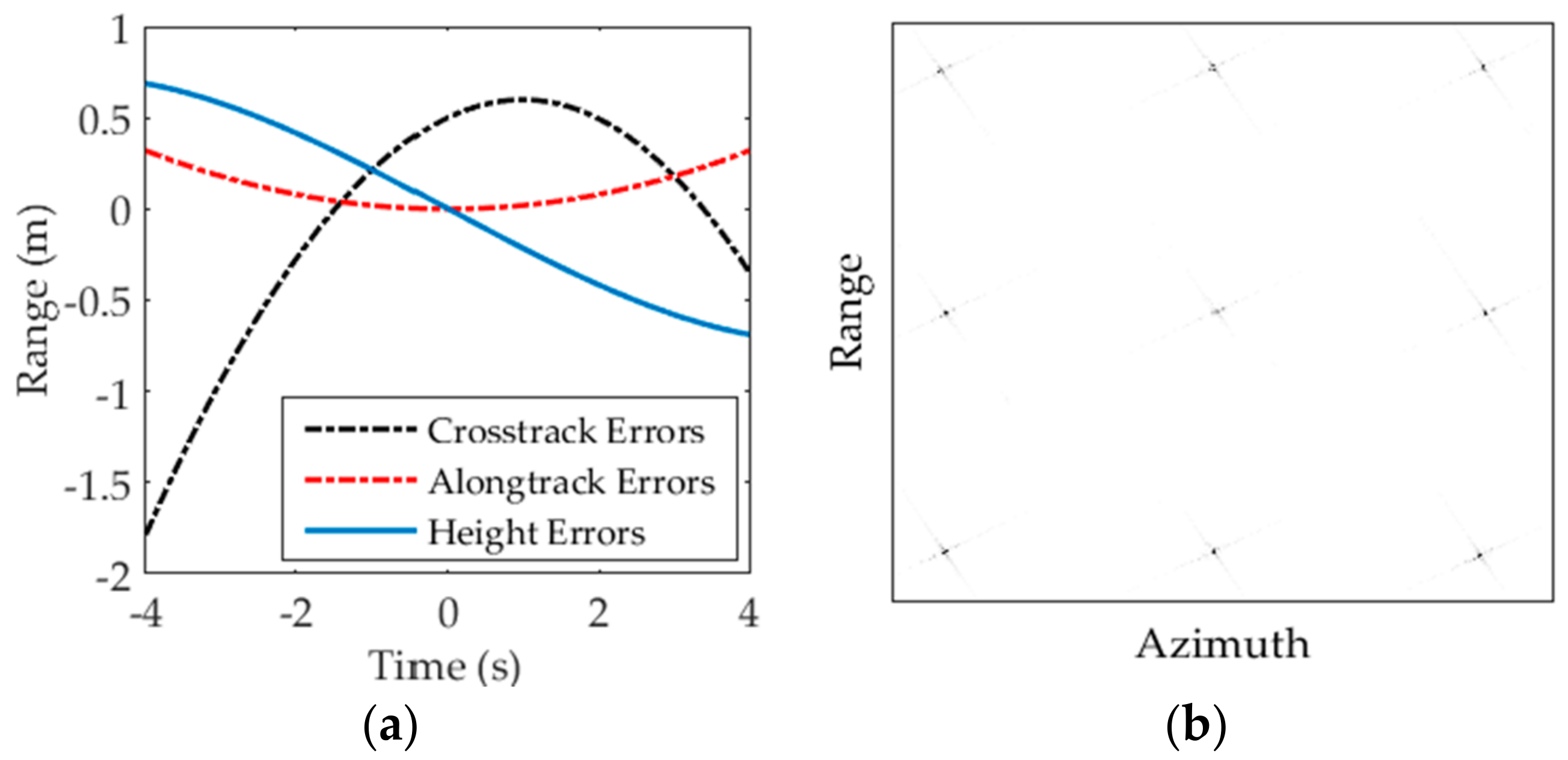
- Three-dimensional (3-D) variations in time-domain. Clearly, the general range history in Equation (1) was a vector variable function, which means that one should consider the changes in range, azimuth, and height directions, when designing the focusing approach in the time-domain. An accurate equation indicates the good performance of the proposed focusing method, or it would lead to a great deterioration in the final imaging result, including the IRW, the peak side-lobe ratio (PSLR), and the integration side-lobe ratio (ISLR).
- (2)
- 3-D variations in the frequency-domain. Because of the complex composition terms in Equation (1), it is difficult to derive the 2-D spectrum, even when using the method of the series reversion (MSR). Moreover, with the complex range history, the focused approach designed in the 2-D frequency-domain would be more complicated than those in the time-domain. Thus, the process directly applied in frequency-domain was not the best choice for an efficient algorithm design for high-resolution airborne SAR in this work.
3. Imaging Algorithm
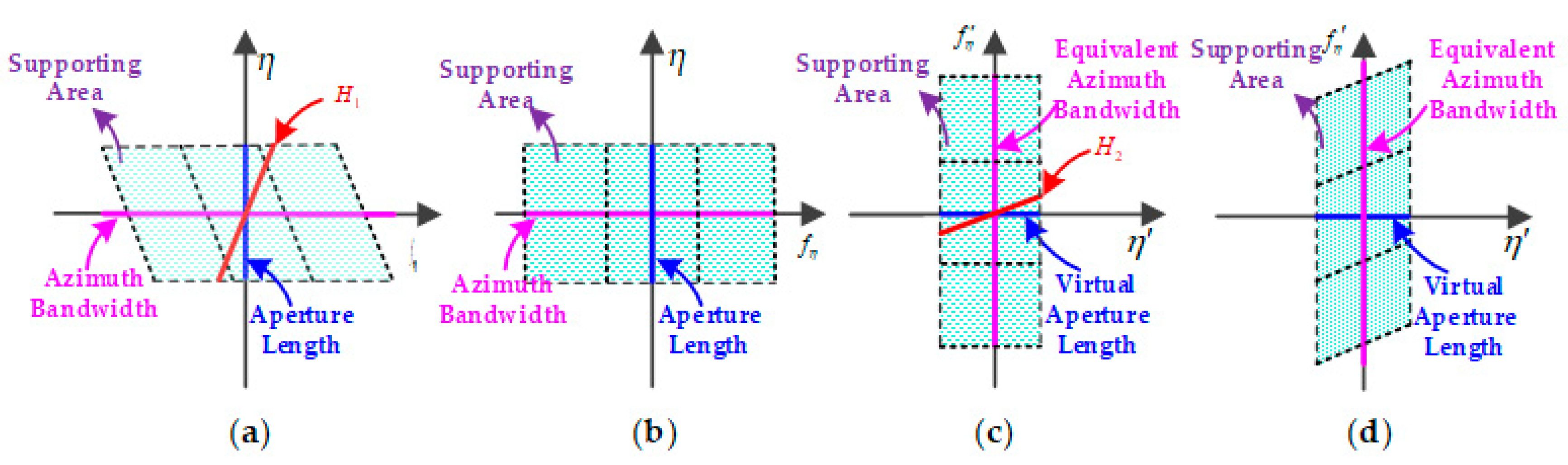
3.1. Frequency-Domain Processing
3.2. Time-Domain Processing
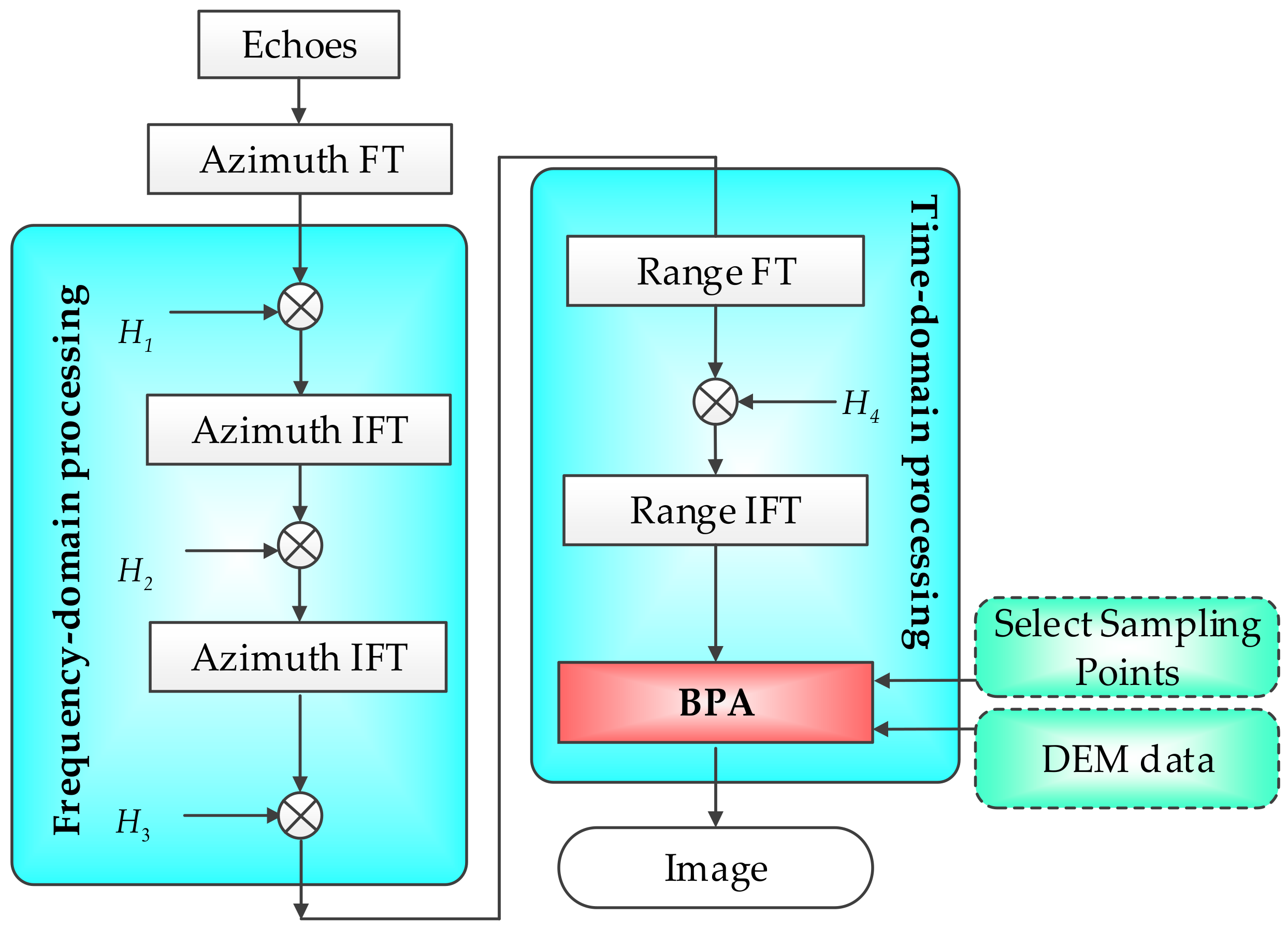
3.3. Flowchart of the EBP Algorithm
- Azimuth Fourier transform (FT). Apply an azimuth FT on the raw data;
- Deramping processing; the first step of the frequency-domain processing. Modulate the raw data with Equation (4);
- Equivalent Azimuth IFT; the second step of the frequency-domain processing. Apply the transformation in the data from the and coordinate, to the and coordinate;
- Residual phase compensation; the final step of the frequency-domain processing. Compensate the data with Equation (7) in the new azimuth frequency-domain;
- Azimuth IFT. Transform the data from the domain to domain;
- Second phase compensation. Compensate the data with Equation (9) in the new azimuth time-domain;
- Range FT. Apply a range of FT on the renovated data. Then, the range compression will be implemented in the range frequency-domain;
- Range compression. Compress the data in the range frequency-domain with Equation (11);
- Range IFT. Transform the data from the domain to domain;
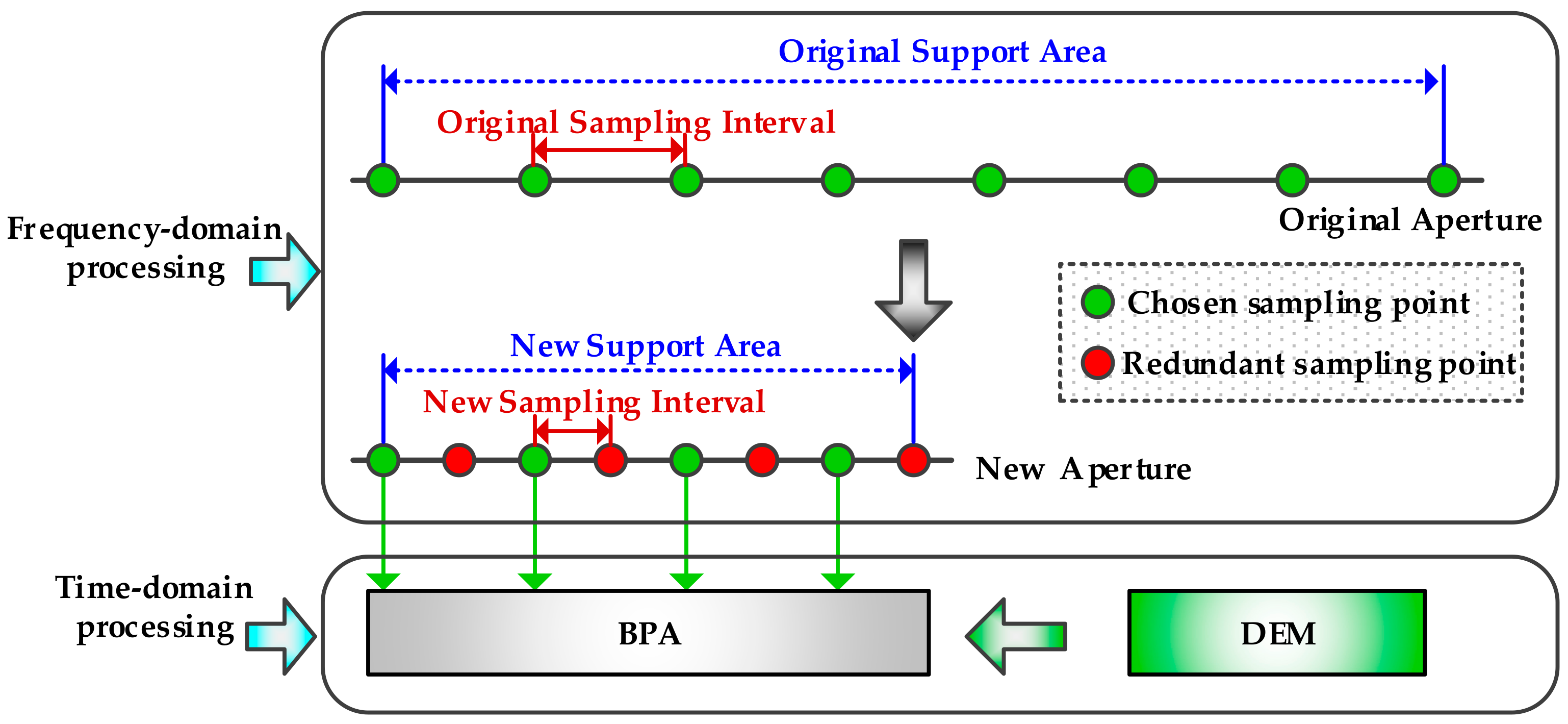
- Selection of samples. The important sampling points are selected appropriately, and the premise is that the echo signal will not alias the azimuth frequency-domain. In this way, the computational burden of the BP algorithm will be reduced;
- BP processing. Calculate the accurate slant range from each azimuth position to the targets, with the combination of the airborne acquisition scenarios and the DEM data. The other substeps in this step are similar to those of the classical BP processing.
4. Simulation Results
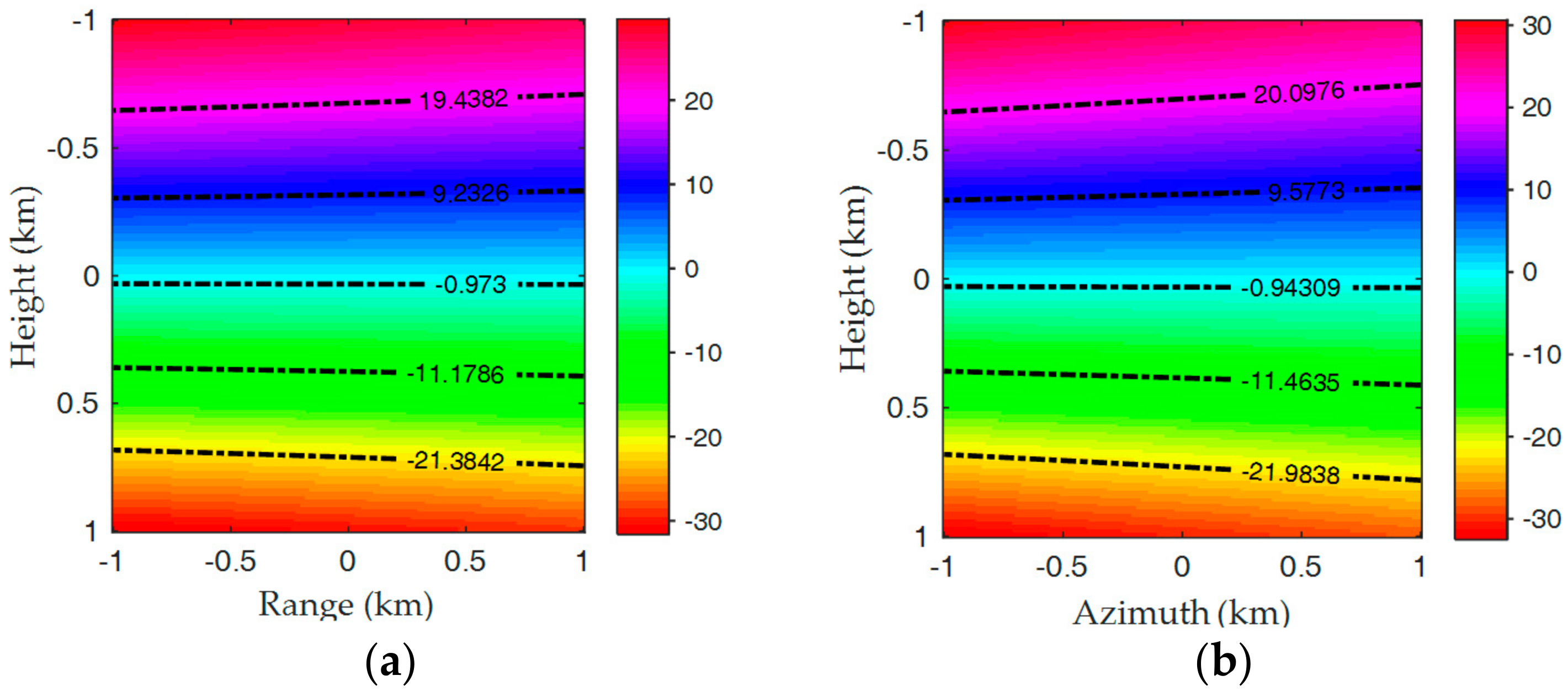
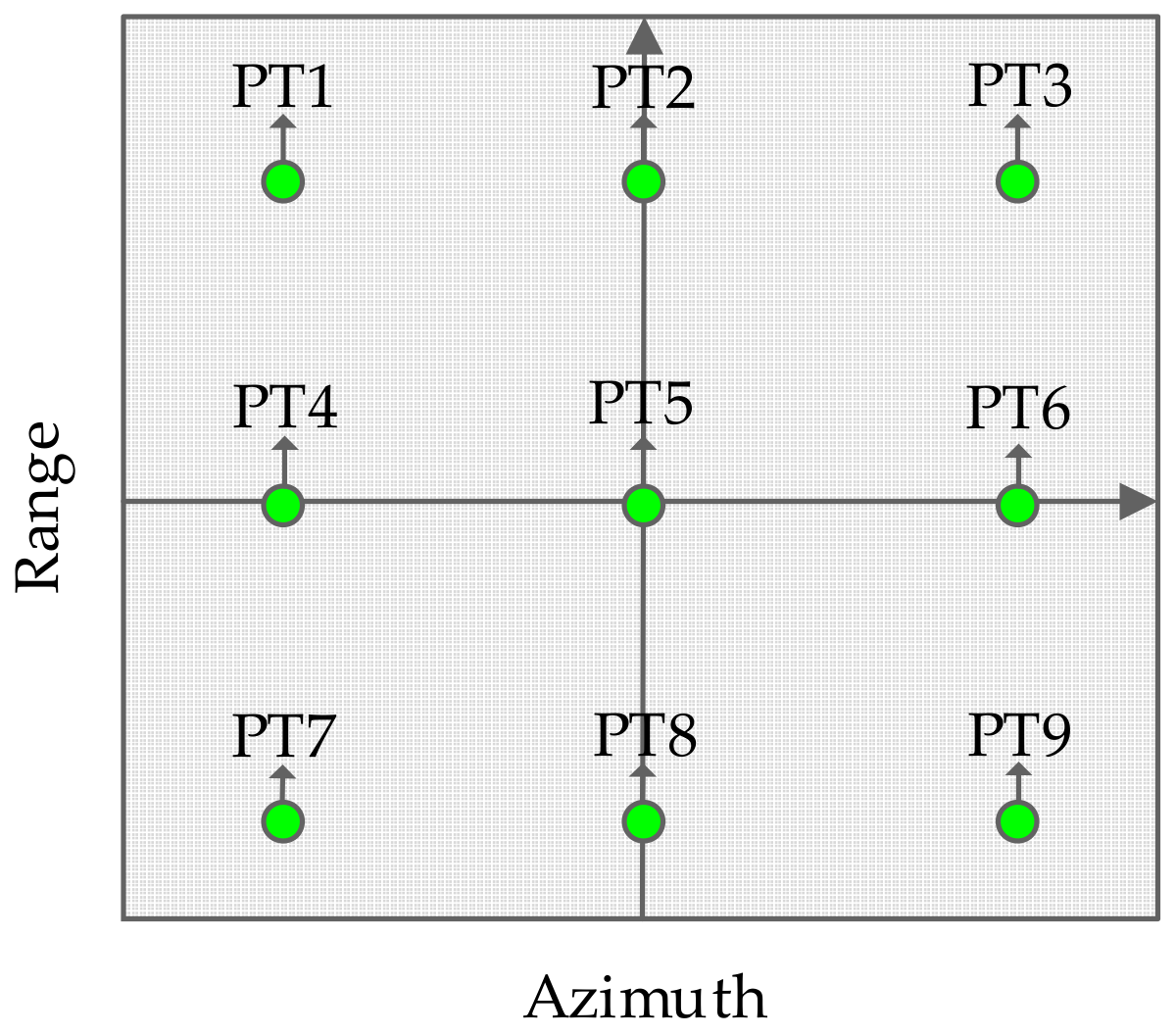
4.1. Spot Matrix Simulation Results
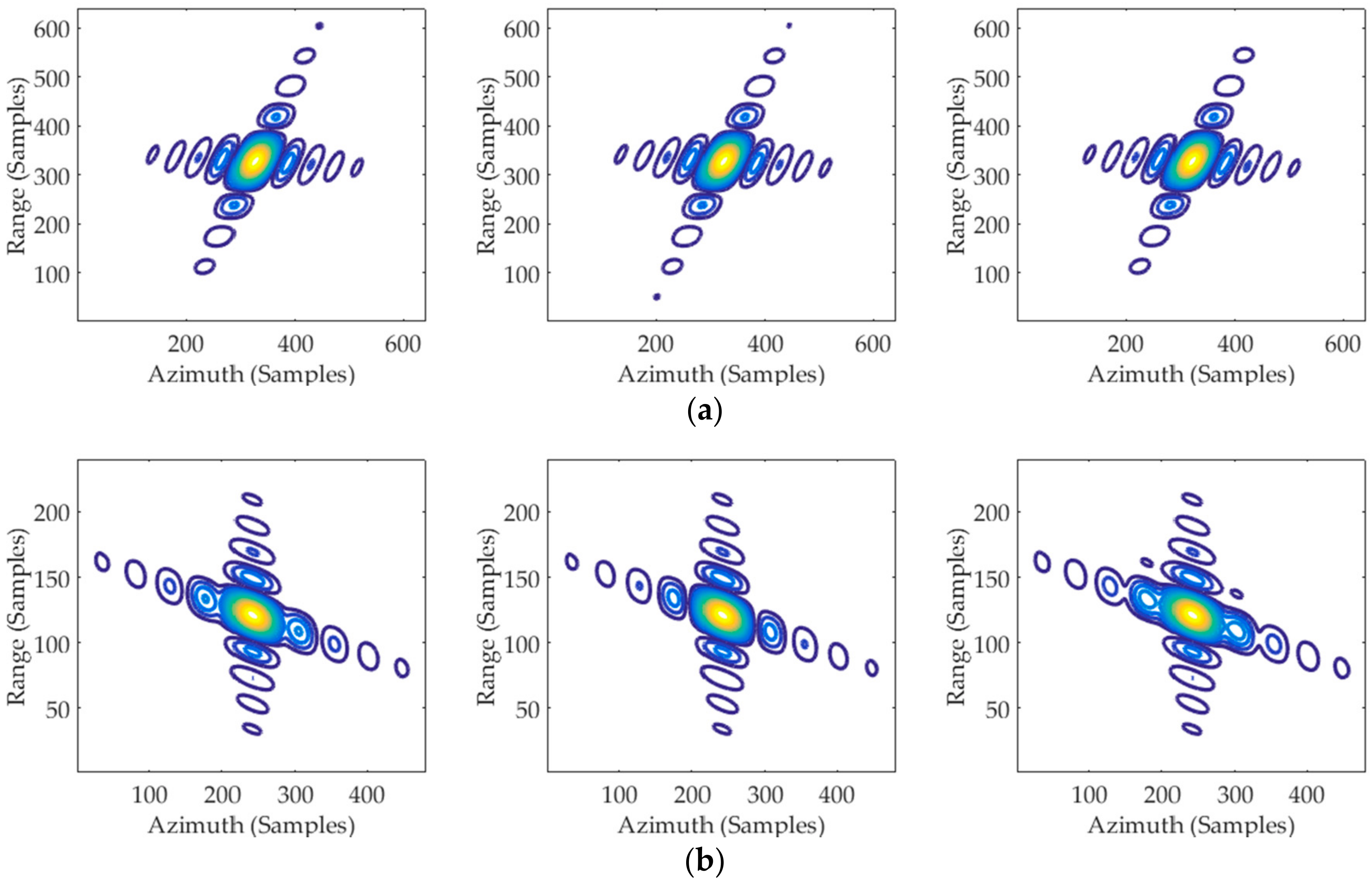
Case I
Case II
4.2. Scene Simulation Results
5. Discussion
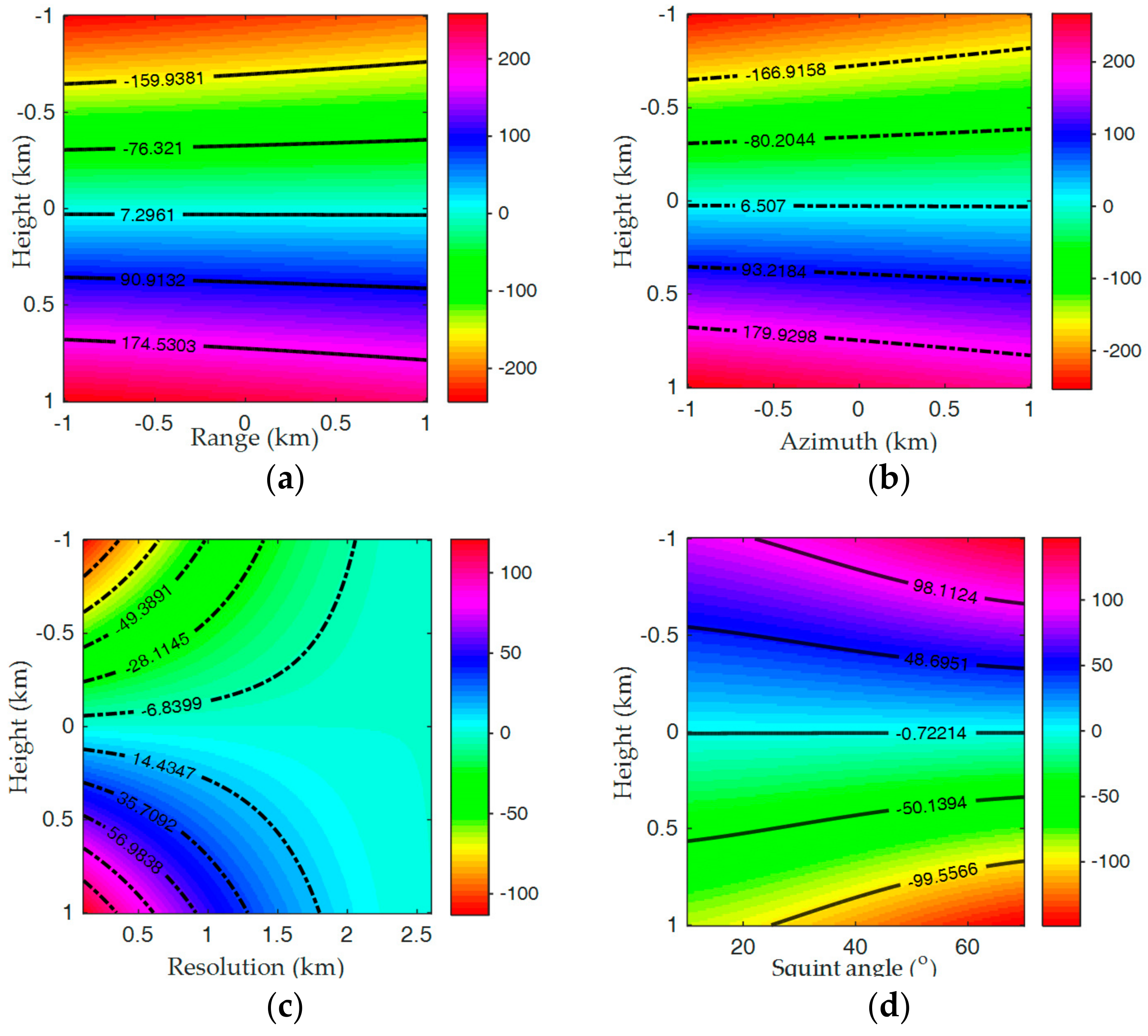
5.1. Parameter Selection
5.2. Computational Burden
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Sun, H.; Shimada, M.; Xu, F.; Xu, F. Recent Advances in Synthetic Aperture Radar Remote Sensing—Systems, Data Processing, and Applications. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2013–2016. [Google Scholar] [CrossRef]
- Carrara, W.G.; Majewski, R.M.; Goodman, R.S. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Dudczyk, J.; Kawalec, A. Optimizing the Minimum Cost Flow Algorithm for the Phase Unwrapping Process in SAR Radar. Bull. Pol. Acad. Sci. Tech. Sci. 2014, 62, 511–516. [Google Scholar] [CrossRef]
- Matuszewski, J. The Analysis of Modern Radar Signals Parameters in Electronic Intelligence System. In Proceedings of the 13th International Conference on Modern Problems of Radio Engineering, Telecommunications and Computer Science (TCSET), Lviv, Ukraine, 23–26 February 2016; pp. 298–302. [Google Scholar]
- Matuszewski, J.; Paradowski, L. The Knowledge Based Approach for Emitter Identification. In Proceedings of the 12th International Conference on Microwaves and Radar, Krakow, Poland, 20–22 May 1998; pp. 810–814. [Google Scholar]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 1999. [Google Scholar]
- Zhang, T.; Ding, Z.; Tian, W.; Zeng, T. A 2-D nonlinear chirp scaling algorithm for high squint GEO SAR imaging based on optimal azimuth polynomial compensation. IEEE J. Sel. Top. Appl. Earth Observat. Remote Sens. 2017, 10, 5724–5735. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Zhang, Y.; Li, Q.; Gu, Y.; Lin, C. Processing of monostatic SAR data with general configurations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6529–6546. [Google Scholar]
- Sun, G.C.; Wu, Y.; Wang, Y.; Xing, M.D.; Bao, Z. Full-aperture focusing of very high resolution spaceborne-squinted sliding spotlight SAR data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3309–3321. [Google Scholar] [CrossRef]
- Hobbs, S.; Mitchell, C.; Forte, B.; Holley, R.; Snapir, B.; Whittaker, P. System design for geosynchronous synthetic aperture radar missions. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7750–7763. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.; Liu, L. A New Analytical Model to Study the Ionospheric Effects on VHF/UHF Wideband SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4545–4557. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the Earth’s surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Fornaro, G.; Franceschetti, G.; Perna, S. Motion Compensation Errors: Effects on the accuracy of airborne SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1338–1352. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Cafforio, C.; Prati, C.; Rocca, E.C. SAR focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Sun, G.C.; Jiang, X.; Xing, M.D.; Qiao, Z.J.; Wu, Y.; Bao, Z. Focus improvement of highly squinted data based on azimuth nonlinear scaling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2308–2322. [Google Scholar] [CrossRef]
- Wong, F.W.; Yeo, T.S. New applications of nonlinear chirp scaling in SAR data processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 946–953. [Google Scholar] [CrossRef]
- Zeng, T.; Hu, C.; Wu, L.; Liu, L.; Tian, W.; Zhu, M.; Long, T. Extended NLCS algorithm of BiSAR systems with a squinted transmitter and a fixed receiver: Theory and experimental confirmation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5019–5030. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; So, H.C. Focusing high-resolution highly-squinted airborne SAR data with maneuvers. Remote Sens. 2018, 10, 862. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. An improved NLCS algorithm with capability analysis for one-stationary BiSAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Yang, J. Wide Nonlinear chirp scaling algorithm for spaceborne stripmap range sweep SAR imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6922–6936. [Google Scholar] [CrossRef]
- Sun, G.C.; Xing, M.D.; Wu, Y.; Wang, Y.; Yang, J.; Bao, Z. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and subband synthesis to process geosynchronous SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4868–4880. [Google Scholar]
- Li, D.; Lin, H.; Liu, H.; Liao, G.; Tan, X. Subaperture approach based on azimuth-dependent range cell migration correction and azimuth focusing parameter equalization for maneuvering high-squintmode SAR. IEEE Trans. Geosci. Remote Sens. 2017, 53, 6718–6734. [Google Scholar]
- Macedo, K.A.C.; Scheiber, R. Precise topography- and aperture-dependent motion compensation for airborne SAR. IEEE Trans. Geosci. Remote Sens. 2005, 2, 172–176. [Google Scholar]
- Prats, P.; Reigber, A.; Mallorqui, J.J. Topography-dependent motion compensation for repeat-pass interferometric SAR systems. IEEE Trans. Geosci. Remote Sens. 2005, 2, 206–210. [Google Scholar] [CrossRef]
- Yang, Z.M.; Sun, G.C.; Xing, M.D. A new fast back-projection algorithm using polar format algorithm. In Proceedings of the Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 373–376. [Google Scholar]
- Rodriguez-Cassola, M.; Prats, P.; Krieger, G.; Moreira, A. Efficient time-domain image formation with precise topography accommodation for general bistatic SAR configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2949–2966. [Google Scholar] [CrossRef]
- Gazdag, J.; Sguazzero, P. Migration of Seismic Data. Proc. IEEE. 1984, 72, 1302–1315. [Google Scholar] [CrossRef]
- Seger, O.; Herberthson, M.; Hellsten, H. Real-time SAR processsing of low frequency ultra wideband radar data. In Proceedings of the EUSAR, Friedrichshafen, Germany, 25–27 May 1998. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Multibaseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
- Ferraiuolo, G.; Meglio, F.; Pascazio, V.; Schirinzi, G. DEM reconstruction accuracy in multichannel SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 191–201. [Google Scholar] [CrossRef]
- Shao, Y.F.; Wang, R.; Deng, Y.K.; Liu, Y.; Chen, R.; Liu, G.; Balz, T.; Loffeld, O. Digital elevation model reconstruction in multichannel spaceborne/stationary SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2080–2084. [Google Scholar] [CrossRef]
- Nilsson, S. Application of Fast Backprojection Techniques for Some Inverse Problems in Integral Geometry. Ph.D. Thesis 499, Linkoping University, Linkoping, Sweden, 1997. [Google Scholar]
- Ulander, L.; Hellsten, H.; Stenström, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.; Glennie, C.; Wang, G.; Lu, Z.; Fernandez-Diaz, J.C. Airborne DInSAR results using time-domain backprojection algorithm: A case study over the slumgullion landslide in Colorado with validation using spaceborne SAR, airborne LiDAR, and ground-based observations. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 108, 4987–5000. [Google Scholar] [CrossRef]
- Heng, Z.; Jiangwen, T.; Robert, W.; Yunkai, D.; Wei, W.; Ning, L. An accelerated backprojection algorithm for monostatic and bistatic SAR processing. Remote Sens. 2018, 10, 140. [Google Scholar] [CrossRef]
- Tang, J.; Deng, Y.; Wang, R.; Zhao, S.; Li, N.; Wang, W. A weighted backprojection algorithm for azimuth multichannel SAR imaging. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1265–1269. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, S.; Zhao, L.; Xing, M. Coherent Auto-Calibration of APE and NsRCM under Fast Back-Projection Image Formation for Airborne SAR Imaging in Highly-Squint Angle. Remote Sens. 2018, 10, 321. [Google Scholar] [CrossRef]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. Fast time-domain algorithms for UWB bistatic SAR processing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1982–1994. [Google Scholar] [CrossRef]
- Walterscheid, I.; Espeter, T.; Brenner, A.R.; Klare, J.; Ender, J.H.G.; Nies, H.; Wang, R.; Loffeld, O. Bistatic SAR experiments with PAMIR and TerraSAR-x; setup, processing, and image results. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3268–3279. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, R.; Deng, Y.; Liu, Y.; Chen, R.; Liu, G.; Loffeld, O. Fast backprojection algorithm for bistatic SAR imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1080–1084. [Google Scholar] [CrossRef]
- Duque, S.; Lopez-Dekker, P.; Mallorqui, J.J. Single-pass bistatic SAR interferometry using fixed-receiver configurations: Theory and experimental validation. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2740–2749. [Google Scholar] [CrossRef]
- Peng, X.; Wang, Y.; Hong, W.; Wu, Y. Autonomous Navigation Airborne Forward-Looking SAR High Precision Imaging with Combination of Pseudo-Polar Formatting and Overlapped Sub-Aperture Algorithm. Remote Sens. 2013, 11, 6063–6078. [Google Scholar] [CrossRef]
- Xu, W.; Deng, Y.; Huang, P.; Wang, R. Full-aperture SAR data focusing in the spaceborne squinted sliding-spotlight mode. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4596–4607. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.C. Acceleration model analyses and imaging algorithm for highly squinted airborne spotlight mode SAR with maneuvers. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR data focusing based on a two-step processing approach. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1993–2004. [Google Scholar] [CrossRef]
- Yang, M.D.; Zhu, D.Y.; Song, W. Comparison of two-step and one-step motion compensation algorithms for airborne synthetic aperture radar. Electron. Lett. 2015, 51, 1108–1110. [Google Scholar] [CrossRef]
- Lanari, R.; Zoffoli, S.; Sansosti, E.; Fornaro, G.; Serafino, F. New approach for hybrid strip-map/spotlight SAR data focusing. Proc. Inst. Elect. Eng.-Radar Sonar Navig. 2001, 148, 363–372. [Google Scholar] [CrossRef]
- Sun, G.C.; Jiang, X.; Xing, M.D.; Xia, X.G.; Wu, Y.R.; Bao, Z. Beam steering SAR data processing by a generalized PFA. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4366–4377. [Google Scholar] [CrossRef]
- Sun, G.C.; Xing, M.D.; Xia, X.G.; Yang, J.; Wu, Y.R.; Bao, Z. A unified focusing algorithm for several modes of SAR based on FrFT. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3139–3155. [Google Scholar] [CrossRef]
- Xie, H.; Shi, S.; An, D.; Wang, G.; Wang, G.; Xiao, H.; Huang, X.; Zhou, Z.; Xie, C.; Wang, F.; et al. Fast factorized backprojection algorithm for one-stationary bistatic spotlight circular SAR image formation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1494–1510. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Carrier frequency | 9.65 GHz |
| Pulse duration | 2.5 μs |
| Pulse Bandwidth | 300 MHz |
| Sampling frequency | 420 MHz |
| Reference slant range | 25.0 km |
| Altitude | 8.0 km |
| Velocity vector | (0, 120, 0) m/s |
| Method | Target | IRW (m) | PSLR (dB) | ISLR (dB) |
|---|---|---|---|---|
| Proposed algorithm | PT1 | 0.687 | −13.22 | −10.03 |
| PT5 | 0.681 | −13.27 | −10.05 | |
| PT9 | 0.679 | −13.24 | −10.02 | |
| CSA | PT1 | 0.795 | −7.23 | −6.65 |
| PT5 | 0.682 | −13.25 | −10.06 | |
| PT9 | 0.813 | −7.14 | −6.37 |
| Method | Target | IRW (m) | PSLR (dB) | ISLR (dB) |
|---|---|---|---|---|
| Proposed algorithm | PT1 | 0.474 | −13.27 | −10.07 |
| PT5 | 0.472 | −13.31 | −10.04 | |
| PT9 | 0.471 | −13.30 | −10.01 | |
| PMA | PT1 | 0.613 | −4.93 | −4.64 |
| PT5 | 0.423 | −13.32 | −10.06 | |
| PT9 | 0.546 | −10.35 | −7.58 |
| Data Size in Azimuth (×103) | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| BPA/CSA | 150.30 | 290.11 | 560.73 | 1084.92 | 2101.48 |
| Proposed/CSA | 12.07 | 22.15 | 41.64 | 79.39 | 152.59 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Tang, S.; Zhang, L.; Guo, P. Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle. Remote Sens. 2018, 10, 1275. https://doi.org/10.3390/rs10081275
Lin C, Tang S, Zhang L, Guo P. Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle. Remote Sensing. 2018; 10(8):1275. https://doi.org/10.3390/rs10081275
Chicago/Turabian StyleLin, Chunhui, Shiyang Tang, Linrang Zhang, and Ping Guo. 2018. "Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle" Remote Sensing 10, no. 8: 1275. https://doi.org/10.3390/rs10081275
APA StyleLin, C., Tang, S., Zhang, L., & Guo, P. (2018). Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle. Remote Sensing, 10(8), 1275. https://doi.org/10.3390/rs10081275





