Seabed Mapping in Coastal Shallow Waters Using High Resolution Multispectral and Hyperspectral Imagery
Abstract
1. Introduction
2. Materials and Methods
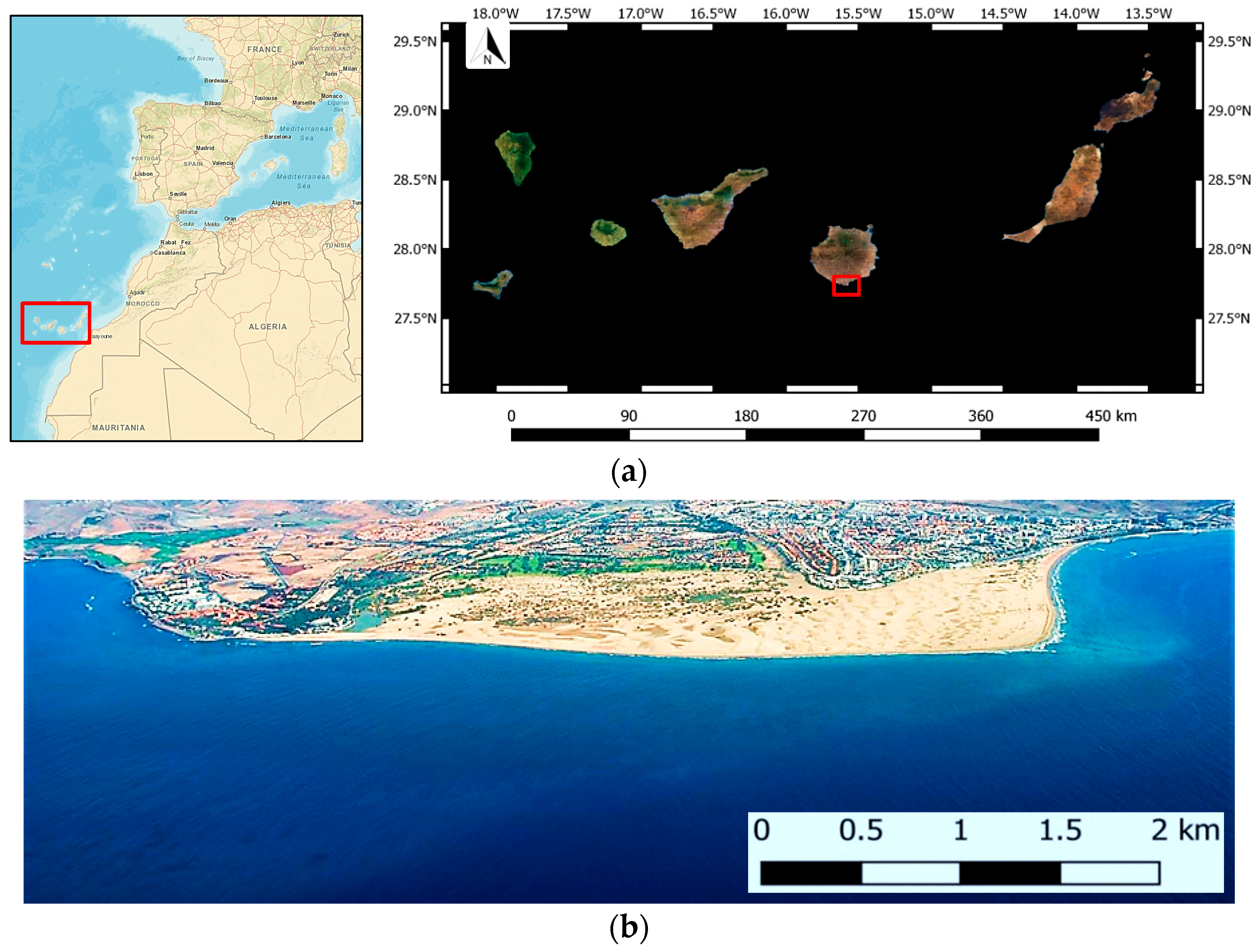
2.1. Study Area
2.2. Multisensor Remotely Sensed Data
2.3. In-Situ Measurements
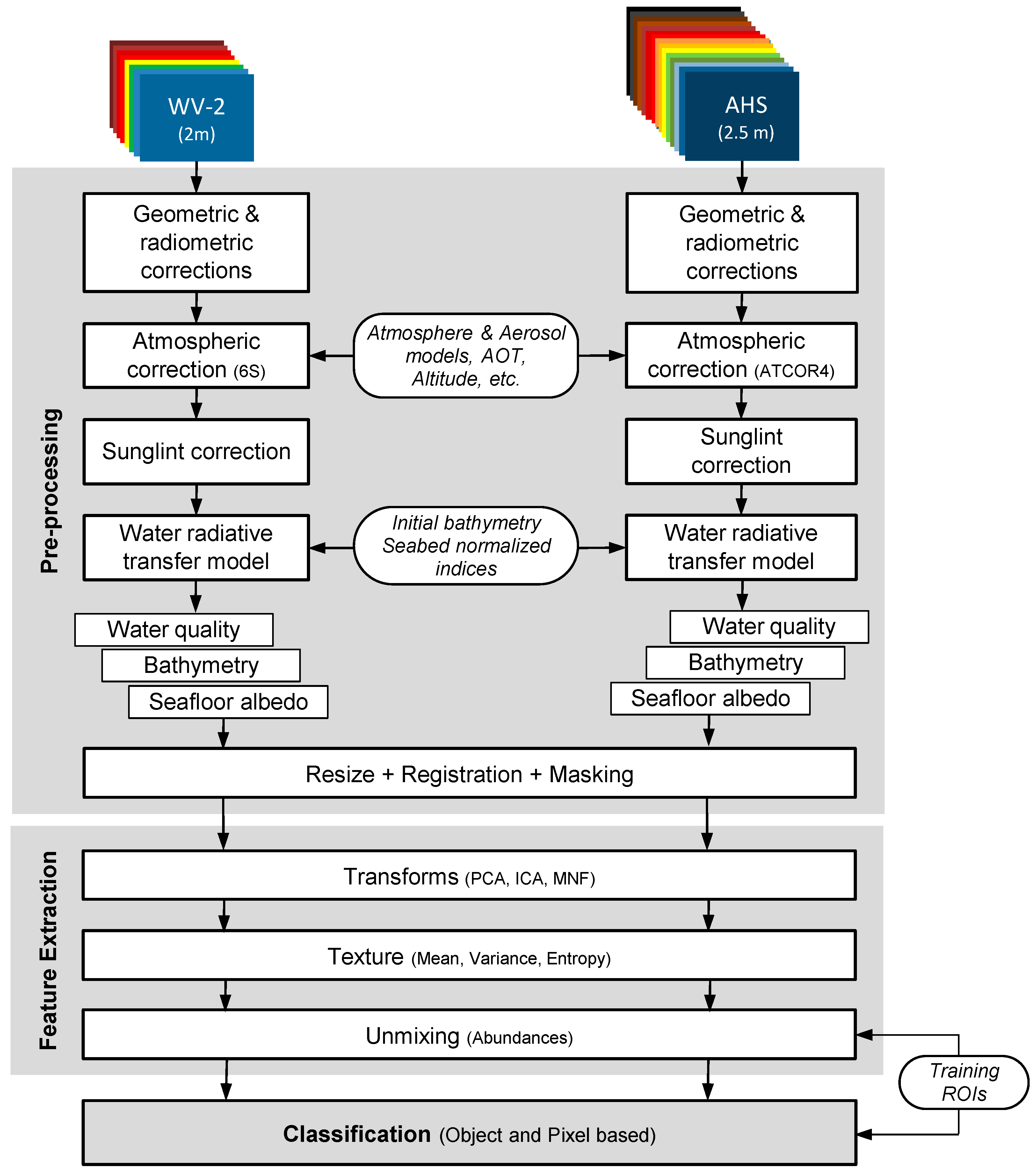
2.4. Mapping Methodology
2.4.1. Multisensor Imagery Corrections
2.4.2. Feature Extraction
2.4.3. Classification
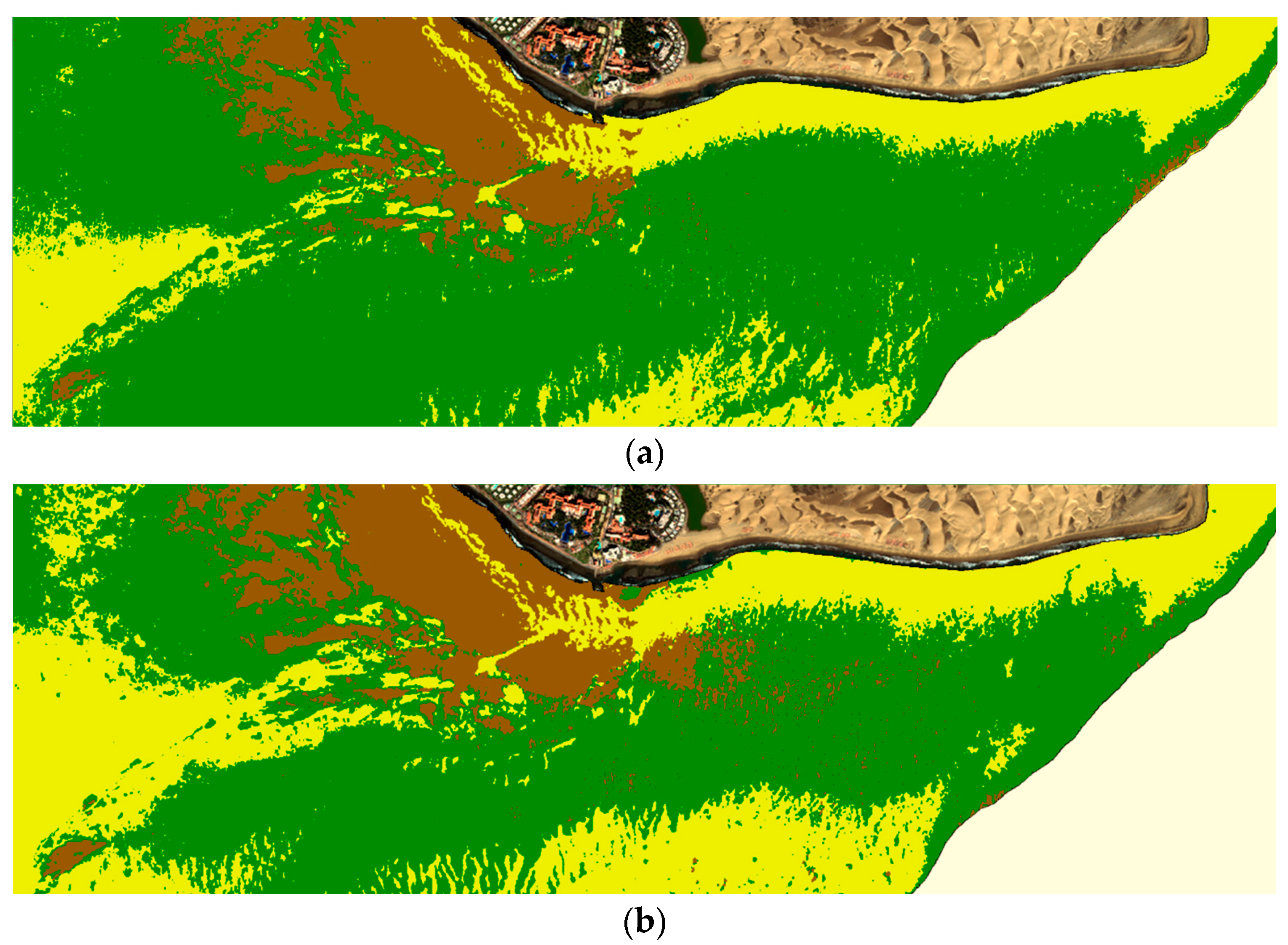
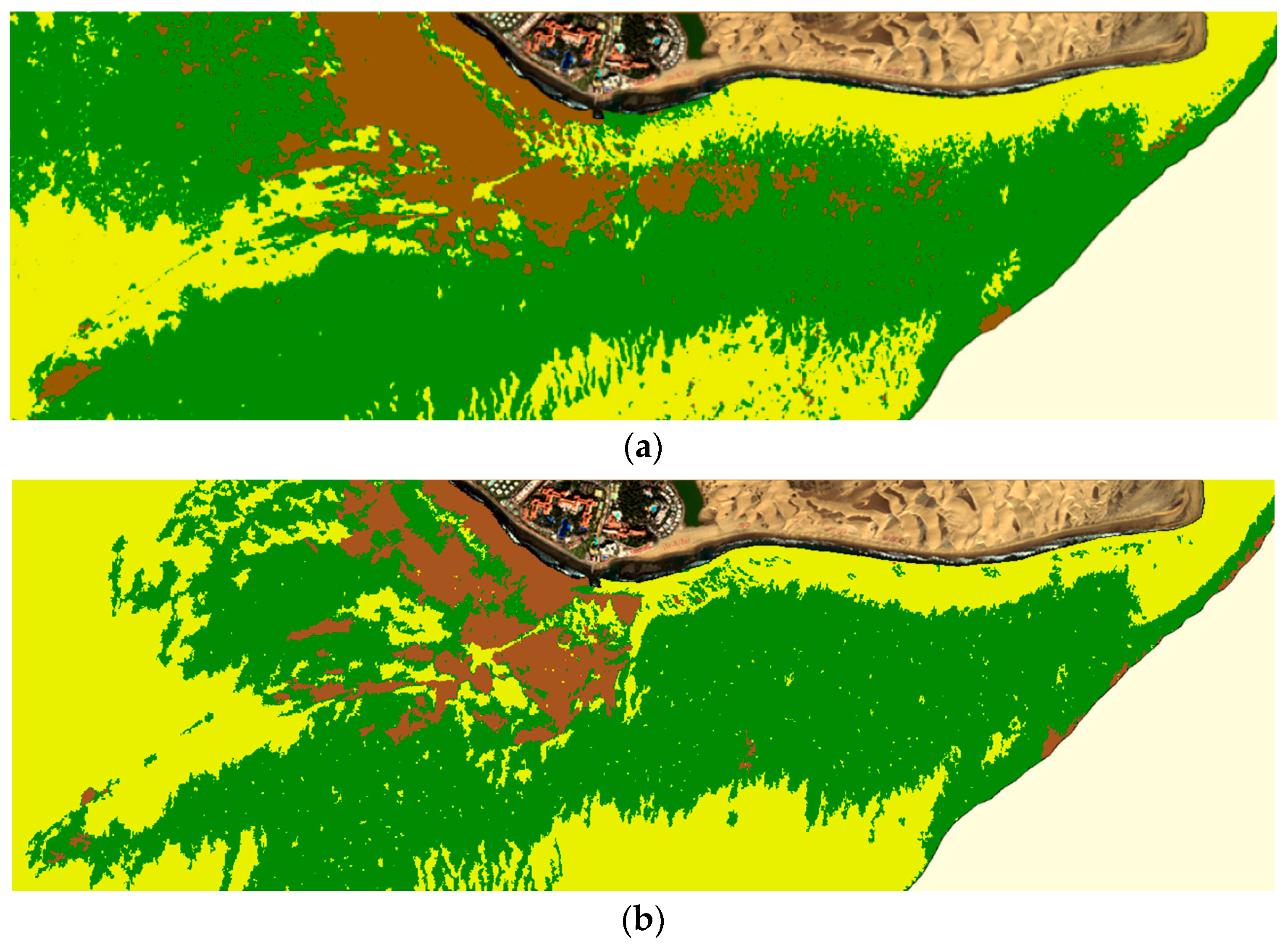
3. Results and Discussion
- Spectral bands after atmospheric and sunglint corrections.
- Components after the application of three-dimensionality reduction techniques (PCA, ICA, and MNF). The complete dataset and a reduced number of bands or components were both tested.
- Abundance maps of each class after the application of linear unmixing techniques.
- Texture information (mean and variance) extracted from the first PCA/MNF component.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horning, E.; Robinson, J.; Sterling, E.; Turner, W.; Spector, S. Remote Sensing for Ecology and Conservation; Oxford University Press: New York, NY, USA, 2010; ISBN 978-0-19-921995-7. [Google Scholar]
- Wang, Y. Remote Sensing of Coastal Environments; Taylor and Francis Series; CRC Press: Boca Raton, FL, USA, 2010; ISBN 978-1-42-009442-8. [Google Scholar]
- Hossain, M.S.; Bujang, J.S.; Zakaria, M.H.; Hashim, M. The application of remote sensing to seagrass ecosystems: An overview and future research prospects. Int. J. Remote Sens. 2015, 36, 61–114. [Google Scholar] [CrossRef]
- Lyons, M.; Phinn, S.; Roelfsema, C. Integrating Quickbird multi-spectral satellite and field data: Mapping bathymetry, seagrass cover, seagrass species and change in Moreton bay, Australia in 2004 and 2007. Remote Sens. 2011, 3, 42–64. [Google Scholar] [CrossRef]
- Knudby, A.; Nordlund, L. Remote Sensing of Seagrasses in a Patchy Multi-Species Environment. Int. J. Remote Sens. 2011, 32, 2227–2244. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-resolution maps of bathymetry and benthic habitats in shallow-water environments using multispectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef]
- Rani, N.; Mandla, V.R.; Singh, T. Evaluation of atmospheric corrections on hyperspectral data with special reference to mineral mapping. Geosci. Front. 2017, 8, 797–808. [Google Scholar] [CrossRef]
- Chavez, P.S. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Chavez, P.S. Image-Based Atmospheric Corrections. Revisited and Improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Bernstein, L.S.; Adler-Golden, S.M.; Jin, X.; Gregor, B.; Sundberg, R.L. Quick atmospheric correction (QUAC) code for VNIR-SWIR spectral imagery: Algorithm details. In Proceedings of the IEEE Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Shanghai, China, 4–7 June 2012. [Google Scholar]
- Marcello, J.; Eugenio, F.; Perdomo, U.; Medina, A. Assessment of atmospheric algorithms to retrieve vegetation in natural protected areas using multispectral high resolution imagery. Sensors 2016, 16, 1624. [Google Scholar] [CrossRef] [PubMed]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Felde, G.; Gardner, J.; et al. Atmospheric Correction for Short-Wave Spectral Imagery based on MODTRAN4. In Imaging Spectrometry V; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3753. [Google Scholar]
- Gao, B.-C.; Davis Curtiss, O.; Goetz, A.F.H. A review of atmospheric correction techniques for hyperspectral remote sensing of land surfaces and ocean colour. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Denver, CO, USA, 31 July–4 August 2006. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J.; Rodríguez-Esparragón, D. Benthic Habitat Mapping Using Multispectral High-Resolution Imagery: Evaluation of Shallow Water Atmospheric Correction Techniques. Sensors 2017, 17, 2639. [Google Scholar] [CrossRef] [PubMed]
- Kay, S.; Hedley, J.; Lavender, S. Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: A Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Simple and robust removal of sun glint for mapping shallow-water bentos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using Aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 72–82. [Google Scholar] [CrossRef]
- Traganos, D.; Reinartz, P. Mapping Mediterranean seagrasses with Sentinel-2 imagery. Mar. Pollut. Bull. 2017. [Google Scholar] [CrossRef] [PubMed]
- Manessa, M.D.M.; Haidar, M.; Budhiman, S.; Winarso, G.; Kanno, A.; Sagawa, T.; Sekine, M. Evaluating the performance of Lyzenga’s water column correction in case-1 coral reef water using a simulated Wolrdview-2 imagery. In Proceedings of IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol; IOP Publishing: Bristol, UK, 2016; Volume 47. [Google Scholar] [CrossRef]
- Wicaksono, P. Improving the accuracy of Multispectral-based benthic habitats mapping using image rotations: The application of Principle Component Analysis and Independent Component Analysis. Eur. J. Remote Sens. 2016, 49, 433–463. [Google Scholar] [CrossRef]
- Tamondong, A.M.; Blanco, A.C.; Fortes, M.D.; Nadaoka, K. Mapping of Seagrass and Other Bentic Habitat in Balinao, Pangasinan Using WorldView-2 Satellite Image. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013; pp. 1579–1582. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Garcia, R.; Lee, A.; Hochberg, E.J. Hyperspectral Shallow-Water Remote Sensing with an Enhanced Benthic Classifier. Remote Sens. 2018, 10, 147. [Google Scholar] [CrossRef]
- Loisel, H.; Stramski, D.; Dessailly, D.; Jamet, C.; Li, L.; Reynolds, R.A. An Inverse Model for Estimating the Optical Absorption and Backscattering Coefficients of Seawater From Remote-Sensing Reflectance Over a Broad Range of Oceanic and Coastal Marine Environments. J. Geophys. Res. Oceans 2018, 123, 2141–2171. [Google Scholar] [CrossRef]
- Barnes, B.B.; Garcia, R.; Hu, C.; Lee, Z. Multi-band spectral matching inversion algorithm to derive water column properties in optically shallow waters: An optimization of parameterization. Remote Sens. Environ. 2018, 204, 424–438. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A. Advanced spectral classifiers for hyperspectral images. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- Bioucas, J.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.M.; Chollett, I.; Harborne, A.R.; Heron, S.F.; Weeks, S.; Skirving, W.J.; Strong, A.E.; Eakin, C.M.; Christensen, T.R.L.; et al. Remote Sensing of Coral Reefs for Monitoring and Management: A Review. Remote Sens. 2016, 8, 118. [Google Scholar] [CrossRef]
- Roelfsema, C.; Kovacs, E.; Ortiz, J.C.; Wolff, N.H.; Callaghan, D.; Wettle, M.; Ronan, M.; Hamylton, S.M.; Mumby, P.J.; Phinn, S. Coral reef habitat mapping: A combination of object-based image analysis and ecological modelling. Remote Sens. Environ. 2018, 208, 27–41. [Google Scholar] [CrossRef]
- Mohamed, H.; Nadaoka, K.; Nakamura, T. Assessment of Machine Learning Algorithms for Automatic Benthic Cover Monitoring and Mapping Using Towed Underwater Video Camera and High-Resolution Satellite Images. Remote Sens. 2018, 10, 773. [Google Scholar] [CrossRef]
- Purkis, S.J. Remote Sensing Tropical Coral Reefs: The View from Above. Annu. Rev. Mar. Sci. 2018, 10, 149–168. [Google Scholar] [CrossRef] [PubMed]
- Petit, T.; Bajjouk, T.; Mouquet, P.; Rochette, S.; Vozel, B.; Delacourt, C. Hyperspectral remote sensing of coral reefs by semi-analytical model inversion—Comparison of different inversion setups. Remote Sens. Environ. 2017, 190, 348–365. [Google Scholar] [CrossRef]
- Zhang, C. Applying data fusion techniques for benthic habitat mapping and monitoring in a coral reef ecosystem. ISPRS J. Photogramm. Remote Sens. 2015, 104, 213–223. [Google Scholar] [CrossRef]
- Leiper, I.A.; Phinn, S.R.; Roelfsema, C.M.; Joyce, K.E.; Dekker, A.G. Mapping Coral Reef Benthos, Substrates, and Bathymetry, Using Compact Airborne Spectrographic Imager (CASI) Data. Remote Sens. 2014, 6, 6423–6445. [Google Scholar] [CrossRef]
- Roelfsema, C.; Kovacs, E.M.; Saunders, M.I.; Phinn, S.; Lyons, M.; Maxwell, P. Challenges of remote sensing for quantifying changes in large complex seagrass environments. Estuar. Coast. Shelf Sci. 2013, 133, 161–171. [Google Scholar] [CrossRef]
- Baumstark, R.; Duffey, R.; Pu, R. Mapping seagrass and colonized hard bottom in Springs Coast, Florida using WorldView-2 satellite imagery. Estuar. Coast. Shelf Sci. 2016, 181, 83–92. [Google Scholar] [CrossRef]
- Koedsin, W.; Intararuang, W.; Ritchie, R.J.; Huete, A. An Integrated Field and Remote Sensing Method for Mapping Seagrass Species, Cover, and Biomass in Southern Thailand. Remote Sens. 2016, 8, 292. [Google Scholar] [CrossRef]
- Uhrin, A.V.; Townsend, P.A. Improved seagrass mapping using linear spectral unmixing of aerial photographs. Estuar. Coast. Shelf Sci. 2016, 171, 11–22. [Google Scholar] [CrossRef]
- Valle, M.; Palà, V.; Lafon, V.; Dehouck, A.; Garmendia, J.M.; Borja, A.; Chust, G. Mapping estuarine habitats using airborne hyperspectral imagery, with special focus on seagrass meadows. Estuar. Coast. Shelf Sci. 2015, 164, 433–442. [Google Scholar] [CrossRef]
- Zhang, C.; Selch, D.; Xie, Z.; Roberts, C.; Cooper, H.; Chen, G. Object-based benthic habitat mapping in the Florida Keys from hyperspectral imagery. Estuar. Coast. Shelf Sci. 2013, 134, 88–97. [Google Scholar] [CrossRef]
- De Miguel, E.; Fernández-Renau, A.; Prado, E.; Jiménez, M.; Gutiérrez, O.; Linés, C.; Gómez, J.; Martín, A.I.; Muñoz, F. A review of INTA AHS PAF. EARSeL eProc. 2014, 13, 20–29. [Google Scholar]
- Gesplan. Plan Regional de Ordenación de la Acuicultura de Canarias. Tomo I: Memoria de Información del Medio Natural Terrestre y Marino. Plano de Sustratos de Gran Canaria; Gobierno de Canarias: Las Palmas de Gran Canaria, Spain, 2013; pp. 1–344. [Google Scholar]
- Digitalglobe. Accuracy of Worldview Products. White Paper. 2016. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/38/DG_ACCURACY_WP_V3.pdf (accessed on 1 June 2018).
- Vermote, E.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second Simulation of a Satellite Signal in the Solar Spectrum—Vector (6SV); 6S User Guide Version 3; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2006.
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J. Validation of vector version of 6s radiative transfer code for atmospheric correction of satellite data. Parth radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Eugenio, F.; Marcello, J.; Medina, A. Automatic sunglint removal of multispectral WV-2 imagery for retrieving coastal shallow water parameters. Remote Sens. 2016, 8, 37. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Heylen, R.; Burazerović, D.; Scheunders, P. Fully constrained least squares spectral unmixing by simplex projection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4112–4122. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/Topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Ibarrola-Ulzurrun, E.; Marcello, J.; Gonzalo-Martin, C. Assessment of Component Selection Strategies in Hyperspectral Imagery. Entropy 2017, 19, 666. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis, 5th ed.; Springer: Berlin, Germany, 2013; ISBN 978-3-54-029711-6. [Google Scholar]
- Benediktsson, J.A.; Ghamisi, P. Spectral-Spatial Classification of Hyperspectral Remote Sensing Images; Artech House: Boston, MA, USA, 2015; ISBN 978-1-60-807812-7. [Google Scholar]
- Li, C.; Yin, J.; Zhao, J. Using improved ICA method for hyperspectral data classification. Arab. J. Sci. Eng. 2014, 39, 181–189. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S.E. Minimum noise fraction versus principal component analysis as a preprocessing step for hyperspectral imagery denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Tso, B.; Mather, P.M. Classification Methods for Remotely Sensed Data; Taylor and Francis Inc.: New York, NY, USA, 2009; ISBN 978-1-42-009072-7. [Google Scholar]
- Li, M.; Zhang, S.; Zhang, B.; Li, S.; Wu, C. A review of remote sensing image classification technique: The role of spatio-contextual information. Eur. J. Remote Sens. 2014, 47, 389–411. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: Berlin, Germany, 1999; ISBN 978-1-47-573264-1. [Google Scholar]
- Yu, X.; Wu, X.; Luo, C.; Ren, P. Deep learning in remote sensing scene classification: A data augmentation enhanced convolutional neural network framework. GISci. Remote Sens. 2017, 54, 741–758. [Google Scholar] [CrossRef]
- Maulik, U.; Chakraborty, D. Remote Sensing Image Classification: A survey of support-vector-machine-based advanced techniques. IEEE Geosci. Remote Sens. Mag. 2017, 5, 33–52. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Support vector machines for classification in remote sensing. Int. J. Remote Sens. 2005, 26, 1007–1011. [Google Scholar] [CrossRef]
- Marcello, J.; Eugenio, F.; Marqués, F.; Martín, J. Precise classification of coastal benthic habitats using high resolution Worldview-2 imagery. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Ibarrola-Ulzurrun, E.; Gonzalo-Martín, C.; Marcello, J. Vulnerable land ecosystems classification using spatial context and spectral indices. In Earth Resources and Environmental Remote Sensing/GIS Applications VIII, Proceedings of the SPIE Remote Sensing, Warsaw, Poland, 11–14 September 2017; SPIE: Bellingham, WA, USA; doi:10.1117/12.2278496. [Google Scholar]
- Baatz, M.; Schape, A. Multiresolution segmentation an optimization approach for high quality multi scale image segmentation. In Proceedings of the Angewandte Geographische Informations Verarbeitung XII, Wichmann Verlag, Karlsruhe, Germany, 30 June 2000. [Google Scholar]
- Jin, X. Segmentation-Based Image Processing System. U.S. Patent 8,260,048, 4 September 2012. [Google Scholar]







| Sensor | Spectral Band | Wavelength (nm) | Bandwidth (nm) |
|---|---|---|---|
| AHS | Visible and Near-IR (20 channels) | 434–1015 | 28–30 |
| WV-2 | Coastal Blue | 400–450 | 47.3 |
| Blue | 450–510 | 54.3 | |
| Green | 510–580 | 63.0 | |
| Yellow | 585–625 | 37.4 | |
| Red | 630–690 | 57.4 | |
| Red-edge | 705–745 | 39.3 | |
| Near-IR 1 | 770–895 | 98.9 | |
| Near-IR 2 | 860–1040 | 99.6 | |
| Panchromatic | 450–800 | 284.6 |
| Sensor | Input | ML | SVM | SAM |
|---|---|---|---|---|
| AHS | AC | 88.87 | 91.34 | 58.13 |
| AC+SC | 91.81 | 92.01 | 58.35 | |
| AC+SC+WCC | 82.42 | 84.66 | 40.44 | |
| WV-2 | AC | 88.08 | 74.66 | 54.68 |
| AC+SC | 88.66 | 80.63 | 58.37 | |
| AC+SC+WCC | 76.76 | 69.17 | 45.76 |
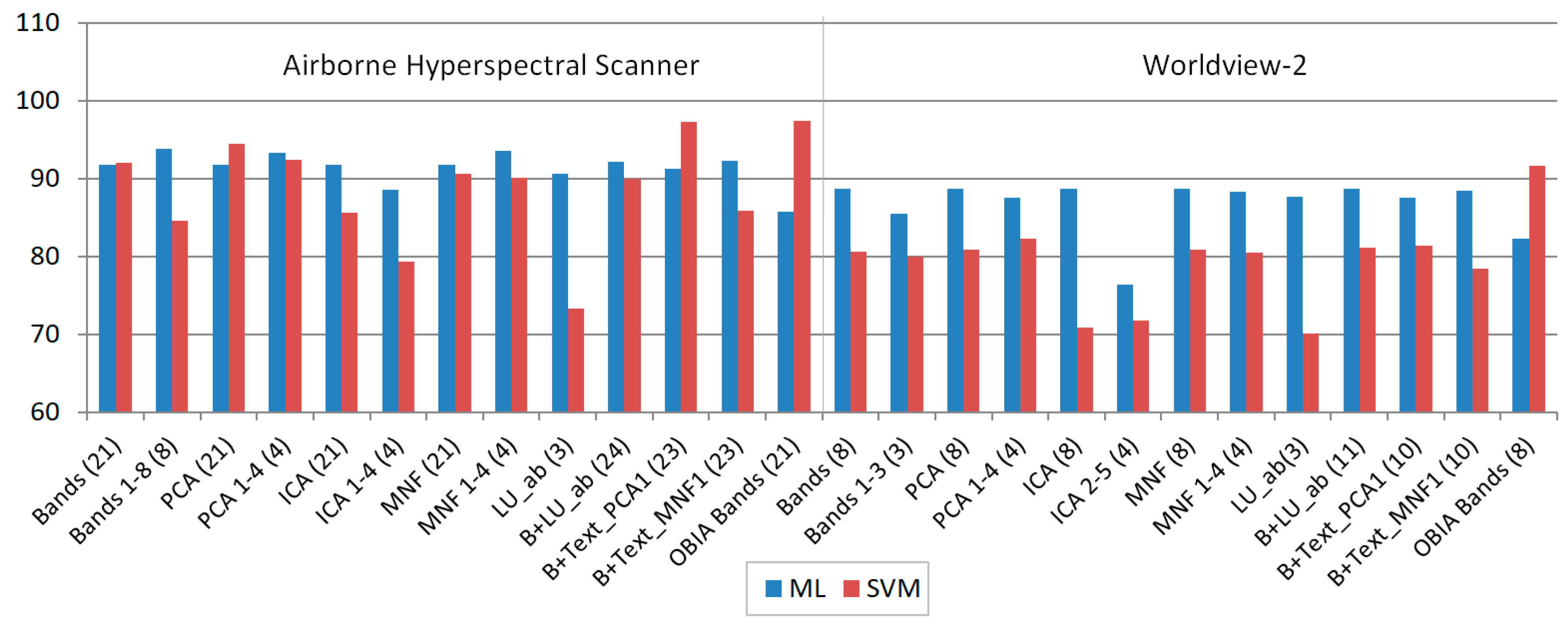
| Sensor | Input | ML | SVM | SAM | Average |
|---|---|---|---|---|---|
| AHS | Bands (21) | 91.81 | 92.01 | 58.35 | 80.72 |
| Bands 1-8 (8) | 93.77 | 84.56 | 57.36 | 78.56 | |
| PCA (21) | 91.81 | 94.48 | 47.39 | 77.89 | |
| PCA 1-4 (4) | 93.25 | 92.39 | 50.54 | 78.73 | |
| ICA (21) | 91.81 | 85.57 | 29.58 | 68.99 | |
| ICA 1-4 (4) | 88.61 | 79.29 | 40.92 | 69.61 | |
| MNF (21) | 91.81 | 90.60 | 36.59 | 73.00 | |
| MNF 1-4 (4) | 93.57 | 90.11 | 39.08 | 74.25 | |
| LU_ab (3) | 90.63 | 73.33 | 48.57 | 70.84 | |
| B+LU_ab (24) | 92.20 | 90.04 | 58.35 | 80.20 | |
| B+Text_PCA1 (23) | 91.30 | 97.29 | 58.35 | 82.31 | |
| B+Text_MNF1 (23) | 92.30 | 85.90 | 58.35 | 78.85 | |
| OBIA Bands (21) | 85.70 | 97.36 | 61.51 | 81.52 | |
| Average | 91.43 | 88.69 | 49.61 | 76.58 | |
| WV-2 | Bands (8) | 88.66 | 80.63 | 58.37 | 75.89 |
| Bands 1-3 (3) | 85.48 | 79.97 | 52.86 | 72.77 | |
| PCA (8) | 88.66 | 80.91 | 69.13 | 79.57 | |
| PCA 1-4 (4) | 87.60 | 82.27 | 68.79 | 79.55 | |
| ICA (8) | 88.66 | 70.90 | 58.26 | 72.61 | |
| ICA 2-5 (4) | 76.44 | 71.72 | 34.40 | 60.85 | |
| MNF (8) | 88.66 | 80.91 | 53.44 | 74.34 | |
| MNF 1-4 (4) | 88.34 | 80.52 | 53.31 | 74.06 | |
| LU_ab(3) | 87.70 | 70.16 | 74.39 | 77.42 | |
| B+LU_ab (11) | 88.71 | 81.16 | 74.38 | 81.42 | |
| B+Text_PCA1 (10) | 87.50 | 81.44 | 58.75 | 75.90 | |
| B+Text_MNF1 (10) | 88.41 | 78.45 | 57.57 | 74.81 | |
| OBIA Bands (8) | 82.27 | 91.66 | 64.55 | 79.49 | |
| Average | 86.70 | 79.28 | 59.86 | 75.28 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcello, J.; Eugenio, F.; Martín, J.; Marqués, F. Seabed Mapping in Coastal Shallow Waters Using High Resolution Multispectral and Hyperspectral Imagery. Remote Sens. 2018, 10, 1208. https://doi.org/10.3390/rs10081208
Marcello J, Eugenio F, Martín J, Marqués F. Seabed Mapping in Coastal Shallow Waters Using High Resolution Multispectral and Hyperspectral Imagery. Remote Sensing. 2018; 10(8):1208. https://doi.org/10.3390/rs10081208
Chicago/Turabian StyleMarcello, Javier, Francisco Eugenio, Javier Martín, and Ferran Marqués. 2018. "Seabed Mapping in Coastal Shallow Waters Using High Resolution Multispectral and Hyperspectral Imagery" Remote Sensing 10, no. 8: 1208. https://doi.org/10.3390/rs10081208
APA StyleMarcello, J., Eugenio, F., Martín, J., & Marqués, F. (2018). Seabed Mapping in Coastal Shallow Waters Using High Resolution Multispectral and Hyperspectral Imagery. Remote Sensing, 10(8), 1208. https://doi.org/10.3390/rs10081208






