GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model
Abstract
1. Introduction
2. Materials and Methods
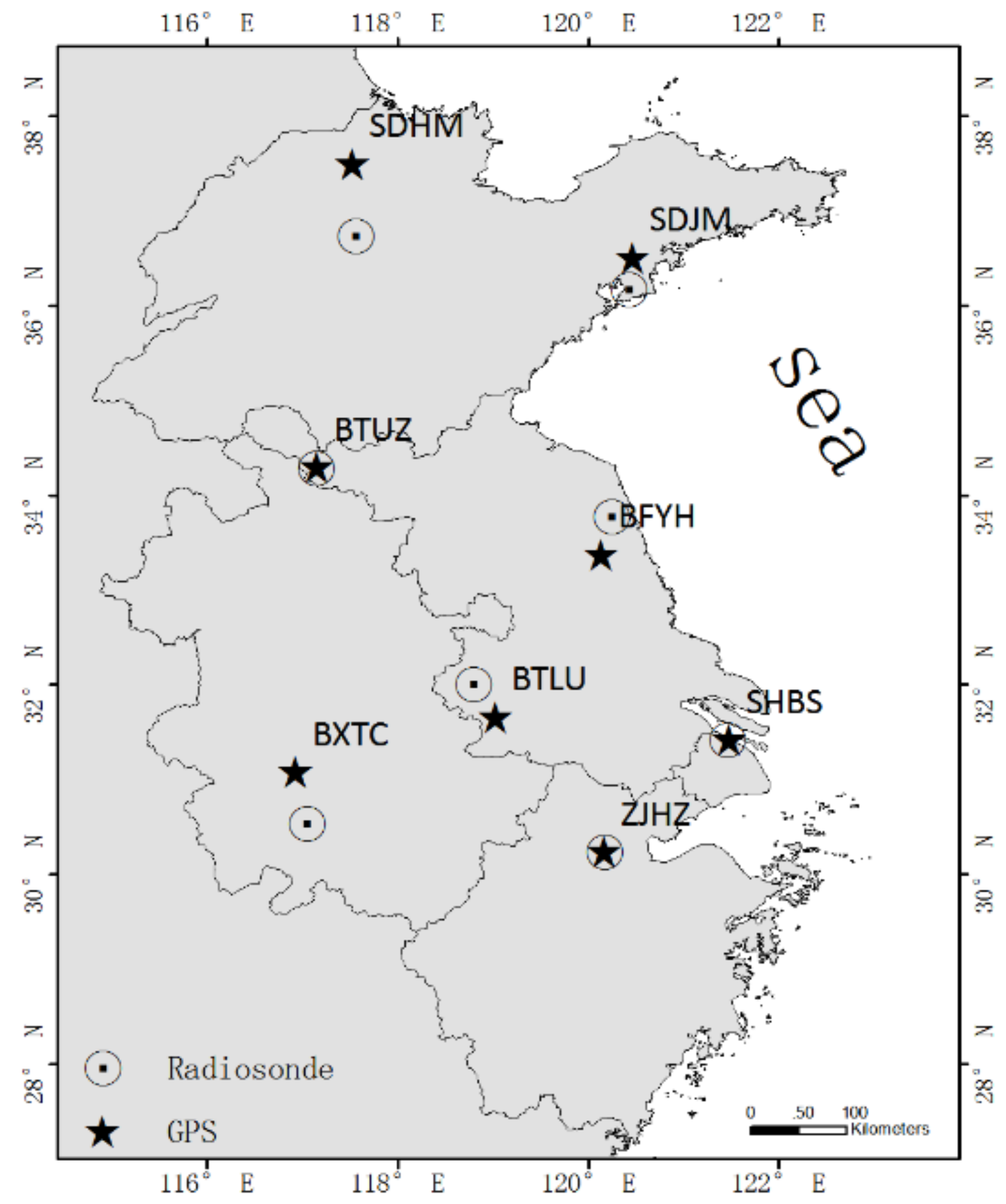
2.1. Data Collection
2.2. NWP ZTD Integral Method
2.3. GPS/BDS Medium/Long-Range RTK Algorithm Constrained with NWP Model
3. Results
3.1. Tropospheric Delay Comparison between NWP and GAMIT
3.2. GPS/BDS RTK Results
4. Discussion
5. Conclusions
- (1)
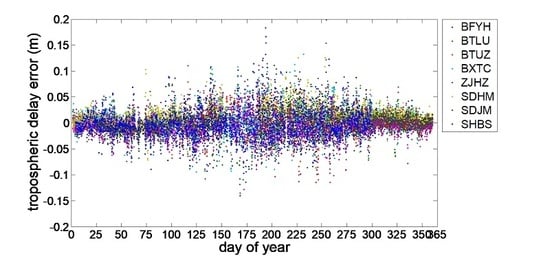
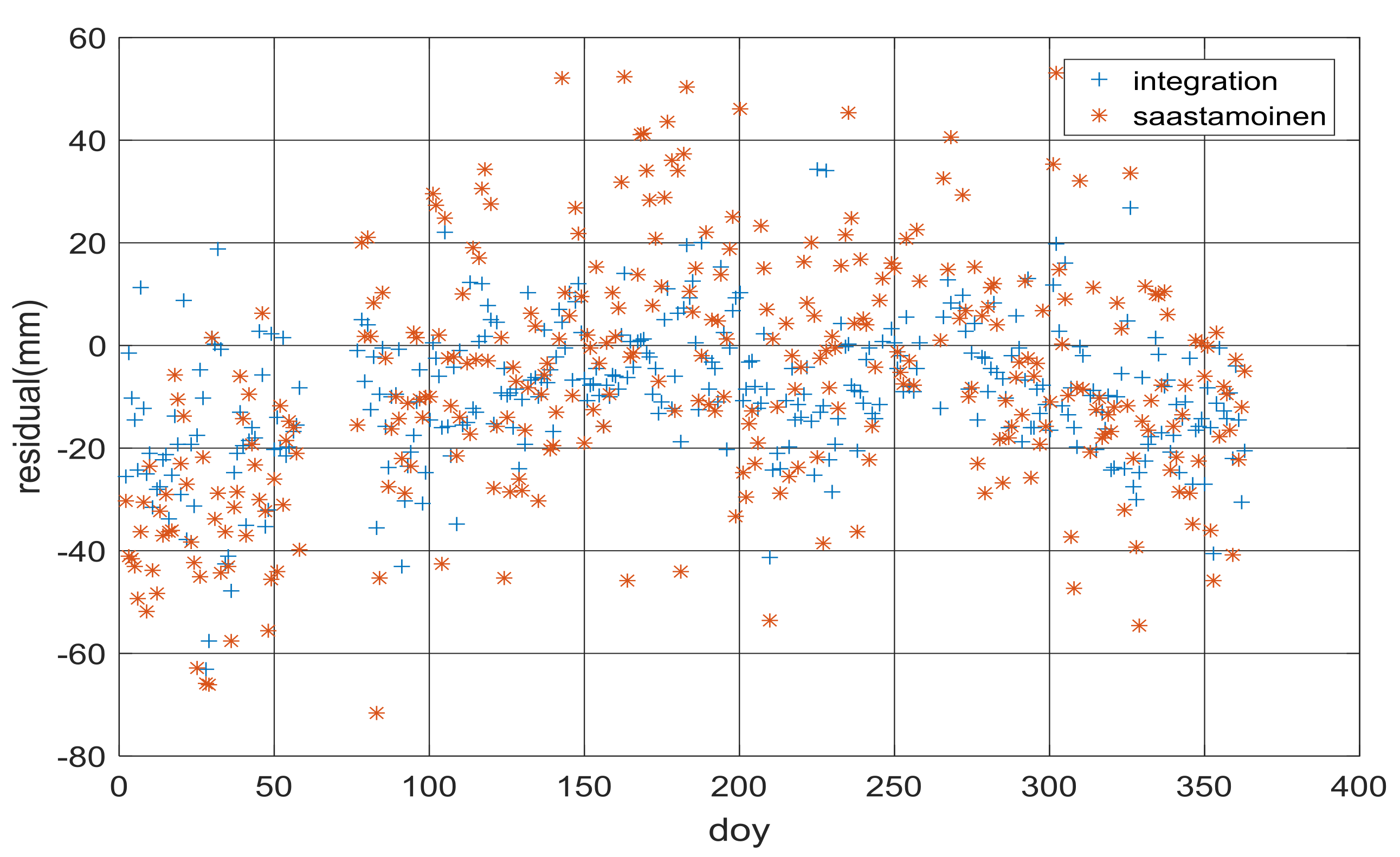
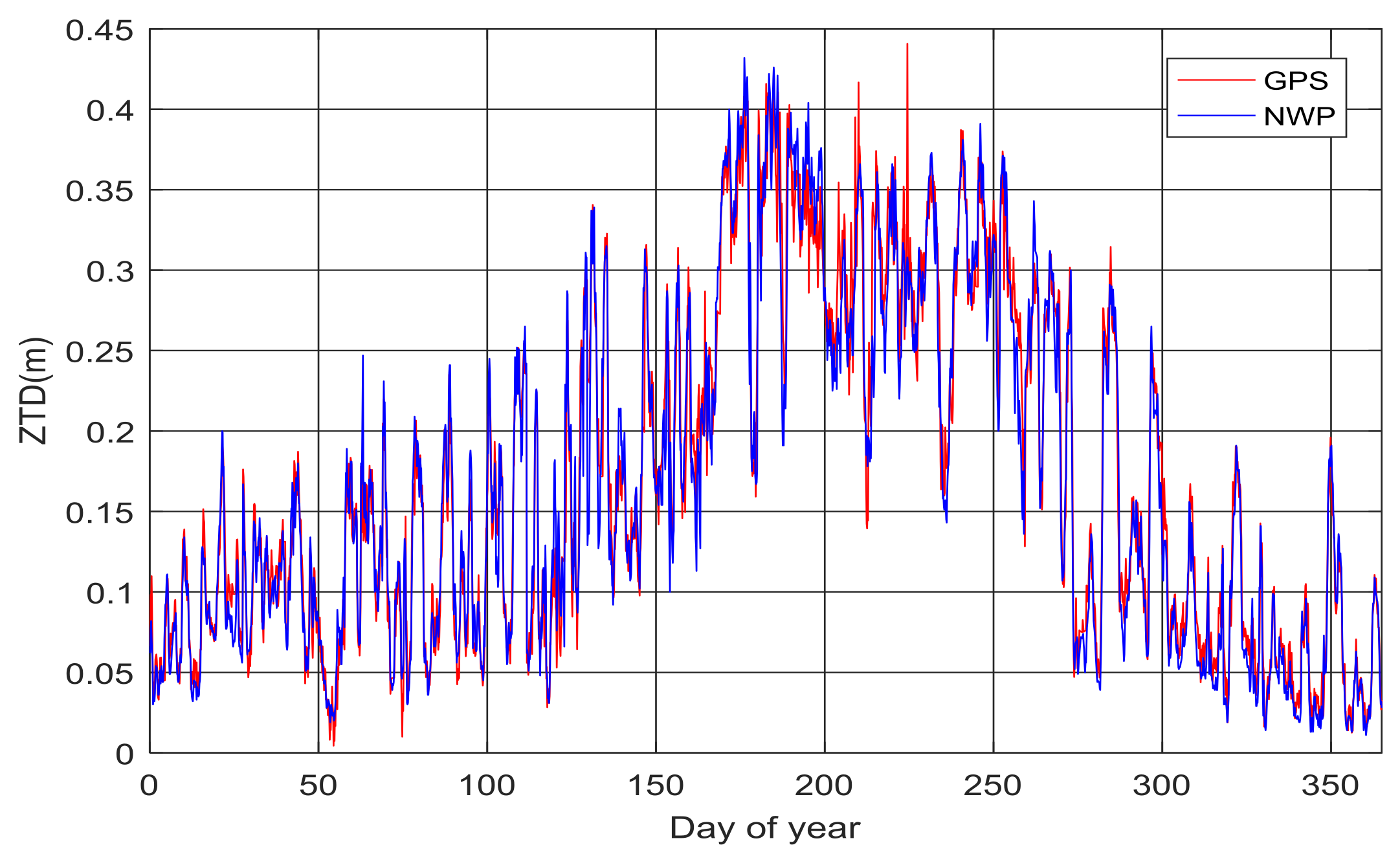
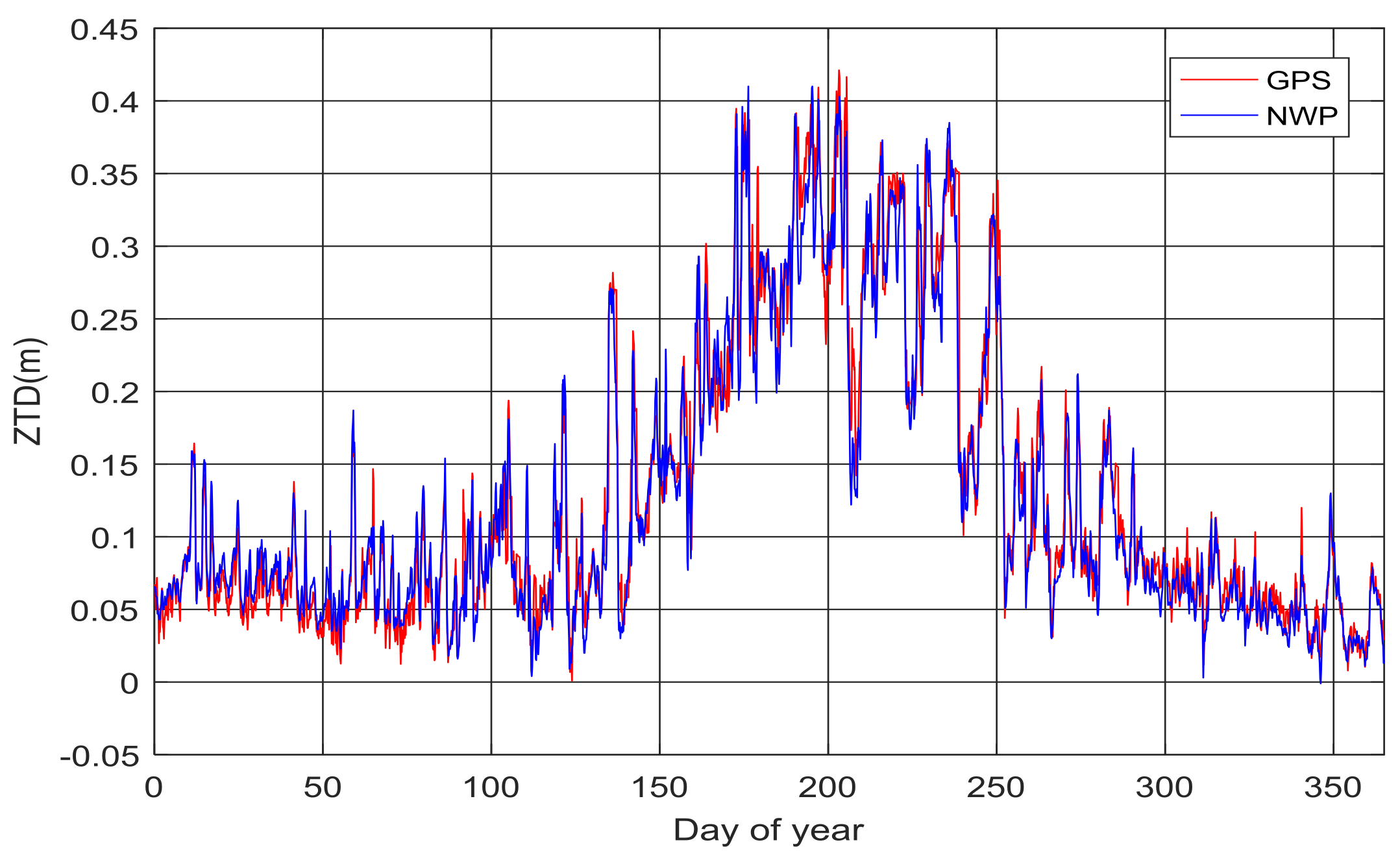
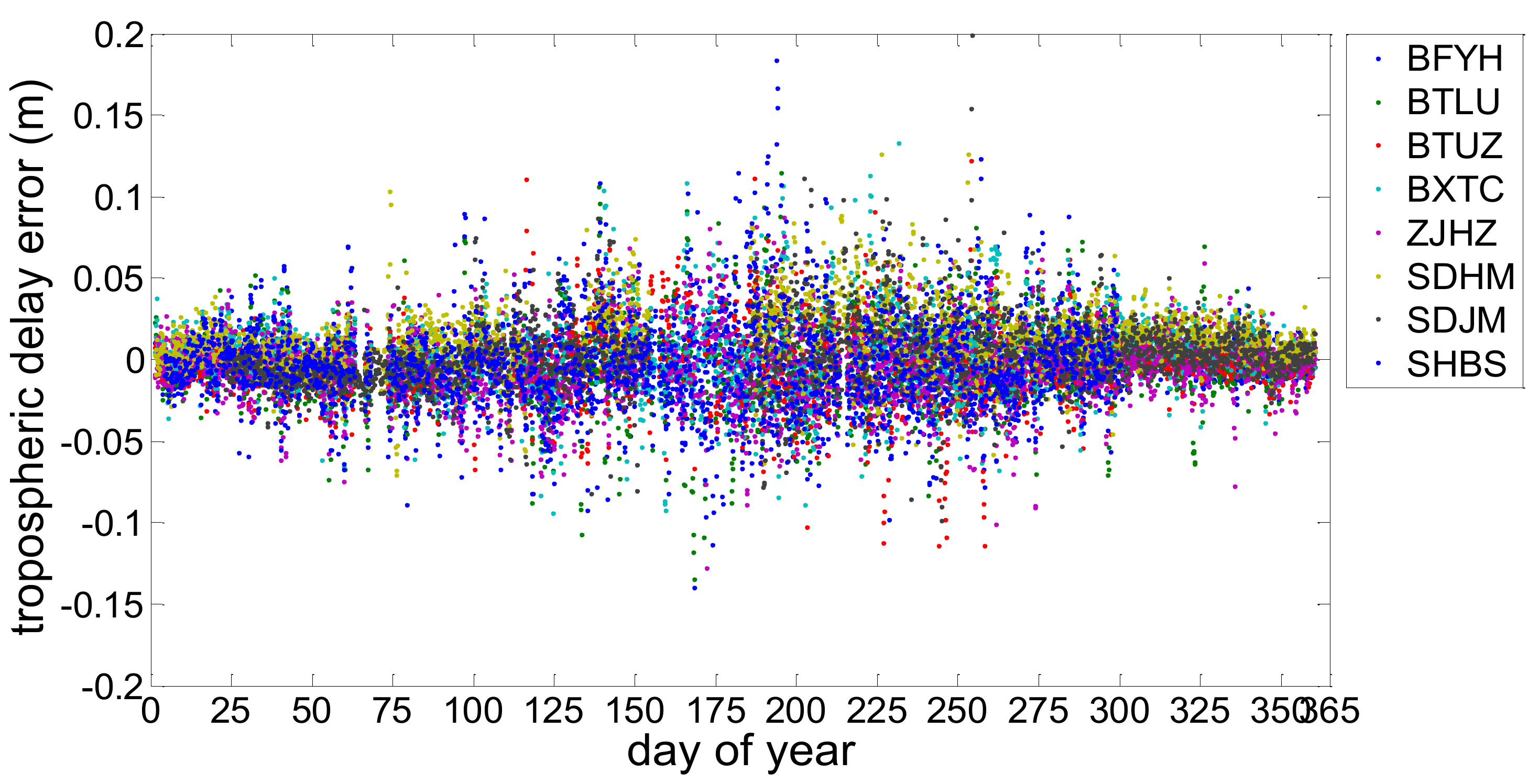
- The mean difference between the NWP and GAMIT ZTD are between −5.50 mm and 5.60 mm, and the RMS values of the NWP ZTD residuals are from 24.02 to 32.62 mm. The tropospheric delay from NWP can not be used in the RTK positioning directly without the estimation of the residual tropospheric delay.
- (2)
- Most of the peaks of the NWP ZTD series appear in the rainy season, and the rapid and large change of water vapor would increase the variability of tropospheric delay. The ZTD from the medium-range NWP model in this study doesn’t show the latitude based characteristics due to the limited area size.
- (3)
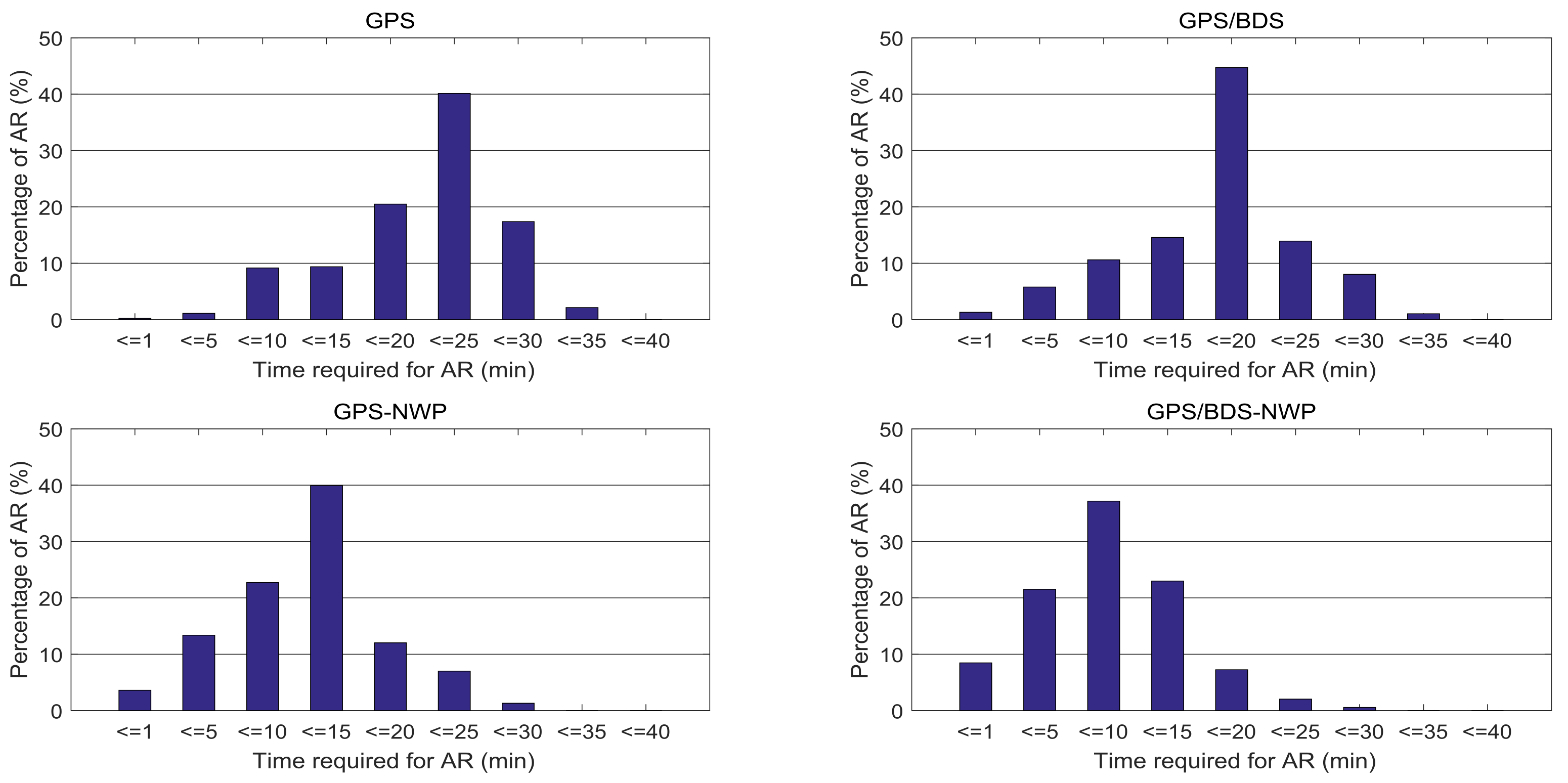
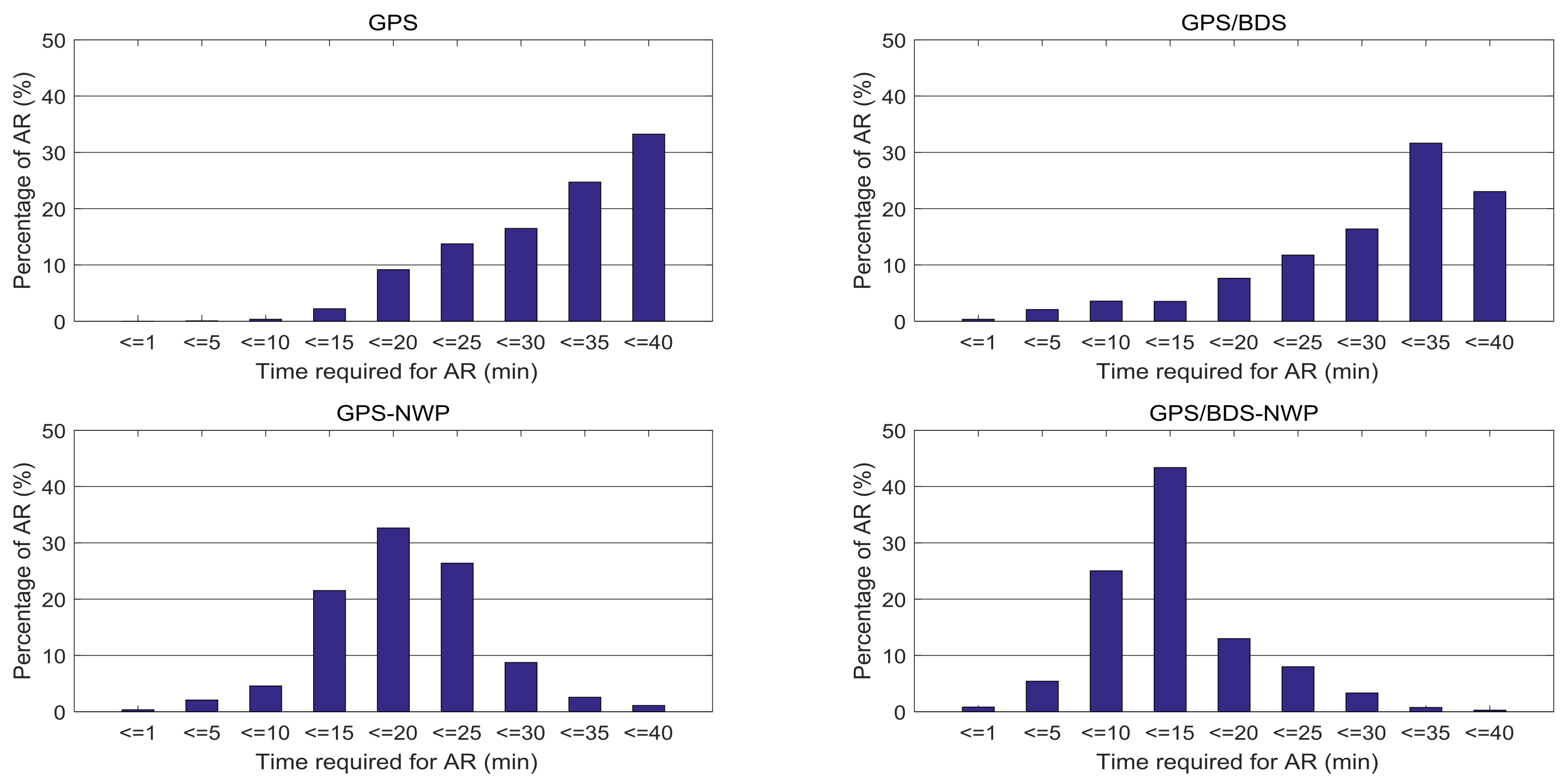
- For the medium-range baseline (80 km), the NWP-constrained RTK (both GPS alone and GPS/BDS RTK solutions) show a reduction of over 41% in the initialization time compared with the standard RTK. This reduction for the long-range baseline (260 km) is over 58%.
- (4)
- An improvement of over 30% in the initialization time can be achieved with the GPS/BDS RTK, compared with that of the GPS RTK for both standard and the NWP-constrained RTK modes.
- (5)
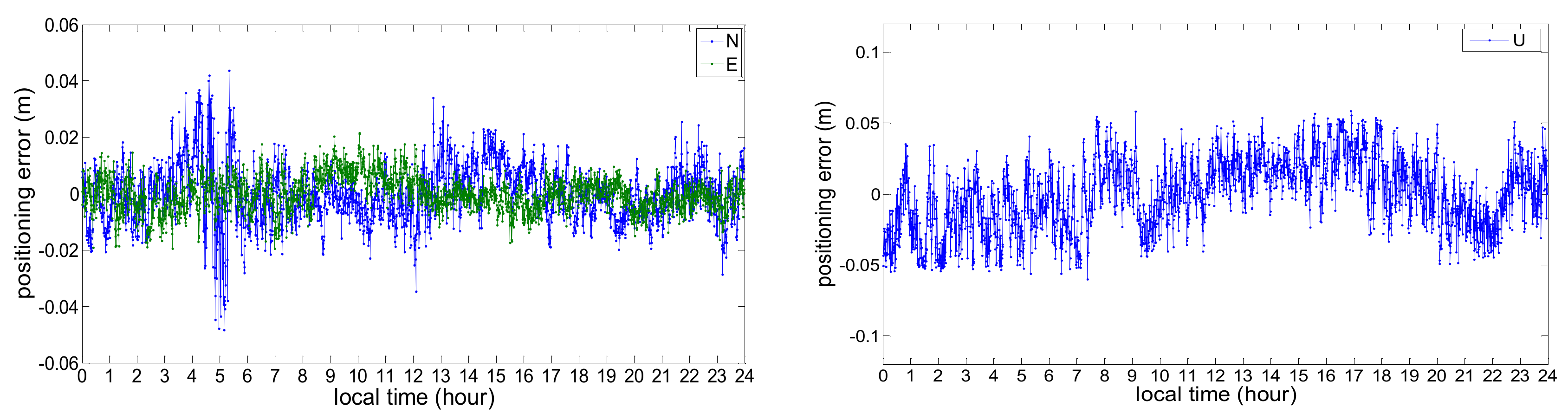
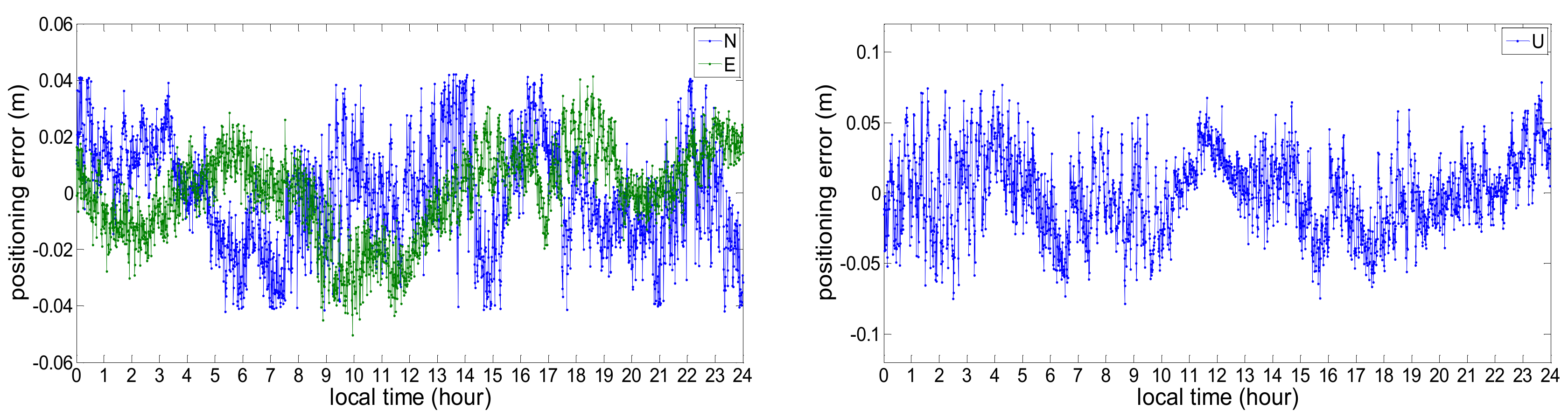
- The positioning precision of NWP-constrained GPS/BDS RTK is better than 3 cm in horizontal direction and better than 5 cm in vertical direction, which satisfies the requirement of the precise positioning service.
Author Contributions
Funding
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current State of Precise Point Positioning and Future Prospects and Limitations; Springer: Berlin/Heidelberg, Germany, 2008; pp. 615–623. [Google Scholar]
- Han, S. Carrier Phase-Based Long-Range GPS Kinematic Positioning. Ph.D. Thesis, UNSW University, Sydney, Australia, 1997. [Google Scholar]
- Teunissen, P.J.G.; Odijk, D. Rank-defect integer estimation and phase-only modernized GPS ambiguity resolution. J. Geod. 2003, 76, 523–535. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y. Performance Analysis of Experimental System of BDS-3; ISGNSS: Hong Kong, China, 2017. [Google Scholar]
- Liang, X.; Huang, Z.; Qin, H.; Liu, Y. GNSS multi-frequency multi-system highly robust differential positioning based on an autonomous fault detection and exclusion method. IEEE Access 2017, 5, 26842–26851. [Google Scholar] [CrossRef]
- He, H.; Li, J.; Yang, Y.; Xu, J.; Guo, H.; Wang, A. Performance assessment of single-and dual-frequency BeiDou/GPS single-epoch kinematic positioning. GPS Solut. 2014, 18, 393–403. [Google Scholar] [CrossRef]
- Ji, S.; Chen, W.; Ding, X.; Chen, Y.; Zhao, C. Potential benefits of GPS/GLONASS/GALILEO integration in an urban canyon–Hong Kong. J. Navig. 2010, 63, 681–693. [Google Scholar] [CrossRef]
- Feng, Y.; Li, B. A benefit of multiple carrier GNSS signals: Regional scale network-based RTK with doubled inter-station distances. J. Spat. Sci. 2009, 53, 135–147. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Shen, Y. Three carrier ambiguity resolution: Distance-independent performance demonstrated using semi-generated triple frequency GPS signals. GPS Solut. 2009, 14, 177–184. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, S.; Chen, W.; Weng, D. A new ionosphere-free ambiguity resolution method for long-range baseline with GNSS triple-frequency signals. Adv. Space Res. 2015, 56, 1600–1612. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuth asymmetry on the analysis of space geodetic data. J. Geophys. Res. 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Schüler, T. On Ground-Based GPS Tropospheric Delay Estimation; University der Bundeswehr München: Neubiberg, Germany, 2001. [Google Scholar]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. (1946–1975). 1972, 107, 13–34. [Google Scholar] [CrossRef]
- Ifadis, I. The Atmospheric Delay of Radio Waves: Modeling the Elevation Dependence on a Global Scale; Technical Report No. 38L; School of Electrical and Computer Engineering, Chalmers University of Technology: Gothenburg, Sweden, 1986. [Google Scholar]
- Mendes, V.B.; Langley, R.B. Tropospheric zenith delay prediction accuracy for airborne GPS high-precision positioning. In Proceedings of the Annual Meeting of the Institute of Navigation 54th Annual Meeting, Denver, CO, USA, 1–3 June 1998; Volume 23, pp. 171–174. [Google Scholar]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS tropospheric correction model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef]
- Lu, C.; Chen, X.; Liu, G.; Dick, G.; Wickert, J.; Jiang, X.; Zheng, K.; Schuh, H. Real-time tropospheric delays retrieved from multi-GNSS observations and IGS real-time product streams. Remote Sens. 2017, 9, 1317. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Cheng, J.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Real-time tropospheric delay retrieval from multi-GNSS PPP ambiguity resolution: Validation with final troposphere products and a numerical weather model. Remote Sens. 2018, 10, 481. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. 2014, 32, 911–923. [Google Scholar] [CrossRef]
- Elgered, G.; Davis, J.L.; Herring, T.A.; Shapiro, I.I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Vedel, H.; Mogensen, K.S.; Huang, X.Y. Calculation of zenith delays from meteorological data comparison of NWP model, radiosonde and GPS delays. Phys. Chem. Earth 2001, 26, 497–502. [Google Scholar] [CrossRef]
- Song, S.; Zhu, W.; Ding, J.; Liao, X.; Cheng, Z. Near real-time sensing of PWV from SGCAN and the application test in numerical weather forecast. Chin. J. Geophys. 2004, 47, 719–727. [Google Scholar] [CrossRef]
- Walpersdorf, A.; Bouin, M.N.; Bock, O.; Doerflinger, E. Assessment of GPS data for meteorological applications over Africa: Study of error sources and analysis of positioning accuracy. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1312–1330. [Google Scholar] [CrossRef]
- Liou, Y.A.; Teng, Y.T.; Van Hove, T.; Liljegren, J.C. Comparison of precipitable water observations in the near tropics by GPS, microwave radiometer, and radiosondes. J. Appl. Meteorol. 2001, 40, 5–15. [Google Scholar] [CrossRef]
- Andrei, C.O.; Chen, R. Assessment of time-series of troposphere zenith delays derived from the global data assimilation system numerical weather model. GPS Solut. 2009, 13, 109–117. [Google Scholar] [CrossRef]
- Chen, Q.; Song, S.; Heise, S.; Liou, Y.A.; Zhu, W.; Zhao, J. Assessment of ZTD derived from ECMWF/NCEP data with GPS ZTD over China. GPS Solut. 2011, 15, 415–425. [Google Scholar] [CrossRef]
- Ghoddousi-Fard, R.; Dare, P. Comparing various GNSS neutral atmospheric delay mitigation strategies: A high latitude experiment. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS), Fort Worth, TX, USA, 26–29 September 2006; pp. 1945–1953. [Google Scholar]
- Ahn, Y.W.; Lachapelle, G.; Skone, S.; Gutman, S.; Sahm, S. Analysis of GPS RTK performance using external NOAA tropospheric corrections integrated with a multiple reference station approach. GPS Solut. 2006, 10, 171–186. [Google Scholar] [CrossRef]
- Cucurull, L.; Sedo, P.; Behrend, D.; Cardellach, E.; Rius, A. Integrating NWP products into the analysis of GPS observables. Phys. Chem. Earth 2002, 27, 377–383. [Google Scholar] [CrossRef]
- Yang, L.; Hill, C.; Moore, T. Numerical weather modeling-based slant tropospheric delay estimation and its enhancement by GNSS data. Geo-Spat. Inf. Sci. 2013, 16, 186–200. [Google Scholar] [CrossRef]
- Lu, C.; Zus, F.; Ge, M.; Heinkelmann, R.; Dick, G.; Wickert, J. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning. Atmos. Meas. Tech. 2016, 9, 1–32. [Google Scholar] [CrossRef]
- Kashani, I.; Wielgosz, P.; Grejnerbrzezinska, D.A. On the reliability of the VCV matrix: A case study based on GAMIT and Bernese GPS software. GPS Solut. 2004, 8, 193–199. [Google Scholar] [CrossRef]
- Rüeger, J.M. Refractive Index Formulae for Radio Waves; International Congress: Washington, DC, USA, 2002. [Google Scholar]
- Hu, Y.; Yao, Y. An Accurate Height Reduction Model for Zenith Tropospheric Delay Correction Using ECMWF Data. In Proceedings of the CSNC, Shanghai, China, 3 May 2017; pp. 337–348. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Verhagen, S. The GNSS ambiguity ratio-test revisited: A better way of using it. Surv. Rev. 2009, 41, 138–151. [Google Scholar] [CrossRef]

| Station | BTLU | BFYH | BTUZ | BXTC | SDHM | ZJHZ | SDJM | SHBS |
|---|---|---|---|---|---|---|---|---|
| Mean (mm) | −4.10 | −0.47 | −5.34 | 3.17 | 5.60 | −3.65 | 0.45 | −5.50 |
| RMS (mm) | 24.02 | 24.08 | 24.47 | 25.08 | 27.63 | 28.10 | 28.22 | 32.62 |
| CC | 0.978 | 0.976 | 0.978 | 0.977 | 0.979 | 0.980 | 0.976 | 0.970 |
| C01 | C02 | C03 | C04 | C05 | |
|---|---|---|---|---|---|
| MP1 | 0.200 | 0.210 | 0.231 | 0.277 | 0.263 |
| MP2 | 0.223 | 0.232 | 0.244 | 0.309 | 0.301 |
| C06 | C07 | C08 | C09 | C10 | |
| MP1 | 0.433 | 0.411 | 0.306 | 0.316 | 0.278 |
| MP2 | 0.381 | 0.392 | 0.371 | 0.382 | 0.384 |
| C11 | C12 | C13 | C14 | ||
| MP1 | 0.366 | 0.432 | 0.356 | 0.367 | |
| MP2 | 0.502 | 0.577 | 0.519 | 0.511 |
| GPS | GPS/BDS | Improvement | ||
|---|---|---|---|---|
| Baseline 80 km | Standard RTK | 22.6 (min) | 15.6 (min) | 31.0% |
| NWP-RTK | 13.3 (min) | 8.8 (min) | 33.8% | |
| Improvement | 41.2% | 43.6% | ||
| Baseline 260 km | Standard RTK | 49.7 (min) | 34.6 (min) | 30.4% |
| NWP-RTK | 20.5 (min) | 12.9 (min) | 37.1% | |
| Improvement | 58.8% | 62.7% |
| Baseline | N | E | U |
|---|---|---|---|
| baseline: 80 km | 0.013 | 0.010 | 0.026 |
| baseline: 260 km | 0.023 | 0.021 | 0.043 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wu, C.; Li, L.; Yan, L.; Liu, M.; Wang, S. GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model. Remote Sens. 2018, 10, 1113. https://doi.org/10.3390/rs10071113
Xu Y, Wu C, Li L, Yan L, Liu M, Wang S. GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model. Remote Sensing. 2018; 10(7):1113. https://doi.org/10.3390/rs10071113
Chicago/Turabian StyleXu, Ying, Chen Wu, Lei Li, Lizi Yan, Min Liu, and Shengli Wang. 2018. "GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model" Remote Sensing 10, no. 7: 1113. https://doi.org/10.3390/rs10071113
APA StyleXu, Y., Wu, C., Li, L., Yan, L., Liu, M., & Wang, S. (2018). GPS/BDS Medium/Long-Range RTK Constrained with Tropospheric Delay Parameters from NWP Model. Remote Sensing, 10(7), 1113. https://doi.org/10.3390/rs10071113